1 Introduction

Strength and stiffness are the most common focus in current steel tubular joint researches. Extensive theoretical calculations and finite element method (FEM) analysis have been studied all over the world. Dexter and Lee (1999a; 1999b), Lee and Gazzola (2006), and Gho and Yang (2008) investigated the tubular cap K-joints and/or overlap K-joints, and developed a set of calculation formulas on the ultimate strength capacity. Soh et al. (2000) established two theoretical models on the strength capacity of axially loaded X-joint, considering the yield line theory. However, the chord members (main pipes) were directly connected without gusset plates or annular plates. Choo et al. (2004) extended the numerical study to doubler plate reinforced tubular X-joints, compared to corresponding un-reinforced joints. However, they did not consider the combined effect of axial force and axial brace force. Paul et al. (1994) studied the ultimate strength capacity of the steel tubular joints under multi-direction axial load through the FEM analysis and the experimental tests, and then obtained the calculation formula according to multiple regression. Liu and Guo (2001) applied the non-linear FEM to analyze the large elastoplasticity deformation of four different types of tubular joint, and obtained the variation rule of the ultimate strength capacity with the geometrical parameter of the joints, but the calculation method on the yield strength was not utilized. Kim (2001) investigated the behavior and ultimate strength of axially loaded tube-gusset connections. An efficient numerical model was suggested to consider the combined effect of axial force and moment. Yam and Cheng (2002) also conducted 13 full-scale tests to investigate the compressive behavior and strength of gusset plate connections. The test results indicated that significant yielding of the gusset plate specimens occurred prior to reaching the ultimate load. You et al. (2010) analyzed the 1/4 annular plate enhanced K-joint, and obtained the influential coefficient of the chord member axial load on the strength capacity. Bao et al. (2008) suggested a cross-section deformation model on the ultimate strength capacity of the K-joint, introduced the ring generatrix model, and obtained the calculation formula on the joint ultimate strength capacity through the virtual work principle of the energy gradient. However, most models mentioned above were proposed for welded joints. Then van der Vegte et al. (2010) gave an overview of the main aspects of the FEM analysis relevant to welded joints and bolted joints. In a further example, relevant details were given of explicit FEM analysis on large-scale bolted connections.

In this study, the X-type steel tubular joint was set as the research object, the former calculation formula deduction methods on the multi-type joint strength capacity were referenced, and the simplified calculation model was established through theoretical analysis. The mechanical characteristics of the joint were analyzed through the experiments and the FEM analysis, and the empirical formula of the joint yield strength was obtained through fitting. The increased coefficient of the gusset plate on the joint strength capacity was considered in the analysis. The yield capacities of the joints with other dimensions were obtained by the FEM analysis, and were compared with the results using an empirical formula.

2 Experiments

2.1 Specimen and loading system

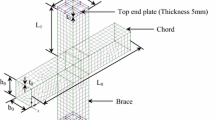
The X-joint in this study was a bolted connection of the steel tubular chord member with the steel tubular branch member by an annular plate and a gusset plate, which could be named as four types: X-1, X-2, X-3, and X-4. The dimension and the detail of the X-joints are shown in Table 1 and Fig. 1, respectively. The loading system was a YAW-10000F microprocessor control electro-hydraulic servo multi-functional testing machine. The photo of the specimen set up on the loading system is shown in Fig. 2.

Table 1 Dimension of specimens
Full size table
Fig. 2
figure 2

Experimental setup photograph

Full size image
Fig. 1
figure 1

Experimental detail of X-joint specimen (a) Plan view; (b) Elevation view

Full size image

2.2 Experimental results and analyses

As shown in Fig. 1, the strain rosette was arranged at the strain monitoring point of the annular plate. The linear strains at three different directional locations of 0°, 45°, and 90° for each measuring point were then obtained, and named as ε0, ε45, and ε90, respectively.

The hoop stress curve for the annular plate cross-section of the X-2 joint under the load is shown in Fig. 3. The horizontal ordinate meant the measure point location, while 0 meant the contact surface of the chord member, and the vertical ordinate meant the normal stress of the cross section. Note that the distribution of the stress with the section height was approximated to be linear, which could be considered as meeting the planar interface assumption. The average stress \(\overline \sigma\) on the section was calculated by

$$\overline \sigma = \frac{{\int_{{A^ + }} {{\sigma ^ + }} {\text{d}}A + \int_{{A^ - }} {{\sigma ^ - }} {\text{d}}A}}{A},$$
(1)

where σ+, σ−, and A are the sectional normal stress, sectional negative stress, and sectional area, respectively. A + and A− are the sectional areas of σ+ and σ−, respectively.

Fig. 3
figure 3

Hoop stress curve for the annular plate cross-section of X-2 joint (a) Hoop stress-measurement location; (b) Measurement location

Full size image

The principal stress could be obtained by the linear strains (ε0, ε45, ε90) at three directional locations measured at each strain measure point as

$${\sigma _1} = \frac{{E({\varepsilon _0} + {\varepsilon _{90}})}}{{2(1 - \upsilon )}} + \frac{{\sqrt 2 E}}{{2(1 + \upsilon )}}\sqrt {{{({\varepsilon _0} - {\varepsilon _{45}})}^2} + {{({\varepsilon _{45}} - {\varepsilon _{90}})}^2}} ,$$
(2)
$${\sigma _2} = \frac{{E({\varepsilon _0} + {\varepsilon _{90}})}}{{2(1 - \upsilon )}} - \frac{{\sqrt 2 E}}{{2(1 + \upsilon )}}\sqrt {{{({\varepsilon _0} - {\varepsilon _{45}})}^2} + {{({\varepsilon _{45}} - {\varepsilon _{90}})}^2}} ,$$
(3)

where E and υ are the elasticity modulus and Poisson’s ratio, respectively. Then the equivalent von Mises stress of the measure point was

$$\tilde \sigma = \sqrt {\sigma _1^2 - {\sigma _1}{\sigma _2} + \sigma _2^2} .$$
(4)

The curves for the equivalent von Mises stress on the middle section of the annular plate with the annular normal stress at each joint under the load are shown in Fig. 4, where they could be found to be relatively close. Therefore, it was reasonable to determine the strength capacity of the joint by directly using the hoop stress in the simplified model.

Fig. 4
figure 4

Hoop stress and von Misses stress on the middle section of the annular plate

Full size image

3 Mechanical model and formula

3.1 Assumptions

For the X-joint, the mechanical characteristic was basically reflected by adopting the simplified mechanical model in Fig. 5. The main mechanical simplifications were as follows:

  1. 1.

    T-type annular beam: T-beam was adopted to replace the annular plate of the joint. The effective length of the chord member and the annular plate were taken as the flange and the web of T-beam, respectively.

  2. 2.

    Flexible support: the support effect of the steel tubes outside the effective flange on the T-type beam and the change of the effective flange width with the arc length of the annular plate were both simulated with the flexible support.

  3. 3.

    Basis of the annular plate stress yield: the load when the hoop stress on the middle section of the annular plate reached the yield stress was taken as the designed value of the load as used normally.

Fig. 5
figure 5

Simplified calculation model for the X-joint

Full size image

According to the simplified method above and the plan cross-section assumption verified by experiments, the yield criterion was chosen according to the normal stress on the section, and the calculation diagram was obtained as shown in Fig. 5. In the mechanical model shown in Fig. 5, R T is the calculated radius of the curvature of the T-annular beam, B e is the effective flange width, T is the flange height, namely the wall thickness of the chord member (main pipe), the web width T r is the thickness of the annular plate, and the web height R is the annular plate width. The spring support set at support A was mainly reflected by the spring stiffness coefficient k θ0 was relevant to the bolt resultant force action point and then determined by the cross-point of the resultant force action point of all the bolts on the one side and the lower edge of the cross-shaped connection plate (Fig. 6c).

Fig. 6
figure 6

Simplified calculation diagram of the X-joint annular plate (a) Computational model; (b) Cross-section of T-type annular beam; (c) Definition of θ 0

Full size image

3.2 Simplified formula derivation

The parameters used in the simplified formula derivation are as follows: I T, A T, and i T are the sectional moment of inertia, the sectional area, and the turning radius, respectively; Y N and Y W are the distances from the section centroid of the T-type annular beam to the inwall of the chord member and the external rim of the annular plate, respectively; I H and R H are the sectional moment of inertia and the curvature radius of the T-type annular beam as only the annular plate is considered, respectively; I Z and R Z are the section moment of inertia and the curvature radius of the T-type annular beam as only the chord member is considered, respectively; I L and H L are the section moment of inertia and the height of the T-type beam, respectively.

The FEM analysis indicated that the effective flange width of the T-type annular beam changed with the arc length. However, the normal stress on the central section of the annular plate was adopted as the control stress to determine the yield point. Therefore, the equivalent flange width of the section was adopted as the flange width of the whole T-type annular beam with a uniform section. The Thurlimann formula as Eq. (5) was adopted to calculate the T-type annular beam flange width in the simplified calculation formula.

$${B_{\text{e}}} = 1.52\sqrt {{R_{\text{Z}}}T} + {t_{\text{r}}},$$
(5)

where R Z=(D−T)/2 and D is the outer diameter of the chord member.

Considering the yield location of the annular plate could be the inside compression yield or the outside tension yield, Eq. (6) was used to determine the yield load.

$${P_y} = \min {\text{(}}{P_{\text{W}}},{P_{\text{N}}}),$$
(6)

where P W is the outside tension yield load, while P N is the inside compression yield load. If the joint plate existed as the experimental result and the FEM result was analyzed, the part outside of the effective flange of the chord member would have a certain restraint effect on the annular plate, and remarkably reduce the yield strength of the annular plate. Therefore, in the simplified calculation model, this factor would be considered as a stiffness support, and the stiffness coefficient was set as k Based on this, the joint yield strength capacity could be deduced as

$${P_{\text{N}}} = 2\eta {\psi _{\text{N}}}{A_{\text{T}}}{\sigma _y},{P_{\text{W}}} = 2\eta {\psi _{\text{W}}}{A_{\text{T}}}{\sigma _y},$$
(7a)

where

$${\psi _{\text{N}}} = \left| {\frac{{i_{\text{T}}^2}}{{\lambda {R_{\text{T}}}{Y_{\text{N}}}/{\gamma _1} + i_{\text{T}}^2}}} \right|,$$
(7b)
$${\psi _{\text{W}}} = \left| {\frac{{i_{\text{T}}^2}}{{\lambda {R_{\text{T}}}{Y_{\text{W}}}/{\gamma _2} - i_{\text{T}}^2}}} \right|,$$
(7c)

where σy is the yield strength of steel, and η, is the load sharing coefficient. The load taken by the annular plate and the gusset plate is distributed according to the stiffness ratio. γ1 and γ2 are the section plasticity development coefficients with reference to the steel structure code (GB50017-2003). λ is the coefficient being relevant with the bending moment on the central section (section A in Fig. 6), i.e.,

$$\lambda = \frac{{\beta \left( {\frac{\pi }{4} + \frac{{E{I_{\text{T}}}}}{{kR_{\text{T}}^3}}} \right) - \alpha }}{{\frac{\pi }{2}\left( {\frac{\pi }{4} + \frac{{E{I_{\text{T}}}}}{{kR_{\text{T}}^3}}} \right) - 1}},$$
(8)

where α and β are the coefficients being relevant with the force action point (determined according to the bolt location). θ0 as shown in Fig. 6 could be calculated by

$$\begin{array}{*{20}{c}} {\alpha = \frac{1}{2}{{\cos }^2}{\theta _0},}&\beta \end{array} = \frac{\pi }{2} - {\theta _0}\sin {\theta _0} - \cos {\theta _0}.$$
(11)

To determine the spring coefficient k in Eq. (8) and the load sharing coefficient η in Eq. (7a), the load proportion distribution coefficient ξ is defined as

$$\xi = {P_{\text{H}}}/{P_{\text{L}}},$$
(12)

where P H is the load taken by the annular plate, and P L is the load taken by the ribbed plate. From the simplified calculation model, k can be calculated with the known load and the bending moment of section A:

$$k = (E{I_{\text{T}}}/{r^3})\left( {\frac{{M/(N{R_{\text{T}}}) - \alpha }}{{\pi M/(2N{R_{\text{T}}}) - \beta }} - \frac{\pi }{4}} \right).$$
(13)

The axial load of the section is

$$N = {A_{\text{T}}}\overline \sigma.$$
(14)

The bending moment M can be calculated according to

$$M = \frac{{{I_{\text{T}}}\overline \sigma _{\text{H}}^{\text{W}}}}{{Y_{\text{H}}^{\text{W}}}}.$$
(15)

From Eq. (11), it can be observed that k is relevant with the ratio of M to N, the changing curves of the section bending moment at the four experimental X-joints with the axial load are shown in Fig. 7. From Fig. 7 it could be found that the relation of M with N was linear, thus the ratio of M to N was constant. The value of k for the four X-joints could be calculated and is listed in Table 2.

Fig. 7
figure 7

Axial force-bending moment relation (a) X-1 and X-2; (b) X-3 and X-4

Full size image
Table 2 Flexible support stiffness coefficients of X-joints (N/mm)
Full size table

The variable was nondimensionalized, then assuming k H=EI H/r H 3 and k Z=EI Z/r Z 3, the experimental result was fitted with the calculated result (Fig. 8), and the empirical formula of k was obtained as

$$\begin{array}{*{20}{l}} {k = 0.0021{{\left( {\frac{{{I_{\text{H}}}R_{\text{Z}}^3}}{{\xi {I_{\text{Z}}}R_{\text{H}}^3}}} \right)}^2}\frac{{E{I_{\text{Z}}}}}{{R_{\text{Z}}^3}} - 8.8348\frac{{E{I_{\text{H}}}}}{{\xi R_{\text{H}}^3}}} \\ {{\text{ }} + 150.44\frac{{E{I_{\text{Z}}}}}{{R_{\text{Z}}^3}},} \end{array}$$
(16)

where I H, R H, I Z, and R Z can be calculated according to Eq. (15), while the section width adopted in I Z was \(1.52\sqrt {{R_{\text{Z}}}T}\), namely,

$$\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} {{I_{\text{H}}} = {R^3}{t_{\text{r}}}/12,}&{{I_{\text{Z}}} = (1.52\sqrt {{R_{\text{Z}}}T} ){T^3}/12,} \end{array}} \\ {{R_{\text{H}}} = (D + R)/2.} \end{array}$$
(17)
Fig. 8
figure 8

Fitting curve for the elastic stiffness k of A N -type joint

Full size image

The load distribution coefficient η is determined by

$$\eta = 1 + 1/\xi.$$
(18)

In the intersecting-beam, as P H and P L were not determined, the load proportion distribution coefficient ξ could be calculated according to the stiffness (or flexibility) of the intersecting beam, namely,

$$\xi = {\delta _{\text{L}}}/{\delta _{\text{H}}},$$
(19)

where δH is the flexibility of the T-type annular plate in the intersecting-beam at the cross point under the unit load, which is expressed as

(20)

δL is the flexibility of the gusset plate in the intersecting-beam at the cross point under the unit load, the gusset plate was also considered as the T-beam, which was shown in Fig. 9. In Eq. (19), l L is the beam length, l H=2H, where H is the distance between the joint annular plate and the structural annular plate. The gusset plate inertia moment I L was calculated according to the T-type section with a uniform section and the flange. The result of the Thurlimann model was then taken as the flange width of the T-type beam section, namely the B e determined in Eq. (6). The web plate width of the T-beam was the web plate thickness b, the equivalent height was adopted to calculate the beam height H L, which is shown in Eq. (20):

(21)
$${H_{\text{L}}} = {H_{{\text{L1}}}} + \rho \mu ({H_{{\text{L2}}}} - {H_{{\text{L1}}}}),$$
(22)

where H L1 is the gusset plate width at the intersection of the gusset plate and the structural annular plate, H L2 is the gusset plate width at the intersection of the gusset plate and the annular plate, and ρ and μ are the reduction coefficients with consideration of the cutting angle θ (Fig. 9). As θ≤π/9, ρ=1.0, and μ=1.0; as θ=π/4, ρ=0.85; as π/9<θ<π/4, ρ could be obtained by interpolation. μ=1.75−3lXL/l L, and μ was 1 if μ was larger than 1. lXL is the length of the cutting angle (0<lXL<0.5l L). The proportionality coefficient of each X-joint was listed in Table 3.

Fig. 9
figure 9

Calculation model of T- type ribbed plate beam

Full size image
Table 3 Load proportion distribution coefficient ξ and the annular plate load sharing coefficient η of each X-joint
Full size table

3.3 Comparison of the simplified result and the code result

Eq. (6) was applied to calculate four specimens X-1, X-2, X-3, and X-4, and by changing the load proportion distribution coefficient ξ, the calculated strength capacities P y of four specimens could be obtained (Fig. 10), where the result of code was also given (Q/GDW391-2009). The ratio curve for the two above is as shown in Fig. 11. It can be observed that the strength capacity obtained by the simplified calculation formula was higher than the code calculation result. As the gusset plate load sharing effect was smaller (ξ>5), and the annular plate width with the same chord member diameter was larger, the simplified calculation result was closer to the code result.

Fig. 10
figure 10

Relation of strength capacity using simplified formula and code formula with ξ

Full size image
Fig. 11
figure 11

Relation of ratio of the calculated strength capacity to the code value with ξ

Full size image

3.4 Yield strength capacity

The total strength capacity of the joint could be divided into two parts, one was undertaken by the annular plate, the other was undertaken by the gusset plate and the bilateral structured annular plate. Therefore, the total strength capacity was relevant with the load distribution ratio. For the convenience of comparison, the calculation result in Fig. 4 was based on the stress of the test point reaching the yield. It could be observed in Table 4 that the results of X-3 and X-4 were quite close to that obtained from the simplified approximation formula, and the deviation for X-1 or X-2 was around 20%.

Table 4 Comparison between experimental and analytical results
Full size table

3.5 Finite element analysis

FEM models for all specimens were established using ANSYS software. The solid45 unit was selected to build the model to ensure calculation accuracy and meanwhile reduce the number of units. Fig. 12 shows the simplified meshed FEM mode of the X-2 joint without a branch member. By the material characteristics test, the four-linear model shown in Eq. (21) was used as the constitutive model of steel in the FEM analysis.

$$\sigma = \left\{ {\begin{array}{*{20}{l}} {E\varepsilon ,{\text{ }}\varepsilon < {\varepsilon _y},} \\ {E{\varepsilon _{y,}}{\text{ }}{\varepsilon _y} \leq \varepsilon < {\varepsilon _1},} \\ {E\prime (\varepsilon - {\varepsilon _1}) + E{\varepsilon _y},{\text{ }}{\varepsilon _1} \leq \varepsilon < {\varepsilon _2},} \\ {E{\varepsilon _{y,}} + E\prime ({\varepsilon _2} - {\varepsilon _1}),{\text{ }}\varepsilon \geq \varepsilon {}_2,} \end{array}} \right.$$
(23)

where the elastic modulus is E=2.07×105 MPa; the yield strain is ε y =0.00165; the initial strain during the strengthening stage is ε1=0.00764 and ε2=0.03; the elastic modulus during the strengthening stage is E′=6463 MPa; and the yield stain is σ y =341 MPa. Fig. 13 shows the four-linear constitutive model of steel.

Fig. 12
figure 12

FEM model

Full size image
Fig. 13
figure 13

Constitutive relation of steel

Full size image

The loading method was the same as the test. The load was distributed to the unit node at the top of branch member by the way of uniformly-distributed node force. The direction of the node force was parallel to the branch member axis. Fig. 14 shows the final failure mode of X-2 joint. At the end stage of loading, the buckling of the annular plate was observed. Moreover, the FEM analytical results show good agreement with the experimental results.

Fig. 14
figure 14

Final failure mode of X-2 joint (a) Experimental result; (b) FEM result

Full size image

3.6 Validation of the proposed model

To discuss the applicability of the simplified formula, namely on the other types of steel tubular X-joints, some imagined X-joints were calculated using the FEM analysis. The dimensions and the relevant experimental, calculation values of the imagined and experimental X-joints (XG and X) are given in Table 5. For the calculation analysis mainly discussed, the annular plate yield strength and the ideal elasto-plastic model were applied in the material constitutive law in the FEM models of these joints. Moreover, the initial imperfection was not considered, and the gusset plate was changed to the uniform section type.

Table 5 Main dimension and yield strength capacity of A N and A G joints
Full size table

The comparison of the finite element analysis, experimental result, simplified formula result, and code result for the eight specimens are shown in Table 6, where the reduction coefficient was not considered in the code value. It was observed that the result obtained by the simplified formula can better reflect the actual yield capacity of the specimen.

Table 6 Comparison of the results from the FEM analysis, experiment, simplified formula, and code
Full size table

4 Conclusions

The yield strength capacity is important in the steel structural design. By comparing the experimental and the FEM analysis, it could be found that the strength capacity calculation formula given by the current code was conservative, and the effect of the joint plate was not considered. However, the joint plate had a great effect on the improvement of the joint strength capacity, neglecting this effect would make the joint yield strength capacity too conservative. Based on the experimental and the FEM analysis, the strength capacity improvement coefficient of the gusset plate was considered in this study, then a simplified calculation model fitting the mechanical performance was proposed, according to which, an empirical formula was deduced. The restraint effect of the part outside the chord member equivalent flange width was considered, and the results obtained from the simplified formula calculation, the FEM analysis, and the experiments all agreed well.