1 Introduction

The expected long-term deformations during the service life of concrete structures are described by creep models, such as those given in Eurocode 2 [1], ACI 209R [2] or fib Model Code 2020 [3] (constant loading). However, measurements of existing reinforced and prestressed concrete bridges have shown that long-term deformations can significantly exceed those predicted by the models [4]. Cyclic loadings are assumed to be one major reason for these increased deformations [5,6,7,8]. However, the magnitude and long-term deformation development of structures subjected to cyclic loading has only been marginally investigated.

Both the elastic as well as the creep deformation behaviour of concrete are significantly influenced by the moisture content of the concrete, whereby creep becomes negligible in very dry concretes (e.g. [9]). The amount and distribution of water in the pore system is of fundamental importance for the magnitude and development of creep deformations. The microscopic origin of the creep deformations of concrete is explained as a result of the rearrangement and transport processes of water in capillary and gel pores, as well as sliding processes between the calcium-silicate-hydrate nanoparticles [10,11,12], confirmed by experimental results of Haist et al. [13] and numerical simulations of Morshedifard et al. [14]. Furthermore, Powers [10] assumed that new, stronger primary bonds within and between the calcium-silicate-hydrate phases can form in the compressed microstructure which prevent creep recovery.

The effect of compressive cyclic loading on the deformations at moderate maximum stress levels Smax ≤ 0.60 has been rarely studied. The results are limited on very few macroscopic investigations (see e.g. [6, 8]), but without taking into account the moisture content of the concrete. First results presented by the authors [15] showed that the moisture content of normal strength concrete affects the strain development significantly even at small maximum stress levels Smax ≤ 0.45. For cyclic loading with higher maximum stress levels Smax ≥ 0.65, significantly lower fatigue resistance was observed for high-strength concrete specimens with higher moisture contents [16,17,18,19]. The reduction of the fatigue resistance due to a high moisture content is more pronounced for a lower test frequency of 0.1 Hz compared to higher test frequencies of 1 or even 10 Hz [19].

The analysis of the stiffness development (development of the secant modulus of stress–strain curve within the cyclic process) has become an essential part of describing the progressive degradation of the microstructure during fatigue loading macroscopically. The fact that the stiffness of the concrete decreases due to fatigue loading at high stress levels is well-documented in literature [20,21,22]. The stiffness development is s-shaped and can be divided into three phases: the stiffness decreases strongly in the first and moderately in the second phase; in the third phase, the stiffness decreases strongly again until failure occurs. A higher degradation of stiffness per load cycle was observed for specimens with a higher moisture content [17,18,19]. No reduction of stiffness in the second phase was measured at moderate maximum stress levels Smax ≤ 0.60 for high-strength concrete specimens which were stored under water until an age of seven days and then stored at 20 °C and 60% RH until testing [23]. In some cases, there was even a slight increase of stiffness in the second phase. These results correspond to results of Kern et al. [24] at maximum cyclic stress levels of Smax = 0.35 and 0.45 for specimens with a moisture content of approx. 100%. Here, a constant stiffness or even a stiffness recovery was observed in the second phase of the stiffness development. Other detailed studies on the stiffness development of concrete subjected to such low maximum cyclic stress levels are not known to the authors.

Smadi and Slate [25] observed by x-ray technique a slow and stable micro cracking process due to sustained constant stresses of 0.40 < Screep ≤ 0.75 for normal strength concretes, which decreases during long-term loading. For creep stresses Screep ≤ 0.40, the micro cracking is almost negligible over that due to drying shrinkage [25]. Based on creep and cyclic tests on a normal strength concrete, Shah and Chandra [16] presented the hypothesis of two opposing effects during loading: on the one hand, consolidation with a consequent strengthening and, on the other hand, cracking with a consequent weakening, assuming that the process of loading and unloading causes additional cracking. This hypothesis is supported by Bažant and Hubler [26], who showed that the additional deformations due to cyclic loading can be well calculated considering the growth of the pre-existing microcracks within fracture mechanics. There are only a few investigations of the damage processes due to fatigue loading (maximum stress levels Smax ≥ 0.65). Oneschkow [27] hypothesised that extremely small-scale structural changes in the concrete microstructure accumulate continuously within the fatigue process as pre-stages of damage visible on a mesoscale. Thiele [28] showed by fluorescence microscopy and scanning electron microscopy that the fatigue process in the first and second phase is apparently not caused by micro cracking and hypothesised that the changes in material properties during the first and second phases are based on structural changes/viscous deformations of the hardened cement. Similar effects are also known from the creep behaviour of concrete. Nevertheless, the macroscopic cyclic investigations showed higher deformations and a much stronger reduction of the stiffness compared to constant loading at a corresponding creep stress level of Screep = Smean. Thus, Thiele [28] hypothesised that cyclic loading leads to an increased activation and accumulation of viscous deformation components and, at the same time, to a more pronounced deterioration of the hardened cement paste compared to constant loading. Using transmission electron microscopy, Schaan et al. [29] found that certain regions of the ultra-high performance concrete paste appeared much more densely packed after a short duration of compressive fatigue loading, while needle- or lath-shaped regions with less density appeared concurrently, which rose in number within the fatigue process. First results from acoustic emission analyses support the hypothesis of structural changes or damage on different scales for creep and cyclic loading [30,31,32].

Despite the lack of knowledge concerning the effect of cyclic loading on long-term deformations and deformation mechanisms, there are some approaches for the prediction of long-term deformations due to cyclic loading. The fib Model Code 2020 [3] provides Eq. (2) for the calculation of cyclic strains due to maximum stresses |σc,max|< 0.60 fck and mean stresses of (|σc,max| +|σc,min|)/2 < 0.50 fck, which is quite similar to Eq. (1) for constant loading |σc,cr|< 0.40 fcm(t0). In Eq. (2), the total strain due to cyclic loading εc,cycl(t,t0) consists of the elastic strain component εel,0 and the time-dependent viscous strain εv,cycl. The amount of elastic strain εel,0 is assumed as a constant value and derived from the maximum peak stress of the cyclic loading divided by the modulus of elasticity. The viscous strain εv,cycl is described according to the creep function for constant loading, considering the mean cyclic stress (mean value of the maximum stress σc,max and the minimum stress σc,min) to be the relevant loading parameter. Determining the viscous strain εv,cycl, the mean cyclic stress is divided by the modulus of elasticity Eci and multiplied by the creep coefficient φ(t,t0).

Strains due to constant loading according to fib Model Code 2020 [3]:

$$ \varepsilon_{{\text{c},{\text{cr}}}} \left( {\text{t},\text{t}_{0} } \right) = \frac{{\sigma_{{c,{\text{cr}}}} }}{{\underbrace {{\text{E}_{{{\text{ci}}}} \left( {\text{t}_{0} } \right)}}_{{\varepsilon_{{{\text{el}},0}} }}}} + \underbrace {{\frac{{\sigma_{{c,{\text{cr}}}} }}{{\text{E}_{{{\text{ci}}}} }} \cdot \varphi \left( {\text{t},\text{t}_{0} } \right)}}_{{ \varepsilon_{{\text{v},{\text{cr}}}} }}$$
(1)

Strains due to cyclic loading according to fib Model Code 2020 [3]:

$$ \varepsilon_{{\text{c},{\text{cycl}}}} \left( {\text{t},\text{t}_{0} } \right) = \underbrace {{\frac{{\sigma_{{c,{\text{max}}}} }}{{\text{E}_{{{\text{ci}}}} \left( {\text{t}_{0} } \right)}}}}_{{ \varepsilon_{{{\text{el}},0}} }} + \underbrace {{\frac{{\sigma_{{c,{\text{max}}}} + \sigma_{{c,{\text{min}}}} }}{{2 \cdot \text{E}_{{{\text{ci}}}} }} \cdot \varphi \left( {\text{t},\text{t}_{0} } \right)}}_{{ \varepsilon_{{\text{v},{\text{cycl}}}} }}$$
(2)

Only a few experimental investigations on normal strength concretes are documented in the literature comparing total strains due to creep and cyclic loading at a maximum stress level of Smax ≤ 0.60. Their results indicate that the mean stress level approach of Eq. (1) underestimates the total strains observed in cyclic tests [6, 8]. Furthermore, the difference between the total strains at maximum peak stress of cyclic loading and the total strains due to creep loading increased with the increasing maximum stress level [8]. In a previous paper [24], the authors already showed that the viscous strains due to cyclic loading for maximum cyclic stresses of Smax = 0.35 and 0.45 and concrete specimens with a moisture content of approx. 100% are higher than those due to creep loading at the corresponding mean stress level (Screep = Smean) within a test duration of 13 days. Furthermore, the viscous strains due to cyclic loading were closer to, but slightly below the viscous creep strains at the corresponding maximum stress level (Screep = Smax).

Prediction models describe the increased viscous strains due to cyclic loading compared to the strains due to creep loading at a corresponding mean stress level (Screep = Smean) as either an acceleration of the creep strain [33,34,35] or an additional strain component [26, 36]. The extent of the acceleration of the creep strain or, rather, the additional strain due to cyclic loading is formulated as a function of the test frequency and either the maximum stress level or the stress amplitude. These models were only validated using the small database documented in literature, which is available only for short test durations ≤ 28 days.

Therefore, fundamental investigations regarding the comparability and differences of strain and stiffness developments due to creep and cyclic loading at corresponding stress levels (Screep = Smean and Screep = Smax) were carried out on a normal strength concrete C30/37 as part of a collaborative research project. In extension to the results presented in [15] and [24], this paper focuses on the influence of the concrete’s moisture content. The development of viscous and viscoplastic strains and the modulus of elasticity over a test duration up to 91 days are presented comparatively for creep and cyclic loading at stress levels of Smax ≤ 0.45. The developments of the viscoplastic strain and the modulus of elasticity due to cyclic loading in comparison to creep loading provide a basic understanding of differentially pronounced deformation mechanisms occurring in the microstructure of concrete due to the load type. Based on this, the overall aim of ongoing studies is to improve approaches describing the cyclic strain development based on creep models.

2 Experimental programme

2.1 Concrete composition and specimens

The investigations were carried out on a normal strength concrete C30/37 as commonly used in bridges (composition see Table 1). The specimens were cast in several batches due to the large number of specimens required. The mean 28-day compressive strength, tested according to DIN EN 12390-3 [37] for at least three specimens, respectively, were determined as fcm,cube = 35.7 ± 0.8 MPa (batch 1), fcm,cube = 37.5 ± 1.7 MPa (batch 3), fcm,cube = 40.3 ± 1.0 MPa (batch 4) and fcm,cube = 42.1 ± 0.4 MPa (batch 5), respectively. The specimens of batch 2 were used for other investigations and are not included in this paper.

Table 1 Concrete composition
Full size table

Creep and cyclic tests were carried out on cylindrical specimens with a height of h = 180 mm and a diameter of d = 60 mm. The specimens were cast, stored and conditioned in a closely defined process. The fresh concrete was filled into cylindrical PVC formworks in two layers and each layer was mechanically compacted using a vibrating table. In order to prevent disturbed areas at the ends of the specimens, the specimens were cast with a height of h = 230 mm. All specimens were stored at 20 °C in boxes covered with a wet cloth for five to six weeks until they were demoulded and cut to the final height of h = 180 mm. Afterwards, the test surfaces were ground and polished plane-parallel to achieve a uniform stress distribution during mechanical testing.

In a next step, the specimens were stored in two different ways to ensure a constant moisture content in the concrete pores of approx. 100% RH (referred to as V100) or approx. 75% RH (referred to as V75). The specimens with the higher moisture content, V100, were entirely sealed with an aluminium-coated butyl tape (Sd-value > 1,500 m) directly after polishing and subsequently stored at 20 °C until testing. The specimens of the lower moisture content V75 were initially sealed only on the test surfaces but not on the circumference and stored for 90 days at 20 °C and 65% RH to ensure a uniform drying over the circumferential surface and obtain a uniform moisture gradient over the entire height of the specimens. Subsequently, they were sealed entirely with an aluminium-coated butyl tape and then stored for a further 40 days at 40 °C to achieve a constant moisture distribution over the cross-section of the specimens. The late and slow drying process of the V75 specimens was chosen to minimise possible differences in the microstructure of specimens with both moisture contents. Thereafter, the V75 specimens remained sealed and were stored at 20 °C until testing. The storage procedure for V75 was chosen based on diffusion calculations using the finite difference method of Acosta Urrea [38]. The concrete moisture content was verified by experimental investigations and were in good agreement to the desired values of 100% RH and 75% RH.

All specimens were tested sealed in the aluminium-coated butyl tape to keep the adjusted moisture content constant and, thus, prevent drying creep and shrinkage. The tests were carried out on specimens with a high age at loading of at least 180 days to ensure an almost complete hydration and avoid additional hardening of the concrete, especially during the long-term loading.

2.2 Experimental set-up

The creep tests (constant loading) were performed using a creep testing machine with a hydraulic load cylinder connected to a high-pressure buffer reservoir. The stress was monotonically increased up to the creep stress level Screep and, subsequently, maintained constant. The cyclic tests were performed using either a servo-hydraulic or an electromechanical universal testing machine. The stress was monotonically increased up to the mean stress level Smean and, afterwards, the load oscillation, defined by the mean stress level Smean, the amplitude and the frequency ft, was started. Hereby, the full amplitude was applied in the first load cycle. The stresses σc,i to be applied were calculated by multiplying the desired stress levels Si with the mean reference compressive strength fcm,ref of parallel specimens tested immediately before creep and cyclic tests (see Sec. 2.3).

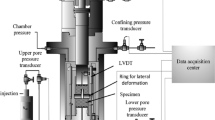
The axial deformations of the specimens were measured continuously throughout the entire creep and cyclic tests using three linear variable differential transformers (LVDTs) positioned on the circumference of the specimen at angles of 0°, 120° and 240° (Fig. 1). In addition, the axial force, the axial stroke of the actuator, the ambient temperature and the temperature of the loading plate were measured and recorded. The data sampling rate was 1 Hz for the creep investigations and 10 Hz for the cyclic investigations.

Fig. 1
figure 1

Test set-up [24]

Full size image

2.3 Test programme

The mean reference compressive strength fcm,ref of the concrete was determined immediately before testing as the mean value of three cylindrical specimens tested force-controlled. Furthermore, the mean modulus of elasticity Ec(t0) of the concrete was determined as the secant modulus of the stress–strain curve due to monotonically increased stress at a rate of approx. 0.5 MPa/s. The respective reference specimens were of the same batch and had the same dimensions and storage conditions (V100 or V75) as those used in the creep and cyclic loading tests. The mean reference compressive strength fcm,ref and the mean modulus of elasticity Ec(t0) are given for each batch in Table 2. As can be seen, there are slight differences in the concrete properties between the batches. Contrary to the intentions, even beyond an age of half a year, the samples show an increase in strength, which has to be accounted in the evaluation of the results. However, an influence of the moisture content of V100 or V75 on the concrete properties cannot be observed macroscopically. No microstructural analyses were carried out to investigate whether the different storage conditions (see Sec. 2.1) had an influence on the microstructure.

Table 2 Mean values of reference compressive strength and modulus of elasticity of the concrete
Full size table

The test programme is given in Table 3 regarding the load type and moisture content of the specimens. The mean reference compressive strength per batch was used for the determination of the stress levels (Si = σc,i/fcm,ref). The maximum and minimum cyclic stress levels (Smax and Smin) and creep stress level Screep were held constant within each test. The test frequency was ft = 0.1 Hz in all cyclic tests, expecting a significant influence of the moisture content [19] and following natural load frequencies of a suspension bridge identified by Xu et al. [39] in the range from 0.068 to 0.616 Hz. Further investigations at 1.0 Hz are published in [24]. The maximum stress level Smax in the cyclic tests was either Smax = 0.35 or 0.45 and the minimum stress level was Smin = 0.05. Creep tests with stress levels of Screep = Smax and Screep = Smean were conducted for comparison with the cyclic tests. The combination consisting of the cyclic test and the two corresponding creep tests is hereafter called “load level set” 0.35 or 0.45. The influence of the moisture content was analysed by comparison of test results at the same stress levels.

Table 3 Overview of creep and cyclic tests conducted
Full size table

The duration of tests was sequenced (3, 6, 13 and 91 days) for each load type to analyse strain components and the modulus of elasticity at uniform logarithmic intervals. The number of tests per loading duration differed between 1 and 4 (see Table 3). After the respective loading duration, the specimens were unloaded and the creep recovery was measured for 24 h after loading durations of 3, 6 and 13 days, and for 5 days after a loading duration of 91 days for further analysis of the strain components. Subsequently, the modulus of elasticity was determined again as the secant modulus of the stress–strain curve due to monotonically increased stress at a rate of approx. 0.5 MPa/s up to 35% of the reference compressive strength.

2.4 Data analysis

2.4.1 Strain development and viscoplastic strain component

The axial deformations were continuously measured using three LVDTs, as described in Chapter 2.2. The development of total strain εtot due to creep or cyclic loading per specimen was calculated as a mean value of the respective three deformation values and plotted as mean deformation curve. In a next step, the peak strains of the cyclic curves εtot,max at the maximum stress level Smax were obtained by peak analyses.

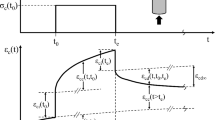
The total strain due to creep εtot,cr or cyclic loading εtot,max consists of an elastic strain component and a time-dependent, viscous strain component (see Fig. 2). The elastic strain component εel,0 was defined as the strain when the creep load level Screep was reached or, in the case of cyclic loading, as the strain when the maximum stress level Smax was reached in the first load cycle. In accordance with fib Model Code 2020 [3] (see Eq. 1), the viscous (index v) strain component εv,cr (creep) or εv,max (cyclic) was determined by subtracting the initial elastic strain component εel,0 from the total strain εtot,cr or εtot,max (mind: sealed samples; no drying shrinkage strains). The mean viscous strain developments presented hereafter are averaged curves of several specimens from the same batch.

Fig. 2
figure 2

Schematic presentation of (a) cyclic loading and (b) creep loading and strain components [24]

Full size image

The viscous strain component εv,cr or εv,max consists of a viscoelastic εv,el and viscoplastic strain component εv,pl, which increase over time during loading. The degraded elastic component εel,d is defined as the part of the strain that decreased until the specimen was completely unloaded and the viscoelastic strain εv,el is defined as the part of the strain that decreases during the time of creep recovery. The viscoplastic strain component εv,pl was determined as the remaining strain at the end of creep recovery. It was analysed as the percentage of the viscous strain at Smax (in the last load cycle) or rather Screep immediately prior to complete unloading to achieve a better comparability between different specimens. Thus, it describes the irreversible proportion of the accumulated viscous strains. The time of creep recovery was 24 h after loading durations of 3, 6 and 13 days, and 5 days after a loading duration of 91 days. As the evaluation of the strain components is based on a limited number of specimens per previous loading duration and type, the viscoplastic strains εv,pl are analysed as mean values from different batches and, therefore, show higher scatter compared to the viscous strain developments.

2.4.2 Relative modulus of elasticity

The modulus of elasticity was analysed in this investigation for both load types (creep and cyclic) in contrast to the stiffness development (usually analysed in fatigue investigations) because no stiffness development is available for creep tests. Furthermore, the stiffness is influenced by the loading velocity and, connected to this, by the moisture content. Therefore, the initial modulus of elasticity Ec(t0) at the beginning of loading and the (degraded) modulus of elasticity Ec(t) after unloading and creep recovery were determined. The initial modulus of elasticity Ec(t0) was determined as the secant modulus of the stress–strain curve due to monotonically increased stress at the beginning of the cyclic tests with the rate of approx. 0.5 MPa/s. It was determined as the mean value of specimens from the same batch and used as the reference for all cyclic and creep tests of this batch. The (degraded) modulus of elasticity Ec(t) was determined after unloading and creep recovery as the secant modulus of the stress–strain curve due to another monotonic loading increased up to 35% of the reference compressive strength at the rate of approx. 0.5 MPa/s. It was also analysed as the mean value of specimens of different batches. The respective number of tests per loading duration can be found in Table 3.

Considering the different concrete batches, slight differences in the initial modulus of elasticity Ec(t0) between the different batches could be detected and, thus, the (degraded) modulus of elasticity Ec(t) cannot be compared as an absolute value throughout different batches. Therefore, the relative modulus of elasticity rel. Ec(t) was analysed as the average (degraded) modulus of elasticity Ec(t) referred to the average initial modulus of elasticity Ec(t0) according to Eq. (3).

$$\it {\text{rel}}.E_{c} \left( t \right)\, = \,E_{c} \left( t \right) / E_{c} (t_{0} )$$
(3)

Similar to the evaluation of the viscoplastic strain component, the evaluation was carried out on a limited number of specimens from different batches, so that there are larger scatters compared to the viscous strain developments. The relative modulus of elasticity Ec(t) gives information about the degraded material behaviour and, thus, supplements the information given by the viscoplastic strain component.

3 Experimental results

3.1 Development of viscous strain

The average temporal developments of viscous strain at maximum stress level due to cyclic loading εv,max (blue) are plotted with the corresponding average developments of viscous strain due to creep loading εv,cr at Screep = Smean (red) and Screep = Smax (yellow) in Figs. 3 and 4. The strains of specimens tested as part of the load level set 0.35 with a moisture content V100 (filled symbols) are presented in Fig. 3a and b and those with V75 (unfilled symbols) in Fig. 3 c and d. The strains of specimens at the higher load level set 0.45 (see Tab. 3) with a moisture content V100 are shown in Fig. 4a and those with V75 in Fig. 4b. The specimens tested at each load level set with the same moisture content were from the same batch. The loading duration of the load level set 0.35 was sequenced up to 91 days (see Table 3). Thus, the results of the load level set 0.35 are presented up to 91 days in Fig. 3 a and c and in a detailed view up to 6 days in Fig. 3b and d for both moisture contents.

Fig. 3
figure 3

Developments of viscous strains due to cyclic and creep loading of specimens with (a, b) moisture content V100 and (c, d) V75 for different loading durations, load level set 0.35

Full size image
Fig. 4
figure 4

Developments of viscous strains due to cyclic and creep loading of specimens with (a) moisture content V100 and (b) V75 for a loading duration of 6 days, load level set 0.45

Full size image

Comparing Fig. 3a and c as well as Fig. 4a and b, it can be seen that the strains of specimens tested with the lower moisture content V75 are generally smaller than those with the higher content V100 for each load type at the same stress level. Furthermore, the cyclic strains εv,max for both moisture contents significantly exceed the corresponding creep strains εv,cr at Screep = Smean for both load level sets (cf. Figs.  3 and 4). Instead, the cyclic strains are smaller but closer to the creep strains at εv,cr at Screep = Smax. Especially for the specimens with V100 and load level set 0.35, the cyclic strains εv,max are very close to the creep strains εv,cr at Screep = Smax (Fig. 3a). Whereby, the difference between εv,max and εv,cr at Screep = Smax is higher for moisture content V75 (Fig. 3c). While the V100-curves show continuous increase of strain combined with a continuous decrease in slope, the V75-curves showing more similarity to a bilinear behaviour with rapid increase of strain immediately after the start of loading and a slower phase afterwards.

As expected, the strains are higher at load level set 0.45 (Fig. 4) than at load level set 0.35 (Figs. 3b and d). Furthermore, the difference between the cyclic strains εv,max and creep strains εv,cr at Screep = Smax and moisture content V100 is higher compared to load level set 0.35 (Fig. 3b). Special attention should be paid to the cyclic and creep strain curves due to Screep = Smax = 0.45 and moisture content V75 (Fig. 4b). Here, the V75-curves show again a more bilinear deformation behaviour. Whereby, the slope of the creep curve at Screep = Smax flattens more strongly in the second phase than the cyclic curve and, consequently, the slope of the cyclic curve is higher. This leads to an intersection point of both strain curves at the sixth day of loading and, thus, higher strains due to cyclic loading can be assumed for a longer loading duration. This is a significant difference to the results for the higher moisture content V100 (Fig. 4a) and, especially, to the results for the same moisture content but at the lower level set 0.35 (Fig. 3c). Whereby the tendency of the creep curve to flatten more than the cyclic curve is also visible in Fig. 3c, but only for a longer load duration above approx. 75 d.

Overall, the strain developments due cyclic loading are more similar to creep loading with Smax instead of Smean which contradicts current modelling approaches (cf. Chapter 1) However, it is shown that the strain developments due to cyclic loading cannot simply be described by a “comparable” creep load as the interdependent influences of type of loading, load level and concrete moisture content are differently pronounced. In order to get more insight into the mechanisms, the viscoplastic strains and the modulus of elasticity (as macroscopic indicators of the underlying deformation processes) are analysed in the following.

3.2 Viscoplastic strain

The viscoplastic strain εv-pl is the irreversible component of the viscous strain and was determined after unloading (see Fig. 2). In the following, the viscoplastic strains are analysed as a percentage of the viscous strains at Smax (in the last load cycle) or rather Screep immediately prior to complete unloading. The viscoplastic strains due to cyclic (blue) and creep loading at Screep = Smean (red) and Screep = Smax (yellow) at load level set 0.35 of the specimens with moisture content V100 (filled symbols) and V75 (unfilled symbols) are shown in Fig. 5 and those at load level set 0.45 in Fig. 6. In addition, lines of the same colour are given, which are no regressions and are rather intended to guide the eye. Please note that the previous loading durations were 3, 6, 13 or 91 days for load level set 0.35 (Fig. 5) and 3, 6 or 13 days for load level set 0.45 (Fig. 6). The mean values presented hereafter are influenced by higher scatter compared to the results in Chapter 3.1 as they were obtained from specimens of different batches.

Fig. 5
figure 5

Viscoplastic strains (percentage) due to cyclic and creep loading of specimens with (a) moisture content V100 and (b) V75 for loading durations of 3, 6, 13 and 91 days, load level set 0.35 (lines are no regressions, rather meant to guide the eye)

Full size image
Fig. 6
figure 6

Viscoplastic strains (percentage) due to cyclic and creep loading of specimens with (a) moisture content V100 and (b) V75 for loading durations of 3, 6 and 13 days, load level set 0.45 (lines are no regressions, rather meant to guide the eye)

Full size image

From Figs. 5 and 6 it is obvious that the viscoplastic strains form with more than 60% the largest part of the viscous strains which develop due to creep or cyclic loading. They increase with the loading duration for all load types and both moisture contents, which was expected. Furthermore, the viscoplastic strains are higher for the higher moisture content V100 than V75 at both load level sets and all load types. The viscoplastic strain component due to cyclic loading tends to be higher than that due to creep loading for specimens of both moisture contents. However, the influence of the moisture content on the viscoplastic strain component seems to be less pronounced for specimens subjected to cyclic loading compared to creep loading. Overall, these results might hint to the fact that there are deformation processes prevailing differently due to creep and cyclic loading whereby the influence of the moisture content is pronounced differently. This is further discussed in the following considering all experimental results.

3.3 Relative modulus of elasticity

The relative modulus of elasticity rel.Ec(t) (related to the initial modulus of elasticity Ec(t0)) is shown in Fig. 7 for the load level set 0.35 and Fig. 8 for load level set 0.45. The rel.Ec(t) due to cyclic loading (blue) and creep loading at Screep = Smean (red) and Screep = Smax (yellow) are shown for both moisture contents V100 (filled symbols) and V75 (unfilled symbols). Linear regressions for the same load type and moisture content are given in the same respective colour. The previous loading durations were 3, 6 or 13 days for both load level sets and additionally 91 days for load level set 0.35.

Fig. 7
figure 7

Relative modulus of elasticity due to cyclic and creep loading of specimens with (a) moisture content V100 and (b) V75 for loading durations of 3, 6, 13 and 91 days, load level set 0.35

Full size image
Fig. 8
figure 8

Relative modulus of elasticity due to cyclic and creep loading of specimens with (a) moisture content V100 and (b) V75 for loading durations of 3, 6 and 13 days, load level set 0.45

Full size image

From Figs. 7 and 8 it is obvious that a decrease in modulus of elasticity is already induced due to a loading of three days for all load types and both moisture contents (hereinafter referred to as initial reduction). Only for creep loading at Screep = 0.25 and moisture content V100 no reduction of the modulus of elasticity is observed. Overall, the smallest initial reduction is observed for creep loading at Screep = Smean, followed by creep loading at Screep = Smax (Figs. 7 and 8). The initial reduction due to cyclic loading is the highest for both load level sets. No distinct influence of the moisture content on the initial reduction can be observed for load level set 0.35 (Fig. 7). By contrast, for load level set 0.45, the initial reduction is higher for specimens with moisture content V75 than V100 (Fig. 8).

Considering longer durations of previous loading of 6, 13 and 91 days, a re-increase of the relative modulus of elasticity rel.Ec(t) is observed for all load types and moisture contents for load level set 0.35 (Fig. 7). Only after 91 days of cyclic loading and V75 a decrease is detected, which might be an artefact and should be considered with caution. However, due to the re-increase, the modulus of elasticity after the maximum duration of loading is, in some cases, even higher than the initial modulus of elasticity (Fig. 7). Regarding load level set 0.45, the re-increase of rel.Ec(t) is only observed for creep loading at Screep = Smean = 0.25 for both moisture contents and at Screep = Smax = 0.45 for the higher moisture content V100. Here, the cyclic loading of specimens with both moisture contents and the creep loading at Screep = Smax = 0.45 with the lower moisture content V75 already lead to a further reduction of rel.Ec(t). The degradation of the modulus of elasticity after the maximum loading duration of either 13 (Fig. 8) or 91 days (Fig. 7) is the highest due to cyclic loading followed by creep loading at Screep = Smax and the lowest due to creep loading Screep = Smean. In general, the moisture content V75 leads to a higher reduction and/or a lower re-increase of the relative modulus of elasticity rel.Ec(t). Therefore, the relative modulus of elasticity rel.Ec(t) tends to be smaller for specimens with a moisture content of V75 compared to those with V100.

Accompanying tests on unloaded specimens show no systematic increase in compressive strength and/or stiffness within the loading duration. This indicates that hydration is not the reason for the re-increase of the modulus of elasticity. However, hydration processes during the loading duration cannot be completely ruled out.

Overall, an interdependence between the influence of load level, type of loading and moisture content on the degradation of the modulus of elasticity is obvious. The reduction of the relative modulus of elasticity rel.Ec(t) is systematically higher due to cyclic loading compared to creep loading. The re-increase is more pronounced by tendency for lower loading, higher moisture content and constant loading compared to cyclic load. On the other hand, further degradation is visible by tendency for higher loading, lower moisture content and cyclic loading compared to constant loading. Altogether, cyclic and creep loading with a certain duration lead to different degradation of the modulus of elasticity. Together with the results of the viscoplastic strains, this is a strong indication for different states of the material after the previous loading maybe due to differently pronounced degradation processes in the concrete.

4 Summary and conclusion

The deformation behaviour of a normal strength concrete under creep and cyclic loading, respectively, was investigated comparatively. Here, significant lower maximum stresses of Smax = 0.35 and 0.45 were investigated compared to usual fatigue investigations. The viscous strain development, the viscoplastic strain component and the relative modulus of elasticity both after creep and cyclic loading were investigated on specimens with moisture contents of approx. 100% (V100) and approx. 75% (V75). Possible differences in the microstructure of specimens with both moisture contents were minimised by a late and slow drying process. However, such differences cannot be completely ruled out, although no differences in the macroscopic properties were found (see Sec. 2.3). The results of the macroscopic creep and cyclic investigations can be summarised as follows:

  1. 1.

    The viscous strains due to cyclic loading are generally higher than those due to creep loading at an equal mean stress level (Screep = Smean) and, furthermore, are closer to the strain caused by creep loading at equal maximum stress level (Screep = Smax) for both moisture contents and maximum stress levels investigated. However, the investigations showed that the cyclic strains of specimens with moisture content V75 may exceed the creep strains at Screep = Smax for longer loading durations. This was determined for moisture content V75 where the development of creep strain flattens earlier, while the slope of the strain curve due to cyclic loading has not yet declined.

  2. 2.

    The viscous strains due to cyclic loading and creep loading at Screep = Smax, respectively, include different percentages of viscoplastic strain and are accompanied with different degraded moduli of elasticity. This indicates different load type dependent processes or different pronounced processes in the microstructure.

  3. 3.

    Viscoplastic strains after 3 days of previous cyclic loading or creep loading were found which contribute more than 60% to the total viscous strains and, furthermore, are higher for moisture content V100 than for V75. These viscoplastic strains increase with longer duration of loading. For creep loading, the creep deformation of hardened cement paste is generally explained as a result of the redistribution and transport processes of water in capillary and gel pores, sliding processes between the calcium-silicate-hydrate nanoparticles and formation of new stronger primary bonds between those calcium-silicate-hydrate nanoparticles preventing creep recovery [10,11,12,13,14]. Thus, the higher viscoplastic strains of the specimens with V100 due to creep loading can be explained by a higher pronouncement of those processes. For cyclic loading, higher percentages of viscoplastic strain are documented, which are less affected by the moisture content.

  4. 4.

    A reduced modulus of elasticity after 3 days of previous cyclic loading or creep loading was found for both moisture contents. For longer loading, a re-increase or further reduction was found dependent on the load type, load level and moisture content. The re-increase is more pronounced by tendency for lower stress level, higher moisture content and constant load compared to cyclic loading. Further degradation is visible by tendency for higher loading, lower moisture content and cyclic load compared to constant load. Regarding cyclic loading, the decrease of the modulus of elasticity is usually assigned to defects and damaging processes in the microstructure from nano- to mesoscale, e.g. [27,28,29,30]. Regarding creep loading, changes in the modulus of elasticity are usually not analysed and, thus, to the best of the authors’ knowledge, no explanations have yet been documented in literature. However, the reduction of the modulus of elasticity due to 3 days of creep loading could also be assigned to defects and damaging processes in the microstructure, which decrease during creep loading [25].

  5. 5.

    Comparing the state of the material after cyclic loading or creep loading of a certain duration at the same moisture content, cyclic loading leads to a higher reduction of modulus of elasticity and higher viscoplastic strains compared to creep loading at Screep = Smax and Screep = Smean. The re-increase of modulus of elasticity is less pronounced. Furthermore, the influence of the moisture content on the viscoplastic strains is lower for cyclic loading compared to creep loading.

  6. 6.

    From the observed macroscopic results, it is assumed that there are on the one hand deformations due to water redistribution and sliding processes, which are partly irreversible due to the formation of new bonds [10,11,12,13,14] and on the other hand deformations due to a degradation of the microstructure in form of extremely small-scale structural changes or damage [25,26,27,28,29,30,31,32]. The viscoplastic strains are considered to be higher for constant loading and high moisture contents. For cyclic loading at increased load levels, the formation of new bonds are assumed to be less pronounced but in addition viscoplastic strains arise as result of a comparatively more pronounced degradation of the microstructure. A re-increase of the elastic modulus arises if the induced irreversible deformations increase the (bulk measured) modulus of elasticity more than the degradation reduces the modulus of elasticity.

It could be shown, that the viscous strains due to cyclic loading and creep loading are the result of differently pronounced deformation/degradation processes. These processes are not yet understood and further investigations are necessary, especially, due to the complex interdependence of load type, load level and moisture content. In particular, microscopic investigations could provide a valuable completion of the overall interpretation of mechanisms.

The results clearly demonstrate, that the calculation of the strains due to cyclic loading by using current models [1,2,3], based on strains caused by creep loading with Screep = Smean, significantly underestimates the actual strains and, thus, is not adequate for the design of bridges, for example. Instead, it would be more secure to model the cyclic strains based on the strains caused by the creep stress at the maximum stress level Screep = Smax. However, the cyclic strains could also exceed the creep strains at the maximum stress level, especially at low moisture contents. Therefore, the proposed approach of using the creep strains for Screep = Smax to model the strains due to cyclic loading is more suitable than the existing approaches but could also lead to an underestimation of strains.