1 Introduction

The cross-section analysis represents a significant tool to investigate the structural response of the buildings by means of moment–curvature M-χ diagrams and axial load-bending moment P-M interaction diagrams. In particular, M-χ diagrams are mainly used in seismic analysis to assess the non-linear response and the ductility of the cross-sections. The ductility of the structures [1, 2] is an important parameter for structural design because the dimensioning of structural elements depends on the energy dissipation and it allows to prevent brittle failures. Pushover analyses are used to assess the non-linear structural capacity of structures under seismic loads. In order to achieve a more accurate simulation of the real structural behaviour, accurate M-χ diagrams are required to describe properly the nonlinear behaviour of the structural elements and, in particular, the plastic hinge behaviour by means of curves with significant points, namely: cracking point, yielding point and ultimate point. In the last decades, the ductility of reinforced masonry cross-sections with fiber reinforced polymer FRP or fiber reinforced cementitious matrix FRCM systems [3, 4] was investigated with M-χ diagrams in order to analyse the benefits on the structural response [5]. In addition, tension stiffening effects are analysed by means of M-χ diagrams and it represents a main aspect in the cracking analysis.

P-M diagrams [6] are generally used to analyse the structural capacity of the cross-section for the design of new buildings or for the vulnerability analysis of existing buildings [7], or even different structures, like as tunnels made of jet grouting [8]. Nowadays, in historical city centres, the rehabilitation of the existing heritage buildings [9] plays an important role in the civil engineering field and therefore, the vulnerability analysis of existing buildings is a debated theme in the scientific community.

Another important aspect of the cross-section analysis is represented by the constitutive model adopted to describe the behaviour of the materials. In addition to a design oriented approach according to code and guidelines proposals, in literature, several experimental studies are available to properly analyse the compressive behaviour of masonry [10,11,12], following a research oriented approach.

The solution of the cross-section analysis is mainly a numerical problem, and it is commonly solved by a fiber discretization of the cross-section. It is important to note that the solution is not exact due to the discretization of the cross-section in fibers or strips; however, the numerical error becomes negligible adopting a high discretization of the cross-section. Howsoever, an iterative process is required in the case of fiber analysis to evaluate the neutral axis depth and the relative force equilibrium, hence yielding to numerical approximations to obtain convergence. In addition, it is important to define properly the convergence with a robust algorithm to prevent wrong solutions or divergence; in fact, the numerical solution is not unique as expected in a non-linear analysis.

Compared to the traditional fiber-section models, the proposed methodology can be more computationally efficient due to the adoption of the closed-form equations for sectional equilibrium.

In fact, the proposed approach represents a computation efficiency optimization of the non-linear cross-section analyses; the theoretical approach is based on the classic theory of the structural mechanics and materials, but it is extended in an unconventional manner, analysing the behaviour even after the attainment of the ultimate strains, accounting for progressive damage.

The development of simplified algorithms to assess the flexural capacity of masonry cross section could be implemented in the risk analyses in order to evaluate the vulnerability of masonry structures within a large scale approach [13, 14].

2 Constitutive models

The proposed approach is based on the stress-block theory and the direct integration of the generic non-linear stress–strain diagram of the continuous material of the cross-section. The stress-block theory allows to substitute the generic non-linear stress-stress diagram by an equivalent rectangular distribution. This was first developed for Reinforced-Concrete, and similarly used for masonry [15], hence theoretically, it is applicable to any non-linear constitutive behaviour, but the complexity of the solution depends on the constitutive model and equations.

2.1 Masonry

The constitutive behaviour of the continuous material of the cross-section in compression is typically described by a non-linear behaviour; several models are proposed in literature [16].

Five constitutive models are analysed herein to compare the stress–strain diagrams provided by codes and experimental studies. In particular, the parabola-rectangle and the linear-rectangle (or bilinear) stress–strain diagrams are analysed according to the Eurocode [17, 18] assumptions, while the stress–strain relations proposed by Turnšek and Cačovic [19], Sawko [20] and Capozucca [21] are assumed to describe the experimental compressive stress–strain relationship according to research oriented constitutive models available in the scientific literature. The tensile behaviour is neglected as basic assumption.

In this paper, the strains are indicated with ε while normalized strains are indicated with e (normalized on the peak strain εk).

The adopted constitutive models (stress as function of strain, σ(ε)) are described by the compressive strength fm, the peak εk (corresponding to fm) and ultimate εu strain. Stresses σ are normalized on the compressive strength, fm, and are indicated with s.

It is important to note that each constitutive model can be described by a parabola equation, s(e) and it depends on the parabola coefficients (Table 1) and the normalized strain \(e\):

$$s\left(e\right)={a}_{1} e-{a}_{2} {e}^{ {a}_{3}}$$

where the coefficients a1, a2 and a3 allow to define the parabola equation. Design oriented models are defined by means of two equations (first portion and second rectangle portion) while research oriented models are defined by a single equation.

Table 1 Parabola coefficients values for each constitutive model
Full size table

The coefficients shown in Table 1 and 2 are those suggested by the orginal models.

Table 2 Peak, ultimate strain and specific compressive fracture energy for each constitutive model
Full size table

In this paper, the design oriented models are code models related to the parabola-rectangle and linear-rectangle models [17, 18] while the research oriented models are parabola models according to Turnšek and Cačovic [19], Sawko [20] and Capozucca [21] proposals.

In addition, the specific compressive fracture energy for masonry, gf,c can be defined, normalized on compressive strength too, according to σ(ε) equation. It is evaluated integrating the general equation of the available model [22]. This parameter could be useful to select the most suitable model to simulate a desired masonry (e.g. based on best fit of available experimental data) or to calibrate the mechanical parameters outlined in Table 2 or even the parabola coefficients outlined in Table 1, in both latter cases, altering the original models.

$${g}_{f,c}={\int }_{{\varepsilon }_{k}}^{{\varepsilon }_{u}}{a}_{1} \frac{\varepsilon }{{\varepsilon }_{k}}-{a}_{2} \frac{{\varepsilon }^{ {a}_{3}}}{{\varepsilon }_{k}^{{a}_{3}}} d\varepsilon =\frac{{a}_{1} {\varepsilon }_{u}^{2}}{2{\varepsilon }_{k}}\left( {\varepsilon }_{u}^{2}- {\varepsilon }_{k}^{2}\right)-\frac{{a}_{2} ({\varepsilon }_{u}^{{a}_{3}+1}-{\varepsilon }_{k}^{{a}_{3}+1})}{{\varepsilon }_{k}^{{a}_{3}}\left({a}_{3}+1\right)}$$

For the proposed constitutive behaviour, it is interesting to note that the compressive fracture energy of Capozucca model is equal to zero due to the brittle behaviour in compression. Design oriented models have a plastic ideal plateau, with different ductility levels, while other two research oriented models are in between, with a softening behaviour after peak, but with different amounts of specific compressive fracture energy (Figs. 1, 2).

Fig. 1
figure 1

Constitutive models adopted for the compressive behaviour of masonry with normalized strain

Full size image
Fig. 2
figure 2

Constitutive models adopted for the compressive behaviour of masonry

Full size image

2.2 Stress-block theory

The stress-block theory allows to convert the parabola-rectangle stress distribution to an equivalent rectangular stress distribution by the means of two dimensionless parameters:

  • ψ: effective height of the compressed masonry cross-section;

  • λ: dimensionless factor that correlates the real distance of centroid of nonlinear stress distribution with the neutral axis depth.

Therefore, the parameters ψ and λ are defined in dimensionless form by the equations:

$$\psi =\frac{{\int }_{{\varepsilon }_{b}}^{{\varepsilon }_{m}}\sigma (\varepsilon ) {\text{d}}\varepsilon }{{f}_{m}{ \varepsilon }_{m}}=\frac{{\int }_{{e}_{b}}^{{e}_{m}}s(e) {\text{d}}e}{{e}_{m}}$$
$$\lambda =1-\frac{{\int }_{{\varepsilon }_{b}}^{{\varepsilon }_{m}}\varepsilon \sigma (\varepsilon ) {\text{d}}\varepsilon }{{f}_{m} {\varepsilon }_{m}^{2} \psi }=1-\frac{{\int }_{{e}_{b}}^{{e}_{m}}e s(e) {\text{d}}e}{{e}_{m}^{2} \psi }$$

where em and eb represent respectively the top εm and bottom εb masonry normalized strain of the cross-section).

The normalized strain em is an input parameter of the proposed algorithm while the normalized strain eb depends on the strain em, the cross-section height t and the neutral axis depth x.

In Fig. 3, b is the width of the cross-section.

Fig. 3
figure 3

Stress-block model

Full size image
$${e}_{b}=\frac{{e}_{m}}{x} \left(x-t\right)$$

2.3 Reinforcement system

The reinforcement system is modelled as a discrete material at the extrados of the cross-section. For unreinforced masonry cross-sections, a typical reinforcement system, applied as strengthening system, is represented by the composite materials like as fiber reinforced polymer (FRP) and fiber reinforced cementitious matrix (FRCM) systems. In the last years, several experimental studies [23] have been performed in order to analyse the behaviour of the composite materials; in fact, depending on the matrix and the fibers, the tensile behaviour could be described by means of linear, bi-linear or tri-linear constitutive models.

In this paper, the strengthening system is described by a linear constitutive model characterized by an ultimate tensile stress ft, an ultimate strain εfu (corresponding to ft) and a Young modulus Ef. This assumption is based on the Italian guidelines CNR-DT 200 R1 [24] and CNR DT 215 [25] where, in the latter, the linear behaviour is justified by the matrix cracking.

$${E}_{f}=\frac{{f}_{t}}{{\varepsilon }_{fu}}$$

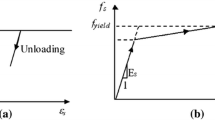
As shown in Fig. 4 (where σf and εf are, respectively, strengthening system stresses and strains), the tensile behaviour of the strengthening system is brittle; therefore, the stress is equal to zero after the achievement of the ultimate strain εfu. Also, for strengthening system the normalized strain is defined as ef = εf/εfu.

Fig. 4
figure 4

Linear stress–strain curve of the strengthening system

Full size image

The mechanical percentage of the strengthening system ω represents a useful parameter to define the properties of the strengthening system in a dimensionless form.

$$\omega = \frac{{t}_{f}}{t}\frac{{\varepsilon }_{k}}{{f}_{m}}{E}_{f}$$

where tf is the thickness of the strengthening system.

3 Cross-section analysis

The cross-section analysis is based on the Eurocode (EC2 [17] and EC6 [18]) assumptions: conservation of plain sections, continuous material does not carry tensile stresses and perfect bond (i.e. strain |εf| equal to |εb|) is assumed between the continuous material and the reinforcement (discrete) material.

The cross-section analysis is related to a generic rectangular masonry cross-section with a discrete reinforcement system, as FRP or FRCM, where the external load is represented by a concentrated axial load.

The unknowns of the problem are represented by the dimensionless neutral axis depth ξ and the dimensionless ultimate bending moment of the cross-section m.

$$\xi =\frac{x}{t}$$
$$m=\frac{M}{b {t}^{2} {f}_{m}}$$

where x is the neutral axis depth and M is the bending moment of the cross-section.

The normalized strain eb at the bottom of the cross-section depends on the normalized strain em and the dimensionless neutral axis depth ξ.

$${e}_{b}=\frac{{e}_{m}}{\xi } \left(\xi -1\right)=-\frac{{\varepsilon }_{f}}{{\varepsilon }_{k}}$$

The unknowns are solved by force and rotational equilibrium equations:

$$p=\frac{P}{b t {f}_{m}}= \frac{\psi x b {f}_{m}-{t}_{f} b {\varepsilon }_{f} {E}_{f}}{t b {f}_{m}}=\psi \xi -\omega \frac{\left(1-\xi \right)}{\xi } {e}_{m}$$
$$m=\frac{M}{{t}^{2} b {f}_{m}}=\psi \frac{x b {f}_{m}}{{t}^{2} b {f}_{m}} \left(\frac{t}{2}-\lambda x\right)+0.5 \frac{{t}_{f} b {\varepsilon }_{f} {E}_{f} t}{t b {f}_{m} t}=\psi \xi \left(0.5-\lambda \xi \right)+0.5 \omega {e}_{m}\frac{\left(1-\xi \right)}{\xi }$$

where p is the dimensionless external axial load.

If the mechanical percentage of the strengthening system ω is assumed null, the equations are those of a simple masonry cross-section without any reinforcement/strengthening system.

The cross-section analysis is based on the direct integration of the constitutive behaviour equation based on the stress-block theory. In particular, 8 cases are identified depending on the failure mode, the strengthening system normalized strain ef and the top and bottom masonry normalized strains (em, eb) of the cross-section (Table 3). The case 0 represents the case where the entire cross-section is compressed, the neutral axis depth is greater than the height of the cross-section and the top masonry strain is equal or less than the ultimate strain; this case is commonly related to low external axial load or to low masonry strains. In the case 1, the neutral axis depth is less than the height of the cross-section and the top masonry strain is equal or less than the ultimate strain. The cases 2 and 3 are respectively related to the failure of the strengthening system and the masonry. The case 4 is a purely theoretical case where both masonry and strengthening system reach the failure; this case has been studied just to analyse the theoretic behaviour of the moment–curvature M-χ chart.

Table 3 Cross-section cases for design oriented constitutive models
Full size table

The sub-cases a and b are related to the material constitutive model characterized by two functions as the design oriented parabola-rectangle and the linear-rectangle proposed by the Eurocodes (EC2 [17] and EC6 [18]).

Therefore, the research oriented constitutive models are characterized by 5 cases (Table 4).

Table 4 Cross-section cases for research oriented constitutive models
Full size table

For each case, the parameters ξ, ψ and λ are evaluated (see Appendix). The proposed equations are in closed form, therefore the convergence algorithm is prevented.

As shown in Fig. 5, the cases 2, 3 and 4 are not conventional cases due to the fact that they analyse the behaviour of the cross-section after the occurrence of the failure of either the masonry or the strengthening system. Conventionally, the cross-section analysis is interrupted when the first element reaches the failure, as described in the main codes [17, 18] and guidelines [24, 25]. This is due to the fact that one of the goals of this research project is to analyse the behaviour of the cross section in the post-failure condition.

Fig. 5
figure 5

Cross-section assumptions (strain ε can be read also as normalized strain e)

Full size image

In addition, a flow chart is proposed in Fig. 6 in order to graphically represent the logic steps related to the proposed algorithm for the cross-section analysis.

Fig. 6
figure 6

Flow chart

Full size image

The algorithm in the flow chart allows to perform the cross-section analysis for a specific masonry normalized strain em; a diagram m-χ∙t is evaluated changing em in a range between 0 and a maximum masonry strain (even higher than the ultimate masonry strain).

It is important to note that the algorithm evaluates the main parameters ψ, λ, ξ, eb and ef for each case shown in Table 3 and 4. The real case is defined by checking conditional expressions on the compatibility equations of masonry and strengthening system strain shown in Table 3 and 4. This approach allows to prevent the iterative analysis in the algorithm.

The proposed algorithm is based on closed-form equations and convergence algorithms are not required. If the compressive behaviour is described by means of parabola models, five functions are plotted and the load-history of the cross-section is defined depending on the conditional expressions shown in Table 3.

In Fig. 7, it is possible to analyse the load-history curves for a generic rectangular cross-section, for p = 0.2 and ω = 0.1, in terms of m-χ∙t diagrams and m-em diagrams, where the cross marker represents a generic point evaluated by the proposed algorithm. In this case, the strengthening system failure is reached before the masonry failure.

Fig. 7
figure 7

Cross-section analysis results for parabola (a, b) models and code models (c, d) assuming p = 0.2 and ω = 0.1

Full size image

The analyses are performed depending on the top masonry strain em and the curvature χ∙t is evaluated depending on the cross-section equilibrium. It is worth noting that dimensionless curvature is obtained by normalizing with respect to (i.e. multiplied by) t. Therefore, in the m-χ∙t diagrams (Fig. 7a, c), the load-history shows a discontinuity due to the strengthening system failure.

The proposed algorithm provides the exact solution without approximation by means of closed form-equations. The structure of the equations is easy to implement in any mathematical software or spreadsheet and the time of the analysis is immediate. In addition, it allows to easily retrieve data about the failure mechanisms of the masonry or of the strengthening system and this is an important aspect if particular constitutive models are adopted to describe the behaviour of the continuous material.

4 Parametric analysis

Several parametric analyses have been performed in order to analyse the effects of the constitutive model, the parameters and the benefits of the strengthening systems; the results are discussed in terms of m-χ∙t diagrams in dimensionless form.

In the parametric analyses, the coefficients shown in Table 1 and 2 are used to describe the compressive behaviour in the constitutive model of masonry.

The maximum investigated normalized masonry strain em is assumed equal to 6 in order to investigate comprehensively the post-peak behaviour of the cross-section.

The external axial load has been changed in the range between 10 and 50% of the ultimate axial load of the masonry cross-section; the minimum and maximum value of the range are defined depending on the common expected values. Similarly, the mechanical percentage of the strengthening system is characterized by 0 as minimum value and 0.25 as maximum value; the minimum value represents the case of the cross-section without any reinforcement/strengthening system, and it is required to analyse the benefits on the strengthening system in terms of ultimate bending moment increment. Several diagrams have been developed but only the most significative will be discussed.

In Fig. 8, the curves become faded at the exceedance of the ultimate masonry normalized strain eu.

Fig. 8
figure 8

Comparison between the constitutive models

Full size image

It is interesting to note that ultimate bending moment of the masonry cross-section is similar changing the constitutive model while significative differences are on the ultimate curvature of the cross-section, hence load-histories are completely different. In fact, the cross-sections modelled by means of the constitutive model proposed by Capozucca [21] are characterized by lower curvature ductility while the Turnšek and Cačovic [19] model provides the highest curvature, and it is fully coherent with the ductility at material level in the relative constitutive models. Furthermore, as expected, the curvature ductility of the cross-section decreases at increasing the external axial load. Similarly, in Fig. 8, it is possible to note the benefits of the strengthening system, however at higher axial loads its contribution reduces as the tension at bottom of the cross section reduces, too, with higher values of dimensionless neutral axis depth.

It is interesting to note that the bending moment of the cross section related to the ultimate masonry normalized strain eu does not correspond to the highest bending moment of its load history; this is due to the softening of the constitutive model assumed to describe the compressive behaviour. In fact, this result is not observed when the design oriented parabola-rectangle and the linear-rectangle constitutive models are adopted.

The parabola-rectangle model proposed by codes should be calibrated, for safety purposes, based on the expected values. In particular, the compressive strength of the design oriented model should be equal to the 80% of the maximum experimental compressive strength commonly adopted directly in research oriented models.

Therefore, m-χ∙t diagrams have to be properly analysed if constitutive models with softening are adopted.

In Fig. 9, parametric analysis results are shown while changing the external axial load p, assuming the constitutive model proposed by Sawko [20]. Conversely, in Fig. 10, the results while changing the mechanical percentage of strengthening system ω are shown assuming the constitutive model proposed by Turnšek and Cačovic [19]. Similarly, in Fig. 11 the parametric analyses are shown assuming the constitutive model proposed by Capozucca [21]. In Figs. 12 and 13 parametric analyses are shown depending on the two design oriented models, parabola-rectangle and linear-rectangle respectively.

Fig. 9
figure 9

Parametric analyses changing the external axial load p, assuming the constitutive model proposed by Sawko

Full size image
Fig. 10
figure 10

Parametric analyses changing the mechanical percentage of strengthening system ω, assuming the constitutive model proposed by Turnšek and Cačovic

Full size image
Fig. 11
figure 11

Parametric analyses assuming the constitutive model proposed by Capozucca

Full size image
Fig. 12
figure 12

Parametric analyses assuming the Parabola-Rectangle constitutive model

Full size image
Fig. 13
figure 13

Parametric analyses assuming the Linear-Rectangle constitutive model

Full size image

The red dashed line represents the behaviour of the cross-section without the strengthening system, and the dot curves represent the behaviour of the cross section after the masonry failure is reached.

In Fig. 10, the case with axial load equal to zero represents a specific theoretical case where the benefits of the strengthening system are remarked; in fact, the masonry cross section would have zero bending capacity, while, with strengthening system and without axial load, it is self-equilibrated by the compressive resultant of the masonry and the tensile resultant of the strengthening system.

The results of the parametric analysis allow to analyse the behaviour of masonry cross sections strengthened with composite material. In particular, the code models are mandatory in case of design process to guarantee safety according to current codes while constitutive models available in literature are useful in case of research oriented analyses, to simulate average behaviour.

In addition, different constitutive models can be adopted calibrating the parameters of the general equation s(e) depending on the fracture energy gf,c parameter to best fit the results of experimental programs.

The performed parametric analyses allow to improve the knowledge on the optimization of the main parameters affecting the strengthening systems in terms of strengthening system mechanical percentage ω and external axial load p depending on the different compressive behaviour of the masonry.

In particular, it is remarked that the strengthening system effect in terms of bending capacity decreases at increasing the external axial load p. The brittle behaviour of the cross-section increases while increasing the mechanical percentage of strengthening system ω. Increasing axial load and mechanical percentage of strengthening system, the impact of different local behaviours of masonry in compression becomes negligible, while the brittle behaviour according to the constitutive model proposed by Capozucca yields always to global most brittle behaviours of cross sections.

5 Conclusions

The analysis of structural cross sections usually requires the iterative search for the neutral axis depth, as main unknown of the problem; conversely, in this study, the main idea, simple yet effective, is that the proposed equations are closed form equations and therefore the convergence algorithm is prevented. This approach is originally implemented for Reinforced-Concrete cross-section analysis and it is useful to evaluate a large number of cross-sections and therefore the proposed tool aims to be useful in the large-scale analyses and in the risk analysis to evaluate the vulnerability of structures; in particular it allows to reduce the time and approximations of the analyses preventing iterative calculations. Similarly, it could be easily implemented in complex algorithms or software.

The proposed approach in the case of Reinforced-Concrete cross-sections requires to account for several more cases to properly evaluate the ultimate bending moment depending mainly on the nonlinear steel behaviour.

Several constitutive models for masonry are assumed in order to analyse the behaviour of cross-sections reinforced with FRP or FRCM systems; in particular, parabola-rectangle and linear-rectangle models are assumed as design oriented main code models while constitutive models proposed by Turnšek and Cačovic, Sawko and Capozucca as research oriented constitutive models available in literature. An elastic behaviour is assumed to analyse the tensile behaviour of the strengthening systems coherently with main codes and guidelines. Each possible failure mode is analysed as shown in Table 3 and 4 depending on the failure of the masonry and the strengthening system. In an unconventional manner, the behaviour of cross sections is analysed even after the attainment of the ultimate strains, accounting for progressive damage.

The parametric analyses allow to appreciate the main differences between the main proposed constitutive models, in terms of peak bending capacity, post-peak behaviour and ductility. In addition, the effects of strengthening system techniques are investigated. The parametric analyses are performed changing the mechanical percentage of strengthening system, the external axial load and the constitutive model adopted for the compressive behaviour of masonry. The strengthening system effect in terms of bending capacity decreases at increasing the external axial load, apart the obvious case of zero bending capacity in unreinforced masonry under pure bending (i.e. with zero axial load). The brittle behaviour of the cross-section increases while increasing the mechanical percentage of strengthening composite system. Increasing axial load and mechanical percentage of strengthening system, the impact of different local behaviours of masonry in compression becomes negligible on the global behaviour, but very brittle masonry has a significant impact on the global behaviour since the considered composite reinforcement is very brittle, too.

The parametric analyses, herein discussed, have been performed assuming the coefficients suggested by original models in Tables 1 and 2, but different values can be adopted by fitting of experimental results also accounting for specific compressive fracture energy.

Future works could provide closed form equations for new constitutive models. In particular, it could be accounted for the direction of compressive stress in a masonry member with respect to main bed joints orientation.