Orthotropic hygroscopic behavior of mass timber: theory, computation, and experimental validation

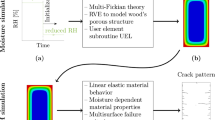
Abstract

Recent rapid improvements in laminated timber technology have led to the increased use of wood in both mid- and high-rise construction, generally posed as a more carbon-friendly alternative to concrete. However, wood is significantly more sensitive to changes in relative humidity than concrete, which may impact the sustainability and durability of mass timber buildings. Moisture cycling in particular affects not only shrinkage and swelling but also strongly influences wood creep. This sensitivity is of high concern for engineered wood used in mass timber buildings. At the same time, wood, considered as an orthotropic material, exhibits varying diffusivity in all three directions, complicating efforts to characterize its behavior. In this work, an orthotropic hygroscopic model was developed for use in laminated timber. A species database for wood sorption isotherm was created and an existing model was used to fit species-based parameters. Diffusion behavior which considers the sorption isotherm was modeled through numerical simulations, and species-dependent orthotropic diffusion parameters were identified. A database of permeability in all directions for various species was created. The resulting model is able to predict diffusion behavior in glulam and cross-laminated timber (CLT) for multiple species of the lab tests. The model also predicts the moisture ranges for a CLT panel under environmental change with parameters from these sorption isotherm and diffusion databases.

Appendices

Appendix 1: Weighted least square method

In the isotherm database, data points are not necessarily distributed evenly along the x-axis (relative humidity). Thus, the data for each curve was divided by intervals of equal size. Noted that if the data points are almost equally spaced, it is not necessary to divide into intervals or add the weight. The number of intervals, n, was defined such that each interval has a similar number of data points, $m_i$, where i = 1, 2,...n. To eliminate human bias, the same weight was assigned to each interval. This is achieved by considering the statistical weights $w_i$ of the individual data points in each interval to be inversely proportional to the number $m_i$ of data points in that interval and $\sum _{i=1}^{n} w_{i}=1$. Then ${\bar{w}} = \sum _{i=1}^n\frac{1}{m_i}$ and $w_i = \frac{1}{m_i{\bar{w}}}$ where the $w_i$ is the $i^{th}$ interval weight

Once the equal-weighted interval was obtained, the standard error s of the prediction model is defined as follows:

$$\begin{aligned} s=\sqrt{\frac{N}{N-p} \sum _{i=1}^{n} w_{i} \sum _{j=1}^{m}\left( Y_{i j}-y_{i j}\right) ^{2}} \end{aligned}$$

(18)

where $y_{ij}$ are the measured isotherm data; $Y_{ij}$ are the corresponding GAB predictions; N is the number of all data points in the database; p is the number of input parameters of the model ($p =3$ for GAB model). $\epsilon _{ij} = y_{ij}-Y_{ij}$ computes the arithmetic difference between the measured points and predictions.

Next, the least square estimation of unknown parameters is found by minimizing Eq. A1 for each individual data curve and the whole database, respectively. Once parameters are identified, it is possible to evaluate the fit and prediction quality. Two statistical indicators are introduced. The first is the coefficient of variation of the regression errors $\omega$ (%) which characterizes the ratio of the scatter band width to the data mean $\omega =\frac{s}{{\bar{y}}}$ and ${\bar{y}}=\frac{{\bar{w}}}{n} \sum _{i=1}^{n} w_{i} \sum _{j=1}^{m_{i}} y_{i j}$ where ${\bar{y}}$ represents the weighted mean value of measured points in the database. The smaller the $\omega$ is, the more accurate the fitting results.

The second term is the coefficient of determination $r^2$, which specifies the ratio of the scatter band width to the overall spread of data and designates what percentage of data variation is accounted for by the model response as $r^2 = 1-\frac{s^2}{\bar{s}^2}$.

$$\begin{aligned} {\bar{s}} = \sqrt{\frac{N}{N-1}\sum _{i=1}^n w_i \sum _{j=1}^m (Y_{ij} - {\bar{y}})^2} \end{aligned}$$

(19)

A value of $r^2=1$ indicates the prediction is closer to measured points.

Appendix 2: Expanded derivation of the finite element implementation

The primary field, relative humidity h, in an infinitesimal control volume $\Omega$ with the boundary subjected to the inflow/outflow of mass $\Gamma _h$, the moisture mass balance equation reads

$$\begin{aligned} \int _\Omega \frac{\partial u}{\partial t}d V=\int _{\Gamma _h} q_{h} d A \end{aligned}$$

(20)

where the rate term (or capacity term) $\partial u/\partial t=(\partial u/\partial h)(\partial h/\partial t)$, the diffusion flux density of water mass per unit time $q_{h}=- {\textbf{J}}\cdot {\textbf{n}}$, ${\textbf{J}}$ is the mass flux density vector per unit time, ${\textbf{n}}$ is the normal vector of the boundary where the flux passes through. The flux density vector per unit time ${\textbf{J}}$ can be associated with the relative humidity gradient $\varvec{ \nabla } h$ by an equivalent Darcy’s law ${\textbf{J}} = - \mathbf {D_u} ~ \varvec{ \nabla }h$ where $\mathbf {D_u}$ is the orthotropic moisture permeability matrix.

To derive the finite element formulation, we need to find the weak form of the governing balance equations mentioned above. For boundary flux term, by using the divergence theorem:

$$\begin{aligned} \begin{aligned}&\int _{\Gamma _h} q_{h} d A=-\int _{\Gamma _h} {\textbf{J}} \cdot {\textbf{n}} d A=-\int _{\Omega } \varvec{ \nabla } \cdot {\textbf{J}} d V \end{aligned} \end{aligned}$$

(21)

Substituting Eq. 21 into Eq. 20 yields

$$\begin{aligned} \begin{aligned} \int _\Omega \left( \frac{\partial u}{\partial t}+ \varvec{ \nabla } \cdot {\textbf{J}}\right) d V&=0 \end{aligned} \end{aligned}$$

(22)

By multiplying arbitrary test functions $\delta h$ to Eq. 22, one obtains

$$\begin{aligned} \begin{aligned} \int _\Omega \left( \delta h \frac{\partial u}{\partial t} + \delta \varvec{\nabla } h\varvec{\nabla }\cdot {\textbf{J}}\right) d V=0 \end{aligned} \end{aligned}$$

(23)

After integral by parts, Eq. 23 becomes

$$\begin{aligned} \begin{aligned} \int _\Omega \left( \delta h \frac{\partial u}{\partial t} + \delta \varvec{\nabla } h\cdot {\textbf{J}}\right) d V+\int _{\Gamma _h} \delta h q_h d A=0 \end{aligned} \end{aligned}$$

(24)

The temporal discretization of rate terms uses the Backward Euler scheme:

$$\begin{aligned} \begin{aligned} \frac{\partial u}{\partial t}=\frac{\partial u}{\partial t} \big |_{t+\Delta t}=\frac{u_{t+\Delta t}-u_{t}}{\Delta t} \end{aligned} \end{aligned}$$

(25)

where the subscript t denotes for the values in the current time step, $t+\Delta t$ denotes for the values in the next time step.

The spatial discretization of the primary field is selected to be consistent with classical Galerkin FEM, which reads:

$$\begin{aligned} \begin{aligned} h&= \sum _{i=1}^{n_{node}}N_i h_i = N_i h_i \\ \delta h&= \sum _{i=1}^{n_{node}}N_i \delta h_i = N_i \delta h_i\\ \varvec{\nabla } h&= \sum _{i=1}^{n_{node}}\sum _{j=1}^{n_{dim}}\frac{\partial N_i}{\partial x_j}h_i = \frac{\partial N_i}{\partial x_j}h_i \end{aligned} \end{aligned}$$

(26)

where $n_{node}$ is number of nodes for the element, $h_i$, and $\delta h_i$ are nodal relative humidity and associated nodal testing function at the $i^{th}$ node, respectively, $N_i$ is the shape function at the $i^{th}$ node, $\partial N_i/\partial x_j$ is the first derivative of the shape function at the $i^{th}$ node with respect to $j^{th}$ dimension. The element-wise Eq. 24 can be discretized as

$$\begin{aligned} \begin{aligned} 0&= {\sum _{i=1}^{n_{node}}\sum _{j=1}^{n_{node}}} \left\{ \int _{\Omega ^{e}} \left[ N_{i} \delta h_{i} N_{j} {\dot{u}}_j \right. \right. \\&+ \left. \left. {\sum _{k=1}^{3}\sum _{l=1}^{3}}\frac{\partial N_{i}}{\partial {{x_k}}} \delta h_{i}\left( { D_{ul}} {\frac{\partial N_j}{\partial x_{l}}h_j}\right) \right] dV \right. \\&- \left. \int _{\Gamma _h} N_{i} \delta h_{i} q_{h} d A\right\} \end{aligned} \end{aligned}$$

(27)

where $\Omega ^e$ denotes the element domain, $D_{ul}$ denotes the diffusivity in $l^{th}$ dimension. By using the Einstein notation, the summations $\sum _{i=1}^{n_{node}}$, $\sum _{i=j}^{n_{node}}$, $\sum _{k=1}^{3}$, $\sum _{l=1}^{3}$ will be simplified in equations below. Since the variational field $\delta h$ can be arbitrarily chosen, the term in the biggest braces of Eq. 27 should equal to 0, which makes:

$$\begin{aligned} \begin{aligned} 0&= \int _{\Omega ^{e}}\left[ N_{j}{\dot{u}}_j +\frac{\partial N_{i}}{\partial {{x_k}}} \left( { D_{ul}} {\frac{\partial N_j}{\partial x_{l}}h_j}\right) \right] dV \\&-\int _{\Gamma _h} q_{h} dA \end{aligned} \end{aligned}$$

(28)

Denotes Eq. 28 as function f, for the situation $f = 0$, use Newton–Raphson method to linearize the equation with the form: $f\left( x_{n+1}\right) =f\left( x_{n}\right) +\frac{\partial f\left( {x}_{n}\right) }{\partial x} \Delta x+ H.O.T$ (high order terms, neglected)

$$\begin{aligned} f\left( h_{n+1}\right) \approx f\left( h_{n}\right) +\frac{\partial f}{\partial h}\Delta h=0 \end{aligned}$$

(29)

rearranging the equations yields

$$\begin{aligned} \frac{\partial f}{\partial h}\Delta h=-f\left( h_{n}\right) \end{aligned}$$

(30)

where the subscript n and $n+1$ denotes the current and the next Newton step, respectively. The matrix on the left hand side is the Jacobian (or tangent stiffness) matrix (AMATRX in user subroutines). The vector on the right hand side is called residual (RHS in user subroutines).

Substituting the discritized rate term in Eq. (28) yields

$$\begin{aligned} \begin{aligned} f&=\int _{\Omega ^e} N_{j}\left( \frac{\partial u}{\partial h} \frac{{h_{j,t+\Delta t}-h_{j,t}}}{\Delta t}\right) dV\\&+\int _{\Omega e}\frac{\partial N_i}{\partial {{x_k}}}{ D_{ul}} {\frac{\partial N_j}{\partial x_{l}}h_j} dV \end{aligned} \end{aligned}$$

(31)

For the variables that depend on humidity, since $h_{t+\Delta t} = N_j h_{j,t+\Delta t}$, the variation with respect to the nodal humidity values can be written:

$$\begin{aligned} \begin{aligned} \frac{\partial f}{\partial {h_{i,t+\Delta t}}}&= \frac{\partial f}{\partial {h_{t+\Delta t}}}\frac{\partial (N_j h_{j,t+\Delta t})}{\partial {h_{i,t+\Delta t}}} \\&= \frac{\partial f}{\partial {h_{t+\Delta t}}} N_j \end{aligned} \end{aligned}$$

(32)

For the partial derivative of f with respect to h, the rate/capacity term reads:

$$\begin{aligned} \begin{aligned}&\int _{\Omega ^e}\frac{\partial }{\partial h_{j,t+\Delta t}}\left[ N_{j}\left( \frac{\partial u}{\partial h} \frac{{h_{j,t+\Delta t}-h_{j,t}}}{\Delta t}\right) \right] d V \\&= \int _{\Omega ^e} N_i N_j \left[ \frac{\partial ^2 u}{\partial h_{t+\Delta t}^2} \left( {\frac{ h_{j,t+\Delta t}-h_{j,t}}{\Delta t}}\right) \right. \\&+ \left. \frac{\partial u}{\partial h_{t+\Delta t}} \frac{1}{\Delta t}\right] d V \end{aligned} \end{aligned}$$

(33)

the gradient term:

$$\begin{aligned} \begin{aligned}&\int _{\Omega e}\frac{\partial }{\partial h_{j,t+\Delta t}}\left[ \frac{\partial N_i}{\partial {{x_k}}}{ D_{ul}} {\frac{\partial N_j}{\partial x_{l}}h_j}\right] d V\\&= \int _{\Omega ^e} \left[ \frac{\partial N_i}{\partial {{x_k}}}\left( N_j\frac{\partial D_{ul}}{\partial h_{j,t+\Delta t}}\right) {\frac{\partial N_j}{\partial x_{l}}h_j} \right. \\&+ \left. \frac{\partial N_i}{\partial {{x_k}}}{ D_{ul}} {\frac{\partial N_j}{\partial x_{l}}}\right] dV \end{aligned} \end{aligned}$$

(34)

Combining Eq. 33 and 34, one gets:

$$\begin{aligned} \begin{aligned} \frac{\partial f}{\partial {h_{j,t+\Delta t}}}=&\int _{\Omega ^e} \left\{ N_{i}N_{j}\left[ \frac{\partial ^2 u}{\partial h_{t+\Delta t}^2} \left( {\frac{ h_{j,t+\Delta t}-h_{j,t}}{\Delta t}}\right) \right. \right. \\&+ \left. \left. \frac{\partial u}{\partial h_{t+\Delta t}} \frac{1}{\Delta t}\right] \right. \\&+\left. \frac{\partial N_i}{\partial {{x_k}}}\left( N_j\frac{\partial D_{ul}}{\partial h_{j,t+\Delta t}}\right) {\frac{\partial N_j}{\partial x_{l}}h_j} \right. \\&+ \left. \frac{\partial N_i}{\partial {{x_k}}}{ D_{ul}} {\frac{\partial N_j}{\partial x_{l}}}\right\} d V \end{aligned} \end{aligned}$$

(35)

Gauss quadrature is a prevalent approach for numerical integration in most finite element methods, it required the space mapping from the parent domain $\varvec{\xi }$ to the physical domain ${\textbf{x}}$, however, this falls in conventional finite element scope and will not be derived here; for details, one may refer to [67].