1 Introduction

Our society stands at a crossroads. Either we fight climate change with all the means at our disposal, or within this century we will see the world as we know it ceases to exist. The long-term usability of existing structures is one way of meeting the challenges ahead. The foundation for this is a profound understanding of the material degradation processes that lead to failure in structures subjected to fatigue loading.

To tackle this task, numerous studies have been conducted in the field of concrete fatigue, addressing diverse topics such as moisture content [1,2,3,4,5], loading frequency and temperature [6,7,8], loading type [9,10,11,12,13,14,15,16] as well as loading sequence and variable amplitude [17,18,19,20,21]. Moreover, various fracture mechanics- and phenomenology-based approaches have been developed to describe the progressive degradation processes that occur during concrete fatigue [22,23,24,25,26,27,28,29].

The authors of this paper have attempted to get to the bottom of the question as well, hypothesizing that the development of fatigue damage in concrete at subcritical load levels is related to a cumulative measure of shear sliding [30]. Based on this idea and experimental observations presented in [31], a model was proposed that incorporates inelastic mechanisms formulated within the thermodynamic framework. First experimental investigations based on this hypothesis have already been performed in [9, 32]. To explore the fatigue behavior under mode II loading in more detail, and to gain more control over the applied loading, the experimental setup was modified. A comprehensive experimental program consisting of 66 monotonic, cyclic, and fatigue tests was conducted and subsequently analyzed.

2 Experimental program

2.1 Test setup and instrumentation

For a systematic and consistent investigation of the material behavior of high-strength concrete under mode II loading, the cylindrical punch-through shear test (PTST) has been re-adapted. It was originally developed by [33, 34] and evokes mode II fracture via combined shear-compression loading. Several studies in recent years have shown that the PTST is ideally suited for exploring mode II behavior [35,36,37,38,39]. Since preliminary tests on similar specimens showed the strong influence of lateral compressive stress on the fatigue life under mode II loading [9, 32], a new test setup was developed to allow simultaneous control of shear and compression loading and simple applicability in monotonic and fatigue tests.

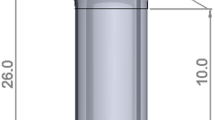
The geometry of the specimen was conceptualized to meet two main requirements: Firstly, the highest shear stresses should occur in the ligament between the notches and, secondly, it should be possible to apply a uniform compressive loading to the ligament. The specimen geometry shown in Fig. 1 fulfills these two requirements and creates a nearly straight fracture surface due to the different notch diameters. Four radial notches were created in the outer concrete ring to prevent self-confinement of the concrete specimen and to enable accurate application of the lateral compressive loading.

Fig. 1
figure 1

Specimen geometry and loading

Full size image

To apply an approximately uniform compressive loading onto the shear surface while visually monitoring the deformation and damage development, the test setup shown in Fig. 2 was developed. The entire setup consists of two parts: the lateral compression unit and the shear unit. The former provides the compressive loading (loading I), which is controlled by two hydraulic cylinders and acts on the entire circumferential surface of the specimen via four steel jaws. Two load cells are located opposite to each hydraulic cylinder to determine the exact loading throughout testing. The shear unit is responsible for the shear loading (loading II) which is applied onto the specimen via the main stamp. Full-surface support on the outer concrete ring and load introduction on the entire inner concrete cylinder ensure a nearly uniform shear stress distribution over the subsequent fracture surface and minimize the resulting tensile strains due to bending. The displacement of the crack surfaces was measured with six linear variable displacement transducers (LVDTs) attached to the bottom and top of the specimen to identify possible tilting of the inner cylinder.

Fig. 2
figure 2

Fully assembled test setup (left) and detail of the shear unit (right)

Full size image

2.2 Material preparation

A high-strength concrete with a maximum grain size of 8 mm was used for all conducted tests. An overview of the concrete composition can be found in Table 1. To evaluate the material properties, different specimens (material samples) were prepared and tested after 28 days. The compressive strength was tested on cube specimens (a = 150 mm) as 96 MPa, while the modulus of elasticity and splitting tensile strength were determined on cylinders (h/d = 300 mm/150 mm) as 39,226 MPa and 4.3 MPa, respectively.

Table 1 Concrete composition
Full size table

The specimens were cast in steel molds, cured together with the material samples for 1 day, and subsequently stored until further preparation. About a week before the test, the radial notches were cut in the specimens with a masonry saw. Afterwards, the circular notches were cut using a core drill and the top surface of each specimen was ground to be parallel to the bottom surface.

2.3 Loading scenarios

To obtain accurate information on fracture behavior, damage evolution and nonlinear shear-compression interaction, a comprehensive experimental program was adopted, which has already been used in various other experimental studies [9, 19, 20]. It provides a sound basis for a systematic calibration and validation procedure for numerical models and engineering design rules. A condensed overview of all load configurations studied in the course of this investigation is shown in Tables 2, 3.

  • LS1: The first loading scenario is used to determine the maximum shear strength τmax as a function of the simultaneously acting lateral compressive stress σc. Furthermore, it allows to obtain the monotonic stress-displacement curve and investigate the fracture behavior under different lateral compressive stresses. The test procedure is described as follows: After the lateral compression unit has applied the desired compression stress (loading I), a monotonically increasing displacement is introduced to the specimen (loading II) at a rate of 0.2 mm/min. This rate is controlled by the displacement of the main hydraulic cylinder and stops after 6 mm.

  • LS2: In the second loading scenario, a displacement-controlled cyclic loading with increasing displacement is applied to the specimen once the lateral compressive loading has been imposed. A minimum of six cycles are performed at a constant rate of 0.2 mm/min (controlled by the displacement of the main hydraulic cylinder). LS2 provides detailed information on the mode II loading and unloading behavior in relation to the concurrent compressive stress. In addition, energy dissipation and strength degradation per load cycle can be determined.

  • LS3: The third loading scenario was developed to fundamentally investigate the loading and unloading behavior at subcritical load levels without having to perform thousands of cycles. Moreover, the evolution of plastic deformation, the size of the hysteretic loops and the influence of small loading steps at subcritical load levels can be investigated. Apart from the constant lateral compressive loading, LS3 comprises load-controlled cyclic loading in a maximum of 132 cycles and a frequency of 0.1 Hz. While Smin remains constant at 5% of τmax (0.05), Smax starts at 0.50 and is increased by 0.05 every ten cycles until failure.

  • LS4: The purpose of the last loading scenario is to study concrete fatigue under mode II loading with constant amplitude in terms of fatigue life, displacement evolution, influence of concurrent lateral compressive stress, and load level. To this end, fatigue-displacement curves, Wöhler curves, and fatigue-compression curves are evaluated. Fatigue tests with a constant amplitude and a loading frequency of 5 Hz form the database. Nine different load configurations are tested and analyzed. Smax varies between 0.95 and 0.75, while Smin remains constant at 0.05. The lateral compressive loading ranges from 15 to 60 MPa.

Table 2 Overview of the investigated load configurations
Full size table
Table 3 Description of the loading scenarios
Full size table

3 Experimental results and discussion

3.1 Lateral compressive loading

To guarantee a stable level of lateral compressive stress, the hydraulic cylinders are operated with constant oil pressure. Thus, an increase in lateral compressive loading is prevented, which would be caused in a passively confined specimen due to concrete dilatation (expansion under shear loading) [9] (Table 3).

As the compressive loading is simply applied to the specimen via two hydraulic cylinders, there is no completely uniform stress distribution over the specimen circumference. The stress perpendicular to the shear surface decreases with cos(α) (Fig. 3). To estimate the effective compressive stress σc,app. acting on the entire specimen, the stress profile is smeared. On average, 90% of the maximum theoretical stress is distributed over the circumference (Fig. 3).

Fig. 3
figure 3

Comparison of the true (σc,true) and approximated (σc,app.) compressive stress distribution and representation of the LVDT arrangement

Full size image

The radial notches divide the outer ring of the specimen into four equal parts, which are all loaded with the same cylinder load Fcyl. If the total load (4 ⋅ Fcyl) is related to the shear surface ALiga and adjusted with the established smeared coefficient of 90%, the effective compressive stress σc,app. can be estimated with Eq. (1).

To evaluate the accuracy and temporal variation of the lateral compressive loading, the force of the compression unit is determined using two load cells. A comparison between the desired compressive load σc,theo. and the actual effective compressive load σc,app. (averaged over the test duration) reveals that there is a mean deviation of 6.2% in the monotonic tests and only 1.4% in the fatigue tests. Thus, it can be assumed that the lateral compressive loading can be maintained very accurately in monotonic and fatigue tests.

$$\sigma_{{c,{\text{app}}{.}}} = \frac{{4 \cdot F_{{{\text{cyl}}}} }}{{A_{{{\text{Liga}}}} }} \cdot 0.9$$
(1)

3.2 Monotonic behavior

Twelve shear tests with six different lateral compressive load levels were carried out to evaluate the influence of compressive loading on the shear strength as well as the fracture and deformation behavior. Figure 4a, b shows the stress-displacement curves of six specimens with different lateral compressive load levels. To determine the shear stress τ, the axial force Fax (loading II) was related to the shear surface area ALiga. Since ALiga decreases with increasing displacement, the surface area reduction was taken into account when calculating τ.

Fig. 4
figure 4

Stress-displacement curves of monotonic shear tests with a lateral compressive loading of: a 0, 2, and 4 MPa and b 8, 16, and 32 MPa, and c summary of the shear strengths of all LS1 tests as a function of compressive stress

Full size image

The lateral compressive stress has a significant influence on the mode II material behavior. The shear strength and post-peak strength (largely determined by friction between inner concrete cylinder and outer concrete ring) rise with increasing lateral compressive stress, which is in good agreement with the studies of [37, 40]. Small compressive stresses (≤ 2 MPa) appear to have no effect on the shear strength (Fig. 4a, c), but are sufficient to reveal post-peak response. While the pre-peak loading behavior seems to be unaffected by the lateral compressive stress (no loading irregularities, no stiffness differences), the post-peak behavior can be divided into three categories: (i) Large lateral compressive stresses (≥ 8 MPa) lead to a uniform decrease in load after reaching the maximum shear strength, whereas (ii) specimens with low lateral compressive stress show a short post-peak slipping of the inner concrete cylinder (recognized by the sudden increase in displacement and the accompanying decrease in load). This behavior is already known from previous investigations [9] and, as indicated by the dotted lines in Fig. 4a, has no effect on the shape of the stress-displacement curve. Lastly, (iii) specimens without lateral compressive loading fail immediately after reaching the maximum shear capacity and show no post-peak behavior at all.

As illustrated by the trendline in Fig. 4c, the shear strength grows sub-proportionally with increasing lateral compressive stress. This seems reasonable, since large compressive stresses would eventually lead to compressive failure. Very low scatter of the individual results suggests good homogenization of the loading, no influence of side effects, and activation of the entire shear surface.

Apart from the results shown in Fig. 4 (LS1), Fig. 5 includes the monotonic reference tests of the test series LS3 and LS4. To allow a better comparison among the tests, the lateral compressive stress was defined as a function of the cylinder compressive strength on the day of testing (σc,app./fcm,cyl). In addition, the ordinate does not describe the absolute, maximum shear stress, but a relative value, which was calculated as a function of the shear strength without lateral compressive stress (τmax,σ/τmax,0).

As can be seen in Fig. 5, above approximately 50% of the lateral compressive loading on the maximum shear stress steadily decreases. However, a negative trend is not yet discernible. Comparing the LS1 series tests with the reference tests, it is noticeable that the capacity of the reference tests is slightly greater. Since the specimens were produced on two separate days, variations in concrete properties due to curing, temperature, and concrete age cannot be excluded. Overall, however, the scatter of the results is very low (Figs. 5).

Fig. 5
figure 5

Influence of the lateral compressive stress on the maximum shear stress

Full size image

Figure 6 shows the inner concrete cylinders of three specimens with a lateral compressive loading of 0, 8, and 32 MPa. The fracture surface is always formed between the inside of the upper circular notch and the outside of the lower notch, which results in an almost straight shear surface.

Fig. 6
figure 6

Inner concrete cylinders after monotonic testing with different lateral compressive load levels

Full size image

A few differences can be observed regarding the condition of the fracture surface. While the aggregate is distinctly visible in the test on the left side (without lateral compressive loading), the concrete matrix is almost completely destroyed on the right (highest lateral compressive loading). The reason for this is friction, which starts immediately after exceeding the maximum shear strength and determines the post-peak strength. Since there was no post-peak behavior in the left test, there is no damage to the fracture surface.

After testing, it was noticed in some specimens with a lateral compressive loading of 0, 2, and 4 MPa that small spalls had formed in the outer concrete ring along the circular notch, below the shear surface. Since these spalls were on the surface of the support, it is not possible to determine at what point during the test they developed. As these spalls no longer occurred under larger lateral compressive stresses, it can be assumed that these are mode I cracks, which are caused by transverse tensile stresses perpendicular to the direct compression transfer (loading I) and result from the sudden slipping of the inner concrete core, immediately after exceeding the maximum shear strength. At higher lateral compressive loadings, these transverse tensile stresses are suppressed and thus cannot cause cracking.

Apart from this, no other visible cracks developed: neither in the outer concrete ring (wing cracks [38] or doughnut fractures [36, 41, 42]), nor in the inner concrete cylinder (wing cracks [36, 41, 42]), or additional cracks along the shear surface (macroscopic en échelon fractures [36, 41, 42]).

3.3 Post-peak cyclic behavior

For a time-efficient evaluation of the dissipative mechanisms under repeated loading, low-cycle tests with displacement-controlled loading and unloading steps at various displacements are suitable. To investigate the influence of the lateral compressive loading on the dissipative mechanisms, five tests were performed with a lateral compressive loading of 15, 30, 45, 60, and 75 MPa, respectively (Fig. 7).

Fig. 7
figure 7

Stress-displacement curves under cyclic mode II loading (LS2) with a lateral compressive loading of: a 15 MPa, b 30 MPa, c 45 MPa, d 60 MPa, and e 75 MPa as well as f the corresponding damage evolutions

Full size image

The stress-displacement curve under cyclic mode II loading behaves very similarly to the static reference test. In particular, the pre-peak unloading step does not seem to have a large influence on the overall shear behavior. Looking at the post-peak regime, however, a clear influence on the shear stress with increasing displacement is noticeable. The reason for this could be the kinetic friction between the shear surfaces. For lateral compressive loadings up to 45 MPa, the loading and unloading results in better interlocking of the grain structures and thus an increase in transferred shear stress.

For a lateral compressive loading above 45 MPa, the structural behavior becomes unstable. As can be seen in Fig. 7d,e, there is no longer a clear increase in shear stress in the post-peak regime, the overall shape of the curve becomes more discontinuous, and the hysteretic loops expand. The positive influence of compressive stress on kinetic friction seems to diminish with increasing compressive loading. Furthermore, the size of the hysteretic loops decreases for displacements w > 3.5 mm. It therefore stands to reason that the mode II capacity is exhausted at this point, and this stress is purely frictional.

In previous research [19, 43], the reloading stiffness decrease is usually used to describe the damage development and is formulated by the damage parameter ω (Eq. (2)).

$$\omega = 1 - \Delta E = 1 - \frac{{E_{i} }}{{E_{0} }}$$
(2)

Since preliminary studies have shown that the stiffness is significantly influenced by the lateral compressive stress [9] and thus the parameter ω is misleading in the context of shear tests, the following discussion will refer exclusively to the stiffness reduction ∆E.

The first unloading step (pre-peak) leads to an increase in reloading stiffness. This behavior under cyclic loading of shear tests is already known from [44, 45]. E0, therefore, refers to the stiffness of the first reloading and not the initial stiffness. To determine the reloading stiffness, the respective slope of the reloading branch was calculated between 15 and 85% of the maximum stress at each step (Fig. 7d).

Figure 7f reveals that there is no significant decrease in reloading stiffness throughout the tests. For tests with lateral compressive loadings up to 45 MPa, ∆Emax varies between 20 and 40%, which corresponds nicely with the results in [9, 44]. The reason for the low stiffness reduction is the lateral compressive loading, which compresses the shear surfaces even after the maximum shear strength has been exceeded, thus preventing further decrease in stiffness. For tests with lateral compressive loads above 45 MPa, ∆E decreases significantly, which is already visible from the unstable structural behavior (Fig. 7d,e). Noteworthy is the anomaly in test LS2.5, which is attributed to an unscheduled minor compressive reloading of ~ 2 MPa in the third load step (comparable to the load jumps in Fig. 8f at a lateral compressive loading of 75 MPa).

Fig. 8
figure 8

Stress-displacement curves under cyclic step-wise increased mode II loading (LS3) with a lateral compressive loading of: a 15 MPa, b 30 MPa, c 45 MPa, d 60 MPa, and e 75 MPa and f the corresponding fatigue-compression curves

Full size image

3.4 Pre-peak cyclic behavior

For a fundamental investigation of the loading and unloading behavior under compressive mode II loading at subcritical load levels, without having to perform thousands of cycles, LS3 was employed. As with LS2, LS3 consists of five tests with various lateral compressive load levels.

In each stress-displacement curve in Fig. 8a–e, both the step-wise increasing cyclic loading and the nonlinear deformation behavior can be observed. Furthermore, Fig. 8f shows that the lateral compressive loading can be kept stable even with repeated cyclic loading. Although there are minor fluctuations, the mean deviation never exceeds 2%.

A fatigue-displacement curve for test LS3.3 (lateral compressive loading of 45 MPa) is depicted in Fig. 9a to illustrate the displacement evolution. In a fatigue-displacement curve, the strains at Smin and Smax of each cycle are plotted as a function of fatigue life. All conducted tests show the same overall behavior, regardless of the lateral compressive loading: little but steadily increasing plastic displacement in the first loading cycles (along with elastic displacement at upper loading due to the loading steps) and the expected nonlinear increase in displacement towards the end of the test.

Fig. 9
figure 9

a Fatigue-displacement curves under cyclic step-wise increased mode II loading (LS3) with a lateral compressive loading of 45 MPa as well as b stiffness degradation development and c stiffness development of all conducted LS3 tests

Full size image

To visualize the pre-peak damage caused by repeated shear loading, the reloading stiffness was determined for every loading cycle (Fig. 9b, c). The overall development is similar for almost all tests. While the stiffness increases slightly at first, it drops to about 80% towards failure. This behavior is already known from other investigations [9, 44]. Backers et al. [44] explains the late decrease in stiffness with the damage of the material structure, which does not occur until 80% of the maximum shear strength is reached. The concrete therefore essentially remains uncracked up to this point, and the final fracture zone is formed only shortly before the maximum strength is reached. Test LS3.5, which was subjected to a lateral compressive loading of 75 MPa, was the only test to show a considerably more pronounced damage development throughout the test (60% drop in stiffness). As in the LS2 test series, very high lateral compressive stresses seem to have a negative influence on the material behavior.

Figure 9c reveals a basic correlation between lateral compressive loading and reloading stiffness. Accordingly, a greater lateral compressive loading leads to a greater initial stiffness E0. Interestingly, all tests seem to eventually tend towards a reloading stiffness of about 180 N/mm, even though E0 of LS3.1 was about half the stiffness of LS3.5.

3.5 Fatigue behavior under constant amplitudes

To investigate the fatigue behavior of concrete under cyclic shear loading with simultaneous constant lateral compressive loading, 32 PTSTs in two separate test campaigns with a total of nine different load combinations were conducted and evaluated. In all tests, Smin was set to 5% of the maximum shear strength τmax, while Smax varied between 75 and 95%. It should be noted that both Smin and Smax always refer to the shear strength under the respective lateral compressive loading. The increase in shear strength due to a lateral compressive loading (cf. Section 3.2) is therefore taken into account.

For each subset (15, 30, 45, and 60 MPa) within each campaign of LS4, at least two monotonic reference tests were performed to determine τmax. Unfortunately, only one reference test could be conducted for the subset LS4.6. Therefore, the reference strength of LS4.6 is composed of an arithmetic mean of the one conducted reference test result and the calculated maximum shear strength determined with the help of the relationship shown in Fig. 6. For the tests LS4.5 -10, -11 and -12, which were tested for up to 10 million cycles, two additional reference tests were conducted following the fatigue tests to account for the increase in concrete strength.

The first LS4 test campaign consisted of twelve individual fatigue tests designed to estimate the influence of lateral compressive stress on the shear fatigue life. The lateral compressive loading was kept constant throughout the entire test, while the shear loading oscillated sinusoidally around a mean load (Smin = 0.05 and Smax = 0.85). To provide an overview of the obtained test results, stress-displacement curves, fatigue-displacement curves and stiffness degradations are shown in Fig. 10. Here, each row represents a specific lateral compressive load level.

Fig. 10
figure 10

a–d Stress-displacement curves under fatigue mode II loading with various lateral compressive loadings (LS4), e–h fatigue-displacement curves, and i–l stiffness degradations of the first test campaign

Full size image

The stress-displacement curves reveal a uniform and continuous loading and unloading behavior, while the strain at shear fatigue failure roughly corresponds to the strain of the softening branch of the reference test at the corresponding load level, comparable to [46, 47]. Noteworthy is that the loading stiffness of the fatigue tests is constantly greater than the loading stiffness of the monotonic reference tests, which is mainly due to the significantly greater loading rate.

Displacement development throughout the fatigue life shows the typical, three-phased S-curve, with an approximately linear increase in the second phase. Apart from the greater strain difference between Smin and Smax (which results from the greater loading), there is no discernible difference in the displacement development among lateral compressive stress levels.

The loss in reloading stiffness is comparatively mild. Over the entire fatigue life, there is a decrease of about 30% across all studied lateral compressive loadings, which correlates well with previous investigations [9]. As with LS2 and LS3, a slightly stronger decrease in stiffness is evident for higher lateral compressive loadings.

A detailed overview of the applied loads and the achieved fatigue lives can be found in Table 4. The compressive loading σc,mean was determined with the help of the two load cells and corresponds to the arithmetic mean of the lateral compressive stress σc,app. at upper loading. Smax was calculated using the arithmetic mean of the upper loading and the respective reference shear strength τmax; hence the values deviate slightly from each other. Figure 11a depicts the test results in respect to the lateral compressive loading. Apparently, the lateral compressive stress has no influence on the fatigue life.

Table 4 Summary of all conducted fatigue tests (LS4)
Full size table
Fig. 11
figure 11

a Fatigue life in respect to the lateral compressive loading (shear fatigue tests of the first campaign), b Wöhler curve (shear fatigue tests of the second campaign), and c fracture development including wing crack formation

Full size image

In other words: The fatigue life scales proportionally with the monotonic shear strength. Furthermore, it appears that the scatter of the results decreases with increasing lateral compressive loading. The reason for this could be an increasing homogenization of the stresses along the shear surface with increasing lateral compressive loading.

Following this first test campaign, further tests were conducted in a second campaign to determine the influence of the upper loading (Smax). A total of 21 tests were planned for this second campaign. Unfortunately, test LS4.6-9 was pre-damaged and could not be tested.

The results of the 20 remaining tests are shown in Fig. 11b and Table 4. To ensure that the lateral compressive loading has no influence on the fatigue life – even across various upper loadings – tests were conducted with a lateral compressive loading of 15 and 30 MPa.

A smaller upper loading has the expected positive influence on the fatigue life. Figure 11b shows that this influence can be assumed to be nonlinear – smaller upper loadings thus lead to a disproportionately strong increase in fatigue life. Since the tests LS4.5-11 and LS4.5-12 were stopped before failure, the disproportionate trendline in Fig. 11b is even underestimated. The tests with a lateral compressive loading of 30 MPa confirm the findings of the first campaign and indicate that there is no influence of the lateral compressive stress on the fatigue life even across varying upper loadings.

Furthermore, Fig. 11b depicts an empirical approximation of the fatigue life under pure compressive loading according to FIB Model Code 2010 [48] – which is applicable for log(N) ≤ 8 (Eqs. (3) and (4)). As described in [48], this approximation represents a mean curve of numbers of cycles to failure.

$$\log \left( N \right) = \frac{8}{{\left( {Y - 1} \right)}} \cdot \left( {S_{\max } - 1} \right)$$
(3)
$$Y = \frac{{0.45 + 1.8 \cdot S_{\min } }}{{1 + 1.8 \cdot S_{\min } - 0.3 \cdot S_{\min }^{2} }}$$
(4)

The test results indicate that concrete under mode II loading has a greater fatigue life than concrete in standard cylindrical specimens under compressive loading, where we expect a uniaxial compressive stress state. While this difference is still small for high upper loadings, significant deviations of about three orders of magnitude occur for Smax = 0.75.

The fracture behavior under fatigue loading is largely comparable to the fracture behavior under monotonic loading. As shown in Fig. 5, the fracture surface is always formed between the inside of the upper circular notch and the outside of the lower notch, which results in an almost straight shear surface. The increased deterioration of the fracture surfaces, as a result of higher lateral compressive loading, can also be recognized.

In the tests LS4.6-7 and LS4.6-8 – which were subjected to a lateral compressive loading of 30 MPa and were tested for a relatively large number of cycles with log(N) ≥ 5 – secondary cracking occurred in addition to the fracture of the shear surface. A similar fracture behavior was also observed in the LS4.3 and LS4.4 test series. Figure 11c shows the final fracture pattern and the analyzed schematic crack development: (1) Initially, as the number of cycles progresses, minor spalling of the outer concrete occurs in the area of load introduction, caused by the transverse tensile stresses at the edge of the main stamp. Since this spalling concerns less than 1.0 mm of concrete, it has no effect on the further fracture process. (2) Subsequently, the shear surface forms steadily and gradually combines microcracks to form a continuous macrocrack. Simultaneously, tensile stresses occur near the lower notch due to a minor bending of the PTST. (3) With long loading periods or high lateral compressive loadings, these tensile stresses lead to tensile fatigue of the concrete, which eventually leads to an advancing tensile crack. [36] already noted this behavior on statically loaded granite specimens and called this fracture wing crack. (4) As the number of cycles increases, this wing crack grows steadily and eventually coalesces, causing the lower part of the concrete cylinder to separate from the upper part. (5) Due to the inclined shape of the wing crack, the final failure of the test provokes the chipping of the concrete between the wing crack and the shear surface.

Even though this behavior does not represent the anticipated fracture pattern, it has no effect on the overall shear fatigue behavior. Since the wing crack starts below the notch, the shear surface remains intact for most of the test. It is only the failure of the shear surface that leads to the chipping of the concrete and the associated disturbed fracture pattern.

4 Conclusions

Within the scope of this paper, experimental tests on the monotonic, cyclic, and fatigue behavior of high-strength concrete under mode II loading – with active control of lateral compression – were presented and analyzed. Based on the presented investigation, the following conclusions can be drawn:

  • The newly developed test setup is capable of introducing a steady compressive-shear stress onto the ligament while actively controlling both the shear and compressive loading with high precision.

  • The positive influence of the lateral compressive stress on the maximum shear strength was confirmed and quantified.

  • In low-cycle shear tests, it was shown that the material behavior in the post-peak regime is largely influenced by crack friction.

  • Shear tests with a step-wise increased cyclic loading showed that the pre-peak loading and unloading behavior is not significantly affected by the applied lateral compressive stress, but is evident in an increased load stiffness.

  • Fatigue test results indicate that the influence of the lateral compressive loading on the shear fatigue life scales proportionally to the influence on the monotonic shear strength.

  • The scatter of the shear fatigue tests seems to reduce with increasing lateral compressive stress.

  • The strain at shear fatigue failure roughly corresponds to the strain of the softening branch of the reference test at the corresponding load level.

  • Concrete under mode II loading tends to have a greater fatigue life than concrete in standard cylindrical specimens under compressive loading.

One potential application for the conducted investigation is the refinement of a promising theory that represents the fatigue behavior of concrete on a thermodynamic basis [30], can be implemented in numerical models [32, 40], and could eventually serve as one element in a complex, all-encompassing mechanical model such as [49]. For a successful implementation, the shear fatigue behavior needs to be further investigated. Since the studies have shown that the developed test setup is ideally suited for this purpose, further investigations on material- and load-related influences are mandatory. In particular, scatter-sensitive investigations on the load sequence effect show great potential.