Validation of reinforced concrete bond stress–slip models through an analytical strain distribution comparison

Abstract

The bond and slip between concrete and the reinforcement bars, cover a key role in the inter-material force transfer of Reinforced Concrete (RC) structures. In light of the lack of tools able to thoroughly inspect the inner workings of RC structures and to extract reliable bond stress values, modern bond stress–slip (Bond–slip) models are often inaccurate and in contradiction with each other. Considering the recent surge of novel hyper-performant strain sampling tools (Distributed Sensing for example), their application for the creation of novel and physically accurate Bond–slip models is just a matter of time. This being said, one of the main reasons behind the modern coexistence of multiple inaccurate and at times contradictory Bond–slip models is the absence of a tool that has allowed researchers to rapidly corroborate and calibrate their newly created models. To this end, the present article proposes such a Bond–slip validation tool for RC elements. This one is designed to extract reinforcement strain profiles at any given load level on the grounds of a specific bond–slip law and geometrical inputs. Said profile is then compared against an experimentally extracted one based on specimens with identical geometrical features. The performance of the validation tool is demonstrated through an application to six existing bond–slip models. Granted the proposal of validation tools is paramount for the future of the discussion on bond–slip modelling, stress-transfer analyses and serviceability of RC structures, the here proposed validation tool is a first significant step in that direction.

1 Introduction

Safety and serviceability are the two essential criteria for the design of reinforced concrete (RC) structures. The latter deals with their working conditions, overall performance and usefulness (intended as their use as originally designed) along their service lives. Serviceability may be evaluated under various headings (deflection, excessive vibration, fire resistance, thermal movements, appearance, etc.) but, in the context of performance-based design, the key requirements are met by controlling deflection and cracking. To this day, the most commonly used approaches to performance-based serviceability analyses assume either a perfect interaction between concrete and deformed reinforcement bars (rebars) or a simplified constant bond relation i.e., the mean strain approach. Whilst these simplifications are reasonable in load bearing capacity analyses, they however should be considered inadequate when the serviceability of RC structures is considered. Furthermore, the approach to the definition of model parameters of said simplified methodologies usually resorts to theoretical, empirical or numerical solutions. This leads to the creation of numerous models with little to no congruence with each other [1,2,3]. Differently so, modern research advocates for a different, experiment-based approach to serviceability analyses called the stress transfer approach (also referred to as partial interaction or discrete crack-based approach). Nowadays, such method is commonly considered as the most realistic depiction of the inner workings of RC structures such as its bond–slip mechanics, tension stiffening effect and crack development [4,5,6,7]. The model acknowledges the presence of a concrete-rebar bond resulting from frictional resistance, chemical adhesion and mechanical interlock between the two materials [4]. Critically, the model suggests that, whenever slip starts occurring between the rebars and its surrounding concrete, an interaction starts developing on their interface i.e., a force transfer commonly referred to as bond stress τ. This one acts against any concrete-rebar relative movement and increases proportionally to the axial force applied on the rebar. On a side note, bond stress is considered to be the result of the mechanical shear interlock between the profiled ribs of the rebars (deformed bars) and the concrete, despite 20% of its total is attributable to the frictional resistances and chemical adhesion [8].

In the last decade, several researchers studied the concrete-rebar bond mechanism, proposing bond stress models related only to the slip between the two materials [9, 10], to the concrete strength [4, 11, 12], to the geometrical features of the case study RC specimen [13] such as concrete cover, rebar diameter and rebar embedment length. Yet, in light of the lack of available tools able to thoroughly inspect the inner workings of RC structures and to extract reliable bond stress values, modern bond stress–slip (henceforth referred to as bond–slip for simplicity’s sake) models are often inaccurate and in contradiction with each other [1,2,3]. To this day, the lack of an adequate bond–slip law embodies the major drawback of the above mentioned stress transfer approach. As such, the authors rely on the importance of furthering the research in this field.

Several experimental testing techniques have been employed for the study of bond stress inside RC structures. These are single pull-out test [14], beam end test [15], beam anchorage [16] and beam splice tests [17] (of which the first two are the most common ones). All of them are based on the measured force–displacement relationship relative to a rebar being pulled out from the concrete and all provide average bond stresses throughout the anchorage length in terms of slip. According to modern research [4, 5], though, these tests fail to provide the real bond condition because of support-induced compressive stress fields in the concrete, of the non-uniform distribution of bond stress around the anchorage length and of the instigation of lateral confining pressure at the concrete-rebar interface. Alternatively, a more realistic way to study the bond–slip relationship is by means of a double pull-out test on RC tension chords (henceforth referred to as RC chord). The reader should note that these kind of specimens are often used to illustrate cracking, deformation and bond behavior of RC structures, thanks to their simplicity and reasonably good representation of the distribution of internal forces and strains in the tensile zones of RC structures [18]. A double pull-out test on RC chords provides a realistic picture of the force transfer mechanism between rebars and concrete [19] which, in turn, allows the extraction of accurate studies on bond stress and slip values. Note that, the most common failure occurring during double pull-out tests is the rupture of the embedded rebar occurring beyond its yielding stage.

Crucially, double pull-out tests rely on the knowledge of the longitudinal strains in the embedded rebar/s, thus the need to deploy strain monitoring tools on them. To this day, said deployment has been achieved by means of several strain monitoring tools, the most common of which are electrical strain gauges [6, 13, 20, 21]. Despite the ensuing accuracy of the strain measurements, the deployment of these sensors requires transversally sawing the rebar, incising grooves, gluing and soldering. Overall, the procedure is time consuming, complex and delicate, in addition to providing measurements with relatively low spatial resolution (around 20 mm). The introduction of Optical Fiber Sensors (OFS) to structural engineering experimentation offered a practical solution to such limitations. Two of the most popular OFS are Optical Fiber Bragg Grating (FBG) sensors [5, 22] and Distributed Optical Fiber Sensors (DOFS). The latter embody the larger potential of the two, as extremely thin sensors (down to 125 µε), can achieve completely distributed measurements (modern interrogation units can attain a spatial resolution of 0.63 mm) and with measurement frequencies of 250 Hz [23]. Recent applications of OFS in the civil and structural engineering field saw their use for the superficial [24] and embedded [25] monitoring of strains and cracks of RC structures, concrete shrinkage and shrinkage-induced compressive strains in embedded rebars [26], tension stiffening [27] and more [28]. Crucially, DOFS were also reported to be effective tools for the study of bond–slip occurring inside RC tension chords [3, 29,30,31]. Considering the rapid popularity of DOFS both in the Structural Health Monitoring field [32, 33] and in the context of structural engineering laboratory experimentation [28], their application for the creation of novel and physically accurate bond–slip models is just a matter of time.

One of the main reasons behind the modern coexistence of multiple inaccurate and at times contradictory bond–slip models (instead of a unique physically substantiated one) is the absence of a tool that has allowed researchers to corroborate and calibrate their newly created models. The presence of a globally approved validation tool would allow to speed up the otherwise long and strenuous process of mathematically and experimentally corroborating, fine tuning and comparing every novel model proposal against other similar ones. As such, the proposal of validation tools is paramount for the future discussion on bond–slip modelling, stress-transfer analyses and, finally, serviceability of RC structures. To this end, the authors here propose a validation tool capable of evaluating the performance with which a bond–slip model assesses the bond and the slip occurring in the interface between deformed rebars and concrete. Given the geometrical and mechanical characteristics of a RC chord, said tool is capable of extracting the specimen’s reinforcement strain profile on the grounds of a case study bond–slip model (at any load). If the bond–slip model is accurate in its predictions, the extracted profile coincides with the one extracted experimentally from a RC chord with the same features as the ones inserted in the validation tool. If instead the calculated and experimental profile do not match, the validation tool quantifies their proximity or lack thereof, indicative of the accuracy of the model. In the present article, the authors will first detail the mathematical and computational steps behind the validation algorithm and then proceed to corroborating it by means of six existing bond–slip models (Nilson [9], Mirza and Houde [10], Shima et al. [11], Kankam [13], Model Code 2010 [4] and Barbosa and Filho [12]) and double pull-out test experimental data. This allowed to assess the performance of each of the above bond–slip models and, in turn, prove the efficiency of the validation tool.

2 Fundamentals of the validation algorithm

In the present section, the authors explain the theory behind the creation of the validation algorithm and sequentially display its fundamental equations. Furthermore, these are combined in a flow chart which schematically represents the logical steps and functioning of the validation tool. The reader should keep in mind that the present bond–slip validation tool deals with the interaction between concrete and deformed rebars.

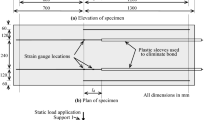
As previously mentioned, the validation of bond–slip models can be performed through the comparison of their respective strain distribution graphs and actual experimental data. The first step towards such comparison was, therefore, the calculation of the reinforcement strain distribution under any specific load and on the grounds of a given bond–slip model. To this end, the authors decided to employ the stress transfer approach—generally considered as the most accurate representation of the composite behavior of a RC structure. Note that, for both the numerical and experimental approach, the authors analyzed these distributions on short RC chords (see Fig. 1a) of general length $(L)$. A RC chord of length equals to the spacing between two primary cracks is considered representative as the average behavior of the entire RC member. From the standpoint of strains present in the constitutive materials, the ends of the RC chord depicts of the situation occurring in two consecutive primary cracks of a standard RC element. That is, nil concrete strain (${\varepsilon }_{\mathrm{c}}$) —assumed absent in a cracked cross-section–and the applied load completely carried by the steel. Indeed, assuming satisfactory the performance of the mean strain approach in providing an accurate average deformation behavior of a full RC element. Therefore, the algorithm requires the input of physical and mechanical characteristics of the full RC element, along with the reinforcement strain at the element end section (${\varepsilon }_{\mathrm{s}}$). Additionally, the following considerations were made:

• The concrete strains at the opposite ends of the RC chord are equals to zero (end-sections in Fig. 1a);

• In any cross section between the two end-sections, the load transmitted to the specimen is shared between the reinforcement and the concrete;

• The change in cross-sectional area of the element is negligible throughout all the test.

Fig. 1

Segment division in half of the specimen and free body diagram of a segment

Acknowledging the presence of symmetry in the RC chord (relative to its mid-section as in Fig. 1a), the analyses were performed on only half the block as in Fig. 1b. Here, one can see how the RC block is further subdivided into $n$ number of equal segments, each of length $\Delta x$. The total number of segments can dictate the fineness, but also the complexity of the analysis. As described later, a series of iterative calculations were sequentially performed on each segment, starting from the right end of the specimen until its mid-section. As visible further on, the calculation of certain physical parameters on the left end-section (henceforth referred to as left end) or the right end-section (henceforth referred to as right end) will allow to extract the values of the steel strain along its embedded length.

Starting from the right end of the specimen, the first segment under analysis is Segment 1 (as in.

Fig. 1b). Here, the equilibrium of forces is represented by Eq. 1 with (${N}_{\mathrm{s}}$) the resisting force in the reinforcement and (${N}_{\mathrm{c}}$) the resisting force in the concrete and ($P$) the applied tensile force.

$$ N_{{\text{s}}} + N_{{\text{c}}} = P $$

(1)

If to isolate segment 1 (see Fig. 1c), Eq. 1 can be rewritten as in Eq. 2 with (${\varepsilon }_{\mathrm{s},1}$) the steel reinforcement strain on the left end of the segment, (${E}_{\mathrm{s}}$) the steel modulus of elasticity, (${A}_{\mathrm{s}}$) the steel cross-section area, (${\varepsilon }_{\mathrm{c},1}$) the concrete strain on the left end of the segment, (${E}_{\mathrm{c}}$) the concrete modulus of elasticity and (${A}_{\mathrm{c}}$) the concrete cross-section area.

$$ \varepsilon_{{{\text{s}},1}} E_{{\text{s}}} A_{{\text{s}}} + \varepsilon_{{{\text{c}},1}} E_{{\text{c}}} A_{{\text{c}}} = P $$

(2)

If to define ($P$) along the lines of the general expression ${\varepsilon }_{\mathrm{s}}{E}_{\mathrm{s}}{A}_{\mathrm{s}}$ in a general section ($\mathrm{i}$), Eq. 2 can be generalized for all segments of our model as in Eq. 3.

$$ \varepsilon_{{{\text{s}},i}} E_{{\text{s}}} A_{{\text{s}}} + \varepsilon_{{{\text{c}},i}} E_{{\text{c}}} A_{{\text{c}}} = \varepsilon_{{{\text{s}},i - 1}} E_{{\text{s}}} A_{{\text{s}}}|\,\, i = 1,2, \ldots ,n $$

(3)

Henceforth the notation $| i=\mathrm{1,2},\dots ,n$ will not be repeated in every equation as parameter ($i$) does not change definition. Note that ($\varepsilon_{{{\text{s}},i - 1}}$) is the steel strain present on the right end of the general ith segment whilst ($\varepsilon_{{{\text{s}},i}}$) is the steel strain on its left end (Fig. 1d). Also, for i = 1, $\varepsilon_{{{\text{s}},i - 1}}$ (aka $\varepsilon_{{{\text{s}},0}}$) refers to a steel strain present on the right end of the first segment i.e., a rebar cross section that is not embedded inside concrete. As such ${\varepsilon }_{\mathrm{s},0}$ is calculated as in Eq. 4.

$$ \varepsilon_{{{\text{s}},0}} = \frac{P}{{E_{{\text{s}}} A_{{\text{s}}} }} $$

(4)

For a general ith segment, Eq. 5 describes the equilibrium of forces on the interface between steel and concrete (represented in Fig. 1d) where (${\tau }_{i}$) is the acting bond stress and ($\varnothing$) is the reinforcement diameter in mm.

$$ \varepsilon_{{{\text{s}},i}} E_{{\text{s}}} A_{{\text{s}}} + \tau_{i} \pi \emptyset \Delta x = \varepsilon_{{{\text{s}},i - 1}} E_{{\text{s}}} A_{{\text{s}}} $$

(5)

The reader will remember that for i = 1–the first segment—the right portion of the equation (${\varepsilon }_{\mathrm{s},i-1} {E}_{\mathrm{s}} {A}_{\mathrm{s}}$) can be simply substituted with ($P$). In order to calculate the steel strain of any section, aka determining the steel strain (${\varepsilon }_{\mathrm{s},i}$), Eq. 5 can be reformulated as Eq. 6.

$${\varepsilon }_{\mathrm{s},i} =\frac{{\varepsilon }_{\mathrm{s},i-1} {E}_{\mathrm{s}} {A}_{\mathrm{s}}-{\tau }_{i} \pi \varnothing \Delta x}{{E}_{\mathrm{s}} {A}_{\mathrm{s}}}$$

(6)

All parameters to solve Eq. 6 are known with the exception of (${\tau }_{i}$). For i = 1, ${\tau }_{1}$ is directly determined from the given bond–slip law ($\tau -S$) and an assumed value of slip ($S$) on the right end of the segment i.e., S₀. This allows for the calculation of ${\varepsilon }_{\mathrm{s},1}$.

For i = 1 and with ${\varepsilon }_{\mathrm{s},1}$ known, ${\varepsilon }_{\mathrm{c},i}$ can be determined rearranging Eq. 3 as in Eq. 7.

$${\varepsilon }_{\mathrm{c},i}=\frac{{\varepsilon }_{\mathrm{s},i-1}{E}_{\mathrm{s}} {A}_{\mathrm{s}}-{\varepsilon }_{\mathrm{s},i} {E}_{\mathrm{s}} {A}_{\mathrm{s}}}{{E}_{\mathrm{c}} {A}_{\mathrm{c}}}$$

(7)

For i = 1 and with (${\varepsilon }_{\mathrm{c},i}$) known, (${S}_{i}$) can be calculated as in Eqs. 8 and 9 where ($\Delta {S}_{i}$) is the variation in slip between the two ends of a segment.

$${S}_{i}= {S}_{i-1}-\Delta {S}_{i}$$

(8)

$$\Delta {S}_{i}=\Delta x\left[\frac{{\varepsilon }_{s,i}-{\varepsilon }_{s,i-1}}{2}-\frac{{\varepsilon }_{\mathrm{c},i}-{\varepsilon }_{c,i-1}}{2}\right]$$

(9)

Note that, for i = 1, (${\varepsilon }_{\mathrm{c},i}$) aka (${\varepsilon }_{\mathrm{c},0}$) is equals to 0 since on the right end of the first segment there is no concrete (Fig. 1c). Finally, for i = 1 and with (${S}_{i}$) known, the analysis of the parameters of the next segment (i + 1) can start with determining the bond stress ${\tau }_{i+1}$ by means of the adopted bond–slip model.

Note that all the above equations exist on both ends of each segment, except for (${\tau }_{i}$) that is constant along all of its length $\Delta x$ (see Fig. 1c, d). That is why, whenever dealing with Eq. 6 for i > 1, the new value of ${\tau }_{i}$ (previously named ${\tau }_{i+1}$) can be expressed as an average of the bond stresses present at the ends of the segments as in Eq. 10.

$${\varepsilon }_{\mathrm{s},i} {E}_{\mathrm{s}} {A}_{\mathrm{s}}+ \left(\frac{{\tau }_{i}+{\tau }_{i-1}}{2}\right) \pi \varnothing \Delta x={\varepsilon }_{\mathrm{s},i-1} {E}_{\mathrm{s}} {A}_{\mathrm{s}} | \quad i=\mathrm{2,3},\dots ,n$$

(10)

Finally, Eq. 10 can be rewritten as Eq. 11 to extract the reinforcement strain of the succeeding section ${\varepsilon }_{\mathrm{s},i}$ for i > 1.

$${\varepsilon }_{\mathrm{s},i}= {\varepsilon }_{\mathrm{s},i-1}- \left(\frac{{\tau }_{i}+{\tau }_{i-1}}{2}\right) \frac{\pi \varnothing \Delta x}{{E}_{\mathrm{s}} {A}_{\mathrm{s}}}| \quad i=\mathrm{2,3},\dots ,n$$

(11)

In the following sections, all the parameters can be calculated by repeating the calculations from Eqs. 7 to  11 updating the parameters of the ith segment, thus proceeding in a loop. Through this methodology, it is possible to calculate the steel strain values present along all the cross sections of the rebar, thus defining a steel strain distribution. The entirety of this process is represented in the form of a flow chart in Fig. 2.

Fig. 2

Flowchart of the validation algorithm aimed at determining a strain distribution on the grounds of an iterative process grounded on a set bond-slip model

As visible in the flowchart, the algorithm requires as input data the (1) features of the RC specimen under analysis ($b,d,L,{E}_{\mathrm{s}},{E}_{\mathrm{c}},\varnothing$), the (2) rebar strain at the end of the specimen ${( \varepsilon }_{s0})$ and the (3) study case parameters i.e., the length of the segments on which the analysis will be run ($\Delta x$) and the case study bond–slip model. The reader should keep in mind that, whenever opting for a particular segment size ($\Delta x$), a “spatial resolution” is also automatically determined. Clearly, a small number of segments might be computationally lighter but might lead to unrepresentative strain distribution profiles, hence inconclusive results. Oppositely, it was determined that an excessively high number of segments does not lead to an equally large increase in quality. These and other aspects will be delved into in Sect. 4.

Moving back to the flowchart of Fig. 2, the algorithm first of all calculates the applied tensile load ($P$) as per Eq. 2 (with ${\varepsilon }_{\mathrm{s},1}={\varepsilon }_{s,0}$ and ${\varepsilon }_{\mathrm{c},1}={\varepsilon }_{\mathrm{c},0}=0$). Then, the algorithm performs a check if ($i=1$) i.e., if the current segment is the first one or not. If this is the case ($S$) will be assumed as a value (${S=S}_{0}$) indicative of the slip at the edge of the specimen. Note that, the veracity of ${(S}_{0})$ is inconsequential as a subsequent iterative process (calculation loop) will narrow it down to the actual value of slip present in the cross-section. If ($i\ne 1$)–all the other segments–the program automatically assumes that ($S$) is equivalent to the one of previous segment (${S=S}_{i-1}$). This assumption ensures the continuity of slip between segments by ensuring that the two adjacent segments (the current one and the previous one) have the same value of slip in their common interface.

On the grounds of the above determined ($S$) and the selected bond–slip model (the one in need of performance assessment), the algorithm computes the bond stress ${(\tau }_{i})$ relative to that particular segment (see Fig. 1c, d). The next step once again differs if the segment under analysis is the first one or not. If so ($i=1$), the algorithm computes the reinforcement strain (${\varepsilon }_{\mathrm{s}i}$) on the grounds of Eq. 6. If not ($i\ne 1$) the algorithm computes the reinforcement strain (${\varepsilon }_{\mathrm{s}i}$) on the grounds of Eq. 11. Next, the concrete strain (${\varepsilon }_{\mathrm{c}i}$) is calculated according to Eq. 7, the difference in slip ($\Delta {S}_{i}$) between the two end-sections of the case study segment according to Eq. 9 and finally the slip (${S}_{i,j}$) at the opposite end of the segment according to Eq. 8. Here, $i$ stands for the number of the segment under analysis and $j$ for the iteration in progress.

On the latter, an iterative process was inserted at this stage with the goal of refining the obtained slip value (${S}_{i,j}$) with each iteration. To do so, the algorithm runs once more the above steps, except this time obtaining the bond stress ${(\tau }_{i})$ on the grounds of the previously obtained slip value (${S}_{i,j-1}$) and the selected bond–slip model (see Fig. 2). The result will be a new slip value (${S}_{i,j |\mathrm{ j }=\mathrm{ 2,3},\dots }$). The algorithm will perform as many iterations as necessary until the slip value obtained in the current iteration (${S}_{i,j}$) is equivalent to the one obtained in the previous iteration (${S}_{i,j-1}$) i.e., convergence has been reached. The (${S}_{i,j}$)—(${S}_{i,j-1}$) comparison is run after every iteration. In summary, the algorithm will perform a new iteration every time if (${S}_{i,j}$) ≠ (${S}_{i,j-1}$) and stop iterating whenever (${S}_{i,j}$) = (${S}_{i,j-1}$). Once the latter occurs, the algorithm records the updated and final $({S}_{i,j})$ for the current segment.

Next, the algorithm checks if ${S}_{i,j}=0$, in order to identify the last segment i.e., the n^th segment (the one bordering the central cross-section as in Fig. 1b). Indeed, as previously mentioned, the slip value is = 0 only in the specimen’s mid-point. Now, if $({S}_{i,j})= 0$ (indicative of the fact that the current segment is the last one) the algorithm records the value and stops. Instead, if $({S}_{i,j})\ne 0$, the algorithm records the value and moves on to next segment ($i=\mathrm{1,2},\dots$), repeating all the above steps on said next segment.

The output of the overall process are multiple values of reinforcement strains (spread thick or thin according to the chosen spatial resolution) on the grounds of which it is possible to plot the strain distribution profile relative to the selected specimen and bond–slip model. The validation tool runs the calculations for half of the specimen only (from one edge to the mid-section). The strain profile is consequently determined for half of the specimen and, on the grounds of the hypothesis of symmetry, duplicated on its other half.

3 Application of the validation tool to assess the performance of bond–slip models

The current section will present several applications of the above illustrated validation tool. In particular, by means of said tool, six bond–slip models will be validated by (1) obtaining the strain profiles corresponding to specific case study loads by means of the algorithm (2) comparing the obtained profiles against the output of five experimental double pull-out tests at the same loads and (3) comparing the accuracy of the bond–slip models by means of a statistical analysis. This last point will be the topic of the following section.

3.1 Assessed models and experimental specimens

Starting from the elucidation of the six selected bond–slip models, these are listed in Table 1 together with their fundamental equation and a brief descriptions.

Table 1 Bond-slip models assessed by means of the newly introduced validation tool

As visible, among the selected bond–slip models half of them consider the influence of concrete strength f_c whilst half do not. Also, half of them were obtained by means of conventional pull-out tests whilst the other half by means of double pull-out tests. Finally note that, unlike others, Kankam [13] included an additional variable i.e., x, indicative of the distance between the measuring point and the middle of the concrete prism along the bar at any load.

Next, the authors will describe the RC chords whose strain profiles will be put against the ones extracted from the six bond–slip models by means of the validation tool. Five RC chords with diverse characteristics were selected. As a matter of fact, four specimens are real-life RC chords whilst one is the result of a numerical simulation. Additionally, the RC chords will differ in their geometry (cross-section, length, reinforcement diameter), mechanical features (concrete strength) and in the strain sampling techniques. Diversification in the specimen selection was essential to verify the performance of the validation tool for varying parameters. It is worth mentioning, that the RC specimens were purposely chosen to be short in length (equal to the average spacing between two primary cracks [3]). This particular feature prevents any distortion of the strain profile caused by out-of-plane transversal cracks in addition to being perfectly compatible with the purpose of the present application i.e., determining the strain distribution along the reinforcement between two cracks. In the following, the specimens will be described in their geometry and strain sampling technology. For a complete reading on the mechanical characteristics of the constitutive materials of the RC chords, the readers are directed to the cited articles. Additionally, it should be noted that the application of the verification tool is limited to the applicability of the bond stress–slip law itself.

The first RC chord, from Dey et al. [6], is a 200 × 200 × 390 mm (Fig. 3a) instrumented with 21 strain gauges positioned in the core of the Ø20 embedded rebar.

Fig. 3

Illustration of double pull-out specimens used for the application of validation tool a Dey et al.[6], b Jakubovskis and Kaklauskas [34], c Bado et al. [31], d Houde [20], (e) Eugenijus [35]

To deploy said gauges, (1) the rebar was cut transversally in two halves, (2) a 10 × 2 mm longitudinal groove was incised in the middle of both halves, (3) the strain gauges were glued in said groove 20 mm apart (see Fig. 4a) and (4) the two halves of the rebar were glued back together with a two component epoxy resin.

Fig. 4

Technology behind the instrumenting of the rebars: a strain gauge sensors placed in 10 × 2 mm groove on one of the two halves of the modified rebar and glued by means of cyanoacrylate b DOFS positioned in a thin grooved previously incised on the longitudinal rib of the rebar, glued by means of cyanoacrylate and protected with a layer of silicone

The second RC chord, from Jakubovskis and Kaklauskas [34], is a 150 × 150 × 270 mm specimen (see Fig. 3b) developed by means of a three dimensional rib-scale finite element model. The third, from Bado et al. [31], is a 150 × 150 × 210 mm RC chord (see Fig. 3c) instrumented by means of a cutting edge monitoring sensor: Distributed Optical Fiber Sensor (DOFS). As deliberated in Bado et al. [28], in light of its small transversal size (125 µm), elevated accuracy (1 µε), sampling frequency (250 Hz), elevate flexibility, electromagnetic interference immunity and more, DOFS are ideal tools to monitor the evolution of strains from the inside of RC structures. For said DOFS-instrumented specimen, the hair-like sensor was first positioned in a small 1.5 × 1.0 mm groove incised along the rebar (see Fig. 4b), glued by means of cyanoacrylate and protected by means of a thin one-component water-proof oxygen-free silicone rubber layer. This layering was found to be the most performant manner of bonding a DOFS to a rebar for concrete embedment [31]. The last two specimens were taken from Houde [20] (150 × 150 × 405 mm concrete prism reinforced with a Ø25 rebar, see Fig. 3d and Eugenijus [35] (150 × 150 × 405 mm concrete prism reinforced with a Ø16 rebar, see Fig. 3e. Both were instrumented by means of a set of strain gauges (in a similar fashion to specimen from Dey et al. [6]), but with different average spacing of 45 mm and 15 mm respectively.

3.2 Application of the validation tool

The present sub-section demonstrates the practical applications of the above illustrated validation tool. As anticipated earlier, given a set of case bond slip models and a case study model RC chord, the first step consists is inserting in the validation model the input data. For example, for Dey et al. [6]’s 200 × 200 × 390 mm specimen the input data is as follows: RC prism width ($b$ = 200 mm), RC prism depth ($d$ = 200 mm), RC prism longitudinal length ($L$ = 390 mm), rebar diameter ($\varnothing$ = 20 mm), the number of segments in which the RC prism will be subdivided by the validation algorithm when running the analysis $n$ = 60, the modulus of elasticity of the concrete and the steel (${E}_{\mathrm{c}}$ = 41,526 MPa and ${E}_{\mathrm{s}}$ = 201,734 MPa respectively), the rebar strain at the end section calculated by means of Eq. 4 as function of the applied load of 45 kN (${\varepsilon }_{\mathrm{s},0}$ = 760 µε) and the assumed slip at the end section (${S}_{0}$ = 0.048 mm). It must be noted that the values of ${\varepsilon }_{\mathrm{s}}$ and ${S}_{0}$ were the real experimental value as per Dey et al. [6]. Note that the compressive strength of concrete ${f}_{c}$ = 71.32 MPa was also inserted in the validation tool as it was required to run the Shima et al., MC2010 and Barbosa and Filho bond–slip models. With the above data input in the validation algorithm, the MatLab program was run and the strain distribution curves were plotted–each corresponding to one of the analyzed bond–slip laws–in combination with the experimental one (Fig. 5a).

Fig. 5

Experimental and predicted strain curve distributions from different bond-slip models

As visible, the strain distribution profiles extracted from each model by the proposed validation tool are represented with solid lines whilst the experimental strain curve with a dotted line. Similarly, Fig. 5b represents the calculated and experimental strain distribution profiles for the load 70 kN (clearly, this second analysis required the input of new ${\varepsilon }_{\mathrm{s},0}$ and ${S}_{0}$ data). In a similar fashion, Fig. 5c–j represent the calculated and experimental profiles of the other bond–slip laws and experimental RC chords. Granted the validation tool can be run for each load level, for simplicity’s sake, Fig. 5 represents only two load levels per each specimen. Note that whilst the values behind said load levels always hover around 45 and 70 kN, these ones might oscillate in light of the conditional availability of data from literature.

At first glance, some clear disparities can be spotted in Fig. 5 between the predicted and experimental strain distributions as described below. Starting from Fig. 5a, b common pattern with all the other Fig. 5 subplots can be observed i.e., the systematic strain value overestimation, particularly evident from the profiles extracted by means of the Nilson & Mirza and Houde models. The other profiles present, instead, a closer agreement with the experimental one, particularly the Shima and Barbosa and Filho models. The above observations are evident valid at both load levels. Moving on to Fig. 5c, d, the best calculated/experimental curve match are the ones of the MC2010 and Barbosa and Filho models, more so for the lower load level of 50 kN. As anticipated earlier, overestimation of the strain data is present for both Mirza and Houde and Nilson models. This time, though, the curves extracted with the Shima and Kankam models significantly underestimate the steel strains. In Fig. 5e, f the experimental curves present a somewhat undulating profile as a byproduct of the sensing technology with which they were sampled i.e., DOFS. As a matter of fact, being the sensor capable of sampling strains with a sub-millimetric spatial resolution, the influence of the transversal ribs on a rebar longitudinal strain profile becomes apparent, in the shape of profile undulations [31]. Similarly to above, the best match is obtained with the Barbosa and Filho model (more so for the lower load level). The others overestimate (Mirza and Houde and Nilson models) or underestimate (MC2010, Kankam and Shima) the experimental strain values. Note that in both cases the margin of under/overshooting is smaller than for the previous specimens (Fig. 5a–d), probably due to the difference in sampling technology.

Figure 5g portrays a moderate match between the experimental curve and the profiles extracted with the Shima and Barbosa and Filho models at 47 kN load. However, this agreement deteriorates at the higher load level 78 kN (Fig. 5h). Note that, in both the figures, the profiles corresponding to the Kankam model seem to match the experimental curve in the central area but fails to reproduce the trend of the latter outside of said area. Finally, similarly as Fig. 5a, b, all the profiles find a certain match with the experimental one with the exception of the overshooting Mirza & Houde and Nilson models. Concluding with Fig. 5i, j, the strain profiles derived from the Kankam and Shima models find a significantly better agreement with the experimental profile than the ones obtained with the other models. At the higher load step 70 kN (Fig. 5j), a good match can only be found with the curve obtained with the Kankam model. For both load steps, all models except for Kankam and Shima overestimate the strain data throughout the RC chord.

Overall, what one can excerpt from Fig. 5 is that, with the exception of the last specimen, the Barbosa & Filho and Shima models produce profiles that match relatively well the experimental strains profiles of the various specimens. Differently so, the other models tend to overestimate the strain values (particularly the Mirza and Houde and Nilson models). Furthermore, Fig. 5 depicts (1) a certain underperformance of most bond–slip models to match the experimental data and (2) a certain discrepancy between the outputs of the former. In the next section the authors will proceed to statistically analyze the results of Fig. 5 in order to mathematically quantify the different model performances.

3.3 Statistical and sensitivity analysis of the validation tool outputs

As anticipated, the present section intends to statistically analyze the strain prediction ability of some of the most commonly used bond–slip models on the grounds of the output of the novel validation tool. The difference between the experimental curves and the ones extracted from the models will be calculated in five equidistant points along the length of each RC chord, as illustrated in Fig. 6.

Fig. 6

Layout of selected points for statistical analysis

The differences at all five locations were then quantified as relative errors as per Eq. 12.

$$\mathrm{Relative\, Error}= \left({\varepsilon }_{\mathrm{exp},i}-{\varepsilon }_{\mathrm{model},i}\right)/{\varepsilon }_{\mathrm{exp},i }| i=\mathrm{1,2},\dots ,5$$

(12)

where ${\varepsilon }_{\mathrm{exp}}$ is the strain value assumed by the experimental curve in any of Fig. 6’s measurement point i and ${\varepsilon }_{\mathrm{model}}$ is the strain value assumed by the model-specific curve in that same measurement point i. The following step consisted in averaging the relative errors at all five locations, thus obtaining a single value of relative error per model and per load level. Given an exemplary RC chord (200 × 200 × 390 mm from Dey et al. [6]) and an exemplary model (Kankam’s), Fig. 7a represents the relative error–as per Eq. 12 − in each of the above mentioned measurement points for two load levels (45 and 70 kN).

Fig. 7

Given the 200 × 200 × 390 RC chord specimen and the above specified 5 measurement points: a relative errors between the experimental strain values and the predicted strain profile calculated (by the validation tool) at each point per Kankam’s bond-slip law at load levels 45 and 70 kN; b Mean relative errors for all the bond-slip models at load levels 45 and 70 kN

As such, five relative errors at five different locations (x-axis) are displayed throughout the bar diagram per each load level (represented in different colors). The average of the five relative errors (mean relative errors) are visible as horizontal dashed lines combinedly with their respective standard deviations. These two mean relative errors constitute 2 of the 12 segments (the ones referred to Kankman’s model) of Fig. 7b which collects the mean relative errors of all the models in reference to specimen 200 × 200 × 390 mm from Dey et al. [6]. Clearly, the smaller the bar heights of Fig. 7b, the smaller the mean relative errors, the more accurate the predictions of the models. Note that positive relative error values reveal an overestimation of the strain values from the part of the model in question and vice versa. Expectedly, Fig. 7b indicates that–for the case study specimen–the strain profiles extracted by means of the Shima model are characterized by the lowest mean relative error of the whole set ( − 0.12 and − 0.04 at 45 and 70 kN respectively), followed by Barbosa and Filho model (0.21 and 0.22 at 45 kN and 70 kN respectively). Oppositely, the Mirza and Houde’s curves present the largest mismatch with their experimental counterpart (reaching a relative error of 5.24 at 45 kN) in addition to the largest error discrepancy among the two case study loads (35%). Interestingly, the only observable strain underestimation is in regard to the Shima model.

In a similar fashion, the mean relative errors were calculated for all models, for each specimen and for each load level. The outcome is summarized in Fig. 8.

Fig. 8

Assessment of bond-slip models based on real-life experiments; a mean relative errors for all the specimens at different loads, b zoomed view of the plot area surrounding the nil mean relative error

Note that each pair of circular marks (one per load level) on the plot lines of Fig. 8 are indicative of the mean relative error of a specific model per one specimen (both the loads and the specimen being indicated on the x-axis).

As visible in Fig. 8a, the mean relative errors relative to Nilson and Mirza and Houde’s models are the most inconsistence along the 5 specimens. For example, the strain overestimation by Nilson’s model varies from 5 to 390% whilst the one from Mirza and Houde’s model varies from 12 to 520%. The other four models, instead, are characterized by a greater consistency in their relative errors (Kankam model 3–94%, Barbosa and Filho model 2–34%, Shima model 4–31%, MC2010 2–66%) as visible in Fig. 8b. This last one highlights, once again, that the mean relative errors of the Barbosa & Filho and Shima models are closer to zero, hence more consistent than the ones of the Kankam and MC2010 models. Indeed, these last two present severe strain value overestimations for the Dey et al. and Houde specimens.

Figure 9 summarizes in one single figure the performance of each model in terms of global mean relative error (Fig. 9a), global standard deviation (Fig. 9b) and probability density (Fig. 9c).

Fig. 9

Overall statistics of all the bond-slip models a means; b standard deviations; c probability density curves

Figure 9 embodies the potential of the novel bond–slip model validation tool. Quintessentially, it provides access to a single mean relative error value (and standard deviation) indicative of the ability of a bond–slip model to provide predictions consistent with experimental data.

Now, on the grounds of Fig. 9, with a single mean relative error and standard deviation value per bond–slip model, it is possible to truly asses the performance of each of them. In Fig. 9a it can be observed that Shima’s model has the smallest mean relative error out of all the models ( − 0.064), signifying that, in an average, the model underestimates the strains by 6.4%. This one is closely followed by Barbosa and Filho’s model (0.104), which overestimates the strain values by 10.4%. Demonstrating moderate performance, the Kankam and MC2010 models are characterized by mean relative errors of 0.164 and 0.19 respectively. Finally, Nilson and Mirza & Houde’s models present significantly higher mean relative errors i.e., 0.95 and 1.28 respectively. The models’ standard deviations (displayed in Fig. 9b) present similar conclusions. The minimum standard deviation can be attributed to Barbosa and Filho’s model (0.14), whereas the maximum one to Mirza and Houde’s model (1.72). The data represented in Fig. 9a, b can be summarized by means of a probability density graph as in Fig. 9c. Expectedly, being characterized by the smallest standard deviation value, the normal distribution of Barbosa and Filho is the tallest and narrowest demonstrating a high concentration of data around the mean value. Differently so, Mirza and Houde’s model shows the maximum spread, indicating a large data spread around the mean value, hence most inconsistent predictions.

In the following, a sensibility analysis will be performed for the newly introduced validation tool. Its goal, assessing the variation of the outputs of the validation tool as a function of the selected “spatial resolution” i.e., the length of each segment ($\Delta x$) in which the case study specimens is subdivided (hence of their total number). Figure 10 represents the experimental and calculated strain distributions obtained by means of the validation tool with different spatial resolutions (specimen 200 × 200 × 390 at load level of 45 kN).

Fig. 10

Experimental and calculated strain curves (specimen 200 × 200 × 390 mm at 45 kN from Dey et al.) on the grounds of different bond-slip models and with different spatial resolution i.e., a 40 b 80 and c 100 segments

The selected spatial resolutions were 40, 60, 80 and 100 segments respectively. Note that the 60-segment resolution is represented in Fig. 5. As visible, no significant changes are present for varying spatial resolution. The strain profile exhibiting the biggest change is the one calculated by means of Kankam et al. which is slightly more curvilinear at its extremities. Yet, the comparison between the prediction performance of the models is not affected by the said change. Hence, it can be stated that, from the validation tool standpoint, the accuracy of the strain distribution output hardly depends on the selected spatial resolution.

Before concluding the present section, the authors would like to display an additional manner in which to run the comparison. This one sees the comparison not of the strain profiles but of the bond stress, slip and bond–slip curves as calculated by the validation tool (Fig. 11).

Fig. 11

Comparison between the experimental results (specimen 200 × 200 × 390 mm at 45 kN from Dey et al.) and several parameters calculated on the grounds of different bond-slip models: a bond stress; b slip and c bond-slip

As anticipated, Fig. 11 represents the (1) bond stress (2) slip and (3) bond–slip relation comparisons between the experimental and bond–slip model extracted results for specimen 200 × 200 × 390 mm at load level 45 kN. As visible, similarly to what concluded above, the Nilson and Mirza & Houde models significantly underestimate the bond stress (Fig. 11a) and overestimate the slip values (Fig. 11b) throughout the specimen length. The MC2010, Barbosa and Filho and Kankam models slightly overestimate the bond stress throughout the initial part of the specimen length whilst they underestimate it in the remainder. Differently so, their slip estimation is relatively in good agreement with experimental one, especially in regards to the shape of the curves. Conformingly to the previous statistical analysis, the Shima model produces the bond–slip curve closest to the experimental one (Fig. 11c). What is also noticeable in Fig. 11c is that most of the models failed to reproduce the downwards segment of the experimental curve corresponding to the specimen’s segment with damaged bond i.e., with degrading bond stresses. The experimental results show the bond stress peak to occur at 7.65 MPa. The Kankam model is the only one displaying a curve with said decreasing trend in the damaged bond segment (despite still underestimating the peak at 4.63 MPa). This observation reiterates the need of novel and more accurate bond–slip models for RC structures.

4 Conclusion

In the last decade, several researchers studied the concrete-rebar bond mechanism of a reinforced concrete (RC) structure, proposing bond stress models related to the slip between the two materials only, to the concrete strength, to the geometrical features of the case study specimen and more. Yet, in light of the lack of systems able to thoroughly inspect the inner workings of RC structures and to extract reliable bond stress values, modern bond–slip models are often inaccurate and in contradiction with each other. One of the main reasons behind this (instead of a unique physically substantiated one) is the absence of a tool that has allowed researchers to rapidly corroborate and calibrate their newly created models.

To this end, the present article proposed a bond–slip validation tool for RC elements. Its fundamental mechanism is (1) extracting strain profiles of embedded rebars on the grounds of a given bond–slip model (the one being evaluated) and of several other geometrical/mechanical features relative to a specific case study RC asset and (2) comparing them against strain profiles extracted from real-life experiments on said RC asset. In the article, the mathematical and computational steps behind the validation algorithm were thoroughly demonstrated. The validation tool is not only useful to corroborate novel bond–slip models but also to assess the performance of existing ones.

This application was demonstrated by means of six case study modern-day bond–slip models and the experimental strain data of five RC chord double pull-out tests. The comparisons between the experimental and model predicted strain distribution curves allowed the authors to, not only demonstrate the efficiency of the novel validation tool, but also to assess the performance of all the case study models (accompanied by a respective statistical analyses).

In light of its potential to speed up the long corroboration process and the model performance assessment, the proposed validation tool represents a step forward for the future of the discussion on bond–slip modelling, stress-transfer analyses and serviceability of RC structures.