Experimental verification of indirect tests for stress-crack opening curve of concrete in tension from a round robin test: application to railway sleeper elements

Abstract

This paper presents experimental verification of indirect tests for the determination of the stress-crack opening curve of concrete, based on the method described in the RILEM TC 187-SOC report and submitted to ACI Committee 446 for Fracture Toughness Testing of Concrete, which relies on the standard cohesive model. In such method, a bilinear approximation of the softening curve is determined from three-point bending tests of notched specimens under crack-mouth-opening-displacement control and from tensile splitting tests, which produces good predictions of the complete crack evolution. The current work focusses on the brittleness length, which is directly related to the parameters of the linear curve defined by the first branch of the bilinear curve, and is one of the main fracture parameters of concrete, since it controls the behaviour of thin cracks. This length can be obtained from a simple version of experiments conducted up to peak load, thus, favouring its application in the industry. In particular, this work presents the results of a round-robin test carried out in collaboration with the Spanish Association of Railway Sleeper Element Manufacturers to determine the brittleness length of concrete. A specific implementation of the method has been proposed in order to perform the tests by using the facilities available in all the factories. The results of the round-robin test have been satisfactory, thus, supporting the viability of the RILEM and ACI proposals. Moreover, a method has been developed which allows the brittleness length of concrete to be determined easily in railway sleeper element factories.

1 Introduction

Fracture of concrete is a quasi-brittle phenomenon. When damage of concrete occurs, there is a residual strength capacity, due to the formation of a damaged zone with micro-crack overlapping and aggregate bridging. The cohesive model, introduced by Hillerborg et al. [1], describes that phenomenon and has been extensively used in the last decades (see [2,3,4] for a detailed description). In that model, the damaged zone is idealised by a crack with finite opening, which transmits stress across its faces. As sketched in Fig. 1, the stress is assumed to depend on the opening of the crack by following a stress-crack opening relation, which is called the softening curve.

Fig. 1

Softening curve of concrete, bilinear approximation and linear approximation. The parameters that define the bilinear and linear approximations are the tensile strength $f_t$, the horizontal intercept of the first branch with the abscissas axis $w_1$, the fracture energy $G_F$ and the stress of the kink point $\sigma _k$

In order to obtain a reliable method for the experimental determination of the stress-crack opening curve for concrete in tension, RILEM Technical Committee TC-187-SOC was launched. In particular, Chapter 3 of the Final Report of that committee describes a method to determine an approximate bilinear softening curve using indirect tests [5], based on the work carried out by Elices, Guinea and Planas in the nineties (see [6,7,8] as main references). This method was included as well in the Draft Report of ACI Committee 446 for Fracture Toughness Testing of Concrete (joint ACI-ASCE Committee) [9], whose final version is currently under revision. It allows a bilinear approach of the softening curve to be obtained by performing an explicit inverse analysis from the results of tensile splitting tests, called Brazilian tests in the following, and three-point bending tests of notched specimens run under crack-mouth-opening-displacement control. The bilinear curve produces good predictions of the complete crack evolution. That method has been successfully applied in the characterisation of the behaviour of ordinary and high strength concrete [10], as well as other much brittler materials, such as brick [11]. However, it entails experiments and calculations which are complex to some extent, and until now there has been no opportunity to validate it through laboratories.

The first branch of the bilinear curve defines a linear approximation, which is frequently used due to its simplicity, since it is adequate to describe the behaviour of thin cracks. The linear curve can be determined from a simpler version of the experiments, with similar basis to those for obtaining the complete curve [6,7,8], as explained in a specific chapter of the Draft Report of ACI Committee 446 [12]. In particular, the parameters that define it can be determined from the maximum load of three-point bending tests and Brazilian tests without the need of measuring kinematical variables such as strain, crack opening or deflection, since they do not enter the calculations. It means that the tests can be run under load or displacement control, which significantly simplifies the experimental equipment and allows standard machines to be used. This curve is related to a characteristic material length that we call the brittleness length $l_1$, which turns out to be an inverse measure of the brittleness of a mixture and is precisely defined in the next section.

The present study focusses on the linear curve and, more particularly, on the brittleness length, in order to provide experimental verification of indirect tests for the determination of the stress-crack opening curve of concrete. A round-robin test¹ has been carried out in collaboration with the Spanish National Association of Railway Sleeper Element Manufacturers, called AFTRAV in the following. The aim was to determine the brittleness length of two mixtures of concrete. Within that purpose, a particular implementation of the method described in [12] has been proposed in order to perform the tests by using the factory facilities.

The mechanical tests carried out routinely in factories are, typically, compression tests and splitting tests [13], although other tests may be performed locally, as for example tensile-bending tests, which are required by the Spanish standard [14]. From those tests, among other parameters, the tensile strength is obtained, which controls crack initiation. However, no other fracture parameters providing information about the crack evolution can be determined. Hence the interest of the method presented here.

The proposed implementation offers the manufacturers a feasible method to characterise the brittleness of a given concrete mixture, which might be a valuable information in certain situations. Indeed, as reported in [15], small longitudinal cracks can develop in prestressed elements at the fastenings, mainly at early ages, when the prestress transfer takes place. Such cracks start from the holes for rail attachment and normally stop after a few centimetres. Although those cracks are not expected to be critical, it is essential to know the brittleness of concrete in order to determine their potential evolution. Thus, a criterion to establish the optimum moment for prestress transfer based on fracture mechanics seems more realistic than the one used in everyday practice, which is founded on the compressive and tensile strengths. Furthermore, fracture parameters may be crucial for sound decision-making when introducing changes, in a given factory, in the materials and proportions of concrete, or in the manufacturing process (curing temperature and delay time between the concrete mix and the prestress transfer).

In the paper, following this introduction, Sect. 2 explains the theoretical basis and background of this work, Sect. 3 describes the experimental method and organisation of the round-robin test, Sect. 4 presents the results and discusses the precision of the method, and Sect. 5 expounds the conclusions.

2 Theoretical basis and background

The current work relies on the standard cohesive model, introduced by Hillerborg et al. [1]. To explain the basis of the model, let us consider an idealised uniaxial tensile test of a concrete bar (see e.g. [2, Fig. 7.1.2]): for monotonic loading, the specimen elongates uniformly, until the tensile strength is reached at the load peak; then a cohesive crack appears at the most unfavourable section perpendicularly to the longitudinal axis of the bar; as the elongation further increases, the crack opens and transmits stress across its faces following a stress-opening relation, called the softening curve, while the uncracked material unloads. Although, actually, the raising branch of the stress-elongation curve does display a certain amount of nonlinearity and irreversibility, in the standard cohesive model, which is the version adopted in this work, it is assumed that the bulk, uncracked concrete behaves as a linear elastic solid and, thus, the loading and unloading curves coincide and are linear, since for ordinary concrete the corresponding inelastic strain before the peak load is negligible. This means that the softening curve is monotonically decreasing, as discussed in [4]. The softening curve displays a high non-linearity [16], as illustrated in Fig. 1, and, therefore, approximations of it are normally used in order to simplify the calculations.

From the typical approximations, the bilinear curve (line ABC in Fig. 1) is frequently used, due to its adequate balance between accuracy and simplicity. This can be defined by the following four parameters, as seen in the figure: the tensile strength $f_t$, the horizontal intercept of the first branch with the abscissas axis $w_1$, the fracture energy $G_F$—which is the area below the curve—and the stress of the kink point $\sigma _k$. These parameters are obtained from the maximum load of Brazilian tests and the analysis of the load-displacement and load-crack opening curves of three-point bending tests of notched beams run under crack-mouth opening displacement, as explained in detail in [5, 10].

Another typical approximation is the linear curve (line AB’ in Fig. 1), which is defined by $f_t$ and $w_1$ according to the figure. This curve is adequate to describe the behaviour of cracks with an opening less than $w_1$, as expected for the potential cracks of concrete sleepers, and is the approach used in this work. It can be characterised from the maximum load of Brazilian tests and bending tests, as described in [12] and mentioned in the previous section.

Let us define the main fracture parameters related to the softening curve:

• (a) The tensile strength $f_t$, interpreted as the maximum cohesive strength in the softening curve, which corresponds to zero crack opening. It is determined from the maximum load of the Brazilian test.

• (b) The brittleness length $l_1$, defined as

  $$\begin{aligned} l_1 = \frac{E w_1}{2 f_t} \end{aligned}$$

  (1)

  where E stands for the elasticity modulus of concrete. The brittleness length indicates the fragility of concrete by comparing the energy the crack can absorb in case of brittle failure and the stored elastic energy [3, 4]: the smaller the brittleness length, the greater the brittleness of concrete. This concept is related to the characteristic length $l_{ch}$ defined by Hillerborg et al [1], which considers the total energy that can be absorbed and is approximately the double of $l_1$. In the practice, the brittleness length is computed from the tensile strength, the net plastic flexural strength and the geometrical characteristics of the beam and test set-up, based on previous works of Planas, Guinea and Elices [8], as it will be explained in Sect. 3.6.

3 Experimental method

In this work, a particular implementation of the method submitted to ACI Committee 446 [12] for determination of the brittleness length is proposed, which has been reviewed in collaboration with the laboratories of AFTRAV, in order to adjust it to the factory facilities.

A preliminary phase of tests was conducted to assess the viability of the tests, which allowed additional modifications to be detected, resulting in the final protocol. Then a definitive phase of tests was carried out, which is used in the verification of the indirect tests. In the following, the main aspects of the definitive procedure and the results of the second phase of tests are presented.

3.1 Geometry of the specimens

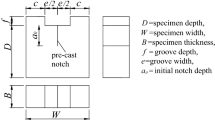
The specimens of the Brazilian tests are cubes with a length L and a depth D equal to 150 mm, as those used in compression tests in the Spanish factories [14] defined in the EN-12390-3 standard [17]. Figure 2a shows a sketch of the cubes.

Fig. 2

Cubic specimen used in Brazilian tests (a) and notched beam used in three point bending tests (b)

The specimens of the three-point bending tests are prismatic beams with a length $L=700$ mm and a rectangular cross-section of 100$\times$150 mm$^2$, as those fabricated in the Spanish factories for tensile-bending tests [14]. During bending the specimen is placed in such a manner that the beam depth is $D=150$ mm and the width $B=100$ mm, as sketched in Fig. 2b. The loading span is equal to $S=4D=600$ mm. Note that the prisms used in this work differ from those in the RILEM and ACI proposals, where beams of square cross-section were proposed for convenience, but both options are adequate for this experiment provided that the span-to-depth ratio is maintained, as explained in Sect. 3.6.

A notch is practiced at the middle cross-section, according to the RILEM and ACI proposals, with a nominal length $a_0=D/3$, i.e., 50 mm, and the following precision:

• 1. The average notch length $\bar{a}_0$ for a series of tests shall not deviate more than 10% from the nominal value, i.e., $|\bar{a}_0 - a_0 |\le 5$ mm in this case.

• 2. The notch length of individual specimens $a_{0i}$ of a series shall not deviate more than 2% from the average value $\bar{a}_0$ of that series, i.e., $|a_{0i} - \bar{a}_0 |\le 1$ mm. (Here, ‘series’ stands for a set of bending tests carried out by a given participant on specimens of the same batch.)

It is recommended that the notch width is $N\le 2\%D$. Note that the notches should be contained in the plane perpendicular to the beam axis, which is crucial in the test results.

It is essential that the loading devices during the test contact only moulded sides. In the case of the bending specimens, it conditions the direction of pouring during casting, as the non-moulded side should be 150$\times$700 mm$^2$, which was taken into account in the preparation of the specimens of this work. Should it be not possible, the non-moulded surface must be treated until complying with the requirements of straightness and perpendicularity of prismatic specimens [18]. Comments about the non-moulded side of the cubes are included in Sect. 3.4.

3.2 Materials and organisation of the round-robin test

Ten laboratories participated in the round-robin test: nine laboratories from AFTRAV, which are distributed along the Iberian Peninsula, and that from the Authors’ institution, called UPM in the following. Due to geographic and logistic reasons, the specimens were cast in two factories. Thus, two types of concrete were fabricated and, accordingly, two groups were formed as shown in Table 1. Four laboratories from AFTRAV participated in one of the groups, five in the other, and the laboratory from UPM in both. Therefore eleven participants are considered, labeled from P1 to P11, from which the UPM was identified as P5 and P11.

Table 1 Organisation of the round-robin test and nomenclature: group, manufacturer, concrete, participant, batch, number of specimens per batch for each laboratory from AFTRAV and for the UPM, where b stands for beams and c for cubes, number of beams per batch, number of cubes per batch, and total number of specimens per group

With regard to the number of tests, in the ACI proposal [12] it is recommended that six specimens are tested per type of experiment, all cast from the same batch of concrete. If not possible, a minimum of three specimens per experiment should be tested for each batch. In the present work, due to the high number of specimens, the specimens of each group were prepared in two batches, maintaining the mix proportions, and they were distributed in such a manner that each laboratory received three prisms and three cubes from each batch, i.e., a total of six beams and six prisms. As an exception, the UPM received twice this number for each group, in order to determine the variability intrinsic to the concrete mixtures and experimental method. In total, 156 specimens were fabricated (72 in a group and 84 in the other). Table 1 displays a summary of the number and type of specimens.

3.3 Curing, transportation and notching conditions

After removing the specimens from the moulds, they were kept submerged into water at $20\pm 2\,^\circ \hbox {C}$ until testing time, except during transportation and notching in which special precautions were taken to avoid drying of the specimen surface.

The specimens were transported with a minimum age of 7 days, adequately protected against knocks. Once received in the laboratories, they were immediately immersed with the conditions previously described.

The specimens were notched with a minimum age of 7 days and after transportation. Notches were performed at each laboratory, in order to avoid damage of the specimen during transportation and to verify the viability of notching in the factories, which was a critical aspect of the round-robin test. They were practiced by using a radial diamond saw with water refrigeration, except for one laboratory of Group 1, participant P3, in which water-jet cutting was used. Although it was verified that such a procedure did not seem to affect the results, it would be preferable to avoid that until an in-depth study on its effects be carried out.

The tests were performed at the age of 28 days. During those, the specimens were constantly sprayed with water to avoid drying of the surfaces.

3.4 Brazilian tests

Cubic specimens were subjected to compression at their middle plane until failure, which results in splitting of the cube in two halves. As mentioned in Sect. 3.1, it is essential that in all the tests the load is applied to moulded sides of the specimen. In the case of the Brazilian tests, there is an additional condition, since the plane of loading must be parallel to the pouring direction, i.e., perpendicular to the non-moulded side, as sketched in Fig. 2a.

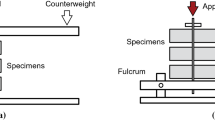
The equipment was that used in the factories for this type of test. Wood load-bearing strips were glued to the specimen, and calibrated steel strips were interposed between those and the loading plates. Fig. 3a shows a picture of the experimental device of the UPM laboratory, in which a centering device was used (for an example of this type of device, see that described in [19]).

Fig. 3

Experimental device of the UPM for Brazilian tests (a) and three point bending tests (b)

The test was carried out according to the EN-12390-6 standard [19], plus additional recommendations from Rocco et al. [20,21,22]. In particular, it is recommended that the width of the load-bearing strips is limited to 4–8% of the beam depth and the loading rate is between 500–1000 kPa/min, which is essential to ensure that the strength inferred from the test is close to the actual tensile strength of the material. In this work, wood strips 6 mm in width were used and a loading rate of 0.3 kN/s was applied, which is the minimum common value applicable in all the factories and leads to a stress rate within the recommended range.

Prior to the test, the depth and length of the loaded section of the cube were measured at its edges, and the mean depth D and mean length L were computed.

3.5 Three-point bending tests

Notched prismatic beams were tested under symmetric three-point bending until failure, with a loading span of 600 mm, as sketched in Fig. 2b, and with the specimen resting over one of the faces 100$\times$700 mm$^2$.

The equipment was that used in the factories for tensile-bending tests [14], which comply with the EN-12390-5 standard [23] (see [12] for additional recommendations for the devices). Figure 3b shows a picture of the experimental device used by the UPM. In this laboratory, servo-hydraulic testing machines were used together with a bending device as that presented in [5]; note that one of the cylinders acting as a support and the cylinder applying the load can rotate perpendicularly to their axis in order to minimise torsion.

Preparation of the specimen for the test includes notching and, if necessary, grinding to eliminate any protuberances from the loading surfaces. During all the processes, the beam must be handled with extreme care, specially after cutting the notch. During the test, the specimen has to be centred in the loading device with an error smaller than 1 mm in the position of the notch, supports and loading plane, and the loading surfaces must be kept clean of small debris.

In this work the tests were performed under a constant loading rate, which was the same in all the laboratories, for the sake of homogeneity, as this parameter may affect the test results [24]. A rate of 0.1 kN/s was applied, which was the minimum common value applicable in all the factories. A small preload was applied, which was limited to 1 kN. In the RILEM proposal, it is advised that the peak load is reached between 3–5 min, in order to perform stable tests. However, the current experiments are not intended to study the whole softening curve, and this condition can be ignored.

After breakage, the weight of the specimen including the fragments detached during the test was measured. Then the beam dimensions (depth, width and notch depth) were measured at the two edges available for each half, and the mean depth D, mean width B and mean notch depth $a_0$ were computed.

3.6 Calculation of results

The procedure for calculating the fracture parameters is as described in [12] (see [6,7,8] for the basis of such method). The main formulae are displayed in the following for completeness of the text. Note that formulae for bending tests only apply for a span-to-depth ratio $S/D=4.0$. Formulae are available as well for a ratio of 3.0 and can be found in [5, 10, 25, 26].

• 1. Firstly, the splitting tensile strength $f_{ts}$ is computed for each cube from the maximum load $F_{\max }$ of the Brazilian test as:

  $$\begin{aligned} f_{ts} = \frac{2F_{\max }}{\pi LD} \end{aligned}$$

  (2)

  where L is the mean length and D the mean depth of that cube. Note that the subindex ‘s’ of $f_{ts}$ stands for splitting test. Then the mean tensile strength $f_{tsm}$ is computed for each series and taken to be a good estimate of the true tensile strength of the corresponding series, provided certain conditions—to be discussed in Sect. 4.5—are met.

• 2. The net plastic flexural strength $f_p$ is defined as the tensile strength of an ideal material behaving as rigid-perfectly plastic in tension and rigid in compression that gives the same peak load as the actual specimen for a beam of identical dimensions. It is computed for each beam from the maximum load $P'_{\mathrm {max}}$ obtained in three-point bending tests as follows. Firstly the self-weight equivalent load $P_0$ is calculated:

  $$\begin{aligned} P_0 = mg \left( 1 - \frac{L}{2S} \right) \end{aligned}$$

  (3)

  where m is the specimen mass, g the specific gravity $g=9.81$ m/s$^2$, L the specimen length and S the loading span. Then the peak load corrected with the self-weight of the specimen $P_{\mathrm {max}}$ is computed:

  $$\begin{aligned} P_{\mathrm {max}} = P'_{\mathrm {max}} + P_0 \end{aligned}$$

  (4)

  The net plastic flexural strength is calculated as:

  $$\begin{aligned} f_p = \frac{P_{\mathrm {max}} S}{2 B b^2} \end{aligned}$$

  (5)

  where $P_{\mathrm {max}}$ is the corrected peak load, S the loading span, B the mean width of the beam, and b the ligament of the beam which is calculated as $b=D-a_0$, with D the mean depth and $a_0$ the notch depth.

• 3. The brittleness length $l_1$ is computed for each specimen from the results of the three-point bending tests and Brazilian tests, according to the equations in [12], which, for convenience, have been rewritten as follows:

  $$\begin{aligned} l_1= & {} \kappa ' \phi (x)\ ,\;\;\; x := \frac{f_t}{f_p}\ , \end{aligned}$$

  (6)
  $$\begin{aligned} \kappa '= & {} (1 - \alpha _0^m) D \ ,\;\;\; \alpha _0 := \frac{a_0}{D} \ , \end{aligned}$$

  (7)
  $$\begin{aligned} \phi (x):= & {} \frac{c_1}{(x^2 - 1)^2} + \frac{c_2}{x^2} \ , \end{aligned}$$

  (8)

  where m, $c_1$ and $c_2$ are constants whose values depend on the span to depth ratio and, for $S/D=4$, are $m=1.45$, $c_1=13.11$ and $c_2=2.68$ as determined in [8]. Most of the quantities entering these equations can be evaluated on a per-specimen basis (geometrical dimensions $a_0$, D and net plastic strength $f_p$), but $f_t$ is not, because we cannot measure the tensile strength directly in this test. We are, thus, bound to estimate its tensile strength based on the mean value $f_{tsm}$ for the series of the splitting tensile strength tests, and thus take $x = f_{tsm}/f_p$. Once the estimates of the individual values of $l_1$ are evaluated, the mean brittleness length $l_{1m}$ is computed for each batch and concrete, for the factories, the UPM and all participants.

Note that if the elastic modulus were known for a particular concrete (from standard tests, for example) the horizontal intercept of the softening curve $w_1$ could be calculated from Eq. (1). With that, the linear softening curve of concrete would be completely defined (see Fig. 1).

4 Results and discussion

In this section the results of the round-robin test are presented. It is important to highlight that the aim of this work is to verify repeatability of the results obtained from indirect tests and to assess the viability of the proposed method to be used in factories. Thus, the reader should not focus on the particular values obtained for a given concrete but on the comparison of results among laboratories.

4.1 Performance of notches

One of the critical aspects of the proposed method is notching of the beams. Prior to the tests, it was verified by visual inspection that no damage was introduced at the base material surrounding the notch front. Then it was verified that notches comply with the two conditions of Sect. 3.1.

Figure 4a shows the results for the first condition, $|\bar{a}_0 - a_0 |\le 5$ mm, which compares the nominal depth and the average of a series, and the allowable limits. Figure 4b shows the results for the second condition, $|a_{0i} - \bar{a}_0 |\le 1$ mm, which compares the individual depths and the average of a series.

Fig. 4

Difference between the nominal notch depth $a_0$ and the mean depth $\bar{a}_0$ of a series (a) and difference between the mean notch depth $\bar{a}_0$ and the individual depth $a_{0i}$ of the specimens of a series (b), for the specimens of all participants P1–P11. The limits for each difference are marked in red. (Colour figure online)

All the specimens comply with those conditions, except for one specimen of participant P6. Precisely, that specimen was discarded in the bending tests due to unexpected breakage.

Therefore, it is considered that notches performed at the laboratories by using the factory facilities are adequate.

It should be noticed that no differences were observed between the notches performed by radial saw (P1–P2, P4–P11) and by water-jet cutting (P3) with regard to their aspect and results of the two conditions. Therefore all the beams were tested.

4.2 Tensile strength

Figure 5 shows the mean tensile splitting strength $f_{tsm}$, together with its standard deviation and its standard error obtained by the factories, the UPM and all participants, for a given concrete and for each batch. For convenience, the results of net plastic flexural strength are displayed as well in the figure.

Fig. 5

Results of tensile strength $f_{ts}$ and net plastic flexural strength $f_p$ of Concrete 1 (a) and Concrete 2 (b), for the factories (F), the UPM (U) and all specimens of a concrete (All), with indication of the concrete (C) and batch (B), according to the nomenclature of Table 1; red bars correspond to standard deviations and blue bars to standard errors. (Colour figure online)

Table 2 displays the corresponding results and the remaining fracture parameters.

Table 2 Results of splitting tensile strength $f_{ts}$, net plastic flexural strength $f_p$, geometry factor $\kappa '$ and brittleness length $l_1$; the mean values are reported with indication of the interval corresponding to the standard deviation (std), and coefficient of variation or relative standard deviation (rsd = std/mean) for each concrete and batch, calculated from the results of all the participants of a given group (All), the factories (F), and the UPM (U)

Note that the results obtained by the UPM are considered as reference in this work, and the corresponding standard deviation is considered as the intrinsic standard deviation of the material. Note as well that the values of Concrete 2 are marked with an asterisk for a comment about their accuracy, which is addressed in Sect. 4.6.

If analysing the influence of the batch, it is observed that the mean strength obtained by the UPM for the two batches of a given concrete (C1B1U, C1B2U for concrete C1, and C2B1U and C2B2U for concrete C2) is within the deviation determined for that concrete (C1U and C2U). Similar comments apply to the results obtained by the factories (C1B1F and C1B2F compared with C1F, and C2B1F and C2B2F with C2F). Thus, it is shown that the results of a given concrete can be analysed regardless of the batch.

With regard to the influence of the laboratory, the mean strength obtained by all the participants for both concretes is within the experimental range determined by the UPM (see C1All versus C1U, and C2All versus C2U). In the case of the factories, the standard deviation is greater than that of the UPM, specially for Concrete 1, but is close to the generally accepted value for this type of parameter.

Figure 6 displays the individual results all the specimens, grouped by concrete, batch and participant, as marked by the squared symbols, and the mean, marked by the dotted line. For convenience, the results of net plastic flexural strength are displayed as well, marked by circles.

Fig. 6

Results of tensile strength $f_{ts}$ for all the specimens of Concrete 1 (a) and Concrete 2 (b) and mean, with indication of the participant and batch, according to the nomenclature of Table 1. (Colour figure online)

Two cubes of the first batch of participant P1 were discarded due to imperfections in the surface close to the plane of loading. It is observed that the results of tensile strength were homogeneous within each laboratory, except for participants P3 and P4, which display a greater deviation, which worsens the standard deviation of the corresponding group. As a possible explanation for those cases, it should be mentioned that the result of this test is very sensitive to small deviations in the alignment of the loading plates and centering of the specimens. However, no specific study has been conducted for the rejection of the values of any participant.

From the foregoing results, it follows that the Brazilian test of cubic specimens is adequate to be performed in the factories.

4.3 Net plastic flexural strength

Figure 5 and Table 2 show the results of mean net plastic flexural strength $f_p$ obtained by the factories, the UPM and all participants for a given concrete. Following an analysis similar to that of the previous section, it is found that the results can be analysed regardless of the batch, and the mean strength determined by all the participants and the factories is within the experimental range determined by the UPM, with excellent results for both groups. Moreover, in the case of Group 1 the results of net plastic flexural strength are more uniform than those obtained for the tensile strength, with a relative standard deviation smaller than 6.3% in all the cases, which supports the viability of performing three-point bending tests and notching in the factories. In the case of Group 2, the standard deviation is slightly greater, but similar to that of the Brazilian test and admissible for a fracture test.

Figure 6 displays the individual results of all the specimens (see the circular symbols) and the mean. Two tests of the first batch of participant P6 were discarded due to unexpected breakage. It is shown that the results are very similar for all the laboratories of a group, except for participants P6 and P7. However, as mentioned in Sect. 4.2, no analysis has been conducted for the rejection of results of any participant.

It should be mentioned that the beams notched by using water-jet cutting, participant P3, display the greatest deviation of its group, but the difference is not significant. Thus, no apparent reason is found to discard the results of the beams notched with that method, and they are included in the analysis. However, as explained in Sec 3.3, it is preferable to avoid that notching method until a deep study on its effect is carried out.

The foregoing results show that three-point bending of notched specimens provides reliable and repeatable results, and notching in the factories is adequate. Note that the net plastic flexural strength is a direct result of the test and, thus, a suitable indicator of the viability of the test procedure.

4.4 Brittleness length

Figure 7 shows the mean brittleness length, standard deviation and standard error obtained by the factories, the UPM and all participants, for a given concrete and for each batch. Table 2 displays the corresponding values. Additionally, the geometrical factor $\kappa '$, defined in Eq. (7), has been included in the table.

Fig. 7

Results of mean brittleness length $l_1$ of Concrete 1 (a) and Concrete 2 (b), for the factories (F), the UPM (U) and all specimens of a concrete (All), with indication of the concrete (C) and batch (B), according to the nomenclature of Table 1, with indication of the standard deviation in red and standard error in blue. (Colour figure online)

As in the case of the tensile strength and net plastic flexural strength, the results fit well inside the global scatter band defined by the results obtained at the UPM, which means that no significative bias is introduced at the participant level.

However, a remarkably large scatter is seen for the values of $l_1$, both in the figures and the table. Indeed, the coefficient of variation for $l_1$ is several times larger than the coefficients of variation of both $f_{ts}$ and $f_p$. This comes from the form of the dependence of $l_1$ on the values of $f_t$ and $f_p$, i.e., of Eq. (8), as we show in detail in Sect. 4.6.

With regard to the value of length itself, the obtained results are physically possible: typical values for ordinary concrete lie within the range 100–150 mm [5], although values of 200 mm are not uncommon, and greater values can be expected for high-strength concrete. Nevertheless, the concrete for sleepers is the result of years of empirical adjustment towards achieving non-brittle behaviour to avoid cracking, and it is normal that values greater that 150 mm be obtained. However it should be highlighted that the mixtures prepared for this work may differ from those actually used by the manufacturers, and, consequently, the mechanical properties reported here should not be taken as fully representative of the actual material used in railway sleeper making.

From the preceding results, it is concluded that the brittleness length can be determined in the factories and the proposed method provides measured reliable results. However, prior to the final validation of indirect tests, it is essential to assess the accuracy of the results and the range of applicability of the available formulae, and explain the high scatter of results, as expounded in the next sections.

4.5 Validation of results

In the foregoing, the tensile strength and brittleness lengths have been calculated from direct experimental measurements using equations that have limited ranges of application because of certain reasons explained next. However, the ranges of applicability are stipulated for the ratio $D/l_1$ which is not known before hand. Thus, after calculation of the brittleness length, the following conditions must be verified for the validity of the results, as indicated in the RILEM report [5]:

• 1. In the bending test, the ratio of the specimen depth and the brittleness length must be within the range

  $$\begin{aligned} 0.15 \le \frac{D}{l_1} \le 2.5 \ . \end{aligned}$$

  This is to ensure an accuracy of $\pm 0.5\%$ in formulas (6)–(8) as established in [8].

• 2. In the Brazilian test, the ratio of the cube depth or cylinder diameter and the brittleness length must satisfy the condition

  $$\begin{aligned} 0.8 \le \frac{D}{l_1}\ . \end{aligned}$$

  (9)

  This is to ensure that the splitting tensile strength $f_{ts}$ is close enough to the true tensile strength $f_t$, according to the results reported in [21, 22].

While all the beams tested in this work verified the first condition, many cubes did not verify the second one, specially for Concrete 2 with 85% of the cubes failing to fulfil condition (9).

Since the nominal dimension for the cubes is the same for all Brazilian tests, namely $D_B =150\,$ mm, the characteristic lengths that fulfilling condition (9) are, very approximately, those satisfying

$$\begin{aligned} l_1 \le \frac{150}{0.8} \approx 188 \,\text{ mm } \ , \end{aligned}$$

(10)

therefore, a single glance to Fig. 7 or Table 2 shows that:

• 1. for Concrete 1, all the mean values of $l_1$, but one, satisfy the foregoing condition and the one exceeding the condition is very close to it (191 vs. 188 mm);

• 2. for Concrete 2, all the mean values of $l_1$ exceed the foregoing limit by a large factor and, moreover, most of the potential values in the scatter bands exceed the limit, which explains why 85% of results on the cubes in this group fall outside the directly acceptable range as indicated by the asterisks in Table 2.

This implies that the analysis of the tests following the simplified method proposed in [5] and [9] is not directly applicable, and so, an iterative corrector method should be applied to the raw results as described in [8].

Such correction uses the size-effect law computed for the Brazilian test in [20, 22] in combination with Eq. (6) to obtain progressively better values of $f_t$ and $l_1$ for each pair of Brazilian-bending test series. In [8] the procedure implied graphical use of the size-effect curves, but, since the publication of [22], equations are available in the following closed-form:

$$\begin{aligned} \frac{f_{ts}}{f_t} = \frac{1}{ b_1 + b_2 D/l_1} + b_3 \ , \end{aligned}$$

(11)

where $b_1, b_2, b_3$ are parameters that depend on the ratio b/D of the width of the bearing bands and the specimen dimension, and on the shape—cylindric or cubic—of the specimen; for the specimens in this work their values are $b_1=2.35,b_2=49.75,b_3=1.0111$.

Unfortunately, the accuracy of that formula has been verified over the range $0.4\le D/l_1 \le 10$, which leads to a lower bound condition for $l_1$ which doubles that in (10), i.e.,

$$\begin{aligned} l_1 \le \frac{150}{0.4} \approx 375 \,\text{ mm } \ , \end{aligned}$$

(12)

which is still not enough to cover all the specimens from Concrete 2. Therefore, further work is necessary and is in progress to extend the computational range of the analysis of the size-effect on the Brazilian test down to ratios $D/l_1$ of 0.25 or less. Moreover, a detailed procedure and a public code should be produced to cover the simultaneous use of the equations of size-effect for bending—Eqs. (6)–(8)—as well as for splitting—Eq. (11) or an extended version of it. This does not affect the purely experimental outcomes of the present round-robin and will be addressed in an independent paper.

Besides, it is worth noting that, in the iterative process indicated before, at each correction step we get a slightly smaller value of $f_t$ from Eq. (11), and, upon substitution of it in Eq. (6), we get a slightly larger value of $l_1$, and so on. In other words: the final result for $f_t$ is approached from above, and that of $l_1$ from below, which means that, of the initial values collected in Table 2, $f_{ts}$ is an upper bound of the actual value of $f_t$, and $l_1$ a lower bound of its actual value.

Let us summarise the main ideas as follows: For the cubes not fulfilling the condition of Eq. (9) an iterative corrector method should be applied as described in [8] by using Eq. (6) and Eq. (11) in order to obtain corrected values of $f_t$ and $l_1$. Currently, this can be applied to the cubes that verify $0.4\le D/l_1 \le 10$. For the remaining ones, no correction is available at this moment. However, as explained in the previous paragraph, the direct results obtained for $f_{ts}$ and $l_1$ without any correction can be interpreted as an upper bound of the actual value $f_t$ and a lower bound for $l_1$, respectively.

4.6 Discussion on the precision and bias

The most striking feature of the results is the very large scatter in the results of $l_1$. This can be explained by an elementary analysis of uncertainty propagation induced by Eqs. (6). Following the standard procedure, we take small variations $(\delta \kappa ',\delta f_t,\delta f_p)$ to get the variation $\delta l_1$ as

$$\begin{aligned} \frac{\delta l_1}{l_{1}} = \frac{\delta \kappa '}{\kappa '} + \frac{x\phi '}{\phi } \left( \frac{\delta f_t}{f_t}-\frac{\delta f_p}{f_p}\right) \end{aligned}$$

(13)

where $\phi '$ stands for the derivative of the function $\phi (x)$ with respect to its argument. If we evaluate the factor $x\phi '/\phi$ for the two concretes at the mean values of $f_{ts}$ and $f_p$ taken from Table 2 for all participants, we get:

$$ \left. {\frac{{x\phi ^{\prime}}}{\phi }} \right|_{{\begin{array}{*{20}l} {f_{t} = \overline{{f_{{ts}} }} } \hfill \\ {f_{p} = \overline{{f_{p} }} } \hfill \\ \end{array} }} = \left\{ {\begin{array}{*{20}l} { - 3.8\;\;\;{\text{ for Concrete 1 }}} \hfill \\ { - 4.4\;\;\;{\text{ for Concrete 2 }}} \hfill \\ \end{array} } \right. $$

(14)

If we interpret, now, the small deviations as uncertainties, an upper bound of the uncertainty in $l_1$ is readily obtained as

$$\begin{aligned} \frac{|\delta l_1|}{l_{1}} \le \frac{|\delta \kappa '|}{\kappa '} + \left| \frac{x\phi '}{\phi }\right| \left( \frac{|\delta f_t|}{f_t}+\frac{|\delta f_p|}{f_p}\right) \end{aligned}$$

(15)

and, thus, the relative uncertainties in $f_t$ or $f_p$ are amplified by a factor of 4, roughly speaking, when we compute $l_1$. This explains the reason why the coefficient of variation of $l_1$ is so large compared to the coefficients of variation of the directly measured quantities $f_{ts}$ and $f_p$.

It should be noticed that the brittleness length was calculated for each specimen according to Equation (6) by considering the net plastic flexural strength of each test and the mean splitting tensile strength of the associated Brazilian test series (3 specimens per series); then the mean and standard deviation were calculated for each group considered and inserted in the table. A deeper study on the convenience of considering the mean tensile strength obtained for the variant under analysis (e.g. group, participant or batch) will be discussed elsewhere, together with other methods to obtain (possibly better) estimators by simultaneous use of Eqs. (6) and an extended version of Eq. (11).

Finally, the minimum number of specimens necessary to obtain a given standard error is calculated, based on a classical analysis of physical measurements (see [27] as a main reference). Assuming that the standard deviation obtained in this round-robin test $\sigma ^*$ coincides with the standard deviation of other samples $\sigma _{n-1}$, and from the definition of the standard error $\sigma _{\mu } = \sigma _{n-1}/\sqrt{n}$, the minimum number of specimens to reach a given target standard error $\sigma _{\mathrm {\mu }}'$ can be computed as:

$$\begin{aligned} n \ge \left( \frac{\sigma ^*}{\sigma _{\mathrm {\mu }}'} \right) ^2 \end{aligned}$$

(16)

Given that the maximum relative standard deviation obtained in the experiments of this work is 12.9% (according to the results of $f_t$ and $f_p$, C1All and C2All in Table 2), a reasonable number of specimens to obtain an error near 5% is six, which coincides with the number of specimens per participant in the current round robin test and as recommended in [12].

4.7 Practical recommendations for the manufacturers

Although it is difficult to propose guidelines on the practical application of the method useful for the different manufacturing methods (long line, short line-carrousel, post-tensioned, etc.), a very general suggestion could be that the proposed method can be a low frequency routine production test (one per month) as complementary to the daily compression tests and to the tensile Brazilian tests included in the routine of some manufacturers and performed before the prestress transfer. Two or three tests at increasing time intervals after the transfer moment can give information of the increase of the brittleness length along the initial hours. These data can be very useful for a particular manufacturer mainly to evaluate the initial brittleness of the concrete along the seasons of the year or the influence of changes in the aggregates (information that cannot be obtained from compression or tensile tests alone). In some countries like Spain and Germany, a flexural concrete tensile test is performed every day at the concrete age of 7 days. Complementing this routine test with the proposed method can be practical to know the fracture properties of the final cured concrete sleepers. The database obtained from this practice can be useful in case of changes in the concrete or manufacturing procedure.

Let us finalise noting that at this moment the method is intended for the particular practice and self-control of each individual manufacturer and is far from becoming a technical standard.

5 Conclusions

From the foregoing presentation and analysis, several conclusions can be drawn regarding three fundamental aspects: (1) feasibility of the tests; (2) reliability of the test results; and (3) validity of the estimated fracture parameters.

Regarding feasibility, the main conclusion of the round-robin is that the tests can be implemented in an industrial environment with relative ease. In particular, all the participants were able to machine the notches within specified tolerances and without damaging the specimen, and the tests were carried out with machines available in most concrete quality control laboratories.

Regarding reliability of the tests, it was observed, first, that the results were not significantly affected by the batch at the participant level, and, second, that, even though the results of some of the participants displayed some more scatter than others, overall there were no significant differences between them and the results were globally consistent with no clear outliers, so that no single result or group of results can be soundly excluded from the analysis. Therefore, the main conclusion is that all the participants were able to measure results that are reliable within the observed scatter which is, on the other hand, perfectly acceptable both for Brazilian and notched beam tests.

Regarding validity of the estimated fracture parameters, tensile strength $f_t$ and brittleness length $l_1$, the following conclusions can be drawn from the analysis in Secs. 4.5 and 4.6:

• The values of $l_1$ obtained for Concrete 2 are far too large for the simplified hypothesis to hold that the splitting strength $f_{ts}$ is ‘close enough’ to the true tensile strength $f_t$.

• The values of $f_t$ and $l_1$ could be iteratively improved using an appropriate closed-form formula for the mutual dependence of $f_{ts}/f_t$ and $D/l_1$ for the cubic splitting specimen (D is the cube side). Unfortunately, the range of applicability of the only available formula is too limited for this procedure to work for Concrete 2.

• An extended version of the available formula down to values of $D/l_1\approx 0.25$ would be necessary to obtain fully valid results of $f_t$ and $l_1$ for that concrete, for which further work is in progress.

• Meanwhile, the results obtained so far must be considered to represent an upper bound for $f_t$ and a lower bound for $l_1$.

Further work is in progress to compile a closed-form formula for the Brazilian tests covering the range required by Concrete 2, together with automated computational procedures to better process the experimental outcomes of the present round-robin.

Finally, let us point that, in spite of the high scatter, this method can be applicable to discern between two concretes, since the difference in the value of this length for different mixtures can be notable, as illustrated by the present results.