1 Introduction

1.1 Motivation

The assessment of existing masonry structures involves various types of uncertainty, making it a challenging task [1]. Since the number of destructive material tests is usually kept to a minimum due to economic and structural reasons and, in some cases, to preserve cultural heritage, statistical uncertainty must be considered; the low number of test results might not be representative of the whole population of masonry. Furthermore, a high level of model uncertainty must be taken into account. In addition to the uncertainty of the resistance model, masonry compressive strength can also be associated with considerable model uncertainty, as masonry compressive strength is usually determined by separate tests on unit and mortar specimens and subsequent application of an empirical model. Approaches to consider statistical and model uncertainty in the assessment of existing masonry structures have been presented in [2].

Apart from statistical and model uncertainty, there is spatial variability of the material properties: Material properties do not only vary from wall to wall but also within a wall. This spatial variability is also present in new masonry structures but becomes particularly apparent in the assessment of older masonry structures with high material variability. The effects of spatial material variability on the out-of-plane flexural resistance and the in-plane shear resistance of masonry walls have been investigated in [3,4,5] and [6], respectively, through Monte Carlo simulations (MCS) employing finite element models. According to these investigations, considering spatial variability causes a decrease in the mean resistance compared to a non-spatial analysis with unit and mortar properties modelled as homogeneous within a masonry wall. However, if spatial variability is considered, the coefficients of variation (CoVs) of the wall resistances are much smaller than the input CoVs of the most influential material properties.

The influence of spatially variable material properties on the resistance of masonry under compression has already been examined by Goretzky [7]. Goretzky’s goal was to compare the resistance of masonry with high spatial variability of strength and elastic modulus of unit and mortar, which is typical for historic masonry, to that of modern masonry with lower variability. For reducing the computational effort associated with using a finite element model, Goretzky developed a simplified numerical model representing masonry as a set of vertical prisms. MCS were then conducted to derive reduction factors for the mean value and the characteristic value (5% fractile) of the resistance in relation to that of contemporary masonry. Lower fractile values, which are essential concerning structural reliability, were not evaluated in [7]. The simulations in [7] were only carried out for a masonry wall with a length of six units per course and a height of only seven courses. Only concentric compression loading and no second-order effects were considered. Therefore, further investigations with varying boundary conditions, such as wall length and slenderness, are needed for a deeper understanding of the influence of spatial variability on masonry under compression.

Current safety concepts for the design and assessment of structures usually do not take spatial variability into account. Instead, masonry compressive strength, for example, is assumed to show only variability from wall to wall. Within a wall, uniformity of the compressive strength (i.e. homogeneity) is assumed. The design value of masonry compressive strength can then be directly determined as a lower quantile value of the respective probability distribution according to the approach with fixed sensitivity factors specified in Eurocode 0 [8]. In the assessment of existing structures, the variance of this probability distribution can be based on (or updated with) results from material tests. For a reliable assessment of existing, as well as a reliable design of new masonry, it is essential to know how these design values differ if they are determined under consideration of spatial variability.

1.2 Objective and outline

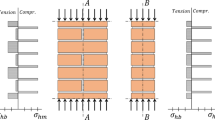
To illustrate the objective of the following study, the general effects of considering spatial variability are presented in Fig. 1. As an example, the figure considers a masonry wall under concentric compression that is not subjected to second-order effects (i.e. with theoretical slenderness of zero). In this case, the resistance is mainly determined by masonry compressive strength. If normalised by cross-section A and mean compressive strength fma,m, the probability density function (PDF) of the resistance Rhom of a homogeneous wall (i.e. the resistance based on a non-spatial analysis) equals the PDF of masonry compressive strength fma normalised by its mean fma,m. The means of the normalised resistance Rhom and the normalised masonry compressive strength fma are one, equalling the normalised resistance Rdet based on a deterministic calculation with fma,m as input material property. If spatial variability is considered, the two previously described effects set in: both the mean and the CoV reduce compared to a non-spatial analysis. Furthermore, the probability distribution of the resistance does not follow the same distribution type as the input material property (here: log-normal distribution for masonry compressive strength).

Fig. 1
figure 1

Expected effects of considering spatial variability on the resistance of a masonry wall under compression

Full size image

Concerning design values for masonry compressive strength, as well as the reliability of masonry walls in general, the left tail of the PDF is essential. To determine the overall effect of spatial variability, the relationship between the probability distribution of spatially variable masonry compressive strength and the resulting probability distribution of the resistance of a masonry wall under compression must be known. Therefore, two main questions need to be answered:

  1. 1.

    How does spatial variability influence the mean value of the resistance of a masonry wall in comparison to that of a homogeneous masonry wall?

  2. 2.

    How can the relationship between the variability of material properties and the resulting variability of the wall resistance be described?

If these two effects are known, and a suitable distribution type is selected, design values for masonry compressive strength can be determined according to the current Eurocode safety format. In the assessment of existing structures, design values are sometimes referred to as assessment values to highlight the different perspectives (see e.g. [9]). Here, the term “design value” is kept to match the well-known nomenclature of the current Eurocodes.

The following analyses focus on solid clay brick masonry walls under compression. In Sect. 2, experimental investigations to study the influence of local weaknesses on the resistance of solid clay brick masonry walls (i.e. their stress redistribution capability) are presented. The experimental results serve as a basis for validating a finite element model, which is illustrated in Sect. 3. The finite element model is then used to conduct Monte Carlo simulations (MCS), in which the compressive strength, elastic modulus, and flexural tensile strength of masonry are modelled spatially variable. The corresponding stochastic model is described in Sect. 4. Finally, the general approach of the MCS and the results of parameter studies are presented in Sect. 5.

2 Experimental investigations

2.1 Experimental programme

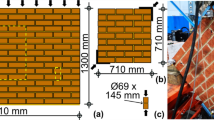
The experiments aimed to investigate the behaviour of solid clay brick masonry with local weaknesses. In total, 24 masonry walls were tested, which were either arranged as single wythe masonry or in cross bond (see Fig. 2). In addition to reference walls, walls with intentionally placed weaknesses were constructed. These weaknesses consisted of either a missing brick in the masonry bond or a particular percentage (25% or 50%) of perforated clay bricks (i.e. bricks with significantly lower compressive strength) within the walls. In walls with a missing brick, stress concentrations occur close to the hole. When the masonry strength is reached locally, stresses need to be redistributed to areas with lower stress levels. The resistance of such walls is thus mainly determined by the post-peak behaviour of the material, making these walls well suited for the validation of the finite element model. In reality, walls with high spatial variability do not only feature a single weak spot but various weaknesses that are randomly distributed over the wall geometry. Furthermore, the weaknesses consist of weaker bricks (i.e. they are less extreme than a hole). Hence, an additional mechanical influence is the confinement of weaker bricks by stronger ones. Therefore, the walls including both stronger and weaker bricks complemented the experimental programme by walls with more realistic boundary conditions to capture the major influences in the validation of the finite element model.

Fig. 2
figure 2

Masonry walls of the experimental programme

Full size image

All the tested walls had a height of 13 courses with five whole bricks per course. For mortar, a factory-mixed dry mortar containing natural hydraulic lime NHL 5 according to EN 459-1 [10], pozzolans, and sand with a maximum aggregate size of 1.2 mm, was chosen. The nominal perpend and bed joint thicknesses were selected as 10 mm and 12 1/3 mm, respectively. The nominal brick dimensions were 240 × 115 × 71 mm3 (length × width × height), corresponding to standard format NF according to DIN 20000-401 [11]. Consequently, the nominal dimensions of the single wythe walls were 1240 × 115 × 1083 mm3 and those of the cross bonded walls 615 × 115 × 1083 mm3.

The walls were erected by trained masons and covered by polyethylene sheets for the first 3 days after construction. Then, until the testing at the age of 32 up to 42 days, the walls were stored under laboratory conditions. Before testing, the top of the wall was capped with a thin gypsum layer. A concentric compression load was then applied via a steel beam, whose support allowed for rotation, with a constant displacement rate to reach the maximum load after 15 to 30 min. Displacements were measured by four linear variable displacement transducers (LVDTs) per wall, each reaching over 10 brick and bed joints. The test setup is depicted in Fig. 3.

Fig. 3
figure 3

Test setup for wall cb-50-1

Full size image

In addition to the tests on masonry walls, the results of which are presented in Sect. 2.3, complementary compression tests on bricks, mortar specimens, and masonry specimens were performed, as presented in Sect. 2.2.

2.2 Results of tests on unit, mortar, and masonry specimens

Unit compression tests according to EN 772-1 [12] were performed on at least n = 6 bricks from each delivered pallet of bricks. The results for the solid and perforated clay bricks are listed in Table 1. In addition to the directly obtained strengths, the normalised compressive strengths based on the shape factors defined in [12] are given. The average normalised unit compressive strengths were 24.9 and 11.6 N/mm2 for solid and perforated bricks, respectively.

Table 1 Experimentally obtained material properties
Full size table

For the construction of each wall, several mortar mixes were needed. From at least one of these mixes, three standard mortar prisms were sampled and tested according to EN 1015-11 [13]. The standard prism mortar tests were conducted on the same day as the corresponding tests on masonry walls. On average, a compressive strength of 2.71 N/mm2 was obtained on the standard mortar prisms. In addition to the standard prisms tests, double punch tests according to procedure III of DIN 18555-9 [14] were performed on small specimens (50 × 50 × 12 mm3) that were extracted from mortar joints within masonry (see Fig. 4). According to this testing method, the load is applied via two loading platens with a diameter of 20 mm. Since these mortar specimens cured under different conditions, namely within masonry instead of in steel moulds, the obtained strengths are much different: 6.50 and 7.44 N/mm2 were determined for mortar cured in solid and perforated clay brick masonry, respectively. It is noted that all the double punch tests were conducted on mortar specimens belonging to the same mortar mix; the average standard prism strength of this mix was 3.48 N/mm2 (i.e. slightly higher than the overall average of 2.71 N/mm2). Hence, the double punch strength was higher by a factor of about two, which approximately matches the findings in [15]. For further information on double punch testing, refer to [16,17,18,19].

Fig. 4
figure 4

Mortar compressive strength testing on standard prisms (left) and double punch testing (right)

Full size image

Furthermore, the compressive strength and the modulus of elasticity of masonry were determined according to EN 1052-1 [20] on six masonry specimens (so-called “RILEM specimens”; see [21]) for both masonry types. These masonry specimens, which were arranged as single wythe masonry, had a height of six and a length of two units. The corresponding results are also listed in Table 1.

2.3 Results of tests on masonry walls

The resulting load-bearing capacities of the tested masonry walls are displayed in Table 2. In addition to the maximum applied load, the testing age, the wall dimensions, and the strength (maximum load per gross cross-sectional area) are listed. Furthermore, the average strength is given and a relative strength, which is the strength related to the respective solid clay brick reference wall.

Table 2 Results of tests on masonry walls
Full size table

The walls with a missing brick (sw-hole, cb-str, cb-head) showed a relative strength of between 70 and 78%. If perfect stress redistribution were possible, the relative load-bearing capacity would be 80%, which is the relative area of the critical cross-section (four instead of five bricks). The strength of walls containing solid and perforated bricks is lower than the strength that is obtained by linear interpolation between the strengths of the two reference walls according to the respective share of solid and perforated bricks. Thus, the load-bearing capacity cannot be directly determined via the average masonry compressive strength in the wall. If only the critical cross-section (i.e. the cross-section with the largest share of perforated bricks) is considered, the extent of this effect reduces, but in principle, the effect remains. Hence, the tests revealed a considerable but not perfect capability of stress redistribution within the walls.

3 Finite element modelling

3.1 General model description

The software DIANA FEA (Version 10.3) is utilised for modelling the masonry walls. The model follows the simplified micro-modelling approach [22]. Hence, the walls are represented by expanded units (i.e. units with their dimensions increased by half of the adjacent mortar joint thicknesses) and interfaces with zero thickness, representing the mortar joints. The simplified micro-modelling approach is chosen as it provides a good compromise between the detailed micro-modelling approach, which represents the interaction of unit and mortar in detail, and the macro-modelling approach, where no discretisation between units and mortar joints is present. On the one hand, detailed micro-modelling would be computationally more demanding and would require much more mechanical and stochastic input parameters. On the other hand, the missing discretisation of a masonry wall into separate units makes macro-modelling inapplicable for walls with unit-to-unit material variability.

Here, the expanded units are modelled by eight-node solid elements, to which the nonlinear behaviour of the composite material masonry is assigned. The dimensions of the expanded units are 250 × 115 × 83.3 mm3 (length × width × height) for the single wythe masonry walls, corresponding to the nominal dimensions of brick format NF plus two halves of the perpend joint thickness (10 mm) in length and two halves of the bed joint thickness (12.3 mm) in height. In the case of the cross-bonded walls, the dimensions are 250 × 120 × 83.3 mm3 for stretchers and 240 × 125 × 83.3 mm3 for headers to obtain a wall width of 240 mm. Each unit is discretised into 8 × 4 × 3 elements. Thus, the elements are approximately cubic with an edge length of approximately 30 mm. The interfaces that are placed at the position of the perpend and bed joints consist of plane quadrilateral elements with four plus four nodes. The purpose of the interfaces is to display the discrete cracking of masonry at the mortar joints under tension.

The load is applied as a line load with a specified eccentricity that is then distributed to the whole cross-section via a rigid plate at the top. At the bottom, the walls are supported vertically along a line, which is similarly connected to a load distribution plate. Furthermore, horizontal supports are placed at the top and bottom. In the simulation of the experiments, the load is applied displacement-controlled, and the top is hinged around the longitudinal axis (x-axis; see Fig. 5). The rotation is restraint at the bottom to model the experimental conditions. The MCS are performed load-controlled. The support at the top allows for rotation around the x- and the y-axis, and the support at the bottom for rotation around the x-axis. Figure 5 displays the geometry, mesh, example stresses, and example strains of the finite element model. The depicted wall corresponds to the reference wall in the MCS.

Fig. 5
figure 5

Geometry, mesh, and example strains of the finite element model (reference wall for the Monte Carlo simulations)

Full size image

3.2 Material modelling

Although the material behaviour of masonry is orthotropic in general, the material behaviour of the extended units is modelled as isotropic here. An isotropic model yields sufficiently accurate results for the following investigations since the vertical compressive stresses dominate. The compressive behaviour of the expanded units is modelled with a Drucker–Prager yield criterion combined with a linear tension cut-off and cohesion hardening/softening. The flow rule is chosen to be associated; that is, the dilatancy angle ψ equals the friction angle φ defining the yield surface [22]. The friction angle is chosen as φ = 12°, as this leads to good agreement between the simulated and the experimental results. Furthermore, the resulting Drucker-Prager criterion agrees well with the biaxial strength of masonry as experimentally determined in [23], considering only the range where the horizontal compressive stress is lower than one-third of the vertical compressive stress. The cohesion hardening/softening law is modelled according to a proposal in [22] (see Fig. 6). Expressed as a uniaxial relationship between the compressive stress σc and the plastic compressive strain εpl, the hardening/softening law is defined as follows:

$$\sigma_{{\text{c}}} \left( {\varepsilon_{{{\text{pl}}}} } \right) = \sigma_{{\text{i}}} + \left( {\sigma_{{\text{p}}} - \sigma_{{\text{i}}} } \right)\;\sqrt {\frac{{2\;\varepsilon_{{{\text{pl}}}} }}{{\varepsilon_{{\text{p}}} }} - \frac{{\varepsilon_{{{\text{pl}}}}^{2} }}{{\varepsilon_{{\text{p}}}^{2} }}} \quad {\text{for}}\;\varepsilon_{{{\text{pl}}}} \le \varepsilon_{{\text{p}}} , \sigma_{{\text{c}}} \left( {\varepsilon_{{{\text{pl}}}} } \right) = \sigma_{{\text{p}}} + \left( {\sigma_{{\text{m}}} - \sigma_{{\text{p}}} } \right)\;\left( {\frac{{\varepsilon_{{{\text{pl}}}} - \varepsilon_{{\text{p}}} }}{{\varepsilon_{{\text{m}}} - \varepsilon_{{\text{p}}} }}} \right)^{2} \quad {\text{for}}\;\varepsilon_{{\text{p}}} \le \varepsilon_{{{\text{pl}}}} \le \varepsilon_{{\text{m}}} , \sigma_{{\text{c}}} \left( {\varepsilon_{{{\text{pl}}}} } \right) = \sigma_{{\text{r}}} + \left( {\sigma_{{\text{m}}} - \sigma_{{\text{r}}} } \right)\;\exp \left( {2\frac{{\sigma_{{\text{m}}} - \sigma_{{\text{p}}} }}{{\varepsilon_{{\text{m}}} - \varepsilon_{{\text{p}}} }}\;\frac{{\varepsilon_{{{\text{pl}}}} - \varepsilon_{{\text{m}}} }}{{\sigma_{{\text{m}}} - \sigma_{{\text{r}}} }}} \right)\quad {\text{for}}\quad\varepsilon_{{\text{m}}} \le \varepsilon_{{{\text{pl}}}} ,$$
(1)

With σp equal to masonry compressive strength fma and εp the corresponding plastic strain. For σc ≤ σi, only elastic strains are present. The post-peak behaviour is defined by σm and εm. The residual stress σr is needed to avoid numerical issues. In [22], the values σi = 0.33 fma, σm = 0.5 fma, and σr = 0.1 fma are proposed, which are also applied here. Setting εm = 6 εp yields results matching the experiments well.

Fig. 6
figure 6

Uniaxial stress–strain relationship for the expanded units

Full size image

For a given modulus of elasticity and a given masonry compressive strength, the plastic strain εp is determined by the stress–strain parameter k, which is the ratio of total to elastic strain at peak stress. The parameter k is a measure for the nonlinearity of the stress–strain curve, with k = 1 leading to a linear curve and k = 2 to a curve resembling a quadratic parabola. From the results of tests on the reference walls, k is determined as 2.31 (single wythe) and 2.38 (cross bond) for solid clay brick masonry, and 1.69 (single wythe) and 2.04 (cross bond) for perforated clay brick masonry. In the MCS, k = 2 is selected, which is representative of solid clay brick masonry in general [24, 25]. For the MCS, an average ratio Ema/fma = 550 is selected based on [24, 26].

To define the tension cut-off of the material model for the expanded units, the horizontal tensile strength fbt of the units is assigned. For this purpose, fbt is set to 0.04 fb for the solid bricks and 0.03 fb for the perforated bricks based on [26], where fb is the unit compressive strength. The MCS are performed based on material properties that are normalised regarding masonry compressive strength fma. Based on typical unit and mortar strengths of fb = 25 N/mm2 and fj = 5 N/mm2, respectively, a characteristic masonry strength of fma,k = 8.1 N/mm2 is obtained according to [27], corresponding to a mean value of fma,m = 9.1 N/mm2 (assuming fma,k = 0.8 fma,m [28]). Hence, the normalised unit tensile strength is fbt/fma = 0.11. Tension softening is selected as linear with a residual tensile strength of 0.1 fbt.

A discrete cracking material model with bilinear softening according to [29] is assigned to the interfaces that represent the mortar joints. As the deformation behaviour under compression is modelled by the expanded units, the stiffness of the interfaces is set very high such that almost no relative displacements occur if the joint is uncracked. The tensile strength ft of the joints represents the flexural tensile strength fx1 of masonry. A typical value of 0.4 N/mm2 [30] is chosen, corresponding to 0.044 fma based on the normalisation described above. The tensile fracture energy is set to 0.0148 ft based on findings in [31]. The selected material properties of the finite element model are summarised in Table 3.

Table 3 Material parameters used in the finite element model
Full size table

3.3 Validation of the model

The finite element model needs to display the behaviour of solid clay brick masonry with local weaknesses sufficiently well. In particular, the relative reductions compared to the reference walls without weaknesses are essential for the subsequent MCS. For the simulation of the experiments, which are performed to validate the model, the compressive strength and the stress–strain parameter k are thus chosen as experimentally determined for the reference walls. The modulus of elasticity is set to the values obtained from the tests on RILEM specimens. Figure 7 illustrates the load–displacement curves from the experiments (average of the four LVDTs) and the corresponding simulations. The displayed loads are normalised regarding the cross-sectional area; that is, they are shown as average stress. The displacements are related to the length of the LVDTs and the height of the finite element wall, respectively. Therefore, they are displayed as an average strain. As evident, the simulated load–displacement curves match the experimental ones very well.

Fig. 7
figure 7

Stress–strain curves obtained from the experiments on masonry walls and corresponding finite element simulations

Full size image

For the following MCS, only the differences between the experimental and simulated peak loads (i.e. the resistances) are important. Thus, the small differences in the post-peak behaviour are of minor relevance. The differences between the experimental and simulated results can—to some extent—be attributed to the inevitable variability of the experimental results themselves. To check the overall accuracy of the finite element model, the ratio θ between the average experimental resistance Rexp and the simulated resistance Rcal is calculated for each wall type with weaknesses. The average ratio θ = Rexp/Rcal is 1.03, which is very close to one. The CoV is 9.5%. Considering the variability of the experimental results themselves, this low CoV affirms that the numerical model is sufficiently precise for the MCS.

4 Stochastic modelling

4.1 General concept

The spatial variability of the material properties is modelled as unit-to-unit variability in the presented investigations. Masonry compressive strength fma, masonry elastic modulus Ema, and joint tensile strength ft are represented by log-normal random variables. An individual random value of fma and Ema is assigned to each expanded unit in the MCS. In the stochastic model, the interfaces at the bed joints are discretised into separate sections according to the units placed at their top, as the mortar is usually placed section by section for the next unit to be laid during construction. Each of these sections receives its individual tensile strength ft,i. The compressive strength fma,i and the elastic modulus Ema,i at one unit i are correlated with the correlation coefficient ρf,E. The spatial correlation between the compressive strengths—as well as between the elastic moduli—at different expanded units i and j is defined by the correlation coefficient ρspat (see Fig. 8).

Fig. 8
figure 8

Correlation between material properties

Full size image

According to this stochastic model, the correlation between the strengths of two expanded units in the wall is independent of their relative location to each other. The reason for the spatial correlation represented by ρspat is that the units within one wall are likely to originate from the same production batch and are thus affected by common production conditions. Within the wall, however, the units from one construction batch are placed in an arbitrary order, which would make any location-related correlation between the unit strengths questionable. Although the compressive strength (and the elastic modulus of masonry) is influenced by the properties of both the units and the mortar, the described correlation structure is modelled according to that of the units. For justification, note that EN 1996-1-1 [32] defines the following empirical relationship between the characteristic masonry compressive strength fma,k and the mean compressive strengths fb,m and fj,m of unit and mortar:

$$f_{{\text{ma,k}}} = K\;f_{{\text{b,m}}}^{0.7} \;f_{{\text{j,m}}}^{0.3}$$
(2)

Equation 2 corresponds to a linear relationship between the units of the logarithms of masonry, unit, and mortar compressive strengths. Hence, the resulting relationship between the respective variances σ2 is

$$\sigma_{{{\text{ln }}f_{{{\text{ma}}}} }}^{2} = 0.7^{2} \;\sigma_{{{\text{ln }}f_{{\text{b}}} }}^{2} + 0.3^{2} \;\sigma_{{{\text{ln }}f_{{\text{j}}} }}^{2} = 0.49\;\sigma_{{{\text{ln }}f_{{\text{b}}} }}^{2} + 0.09\;\sigma_{{{\text{ln }}f_{{\text{j}}} }}^{2}$$
(3)

Equation 3 demonstrates the dominating influence of the unit properties on the variability of masonry compressive strength. This much stronger influence of the unit properties on masonry compressive strength justifies the choice of modelling correlation according to the unit properties. Analogous considerations apply to the modulus of elasticity.

4.2 Stochastic parameters

The CoVs of the material properties are varied in the parameter studies presented in Sect. 5. Therefore, typical ratios between the CoVs of the different material properties are specified rather than fixed CoVs. The CoVs of masonry compressive strength, masonry elastic modulus, and joint tensile strength are found to be 17%, 22%, and 35%, respectively, in experimental investigations by Schueremans [31]. Therefore, the relative CoVs of masonry elastic modulus and joint tensile strength are defined as 1.3 and 2 times the CoV of masonry compressive strength. These ratios also approximately match the CoVs specified in the JCSS Probabilistic Model Code [33]. The correlation between the compressive strength and the elastic modulus of masonry is set to ρf,E = 0.72, as evaluated in [31] based on experimental investigations. The spatial correlation coefficient ρspat is varied between zero and one in the parameter studies.

4.3 Generation of random material properties

The generation of the random material properties masonry compressive strength and masonry elastic modulus according to the correlation structure in Fig. 8 and the stochastic parameters in Table 4 is performed according to an approach previously presented in [34]. The random values for fma and Ema at a specific expanded unit i are obtained as the product of four independent random variables:

$$f_{{{\text{ma}},i}} = W\;f_{{\text{w}}} \;U_{i} \;f_{{{\text{u}},i}} ,$$
(4)
$$E_{{{\text{ma}},i}} = W\;E_{{\text{w}}} \;U_{i} \;E_{{{\text{u}},i}} ,$$
(5)

where W, Ew, fw, and Ui are auxiliary random variables shared by particular pairs of the material properties fma,i and Ema,i. Since the same random values of W and Ui are applied to calculate fma,i and Ema,i, these random variables cause a correlation between the compressive strength and the modulus of elasticity at a specific unit i. In the same way, W and fw cause a correlation between the compressive strengths fma at two different units i and j. Finally, the correlation between the moduli of elasticity Ema at different units is caused by W and Ew.

Table 4 Stochastic parameters of the material properties
Full size table

All random variables in Eqs. 4 and 5 are log-normally distributed. Furthermore, they have a mean value of one, except for fma,i and Ema,i, the mean values of which equal the actual mean values of fma and Ema. If the CoVs of the auxiliary variables are determined according to the following equations, the desired correlation coefficients ρf,E and ρspat and the CoVs Vf and VE are obtained:

$$V_{W} = \sqrt {\rho_{{{\text{spat}}}} \;\rho_{{f,E}} \;V_{{E}} \;V_{{f}} } ,$$
(6)
$$V_{{f_{{\text{w}}} }} = \sqrt {\frac{{\rho_{{{\text{spat}}}} \;\left( {V_{{\text{f}}}^{2} - \rho_{{f,E}} \;V_{{E}} \;V_{{f}} } \right)}}{{1 + \rho_{{{\text{spat}}}} \;\rho_{{f,E}} \;V_{{E}} \;V_{{f}} }}} ,$$
(7)
$$V_{{U_{i} }} = \sqrt {\frac{{\left( {1 - \rho_{{{\text{spat}}}} } \right)\;\rho_{{f,E}} \;V_{{E}} \;V_{{f}} }}{{1 + \rho_{{{\text{spat}}}} \;\rho_{{f,E}} \;V_{{E}} \;V_{{f}} }}} ,$$
(8)
$$V_{{f_{{{\text{u,}}i}} }} = \sqrt {\frac{{\left( {1 - \rho_{{{\text{spat}}}} } \right)\;\left( {V_{{f}}^{2} - \rho_{{f,E}} \;V_{{E}} \;V_{{f}} } \right)}}{{\left( {1 + \rho_{{{\text{spat}}}} \;V_{f}^{2} } \right)\;\left( {1 + \rho_{{f,E}} \;V_{{E}} \;V_{{f}} } \right)}}} .$$
(9)

The CoVs of Ew and Eu,i can be calculated analogously to those of fw and fu,i (i.e. by swapping the indices “f” and “E”). Equations 6 to 9 are derived from the well-known relationships for the variance of the product of random variables and the correlation coefficient of two random variables. Random material properties for the joint tensile strengths ft,i can be directly generated according to the desired mean and CoV, as they are not modelled as correlated.

5 Monte Carlo simulation

5.1 Approach

The reference wall for the following parameter studies is illustrated in Fig. 9. It is arranged in cross bond with a thickness of two unit widths. Each of the 36 courses consists of five units of standard format NF [11], resulting in the height of 3 m, the thickness of 0.24 m, and the length of 0.625 m. The ratio of mean elastic modulus to mean compressive strength is set to Ema,m/fma,m = 550 for the reference wall. The wall is loaded concentrically, and the supports are modelled as hinged around the longitudinal axis. The reference wall is simulated without consideration of geometrical nonlinearity (i.e. without second-order effects) since this leads to the most critical influence of spatial variability, as shown in the following. The CoV of masonry compressive strength is set to Vf = 30% for the reference wall, which is typical for existing solid clay brick masonry [2]. Based on the ratios in Table 4, the CoVs of masonry elastic modulus and joint tensile strength are 39% and 60%, respectively. Furthermore, no spatial correlation (i.e. full spatial variability) of the material properties and, hence, ρspat = 0 is assumed for the reference wall. In each parameter study in the following, one of the parameters of the reference wall is varied.

Fig. 9
figure 9

Geometry and structural system of the reference wall

Full size image

In the MCS, all material properties are normalised by the mean masonry compressive strength fma,m. In most parameter studies, 200 simulations with random material properties are conducted for each parameter combination. Subsequently, the mean Rm and the CoV VR of the resistance are estimated by the arithmetic mean and the sample CoV of the simulation results.

Since lower quantile values are essential regarding structural reliability, design values of the resistance are also determined. As the focus is on existing structures, a corresponding target reliability index is chosen, which—due to higher costs of measures for increasing structural reliability—is typically lower than for the design of new structures [35, 36]. The target reliability index is selected as βt,1a = 3.3 for a one-year reference period, as specified in ISO 2394 [37] for high relative costs of safety measures and medium failure consequences. Since the fixed sensitivity factor αR = 0.8 from EN 1990 is mainly defined for a 50-year reference period, a modified sensitivity factor αR,1a = 0.7 is used, which is more suitable for a one-year reference to achieve compatibility with design values based on a 50-year target reliability index βt,50a [38].

Although the input material properties are log-normally distributed, the resulting probability distribution of the wall resistance is not necessarily log-normally distributed. Anderson–Darling tests for goodness-of-fit [39] indicate that the most suitable distribution type varies between the parameter combinations. Nevertheless, all design values are evaluated assuming a log-normal distribution to gain better comparability. However, the respective variance is not estimated by the variance of the simulation results directly. To consider the skewness of the simulation results that might differ from that of a log-normal distribution, the distribution parameters μlnR and σlnR2 (i.e. the mean and variance of the logarithm of the resistance) are chosen such that the mean and the 5% fractile of the distribution match the arithmetic mean and 5% fractile of the simulation results. The design value is then determined by

$$\begin{aligned} R_{{\text{d}}} & = R_{{\text{m}}} \exp \left( { - 0.5\;\sigma_{\ln R,5\% }^{2} - \alpha_{R} \;\beta_{{\text{t}}} \;\sigma_{\ln \,R,5\% } } \right) \\ & = R_{{\text{m}}} \exp \left( { - 0.5\;\sigma_{\ln R,5\% }^{2} - 0.7 \cdot 3.3\;\sigma_{\ln \,R,5\% } } \right), \\ \end{aligned}$$
(10)

where σlnR,5%2 denotes the variance derived from fitting the distribution parameters to the mean and 5% fractile of the results.

These design values are not directly suited for engineering practice, as model uncertainty has not been considered yet. The design values determined by Eq. 10 are compared to design values Rd,hom obtained by the approach without considering spatial variability. Therefore, a deterministic calculation based on mean material properties is conducted first to obtain the deterministic resistance Rdet assuming homogeneity. According to the traditional approach without considering spatial variability, design values are determined based on the variability of the material properties. Here, masonry compressive strength fma is the most relevant material property:

$$R_{{\text{d,hom}}} = R_{{{\text{det}}}} \exp \left( { - 0.5\;\sigma_{\ln { f}}^{2} - 0.7 \cdot 3.3\;\sigma_{\ln \,{ f}} } \right)$$
(11)

with σln f2 the variance of the logarithm of masonry compressive strength.

5.2 Influence of material variability

The evaluated simulation results for varying CoVs Vf of masonry compressive strength are displayed in Fig. 10. As the spatial correlation coefficient ρspat is zero, the CoV Vf fully corresponds to unit-to-unit variability (Vf = Vf,spat). The resistance is normalised by cross-sectional area A and mean masonry compressive strength fma,m. The normalised deterministic resistance Rdet/(A·fma,m) is one since no load eccentricity and no second-order effects are considered.

Fig. 10
figure 10

Influence of the coefficient of variation of masonry strength on the wall resistance

Full size image

Two main effects are evident. First, the mean resistance Rm decreases with an increasing CoV of spatially variable masonry strength. This effect is caused by an increasing number of expanded units with very low compressive strength within the wall, combined with a limited stress redistribution capability. The mean resistance Rm can be approximated as a function of Vf,spat as follows:

$$R_{{\text{m}}} \approx R_{{\text{m,appr}}} = R_{\det } \exp \left( { - 1.62\;V_{{f}}^{1.44} } \right).$$
(12)

Figure 10 demonstrates the excellent fit of the approximation.

The second effect is that the resulting CoV of the wall resistance VR is significantly smaller than the input CoV of masonry compressive strength Vf. The relationship between Vf and VR can be approximated by

$$V_{{R}} \approx V_{{R,\text{appr}}} = 0.17\;V_{{f,\text{spat}}}$$
(13)

The CoV VR,5% corresponding to the variance σln R,5%2 can analogously be approximated by 0.21 Vf,spat. All coefficients in the approximative equations are determined using the method of least squares.

The reduction of the mean Rm is a negative effect of considering spatial variability, whereas the effect that VR is much smaller than Vf is positive. The overall influence of considering spatial variability is apparent when comparing the design value Rd under consideration of spatial variability to the design value Rd,hom obtained by the traditional approach without spatial variability. Figure 10 shows that the consideration of spatial variability leads to significantly higher design values here. Considering spatial variability thus has a positive influence on obtained design values or partial factors in this case.

5.3 Influence of spatial correlation

The spatial correlation coefficient ρspat is varied between 0 and 1 in this next parameter study. The total CoV of masonry compressive strength is constant with Vf = 0.3, but the choice of ρspat determines which part of the CoV corresponds to unit-to-unit and which to wall-to-wall variability. The case ρspat = 0 is identical to the reference case; all the variability of masonry compressive strength belongs to spatial (i.e. unit-to-unit) variability within the wall. For ρspat = 1, the compressive strengths at the different units within the wall are perfectly correlated. Hence, no spatial variability exists within the wall; the CoV of masonry compressive strengths fully corresponds to variability between different walls. In the intermediate cases, the variability consists of both a unit-to-unit and a wall-to-wall component, represented by Vf,spat and Vf,wall, respectively. Based on Eqs. 6 to 9, these component CoVs are given by

$$V_{{f,\text{wall}}} = V_{{f}} \;\sqrt {\rho_{{{\text{spat}}}} } ,$$
(14)
$$V_{{f,\text{spat}}} = V_{{f}} \;\sqrt {\frac{{1 - \rho_{{{\text{spat}}}} }}{{1 + \rho_{{{\text{spat}}}} \;V_{{f}}^{2} }}} .$$
(15)

In this parameter study, 100 simulations are performed for each parameter combination. The reduction of the simulation runs is possible, as the random numbers for the auxiliary variables W, Ew, and fw, which are much more influential than those for the individual units, are generated using Latin hypercube sampling.

Figure 11 presents the MCS results for varying values of ρspat. In the case of ρspat = 1 (i.e. homogeneity), the mean resistance equals the deterministic resistance Rdet. Furthermore, the CoV VR of the resistance equals the CoV Vf of masonry compressive strength. Since this situation is identical to the traditional approach for determining design values, the design value Rd derived from the MCS equals the design value Rd,hom (except for minor deviations due to the limited number of simulation runs). As soon as ρspat < 1, spatial variability is present, including its previously described effects on the wall resistance, namely the reduction of the mean Rm and the CoV VR. The positive effect of considering spatial variability on the design value is only present for a small correlation coefficient. For ρspat around 0.5, the two effects of reduced mean and reduced variability approximately cancel each other out.

Fig. 11
figure 11

Influence of the spatial correlation coefficient on the wall resistance

Full size image

Based on Eqs. 11 and 12, the results for varying ρspat can also be determined analytically. The reduction in Rm is caused by only the spatial component of Vf, which can be determined with Eq. 14 to be inserted into Eq. 11. The CoV VR can be determined by considering that the resistance R can be viewed as a product of two random variables: one representing a wall with ρspat = 0 and Vf = Vf,spat and one for a wall with ρspat = 1 and Vf = Vf,wall. Since only the CoV of the first random variable is reduced according to Eq. 12, the CoV of the resistance is

$$V_{{R}}^{2} = 0.17^{2} \;V_{{f,\text{spat}}}^{2} + V_{{f,\text{wall}}}^{2} + \;0.17^{2} \;V_{{f,\text{spat}}}^{2} \;V_{{f,\text{wall}}}^{2} .$$
(16)

The CoV VR,5% can be calculated analogously with the coefficient 0.21 instead of 0.17, enabling the determination of design values Rd. As illustrated in Fig. 11, the analytically determined values Rm,appr, VR,appr, and Rd,appr excellently match the simulation results. Hence, MCS with the finite element model are only required for ρspat = 0 since the intermediate cases can be captured analytically.

5.4 Influence of wall length

The number of units per course of the masonry wall is varied to study the influence of wall length. At first, a masonry pillar with just one undivided unit per course is investigated, followed by a pillar having two undivided units per course (with the next course always rotated by 90°). Then, walls in cross bond with three, five, seven, nine, and 11 units per course are investigated. The results are presented in Fig. 12. Although the number of potential weaknesses in the long walls is higher, the mean value Rm increases with higher wall length. This is due to the higher number of units in a course involved in stress redistribution when the weakest unit in this course reaches its strength. Due to stress redistribution, the strengths of the expanded units are—to a certain extent—averaged out within a course, which leads to a lower CoV of the resistance for long walls. Because of these two positive effects, the design values significantly increase with higher wall length. Hence, this parameter study confirms the need for a reduction factor for the design value of walls with a small cross-sectional area A. In EN 1996-1-1 [32], such a reduction factor is specified as 0.7 + 3 A for A < 0.1 m2, leading to 0.79, 0.88, and 0.97 for the investigated walls with one, two, and three units per course.

Fig. 12
figure 12

Influence of the wall length on the wall resistance

Full size image

5.5 Influence of slenderness

This last parameter study aims at investigating the transition between material failure and stability failure. Therefore, geometrical nonlinearity is considered in this parameter study, and the wall slenderness is varied. In this context, it is helpful to define a material-related slenderness λ that includes the ratio of elastic modulus Ema,m to compressive strength fma,m. Slenderness λ is defined according to [40]:

$$\lambda = \frac{{h_{{{\text{ef}}}} }}{t}\;\sqrt {k\;\frac{{f_{{\text{ma,m}}} }}{{E_{{\text{ma,m}}} }}\;} = \frac{{h_{{{\text{ef}}}} }}{t}\;\sqrt {\varepsilon_{{f,\text{m}}} } ,$$
(17)

with εf,m the compressive strain at peak stress (based on the mean of fma and Ema), k the stress–strain parameter, hef the effective height of the wall length (i.e. buckling length), and t the thickness of the wall.

To avoid effects from changing the number or dimensions of the units, slenderness λ is varied by altering the ratio Ema,m/fma,m between 10,000 and 75. With decreasing elastic modulus, second-order effects gain more and more influence until the failure mode switches from compression to stability failure. The load eccentricity e is chosen as 0.1 t in this parameter study. Thereby, an initial eccentricity is present that is increased at the mid-height of the wall as a result of second-order effects. Due to hinged supports, hef equals the actual wall height h. The results are presented in Fig. 13, where λ = 0 corresponds to a Monte Carlo simulation without considering geometrical nonlinearity. In addition to the mean Rm, the CoV VR, and the design values Rd and Rd,hom of the resistance, the resistance Rdet based on a deterministic simulation with mean material properties is shown, as Rdet/(A·fma,m) ≠ 1 here.

Fig. 13
figure 13

Influence of the slenderness on the wall resistance

Full size image

The influence of masonry compressive strength reduces with increasing slenderness λ. In the case of high slenderness λ, with most of the walls showing stability failure, only the overall stiffness, determined by the elastic moduli of the expanded units in the wall, is essential. While material failure is initiated by the failure of the weakest spots in the wall (i.e. the “weakest link”), the overall stiffness that determines the resistance in the case of stability failure is given by a weighted harmonic mean of the varying stiffness of the courses within the wall. Consequently, the gap between the mean resistance Rm and the deterministic resistance Rdet gets smaller for increasing slenderness. Furthermore, the CoV VR of the resistance is smaller in the case of high slenderness λ, although the CoV of the elastic modulus is higher than the CoV of masonry compressive strength. As a result, the ratio Rd/Rd,hom and, hence, the positive effect of considering spatial variability is higher for slender walls showing stability failure than for non-slender walls with material failure.

6 Conclusions

The influence of spatially variable material properties on the resistance of solid clay brick masonry under compression has been investigated in the presented study. A finite element model was developed based on the simplified micro-modelling approach. The model proved its suitability by comparing experimental results on masonry walls featuring local weaknesses with corresponding finite element simulations. The finite element model was then utilised for Monte Carlo simulations, in which the spatial variability of masonry compressive strength, masonry elastic modulus, and joint tensile strength was modelled as unit-to-unit variability. Various parameter studies were performed to quantify the influence of spatial variability on the resistance of masonry under compression concerning the mean resistance, the CoV of the resistance, and the design value of the resistance. From these parameter studies, the following conclusions can be drawn:

  • The mean resistance decreases with increasing spatial variability of the material properties within the wall. However, the CoV of the resistance is much smaller than the input CoV of the relevant spatially variable material property. Approximate equations were found for describing both effects.

  • If the spatial correlation coefficient of the material properties within the wall is small, considering spatial variability usually leads to much higher design values of the resistance than the traditional approach that is based on the deterministic resistance assuming homogeneity and the variability of the most important material property. If the spatial correlation coefficient is around 0.5, both approaches approximately lead to the same design values for the investigated reference wall.

  • Due to an improved stress redistribution capability, longer masonry walls perform better than short walls if spatial material variability is present.

  • The relative reduction of the mean resistance caused by spatial variability is smaller for slender walls with stability failure, as average material properties are more relevant than the “weakest link” in this case.

The results of the study thus provide valuable insights into the effects of spatial variability on the resistance of solid clay brick masonry under compression, which is particularly relevant for the assessment of existing masonry structures.