1 Introduction

The problem of cracks in cementitious materials is a widespread and thorough engineering problem [1]. Although small cracks do not directly cause structural failure, they can also accelerate the deterioration of a structure [2]. The presence of cracks not only affects the permeability of building structures and reduces their freeze–thaw resistance, but also many enhance the chloride attack of concrete [3,4,5,6]. Inspired by nature, a variety of self-healing mechanisms have been developed for cementitious materials [7,8,9,10,11], which has led to concrete materials becoming intelligent and capable of detecting the damage and repairing themselves. According to the report RILEM TC-221-SHC, the self-healing mechanism can be classified into “autogenic” and “autonomic” [12]. The autogenous self-healing is mainly based on the original composition of cementitious materials, which consists of three mechanisms: (1) the cement matrix on the crack surface absorbs water leading to volume expansions [12], (2) further hydration of the unhydrated cement clinker [13], and (3) carbonation of the additionally formed portlandite [14]. The autonomous self-healing is carried out with the help of healing agents. Depending on its composition, the healing agent can be divided into polymers [15], minerals [16] and bacterial spores [17].

The currently available numerical methods for self-healing can be grouped according to the nature of their self-healing mechanisms into: (1) chemical reaction-based models, for predicting carbonation [18], further hydration [13, 19,20,21,22,23,24,25], precipitation [26, 27] and encapsulation [28,29,30,31]; and (2) transport-based models [18, 27], in which the phases affecting the healing processes are transported through the pore-structure network. A few models involve thermodynamics. Huang and Ye [32] modeled the further hydration of unhydrated cement particles based on a thermodynamic-diffusion model with coupled mass balance, charge balance and chemical equilibrium. In addition, Lattice–Boltzmann Method (LBM) as a class of computational fluid dynamics (CFD) methods for fluid simulation has been used for self-healing materials in non-equilibrium thermodynamic states, such as polymer [33] and cementitious materials [34]. For the carbonation reaction, which is one of the important mechanisms of self-healing in cementitious materials, there are numerous studies that consider it as a moving boundary problem since the position of the free boundary is a function of time [35,36,37,38].

Based on the present literature review, it can be summarized that self-healing of cementitious materials is treated analytically and numerically mainly using reaction–diffusion equations. However, these models have several limitations. Firstly, the solid–liquid interface is treated as a sharp interface, which leads to the discontinuity in some of the continuously varying parameters at the interface (e.g. ionic concentration field), making it difficult to trace the evolution of certain physical processes, notably, the concentration profile across the interface. Secondly, sharp interfaces have to be explicitly tracked, especially for the evolution of high-dimensional, microstructurally complex interfaces, which can make numerical calculations extremely difficult. Thirdly, only single solid–liquid interface has been investigated in existing models. The effect of dissolution of soluble minerals on the fracture surface on the initial solid-phase boundary is not yet considered. Finally, these models are concentrated solely on the standalone self-healing process, neglecting interactions between the concentration of aqueous species in the solution, the moving front of self-healing products, and the morphology of the interface. The above limitations will be overcome by applying the phase-field (PF) method presented in this study.

The PF method provides an effective way to simulate migration problems of thermodynamically driven interfaces, which applies order parameters (OPs) to represent microstructures (e.g. pores, liquid and solid phases) and can include natural thermodynamic quantities such as concentration and temperature. The OPs take different constant values in different regions and have a continuous spatial variation across the interface. The microstructure and its evolution is thus reproduced by the spatial and temporal distribution of the OPs, without the need for interfacial tracking [39]. Several PF models for dissolution and/or precipitation simulations have been proposed: solutes in liquids [40,41,42], tri phases in porous media (two immiscible fluids and a solid phase) [43], binary or ternary alloys [44,45,46]. Moreover, some PF models for simulating metal corrosion are also worthy of reference [47,48,49].

Unlike the conventional sharp and/or single interface PF models, the contribution of presented novel PF model is based on thermodynamics to simulate the evolution of multi diffusion interfaces of self-healing process. We used the physicochemical principles of the self-healing problem to construct a free energy function that incorporates the mechanism of dissolution and precipitation interactions. By introducing an auxiliary (phase) field as a front tracking tool, the complex interface migration are implicit solved. Specifically, the solution of the model consists of determining the concentration fields of the active species and the PF.

Based on the above overview, this study will report numerical simulations of the carbonation reaction of cementitious materials using the PF method from the perspective of dissolution and precipitation. The numerical model is introduced in Sect. 2, including the novelty on the construction of energy functions for multiphase dissolution and precipitation. Numerical simulation and experimental methodology is presented in Sect. 3. The experimental validation and the model application are demonstrated in Sect. 4, followed by a series of parametric studies. Finally, concluding remarks are provided in Sect. 5.

2 Phase-field model of self-healing

2.1 Phase-field scenario

From a chemical point of view, the hydration reaction of cementitious materials is a complex dissolution–precipitation reaction in which, unlike the reaction of a single component, numerous components of cementitious materials react simultaneously with different thermodynamics and kinetics, and the various mineral components interact with each other. This poses a great challenge for modeling. However, the carbonation reaction, which is one of the main mechanisms of self-healing in cementitious materials, could be simplified as a \({\hbox {Ca(OH)}_{2}}\) dissolution and \({{\text {CaCO}}_{3}}\) precipitation process. From the modeling point of view, a simplified approach to the analysis of the carbonation reaction (Eq. 1) [35, 50] can help to analyze and understand the complex self-healing mechanism based on nonequilibrium thermodynamics.

$$\begin{aligned} \left\{ \begin{array}{lr} {{\text {CO}}_{2}}(\text {g})+{{\text {H}}_{2}{\text {O}}}{\mathop {\longleftrightarrow }\limits ^{\langle 1\rangle }}{{\text {CO}}_{2}}(\text {aq})+{{\text {H}}_{2}{\text {O}}}\\ {\mathop {\longleftrightarrow }\limits ^{\langle 2\rangle }}{{\text {H}}_{2}{\text {CO}}_{3}}(\text {aq}){\mathop {\longleftrightarrow }\limits ^{\langle 3\rangle }}{{\text {HCO}}^{-}_{3}}(\text {aq})+{{\text {H}}^{+}}(\text {aq})\\ {\mathop {\longleftrightarrow }\limits ^{\langle 4\rangle }}{{\text {CO}}^{2-}_{3}} (\text {aq}) + 2{{\text {H}}^{+}}(\text {aq}), \textcircled{1}\\ {\hbox {Ca(OH)}_{2}}(\text {s}){\mathop {\longleftrightarrow }\limits ^{{{\text {H}}_{2}{\text {O}}}}}{{\text {Ca}}^{2+}} (\text {aq}) +2{{\text {OH}}^{-}} (\text {aq}), \textcircled{2} &{} \\ {{\text {Ca}}^{2+}}(\text {aq})+{{\text {CO}}^{2-}_{3}}(\text {aq})\longleftrightarrow {{\text {CaCO}}_{3}}(\text {s}), \textcircled{3} &{} \end{array} \right. \end{aligned}$$
(1)

where “aq” , “g” and “s” refer to species which are in an aqueous, gaseous and solid states, respectively.

Figure 1 shows the carbonation process and the corresponding profiles of the OPs in the PF model. Generally, the carbonation based self-healing consists of three main mechanisms: (1) \({{\text {CO}}_{2}}\) dissolves in water to form carbonate ions, (2) dissolution of \({{\text {Ca}}^{2+}}\) ions source phase \({{\text {Ca(OH)}}_{2}}\), hydration product, e.g. calcium silicate hydrate (C–S–H or \(3{\hbox {CaO}}\cdot 2{\hbox {SiO}_2}\cdot 3{{\text {H}}_{2}{\text {O}}}\)) and non-hydrated cement phases, e.g. tricalcium silicate (\({{\text {C}}_{3}{\text {S}}}\) or \(3{\hbox {CaO}}\cdot {\hbox {SiO}_2}\)) and dicalcium silicate (\({{\text {C}}_{2}{\text {S}}}\) or \(2{\hbox {CaO}}\cdot {\hbox {SiO}_2}\)) [51] in the unsaturated solution, and (3) nucleation and growth of precipitated \({{\text {CaCO}}_{3}}\) in the supersaturated solution [52]. The dissolution of \({{\text {CO}}_{2}}\) (g) in water proceeds through a multi-step equilibrium reactions (mechanism 1, reaction \(\langle 1\rangle\)), where the reaction \(\langle 2\rangle\) is the bottleneck process, as only a very small fraction of \({{\text {CO}}_{2}}\) (aq) is transformed into \({{\text {H}}_{2}{\text {CO}}_{3}}\). In our first PF approach, a full availability of \({{\text {CO}}_{3}^{2-}}\) species is considered, thus neglecting the kinetic effects of \({{\text {CO}}_{2}}\) dissolution steps \(\langle 1\rangle {-}\langle 4\rangle\). A more detailed modeling approach for the carbonation of cement pastes considering chemical thermodynamics and diffusive and convective transports can be found in recent literature, e.g. [53]. Following the PF scenario, the ion diffusion in each phase (labeled as i) is described with a conserved field variable, i.e. \(c_i\) adopting physical meaning of the concentration and track the phase evolution with a non-conserved field variable, i.e. \(\phi _i\) adopting the physical meaning of the volumetric fraction of the phase i. Note here the \(c_i\) refers to the ratio of the actual ionic concentration \(C_i\) at a certain position and time to the initial concentration of the source phase \(C^0_\text {sou}\), both in units of mol/\(\hbox {m}^3\) (see Table 1, Sect. 3.1.2). The calcium ion source phase \(\phi _\text {sou}\) (hereafter referred to as the source phase), the precipitation phase \(\phi _\text {pre}\) and the aqueous solution phase \(\phi _\text {aq}\) together form a multiphase system.

In the initial stage (\(0< \ t\ < t_p\)), when the dissolution begins, i.e., only \(\phi _\text {sou}\), \(\phi _\text {aq}\) and their interface \(I_{\text {a}{-}\text {s}}\), are present in the system. Then \({{\text {Ca}}^{2+}}\) ions diffuse from \({\hbox {Ca(OH)}_{2}}\), hydration products and unhydrated cement particles (\(t\ >\ t_p\)), and react with dissolved \({{\text {CO}}_{2}}\) in water to form suspended \({{\text {CaCO}}_{3}}\). As its concentration reaches a saturation \(c^\text {E}_\text {aq}\) and even an oversaturation state \(c^\text {sat}_\text {aq}\), calcium carbonate pre-nucleates, nucleates, and eventually later forms crystals, precipitating on the crack surface. The interaction energy of \({{\text {CaCO}}_{3}}\) particles is strongly dependent on the ionic concentration in the solution [54]. This is mainly due to the fact that \({{\text {Ca}}^{2+}}\) ions in solution produce short-range attractive and long-range repulsive interactions [55]. \({{\text {CaCO}}_{3}}\) particles accumulate more in ion-concentration-enriched regions. Therefore, the ion concentration can be used to express the local packing density of precipitated \({{\text {CaCO}}_{3}}\) particles. The corresponding interfaces of \(\phi _\text {pre}\) with \(\phi _\text {sou}\) and \(\phi _\text {aq}\) are denoted by \(I_{\text {s}{-}\text {p}}\) and \(I_{\text {p}{-}\text {a}}\), respectively.

Fig. 1
figure 1

Schematic diagram of the simplified self-healing mechanism and profiles of the order parameters of the corresponding phases; \(t_p\) is the time to start precipitating

Full size image

Based on the self-healing mechanism described above, several modeling assumptions have been made:

  • only the reaction of \({{\text {Ca}}^{2+}}\) with \({{\text {CO}}_{3}^{2-}}\) ions to form \({{\text {CaCO}}_{3}}\) is considered. The carbonation products do not contain other intermediate substances;

  • all \({{\text {Ca}}^{2+}}\) ions localized in the crack solution may eventually be equilibrated with respect to \({{\text {CaCO}}_{3}}\) precipitates;

  • since the number of moles of \({{\text {CaCO}}_{3}}\) is the same as that of \({{\text {Ca}}^{2+}}\) ions it contains, the diffusion of all aqueous species (\({{\text {Ca}}^{2+}}\) ions and suspended \({{\text {CaCO}}_{3}}\)) can be expressed as a single ionic concentration \({c_i}\);

  • the diffusion coefficients of aqueous substances in phase (\(\phi _\text {pre}\), \(\phi _\text {sou}\) and \(\phi _\text {aq}\)) and the corresponding interface (\(I_{\text {s}{-}\text {p}}\) and \(I_{\text {p}{-}\text {a}}\)) are constant, respectively (see Fig. 1).

2.2 Thermodynamic and kinetic formulations

The multi non-conserved OPs \(\{\phi _i\}\) are continuous functions of time t and space x, which indicate each phase to convert between 0 and 1 within a thin diffusion translation interface. Subscription \(i=\mathrm {sou,\,pre\,and\,aq}\) is used further. The three phase contributions (\(\phi _\text {sou}\), \(\phi _\text {pre}\) and \(\phi _\text {aq}\)) are constrained following [56], i.e.,

$$\begin{aligned} \phi _\text {sou}+\phi _\text {pre}+\phi _\text {aq}=1. \end{aligned}$$
(2)

Considering this multi-phase constraint, the free energy \({\mathscr {L}}\), within the simulation domain \(\varOmega\) with the Lagrangian multiplier \(\lambda\), is written as

$$\begin{aligned} \begin{aligned} {\mathscr {L}}\left( \{c_i\},\{\phi _i, \nabla \phi _i\}\right)&=\int _{\varOmega }[f_\text {loc}(\{c_i\},\{\phi _i\})\\&\quad +f_\text {int}(\{\nabla \phi _i\})\\&\quad +\lambda (1-\sum \phi _i)]\text {d}\varOmega , \end{aligned} \end{aligned}$$
(3)

where \(f_\text {loc}\) and \(f_\text {int}\) are the terms for local and interface free energy density, respectively. The local free energy \(f_\text {loc}\) can be formulated as an extension of the double-well function as

$$\begin{aligned} f_\text {loc}(\{c_i\},\{\phi _i\})=\sum _i\left[ \varPhi _i(\phi _i)f_i(c_i)+\omega _i g(\phi _i)\right] \end{aligned}$$
(4)

where \(\varPhi _i(\phi _i)\) are originally the tilting functions [57], which is reduced in this work in a two-phase interpolating function as: \(\varPhi _i(\phi _i)=(10 - 15\phi _i + 6\phi _i^2)\phi _i^3\). \(\omega _i\) is the height of the imposed double-well energy barrier of each phase. \(g(\phi _i)=\phi _i^2(1-\phi _i)^2\) is the double-well potential. The free energy density of each phase \(f_i(c_i)\) is approximated by a parabolic function as follows

$$\begin{aligned} f_\text {sou}(c_\text {sou})= & {} A_\text {sou}(c_\text {sou})^2, \end{aligned}$$
(5)
$$\begin{aligned} f_\text {pre}(c_\text {pre})= & {} A_\text {pre}(c_\text {pre}-c_\text {pre}^\text {E})^2-\varDelta _\text {r}f, \end{aligned}$$
(6)
$$\begin{aligned} f_\text {aq}(c_\text {aq})= & {} A_\text {aq}(c_\text {aq}-c_\text {aq}^\text {E})^2, \end{aligned}$$
(7)

where \(A_i\) is the potential parameter employed to construct the local free energy of distinct phases in order to approximate the actual thermodynamic system.

Figure 2 illustrates the path of local free energy variation with the concentration \(\{c_i\}\) and the order parameters \(\{\phi _i\}\) for the three stages of the self-healing reaction, i.e. (0) undersaturation, (1) saturation and (2) oversaturation. In the unsaturated state, \({{\text {Ca}}^{2+}}\) ions dissolve from the cementitious matrix and diffuse into the solution to form suspended \({\text {CaCO}_{3}}\), which is accompanied by a decrease in the solute concentration in the cementitious matrix from \(c^{(0)}_\text {sou}\) to \(c^{(1)}_\text {sou}\) and an increase in the solute concentration from \(c^{(0)}_\text {aq}\) to \(c^{(1)}_\text {aq}\) in the solution. The difference in the diffusion energy of the cementitious matrix changes from \(\varDelta _\text {dis}f^{(0)}\) to \(\varDelta _\text {dis}f^{(1)}\). The precipitation chemical driving force \(\varDelta _\text {pre}f^{(0)}\) is negative when the solution is not saturated, which corresponds to the inability to precipitate but only to dissolve. When the solution is saturated or even supersaturated (\(c^{(1)}_\text {sou}\) to \(c^{(2)}_\text {sou}\) and \(c^{(1)}_\text {aq}\) to \(c^{(2)}_\text {aq}\)), i.e. the chemical driving force \(\varDelta _\text {pre}f^{(2)}\) is positive, after which the suspended \({\text {CaCO}_{3}}\) starts to precipitate. In order to properly emulate this process, \(A_\mathrm {sou}<A_\mathrm {aq}\ll A_\mathrm {pre}\) should be numerically satisfied. Meanwhile, the thermodynamic driving force for the precipitation of \({\text {CaCO}_{3}}\) consists of the contribution of the reaction part \(\varDelta _\text {r}f^{(2)}\) and the diffusion part \(\varDelta _\text {dif}f^{(2)}\).

The precipitation follows a non-equilibrium process in which \({{\text {CaCO}}_{3}}\) aggregates with characteristic mean cluster size form and grow, thus filling the cracks. For \({{\text {CaCO}}_{3}}\) nanoparticles present in solution, their mutual clustering is strongly dependent on the ionic concentration of the solution. When the ionic concentration is small, dissolution of the reactants is promoted. An increase in the ionic concentration rapidly promotes the production of more precipitation. The precipitation reaction term \(\varDelta _\text {r}f\) should be an expression of the free energy density related to the chemical formation of \({{\text {CaCO}}_{3}}\) particles [58]. In this PF model, we simplify the precipitation term to a non-negative constant. With this constant we are able to define the free energy of the precipitation phase \(f_\text {pre}(c_\text {pre})\) (as shown in Eq. 6) in the region that allows the \({{\text {CaCO}}_{3}}\) precipitation, i.e. located in the oversaturation (OS) regions.

Fig. 2
figure 2

a Processes and driving forces for the three stages. b Logarithmic free energy density landscape among the source phase, the precipitation phase, and the aqueous solution as the junction phase. Energy variation paths (of dissolution and precipitation) are also illustrated

Full size image

The energy contributions at the diffusive interface is formulated [59] as

$$\begin{aligned} f_\text {int}(\nabla \{\phi _i\})=\sum _i\frac{\kappa _i}{2}\left| \nabla \phi _i\right| ^2 \end{aligned}$$
(8)

where \(\kappa _i\) is the gradient energy coefficient of each phase. Based on the formulations of [59], the interface is described as a mixture of multi-phase with different compositions, but with the same chemical potential. The local concentration c is thus defined as the weighted superposition of each phase \(c_i\)

$$\begin{aligned} c=\varPhi _\text {sou}c_\text {sou}+\varPhi _\text {pre}c_\text {pre}+\varPhi _\text {aq}c_\text {aq}. \end{aligned}$$
(9)

These phase concentrations are further constrained by an equal-chemical–potential condition, i.e.

$$\begin{aligned} \mu =\frac{\partial f_\text {sou}}{\partial c_\text {sou}}=\frac{\partial f_\text {pre}}{\partial c_\text {pre}}=\frac{\partial f_\text {aq}}{\partial c_\text {aq}}. \end{aligned}$$
(10)

The temporal evolution of the non-conserved order parameters \(\{\phi _i\}\) is governed by the Allen–Cahn equation [60] as

$$\begin{aligned} \frac{\partial \phi _i}{\partial t}= -L_i \frac{\delta {\mathscr {L}}}{\delta \phi _i} \end{aligned}$$
(11)

with the corresponding interface mobility coefficient \(L_i\). On the other hand, the conserved local concentration field c is governed by diffusion equation [59] as

$$\begin{aligned} \frac{\partial c}{\partial t}= \nabla \cdot \left( D\sum _{i} \varPhi _{i} \nabla c_{i} \right) , \end{aligned}$$
(12)

which can be also regarded as the reduced version of Cahn–Hilliard equation by applying the chain rule on the chemical potential [59]. The solute diffusion coefficient can be formulated as \(D=\sum _{i}\varPhi _i D_i\) considering the effective value of each phase \(D_i\) and corresponding interpolation \(\varPhi _i\).

Analyzing the equilibrium properties of the kinetic equations (11) and (12) by means of the thin interface limit analysis [59], the unknown model parameters \(\kappa _i\) and \(\omega _i\) can be expressed by the interfacial energy \(\sigma _{i{-}j}\) and the interfacial width \(l_{i{-}j}\). As the general formation, \(\kappa _i\) and \(\omega _i\), corresponding to the OP \(\phi _i\), are calculated as follows

$$\begin{aligned} \kappa _i= & {} \frac{3}{4}\left( \sigma _{i{-}j}l_{i{-}j}+\sigma _{i{-}k}l_{i{-}k}-\sigma _{j{-}k}l_{j{-}k}\right) , \end{aligned}$$
(13)
$$\begin{aligned} \omega _i= & {} 6\left( \frac{\sigma _{i{-}j}}{l_{i{-}j}}+\frac{\sigma _{i{-}k}}{l_{i{-}k}}-\frac{\sigma _{j{-}k}}{l_{j{-}k}}\right) , \end{aligned}$$
(14)

where i,  j,  k are distinct phase subscriptions, i.e. \(\text {sou, pre or aq}\).

3 Method

3.1 Numerical method

3.1.1 Simulation setup

Figure 3 shows a 2D schematic view of a simulation domain of size 375 \({\upmu }\)m \(\times\) 750 \({\upmu }\)m for the parameter research. The initial width of the crack is set to 150 \({\upmu }\)m. In this model, the solid calcium hydroxide provides a source of calcium ions. When the crack width is much smaller than the size of the source phase and the number of cracks is sufficiently few, it can be considered as a constant supply of calcium ions in the system. However, when the cracks are densely distributed, this causes competition for the supply of \({{\text {Ca}}^{2+}}\) ions around the cracks. Therefore, only a limited ions supply is available. This phenomenon can be simulated by two boundary conditions (BC), i.e. BC1: the boundary of the domain \(\Gamma _1\) is a constant concentration ion reservoir following (Eq. 9); BC2: there is no mass exchange between the domain and the environment along the outward unit normal of the boundary \(\Gamma _2\). \({\mathbf {n}}\) is the normal vector. For the realistic simulation of the model, binary large objects (BLObs) were converted from the experimental images derived from the stereo microscope (see Sect. 4.3), imported and processed using the MOOSE-embedded ImageFunction and associated utilities.

Fig. 3
figure 3

Schematic view of a typical crack and the initial and boundary conditions used in the PF model. The source phase and the aqueous solution phase are separated by the diffusion interface \(I_{\text {a}{-}\text {s}}\)

Full size image

3.1.2 Parameter normalization

To ensure the convergence of the model and to improve the computational efficiency of solving the non-linear governing equation sets, all variables are normalized. Spatial derivatives are normalized with respect to the reference length r, which is set to 5% of the initial crack width. Dimensionless forms of other quantities are given in Table 1.

Table 1 The dimensionless forms of the parameters
Full size table

In order to enable a valid comparison of the varying order parameters in the same time frame, the original data were linearly transformed by equation 15.

$$\begin{aligned} \phi ^*_i=\frac{\phi _i^t-\phi _i^\text {min}}{\phi _i^\text {max}-\phi _i^\text {min}} \end{aligned}$$
(15)

where \(\phi _i^t\) is the integration of the corresponding phase at the time t over the 2D domain, while \(\phi _i^\text {min}\) and \(\phi _i^\text {max}\) represent the minimum and maximum integration of the corresponding phase, respectively. The residual source phase ratio, the precipitation generation ratio and the self-healing ratio can be expressed as the corresponding normalized phase ratio \(\phi ^*_\text {sou}\), \(\phi ^*_\text {pre}\) and \(\phi ^*_\text {aq}\), respectively. The physical meaning for the integration, could be related in terms of the derivative of the porosity integral on the surface.

3.1.3 Finite element implementation

The PF model was implemented using the finite element method (FEM) in the framework of the multiphysics object-oriented environment (MOOSE) [61]. 4-node quadratic Lagrangian elements were chosen to mesh the geometry. Transient solver with preconditioned Jacobian-Free Newton–Krylov method (PJFNK) and backward Euler algorithm were employed. Adaptive mesh and time stepping schemes are used to reduce computation costs. Error indicators employed in H-adaptive meshing scheme on both \(\{\phi _i\}\) and \(\{c_i\}\), with the h-level as four, were specified to guarantee the precision requirement of the diffusive interface.

3.2 Experimental method

Experimental studies were conducted at the Institute of Construction and Building Materials of the TU Darmstadt. The \({\hbox {Ca(OH)}_{2}}\) powder (ROTH, >96%) was compressed by a hydraulic press (ENERPAC P142, USA) at 40 MPa pressure into tablet specimens having dimensions of 15 mm diameter and 10 mm height (Fig. 4). The specimens were completely sealed using a vacuum impregnation device (EPOFIX from Struvers, Denmark) at a pressure of 20 kPa then a fissure opening with a width of 1.0 mm was carved along its diameter. This geometry was chosen to ensure one dimensional advancement of the carbonation reaction front. Each specimen was immersed in 200 mL distilled water and transferred to a regulated environmental chamber (ICH-C 110, Memmert, Germany) and carbonized for 3, 7, 14 and 21 days at a temperature of 20 \({^{\circ }}\)C, a relative humidity of 80% (to avoid the evaporation of water from the vessel).

Due to the low concentration of \({{\text {CO}}_{2}}\) in the atmosphere (about 0.03% by volume), the carbonation process of \({\hbox {Ca(OH)}_{2}}\) and cementitious materials is very slow in the natural environment. Accelerated carbonation experiments are usually performed in the laboratory to quickly assess the carbonation process. In the literature, the \({{\text {CO}}_{2}}\) concentration for accelerated carbonation varies from 3 to 100% [62, 63]. The carbonation rate increases with increasing \({{\text {CO}}_{2}}\) concentration. However, this development is not significant at \({{\text {CO}}_{2}}\) concentrations above 20%, due to the fact that at high \({{\text {CO}}_{2}}\) concentrations, in the outer layers of the concrete, dense carbonation microstructures are formed, which prevent further penetration of \({{\text {CO}}_{2}}\) [64]. In order to ensure that the accelerated carbonation produces a sustained self-healing effect, a \({{\text {CO}}_{2}}\) concentration of 5% by volume was chosen for this study. Here it is important to note that our model disregarded the \({{\text {CO}}_{2}}\) dissolution kinetics, by assuming that the \({{\text {CO}}^{2-}_{3}}\) is fully available in the pore system, i.e. the dissolution kinetics is instantaneous. In future modeling works, the \({{\text {CO}}_{2}}\) dissolution kinetics should be considered as well.

At each exposure time period, the corresponding specimen was taken out of the water and dried at 40 \({^{\circ }}\)C for 24 h. The crack opening was then vacuum filled with a low viscosity (nominally 0.6 mPa s) epoxy resin. After the epoxy resin hardened, the specimens were polished using a semi-automatic grinding–polishing machine (LaboSystem, Struers, Denmark), initially using a disc in hardness range HV 150–2000 at a rotational speed of 300 rpm, followed by a lubricated cloth and polycrystalline diamond spray of, consecutively, 9, 3, and 1 \({\upmu }\)m sizes at a rotational speed of 150 rpm. The polished cross-sections of the specimens were imaged by an environmental scanning electron microscopy using a back-scattered electron detector (SEM-BSE, Zeiss EVO LS25, Germany). The chemical analysis of the polished cross sections of the samples were conducted using the energy dispersive spectroscopy (EDS) detector.

Fig. 4
figure 4

Schematic procedure of \({\hbox {Ca(OH)}_{2}}\) carbonation experiments

Full size image

4 Results and discussion

4.1 Experimental validation

The purpose of the experimental observation of the carbonation reaction of a single substance, \({\hbox {Ca(OH)}_{2}}\), is to verify the appropriateness of the multiple interfaces settings in the PF model. Figure 5a shows the SEM images of specimens after different repair time. The dashed line indicates the initial solid–liquid interface \(I_{\text {a}{-}\text {s}}\). The dissolution process of calcium hydroxide occurs first on the exposure surface. As the solution penetrates the surface layer of \({\hbox {Ca(OH)}_{2}}\) is exfoliated. By day 7, typical dendritic calcium carbonate crystals can be clearly observed on the stripped layer. Based on this dendritic layer of \({{\text {CaCO}}_{3}}\) crystals, \({{\text {CaCO}}_{3}}\) will continue to precipitate and fill the voids, resulting in a porous layer. The pore system provides a channel for further bi-directional diffusion of \({{\text {CO}}_{3}^{2-}}\) and \({{\text {Ca}}^{2+}}\) ions. By day 14 it can be seen that the carbonate ions diffuse through the porous \({{\text {CaCO}}_{3}}\) layer generated at the crack surface into the \({{\text {Ca(OH)}}_{2}}\) matrix and undergo precipitation reactions, which allows the interface \(I_{\text {s}{-}\text {p}}\) to continue to move deeper into the matrix. At the same time, the interface \(I_{\text {p}{-}\text {a}}\) continued to grow toward the solution, and by day 21, the cracks had completely healed. Non-homogeneously distributed light-colored patches in the healed regions were observed in the SEM images, which was due to the studied cross-section of the precipitation region containing crystalline \({{\text {CaCO}}_{3}}\) [65]. We also analysed the different depths of the cracks in combination with stereo microscopy and found that in the 21-day sample, the deeper areas of the cracks were completely filled with calcium carbonate. \({{\text {CaCO}}_{3}}\) composition was confirmed using EDS point analysis (average composition of 40.05 wt% Ca, 15.71 wt% C, 44.24 wt% O, Fig. 5c). From the experimental results in Fig. 5b, it can be seen that by 21 days, the total moving distance of single side of \(I_{\text {p}{-}\text {a}}\) is 2.7 times greater than that of \(I_{\text {s}{-}\text {p}}\).

Fig. 5
figure 5

Image and data analysis of the interfacial migration of \({\hbox {Ca(OH)}_{2}}\) carbonation over time. a SEM image after different self-healing exposure times, i.e. 3, 7, 14 and 21 days; b comparison of numerical and experimental results of the interface migration distance, model case is abbreviated as MC and c the EDS spectrum of the self-healing product

Full size image

The experiment results also showed that \(I_{\text {s}{-}\text {p}}\) receded rapidly during the first 7 days of the experiment and moved slowly thereafter. The reason for this phenomenon is that the solute concentration of the exposed solution is zero (initial condition), i.e. the diffusion flux is initially very high. This leads to a rapid retreat of the interface due to the continuous dissolution controlled by \(L_\text {sou}\). As the precipitation reaction continues on the fracture surface, a structurally dense \({{\text {CaCO}}_{3}}\) layer is formed, which prevents the penetration of \({{\text {CO}}_{3}^{2-}}\) ions into \({\hbox {Ca(OH)}_{2}}\) matrix on the one hand, and the leaching of \({{\text {Ca}}^{2+}}\) ions into the solution on the other hand. This rate of interface migration in the PF model may be considered in the future in \(L_\text {sou}\), where this mobility should vary with time and is fundamentally a function of solute concentration and porosity. However, in this study, \(L_\text {sou}\) is simplified to a constant. The effects of varying \(L_\text {sou}\) (case 1, 2, and 3) on the evolution of \(I_{\text {s}{-}\text {p}}\) are compared with the experimental results.

The migration distances of the single side of \(I_{\text {p}{-}\text {a}}\) and \(I_{\text {s}{-}\text {p}}\) are calculated from the integration lengths of \(\phi _\text {aq}\) and \(\phi _\text {sou}\) in the 1D simulation, respectively. The model parameters for case 1 are summarized in Table 2.

The parameter \(A_i\) is taken to construct the free energy of the cementitious system (Fig. 2). The interface mobility coefficient \(L_i\) is related to the interface velocity and the driving force according to the chemical rate theory. In most of the studies, the values of interface mobility are used as empirical or hypothetical ones [49, 66]. In our study, the interface mobility was determined based on experiment results. For case 2 and case 3, \(L_\text {sou}\) has the value of \(5\times 10^{-5}\) and \(3.5\times 10^{-5}\), respectively. Other parameters are the same as that of case 1. \(c^E_\text {aq}\) is derived from the solubility of \({{\text {CaCO}}_{3}}\) at 20 \({^{\circ }}\)C and 1 atm. \(c^E_\text {pre}\) is the molar concentration of the calcium ion of \({{\text {CaCO}}_{3}}\) with a porosity of 47%. \(C^0_\text {sou}\) is calculated by dividing the density of \({{\text {CaCO}}_{3}}\) by its average molar mass [67]. The porosity of the diffusion coefficient of the source phase \(D_\text {sou}\) is obtained from the compaction density and the particle density of \({\hbox {Ca(OH)}_{2}}\) specimens, i.e. 30%. Based on the relationship between the diffusion coefficient, the open porosity and the pore morphology [68, 69], \(D_\text {sou}\) is set to be 5 orders of magnitude smaller than in its solution. As this is a crack scale model, it operates both with ion diffusivity in pore (crack) solution and effective diffusivity through porous matrix. The value of \(D_\text {pre}\) was determined by choosing the ion diffusion coefficient of a cementitious material with approximate porosity to the precipitated phase.

Figure 5b shows that the profiles of \(I_{\text {p}{-}\text {a}}\) in the three cases were in good agreement with the experimental results, although the measured value on day 7 is slightly lower than that of the simulation where the measured value on day 14 is higher than the simulated values. The results for the three models cases show a slowdown in the rate of interface migration after day 16, which is consistent with the results of the parametric analysis in Fig. 6a in Sect. 4.2. For the evolution of \(I_{\text {s}{-}\text {p}}\) it can be seen that for an increasing \(L_\text {sou}\), it is possible to facilitate the \(I_{\text {s}{-}\text {p}}\) migration in case 1 (\(7\times 10^{-5}\)) and case 2 (\(5\times 10^{-5}\)) and to make the total distance consistent with the experiments. However, the backward distance of \(I_{\text {s}{-}\text {p}}\) grows rapidly during the first 7 days of the experiment, which is not reflected in the model results, which is due to the detachment of the surface layer after soaking of the \({\hbox {Ca(OH)}_{2}}\) specimens. However, it should be noted that only the continuous dissolution is considered in this model.

Table 2 Model parameters
Full size table

4.2 Parameter research

An exhaustive series of parametric studies was conducted to identify the effect of each parameter containing an actual physical significance on the model results. Firstly, the effect of the morphology of the crack on the healing effect was analyzed. The cracks are represented by two parallel sine waves. The surface roughness is constructed by adjusting the sinusoidal frequency. The amplitude of four cases is 2 and the frequencies are 1, 5, 10 and 20 respectively. As the surface roughness increases, the precipitation fills first in the areas of greater curvature. Then the interface \(I_{\text {p}{-}\text {a}}\) gradually becomes flat. As seen in Fig. 6a1, case 4 is the first to be completely healed, while case 1 only reaches 0.8. From Fig. 6a3, it can be observed that the growth rate of self-healing ratio keeps increasing until 0.04 s, while it gradually decreases afterwards, which makes the four curves almost parallel after 0.5 s (in Fig. 6a2). This is due to the curved interface which migrates spontaneously toward the center of the curvature. The larger the curvature of the interface, the smaller the radius of the curvature, the faster the interface migration, and the faster the interface will move.

The rate of the interface migration resulting from the thermodynamic driving force of precipitation and dissolution is controlled by \(L_i\). In this model, \(L^*_\text {sou}\) and \(L^*_\text {pre}\) is referring to the normalized interface mobility coefficient of \(I_{\text {s}{-}\text {p}}\) and \(I_{\text {p}{-}\text {a}}\), respectively. Figure 6b1 shows snapshots of crack simulations with three coefficient ratios (\(L^*_\text {pre}/L^*_\text {sou}=1, 10\) and 100) at 0.3\(t^*\) and 0.6\(t^*\). It is obvious that when the coefficient ratio increases from 1 to 100, the self-healing ratio increases (Fig. 6b2) while the residual source phase ratio decreases (Fig. 6b3) significantly.

In order to simulate the physicochemical reactions correctly, the thickness of the interface has to be sufficiently small compared to the mesoscopic structure of the system; however, from a computational point of view, it is expected that the thickness of the interface has to be as large as possible in order to keep the interface from being overly densely meshed, which increases the computational effort. Therefore, for the simulation of crack healing with sinusoidal morphology, we quantitatively evaluated the effect of different interfacial widths (\(l_{i{-}j}=1, 2\) and 4) on the model behavior. Figure 6c1 shows that the operating state of sinusoidal cracks is sensitive to the interface thickness. It is evident that when the interface thickness is 1, there is a clear boundary between the two phases. And when the interfacial thickness increases to 4, the interface morphology becomes blurred. Figure 6c2 shows the spatial distribution of \(\phi _\text {pre}\) at 0.25\(t^*\) along the dashed line. As the interfacial width increases, the value of \(\phi _\text {pre}\) at the crack location becomes larger, which implies that the cracks can heal faster.

Fig. 6
figure 6

The effect PF parameter on profile of OP \(\{\phi _i\}\). a1 Simulation of self-healing with different crack morphologies, a2, a3 the evolution of normalized phase ratio and its slope; b1 Evolution of self-healing with variation of interface mobility coefficient \(L_i\), b2, b3 normalized phase ratio \(\phi ^*_\text {pre}\) and normalized phase ratio \(\phi ^*_\text {sou}\) as a function of time, respectively; Effect of interfacial width and c2 phase \(\phi _\text {shp}\) profile evolution

Full size image

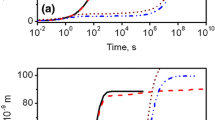
So far, for all simulations the same diffusion coefficient was assumed for each phase. Therefore, the performance of the model will be tested when varying the effective diffusion coefficient of ions in the source phase \(D_\text {sou}\) and that in the precipitation phase \(D_\text {pre}\). All of them are normalized (\(D^*_\text {sou}\) = \(5\times 10^1\), \(5\times 10^2\) and \(5\times 10^3\); \(D^*_\text {pre}\) = \(4\times 10^1\), \(4\times 10^2\) and \(4\times 10^3\)) with \(D_\text {aq}=1\times 10^{-9}\) \(\text {m}^2\)/s (see Table 1, Sect. 3.1.2). Figure 7a2 shows that the concentration profile of \(D^*_\text {sou}=5\times 10^1\) is higher compared to that of \(D^*_\text {sou}=5\times 10^2\) and \(D^*_\text {sou}=5\times 10^3\) at 0.4\(t^*\) in the ion source phase and clearly decreases from the boundary of the ion source phase to the fracture surface, especially with a low concentration spike at \(x = 34\). This is due to the large difference between \(D^*_\text {sou}\) and \(D^*_\text {pre}\), which drives the ions appearing at the crack surface to diffuse rapidly into the precipitation region forming a concentration depletion zone at the crack surface. At 0.8\(t^*\) (Fig. 7a3) the concentration spike rises due to more ions being transported to the fracture surface, thus compensating for the local concentration depletion. Figure 7a4 presents that the high concentration region (\(c^*\)=1) widened significantly with increasing \(D^*_\text {pre}\). Higher \(D^*_\text {pre}\) promotes rapid ion abstraction from the source phase, which causes the concentration to decrease with increasing \(D^*_\text {pre}\) in the ion source phase. Figure 7a5 shows the concentration profiles from 0.2\(t^*\) to 0.8\(t^*\) for \(D^*_\text {pre}=4\times 10^3\). Combining Fig. 7a5, a6, it can be observed that the expansion of the high concentration region (\(c^*=1\)) slows down with time which leads to a decrease in the precipitation phase \(\phi _\text {pre}^*\). The above results indicate that an increase in the effective diffusivity of ions produces a significant increase in the precipitation width. It is worth emphasizing that in the PF method the order parameter and the concentration field are defined based on the mean field theory, which means that the fluctuated property of the concentration coefficients in the same phase are homogenized and therefore represented by a constant value. For the case where the mass transfer (incl. diffusion and fluid transfer) depending on the local pore structures, an additional conserved order parameter and corresponding fluid dynamics should be implemented [75].

The effect of two boundary conditions (BC1 and BC2) on the self-healing efficiency is discussed next. Under BC1, the effects caused by ion concentrations of 0.5 and 1.0 are compared. The position of the studied profiles is shown in Fig. 7a1. Figure 7b investigates the self-healing ratio \(\phi _\text {pre}^*\) and normalized concentration profiles \(c_\text {i}^*\) with the above boundary conditions. As shown in Fig. 7b1, when the constant concentration \(c_\text {o}^*\) of the boundary (Fig. 3) is increased from 0.5 to 1.0, the ratio of self-healing increases. As time increases from 0.2\(t^*\) to 0.8\(t^*\), there is no change in the concentration profiles in the source phase in case of boundary with a constant concentration. In contrast, the normalized ion concentration in the source phase under BC2 decreases from 0.61 to 0.39 due to further diffusion of calcium ions from the boundary to the crack surface (Fig. 7b2, b3).

Since it is not clear whether and how the precipitation reaction term \(\varDelta _\text {r}f\) affects the concentration profiles, the effect of three cases \(\varDelta _\text {r}f\) = 5, 9 and 13 will be discussed now. The results in Fig. 7c1, c2 indicates a strong dependence of the concentration profiles on \(\varDelta _\text {r}f\). Changing \(\varDelta _\text {r}f\) from 5 to 13 produces a significant decrease of the ion concentration in the source and solution phase, which finally results in a wider precipitation region. From 0.2\(t^*\) to 0.7\(t^*\), all depressions in the middle of the curve with OS = 13 are replaced by a high concentration, indicating that the crack is completely healed. The driving force contributed by \(\varDelta _\text {r}f\) drives the ions to diffuse from the source phase into the solution eventually accumulating at the crack surface. As a result, the ion concentration in the source phase and solution decreases rapidly, while the high concentration region in the phase with self-healing products increases. The above results show that the precipitation reaction progress can be effectively controlled by adjusting \(\varDelta _\text {r}f\).

Fig. 7
figure 7

The effect PF parameter on profile of concentration \(c_i\). a1 The position of the studied profiles, a2, a3 the distribution profiles of \(c^*\) at 0.4\(t^*\) and 0.8\(t^*\) with the variation of \(D^*_\text {sou}\), respectively, a4 the distribution profiles of \(c^*\) at 0.8\(t^*\) with the variation of \(D^*_\text {pre}\), a5 the distribution profiles of \(c^*\) of the case \(D^*_\text {pre}=4\times 10^{3}\) at four time points, a6 the evolution of the normalized phase ratio \(\phi ^*_\text {pre}\) with the variation of \(D^*_\text {pre}\); b1 Evolution of self-healing ratio \(\phi ^*_\text {shp}\) with different boundary conditions, normalized concentration profile evolution b2 at 0.2\(t^*\) and b3 at 0.8\(t^*\); Evolution of normalized concentration profile with the different oversaturation terms \(\varDelta _\text {r}f\) at c1 0.2\(t^*\) and c2 0.7\(t^*\)

Full size image

4.3 Modeling applications

The following two examples (Fig. 8) demonstrate that the PF model can be used to quantitatively simulate the morphological migrations of self-healing cementitious materials. Example 1 is the autogenous self-healing studied by Lee and Ryou [16], while example 2 is bacteria-based self-healing studied by Erşan et al. [76]. The reasons for choosing these two examples are as follows. First of all, the primary mechanism of the autogenous self-healing is the crystallization of \({{\text {CaCO}}_{3}}\) [77]. Secondly, the principle mechanism of bacterial self-healing is that the bacteria act primarily as catalysts, and convert the organic biomineral precursor compound into insoluble inorganic \({{\text {CaCO}}_{3}}\) based minerals [78,79,80,81]. When bacteria control the catalytic reaction much faster than diffusion, the self-healing process is mainly controlled by diffusion. In conclusion, these two examples can be numerically treated as a dissolution and precipitation process of solutes, which is time-dependent and controlled by diffusion. Therefore, both can be simulated using the PF model proposed in this study.

The initial widths of examples 1 and 2 are taken from the experimental data, i.e., 174 \({\upmu }\)m and 318 \({\upmu }\)m, respectively. The model parameters are the same as that in Table 2 except \(L_\text {aq}= 1\times 10^{-7}\) \(\text {m}^{3}/(\text {Js})\), \(L_\text {pre}=1\times 10^{-4}\) \(\text {m}^{3}/(\text {Js})\) and \(L_\text {sou}=1\times 10^{-10}\) \(\text {m}^{3}/(\text {Js})\) used for example 1 and \(L_\text {aq}\)=\(1\times 10^{-5}\) \(\text {m}^{3}/(\text {Js})\), \(L_\text {pre}\)=\(1\times 10^{-4}\) \(\text {m}^{3}/(\text {Js})\) and \(L_\text {sou}= 1\times 10^{-10}\) \(\text {m}^{3}/(\text {Js})\) used for example 2, respectively. The precipitation reaction term \(\varDelta _\text {r}f\) is an expression of the free energy density related to the chemical formation of \({{\text {CaCO}}_{3}}\) particles (Eq. 6). In this PF model, we simplify the precipitation term to a non-negative constant. Based on the authors’ research experience, a reasonable range of values for \(\varDelta _\text {r}f\) is from 1 to 20. In order to focus on the effect of other parameters on the self-healing effect and to avoid the model being subjected to a large \(\varDelta _\text {r}f\) that would lead to too rapid healing, \(\varDelta _\text {r}f\) was taken as 5 in both examples.

Figure 8 shows schematically the concentration field c, the phase field \(\phi _i\) and the experimental results for the 2 examples at different times, respectively. At the beginning of cracking, the reactant ion concentration c is highest in the cementitious matrix and nearly 0 in the solution. At 14 days, c at the crack surface reaches 1, while a layer of self-healing products. This indicates that the \({{\text {Ca}}^{2+}}\) ions in the solution are carbonated and the concentration of \({{\text {CaCO}}_{3}}\) reaches the saturation state forming a layer of self-healing products. The concentration in the cementitious matrix is low compared to that on the crack surface. Such a difference is set to numerically reflect a physical meaning, i.e., \({{\text {CaCO}}_{3}}\) precipitation is difficult to form in the deep cementitious matrix due to the lack of \({{\text {CO}}_{2}}\). It can be carbonated only when \({{\text {Ca}}^{2+}}\) ions diffuse to the crack surface. It is one of the innovations of our model that c can reach 1 only near the crack surface, thus allowing the formation of the self-healing products locally. With this strategy, the different phases can be effectively distinguished by their concentrations and tracked by the corresponding order parameters.

It is clear from the experimental results that the morphology of the cracks largely influences their local healing effect. At the same time the morphology of the crack is constantly changing with the healing process. In the depression out of the crack surface, the healing products precipitate faster and more frequently due to the higher concentration of solutes. Therefore, its local boundary moves faster than that of other locations.

The effect of crack width on the self-healing efficiency can also be seen in the simulation results of examples 1 and 2. This effect has also been mentioned in the literature [82, 83]. From the simulation results of example 1, it can be seen that the crack healing rate from 0 to 15 days is slower than that from 15 to 23 days. This is due to the slow diffusion process of \({{\text {Ca}}^{2+}}\) ions from the cement matrix to the crack surface and their gradual accumulation in the early stage of crack appearance. Precipitation occurs only when ions concentration reaches the saturation state. The results from days 0–15 reflect the gradual accumulation of reactant concentrations. After 15 days, the crack healing rate is accelerated. This is due to the synergistic effect of \({{\text {Ca}}^{2+}}\) ions diffusing from both crack sides. However, the width of example 2 is 1.8 times wider than that of example 1, which leads to the fact that the processes of diffusion of \({{\text {Ca}}^{2+}}\) ions and occurrence of precipitation reactions on both sides of the crack are independent of each other and have no synergistic effect. Therefore the self-healing rate of example 2 was almost constant until 20 days. The self-healing rates of the two examples slowed down after 23 and 20 days, respectively. This is due to the formation of a \({{\text {CaCO}}_{3}}\) layer on the crack surface thereby preventing further diffusion of \({{\text {Ca}}^{2+}}\) ions outward.

The above two numerical simulations provides consistent results with experiments, which is encouraging as for the capacity of the present model to predict the morphology and the geometrical details of the interface migration of self-healing processes in cementitious materials. However, we should keep in mind that the comparison between numerical and experimental results is mainly qualitative, since we have focused only on the dissolution–precipitation mechanism, whereas for cementitious materials containing mineral additives, the corresponding self-healing processes have to be extended to consider more types of reactions (e.g. hydration) and additional physicochemical effects (e.g. swelling and dissolution). In addition, although the empirical relationship between effective diffusivity and porosity (single value) takes into account the effect of w/c ratio, the variation of porosity is not studied in this study. The porosity should be related to the local concentration of ions and the phase in which they are located. The diffusion coefficient could be expressed as an equation related to the porosity and pore structure [68]. This model can be flexibly extend to a multiphase multicomponent form to analyze the effect of real cementitious materials on self-healing, e.g., by adding a order parameter ϕsou_csh for \(\text {C-S-H}\) in the phase of \(\phi _\text {sou}\). For this, a thermodynamic dissolution-precipitation description should be implemented as well as a change of the homogenized properties. The fluctuated properties should be homogenized and generally represented by a non-constant value, where e.g. the effective diffusion coefficient depends on the pore structure (e.g. using empirical relations [53, 68]).

Fig. 8
figure 8

Two examples demonstrating the practical application of the PF model. a Example 1: the autogenous self-healing, reproduced with permission from the authors of [16], copyright 2014, Constr Build Mater, Elsevier; b example 2: the bacteria-based self-healing, reproduced with permission from the authors of [76], copyright 2016, Cem Concr Compos, Elsevier

Full size image

5 Conclusion

In this study, a novel PF model for self-healing of cementitious materials is presented. The model can effectively capture the evolution of dissolution and precipitation interfaces controlled by diffusion and the behavior of solute concentration profiles. From the results of this study following conclusion can be drawn:

  1. (1)

    The free energy of the system, approximated by a set of parabolic functions, varies with solute concentrations and order parameters, which is able to describe the self-healing processing by analyzing the thermodynamic driving force of the solute diffusion and precipitation in a thermodynamic-consistent way and thereby capable in recapitulating the process under various solute conditions, i.e. undersaturation, saturation and oversaturation;

  2. (2)

    Calcium hydroxide-based carbonation measurements confirm that multiple interface evolution occurs during the self-healing process. Using the derived interfacial mobility, the PF numerical simulations show a consistent agreement with the experimental results;

  3. (3)

    By conducting a series of parametric studies, it was confirmed that model parameters with clear physical meanings can reflect the evolution of multiple interfaces under different conditions;

  4. (4)

    2D simulations of the interfacial growth kinetics during the self-healing of cementitious materials were carried out. Comparison with experimental results shows that the PF model is able to provide good qualitative predictions of the morphological and geometric details of interfacial migration during self-healing of cementitious materials in terms of minerals dissolution and precipitation (Fig. 8). For a further quantitative analysis, additional types of chemical reactions and additional physical factors need to be considered.

In future studies, the free energies and the corresponding thermodynamic parameters of the involved phases will be examined to quantify mechanisms for the formation of the self-healing products, e.g. hydration kinetics, crystallization kinetics and swelling. Due to the dependence on the ion type, ion concentration, capillary pore structure, degree of chemical reaction, etc. an explicit formulation of the diffusion coefficient on relevant factors shall be derived and validated with experiments [84]. The chemistry modeling should be extended with the \({{\text {Ca}}^{2+}}\) ion diffusion coefficient to be subject to the interaction of porosity and chemical reaction rate. Ion transport and local chemical reactions can be calculated using PHREEQC (a computer program for speciation, reaction-path, advective transport, and inverse geochemical calculations). The yielded results are then transferred to the PF model for the further phase transformation analysis. The complex evolution of crack healing morphology in physicochemical processes can be accurately evaluated only in a full 3D system. All the above should be considered for further development of a comprehensive self-healing modeling tool for cementitious materials.