1 Introduction

Additive manufacturing, more commonly known as 3D printing, is an umbrella term comprising a multitude of manufacturing processes. While the exact processes differ among the individual types of additive manufacturing, these methods broadly share a mechanism by which a digitally created 3-dimensional structure is constructed by depositing a usually molten or liquid material in a layer-by-layer fashion. The structure is finished once the deposited material undergoes a physical or chemical solidifying process. While more established 3D printing methods using polymer strands have been already successful in penetrating professional and amateur markets [1, 2], methods using construction materials have been a field of mostly academic research until very recently.

Additive manufacturing using cementitious materials is often referred to as ‘3D concrete printing’ (3DCP) [3]. 3DCP processes mainly fall into one out of two categories. There are processes that rely on a particle bed being intruded by a liquid introduced from a moveable nozzle. These methods are often encountered under the terms ‘3D Particle Bed Printing’ or ‘Binder Jetting’ and are commonly abbreviated as ‘3DP’. Either the particles are inert filler (most commonly sand), the liquid acts as a binder (usually a cement paste), or the particle bed itself already contains reactive cementitious particles that are infiltrated by water. Both methods lead to a printing process where the wetted sections of material start hardening, while the nonwetted sections remain as powder and are easily separated from the final structure [4].

The second and more common process used in 3DCP is based on the extrusion of a premixed cement paste, mortar or concrete mix. Often, an extruder mounted on an industrial robot, gantry crane or a similar system is employed and used to deposit the material. This process was originally invented under the name ‘contour crafting’ [5] but is also often termed ‘liquid deposition’ (LD) in the literature. As the chemical processes that govern the early hydration kinetics of cementitious materials take several hours to complete, the mixtures being used are often highly viscous or make use of admixtures after extrusion to severely accelerate early stiffening [6].

While cementitious materials perform very well under compressive loads, the introduction of an even moderate tensile load can lead to sudden failure. Thus, the introduction of tensile reinforcement is ubiquitous when structural use is considered. The most common example is the use of reinforcing steel in concrete, a technology known since the middle of the nineteenth century [7]. Alternatively, reinforcement can be introduced in the shape of discontinuous fibers or continuous fiber-derived textile products (mats, meshes, rods, etc.). In particular, continuous meshes made from carbon fibers have started to see some use in practical applications [8, 9]. However, these continuous reinforcements must be manually introduced into the matrix and thus do not translate well into fully automated processes [10]. Recent research shows promising results with the integration of continuous yarn when using specialized printing equipment capable of realizing a flow-based pultrusion process [11,12,13].

Discontinuous chopped fibers are considerably easier to introduce into a common extrusion-based additive manufacturing process without the need for additional specialized equipment. However, their contribution to strength depends on a multitude of factors (dispersion of single fibers in the fresh paste, wetting, fiber alignment in the final specimen, etc.), and thus these systems possess a very narrow processing window and are highly sensitive to the mixing equipment used for the introduction of fibers. Systems within this processing window have been shown in recent research on multiple systems to possess an intriguing characteristic: as the material is extruded, the fibers align themselves along the travel path of the nozzle, given that the nozzle’s diameter is similar to the length of the fibers [14,15,16,17,18,19]. This allows for the creation of structural members with a fiber alignment tailor-made to a given loading scenario [20].

By using chopped fibers as reinforcement, a specific kind of cementitious composite material can be created. By fine-tuning fiber-matrix adhesion on a micromechanical level, the material no longer reacts in a brittle fashion under tension but rather shows a certain amount of pseudoductility. Instead of failing instantly, cracks are bridged by the fibers and transmit the load further along the specimen. This leads to the formation of a multitude of stable microcracks across the loaded area. Mechanistically, this behavior manifests itself in a roughly bilinear stress–strain pattern. The composite behaves in a linear-elastic fashion until the first major crack is introduced. Thereafter, the composite shows a behavior known as ‘strain hardening’; it can handle a further increasing load but at the cost of decreased stiffness. Failure occurs once fibers start rupturing or are pulled out, leading to microcracks being loaded past their point of stable crack growth. Cementitious materials meeting these criteria have been dubbed ‘engineered cementitious composites (ECC)’ or ‘strain hardening cementitious composites (SHCC)’ in the literature [21, 22]. As crack widths are limited to a few micrometers, such materials generally show superior durability, as the permeability of aggressive substances is hindered [23, 24]. The small crack width also highly facilitates the self-healing of those structures [25,26,27]. Due to these properties, this class of material is often suggested for use as a repair mortar. While structural uses have been suggested by some researchers, the achieved tensile or flexural strength is usually perceived as a limiting factor [16, 28, 29].

It has been shown that chopped and thermally oxidized carbon fibers show very good compatibility with cementitious mixes rich in silica fume, and up to 3 vol.-% can be effectively dispersed. Such a system can yield composites with a flexural strength above 100 N/mm2, given that the fibers are aligned in correspondence to the acting tensile force [15]. Promising first insights into the capability of this system as a material for additive manufacturing were published in earlier articles by our group; however, the sample dimensions were limited to a few millimeters, and mixture designs with a fiber content above 1 vol.-% turned out to be unprintable at the time. Printed samples did not reach the same strength values as manually extruded samples, likely due to questionable fiber integrity after being extruded by an auger screw [14, 15].

In this article, we present an upscaled version of this 3D printing process capable of producing specimens able to withstand flexural stresses above 100 N/mm2, and the fiber reinforcement is fully integrated into the automatic printing process. Alterations to both the mechanism of extrusion during the 3D printing process and the mixture design of the paste allowed prints with repeatable results. Specimens with fiber contents between 1 and 3 vol.-% were found to be printable without issue. The results promise the possibility of further upscaling procedures, to allow for eventual printing of larger scale elements. Great parts of this research are based on the adjustment of paste consistency to improve process stability, thus our findings indicate that further research into the influence of fluid dynamics and rheology will prove to be fruitful for understanding the processes governing fiber dispersion and alignment.

Both monolithic and mixed-material specimens were tested for their mechanical strength under flexural and compressive loads. A range of imaging techniques (i.e., optical microscopy and X-ray Computed Tomography) were used to investigate parameters critical to strength, especially porosity, fiber length and fiber alignment. In addition to regular mechanical tests under compressive and flexural loads, micromechanical single-fiber push-out tests were performed to gain insight into the fracture toughness of the transition zone between the fiber and matrix and its relation to the material’s behavior under loading. To our knowledge, this is the first time that cementitious material with the ability to withstand such loads has been successfully created by means of a fully automated 3D printing process.

2 Materials and methods

2.1 Optimization of printability and mixture design

The materials used in this research are based on prior publications of our working group [14, 15, 19]. Using the exact mixture described in Ref. [14] (termed ‘MH-2017’ for use in this publication) leads to specimens with insufficient dimensional stability and severe gaps due to failures to extrude material (also called ‘underextrusion’ by the 3D printing community). This often causes failed prints due to fiber aggregates blocking the nozzle [30]. Both issues can be addressed by raising viscosity by means of lowering the w/c ratio of the mixture, resulting in an optimized mixture referred to as ‘MR-2021’. The original and optimized mixture design can be seen in Table 1.

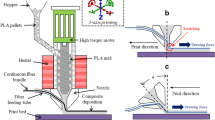
Table 1 Mixture designs used in the additive manufacturing of cementitious composites. Mixture MH-2017 was previously published by our group [14], and mixture MR-2021 is optimized for printing larger-scale specimens and used for the specimens in this publication
Full size table

The (initially seemingly paradoxical) improvement of extrusion behavior when raising viscosity has already been noted in research on fiber-reinforced epoxy-based 3D printing inks. The authors theorize that a higher viscosity considerably increases drag forces between fibers and binder paste, causing the fibers to be continuously extruded along with the fluid instead of forming aggregates [17, 18]. Print results were considerably improved by reducing the w/c value (including water from the plasticizer) from 0.28, as published in [14], down to 0.22. Measuring the change in flow behavior using a Hägermann cone (diameter: 100 mm) and flow table, the value decreased from a flow value after 15 shocks of 181 mm for the initial mixture down to 125 mm for the new stiffer mixture. A typical printing result for each mixture is illustrated in Fig. 1. Barium sulfate was added to improve the contrast between the cementitious matrix and fibers or other inclusions [31].

Fig. 1
figure 1

Typical printing result at 2 vol.-% fiber content for mixtures MH-2017 (left) and MR-2021 (right). Optimization of paste consistency leads to specimens with vastly improved dimensional stability and a more stable printing process

Full size image

The mixtures were prepared in an Eirich EL1 laboratory mixer (Maschinenfabrik Gustav Eirich GmbH & Co KG, Hardheim, Germany). Cement (CEM I 52.5 R, supplied by Schwenk Zement KG, Karlstadt cement plant), silica fume (brand name ‘EFACO’, supplied by Egyptian Ferro-Alloys Company, Cairo, Egypt) and barium sulfate (supplied by Acros Organics, Geel, Belgium) were dry-mixed at 300 RPM for 30 s. Water and superplasticizer (MasterGlenium ACE 430, Master Builders Solutions Deutschland GmbH, Trostberg, Germany) were premixed in a glass beaker and added while retaining the speed of 300 RPM for a 30-s timeframe. Once all the fluid was added, the mixture was stirred at 1000 RPM for 180 s; thereafter, mixing was paused for 30 s. Unhomogenized material stuck to the mixing container walls and stirring tool were removed and added back into the paste, and the mixture was homogenized further at 3000 RPM for 90 s. Once the paste was properly homogenized, carbon fibers (Tenax-J HT C 261, Teijin Ltd., Tokyo, Japan) were added and admixed at 300 RPM for 60 s.

Prior to use, the fibers were thermally desized at 425 °C for 2 h in an open furnace, resulting in an oxidized surface treatment and improved wettability. The carbon fibers were produced with the following specifications: length: 3 mm, diameter: 7 µm, tensile strength: 4000 N/mm2, Young’s modulus: 238 GPa.

2.2 Sample preparation and printing parameters

The original.stl files were created using FreeCAD 0.18 and sliced into.gcode format with Ultimaker Cura 4.8. Samples were printed using a 3D Potter 9 XL printer (3D Potter Inc., Stuart, FL, USA) with a 4-mm diameter nozzle at a layer height of 2.5 mm and a line width of 3.8 mm. The previous system [14] made use of an auger screw to extrude the material through a nozzle with a 3 mm diameter at a layer height of 1.5 mm. In contrast, the material was put under direct pressure using a linear actuator ram with the new 3D Potter system. This new process closely mimicked the originally published method of extruding the material through a syringe (nozzle diameter: 2 mm) [15] and was thus considerably less likely to lead to fiber degradation during printing.

The print was carried out at a printing speed of 50 mm/s (while extruding material) and a travel speed of 120 mm/s (when not extruding material). As the layer height is smaller than the nozzle diameter, the extruded strands are deformed upon deposition, leading to the extrudate being overlapped horizontally and squished vertically. This reduces excess porosity by increasing the packing factor, as the strands would be oriented in a square packing lattice if left uncompacted. Finished samples were left to harden at 100% relative humidity for 24 h and were transferred into underwater storage for another 6 days. After this period, the samples were stored in a desiccator at 59% relative humidity for 21 more days. Proper humidity levels were controlled by an oversaturated sodium bromide solution. As the printing process leaves the samples with a rough surface, samples were smoothed using a mounted die grinder (Makita GD800C, Makita Corporation, Anjo, Japan) with a cylindrical diamond grinding point installed.

2.3 Fiber integrity before and after printing

Carbon fibers are very sensitive to transversal loads, which can occur during both mixing and printing. As fibers need to retain a minimum length to be effective as reinforcement, an assessment of the remaining fiber length along the process chain is necessary. A small amount of fresh paste was taken as a sample after mixing and after printing and heavily diluted in water. After stirring, the mixture was decanted over a paper filter. To obtain reference data, this process was repeated on a sample of pristine fibers. After drying, the fiber length was measured by optical microscopy (microscope used: Leica EZ4 HD, Leica Microsystems GmbH, Wetzlar, Germany).

2.4 Mechanical testing

2.4.1 Flexural strength in 3-point-bending

Flexural testing was performed on a 3-point-bending setup in a ZwickRoell ZMART PRO (ZwickRoell GmbH & Co. KG, Ulm, Germany) universal testing machine using a 50 kN load cell. The span between the supports was set to 180.0 (± 0.1) mm. The tests were deformation controlled with a loading rate of 0.5 mm/min. Midspan deflection of the beam was measured using a ZwickRoell videoXtens 1–120 optical extensometer. The extensometer measures the vertical distance between two high-contrast black-and-white stickers once the load cell starts to register a force. The first sticker is attached to the (static) loading pin of the machine, while the second sticker is attached to the (moving) frame; thus, the difference between them relates to the midpoint deflection of the prism being tested.

The flexural stress σB is calculated from the force F continuously registered during testing according to:

$$ \sigma _{b} = 3 \cdot F_{{{\text{max}}}} \cdot c/~2 \cdot a^{2} \cdot b $$
(1)

The highest strength value measured during the test is considered to be the material’s flexural strength fct.

The flexural strain εf for each σB is calculated from the deflection d at the beam midpoint according to:

$$ \varepsilon _{f} = 6 \cdot d \cdot a/c^{2} $$
(2)

where c is the length of the span between the supports, a is the specimen thickness, and b is the specimen width.

The finished bending beams had dimensions of 40 mm × 40 mm × 220 mm, which was an elongated version of the standardized mortar prism described in DIN EN 196–1 [32]. A longer geometry was chosen to spread out transversal force, as fiber-reinforced beams tested with standard geometry can sometimes show shear failure going from a loading pin to a support instead of bending failure at the midpoint. Samples were printed using a concentric tool path, leading to fiber orientation alongside the length of the beam and thus in accordance with the tensile forces during flexural testing. An overview of all sample geometries, printing paths and definition of angles can be seen in Fig. 2, with the prism for flexural testing being represented by Fig. 2b.

Fig. 2
figure 2

Sample geometries used for mechanical testing. a Cylindrical specimens printed with a concentric circular path. b Prisms for flexural testing printed using a concentric rectangular path. c Definition of alignment angle used in this publication. The in-plane alignment is given by \(\theta \) (also called yaw), and the out-of-plane alignment is given by \(\varphi \) (also called pitch). Fibers with an in-plane alignment angle of 0° and an out-of-plane alignment angle of 90° are considered to be optimally aligned

Full size image

2.4.2 Compressive strength of cylindrical specimens

The compressive strength was tested on cylindrical samples 100 mm in length and 50 mm in diameter. The specimens were printed using a concentric circular printing path (see Fig. 2a). This allowed the fibers to transmit transversal tensile forces occurring during compressive testing.

For testing, a 1000 kN universal compression testing machine from Toni Technik GmbH (Berlin, Germany) was used. For load measurement, an external 500 kN load cell was used for displacement measurement, and two 20 mm inductive distance sensors (product name: WA-T, Hottinger Brüel & Kjaer GmbH, Darmstadt, Germany) were deployed. For deformation calculation, the two displacement signals were averaged. To survey the load bearing capacities after primary failure, tests were carried out with deformation controlled at a speed of 0.004 mm/s.

2.5 Multicomponent materials and usage as lost formwork

A concept very commonly employed in research concerning 3DCP is the use of the printed material as ‘lost formwork’, i.e., the printed material is used as a self-supporting shell that is filled with other (functional or more cost-effective) materials such as pumpable concrete mixes, manually inserted reinforcement or insulation material [5, 10]. Since specimens of our cementitious composite material already possess high amounts of load-bearing capacity when printed with high fiber content, a lost formwork approach can lead to structures with high strength while both printing time (the full volume need not be printed) and cost (as use of expensive carbon fiber is kept to a minimum) are kept low. This kind of approach also allows printing of structural members with varying amounts of (mean) fiber content without having to switch material during the printing process. Such a multimaterial approach is tested by printing the hollowed-out bending beam geometry described in Sect. 2.4.1. To achieve a wide range of fiber contents, the prisms for the lost formwork approach are printed with a fiber content of 2 or 3 vol.-% and are hollowed out in the middle by creating a pocket of variable height in the CAD model, creating specimens with a U-shaped cross-section (see Fig. 3). The pocket measures 30 mm in width and 200 mm in length. The pocket height is set to 38 mm (corresponding to a single layer of fiber-reinforced material being printed as the bottom layer), 30 mm, 20 mm and 15 mm.

Fig. 3
figure 3

Dimensions of the lost formwork printed for the multicomponent approach. a Top-down view. b Cross-section. c 3D model used to generate printing paths for additive manufacturing. d Picture of a fully hardened sample after preparation

Full size image

The mixture design of the infill mortar is given in Table 2.

Table 2 Mixture design of the infill mortar used to prepare multicomponent prisms for bending tests
Full size table

Materials already mentioned in Sect. 2.1 are from the same suppliers mentioned there. Sikron SF500 and sand H33 were supplied by Quarzwerke GmbH (Frechen, Germany). Hematite (Sigma-Aldrich, St. Louis, MO, USA) was added as a red pigment so that the fiber-reinforced material could be easily differentiated from the nonreinforced mortar. The mortar was mixed using an Eirich EL1 laboratory mixer. The solids of the infill mortar were premixed in a dry state at 300 RPM for 30 s. Water and superplasticizer were premixed in a glass beaker and added after premixing over a time span of 30 s while retaining 300 RPM. The mortar was mixed at 1000 RPM for 60 s and then mixed for 30 s to remove the undispersed material from the stirring tool and container wall and place it back into the mixture. The mortar was then homogenized for another 30 s at 1000 RPM.

The multicomponent specimens were printed using mixture MR-2021 with the same parameters laid out in Sect. 2.2 and allowed to harden for 30 min to gain some dimensional stability. After this timeframe, the infill mortar was prepared and cast into specimen pockets. Specimens were stored under the identical conditions laid out in Sect. 2.2.

2.6 Microstructural parameters derived from X-ray CT

X-ray CT was measured using a Phoenix nanotom m tomograph (GE Inspection Technologies LP, Lewistown, PA, USA). The acceleration voltage was set to 70 kV, and the beam current was set to 190 µA. The integration time was set to 2000 ms with one scan consisting of a total of 2000 single images. Images were reconstructed using Phoenix datos|x. Before reconstruction, the center of rotation for the image stack was identified using the ‘agc’ module (‘automatic geometry correction’). During reconstruction a Gaussian smoothing filter (datos|x setting: Gauss radius = 5), a USM filter (unsharp masking, datos|x settings: USM radius = 5, USM contrast = 10, USM iterations = 2) as well as an automatic ring artifact reduction were applied. The reconstructed volumes were exported into raw format and imported into ORS Dragonfly version 2020.2 (Object Research Systems (ORS) Inc., Montreal, Canada) for metrological analysis.

2.6.1 Porosity and pore size distribution

A porosity analysis was carried out on prisms with a quadratic cross-section of 10 × 10 mm. They were cut out of a printed bending beam using a Buehler IsoMet low-speed saw (Buehler Ltd., Lake Bluff, IL, USA). The scan was carried out with a voxel size of 8.6 μm, which resolves all macropores and a large number of capillary pores.

The grayscale value used as a threshold to differentiate between porosity and material was obtained by overlaying the grayscale value distribution with 2 tangents before and at the slope of the main peak and calculating their intersection. All voxels below the threshold were treated as pores, and all voxels above the threshold were treated as material. A visual representation of the process can be seen in Fig. 4. After thresholding, the segmented voxels were transferred into discrete pores by means of a connectivity analysis.

Fig. 4
figure 4

Thresholding method for segmentation of pores. By intersecting two tangents before and at the grayscale value peak, a threshold value is obtained

Full size image

For pore size distribution analysis, the equivalent radius of an ideal sphere for each individual pore is calculated from its volume according to:

$$ r_{{{\text{eq}}}} = \sqrt[3]{{(3 \cdot V_{{{\text{por}}}} /4 \cdot \pi )}} $$
(3)

where req is the equivalent radius and Vpor is the measured volume of the individual pore.

2.6.2 Fiber alignment

A fiber alignment analysis was carried out using miniature prisms with a cross-section of 1 × 1 mm. They were cut out of a printed full-size prism sample using a Buehler IsoMet low-speed saw with a diamond sawblade. The scan was taken at a voxel size of 1 µm and digitally scaled down to a voxel size of 2 µm when imported into ORS Dragonfly to lower computational demand. As the grayscale value of the carbon fibers overlaps with the values of the cementitious matrix rather than showing a separated peak in the histogram, purely threshold-based segmentation methods will not yield satisfactory results.

Instead, a method that emphasizes local gray-value deviation and geometric parameters is used, similar to other successful methods applied in the literature [33, 34]. As the fibers show very little deviation in grayscale value along their length, they appear as nearly monochromatic black features after such treatment. This in turn makes it possible to set a threshold to begin a segmentation procedure. Implementation of this method in ORS Dragonfly is realized by filtering the scan through a ‘Local Histogram Equalization’ filter. After thresholding, segmented voxels are passed through a connectivity analysis to identify discrete objects. Dragonfly automatically calculates various geometric properties (volume, surface area, aspect ratio, alignment angles, etc.) of each discrete object. This can be used for further refinement of the segmented material. The final segmentation is achieved by removing material not in line with the rodlike geometry of a fiber, i.e., objects that are unusually small or large, as well as objects with an aspect ratio approaching 1.

2.7 Single-fiber push-out tests

2.7.1 Sample preparation

For single-fiber push-out testing, plane-parallel samples with a thickness below 100 µm are required. The reinforcing fibers must be oriented perpendicular to the sample surface. To this end, thin slices of the cementitious composite with dimensions of approximately 5.0 mm x 3.0 mm x 0.7 mm were cut by a diamond saw, with the cut direction oriented perpendicular to the orientation of the carbon fibers (i.e., the printing direction). The slices were thinned to a thickness of 30–70 µm by a two-sided lapping and polishing process (Precision Lapping and Polishing System PM5, Logitech Ltd.). A lapping suspension of boron carbide particles with a grain size of 3 µm and a polishing suspension of diamond particles with a grain size of 0.25 µm were used. Four samples with different, well-defined sample thicknesses of 33 µm, 48 µm, 54 µm, and 66 µm were prepared. The thinned slices were fixed by quartz wax on glass substrates with a groove of approximately 50 µm in width located below the fibers to be tested.

2.7.2 Cyclic single-fiber push-out tests

Cyclic single-fiber push-out tests were performed using a Universal Nanomechanical Tester (Asmec GmbH). It permits displacement-controlled measurements in the normal direction with a force and displacement accuracy of 0.01 mN and 1 nm, respectively. In the lateral direction, the positioning accuracy of the indenter tip is 1 μm. The push-out tests were performed with a flat-end diamond indenter tip of approximately cylindrical shape (diameter at the tip: 4.6 µm, length: approximately 7 µm). This indenter tip allows area loading of the tested fibers without touching the surrounding matrix. In addition, it is characterized by a high stiffness and abrasion resistance. A cyclic loading schedule was used, which consisted of subsequent unloading–reloading cycles in regular steps of 100 nm. The unloading/loading segments were performed at displacement rates of 25 nm/s (first cycle), 50 nm/s (second to fourth cycle), and 100 nm/s (from the fifth cycle). The force was measured with a sampling rate of 5 Hz, which resulted in displacement resolutions of 5 nm, 10 nm, and 20 nm. Energy analysis of the load–displacement curves reveals the energy of stable crack growth. Testing of the four samples of different thicknesses allows for evaluation of the interfacial fracture toughness [35, 36].

The cementitious material is characterized by a certain porosity. To characterize the interfacial fracture toughness between the carbon fibers and cement matrix, the intact composite material and sample regions without pores were chosen for single fiber push-out testing. A distance of at least 100 µm to existing pores was upheld for every measurement. A total of 18–21 fibers were tested for each sample thickness. The surroundings of each tested fiber were documented by optical microscopy.

3 Results

3.1 Fiber integrity after printing and mixing

The histograms in Fig. 5 show the distribution of fiber length after various processing steps. Pristine, unused fibers are represented in Fig. 5a, fibers after the mixing procedure in Fig. 5b and fibers after being extruded in Fig. 5c. To place these values in perspective with our previous publications, fiber lengths after manual extrusion through a disposable syringe (Fig. 5d) and printed through an extruder using an auger screw for extrusion (Fig. 5e, Delta WASP 2040, WASP SRL, Massa Lombarda) are also included.

Fig. 5
figure 5

Histograms of length distribution of a pristine carbon fibers before use, b carbon fibers after the mixing process, c carbon fibers after being extruded by a 3D printer using a ram extruder, d carbon fibers after being extruded manually using a syringe, e carbon fibers after being extruded using a 3D printer using a screw-based extrusion process

Full size image

Prior to use, the carbon fibers show a single clear peak around a fiber length of 3 mm. Minor fiber damage is visible after mixing, with a small amount of fibers below a length of 1 mm becoming visible. Fully manual extrusion using a disposable syringe, as in [15], leads to no further observable damage. Automatic extrusion using the 3D Potter 9 XL ram extruder system leads to a slight amount of further reduction in fiber length, although a majority of fibers still retain a length of 3 mm.

Using a system dosing with the help of an auger screw, as in [14], leads to the fibers being considerably milled down in size, and a majority of the observed fibers are below a length of 1 mm. Considering that fibers need to retain a minimum length to act as tensile reinforcement [37] and to be effectively aligned by the extrusion process [18], this gives a clear explanation as to why the previously published strength values fell short of the material’s potential.

3.2 Fiber alignment in prism-shaped specimens

Figure 6 shows the distribution of fiber alignment angles measured within the sample. Figure 6a shows the in-plane alignment angle (also called yaw and denoted as \(\theta \)), while Fig. 6b shows the out-of-plane alignment angle (also called pitch and denoted as \(\varphi \)). Fibers are considered ideally aligned with the tensile force if their in-plane alignment is at 0° and their out-of-plane alignment is at 90° (see also Fig. 2c). The most well-aligned fibers are marked by the red area around the mode value of the distribution. Its width represents a one-sigma standard deviation, comprising 68% of all angles measured in the segmented dataset.

Fig. 6
figure 6

Distribution of in-plane a and out-of-plane b alignment angles obtained from the segmentation of carbon fibers present in the X-ray CT scan. The area shaded in red indicates the standard deviation (68% of all measured data points) of the dataset around the mode value, indicating the best aligned fibers. c Excerpt from a tomographic slice showing segmented fibers considered in the alignment analysis in blue

Full size image

The in-plane alignment visible in Fig. 6a shows a very sharp peak at approximately 0°, most fibers are oriented within ± 5° of the mode value, and nearly no fibers deviate more than 15° from the ideal alignment angle. The distribution of out-of-plane alignment scatters at approximately 90°. While the distribution is slightly broader in comparison to the in-plane angle, the majority of fibers are aligned within ± 10° of the ideal angle.

These values agree strongly with our prior research concerning the control of alignment angles using manual extrusion techniques [19]. In direct comparison, the alignment distributions achieved by automated 3D printing appear narrower, thus suggesting a more reliable process than manual extrusion.

3.3 Porosity and pore size distribution

Figure 7a shows the cumulative distribution of pore size by contribution of pore volume for pores of a given radius. Figure 7b shows a 3-dimensional visualization of pores segmented from the X-ray CT scan. Specimens are characterized by largely unconnected porosity with a large number of pores appearing very ellipsoidal in shape. Their longest axis seems to follow the print direction, hinting at the fact that they are caused by air entrapped in the paste during the printing process. The distribution in Fig. 7a clearly shows that smaller pores between 50 and 200 µm are the largest contributor to the total pore volume, while the larger macropores play a smaller role in terms of volume, even if they appear more visible to the naked eye. Nonetheless, their role as flaws for crack initiation must be kept in mind.

Fig. 7
figure 7

a Cumulative distribution of pore volume. The diagram shows the contribution of pores of a given radius to the total pore volume. b Three-dimensional visualization of porosity at 2 vol.-% fiber content obtained from an X-ray CT scan. The front part of the cementitious matrix was digitally removed to make the segmented pores visible

Full size image

The porosity values in Table 3 suggest that there is no direct correlation between fiber content and total porosity, with values ranging from 3.6 to 5.9%. However, the pore size distribution shows larger pores present in the specimens with 2 and 3 vol.-% fiber content, hinting at the fact that the higher viscosity of pastes with high fiber content may counteract compaction of the matrix.

Table 3 Total porosity for specimens with a fiber content between 0 vol.-% and 3 vol.-%
Full size table

3.4 Mechanical testing

3.4.1 Flexural strength of prism-shaped specimens

Figure 8a shows the stress–strain diagrams for printed prism specimens with fiber contents varying between 0 vol.-% and 3 vol.-%, and Fig. 8b shows the change in ultimate flexural strength with the fiber content. The gain of flexural strength in printed fiber-reinforced beam specimens is very pronounced, jumping from 10.8 (± 3.3) N/mm2 for unreinforced specimens to 56.7 (± 6.5) N/mm2 when admixing 1 vol.-% of carbon fibers and even further to 94.1 (± 1.0) N/mm2 when adding 2 vol.-% of fibers. The additional introduction of fibers can further improve flexural strength; however, the effect starts to suffer from severely diminishing returns. The strength only increases to a value of 106.0 (± 4.1) N/mm2 at a fiber content of 3 vol.-%. This is likely caused by the increasing tendency of the fibers to aggregate at higher volume content. Aggregated fibers do not contribute to the specimen’s tensile properties and can act as weak spots, as has been observed in prior research on this system [14, 15].

Fig. 8
figure 8

Results from flexural tests. a Stress–strain diagrams of the prisms at varying fiber contents. b Visualization of ultimate flexural strength at different fiber contents. c Crack pattern after bending failure of prisms without fiber reinforcement (top), 1 vol.-% fiber reinforcement (middle), and 3 vol.-% fiber reinforcement (bottom)

Full size image

Figure 8c shows the shape of the developing macroscopic cracks for an unreinforced prism (top), a prism with 1 vol.-% fibers (middle) and a prism with 3 vol.-% fibers (bottom). The higher the fiber content, the more crack deflection can be seen in the specimens, indicating that prisms with fiber contents of 2 vol.-% and above show an interlocking crack pattern causing secondary cracks to appear as the edges lever against each other. Further information about the mechanical properties of the specimens can be found in the supplementary material.

Aside from the pure increase in strength, a considerable increase in deformation capacity can be seen as the fiber content increases. While the unreinforced prisms show immediate brittle failure at a deformation of approximately 0.1%, admixing 1 vol.-% of fibers leads to significant microcracking that manifests itself in the characteristic pseudoductile behavior, increasing the strain-at-break values to approximately 1%. At 2 and 3 vol.-%, this strain-hardening behavior is even more pronounced, with failure occurring at approximately 1.2% deformation. Furthermore, Fig. 8a suggests that fibers improve the load-bearing capacity during linear-elastic behavior. Prisms with 1 vol.-% fiber content show linear behavior up to loads of approximately 20 N/mm2, those with 2 and 3 vol.-% even up to 40 N/mm2.

Strength values correspond very well with data previously published by our group measured on manually extruded miniature (mm scale) beam specimens [15, 19], suggesting that the size effect on strength in this material is either generally small or is being compensated by a stronger matrix caused by the (slightly) lower w/c value of the adapted mixture design or a possible reduction of porosity when moving from a manual toward an automated process.

3.4.2 Determination of interfacial fracture toughness by single-fiber push-out test

The pseudoductile failure behavior and the high toughness of cementitious composites result from multiple microcrack formations and crack bridging by the reinforcing fibers during load application. Energy dissipation through fiber-matrix debonding, frictional sliding, and fiber pull-out takes place. The microscopic failure behavior strongly depends on the fiber-matrix interfacial properties, which are characterized, e.g., by the interfacial fracture toughness.

To determine the interfacial fracture toughness between individual carbon fibers and the cement matrix, to our knowledge, micromechanical single-fiber push-out tests are applied to cementitious composites for the first time. The tested fiber, which is oriented perpendicular to the surface of a thin (thickness below 100 µm), plane-parallel sample, is loaded by a rigid indenter tip with increasing load (see Fig. 9a, left image). The increasing shear stress results in debonding of the fiber and matrix and subsequent push-out of the fiber to the sample backside (Fig. 9a, right image). The use of a cyclic loading schedule and energy analysis of the resulting load–displacement curves allows determination of the interfacial fracture toughness [35, 36].

Fig. 9
figure 9

a Schematic of the single-fiber push-out experiment with the first loading of fiber (left), crack initiation and crack growth (middle), and fiber push-out (right). b Exemplary load displacement curve of the cyclic single-fiber push-out test

Full size image

Figure 9b shows an exemplary cyclic single-fiber push-out load–displacement curve of the cementitious composite. The curve is characterized by increased and decreased hysteresis loops of force (for one cycle marked by arrows), which result from energy dissipation during loading and unloading of the fiber. The curve shows an abrupt load drop at an indenter displacement of approximately 0.86 µm. Here, complete fiber debonding and fiber push-out, i.e., an abrupt relative movement of the fiber toward the back side of the sample, was achieved [35, 38]. To date, abrupt push-out behavior during cyclic loading has been reported for fiber-reinforced ceramics (SiC/SiC) [38] and carbon fiber-reinforced polymers [35, 36, 39, 40]. This investigation shows that this behavior is also typical for cementitious composites.

Evaluation of the interfacial fracture toughness G was performed according to our previous publications [35, 36]. G is defined by the energy dissipated in stable mode II crack growth \(\Delta {E}_{\mathrm{crack},\mathrm{stable}}\) normalized to the resulting fracture surface area \({A}_{\mathrm{crack},\mathrm{stable}}\) (see (4) with fiber radius \({r}_{F}\), length of stable crack propagation \({l}_{\mathrm{stable}}\), sample thickness \(l\)):

$$G=\frac{\Delta {E}_{crack,stable}}{{A}_{\mathrm{crack},\mathrm{stable}}}=\frac{\Delta {E}_{\rm crack,stable}}{2\pi {r}_{F}{l}_{\rm stable}}=\frac{\Delta {E}_{\mathrm{crack},\mathrm{stable}}}{2\pi {r}_{F}({l-l}_{\rm unstable})}$$
(4)

To determine \(\Delta {A}_{\rm crack,stable}\), a linear relationship between the energy dissipated in stable crack growth and the sample thickness is assumed (see 5).

$$\frac{\Delta {E}_{crack,stable}}{2\pi {r}_{F}}=G\left(l-{l}_{unstable}\right)$$
(5)

From the push-out load–displacement curves, the energies of stable crack growth were determined for each tested fiber according to Refs. [35, 36]. To this end, the total plastic energy is evaluated, which includes the plastic deformation energy of the fiber and matrix and the energy of stable crack growth. The total plastic energy is the sum of all preceding plastic energy contributions, which are determined by integrating the areas between two successive loading curves.

Figure 10 shows the normalized energies of stable crack propagation for all tested fibers as a function of sample thickness together with the linear fit line. According to (5), the slope of the linear fit line defines the interfacial fracture toughness, and the intercept with the x-axis defines the length of unstable crack growth.

Fig. 10
figure 10

Normalized energy of stable crack growth together with the fit line

Full size image

The cementitious composite is characterized by an interfacial fracture toughness of 2.3 (± 0.5) J/m2. This value is significantly lower than the values reported for carbon fiber-reinforced polymers (24 J/m2 to 205 J/m2 [36, 40, 41]) and fiber-reinforced ceramics (85 J/m2 to 308 J/m2 [38]). This trend is supported by micromechanical pull-out experiments described in the literature, which report interfacial shear strength values of cement-based composites (1–8 MPa [42]) clearly below those of polymer composites (50–230 MPa [43,44,45]). The relatively low fiber-matrix adhesion thus seems to be typical for carbon fiber-reinforced cementitious composites.

The length of unstable crack propagation of the cement-based composite amounts to 22 (± 7) µm. A relatively high value is typical for brittle matrix composites. The values for brittle SiC/SiC materials range between 40 µm and 50 µm [38]. Polymer composites with a more ductile matrix, in contrast, are characterized by unstable crack growth lengths below 20 µm [35, 40, 46].

The low interfacial fracture toughness and the high length of unstable crack propagation are assumed to further the pseudoductile behavior of the cementitious composites. They facilitate microscopic failure processes such as fiber-matrix debonding and fiber pull-out, which are crucial for establishing composites with high toughness. In fact, some research in the field of SHCC recommends an interfacial fracture toughness below 2 J/m2 as an explicit design goal [47, 48]. Exceedingly high interfacial fracture toughness has been discussed as preventing pseudoductile behavior from occurring [49].

3.4.3 Compressive strength of cylindrical specimens

The influence of fibers on compressive strength can be seen in Fig. 11. The measurements suggest a slightly positive correlation between strength and fiber content, with unreinforced specimens having an average compressive strength of 104.1 (± 4.2) N/mm2 and reinforced specimens showing a strength of 117.0 (± 8.6) N/mm2 at 1 vol.-% fiber content, 107.8 (± 15.6) N/mm2 at 2 vol.-% fiber content and 131.1 (± 6.6) N/mm2 at 3 vol.-% fiber content. The deformation behavior is mostly linear-elastic, regardless of the fiber content. However, the effect of fiber reinforcement is rather small and overlaid with scattering. The improvement is likely caused by the carbon fibers transmitting transversal tensile forces that occur during compression. This trend is insofar significant, as previous research indicated a pronounced loss in compressive strength when admixing carbon fibers [15] as well as generally low compressive strength for printed specimens due to poor interlayer adhesion [14]. As the data in Fig. 11 suggest, this loss in compressive strength can be mitigated or even fully avoided with an optimized mixture design leading to well-dispersed fibers and ensuring that fibers are aligned in the direction of occurring (transversal) tensile forces. Further information about the mechanical properties of the specimens can be found in the supplementary material.

Fig. 11
figure 11

Results concerning compressive strength. a Stress–strain diagrams of cylindrical specimens at varying fiber contents. b Visualization of compressive strength at different fiber-volume contents. The dashed line represents a least-square regression suggesting slight improvement of strength with increasing fiber content. Typical appearance of a sample before c and after d testing

Full size image

3.4.4 Flexural strength of multicomponent materials

The flexural strength of the different multicomponent prisms (for geometry, see Fig. 3) obtained by the lost formwork approach can be seen in Fig. 12. As a reference, the flexural strength of monolithic prisms is shown as a gray dashed line. Specimens printed with 2 vol.-% are shown as red dots, and those printed with 3 vol.-% are shown as black dots. The depth of the pocket is given in the respective annotations. As each specimen underwent grinding during preparation, the dimensions of each individual sample could vary slightly, leading to small differences in fiber content. Thus, the fiber content was calculated individually for each sample based on the actual dimensions of the prisms being put under load during testing (i.e., everything within the load span of 180 mm).

Fig. 12
figure 12

Strength of multimaterial beams compared to monolithic printed specimens. a Flexural strength of the multimaterial prisms. The gray dashed line represents the flexural strength of printed monolithic prisms (as also seen in Fig. 8). Dots represent measured values of multicomponent prisms printed with 3 vol.-% fibers (red) and 2 vol.-% fibers (black). The annotations give the depth of the pocket filled with mortar. b Schematics of the cross-sections illustrating pocket depth in relation to specimen geometry

Full size image

Generally, the flexural strength of a multicomponent prism with a given fiber content corresponds to the strength of a monolithic prism with an equivalent fiber volume content. The main exceptions visible in Fig. 12 are the samples printed with 3 vol.-% fibers and a pocket depth of 38 mm. This is not fully unexpected, as the flexural stress is at a maximum at the bottom of the sample. The deep pocket only leaves very little fiber-reinforced material to carry this load. Once the thin layer of reinforced material breaks, only the sidewalls of the prism are able to counteract the tensile force. As a clear and expected consequence, enough reinforced material should be printed as bottom layers when producing elements that are planned to be placed under flexural load.

4 Conclusion

The use of extrusion-based manufacturing methods is a viable way to create cementitious composites with controlled fiber alignment, given that fresh paste properties fall within a viable processing window. The most important factor identified was the flow value of the paste. Remarkably, pastes more easily extrude as their flowability decreases, likely because the higher viscosity of the fresh paste acts against the tendency of dispersed fibers to separate and form aggregates. Pastes that are too fluid will lead to samples insufficient in dimensional stability and riddled with macroscopic flaws, as extrusion is prevented by blockages in the nozzle. The integrity of the dispersed fibers must be ensured throughout the whole mixing and printing process, as the brittle fibers tend to break when in direct contact with mechanical mixing tools. If a critical fiber length is to be upheld, mixing must occur briefly and at low mixing speeds only once the fibers are added. Extrusion methods that are not reliant on the paste being in direct contact with a screw are preferred. Given that both of these points are considered, specimens with exceptional flexural strength of more than 100 N/mm2 can be printed in a fully automated process. The samples are characterized by a dense matrix with largely unconnected porosity. A multimaterial approach using a combination of reinforced composite and unreinforced mortar shows that the material can be successfully used for ‘lost formwork’-type structures. The flexural strength of a given structure will be in line with its integral fiber content, given that enough composite material is present in the tensile zone of the bending beam.

As confirmed by X-ray CT, the extrusion process leads to fiber alignment following the printing path very accurately. When looking at in-plane alignment, approximately 68% of fibers are aligned within ± 5° of the nozzle’s travel path. This high number of aligned fibers leads to a pseudoductile response when the material is put under tensile loads. As cracks are formed, they are bridged by the fibers, resulting in multiple cracks over a large area instead of the formation of a critical single crack. Consequently, both flexural strength and strain-at-break values increase. Investigation of the interfacial fracture toughness can also predict the material’s pseudoductile strain-hardening behavior.

While the results obtained in this research paint a very optimistic picture for further upscaling the use of carbon fiber-reinforced cementitious composites at the structural level, further investigations on several topics will need to be addressed. Given the complex interaction of viscosity and printability of the fresh paste, further studies on the rheological parameters of the material are advised. Gaining further insights into rheology will also play an important role in the dimensional stability of larger structures. Given the need to upscale the process further to an element size relevant to buildings, further research into the relationship between nozzle geometry, fiber geometry and extrusion parameters may yield interesting results. Further insight on how the system will work with the addition of aggregates will also aid upscaling, as parameters such as shrinkage will likely to play a larger role in elements of that size.

As these materials show great promise under flexural loading, further investigations of uniaxial tensile strength also seem fruitful. Material properties derived from direct tension will also facilitate future mathematical modeling of material behavior, a further endeavor that will allow for further upscaling and aid in directed optimization of performance.