Abstract
In this recommendation, standard testing methods for determination of the double-K criterion for Mode I crack propagation in concrete using wedge-splitting tests and three-point bending beam tests are specified for the fracture parameters of the initial cracking toughness \(K_{Ic}^{ini}\) and the unstable fracture toughness \(K_{Ic}^{un}\). Along with the recommendation of the standard testing methods, the theoretical background of the double-K criterion, the calculation methods and the results of round-robin testing for determining the double-K fracture parameters are presented in technical reports [1, 2]. The recommendation of the standard testing methods includes geometry for specimens, fabrication of specimens, testing machine, load transmission system and supports, measuring instruments, determination of initial cracking load Pini, determination of measured maximum load Pmax and initial compliance ci, calculation methods for wedge-splitting test and three-point bending beam test, as well as the testing results and testing report forms. According to these methods, the measured fracture parameters of double-K criterion can be used to describe the onset of cracking, and the onset of unstable cracking or failure for predicting crack initiation, structure failure and crack stability in concrete structures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Scope
Two methods are specified in this recommendation for the determination of the initial cracking toughness \(K_{Ic}^{{{\text{ini}}}}\) and the unstable fracture toughness \(K_{Ic}^{{{\text{un}}}}\) by means of wedge-splitting tests and three-point bending beam tests. Note that these methods are specially recommended for mortar and concrete.
The initial cracking toughness \(K_{Ic}^{{{\text{ini}}}}\) defines the onset of cracking which can be directly evaluated by the initial cracking load, Pini, and the precast crack length, a0, using a formula of LEFM (Linear Elastic Fracture Mechanics). The unstable fracture toughness \(K_{Ic}^{{{\text{un}}}}\) judges unstable crack or failure, which is determined by substituting the maximum load Pmax and the critical effective crack length ac into the same formula.
Testing methods are recommended for the determination of double-K criterion. Standard cylinder compressive tests (ASTM C469/C469M-10) are employed as assistant tests to obtain the compressive strength and elastic modulus of concrete.
2 Specimens
2.1 Geometry for specimens
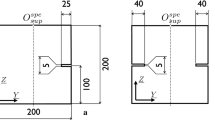
The geometries for wedge-splitting specimen and three-point bending beam are illustrated in Figs. 1 and 2 respectively.
Consider the following items to get appropriate size of specimen.
-
1.
The size of specimen depends on the maximum size of aggregate dmax. dmax can be determined by sieve analysis. When the percentage of mass passing through sieve with a certain opening size exceeds 95%, this size can be regarded as dmax.. Recommended sizes are provided in Tables 1 and 2.
-
2.
If the maximum aggregate size exceeds 40 mm, sizes listed in Tables 1 and 2 must increase proportional except for the thickness B and groove width e of wedge-splitting specimens.
-
3.
Since larger the specimen is, greater stiffness the test machine should provide, size of the specimen should be limited for less-equipped laboratories to perform tests.
-
4.
The ligament of the specimen is recommended to be larger than 5 times the maximum aggregate size dmax.
2.2 Fabrication of specimens
To help ensure the stability of the testing methods, the strength class of concrete is suggested to be no less than C20.
Both pre-cast notched specimen and saw-cut notched specimen are allowed in the recommended methods.
For pre-cast notched specimens, the original depth a0 is made by inserting a greased 3 mm-thick steel plate in the mould before casting the specimen, and the plate shall be taken out 1 day after concrete is initially set. The tip of the steel plate should be wedge-shaped with an angle of 15–30°. Note that the plate must be carefully removed from the mould without damaging the test specimen especially the initial crack tip of the specimen.
For saw-cut notched specimens, the width of the notch should be restricted to 3 mm ± 1 mm. The angle between crack plane and specimen surface is 90° ± 0.5°.
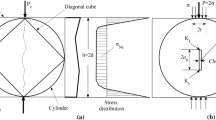
When it comes to the case of an existing structure, suitable specimens shall be cut from drilled cores. The recommended sizes in Tables 1 and 2 are still applicable to drilled core specimens but the sizes for drilled specimens are not necessary to be chosen according to dmax. A three-point bending beam can be cut directly from a core for testing. However, for wedge-splitting test, if the specimen cut from drilled core is a cube, metal blocks are needed to make a groove. Blocks shall be glued to the specimen as shown in Fig. 3 and relevant dimensions are the same as in Table 1. The glue faces shall be burnished to smoothness over 99.5% and cleaned before affixing the metal blocks with epoxy.
At least 5 specimens are needed for each group in case of damage in fabricating specimens. Besides, 3 standard cylinder compressive specimens shall be cast from the same batch of concrete to determine cylinder compressive strength and elastic modulus. For pre-cast specimens, steel mould is recommended for reducing the errors in specimen sizes caused by the deformation of mould. The cast specimen should remain in the mould, protected from shock, vibrations and drying, for at least 16 h. Then the specimen shall be removed from the mould. The specimen should be cured in the curing room with 100% relative humidity at 23 ± 2 °C for 28 days (which can be modified according to the required curing age) until about 3 days before testing.
If notches are to be cut, they are recommended to be cut 1 day before testing. Then the specimens are stored in the testing room. Shortly before test, strain gauges can be applied.
3 Apparatus
3.1 Testing machine
A loading machine with stiffness no less than 100 kN/mm is recommended to achieve a stable fracture process. Figures 4 and 5 are testing setups for wedge-splitting test and three-point bending beam test.
3.2 Load transmission system and supports
As shown in Fig. 4, load is applied through a wedging device and two steel platens (with roller bearings) during wedge-splitting test. It should be noted that inappropriate design of the steel platens, such as a wrong position of roller bearing, may cause rotation of the steel platens leading to eventual failure of test or error test results. Hence, the position of roller bearings should be designed properly in order to facilitate the installation of wedging device and measuring instrument for gaining the value of crack mouth opening displacement CMOD. Once the position of roller bearings is determined, specimen depth D denotes the distance from the center of roller bearings to the bottom of specimen while initial notch depth a0 indicates the distance from the line of the center of roller bearings to the initial crack tip. To simplify, the distance from the center of roller bearings to the top of specimen or metal block is equal to f, as described in Fig. 6. With the geometry of the wedging device, downward displacement due to vertical loading will induce horizontal movement of the roller bearings and splitting force on the concrete specimen. The bottom of the specimen rests on two linear supports (two rollers), which are located at two quartered points of specimen width W. Spherical hinges should be set under both the supports and the loading device to avoid torsion during the loading.
The required stiffness is not smaller than 100kN/mm as well for the load transmission system.
With regard to the three-point bending beam test, the width of the loading jack in a three-point bending beam test is at least equal to the thickness of the specimen. If the width of the loading jack in three-point bending beam test is less than the specimen thickness, a steel plate which is 10 mm in width, 5 mm in thickness, with a length at least equal to the thickness of the specimen is placed under the loading jack so that the load uniformly applied along specimen thickness. For better distributing the load, a rubber strip with sufficient rigid is also recommended between the loading jack and the beam. At the bottom, there should be two roller supports, providing sufficient lifting distance to install clip gauges at the bottom of the beam.
The length of the supports has to be no less than the specimen thickness for all tests.
The supports and the loading arrangements shall be such that the torsion is prevented and the applied forces acting on the beam are statically determinate.
If the load acts on casting surface of the specimen, the casting surface has to be flattened and make sure the specimen is loaded with the same rate, seen from its thickness direction.
3.3 Measuring instruments
Application of load cell is recommended. To minimize errors of the test results, capacity of load cell is 10kN. For concrete whose strength class is lower than C30, a load cell with smaller capacity is advised. The precision of the load cell is suggested to be 1% or below. To measure the value of CMOD, a clip gauge with accuracy within 0.5% is recommended. However, when a clip gauge is not available, other displacement measuring instruments with similar accuracy and resolution can also be employed.
The CMOD for wedge-splitting specimen refers to the crack opening displacement at loading line, which is the line through the center of the two roller bearings in Fig. 4. To fit the particular instrument, the width of the groove e in Fig. 4 may be increased if necessary. During the test, all test data are collected through auto data acquisition system.
In order to determine the load at initial cracking, the specimen surface should be polished before the bonding of two strain gauges in full bridge with a distance of 10 mm apart from the centerline of the original notch, as shown in Fig. 7. Given that slight damage could happen during the fabrication or transport of specimens, and the actual crack tip is hard to distinguish with naked eyes, it is suggested to glue two pairs of strain gauges to detect crack initiation. Along specimen depth direction, one pair is close to the preformed notch tip, another is 20 mm far from it, see Fig. 7. In case the torsion might occur during the loading, such gauges in Fig. 7 should be glued on both sides of the specimen, front and back.
4 Test procedure
Before testing, all geometrical dimensions of the specimen and the notch depth shall be confirmed in accordance with above recommendations. The specimen is then fixed in the loading machine with all measuring devices. The test is performed at an approximately constant loading rate controlled by CMOD. The recommended loading rate is 2 μm/min. The CMOD and the applied load are recorded continuously until the load is beyond its maximum value and decreases by 5%. Specimens in one group shall all be tested within 24 h without interruption. In three-point bending beam test, weight of the beam should always be determined while in the wedge-splitting test, weight of the wedging device needs to be measured only if it is not fixed to the testing machine.
5 Calculations
A load-CMOD curve and a load-strain curve are plotted after every test. Based on the two curves, parameters such as initial cracking load Pini, measured maximum load Pmax, critical crack mouth opening displacement CMODc and initial compliance ci shall be obtained. Then Young’s modulus E shall be computed by the initial compliance ci. Knowing value of E, Pmax and CMODc, the critical effective crack length ac can be derived. With ac and the maximum measured load Pmax, the unstable fracture toughness \(K_{Ic}^{{{\text{un}}}}\) is determined. The initial cracking toughness \(K_{Ic}^{{{\text{ini}}}}\) is calculated by Pini and the original notch depth a0.
5.1 Determination of initial cracking load P ini
Figure 8 shows the measured result from two strain gauges in full bridge configuration. When fracture initiates, propagation of the crack is accompanied by unloading at the strain gauges, as reflected by the sudden drop in strain followed by continuous decrease. The smaller one of the two initial cracking loads obtained from the two sides of the specimen is taken as the initial cracking load of the specimen Pini, and the difference between them should be less than 15%.
5.2 Determination of measured maximum load P max and initial compliance c i
Measured maximum load Pmax is the load at peak point on the load-CMOD curve, which can be directly read from Fig. 9.
For wedge-splitting test, the initial compliance ci is computed as follows:
PHi relies on Pi according to the relationship:
θ is the wedge angle of wedging device. The calculation of the initial compliance ci for three-point bending beam test is:
Pi and CMODi are the corresponding coordinate values of an arbitrary point on the linear ascending part of the load-CMOD curve, see Fig. 9.
5.3 Calculations for wedge-splitting test
Attaching the wedging device to the testing machine has a priority. If this is unavailable, test setup for wedging device not connected to the testing machine can be employed as well. For these two situations, the calculations are different.
For the situation that the wedging device is attached to the testing machine, the formulas are as follows:
The unstable fracture toughness \(K_{Ic}^{{{\text{un}}}}\) is calculated from the equation:
where
in which.
\(\alpha = \frac{{a_{{\text{c}}} + h_{{0}} }}{{D + h_{{0}} }}\)
PHmax—maximum horizontal splitting force [N];
h0—thickness of holder of clip gauge [m];
B—specimen thickness [m];
D—specimen depth [m], is the distance from the line of the center of roller bearings to the bottom of specimen;
ac—critical effective crack length[m], is composed of a0 and stable crack growth at peak load.
The maximum horizontal splitting force PHmax is related to the maximum load Pmax using Eq. 6:
where
θ—wedge angle of wedging device;
Pmax—measured maximum load [N];
The critical effective crack length ac is calculated by:
in which.
CMODc—critical crack mouth opening displacement [μm], crack mouth opening displacement collected by auto data acquisition system at the maximum load;
E—Young’s modulus [MPa], can be measured from the standard compression cylinder test or computed by Eq. 8 as follows.
where
a0—initial notch depth [m], is the distance from the line of the center of roller bearings to the initial crack tip;
ci—initial compliance [μm/N], is calculated through Eq. 1.
It is worth mentioning that the Young’s modulus E determined by Eq. 8 should be compared with the one measured from standard cylinder compressive test. Normally, the two values are close. However, if the variation of them is larger than 10% but no large than 20% of the average modulus E measured from the standard cylinder compressive tests, the specimen can be seen as slightly damaged, and the initial notch depth a0 should be recalculated by Eq. 8 with the average modulus E. Otherwise, the specimen should be taken out since there must be some damage that could not be disregarded.
The initial cracking toughness \(K_{Ic}^{{{\text{ini}}}}\) is calculated from equation:
in which
in which.
\(\alpha = \frac{{a_{{0}} + h_{{0}} }}{{D + h_{{0}} }}\),
PHini-initial horizontal splitting force [N], is given by
where
Pini—initial cracking load [N], which is measured by the strain gauge technique.
For the situation that the wedging device is not attached to the testing machine, the formulas are listed below.
The unstable fracture toughness \(K_{Ic}^{{{\text{un}}}}\) is calculated from the equation:
where
in which
\(\alpha = \frac{{a_{{\text{c}}} + h_{{0}} }}{{D + h_{{0}} }}\),
PHmax—Maximum horizontal splitting force [N];
h0—Thickness of holder of clip gauge [m];
B—Specimen thickness [m];
D—Specimen depth [m], is the distance from the line of the center of roller bearings to the bottom of specimen;
ac—Critical effective crack length[m], is composed of a0 and stable crack growth at peak load.
The maximum horizontal splitting force PHmax is given by
where
θ—wedge angle of wedging device;
Pmax—measured maximum load [N];
m—mass of the wedging device [kg];
g—acceleration due to gravity [m/s2].
The critical effective crack length ac is calculated:
in which
CMODd—Crack mouth opening displacement at the maximum load considering the influence of wedging device weight [μm], described in Fig. 9 and can be computed by the following formula.
CMODc—Critical crack mouth opening displacement[μm], crack mouth opening displacement collected by auto data acquisition system at the maximum load[μm];
ci—Initial compliance [μm/N], is calculated through Eq. 1.
E—Young’s modulus [MPa], can be measured from the standard compression cylinder test or computed by Eq. 17 as follows.
where
a0—Initial notch depth [m], is the distance from the line of the center of roller bearings to the initial crack tip.
The Young’s modulus E determined by Eq. 17 shall be compared with the one measured from standard cylinder compressive test. The specimen shall be regarded as damaged to a small extent if the variation of them is larger than 10% and less than 20% of the average modulus E measured from the standard cylinder compressive tests, and the initial notch depth a0 should be recalculated by Eq. 17 with the average modulus E. Otherwise, it indicates that the specimen become invalid with significant damage.
The initial cracking toughness \(K_{Ic}^{{{\text{ini}}}}\) is calculated from equation:
in which
in which.
\(\alpha = \frac{{a_{{0}} + h_{{0}} }}{{D + h_{{0}} }}\),
PHini-initial horizontal splitting force [N], is calculated through Eq. 11.
where
Pini—initial cracking load [N], which is measured by the strain gauge technique.
5.4 Calculations for three-point bending beam test
The unstable fracture toughness \(K_{Ic}^{{{\text{un}}}}\) is calculated from equation:
where
in which.
\(\alpha = \frac{{a_{{\text{c}}} + h_{{0}} }}{{D + h_{{0}} }}\),
Pmax—Measured maximum load [N];
h0—Thickness of holder of clip gauge [m];
B—Specimen thickness [m];
D—Specimen depth [m];
Pd—The additional central load [N], which gives rise to the same central bending moment as (M1–M2), is computed by Eq. 23;
M2—The central bending moment compensated by the support moments [N·m];
M1—The central bending moment [N·m], caused by the self-weight of the beam between the supports adds the weight of the loading arrangements which is not attached to the machine;
m1—mass of the beam [kg];
m2—mass of the loading arrangement which is not attached to the machine [kg];
g—acceleration due to gravity [m/s2];
L—specimen length [m];
S—specimen loading span [m];
ac—critical effective crack length[m], is composed of a0 and stable crack growth at peak load.
The critical effective crack length ac is given by:
in which.
CMODd—Crack mouth opening displacement at the maximum load considering the influence of additional central load [μm], shown in Fig. 9 and is computed by the following equation.
CMODc—critical crack mouth opening displacement[μm], crack mouth opening displacement collected by auto data acquisition system at the maximum load[μm];
E—Young’s modulus [MPa], can be measured from the standard compression cylinder test or computed by Eq. 27 as follows.
The computed Young’s modulus E is calculated:
where
a0—initial notch depth [m];
ci—initial compliance [μm/N].
Similarly, the Young’s modulus E determined by Eq. 27 also needs to be compared with the one measured from standard cylinder compressive test. If they vary to an extent greater than 10% but within 20% of the average modulus E calculated from the standard cylinder compressive tests, then the specimen suffers minor damage, and the initial notch depth a0 should be recalculated by Eq. 27 with the average modulus E. If the variation is larger than 20%, the specimen ceases to be effective.
The initial cracking toughness \(K_{Ic}^{{{\text{ini}}}}\) is calculated from equation:
where
in which.
\(\alpha = \frac{{a_{{0}} + h_{0} }}{{D + h_{0} }}\),
Pini—initial cracking load [N], which is measured by the strain gauge technique.
6 Test results
After the values of \(K_{Ic}^{{{\text{ini}}}}\) and \(K_{{{\text{Ic}}}}^{{{\text{un}}}}\) for each specimen in one group have been computed, the average value, standard deviation and variation coefficient of \(K_{Ic}^{{{\text{ini}}}}\) and \(K_{Ic}^{{{\text{un}}}}\) need to be calculated respectively without excluding any values of the 5 specimens. The final value of fracture parameters \(K_{Ic}^{{{\text{ini}}}}\) and \(K_{Ic}^{{{\text{un}}}}\) should be determined as the average of 5 measured values from 5 specimens in one group respectively. Values exceeding the average value by over 15% should be excluded and the remaining values are averaged to obtain the final result. If the number of usable data in one group is less than 3, the group of tests should be performed again.
7 Test report
The following information is recommended to include in the test report:
-
1.
Number of specimens tested, age of testing.
-
2.
Specimen dimensions, mass of specimen, mass of the wedging device which is not attached to the testing machine.
-
3.
Fabrication of pre-cast notch.
-
4.
Apparatus.
-
5.
Measuring instruments, accuracy of measurements.
-
6.
Test procedure description.
-
7.
Load—CMOD curve.
-
8.
Load—strain curve.
-
9.
Measured maximum load Pmax, critical crack mouth opening displacement CMODc and initial compliance ci measured from load- CMOD curve.
-
10.
Initial cracking load Pini determined by load-strain curve.
-
11.
Young’s modulus E computed with initial compliance ci.
-
12.
Critical effective crack length ac calculated by Young’s modulus E, measured maximum load Pmax and critical crack mouth opening displacement CMODc.
-
13.
Initial cracking toughness \(K_{Ic}^{{{\text{ini}}}}\) for each specimen computed with initial cracking load Pini and initial notch depth a0.
-
14.
Unstable fracture toughness \(K_{{{\text{Ic}}}}^{{{\text{un}}}}\) for each specimen computed with measured maximum load Pmax and critical effective crack length ac.
-
15.
Average values, standard deviations and variation coefficients of \(K_{Ic}^{ini}\) and \(K_{{{\text{Ic}}}}^{{{\text{un}}}}\).
In addition, the following information shall be provided:
-
1.
Type of concrete and type of raw materials used in concrete.
-
2.
Cement content and mix proportions of concrete.
-
3.
Compressive strength of concrete, determined by standard cylinder compressive testing method.
-
4.
Young’s modulus E, determined by the standard cylinder compressive testing method.
-
5.
Phenomenon and its analysis.
-
6.
Special events to be specified.
Abbreviations
- a 0 :
-
Initial notch length
- a c :
-
Critical effective crack length, corresponding to the maximum load
- B :
-
Thickness of the specimen
- c i :
-
Initial compliance
- CMOD :
-
Crack mouth opening displacement
- CMOD c :
-
Crack mouth opening displacement corresponding to the maximum load
- CMOD d :
-
Crack mouth opening displacement at the maximum load considering the influence of wedging device weight in a wedge-splitting test or additional central load in a three-point bending test
- CMOD i :
-
Crack mouth opening displacement to an arbitrary point on the linear ascending part of a load-CMOD curve
- d max :
-
Maximum size of aggregate
- D :
-
Specimen depth
- e :
-
Width of groove for a wedge-splitting specimen to affix the necessary devices for performing the test
- E :
-
Elastic modulus, calculated by initial compliance of a load-CMOD curve or determined by standard cylinder compressive test
- f :
-
Depth of groove for a wedge-splitting specimen to affix the necessary devices for performing the test
- f c :
-
Concrete compressive strength, determined by standard cylinder compressive test
- f cu :
-
Concrete compressive strength, measured by cube specimen of 150 mm × 150 mm × 150 mm
- g :
-
Acceleration due to gravity
- G F :
-
Fracture energy
- h 0 :
-
Thickness of holder of clip gauge
- K :
-
Stress intensity factor at the tip of an elastic crack
- K Ic :
-
Fracture toughness in opening mode I
- K Ic ini :
-
Initial fracture toughness
- K Ic un :
-
Unstable fracture toughness
- L :
-
Specimen length for s three-point bending beam
- M :
-
Mass of a wedge device in a wedge-splitting test
- m 1 :
-
Mass of a three-point bending beam
- m 2 :
-
Mass of loading arrangement not attached to machine in a three-point bending test
- M 1 :
-
Central bending moment caused by beam weight between supports adds loading arrangement weight not attached to machine in a three-point bending test
- M 2 :
-
Central bending moment compensated by support moments
- P :
-
Load
- P d :
-
Additional central load gives rise to the same central bending moment as (M1–M2)
- P H :
-
Horizontal load
- P Hi :
-
Horizontal load corresponding to an arbitrary point on the linear ascending part of a load-CMOD curve for a wedge-splitting test
- P Hini :
-
Initial horizontal splitting force
- P Hmax :
-
Maximum horizontal splitting force
- P i :
-
Load corresponding to an arbitrary point on the linear ascending part of a load-CMOD curve
- P ini :
-
Initial cracking load
- P max :
-
Maximum load
- S :
-
Span length in a three-point bending test
- W :
-
Wedge-splitting specimen width
- α :
-
Notch to depth ratio, calculated by (a + h0)/(D + h0)
- θ :
-
Wedge angle of a wedging device in wedge-splitting test
- σ N :
-
Nominal strength, calculated by Pmax/BD for three-point bending test and PHmax/BD for wedge-splitting test
- FPZ:
-
Fracture process zone
- LEFM:
-
Linear elastic fracture mechanics
- SIF:
-
Stress intensity factor
- TPB:
-
Three-point bending test
- WS:
-
Wedge-splitting test
References
Xu S, Li Q, Wu Y, Dong L, Lyu Y, Reinhardt HW, Leung CKY, Ruiz G, Kumar S, Hu S (2021) The theoretical basis of testing methods to determine double-K criterion for crack propagation in concrete: technical report of the RILEM TC265-TDK. Mater Struct
Xu S, Li Q, Wu Y, Dong L, Lyu Y, Reinhardt HW, Leung CKY, Ruiz G, Kumar S, Hu S (2021) Results of round-robin testing for determining the double-K fracture parameters for crack propagation in concrete: technical report of the RILEM TC265-TDK. Mater Struct. https://doi.org/10.1617/s11527-021-01788-6
Acknowledgements
The development procession of this standard was partly financially supported by the National Natural Science Foundation of China (Nos. 51310305028 and 51378461)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The “RILEM Standard Testing methods for determination of the double-K criterion for crack propagation in concrete using wedge-splitting tests and three-point bending beam tests” has been developed by members of RILEM TC265-TDK (Shilang Xu, Qinghua Li, Yao Wu, Lixin Dong, Yao Lyu ,Hans W. Reinhardt, Christopher K.Y. Leung, Gonzalo Ruiz López, Shailendra Kumar, and Shaowei Hu) within RILEM TC265-TDK ‘Testing methods for determination of double-K criterion for crack propagation in concrete’ and further reviewed and approved by all members of the RILEM TC265-TDK.
TC Membership:
Chair:Shilang Xu
Secretaries:Yao Wu.
Members: Hans W. Reinhardt, Germany; Christopher K. Y. Leung, Hong Kong, China; Gonzalo Ruiz López, Spain; Shailendra Kumar, India; Qinghua Li, China; Yao Wu, China; Yao Lyu, China; Shaowei Hu, China; Lixin Dong, China
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xu, S., Li, Q., Wu, Y. et al. RILEM Standard: testing methods for determination of the double-K criterion for crack propagation in concrete using wedge-splitting tests and three-point bending beam tests, recommendation of RILEM TC265-TDK. Mater Struct 54, 220 (2021). https://doi.org/10.1617/s11527-021-01786-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1617/s11527-021-01786-8