1 Introduction

Reinforced concrete (RC) is efficient, cost-effective, malleable and it has become the most important building material in terms of quantity. Despite its many advantages, there is still great potential for improvement, especially since a large part of the damages to RC structures is due to corrosion of the reinforcing steel [1].

As a result, it is often not possible to achieve the service lives assumed in the design of RC structures, so that either expensive repairs or entire replacement structures are required. In order to counteract this issue, researchers all over the globe investigate the potential of alternative reinforcement materials such as fibre-reinforced polymers (FRP) [2,3,4,5,6,7,8,9,10]. Carbon fibre-reinforced polymer (CFRP) reinforcement in particular has proven to be a reasonable alternative due to its resistance to corrosion and other chemical and physical attacks as well as its high tensile strength and relatively high modulus of elasticity compared to other fibre materials. In order to reach or even extend the planned service lives of RC structures through the use of CFRP reinforcement, precise knowledge of the behaviour of CFRP RC members under monotonic and cyclic long-term loading is required.

Within the scope of the joint research project Carbon Concrete Composite [11], structural tests under monotonic and cyclic long-term loading on RC members with different types of reinforcement (CFRP textile fabrics, CFRP bars, steel bars B500), cross-section (slabs, beams), load position and failure mode were carried out.

The material properties are determined experimentally and are used in the context of analytical investigations of long-term deflections as well as for the evaluation of the load-bearing capacity depending on effects due to permanent load. The results of the experimental investigations on the structural behaviour of the RC members under short-term loading have been reported in a previous publication [12].

2 Test-setup and material properties

2.1 Test-setup

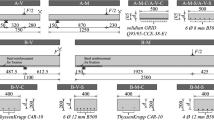
The main parameters of the RC members tested under monotonic and cyclic long-term loading are summarised in Table 1 and Fig. 1. The mean effective depths of the specimens dm were measured in the critical cross section. The RC members with reinforcing steel were designed in such a way that the mechanical reinforcement ratio ωm = As/f · ftm/(bm · dm · fcm) of the corresponding CFRP RC members is comparable. Due to the different tensile strengths of the reinforcement, the geometric reinforcement ratio ρl = As/f/(bm · dm) for the steel RC members is significantly higher compared to the CFRP RC members. The midspan deflections were measured using a wire transducer.

Table 1 Overview of the investigated test-specimens
Full size table
Fig. 1
figure 1

Cross-sections of the test specimens and test-setups

Full size image

2.2 Concrete

Two different normal strength concretes (C 40/50 and C 50/60) were used for the test series A and B, respectively (see also Table 1). The concrete properties were determined by experiments on cubes, cylinders and drill cores at different concrete ages and converted to the uniaxial compressive strength f1,c,m according to [13]. The ratios of the uniaxial compressive strength f1,c,m compared to the compressive strength fcm,cyl determined on concrete cylinders (h = 300 mm, d = 150 mm) and fcm,cube determined on concrete cubes (150 mm) are approximately 0.93 and 0.81, respectively. The uniaxial concrete tensile strength fctm is determined by converting the strength from tensile splitting tests with a conversion factor of 1.0 according to fib Model Code 2010 [14]. The experimental values as well as the results derived from mathematical functions of the time-dependent concrete compressive and tensile strengths are shown in Fig. 2.

Fig. 2
figure 2

Time-dependent concrete compressive and tensile strength

Full size image

The modulus of elasticity of the concretes were determined using concrete cylinders prepared with measuring marks and strain gauges for a stress level of σc = 0.4 · fcm at a concrete age of 276 days and 145 days for the concretes of the test series A and B, respectively. The time-dependent development of the modulus of elasticity can be calculated using Eq. (1).

$$E_{{{\text{cm}}}} (t) = \left[ {\frac{{f_{{\text{1,c,m}}} (t)}}{{f_{{\text{1,c,m,28}}} }}} \right]^{0,3} \cdot E_{{{\text{cm}}}} = \left[ {\frac{{f_{{\text{1,c,m}}} (t)}}{{f_{{\text{1,c,m,28}}} }}} \right]^{0,3} \cdot \alpha_{{\text{i}}} \cdot 21{,}500 \cdot \left( {\frac{{f_{{\text{1,c,m,28}}} }}{10}} \right) \cdot \alpha_{{{\text{Ecm}}}}$$
(1)

αi—0.8 + 0.2 · fcm/88; αEcm—1.06 for concrete grade C 40/50 (test series A)—0.93 for concrete grade C 50/60 (test series B); f1,c,m(t), f1,c,m,28—according to values given in Fig. 2.

To evaluate the concrete creep coefficients, drill cores (h ≈ 200 mm, d ≈ 00 mm) drilled out from casted cylinders were loaded in a pneumatically controlled test rig at different stress levels over a period of 224 days including a strain measurement. The experimentally determined creep coefficients φexp(t,t0) refer to the initial modulus of elasticity at a concrete age of 28 days and are compared with the creep coefficients φcalc,EN1992(t,t0) according to [15], see Fig. 3. The coefficients according to [15] are based on simplifications, since it is assumed that the moduli of elasticity are fully correlated with the concrete compressive strength. However, this is not always the case, especially with regard to the large number of possible concrete mixtures and types of aggregate. For this reason, the normative creep coefficients were modified according to the ratio of calculated and empirically obtained modulus of elasticity Ec,i,28,EN1992/Ec,i,28,exp after 28 days. In addition to the ratio of experimentally determined and calculated creep coefficients, a grey highlighted scatter range of ± 30% is shown in Fig. 3a, b. The experimentally determined creep coefficients over time are plotted in Fig. 3c, d. For stress levels up to 53% a good agreement between the experimental data and the prediction model can be seen. For stress levels higher than 70%, for which the prediction model in [15] is not calibrated, the calculated values deviate significantly from the experimental values due to highly non-linear creeping.

Fig. 3
figure 3

Comparison of experimental and calculated creep coefficients

Full size image

2.3 Reinforcement

The short-term material properties of the steel and CFRP reinforcement are listed in Table 2. The CFRP textile strands are impregnated with epoxy resin, have a cross-sectional composite area of 8.16 mm2 per strand, a fiber volume ratio of 44%, a mesh size of 38 mm and a smooth surface. The ribbed CFRP bars are also impregnated with epoxy resin, have a cross-sectional composite area of 70.12 mm2 and a fiber volume ratio of 68%. The cross-sectional composite areas are based on an immersion weighing as it is suggested in [16].

Table 2 Material properties of the reinforcement
Full size table

While epoxy resins are viscoelastic and show a significant creep behaviour, carbon fibres are comparatively creep resistant up to a temperature of 1200 K according to [17]. As a result, initial stresses in the composite cross-section that are distributed in accordance with the stiffness ratios of fiber and matrix are progressively transferred to the fibres and the strains therefore increase [18]. Assuming a mean modulus of elasticity of the epoxy resin of Em = 3000 MPa (cf. [19, 20]), the modulus of elasticity of the CFRP textile fibres and the CFRP bar fibres are Ef = 236,777 MPa and Ef = 197,296 MPa, respectively. As the fibre contents are known, the ratio of strains at t = ∞ and the initial strains can be calculated. For the CFRP reinforcement shown in Table 2, the increase in strain is calculated to be less than 1.6% of the initial strain and therefore negligible. This FRP internal creep effect can be relevant for materials with fibres of low modulus of elasticity (i. e. glass or basalt) and low fibre content, where the strain increase can reach up to 10% as it is demonstrated in several experimental investigations [21,22,23,24,25,26,27].

Due to the brittle behaviour of FRP reinforcement, the tensile strength is reduced depending on the length under tension and the number of parallel elements. The size effect underlying this phenomenon was analysed in [12, 28, 29]. For the RC members presented in this article, the reduced mean tensile strength of the CFRP textile strands and the CFRP bars can be taken as ftm = 1189 N/mm2 and ftm = 1857 N/mm2, respectively.

3 Moment–curvature relations

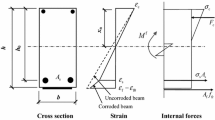
To calculate deflections, precise knowledge of the moment–curvature relations of RC cross-sections is required. In general, a trilinear moment–curvature relation as it is shown in Fig. 4 can be assumed [14, 30, 31]. In the uncracked state I up to the cracking moment Mcr, the concrete contributes in the compression as well as the tension zone, leading to a high stiffness and a low curvature. The following crack formation stage usually reaches up to a moment of 1.3 Mcr, which corresponds to the 95% quantile of the concrete tensile strength. As can be seen in Fig. 4, the curvatures in the subsequent stabilised cracking stage do not reach the pure state II, in which the concrete tensile strength is completely neglected. This is due to the so-called tension stiffening effect. In the tension zone of a cracked cross-section, the concrete strain equals zero and the tension force is fully carried by the reinforcement. Next to the crack, forces are transferred from the reinforcement to the concrete in the tension zone due to bonding. This reduces the mean strains in the reinforcement and therefore also the curvature.

Fig. 4
figure 4

Moment–curvature relation for RC cross-sections

Full size image

To take the tension stiffening effect into account, the reduced mean curvature κm can be calculated if the coefficient βt,m is known. This coefficient is dependent on the bond behaviour of concrete and reinforcement and relates the mean concrete tensile strain εcm to the maximum concrete tensile strain εct. If the ascending branch of the relation between bond stress τ and slip s is described by Eq. (2), the coefficient βt,m can be calculated via Eq. (3) according to [30, 32].

$$\tau (s) = C \cdot s^{\alpha }$$
(2)

τ(s)—bond stress depending on slip s; C—coefficient depending on reinforcement type and concrete strength; α—coefficient depending on reinforcement type and bond behaviour

$$\beta_{{\text{t,m}}} = \frac{{S_{{\text{r,m}}} }}{{S_{{\text{r,max}}} }} \cdot \frac{1 + \alpha }{{2 + \alpha }} \cdot \frac{1}{{\varphi_{{\text{b}}}^{\alpha } }} \approx \frac{2}{3} \cdot \frac{1 + \alpha }{{2 + \alpha }} \cdot \frac{1}{{\varphi_{{\text{b}}}^{\alpha } }}$$
(3)

sr,m—mean crack spacing; sr,max—maximum crack spacing; φb—bond creep coefficient; φb = (1 + 10 t)0.08—for steel reinforcement and monotonic long-term loading with t as load duration in h, according to [33]; φb = (1 + N)0.107—for steel reinforcement and cyclic long-term loading with N as number of cycles, according to [34].

For typical ribbed steel reinforcement, the coefficient α can be taken as 0.3 according to [30]. If the state of maximum crack spacing sr,max is analysed, the coefficient yields to a value of βt = (1 + 0.3)/(2 + 0.3) = 0.57 under short-term loading and is in agreement with the suggestions in [14, 15]. For the calculation of deflections, however, the mean crack spacing sr,m has to be considered and the coefficient βt,m is reduced with a factor of sr,m/sr,max = 2/3. Furthermore, the coefficient βt,m is reduced by the bond creep coefficient φb due to increasing slip resulting from monotonic or cyclic long-term loading.

To determine the bond properties and the tension stiffening coefficient βt,m, pull-out tests were conducted and reported in [12]. An analysis of the bond stress-slip relation leads to the following coefficients under short-term loading:

  • Concrete A/CFRP textiles: α = 0.44 → βt,m = 0.39.

  • Concrete A/Steel: α = 0.40 → βt,m = 0.39.

  • Concrete B/CFRP bars: α = 0.93 → βt,m = 0.44.

  • Concrete B/Steel: α = 0.56 → βt,m = 0.41.

For the CFRP bars, it could be observed, that an adhesive bond was contributing to the bond stress-slip relation. After reaching the adhesive bond strength, a high slip with no force increase occurred until the reinforcement ribs interlocked with the surrounding concrete. As the bond law in Eq. (2) has its origin at τ (s = 0) = 0, the mathematical description compensates this adhesive bond leading to a high coefficient α and therefore to an almost linear regression of the bond stress-slip relation for small values of slip.

4 RC members under monotonic loading

4.1 Test-setup and procedure

For the analysis of the structural behaviour under monotonic long-term loading with predominant bending, a total of six RC member tests were carried out over a loading period of at least 5000 h. The RC members are loaded with weights, consisting of pre-weighed concrete blocks and steel plates. These weights were lifted onto the RC members by means of a crane and slowly lowered. The weights were placed over steel plates and rods on load introduction beams, which were fixed to the RC members with gypsum lime mortar.

Due to the higher loads for the RC members under predominant shear, a test rig was constructed with which the RC members could be loaded. This construction consists of two vertical anchors, which are passed through two crossbars and fixed against the strongfloor with an interposed spring. A hydraulic jack is installed centrally between the two crossbars to apply the load. During the loading process, the hydraulic jack presses against the fixed upper crossbar thus transmitting the load to the RC member via the lower crossbar. During the loading process the actual load applied is determined and monitored by a load cell. At the same time, the high performance compression spring located below the strongfloor is compressed. The stiffnesses of the individual springs were determined in previous tests, so that the current force and the force losses in the system over time can be determined by the deformations of the springs. After reaching the test force (including an overstressing of approx. 5%), the force is first held by the hydraulic jack and time-dependent force losses due to the decreasing stiffness of the RC members are compensated. After a period of approx. one hour, the lower crossbar is fixed at the top and the hydraulic jack is removed. It was not necessary to readjust the applied force on the RC members, as the force did not drop by more than 10% during the entire test period of 5000 h.

After the test period of 5000 h the RC members were transferred to a different test rig and tested regarding their residual load-bearing capacity. The test-setup of the RC members under predominant bending and shear during the period of long-term loading are shown in Fig. 5.

Fig. 5
figure 5

Test-setup of the RC members under monotonic long-term loading

Full size image

4.2 Results and discussion

The relevant results of the experimental investigations on RC members under monotonic long-term loading including the time-dependent deflections are shown in Table 3 and Fig. 6.

Table 3 Summarised results of the member tests under monotonic long-term loading
Full size table
Fig. 6
figure 6

Time-dependent midspan deflections of the RC members under monotonic long-term loading

Full size image

To calculate the initial stress level of the RC members under predominant bending, the stresses in the reinforcement σs/f are calculated based on an iteration of the cross-section strain plane using the applied loads and the mean effective depth dm measured after the test period. These stress values are first set in relation to the expected mean value of the reinforcement tensile strength ft,m. The second stress level given in Table 3 is based on the ultimate residual tensile strength ft,m,post, which is recalculated from the load-bearing capacity of the saystem. All CFRP members showed a tension failure of the reinforcement in the residual strength tests. The experimentally determined time-dependent midspan deflections are compared to a numerical calculation showing a good agreement. The coloured areas in Fig. 6 represent a scatter range of the calculation of ± 15%. The calculation is done using a numerical approach, which divides the system into 100 elements. For each element, the individual curvature based on the relations in Fig. 4 is calculated. Creeping of the concrete compression zone is taken into account via an effective modulus of elasticity of the concrete Ec,eff (t,t0) = Ecm (t)/[1 + φ(t,t0)], although the creep coefficient is technically referred to the tangent modulus leading to a slightly lower effective modulus of elasticity Ec,eff. The bond creep equation for monotonic long-term loading given in Eq. (3) had to be adjusted for a better match of the experimental and calculated values. Keeping the same value of φb for a period of 50 years, the adjusted equation Eq. (4) was calibrated based on the experimentally derived time-dependent deflections.

$$\varphi_{{\text{b}}} \left( {t,t_{0} } \right) = 1 + 2.4 \cdot \left( {\frac{{t - t_{0} }}{{5000 + t - t_{0} }}} \right)^{0.8}$$
(4)

As it can be seen in the deflections of member B-M-C-D2, there is a sudden increase in deflection at approximately 3200 h. This is due to an additional crack that occurred. The effect of decreasing strength of concrete under sustained loading is well known and has been proven by numerous investigations [35,36,37,38]. According to [39], the concrete tensile stength under sustained loading reaches approximately 75% of the value under short-term loading.

For the interpretation of the results of the RC members under predominant shear, it is necessary to understand that the load is applied differently. When using weights, the load is applied force-controlled. In the case of shear loading, the system is partly displacement-controlled as it is loaded by the fixed crossbar described in Sect. 4.1. The irregularities in some parts of the curves in Fig. 6c, d can not be fully explained but are assumed to be caused by unstable measuring at small values of deformation. In Table 3, the shear strength under short-term loading Vexp,ref is based on the experimental investigations reported in [12]. The applied loads are given for different points in time. The first time t0 describes the loading sequence in which the load is applied by the hydraulic jack. The second time t1 describes the point at which the hydraulic jack is released. The reduction of the load is calculated by the difference of the spring compression. The third time t2 marks the end of the load duration of 5000 h. After reaching the end of load duration, the RC members were tested for their residual strength. The members A-V-C-D1 and A-V-C-D2 did not fail in shear anymore but in bending, even though the reference tests with the same geometry, reinforcement and shear slenderness showed a typical shear failure. The first reason for this is the increase of concrete strength over time due to hydratation processes as the reference tests under short-term loading were conducted at a concrete age of 54–66 days. At the time of the residual strength tests the concrete age was over 500 days and the concrete strength had increased by approximately 6%. However, the main reason for the increase of the shear strength is attributed to the increase of the concrete compression zone due to creeping of the concrete. For the members A-V-C-D the calculated increase of the concrete compression zone is approximately 34% allowing for a larger area to transfer shear stresses in the uncracked concrete compression zone. For the member B-V-C-D1, the shear strength is about 4% lower compared to the values of the reference tests. This is partly attributed to a slightly lower effective depth in the critical cross-section. Both members, B-V-C-D1 and B-V-C-D2, showed a shear failure in the residual strength tests. The increase in strength of member B-V-C-D2 was in the same order of magnitude as for the members A-V-C-D. These experimental results show good agreement with data in the literature, where similar tests were conducted on RC members with steel reinforcement [40].

5 RC members under cyclic loading

5.1 Test-setup and procedure

Cyclic loading and the resulting crack friction can cause damage to individual outer fibers in the area of the crack due to changing relative displacements and friction-induced increased temperature. Furthermore, the concrete strength decreases due to cyclic loading with increasing number of load cycles, which can lead to a critical exceeding of the shear strength. To investigate this influence, a total of 10 member tests were carried out under cyclic long-term loading with a maximum target number of load cycles of N = 106 and a load frequency of f = 1 Hz, where geometry and reinforcement were left unchanged compared to the tests under monotonic loading. The maximum and minimum load values are varied leading to different stress ranges in the reinforcement.

At first, the load is increased displacement-controlled until the upper load Fu is reached. Then the members were unloaded completely. After this first load cycle, the load application system was changed into a force-controlled programme. At the beginning of the cyclic loading, the load frequency and the amplitude were increased continuously until the target values were reached. If the members passed the 106 cycles, the residual load-bearing capacities were determined in the same test rig. The test-setup of the RC members under cyclic long-term loading is shown in Fig. 7.

Fig. 7
figure 7

Test-setup of the RC members under cyclic long-term loading

Full size image

5.2 Results and discussion

The main experimental results of the RC members under cyclic long-term loading are summarised in Table 4.

Table 4 Summarised results of the member tests under cyclic long-term loading
Full size table

Columns 4 and 5 show the upper and lower loads Fu and Fl, leading to the stress values of σs/f,u/l in the reinforcement axis at the critical cross-section given in columns 6 and 7. For the members that failed due to shear, the load levels in column 11 and 12 are calculated as the upper and lower shear forces related to the shear force capacity of the reference members (column 2). The maximum load at failure measured during the residual strength tests Fmax,post is given in Column 14. Column 15 or Failure A describes the mode of failure of the reference members under short-term loading. If a failure occurred during the cyclic loading, it is described as Failure B in column 16. If the members resisted the 106 load cycles, Failure C in column 17 describes the mode of failure in the residual strength tests.

The stress ranges and load levels were varied when more than one test per configuration could be conducted. The load level for the first test was chosen higher to target a fatigue failure of the reinforcement in case of predominant bending and shear failure in case of predominant shear. The load level for the second test was chosen lower to simulate a more realistic loading which is relevant for the analysis of deflections.

The test parameters of the four RC members under cyclic long-term loading and predominant bending (A-M-C-E1, B-M-C-E1, B-M-C-E2, B-M-S-E1) can be taken from Table 4. The stress levels are related to the reduced mean tensile strength of the CFRP reinforcement. The dead weight of the members is also taken into account. The low reinforcement ratios and high load differences lead to large deformation differences between the state of the upper and lower load, which results in high demands on the test rig and the hydraulic jack. Furthermore, the control system and hydraulic circuit react sensitively to the different stiffnesses and load scenarios of the member tests, which makes the optimisation of the control parameters indispensable. Figure 8a, b show the force–deflection curves and the deflection curves as a function of the number of load cycles of the members A-M-C-E1 and B-M-C-E1. In Fig. 8b, d, the calculated deflections and a hatched scatter range of the calculated deflections of ± 15% are also shown. The calculation is predicting the deflections under the upper load and therefore the top edge of the coloured areas. First, the maximum deflection under the upper load is calculated for the analysis. The additional deflections from cyclic long-term loading are calculated as creep deformations under the middle load Fm = (Fu + Fl)/2. In contrast to the monotonic long-term tests, it could be observed that during the cyclic loading further cracks formed. This is an indication that a reduction of the concrete tensile strength is justified under cyclic loading, see Eq. (5) according to [14].

$$f_{{\text{ct,fat}}} (N) = f_{{{\text{ct}}}} \cdot \left( {1 - \frac{\log (N)}{{12}}} \right)$$
(5)
Fig. 8
figure 8

Results of RC members under cyclic long-term loading (A-M-C-E1, B-M-C-E1, B-M-C-E2, B-M-S-E1)

Full size image

Figure 8a, c show the initial loading process, the cyclic long-term loading and the subsequent determination of the residual load-bearing capacity. All members reach the stabilised cracking stage under the upper load. Regarding the deflections w over the applied number of load cycles N, a good agreement between the experimentally and analytically determined values can be found for member A-M-C-E1. The dashed line runs along the upper edge of the red area, which represents the deflections under the upper load. Upon closer examination of the B-M-C-E1 test, it is noticeable that the measured deflections are higher than the calculated values. This is attributed to the high load level and the fact, that the maximum bond stress between concrete and CFRP reinforcement is exceeded at such high loads. The tension stiffening effect is thus overestimated, which leads to an underestimation of the deflections.

Figure 8c, d also show the results of the two members B-M-C-E2 and B-M-S-E1. As can be seen in Fig. 8d, the initial deflection of B-M-C-E2 can be calculated accurately. In this case, however, the increase in deflections exceeds the predicted value, but remains within the scatter band of ± 15%. In principle, a good agreement between the experimental and calculated values can be determined. However, members under cyclic-loading show larger additional deflections, which results from the reduced tensile strength of the concrete as well as from the more severe damage of the bond between concrete and reinforcement.

The test parameters of the six RC members under cyclic long-term loading and predominant shear can be taken from Table 4.

Figure 9 shows the test results of the four shear-members that did not fail during the cyclic long-term loading process (A-V-C-E1, A-V-C-E2, B-V-C-E2, B-V-S-E1). In the A-V-C-E2 test, shown in Fig. 9b, a decrease in stiffness at a load cycle number of approximately N = 300,000 can be seen, which is attributed to the formation of further cracks. The calculation of the deflections shows a good agreement between the experimental and calculated values. In contrast to the residual strength tests of the same members under monotonic loading (A-V-C-D1, A-V-C-D2) showing a flexural failure, the members A-V-C-E1 and A-V-C-E2 showed a shear failure. The determined residual shear force capacity after the cyclic long-term loading period was on average approximately 10% higher than the reference shear force capacity under short-term loading.

Fig. 9
figure 9

Results of RC members under cyclic long-term loading (A-V-C-E1, A-V-C-E2, B-V-C-E2, B-V-S-E1)

Full size image

The aforementioned increase of the height of the concrete compression zone due to creeping thereby increasing the shear capacity of the RC member shows its positive impact under cyclic long-term loading as well as under monotonic long-term loading. On the other hand, the concrete tensile strength is reduced by cyclic loading damage, which results in the observation that the loads cannot be increased to the same extent as under monotonic long term loading.

Figure 9c, d also show the results of the two member tests B-V-C-E2 and B-V-S-E1. No fatigue failure occurred under cyclic loading and the calculation of the deflections shows a good agreement with the experimental data. In both tests, like in the two tests A-V-C-E1 and A-V-C-E2, there was a slight increase in the shear force capacity compared to the reference values under short-term loading. Member B-V-C-E2 failed at a maximum shear force of Vmax,post = 65.5 kN which is approximately 3% more than the reference shear force capacity. At a load of Fmax,post = 208.0 kN the longitudinal steel reinforcement in member B-V-S-E1 reached the yield strength, which marks bending failure. Accordingly, the shear force capacity is at least 11.6% higher than the value of the reference members under short-term loading.

Figure 10 shows the test results of the members A-V-S-E1 and B-V-C-E1, which both failed during the cyclic long-term loading period. As described previously, the reference member of A-V-S-E1 under short-term loading did not fail due to shear but showed a flexural failure (see column 15 in Table 4). Therefore member A-V-S-E1 also did not show a shear failure but a fatigue failure of the steel reinforcement. The absolute stress range in the steel reinforcement is Δσ = 173 N/mm2 (column 6 minus column 7 in Table 4). For a number of load cycles of N = 106, the characteristic maximum stress range of welded bars and of reinforcing steel meshes according to [15] is ΔσRsk = 85 N/mm2. The actually applied stress range is more than twice this value. At a number of load cycles of N ≈ 570,000, one of the six bars of the reinforcing steel mesh failed, which can be seen from the significant deflection increase. However, the failure of one of the bars did not lead to failure of the member because the new upper stress reached a value of σu = 356 N/mm2 and was therefore still lower than the yield strength. In this state, the stress range was significantly increased to a value of Δσ = 207 N/mm2 leading to a tensile fatigue failure of the steel reinforcement at a load cycle number of N = 650,000.

Fig. 10
figure 10

Results of RC members under cyclic long-term loading (A-V-S-E1, B-V-C-E1)

Full size image

Test B-V-C-E1 failed at a number of load cycles of approximately N = 3000. It could already be observed during the first loading stage that the critical shear crack had already propagated into the compression zone. This clearly indicates that the shear force capacity of this member was lower than expected. On the one hand this is due to the large possible scattering of the shear force capacity, on the other hand the effective depth of dm = 161.7 mm (see Table 1) of this member B-V-C-E1 was approximately 10 mm (approximately 6%) lower than the mean effective depth of the reference members under short-term loading with a value of dm,short = 171.3 mm reported in [12]. The load level at the beginning of the cyclic loading must therefore be significantly higher than the calculated 80% (see column 11 in Table 4). After the critical shear crack breaks through the compression zone, the areas near the critical shear crack experience progressive damage, which ultimately leads to a brittle failure of the member. As a secondary shear failure, the CFRP bars are completely sheared off.

6 Summary and conclusions

Based on the reference tests under short-term loading reported in [12], the results of the experimental investigations on CFRP RC members under monotonic and cyclic long-term loading are presented in this article.

At first, the material properties of concrete and reinforcement were analysed in detail. For this purpose, experimental investigations were carried out on the time-dependent development of the concrete compressive and tensile strength. The creep parameters of the concretes were determined by experimental investigations and compared with prediction models. It turned out that the model in [15] provides accurate results at stress levels of 30% and 50%. At high stress levels, where non-linear creep is dominant, the creep deformations are underestimated.

To investigate the structural behaviour of CFRP RC members under monotonic long-term loading, 10 large-scaled tests with varying test parameters were conducted. None of the members failed within the long-term loading period of 5000 h. The member tests were recalculated with the help of the previously explained input parameters with regard to the time-dependent deflections, taking into account creeping of the concrete compression zone and the decreasing tension stiffening effect. A good agreement between the calculated and experimental results was observed. After the long-term loading period, the residual load capacities were determined. No significant loss of load-bearing capacity due to the applied preload was detected. The determination of the residual load-bearing capacity showed that the shear capacity increased significantly compared to the load capacity under short-term loading reported in [12]. These results correspond with the shear tests carried out on RC members with steel reinforcement in the literature, where an increase of the shear capacity was also observed. This aspect can be attributed in particular to the creep-induced increase of the height of the concrete compression zone as well as the post-hardening of the concrete.

For the investigation of the load-bearing capacity and deflection behaviour of the CFRP RC members under cyclic long-term loading, a total of 10 large-scaled tests with a maximum load cycle number of N = 106 were carried out. Despite the partly high stresses and stress ranges, no fatigue failure of the CFRP reinforcement could be observed. In two cases, members failed prematurely under cyclic loading. Member B-V-C-E1 with a maximum shear force load level of approximately 80% (related to the average value of the shear force capacity of the reference tests) failed at a load cycle number of approximately N = 3000. However, it was observed that the member showed a critical crack pattern during the initial loading process, where the critical shear crack already propagated into the compression zone. Since the shear capacity is subjected to strong scattering, the load level was probably higher than the calculated 80%. Member A-V-S-E1, which was reinforced with conventional reinforcing steel, failed after a number of load cycles of approximately N = 650,000 due to material fatigue of the reinforcing steel. The stress range was more than twice the permissible characteristic stress range for reinforcing steel meshes according to [15]. The members that did not fail during the cyclic long-term loading process were tested for their residual load-bearing capacity. Again, no general load-bearing capacity decrease could be determined. The members under cyclic long-term loading and predominant shear, similar to the members under monotonic long-term loading, tended to an increase of their shear force capacity.

In conclusion, it can be stated that concrete members with CFRP reinforcement have a high resistance to monotonic and cyclic loading. If there is no failure during long-term loading, an increase in the load-bearing capacity can be expected, especially in the case of predominant shear. The existing models for the calculation of deflections in RC structures are applicable to concrete members with CFRP reinforcement if the specific material and bond parameters are known. For FRP reinforcement with a low ratio of fibre to matrix stiffness, the FRP reinforcement tends to creep. This effect has to be taken into account when calculating deflections.