1 Introduction

Throughout the entire history of building construction, masonry has been one of the most common and efficient techniques, due to the simple geometry of units, their affordability, and great structural properties. The discontinuous and non-homogenous nature of the constitutive elements of masonry, i.e. units and mortar, strongly affects the in-plane and out-of-plane behaviour of masonry walls under various external loading. In traditional masonry block structures subjected to seismic loading, the joints between units act as planes of weakness due to their low tensile and shear bond strength, while the use of non-planar interlocking joints is recently becoming very popular to improve the mechanical behaviour at block interfaces.

The interface behaviour of traditional planar masonry joints has been widely studied with advanced non-linear computational formulations, mostly based on the homogenized finite element analysis (FEA) at the micro-scale level, detailing blocks, mortar and the block/mortar interface [1]. As an alternative, the assessment of discontinuous media composed of discrete bodies and contacts in between has increasingly been investigated using the discrete element method (DEM) first developed by Cundall [2]. This approach, specifically its version based on an explicit time integration method [2, 3], is the core of the software 3DEC [4], suitable to model 3D masonry systems as assemblages of deformable or rigid blocks with contacts representing dry or mortar joints [5,6,7,8,9,10,11,12]. The greatest advantage of DEM compared with FEA is its capability to simulate the large displacements between the bodies as well as sliding and partial or complete separation of neighbouring blocks. However, both FEA and DEM require high computational cost and advanced operational knowledge to properly define material properties, discretization, boundary conditions, input parameters, etc., which make them less convenient for everyday engineering professional applications.

Less demanding methods in terms of computational effort and accurate knowledge of state characteristics are those based on limit analysis procedures, assuming the masonry structure as an assemblage of rigid blocks and contact interfaces, with infinitive or finite friction [13]. The yield domains in terms of ultimate shear, torsion-shear and torsion-shear-bending moment interactions at joints are taken into account using convex and concave formulations [13,14,15], and experimental results carried out on 3D dry-stacked units [16, 17]. For these simplified methods, several contributions were recently proposed to assess the seismic vulnerability of masonry buildings [18, 19].

On the other hand, increasing interest has recently been devoted to interlocking blocks capable to enhance the sliding resistance of masonry joints. These blocks are rigid units which, on their faces, have locks keeping the blocks together, preventing them from sliding. Experimental and numerical tests [20] investigated the in-plane and out-of-plane capacity of masonry walls composed of blocks with corrugated interfaces. Out-of-plane behaviour of osteomorphic blocks and interfaces with cross-shaped locks were also experimentally investigated by Dyskin et al. [21] and Ali et al. [22], respectively. Similarly, experimental and numerical investigations were carried out on the different behaviour of wooden joinery connections with different geometric properties [23,24,25,26]. A digital tool to design structurally feasible masonry structures composed of interlocking blocks has been developed by some of the presenting authors [27,28,29].

One of the key factors influencing the behaviour of the conventional mortared block masonry is the bond strength between the mortar and the units, which also affects the pull-out strength of injected anchors frequently used in masonry walls [30]. Similarly, the shear strength between the locks and the main body of an interlocking block is of utmost importance for dry masonry structures made of units with corrugated interfaces. This means that, if interlocking blocks are composed of cohesive material at the interfaces between their locks and main bodies, the Mohr–Coulomb criterion can be adopted for both systems, for which the bond strength itself depends on the initial shear strength (cohesion) and the coefficient of friction, as well as the level of normal stresses. To determine the initial shear strength and the coefficient of friction, only European Standard EN 1052–3 [31] test method is available so far. However, the scientific literature shows that different domestic test methods have been developed worldwide, indicating the difficulty of finding a general consensus [32].

This paper is particularly focused on the assessment of the torsion-shear capacity of the contact interface between the lock and the main body of an interlocking block, assumed to have a cohesive behaviour. To this aim, two numerical approaches and a novel ad hoc experimental investigation are herein proposed to simulate this behaviour by applying eccentrical shear forces to the upper lock.

The paper is organised as follows. In Sect. 2, the analytical formulations of the concave, convex and corrected concave models proposed by Casapulla and Maione [14] are extended to such an interface, considering the shear resistance different from the frictional resistance. Section 3 explores the DEM capability to model interlocking joints for the simplest case study of an interlocking cuboidal block with a square cuboidal lock on its main body. A novel test method is then proposed in Sect. 4 to evaluate the initial shear and torsion-shear capacity of a single lock of an interlocking block. The test setup is similar to that used for dry-stacked tuff blocks [16], but with different load applications and constraints, to allow the absence of normal force on the cohesive interface between the two parts of the block (lock and main body) kept rigid during the tests. Section 5 presents the comparison of the analytical and numerical results against the experimental ones, with interesting remarks on the application of the different approaches. Finally, the conclusions are summarized in Sect. 6.

2 Analytical contact formulations for torsion-shear interactions in limiting conditions

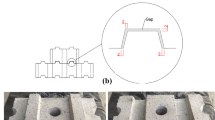
An assemblage of interlocking blocks can be modelled as a set of units with potential failure surfaces at their inner sides and boundaries. For an interlocking block represented in Fig. 1a, its main body and locks (projections keeping the blocks together) can be considered rigid enough, so that the failure surfaces are assumed to be the dry joints between two blocks (blue planes), with potential sliding along the locks, together with the fracture planes at which each block might crack (red planes). The assumption of rigid bodies for the main body and the locks becomes even more reliable as the number of locks is increased; therefore, the key issue is to define the load-bearing capacity of each lock connection.

Fig. 1
figure 1

3D representation of an interlocking block with a three locks and b only one lock

Full size image

Basically, a lock connection can be cracked due to bending or torsion-shear failure when the lock is subjected to lateral forces. Considering a sufficiently thick lock to avoid its bending failure [27], the cracking at the interface with the main body may occur for different combinations of torsion moment and shear force.

The main objective of this paper is to investigate these yield conditions at the single lock connection (Fig. 1b), which is carried out using different idealizations of the contact interfaces (listed above), among which the convexity and the concavity models are the most common ones [13]. These models are generally used for the dry contact interfaces between masonry units, governed by the cohesionless Coulomb’s law of friction, to predict the limiting forces at the interface, though providing some discrepancy in the evaluation of the torsion capacity [33]. The related analytical formulations have recently been validated by comparison of the results with the experimental investigation carried out by Casapulla and Portioli [16], based on an ad hoc setup of two dry-stacked tuff stones. A reliable corrected concave formulation has then been developed to account for the discrepancy in the torsion capacity [14].

However, to apply these models to the lock connections, a shear resistance different from the frictional resistance should be defined. The following sections will address the extension of these two formulations to the lock connection, together with the assumed interface law.

2.1 Convex and concave formulations

The concave or point contact formulation is a dominant approach to model the stress states of assemblages of rigid blocks, first developed by Livesley [13]. In this method, the contact interfaces are idealized so that the internal forces are distributed on a few contact points, usually located at the vertices of these interfaces. The stress resultant vector at each point has only a normal and a shear component, while the torsion capacity of the interface is represented by two couples of shear forces orthogonal to the interface diagonals. Moreover, different twisting centres are possible for uniform and non-uniform distributions of shear components and normal forces.

Instead, the convex contact formulation represents the interaction between two blocks via the stress state at a single point on their interface [13]. The stress resultant vector at this point includes six components of normal and shear forces as well as bending and torsion moments. It is worth noting that, although this formulation implies that the contact occurs at a single point, as if the two surfaces in contact were slightly convex, the shear, bending and torsion components imply their interactions along the entire surfaces [16].

To apply these formulations to the contact interface between the main body and the lock of an interlocking block, first the shear resistance of the interface should be introduced. In the case of cohesive-frictional material at this interface, the Mohr–Coulomb law may be used, which considers the shear resistance of a lock subjected to shear and compressive forces greater than the shear resistance of a lock only subjected to pure shear forces, because of the effect of the compression. However, for the sake of safety and to make the shear resistance independent of the normal force, the Tresca yield criterion [27, 34] is herein assumed and the pure shear resistance, e.g. due to cohesion, is considered as the limiting value, neglecting the contribution of the compressive forces. This means that the limiting pure shear force for the lock interface is (Fig. 1b):

$$V_{0} = \tau_{0} {\text{ab}}$$
(1)

where τ0 is the cohesion or the pure shear strength depending on the material properties. Based on the so defined pure shear resistance, the two formulations for torsion-shear interaction previously developed for dry contact interfaces in [14] can easily be applied to the lock interface, as summarised in the following.

The interaction effect of the torsion moment MT and the shear force V (Vx, Vy) occurs when the shear force is applied to the lock with some eccentricity e (ex, ey) with respect to the centroid O of the contact interface (Fig. 2a, b) so that MT = Vxey + Vyex. In this case, using the superimposed symbols \(\wedge\) and \(\vee\) to denote convexity and concavity, respectively, the convexity model (Fig. 2a) provides highly non-linear relationships among the variables \({\hat{V}}_{x}\), \({\hat{V}}_{y}\), \({\hat{M}}_{T}\) and the coordinates of the torsion centre T (xT, yT), as described by Casapulla [35]. In particular, when \({\hat{V}}_{x}=0\) (torsion centre on the X axis), still assuming that the shear stress at each point of the interface is orthogonal to a line connecting the point and T, the torsion-shear interaction is described by the following equilibrium equations (Fig. 2c):

$$\hat{{V_{y} }} = \hat{V} = \frac{{V_{0} }}{{4{{ab}}}}\left[ {b\left( {A - B} \right) + 2\left( {x_{T} + a} \right)^{2} \ln \frac{b + A}{{ - b + A}} + 2x_{T}^{2} \ln \frac{ - b + B}{{b + B}}} \right]$$
(2)
$$ \hat{M}_{T} = \frac{{V_{0} }}{{6{{ab}}}}\left[ { - x_{T} {{bB}} + \left( {x_{T} + a} \right){{bA}} + x_{T}^{3} \ln \frac{ - b + B}{{b + B}} + \left( {x_{T} + a} \right)^{3} \ln \frac{b + A}{{ - b + A}} - \frac{{b^{3} }}{4}\ln \frac{{2x_{T} + B}}{{2\left( {x_{T} + a} \right) + A}}} \right] - \hat{V}_{y} \left( {x_{T} + \frac{a}{2}} \right)$$
(3)

where:

$$A = \sqrt {4\left( {x_{T} + a} \right)^{2} + b^{2} } ;\;B = \sqrt {4x_{T}^{2} + b^{2} }$$
(4)
Fig. 2
figure 2

Torsion-shear interaction by the a, c convex and b, d concave contact interfaces

Full size image

Like the convexity model, the concavity model also assumes that the shear strengths at the contact points are orthogonal to the lines connecting them to T, but these strengths are concentrated in four vertices whose distances from T are denoted as di, with i = 1 to 4 (Fig. 2b). Assuming again \(\check{V}_{x} = 0\), the torsion centre is on the X axis and the following relations can be derived depending on the block dimensions (Fig. 2d):

$$\check {V}_{y} = \check {V} = \frac{{V_{0} }}{2}\left( {\sin {\upalpha }_{1} + \sin {\upalpha }_{2} } \right)$$
(5)
$$\check {M}_{T} = \left[ {\frac{{b^{2} \left( {d_{1} + d_{2} } \right) + 4d_{1} a\left( {a + x_{T} } \right)}}{{8d_{1} d_{2} }}} \right]V_{0} - \frac{a}{2}\check {V}$$
(6)

where:

$$d_{1} = \sqrt {x_{T}^{2} + \left( \frac{b}{2} \right)^{2} } ;\;d_{2} = \sqrt {\left( {x_{T} + a} \right)^{2} + \left( \frac{b}{2} \right)^{2} }$$
(7)

A family of interaction curves can numerically be obtained for both formulations, for different aspect ratios a/b. However, the results obtained by the two models are not coincident with each other, and their difference increases with the prevalence of the torsion moment, as highlighted in [14]. In that paper, it was also demonstrated how this difference is related to the overestimation of the pure torsion capacity in the concavity model, and therefore a “corrected” concave formulation was proposed. This can also be applied to the lock connection, as developed in the following.

2.2 Corrected concave formulation

As remarked in the previous section, the torsion and torsion-shear yield domains obtained by the concave formulation appear to be less reliable in comparison with those obtained by the convex formulation, but the former allows enhancing the computational efficiency when it is used in micro-modelling approaches for limit analysis of masonry walls [13].

To benefit from this advantage, the efficient correction of the torsion capacity proposed by Casapulla and Maione [14] is herein applied to the lock connection of the interlocking block (Fig. 1b), with its direct effects on the torsion-shear interaction. It is based on finding the corrected positions of the contact points in the concave model that provide the pure torsion capacity equal to the convex formulation (Fig. 3a). In fact, from the equation:

$$\hat{M}_{T0} = V_{0} c_{T} = \check {M}_{T0} = V_{0} c_{1}$$
(8)

it is derived that the position c1 of the single contact point in Fig. 3b will be:

$$c_{1} = c_{T} = \frac{1}{{12{{ab}}}}\left( {a^{3} {\text{ln}}\frac{b + d}{a} + b^{3} {\text{ln}}\frac{a + d}{b} + 2{{abd}}} \right)$$
(9)

where \(d = \sqrt {a^{2} + b^{2} }\) is the length of the diagonals.

Fig. 3
figure 3

Shear stresses and/or forces over the a convex and b corrected concave contact interfaces under axial compression and pure torsion moment

Full size image

This means that a reduced effective area can be derived, with dimensions:

$$a_{1} = \frac{{c_{T} }}{c}a;\;b_{1} = \frac{{c_{T} }}{c}b$$
(10)

where c is the actual half-diagonal, i.e. c = d/2. Therefore, Eqs. (5) and (6) become:

$$\check {V}_{y} = \check {V} = \frac{{V_{0} }}{2}\left( {\sin {\upalpha }_{1} + \sin {\upalpha }_{2} } \right)$$
(11)
$$\check {M}_{T} = \left[ {\frac{{b_{1}^{2} \left( {d_{1} + d_{2} } \right) + 4d_{1} a_{1} \left( {a_{1} + x_{T} } \right)}}{{8d_{1} d_{2} }}} \right]V_{0} - \frac{{a_{1} }}{2}\check {V}$$
(12)

where V0, d1 and d2 are derived by Eqs. (1) and (7), respectively, by replacing a and b with a1 and b1 in Eq. (10).

As will be shown in Sect. 5, this criterion also affects the torsion-shear interaction and can therefore be used as a potential yield domain for the lock connection.

3 Numerical analysis for torsion-shear interactions in limiting conditions using discrete element modelling (3DEC)

The torsion-shear capacity of the lock connection in Fig. 1b is herein also investigated using the discrete element approach by means of 3DEC [4], a 3D numerical modelling code for advanced analysis of discontinuous media subjected to either static or dynamic loading [2, 3].

Generally speaking, a concave-shaped element simulating the interlocking block in Fig. 1b could be modelled in 3DEC by joining two convex polyhedrons, representing the lock and the main body (Fig. 4a). However, to reproduce the torsion-shear behaviour at their interface better, these two convex polyhedrons are herein considered as individual rigid units stacked over each other with a cohesive contact in between (Fig. 4b). Each of the rigid blocks is a body with three translational and three rotational degrees of freedom, while the deformable contact is discretized into finite elements, with three translational degrees of freedom at each vertex, based on the contact stress-displacement law.

Fig. 4
figure 4

a Concave-shaped block modelled in 3DEC, b 3DEC interlocking block modelled in this paper with a cohesive contact between its main body and lock, c to f replacing the pointed force normal to the X axis with a linearly distributed force

Full size image

Considering the interlocking block under study, high stiffnesses and Mohr–Coulomb criterion are assumed for the deformable interface between the two rigid parts (lock and main body). In particular, to approach the rigid-plastic behaviour assumed within the analytical formulations in Sect. 2, the normal and tangential stiffnesses of the contact interface can be considered equal to (or greater than) 1010 N/m, while to avoid the tensile failure at the same contact, the tensile strength is considered large enough, i.e. 105 N/m2. On the other hand, while the cohesion value is equal to the material shear strength, as applied in Sect. 5, to make the shear resistance independent of the normal stress (like the Tresca model), the contact friction angle is set to be zero.

To investigate the torsion-shear behaviour of the lock connection, the lower main body is fully fixed, while the upper lock is subjected to lateral point loads. These have different eccentricities with respect to the contact centroid to find the maximum load the contact can bear. Since applying point loads to the rigid block boundary is not possible in 3DEC, boundary stresses are instead applied as non-uniformly distributed forces, equivalent to a point load with some eccentricity.

Two directions of the point load are herein considered, including the lateral force normal to X (Fig. 4c) and 45° inclined with respect to this axis (Fig. 5a).

Fig. 5
figure 5

Replacing the pointed force 45° inclined with respect to the X axis with two linearly distributed forces

Full size image

A force Vy normal to the X axis with eccentricity ex can be substituted by the same force and a torque My = Vyex applied to the centroid of the vertical lock face (Fig. 4d). Their distributions on the 2D lateral face of the lock (equal to ah) are displayed in Fig. 4e, where:

$$V_{dy,h} = \frac{{V_{y} }}{ah};\;M_{dy,h} = \frac{{6M_{y} }}{{a^{2} h}}$$
(13)

and the slope ky of the linear distribution is:

$$k_{y} = \frac{{12M_{y} }}{{a^{3} h}}$$
(14)

On the other hand, an inclined force V with eccentricity e can be decomposed by two components normal to the X and Y axes, i.e. \({V}_{x}={V}_{y}=\frac{\sqrt{2}}{2}V\) and \({e}_{x}={e}_{y}=\frac{\sqrt{2}}{2}e\) (Fig. 5a,b). The components of the force and torque in the two directions can be substituted by {Vdy,h, Mdy,h} and {Vdx,h, Mdx,h} (Fig. 5c), respectively defined by Eq. (13) and by:

$$V_{dx,h} = \frac{{V_{x} }}{bh};\;M_{dx,h} = \frac{{6M_{x} }}{{b^{2} h}}$$
(15)

while the slope kx of the linear distribution is:

$$k_{x} = \frac{{12M_{x} }}{{b^{3} h}}$$
(16)

Summing up each pair of the distributed forces representing V and M, a linearly non-uniform distributed force is obtained (Figs. 4f and 5d).

To study the torsion-shear behaviour of the cohesive contact, the ultimate normal and inclined V are found for different eccentricities, by incrementally increasing V. The ultimate V is, in fact, the maximum lateral force equilibrating the system. However, in the case of the pure shear condition, the shear stress at the interface multiplied by the contact area has turned out to be different from the applied V. This discrepancy occurs when the width of the lock is smaller than that of the main body, and to remedy this drawback, the main block has been divided into three fixed parts (Fig. 6a). The shear and tensile strengths at the vertical contacts between them are considered very large to simulate they are part of a unique rigid block.

Fig. 6
figure 6

a, b Discretisation of the main body to remove the equilibration error; different face triangulation models for the contacts between rigid blocks as: c radial, d rad8 and e divide-join rad8

Full size image

Furthermore, it has been observed that applying the non-uniformly distributed force on a rigid model, the shear stress distribution varies for different types of face triangulations. A contact can be discretised using different triangulation commands provided by 3DEC and the ideal commands are those that can discretize a contact symmetrically. Two of these commands are “radial” and “rad8”, where the former adds a vertex on the face centroid, the latter adds vertices on the face centroid and on the middle of boundary edges (Fig. 6b–d).

Also, the contact can be discretised into smaller sub-contacts with more contact points through dividing and then joining the related polyhedrons. Figures 6c–e show a cohesive interface divided into four pieces, triangulated using rad8, and joined again (divide-join rad8), respectively.

Difference in the shear stress distribution results in finding different ultimate force V, and the difference increases with the eccentricity. Later in Sect. 5, the obtained ultimate V found by these four face triangulation types are compared to those obtained by analytical and experimental investigations.

4 Experimental investigation on the lock under torsion-shear loading

In this section, an experimental investigation on the limiting pure shear and torsion-shear combinations at the lock interface of a simple interlocking block made of cohesive material is presented. An ad hoc test setup was realized to estimate these resistances at the interface between the lock and the main body, while keeping them rigid.

Two different mortars were chosen to make the specimens, which were casted using 3D printed moulds, and four different test configurations (sets) were set up to simulate shear and torsion-shear failures. Combining the four sets and the two mortars, eight samples were tested. Two samples were tested in pure shear (each involving four specimens), while six samples were tested in torsion-shear condition (each involving three specimens), in total providing twenty-six experimental results.

The experimental investigation was carried out with standard and non-standard equipment at Laboratory of the Department of Structures for Engineering and Architecture (DiSt) of the University of Napoli Federico II (Italy).

4.1 Specimen shape and characterization of two mortars

The first phase of the experimental investigation focused on finding the proper shape and dimensions for the interlocking block and appropriate mechanical properties for the specimens made of cohesive material.

The designed specimen is composed of a main body, which is a 100 x 90 x 50mm3 cuboid, with a 100 x 30 x 15mm3 cuboidal lock located on its upper face (Fig. 7a). Before defining this final shape, several specimens were made by casting mortars with different mixtures in a mould (an ad hoc formwork to make the customized lock dimensions), and different moulds were also explored. The final formwork was composed of pieces provided in the desired shape and dimension by a 3D printer (Fig. 7b, c).

Fig. 7
figure 7

a Designed specimen (the dimensions are in mm); b, c printed moulds; d curing phase

Full size image

On the other hand, calibrating the mechanical properties of the appropriate mortar was a crucial issue, and the first phase of the experimental program was aimed to obtain: (1) failure load values consistent with the designed setup (limit load = 500 N) and within the valid range of the employed instrumentation; (2) failure modes corresponding to instantaneous and clear cutting of the lock from the main block (cohesive crack). After several attempts with traditional mortars, non-standard M1 and M2 mortars were finally defined, whose composition and curing time are reported in Table 1.

Table 1 Composition and mechanical properties of the tested mortars
Full size table

The main components of M1 are Pozzolana, a volcanic material from Pozzuoli (Naples, Italy) with a range of colours between grey and red [36, 37], and lime, supplied by the Neapolitan company Cimmino Calce s.r.l., which is a calcium-containing inorganic mineral still extensively used as a building and engineering material. M2 is instead a cement-based mortar in which the cement took the place of lime, with different percentages. The mixtures were prepared using the amount of water required to ensure enough workability and normal consistency. According to the European Standard UNI EN 1015–2 [38], the pastes were compacted during the casting process to remove any air bubbles and voids. Curing was performed in ambient laboratory conditions (relative humidity 60 ± 10% and 20 ± 5 °C) until the test day (Fig. 7d). Flexural and compressive tests were also carried out using standard equipment, based on the UNI EN 1015–11 [39], and the mean values of the measured density and strengths are summarized in Table 1.

4.2 Test setup

The test setup was specifically designed to investigate the pure shear and torsion-shear resistances of the lock interface, and to this aim several issues were taken into account. To minimise the effect of bending usually experienced during shear tests [32] and to neglect the pre-compression force, which are the main challenges of the classical experimental setup [31], a new setup was developed for the experimental tests.

Actually, a horizontal load was directly applied on the front face of the lock by the static gravity load via a pulley system, while the main body of the interlocking block was held fixed, until the collapse of the lock. On the other hand, to consider the pure shear resistance and torsion-shear combinations, different positions and orientations of the designed pulley system were explored.

The test setup is schematically shown in Fig. 8a, b: the horizontal point-load was applied to the side face of the specimen lock by means of an electric hydraulic jack, monotonically increasing until the failure mechanism. As shown in Fig. 8b, c, the main body of the block was fixed to a wooden board to avoid sliding and to the upper support to avoid rotation, while the board was fixed to the upper support against sliding as well.

Fig. 8
figure 8

Test setup. a, b Displacement and load measurement; c, d constraints; e interlocking block with steel cup; f LVDT’s position in the plan view

Full size image

It is worth noting that this setup only allows torsion-shear combinations with low and intermediate eccentricities of the applied force (Fig. 8c), while the simulation of the pure torsion moment would require the application of a couple of forces as carried out for dry-stacked units [16].

The application of an iron cup on the lock allowed both to simulate this body as a rigid block and to distribute the applied shear force along the whole lock face (Fig. 8e). On the other hand, the main body of the interlocking block was kept rigid during the tests by using a 3D printed rigid cup-shaped box. The load was applied under displacement control at a constant rate of 3 mm/min.

Forces were measured using a load cell with 500 N maximum capacity and 10 Hz acquisition frequency, while the displacements were measured using linear variable displacement transducers (LVDTs) with a displacement range of ± 50 mm. A digital scanner, distributed by Vishay Measurements Group, was employed to acquire transducers data.

To record both pure shear and torsion-shear failures, three LVDTs, supported by a steel frame, were positioned to the lateral and back sides of the lock, and numbered as shown in Fig. 8f.

4.3 Testing program

The experimental program was planned to analyse the shear resistance of the lock interface in the case of pure shear (S1) and torsion-shear (S2, S3 and S4). The horizontal force, representing the shear force V, was applied at variable eccentricity and direction with respect to the vertical midplane of the lock.

As introduced above, the specimens made of two chosen mortars, M1 and M2, were tested using four setups, resulting in eight samples (Table 2):

  • S1M1 and S1M2 for the limiting pure shear evaluation, each comprising four specimens;

  • S2M1, S2M2, S3M1, S3M2, S4M1, S4M2 for the limiting torsion-shear evaluation, each comprising three specimens.

Table 2 Experimental set configurations (the distances are in mm)
Full size table

As shown in Table 2, the shear setup S1 was modified in S2-4 to allow the expected torsion-shear behaviour, in different ways:

  • for S2, the force application point was moved along the lock, while V was still orthogonal to the lock front side, with the eccentricity e = 25 mm from point O;

  • for S3, the force application point was only distanced from the centroid of the vertical lock face, with V rotated 45° counter clockwise, providing the eccentricity e = 29 mm;

  • for S4, the force application point was spaced from the lock and moved to a different position, with V rotated 45° clockwise, applying the eccentricity e = 51 mm.

4.4 Experimental results

To determine the pure shear strength (cohesion) of the two mortars, 8 tests were carried out using the M1 and M2 mortar samples and the S1 shear test setup described in the previous sections. The limiting pure shear force for M1 and M2 are collected in Table 3, together with the other sets. The coefficients of variation (CV) show a low dispersion of the frequency distributions and therefore a good reliability of the test setup. The averages of the limiting forces related to the pure shear failure are 430 N and 240 N for M1 and M2, respectively. The greater shear resistance of M1 compared to M2 is in good agreement with similar trends for the compressive and flexural strength results shown in Table 1.

Table 3 Pure shear and torsion-shear resistances of the 26 specimens
Full size table

For this setup (pure shear), two LVDTs were used to verify the effective displacements of the lock in the absence of torsion. Figure 9a,b show the load–displacement curves referred to some of the four tests performed on each of M1 and M2, i.e. T2 test in Fig. 9a, and T1 and T3 Tests in Fig. 9b. From these figures it is first evident the quasi-brittle behaviour of the material for both mortars. It is then worth emphasizing that the displacements of the two LVDTs, registered as channels Ch.2 and Ch.3 in the figure, substantially tend to overlap for each test. This result confirms once again the reliability of the setup realized ad hoc, since the specimens collapsed in pure shear without torsion effect. The maximum capacity values shown in the graphs correspond to the limiting forces collected for the corresponding tests in Table 3.

Fig. 9
figure 9

Load–displacement curves for S1 tests: a M1_T2 – M2_T2 and b M1_T1– M2_T3. Load–displacement curves for S2 and S3 tests and: c, d M1 and e, f M2

Full size image

The S2-3-4 setups were developed to analyse the torsion-shear resistance of the lock. These setups differ from each other in the eccentricity of the applied force. To determine the torsion-shear strength of the two mortars, a total of 18 specimens, three per each set and mortar, were made out on the M1 and M2 samples, as reported in Table 3. The first interesting remark is that the values of the forces V related to the torsion-shear failure of each mortar decrease with increasing eccentricity, as expected. The small coefficients of variation CV, except one, still show quite a good reliability of the setup adopted.

On the other hand, through the load–displacement curves in Fig. 9c–f, it is possible to confirm the quasi-brittle behaviour of the involved materials and to analyse the rotation of the lock until collapse and its consistency with the eccentric load applied. Unlike the curves for pure shear in Fig. 9a,b, where the displacements of LVDTs Ch.2 and Ch.3 tend to coincide, for the torsion-shear condition the displacements are very different from each other. In particular, before the collapse of the lock, the displacements of LVDT Ch.3 are generally limited into 0.5 mm, while the displacements recorded by LVDT Ch.2 are even six times higher than those reported by LVDT Ch.3. Using three LVDTs allows to record three final displacements at the moment of the lock failure and therefore to build the final deformation. Further investigation will be carried out to define the pure torsion strength as well, so that analytical yield domains in torsion-shear interaction can be experimentally validated, similarly to what developed in [16] for dry-stacked tuff blocks.

5 Comparison of analytical, numerical and experimental results

This section presents the analytical and numerical results and their comparison with each other and against the experimental outcomes, with reference to the torsion-shear interactions on the lock interface of the simple interlocking block experimentally investigated (Fig. 7a). The analytical results include those obtained by the convex, concave and corrected concave formulations described in Sect. 2, while the numerical results are referred to the three face triangulation types (normal, radial and rad8) used in 3DEC. For each mortar, the value of the pure shear force is considered as the mean value of the experimental results displayed in Table 3, that are 430 N and 240 N for M1 and M2, respectively. The cohesion values adopted for the 3DEC analyses are τ0 = 0.14 N/mm2 for M1 and τ0 = 0.08 N/mm2 for M2, which are obtained applying Eq. (1).

The first remark is that the curves related to the two different orientations of the applied shear force (orthogonal and 45° inclined to the vertical lock face) provide close results for both the 3DEC and the convex models, as shown in Fig. 10a, b referred to M1. In particular, the curves referred to 45° inclined forces provide slightly higher values for all the cases and this allows to proceed with the more conservative results related to the orthogonal shear force. The similarity of these results is mainly due to the fact that both the distances of the instantaneous twisting centre and the corresponding applied shear force from the centroid of the interface almost lay on the same line, whatever the inclination of the force, as highlighted in [35]. It is also important to note that the outcomes of the 3DEC model in Fig. 10a are represented by quite linear curves, with the same pure shear force but different pure torsion moments. This tendency is also followed by the analytical curves, though they are not linear but parabolic arcs.

Fig. 10
figure 10

Numerical results for orthogonal and 45° inclined shear forces and M1, obtained by the: a 3DEC model and b convex model

Full size image

In order to be compared, all the numerical and experimental results are collected in Figs. 11a and 11b with reference to M1 and M2, respectively.

Fig. 11
figure 11

Numerical and experimental results for orthogonal shear forces and a M1 and b M2

Full size image
Fig. 12
figure 12

S4-M2 case. a Experimental cracking and shear stress distributions for the b convex model and the c-e 3DEC face triangulation types

Full size image

By comparing the numerical and analytical results, from both figures it emerges that the upper and lower lines of the 3DEC results seem to be the chords with the same endpoints as the parabolic curves provided by the concave and convex formulations, respectively. This suggests that the 3DEC normal model is more similar to the concave model, while the 3DEC rad8 model is close to the convex model and even closer to the corrected concave model (CCM in the figure).

The most interesting remark regards the comparison of the analytical/numerical results with the experimental ones, based on the assumption that the value for the pure shear condition of both mortars is the mean value of the corresponding experimental results for S1. Figure 11a shows that, for the M1 specimens, the torsion-shear with low eccentricity (S2) provides results between the two upper curves obtained by 3DEC and the concave formulations, while the experimental results corresponding to the 45° inclined forces (S3 and S4) with increasing eccentricities mostly straddle the curve obtained by the convex model. It is also evident that one of the S4 specimens is very far from the others and can be discharged. On the other hand, similar results can be observed for M2 from Fig. 11b, though with lower results predicted by the same models as for M1 and some anomaly for S3. In fact, from this figure it can be observed that both the 3DEC normal and the concave models underestimate the experimental values for S2, while the 3DEC rad8 and the convex model underestimate the experimental values for S4, but the results for the S3 sample are even higher than the concave curve.

Increasing the density of the interface subdivision by 3DEC will provide greater discrepancies with the analytical and experimental results, as shown for the 3DEC divide-join rad8 model in Fig. 11a.

Besides, it should also be considered that the experimental results on the cohesive joint are affected by the mechanism of dilatancy, which tends to increase with the decrease of shear displacement and compression [1, 40] and therefore to provide larger values of the initial shear strength (cohesion) [41]. Although this is a complex issue as addressed in [42], it suggests that the analytical and numerical curves herein obtained in favour of safety and without considering dilatancy would be sufficiently reliable even in the presence of compression on the joints, as actually occurs in real structures.

Another interesting remark is that the shear stress distributions at the contact for the different models and types of discretization are in good agreement with the compared results. As an example, Fig. 12 reports the stress distributions for the S4-M2 case (torsion-shear with large eccentricity), where the position of the torsion centres of the conservative models, i.e. the analytical convex (Fig. 12b) and the 3DEC rad8 (Fig. 12e) models, are very close to each other and they both well represent the experimental cracking of the lock (Fig. 12a).

It can be concluded that, although further experimental results are needed, especially referred to larger eccentricities towards the pure torsion moment, the comparison of all the results show that the analytical concave and corrected concave models may respectively represent the upper and lower bounds of the torsion-shear behaviour of a cohesive joint. Moreover, the curves obtained by 3DEC normal and rad8 models are the conservative lines of these curves.

6 Conclusions

Analytical, numerical and experimental approaches have been presented in this paper to investigate the torsion-shear capacity of the contact interface between the lock and the main body of an interlocking block, assumed to have a cohesive behaviour.

Three analytical formulations, i.e. the concave, convex and “corrected” concave models, previously developed for assemblages of rigid blocks with conventional planar joints, have been extended to investigate the torsion-shear capacity of the lock connection, introducing a shear resistance independent of the normal force, based on the Tresca yield criterion and the cohesion as limiting value. Like the conventional planar dry interface, the overestimation of the pure torsion capacity in the concavity model with respect to the convex formulation has also been observed in the lock connection of the interlocking block, confirming the higher reliability of the “corrected” concave model.

Numerical analyses employing the modelling code 3DEC for advanced analysis of discontinuous media have been carried out on an interlocking cuboidal block with a cuboidal lock on its main body, to model the interlocking interface. As point loads cannot be applied to the rigid block boundary in 3DEC, lateral forces applied to the lock have been simulated as non-uniformly distributed forces with a linear gradient, and with different shear stress distributions varying with the face triangulation type. In particular, “radial” and “rad8” triangulations provided by 3DEC have been used, obtaining different ultimate forces, with differences increasing with eccentricity.

The third approach herein presented is the experimental investigation carried out on the simplest interlocking block, composed of a main body with a square cuboidal lock located on its upper face and subjected to lateral loading in absence of normal force. An ad hoc test setup was realized to estimate the initial shear and torsion-shear strengths at the lock interface, with results reported in terms of load–displacement curves. Two cement-based mortars M1 and M2 were used for specimens, casted using moulds provided by a 3D printer.

Comparing analytical and numerical results on the interlocking block experimentally tested, the following comments are interesting to underline:

  • in both cases, the two different orientations of the applied shear force (orthogonal and 45° inclined to the vertical lock face) provide close results, with more conservative values obtained for the orthogonal direction;

  • assuming the same pure shear values, different pure torsion values are attained by the four numerical models for the interlocking interface (normal, radial, rad8, and divide-join rad8) and analogous observations can be made for the three analytical models (concave, convex and “corrected” concave);

  • the 3DEC normal model is similar to the concave model, while the 3DEC rad8 model is close to the convex model and even closer to the “corrected” concave model;

Comparing the analytical and numerical results with experimental ones allows the following comments:

  • both for M1 and M2, experimental results corresponding to the 45° inclined forces with increasing eccentricities mostly straddle the curve obtained by the convex model, while the torsion-shear condition with low eccentricity and orthogonal shear forces provides results between the two upper curves obtained by 3DEC and the concave formulations, though with upper values for M2;

  • increasing the density of the interface subdivision by 3DEC, e.g. with divide-join rad8, is not convenient since providing greater discrepancies with both analytical and experimental results.

In conclusion, the analytical concave and “corrected” concave models, and the corresponding parabolic curves obtained, can be assumed as the upper and lower bounds of the torsion-shear behaviour of a cohesive joint, while the 3DEC normal and rad8 models, and the corresponding linear curves obtained, can be considered their conservative interpretation.