1 Introduction

Recently, the use of post-tensioned lateral bearing structural systems, such as self-centering/rocking walls, has been receiving much attention due to their post-earthquake full-operability as well as negligible downtime and repair costs following seismic events [1, 2]. Moreover, due to the restoring forces developed in the unbonded post-tensioning (UPT) tendons, in self-centering walls, the structure’s residual drift was expected to be small and make the system robust and reliable especially for vital/critical infrastructures [1, 2]. It has been suggested in the literature that the single rocking walls’ (SRWs) axial stress and tendons’ prestressing ratios be the most influential parameters during seismic events [3, 53, 4,5,6,7,8]. Due to the lack of longitudinal rebars passing through the wall-foundation interface of the SRWs, when applying a sufficiently large lateral load to walls, a gap develops at the interface (i.e., the decompression state). During decompression state, compressive stresses concentrate near one corner of the wall over the toe region, while the opposite corner experiences uplift (i.e., rocking mechanism) [9, 10]. Due to the rocking mechanism, steep, compressive strain gradients occur in the toe regions, making it challenging to accurately estimate/determine the strain by experimental methods. Data obtained from the numerical investigations of SRWs, therefore, particularly in the toe regions, could be used as a useful analytical tool [6, 11,12,13].

Preventing damage in the walls’ toe regions could provide a better serviceability level after seismic events. Furthermore, due to the relatively small size of the compression region in SRWs, damage at the toe regions may result in a reduction in the wall’s resistive moment. The ability to delimit the damaged region, and subsequently to minimize/prevent damage, therefore, could be considered as a vital issue in SRWs. In the past, several strengthening solutions have been recommended to prevent/minimize damage in SRWs. Some examples of strengthening solutions consisted in replacing the damaged toe region of SRWs by high-performance fiber-reinforced concrete (HPFRC) [14], using steel-plates at SRWs’ toe regions [15, 16], placing either steel rollers or steel U-shaped section profiles at the corners of SRWs [17, 18], and using an armoring steel frame in the SRWs’ wall-foundation interface [19,20,21].

Considering the high workability, enhanced compressive/tensile strength and toughness of both high-performance concrete (HPC) and HPFRC [22,23,24,25], and the reported SRWs’ damage which mainly concentrates in the wall’s toes [3, 5,6,7,8,9, 26,27,28,29], HPC/HPFRC replacement of the damaged region could be considered as the fastest, cheapest, and least invasive strategy either for retrofitting or rehabilitating SRWs. However, to apply this strategy, the expected SRW’s damaged region needs to be estimated in advance together with the concrete’s strain demand corresponding to walls’ limit states in design/retrofit stage at the toe regions. In this work, a parametric study was conducted using proven, finite element (FE) models of SRWs, by considering the SRWs’ axial stress and tendons’ prestressing ratios as the design variables. To this end, 40 different loading scenarios were considered, and for each scenario damage estimations were carried out in 3 distinct cases (i.e., original, retrofitting, and rehabilitating) at 3 different states (i.e., nominal, design, and ultimate). Overall, 360 damage estimations were performed and compared. Assuming both linear and uniform strain distribution at damaged region, the maximum compressive strain of the concrete, \({\varepsilon }_{cu}\), in SRWs’ toe regions, was defined/formulated at the nominal state. Using the defined \({\varepsilon }_{cu}\), and considering the wall response, a practical approach was proposed to estimate the extent of the damaged region. The goal of the study was to help provide a practical approach for delimiting the damaged region at the toe region of SRW and subsequently assessing the feasibility of both a repairing strategy using HPC/HPFRC material locally at the damaged regions in toes, and a reconfiguring strategy by replacing/casting the toe regions/initial height of a new SRW using HPC/HPFRC material.

2 Study benchmark experimental program

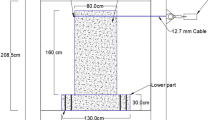
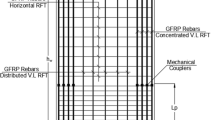
An earlier, full-scale experimental test of an SRW results [14, 30, 31] was selected as the study’s benchmark. A unique feature of the experimental study was the lack of longitudinal steel reinforcements at the wall’s cross-section. The longitudinal rebars necessary to support the stirrups were replaced by plastic pipes in the wall construction [14]. The full-scale test walls (action and reaction walls), the wall cross-sectional details (transverse reinforcements and stirrups), UPT tendons layout and vertical and horizontal loads’ position are illustrated in Fig. 1. Considering the lack of longitudinal reinforcements, the results of the test could be extended to poorly designed/built walls after strengthening interventions with shear resistance and concrete confinement provided by external horizontal ties [30]. The experimental program included two cyclic loading histories: (i) the loading history consisted of 7 complete cycles including 0.1, 0.25, 0.5, two cycles of 1, 1.5, and 2%, and (ii) the loading history consisted of 11 complete cycles including five cycles of 0.5, three cycles of 2, and three cycles of 2.5%. The second loading history was applied to the wall twice, the second time after repairing the damage associated with the first loading history at the toe regions. The second loading history was applied to the repaired wall (i.e., after applying the second loading history) using HPFRC. Further information regarding the experimental setup, instrumental apparatus, and material properties can be found in previously published research [14, 30, 31].

Fig. 1
figure 1

Experimental program details [14, 30, 31]

Full size image

3 Feasibility of strengthening self-centering walls

The idea of partial usage of HPFRC for rehabilitating SRWs was proposed and successfully tested in a previously published research [14]. Figure 2 shows the repair intervention including removing the damaged sections, casting the removed part with HPFRC (only at toe region), and finally reloading the repaired wall. The repaired wall toe, as shown in Fig. 2, did not experience significant damage, and the observed damage was rated as “cosmetic/negligible”.

Fig. 2
figure 2

Modified from Preti, Meda [14]

The repair intervention of the tested wall and the obtained results.

Full size image

According to both recent results [14] and the existing body of literature [3, 5,6,7,8,9, 26,27,28,29], no structural damage has been reported at non-toe regions of SRWs. The walls’ material strength, therefore, does not play a prominent role in the SRWs’ response. Damage prevention at the toe regions, therefore, could be considered as both a simple and highly effective solution to rehabilitate/reconfigure SRWs.

Based on the idea proposed and tested in the previously published research [14], two potential design approaches were considered to prevent/minimize damage in newly-constructed SRWs using HPC. As schematically shown in Fig. 3, the approaches would either cast the bottom height of a newly-constructed SRW with HPC or use HPC replaceable toe-blocks plus adding external shear ties for connecting the HPC blocks to the repaired wall body. To reconfigure SRWs at the design stage, the potential damaged region of SRWs (i.e., \({h}_{D}\times {l}_{C}\)) has to be initially delimited. To this end, estimation of the damaged region’s size is addressed in the following section.

Fig. 3
figure 3

Schematic potential solutions for preventing/minimizing SRWs’ damage, using HPC replaceable toe blocks, and casting the toe region of SRWs with HPC

Full size image

4 Modeling and damage estimation of SRWs

In this work, a numerical model for the SRW was developed using PERFORM 3D software [32]. Using multi-layer shell FEs with fiber sections, the tested wall’s response to external loading was simulated. A multi-layer shell FE consists of several layers (i.e., steel layer, concrete layer, shear behavior layer, etc.) connected in parallel to suitably simulate the behavior of concrete elements. Although the modeling procedure was carefully described in previously published research [3, 33, 34], the adopted mechanical properties in the developed numerical models are briefly summarized herein. To define each layer of an element, a suitable constitutive behavior (i.e., stress–strain relationship), and cross-section must be assigned to each layer. To this end, the stress–strain relationships provided by Mander et al. [35] were used to model confined and unconfined concrete’s behavior. HPFRC behavior was modeled using the results obtained in the experimental studies [14], and the proposed behavior by Hassan et al. [22]. The shear behavior of the wall was modeled using the relationships and recommendations given by Esfandiari [36], Hassani, Jafari [54], and Wallace [37]. Different shear behaviors were defined and used in the model depending on the wall’s structural details. The unbonded tendons were modeled using bar elements and their behavior was defined using equations and considerations provided by Devalapura, Tadros [38], and Walsh, Kurama [39]. To simulate the wall’s rocking response, gap-hook elements with negligible and very large values were defined for positive and negative stiffness, respectively; moreover, the positive and negative gap displacements were defined as a large value and zero, respectively. More explanations on the modeling and the detailed schematic of the developed numerical model are shown in Fig. S1 of the electronic supplementary material (ESM). The hysteresis loops and the wall’s centerline uplift obtained from both the developed model and the tested wall are also demonstrated in Fig. S2 of the ESM.

The results obtained from the cyclic loading were post-processed, and the extent and severity of damage was estimated using the damage index (DI) approach developed by Kim et al. [40]. According to Kim et al.’s DI, for DI ≤ 0.1, damage should not be observed in concrete elements; for DI within the range of 0.1–0.4, the concrete elements experienced damage ranging from ‘negligible/no damage’ to ‘not easily repairable damage’. For concrete elements with DI = 0.4, the elements’ principle strain reaches the strain corresponding to the maximum concrete’s compressive strength. Concrete elements displaying 0.4 ≤ DI ≤ 0.75, experience damage spanning from ‘cover spalling’ to ‘concrete crushing’. Finally, concrete elements with DI = 1 are expected to collapse. To further validate the model’s accuracy in a local-scale, the predicted damage was compared with the observed damage in the experimental tests [14, 30]. The estimated damage (DI surface) in the model, and the observed damage in the experimental tests corresponding to two, separate cyclic loadings (up to lateral drift of 2 and 2.5%), and the repaired wall up to lateral drift of 2.5% are illustrated in Fig. 4. Comparing the estimated damage from the numerical results to the observed experimental damage, provides further reassurance that the proposed model is also appropriate for accurately predicting the extent and severity of the SRWs’ damage. A detailed explanation of how to calculate DI can be found in the ESM and in previously published work [10].

Fig. 4
figure 4

Observed damage in the experimental test, and estimated damage (DI surface) in the model at 2% drift level [30] (a), at 2.5% drift level after removing damaged region [14] (b), and at 2.5% drift level after using HPFRC material at the toe regions [14] (c)

Full size image

5 Parametric study

The SRWs’ axial stress ratio (\({\rho }_{Axial}\)) and tendons’ prestressing ratio (\({\rho }_{UPT}\)) have been shown in previous studies to be the determinative parameters for walls’ response and damage [3, 5,6,7,8,9, 26,27,28,29]. The walls’ axial stress and tendons’ prestressing ratios were defined through Eq. (1) and Eq. (2), respectively:

$${\rho }_{UPT}=\frac{{f}_{se}}{{f}_{y}}$$
(1)
$${\rho }_{Axial}=\frac{{f}_{c}}{{f}_{c}^{^{\prime}}}$$
(2)

where, \({f}_{se}\) is the UPT tendons’ initial stress after losses (MPa), \({f}_{y}\) is the UPT tendons’ yield stress (i.e., 1640 MPa),\({f}_{c}\) is the wall section's average compressive stress at zero lateral displacement (MPa), and \({f}_{c}^{^{\prime}}\) is the concrete compressive stress (MPa). In the parametric study conducted in this work, the minimum values of the tendons’ prestressing ratio and the axial stress ratio were selected as 0.35 and 0.055, respectively, based on the recommendation by ACI [41], as well as the experimental setup [14]. The maximum values of \({\rho }_{UPT}\) and \({\rho }_{Axial}\), were selected based on the highest values reported in the existing literature [3, 5,6,7,8,9, 26,27,28,29]. However, the maximum considered values for these ratios were tailored in such a way that the risk of premature yielding of UPT tendons and extensive crushing in the toe regions was minimized. Therefore, the maximum values of the walls’ axial stress and tendons’ prestressing ratios were chosen as 0.75 and 0.125, respectively. To increase \({\rho }_{Axial}\), the applied axial force on the wall was increased. \({F}_{v}\) (see Fig. 1) was held constant by keeping \({\rho }_{Axial}\) constant and \({\rho }_{UPT}\) was increased by proportionally decreasing the UPT tendons’ cross-sectional area. The summary of the 40 loading scenarios considered in this study is shown in Table 1.

Table 1 Parametric study’s design matrix
Full size table

Considering the guidance offered by ACI [42], a cyclic loading, \({F}_{h}\), (see Fig. 1) was applied laterally to the wall’s model. The cyclic loading history includes pushing up the wall to lateral drift levels of ± 0.1, ± 0.125, ± 0.175, ± 0.25, ± 0.375, ± 0.5, ± 0.75, ± 1, ± 1.5, ± 2, ± 2.5 and ± 3% (i.e., 36 full cycles, and three cycles for each lateral drift). To consider the highest extent and severity of the induced damage at each level of lateral drift, conservatively, the third cycle’s results for that level was considered herein.

Two distinct strengthening strategies including (i) retrofitting of damaged SRWs using HPFRC materials only at the damaged toe regions after loading, and (ii) rehabilitating/redesigning of newly constructed SRWs using HPFRC toe block/HPFRC casting at the bottom part were considered and their performances were carefully examined. To this end, the damage of the original walls (40 scenarios in Table 1), the repaired walls using both rehabilitation strategy, and the redesigning strategy for the same scenarios were estimated and compared for 3 seismic hazard levels, namely nominal state, design basis earthquake (DBE), and maximum considered earthquake (MCE). A lateral drift of 2% and 3% are commonly accepted as the design’s lateral drift, and the maximum applicable drift of SRWs, respectively [42,43,44,45]. Moreover, to evaluate the seismic performance of hybrid SRWs, the maximum transient lateral drift of 2% and 3% were recommended by Rahman, Sritharan [46] as the seismic hazard level of DBE and MCE, respectively. Therefore, the damage status of the scenarios (extent and severity) were estimated at the third cycle of the hysteresis loop at drift level of 2% (DBE hazard level) and 3% (MCE hazard level) in the 3 mentioned cases.

5.1 SRWs’ maximum compressive strain

The ‘plastic hinge’ concept in shear walls assumes that the entire plastic deformation of the concrete elements is confined within the plastic hinge region [47], and the widely used range of \({\varepsilon }_{cu}\) = 0.0030–0.0035 (i.e., generally for unconfined concrete) is assumed to be constant and uniformly distributed over the plastic hinge region’s height [48]. In SRWs, due to rocking mechanism, the toe regions of SRWs experiences compressive stress concentration and the concrete strain varies steeply over a short length. In SRWs, therefore, the use of the plastic hinge concept or the working value of \({\varepsilon }_{cu}\) (0.0030–0.0035) is unlikely to yield reasonable results. Any attempt to establish \({\varepsilon }_{cu}\) at a flexural strength level, using experimental means is likely to be affected by the size, type, and placement of the measuring device(s). Conversely, the use of FE numerical models allowed to estimate the concrete’s strain over a short length at the wall’s toe region [6, 11, 12]. As in this research, the extent and severity of damage can be satisfactorily estimated by the developed numerical model, the numerical models’ damage estimation together with the modified version of plastic hinge concept could be used to circumvent the mentioned difficulties about estimating \({\varepsilon }_{cu}\) in SRWs due to rocking mechanism.

Paulay and Priestley’s plastic hinge model assumes that the plastic deformation of the shear wall is confined within the plastic hinge’s equivalent length, \({L}_{Pl}\) (see Fig. 5). Using Eq. (3), the total rotation of the wall, \({\theta }_{T}\), was estimated as [45]:

$${\theta }_{T}={\int }_{0}^{{L}_{Pl}}\frac{{\varepsilon }_{c}(y)}{{l}_{c}} dy$$
(3)

where \({l}_{c}\) is the wall’s compression zone length, and \({\varepsilon }_{c}(y)\), is the distribution of concrete compressive strain at the wall edge along wall height. Assuming the maximum concrete strain, \({\varepsilon }_{cu}\), being constant along the equivalent length, (Fig. 5) the plastic hinge’s length, \({L}_{Pl}\), was estimated as:

Fig. 5
figure 5

Concrete strain (\({\varepsilon }_{c}\)) distribution over shear wall height, and the plastic hinge concept, and \({\varepsilon }_{c}\) distribution over SRW’s height and the modified plastic hinge concept

Full size image
$${L}_{Pl}\cong \frac{{\theta }_{T}{l}_{c}}{{\varepsilon }_{cu}}$$
(4)

Although shear walls and SRWs are inherently different, this approach was implemented to estimate the SRWs’ plastic hinge length, and the reported plastic hinge lengths were found to be considerably shorter than the ones in shear walls [10, 49]. In those works, the assumed value for \({\varepsilon }_{cu}\) (i.e., constant value of 0.005), and the underlying assumption for choosing \({\theta }_{T}\) (i.e., the wall rotation corresponding to the peak strength capacity of an SRW) in the calculation of \({L}_{Pl}\) were questionable.

In this work, to determine \({\varepsilon }_{cu}\) in SRW, the plastic hinge concept was modified to account for the expected distribution of the concrete’s strain at the wall’s toe region. As it can be seen in Fig. 5, in an SRW, a solid curve represents a reasonable distribution of the concrete’s strain over the wall’s height; however, due to integration difficulties, a simplified, linear strain distribution (i.e., the dashed line) is proposed in the calculations. The concrete strain was set to vary linearly from \({\varepsilon }_{cu}\) to \({\varepsilon }_{D}\) (i.e., the strain corresponding to the onset of damage at the wall edge) over the damaged length of the wall, \({h}_{D}\). In reality, due to the rocking mechanism, the concrete strain in the wall corner at the wall-footing interface may reach \({\varepsilon }_{cu,f}\) (i.e., the concrete strain-based failure criterion [47]; more information can be found in the ESM); however, just above the wall-footing interface, the concrete’s strain is expected to drastically decrease. Although using a linear strain distribution leads to underestimation of concrete strain at the wall-footing interface (see Fig. 5), the assumption can simplify the estimation of \({\varepsilon }_{cu}\), and facilitate the calculation of damaged/crushed height.

By combining Eq. (3) with the linear concrete strain distribution, \({\varepsilon }_{cu}\) can be expressed as:

$${\varepsilon }_{cu}\cong \frac{{2\theta }_{T}{l}_{c}}{{h}_{D}}- {\varepsilon }_{D}$$
(5)

In both the plastic hinge, and the modified plastic hinge scenarios, using either Eq. (4) or (5), respectively, \({\theta }_{T}\), \({h}_{D}\), \({l}_{c}\), and \({\varepsilon }_{D}\) (for Eq. (5)) should be estimated in order to determine \({\varepsilon }_{cu}\). The first step, therefore, is establishing a suitable level of wall rotation, \({\theta }_{T}\), wherein \({\varepsilon }_{cu}\) to be determined.

Taking a simplistic approach to estimate the SRWs’ rotation, \({\theta }_{T}\), the wall rotation was decomposed into the elastic lateral rotation before decompression state, and the rigid rotation after decompression state (see Fig. 6). In previously published research [10], neglecting the shear rotation, the elastic rotation of an SRW, \({\theta }_{e}\), at the decompression state was estimated using Eq. (6):

$${\theta }_{e}\cong \frac{2{h}_{w}{f}_{c}}{3{l}_{w}{E}_{c}}$$
(6)

where, \({h}_{w}\) and \({l}_{w}\) are the height and width of the wall (mm), respectively, \({E}_{c}\) is the concrete’s modulus of elasticity (MPa), and \({f}_{c}\), is the average axial stress of the wall at zero lateral displacement.

Fig. 6
figure 6

SRW’s rotation schematic, elastic rotation mode of the wall before decompression state, rigid rotation mode of the wall after decompression state, and schematic detailed deformation in a SRW after decompression state, and displacement compatibility

Full size image

The second term of the wall’s rotation, the rigid rotation, \({\theta }_{r}\), is mainly controlled by the wall’s UPT tendons elongation, and was estimated by assuming small displacements/rotations. The SRW’s rigid rotation after the decompression state is shown at the bottom section of the wall in Fig. 6, and, for small displacements, is expressed as:

$${\mathit{tan}{ \theta }_{r}\cong \theta }_{r}= {\Delta }_{w}/{(l}_{w}-{l}_{c})$$
(7)

where \({\Delta }_{w}\) is the wall’s outermost edge uplift (mm) caused by the lateral load, \({F}_{h}\), (see Fig. 1). Since the elastic rotation of the wall due to the wall flexure and shear deformation beyond decompression state is negligibly small, the rigid rotation, \({\theta }_{r}\), was approximated by the expression:

$${\theta }_{r}\cong {\theta }_{T}-{\theta }_{e}$$
(8)

Since \({l}_{c}\) is expected to remain nearly unchanged for \({\theta }_{T}>\) 0.5% [50], and the system’s functionality in terms of wall rotation (\({\theta }_{T}\)) is wide, then, the critical factors in determining \({\varepsilon }_{cu}\) are the estimated \({\theta }_{T}\), \({h}_{D}\), and \({\varepsilon }_{D}\). In this research, \({\varepsilon }_{cu}\) was estimated at the SRWs’ nominal limit state rotation. To this end, the wall rotation corresponding to either occurrence of crushing at any place in the wall’s toe region or UPT tendons yielding, was considered as the nominal limit state’s rotation [11]. In this study, crushing was expected when the compressive strain of an element, either at the center or the edge, reached the strain corresponding to the peak stress of confined/unconfined concrete (depending on the elements’ properties). To measure the elements’ strain, ‘strain gage elements’ [32] were placed at the edge of all elements. To define tendons’ yielding, the tensile strain of each cable was compared with the yielding strain of the steel in UPT tendons. Nonlinear static analysis (pushover) was then used to estimate the nominal rotation. Analyzing the defined scenarios, the wall rotation at the nominal limit state of scenarios, \({\theta }_{T, Nominal}\), were estimated, and is illustrated in Fig. S3a of the ESM.

Substituting Eqs. (6) and (7) into Eq. (8), and using the results obtained from the numerical analysis (i.e., \({\Delta }_{w}\) corresponding to the nominal limit state), the wall’s compression zone’s length was estimated as:

$${l}_{c}\cong {l}_{w}-\left({\Delta }_{w}/\left({\theta }_{T}-\frac{2{h}_{w}{f}_{c}}{3{l}_{w}{E}_{c}} \right)\right)$$
(9)

Using Eq. (9), \({l}_{c}\) was calculated at the nominal rotation of each scenario and the results are shown in Fig. S3b of the ESM. According to the employed DI definition, DI = 0.1, in an element could be considered as damage initiation in the element. Therefore, the employed DI [40] was solved for DI = 0.1 to estimate \({\varepsilon }_{D}\). Equation (10) was proposed by Kim et al. [40] to estimate the DI:

$$DI=1- \alpha {\left[\frac{2{\varepsilon }_{cu,f}-{\varepsilon }_{cs}}{2{\varepsilon }_{cu,f}}\right]}^{2}$$
(10)

where \({\varepsilon }_{cs}\) is the principle strain of the element in a specific rotation, and \(\alpha\) is the concrete fatigue parameter, which can be expressed implicitly as:

$$\alpha =f(n,{f}_{cc}^{^{\prime}},{f}_{co}^{^{\prime}},{\varepsilon }_{co},{\varepsilon }_{max},{\varepsilon }_{min}, {\varepsilon }_{cu,f})$$
(11)

More information to state \(\alpha\) explicitly, can be found in the ESM (i.e., damage estimation section). As shown in Eq. (11), \(\alpha\) is the function of the number of complete load cycles, \(n\), applied to the element, the element’s confined and unconfined concrete compressive strength, \({f}_{cc}^{^{\prime}}\), and \({f}_{co}^{^{\prime}}\) respectively, the element’s strain corresponding to the peak stress of unconfined concrete, \({\varepsilon }_{co}\), and the maximum and minimum cyclic strain of the element at each step of a cyclic analysis, \({\varepsilon }_{max}\) and \({\varepsilon }_{min}\), respectively. Considering the cyclic loading applied to the defined scenarios (see Sect. 5) and the materials properties, the value of \(\alpha\) was found to be within the range of 0.965–1.00 and hence, for simplicity, it was assumed \(\alpha \approx\) 1.0. Considering damage estimation at the outermost edges of an SRW, \({\varepsilon }_{cs}\) could be replaced by the axial strain of the corresponding concrete element (i.e., at the wall edge), \({\varepsilon }_{c},\) which can be expressed as:

$${\varepsilon }_{c}\cong 2{\varepsilon }_{cu,f}\left(1-\sqrt{\left(1-DI\right)}\right)$$
(12)

Substituting DI = 0.1 in Eq. (12), and setting \({\varepsilon }_{cu,f}\) of the defined concrete in the scenarios, leads to \({\varepsilon }_{D }\approx\) 0.0017.

Using Kim, et al.’s DI, the height of the region that experiences damage more severe than hairline/slight flexure cracks (i.e., DI ≥ 0.1) at the wall’s nominal limit state was considered as the damaged height, \({h}_{D}\). The walls’ DI contour lines at the nominal limit state’s rotation are shown in Fig. S4 of the ESM (i.e., original wall). Using both the plastic hinge and the modified plastic hinge concepts (Eq. (4), and Eq. (5)), \({\varepsilon }_{cu}\) could then be estimated. To this end, the plastic hinge length (\({L}_{Pl}\)) in Eq. (4) was replaced with the estimated \({h}_{D}\) at the nominal limit state of SRWs (Fig. S4 of the ESM), the values for \({l}_{c}\) and \({\theta }_{T, Nominal}\) were calculated via numerical analyses. The \({\varepsilon }_{cu}\) for both cases are illustrated in Fig. 7.

Fig. 7
figure 7

Calculated \({\varepsilon }_{cu}\), at the nominal limit state of SRWs using both plastic hinge and modified plastic hinge concepts, and the experimentally measured \({\varepsilon }_{cu}\) at the toe region (close to the wall-footing interface) as reported in [6]. Note: plastic hinge (PH)

Full size image

Using embedded strain gages placed in the toe region (close to the wall-footing interface), Henry [6] measured \({\varepsilon }_{cu}\) for SRWs with axial stress ratio spanning from 0.033 to 0.105 at the nominal flexural limit state (see Fig. 7). The reported strains for \({\varepsilon }_{cu}\) were between 0.005 (at \({f}_{c}/{f}_{c}^{\mathrm{^{\prime}}}\) = 0.105) and 0.015 (at \({f}_{c}/{f}_{c}^{\mathrm{^{\prime}}}\) = 0.033) and the effect of the axial stress ratio was clearly to decrease the magnitude of \({\varepsilon }_{cu}\) corresponding to the nominal limit state.

As it can be observed in Fig. 7, the axial stress ratio had a decreasing effect on the local strain demand at the toe region (particularly at the wall-footing interface), whereas no clear trend was observed by increasing/decreasing of\({f}_{se}/{f}_{y}\). In this study, unlike the locally measured strain by Henry, the calculated strain was assumed to be distributed uniformly (plastic hinge concept) or linearly (modified plastic hinge concept) over the damaged height (\({h}_{D}\)) at the SRW’s toe region. As expected, the obtained magnitudes of \({\varepsilon }_{cu}\) were relatively less pronounced than the experimentally measured strains [6]; a similar trend between \({\varepsilon }_{cu}\) and \({f}_{c}/{f}_{c}^{^{\prime}}\) was obtained based on the numerical model. Furthermore, the modified plastic hinge concept yielded a better prediction of \({\varepsilon }_{cu}\) versus \({f}_{c}/{f}_{c}^{^{\prime}}\) at the SRWs’ toe regions. Although the nominal limit state was defined as the initiation of concrete crushing in wall-footing interface, \({\varepsilon }_{c}={\varepsilon }_{cc}\) (i.e., concrete strain corresponding to the peak stress of confined concrete; \({\varepsilon }_{cc}=0.0052\)), the obtained results for the modified plastic hinge are higher than\({\varepsilon }_{cc}\). In fact, in this research the concrete’s strain was measured using strain gage elements [32] located on the wall elements, which explains why real strains could be larger than the measured ones. Mesh sensitivity analysis, showed that in the toe regions, a mesh size smaller than 5 cm had no effect on both the predicted response and damage estimation. This length was selected, therefore, as mesh size in the toe regions at wall-footing interface, and concrete strain was measured over this length. Comparing the obtained results from both plastic hinge and modified plastic hinge concepts (see Fig. 7) and experimentally-measured strains shows that the modified plastic hinge concept for SRWs could provide better estimation of the concrete strain.

Assuming either plastic hinge or the modified plastic hinge distributions, Eqs. (13) and (14) were proposed, respectively, to describe the approximate relation between \({f}_{c}/{f}_{c}^{^{\prime}}\) and \({\varepsilon }_{cu}\) at the SRWs’ toe region:

$${\varepsilon }_{cu} = \left\{\begin{array}{cc}0.00671-0.0268({f}_{c}/{f}_{c}^{^{\prime}});& {0.055 \le f}_{c}/{f}_{c}^{^{\prime}}\le 0.105\\ 0.0039& { f}_{c}/{f}_{c}^{^{\prime}}> 0.105\end{array}\right.$$
(13)
$${\varepsilon }_{cu,m}= \left\{\begin{array}{cc}0.01154-0.0519({f}_{c}/{f}_{c}^{^{\prime}});& {0.055 \le f}_{c}/{f}_{c}^{^{\prime}}\le 0.105\\ 0.00645& { f}_{c}/{f}_{c}^{^{\prime}}> 0.105\end{array}\right.$$
(14)

Choosing a reasonable value/trend for \({\varepsilon }_{cu}\) strongly depends on the designers’ attitude and intention toward \({\varepsilon }_{cu}\). However, considering the experimental results [6, 11], and the calculated values, the modified plastic hinge concept yields more reasonable results. With respect to the capacity, underestimating the wall’s capacity is more conservative. To this end, the lower bound of \({\varepsilon }_{cu}\) = 0.0055 could be set for repair issues/capacity estimation. With respect to the demand, using Eq. (14), indicates that \({\varepsilon }_{cu}\) = 0.0055 cannot be considered as a safe choice for designing the SRWs’ toe regions. Considering the effect of \({f}_{c}/{f}_{c}^{^{\prime}}\) on \({\varepsilon }_{cu}\), the material used in the toes should at least accommodate the demand strain of 0.0055. It is quite clear that this strain represents the lower bound of the demand strain that could be attained using either stirrups at the toe regions or more ductile and stronger materials.

5.2 Simplified and practical approach for estimating SRWs’ damaged region

It is reasonable to expect that the most severe and extensive damage is encountered at the highest hazard level (MCE). Considering the limited strength capacity of the toe material (concrete), and the high strain demand at the toe region, estimating an SRW’s strain profile either analytically or numerically is unpractical. Therefore, choosing an idealized strain profile could further simplify the estimation of SRWs’ damaged region. Considering the brittle nature of concrete, it is clear that at a relatively small wall rotation (even in \({{\theta }_{T}\ll \theta }_{T, Nominal}\)) the wall’s toe region at the wall-footing interface experiences severe crushing (i.e., local collapse). As concrete does not resist axial stress increment, once the axial stress reaches the concrete peak strength (\({f}_{cc}^{^{\prime}}\)), the applied stress is not transferred from the crushed regions (\({\sigma }_{c}\ge {f}_{cc}^{^{\prime}}\) or \({\varepsilon }_{c}\ge {\varepsilon }_{cc}\)) to the undamaged regions and damage does not propagate further. Therefore, without losing much accuracy, the nominal limit state strain profile could be selected to estimate the damaged region at the highest hazard level (MCE). As discussed earlier, a linear strain distribution can be used to describe the \({\varepsilon }_{c}\) behavior and simplify the existing nonlinearity. Furthermore, due to the limited strength capacity of the toe materials, damage could not progress steadily upward; the estimated damaged/crushed length in the nominal limit state, therefore, could be considered as the approximate damaged/crushed length at higher hazard level.

Considering the SRWs’ behavior, SRWs’ damaged regions can be delimited as \({h}_{D}\times {l}_{c}\) (see Fig. 3). As mentioned above, for \({\theta }_{T}>\) 0.5% [50], SRWs’ \({l}_{c}\) remains nearly unchanged. Considering the range of values obtained for \({\theta }_{T, Nominal}\) (see Fig. S3a of the ESM), the \({\theta }_{T, Nominal}\) of 1% was chosen to simplify the model. Although the calculation of the SRWs’ \({l}_{c}\) at a specific level of rotation could be carried out analytically [5, 13, 49], in this research, \({l}_{c}\) was calculated numerically via Eq. (9) at \({\theta }_{T}\) of 1% and referred to as \({l}_{c,0.01}\) hereafter. Using Eqs. (5) and (14), and the calculated \({l}_{c,0.01}\), \({h}_{D}\) can be expressed as:

$${h}_{d}\cong \frac{0.02{l}_{c,0.01 }}{{\varepsilon }_{cu,m}+{\varepsilon }_{D}}$$
(15)

As discussed above, the calculated \({h}_{D}\) (at the nominal limit state) can be considered as \({h}_{D}\) at the higher hazard levels (DBE and MCE). To examine the validity of the assumption, the calculated values for \({l}_{c}\) and \({h}_{D}\), using Eqs. (9) and (15) respectively, are shown in the same graph with the calculated DI (Fig. S5 of the ESM) at both DBE and MCE levels.

As shown in Fig. 8, beyond the nominal limit state, plastic deformation mainly develops within the potentially crushed region of height \({h}_{C}\). Considering the existing nonlinearity, beyond the nominal limit state, Eq. (3) was rewritten as:

$${\theta }_{T}=\frac{1}{{l}_{c}}\left[{\int }_{0}^{{h}_{C}}{\varepsilon }_{c,BTC}(y) dy+{\int }_{{h}_{C}}^{{h}_{D}}\left({\varepsilon }_{cu,m}-\left(\frac{{\varepsilon }_{cu,m}-{\varepsilon }_{D}}{{h}_{D}}\right)y\right) dy\right]+{\theta }_{e}$$
(16)

where \({\varepsilon }_{c,BTC}(y)\) is the concrete strain distribution along \({h}_{C}\) beyond toe crushing (BTC).

Fig. 8
figure 8

\({h}_{D}\), \({h}_{C}\), and the distribution of \({\varepsilon }_{c}\) along wall edge at the toe region applying the modified plastic hinge at the nominal limit state, and beyond the nominal limit state

Full size image

Due to the high nonlinearity of the concrete after crushing, the presence of local collapsed regions at the toe, and the effect of UPT tendons’ yielding on \({\varepsilon }_{c,BTC}(y)\), determining \({\varepsilon }_{c,BTC}(y)\) is significantly challenging. However, considering the brittle nature of concrete, and lower level of nonlinearity at the nominal limit state, the estimated value of \({h}_{c}\) at this state was assumed as \({h}_{c}\) for higher hazard levels (i.e., DBE/MCE), too. Therefore, by applying the modified plastic hinge concept (linear \({\varepsilon }_{c}\) distribution), and using the calibrated \({\varepsilon }_{cu,m}\), Eq. (14), \({h}_{C}\) was estimated as:

$${h}_{C}\cong {h}_{D}\left(1-\frac{{\varepsilon }_{cc}-{\varepsilon }_{D}}{{\varepsilon }_{cu,m}-{\varepsilon }_{D}}\right)$$
(17)

The values of \({h}_{C}\) estimated using Eq. (17) are shown in Fig. 9. Figure 9 also shows Thomas, Sritharan [51] estimated value, \({h}_{c}={0.08h}_{w}\) which was obtained using the monolithic beam analogy (MBA) proposed by Pampanin et al. [52]. The uniform strain distribution assumption, the modeling of SRW as a cantilever beam, and the lack of differentiation between beams and walls (i.e., smaller aspect ratio of walls) might explain the conservative estimation. Figure 9 also shows Jafari et al. [10], and Hassanli et al. [49] proposed relationships based on the plastic hinge concept. Although these relationships can predict \({h}_{c}\) better than Thomas’s relationship (see Fig. 9), both appear to overestimate \({h}_{c}\).

Fig. 9
figure 9

Calculated \({h}_{c}/{h}_{w}\) using the proposed simplified approach, obtained values for \({h}_{c}/{h}_{w}\) from numerical analysis at MCE level, and proposed \({h}_{c}/{h}_{w}\) by Jafari et al. [11], Hassanli et al. [51], and Thomas, Sritharan [53]

Full size image

Considering the applied simplifying assumptions, \({h}_{c}\) cannot be expected to be calculated using Eq. (17). However, Eq. (17) yields a better estimation of \({h}_{c}\) than existing relations in the literature [10, 49, 51], taking into account the obtained results by numerical analyses (see Fig. 9). The existing difference between the proposed approach’s results and numerical results could be mainly attributed to not considering UPT tendons’ yielding in calculation of \({h}_{c}\). To gain a better insight into this effect, the rotation corresponding to the yielding of UPT tendons in all defined scenarios is illustrated in Fig. S6 of the ESM. As the scenarios with greater \({f}_{se}/{f}_{y}\) (within the range of 0.55–0.75) experienced tendons’ yielding in a lower level of wall rotation (equal or greater than 1.5%), a lower level of axial stress can be expected at the toe regions, and as a result less/no crushing is expected. Therefore, the existing discrepancy between numerical results and the proposed approach results, particularly for scenarios with \({f}_{c}/{f}_{c}^{^{\prime}}\) < 0.095 and \({f}_{se}/{f}_{y}\) > 0.55, might be better explained. The calculated values for \({l}_{c}\) and \({h}_{C}\) using Eqs. (9) and (17), respectively, are shown in Fig. S5 of the ESM as a crushed region (\({h}_{C}\times {l}_{c}\)) by grey-filled rectangles at both DBE and MCE levels.

6 Strengthening strategies

To strengthen damaged SRWs, the simplest retrofitting strategy with the least intervention is to locally replace the toe regions with HPC. Similarly, for newly constructed SRWs, using HPC toe blocks/casting the bottom part with HPC could be among the most efficient rehabilitating strategies. In this section, the capability of each strategy was examined, after estimating the crushed and damaged regions of relevant scenarios (see Fig. S4 of the ESM). In retrofitting strategy, based on the damage estimation results, the delimited crushed regions (DI > 0.4) were replaced by elements with the HPFRC, as in the experimental program [14]. Subsequently, damage was estimated in the retrofitted wall in three different loading levels (nominal, DBE, and MCE) and displayed in Fig. S4. In rehabilitating strategies, using Eqs. (15) and (9) scenarios’ damaged region (\({h}_{D}\times {l}_{c}\)) were estimated, and the toe regions replaced by HPFRC toe blocks of height and width \({h}_{D}\) and \({l}_{c}\), respectively. Due to the extensive damage for scenarios with \({f}_{c}/{f}_{c}^{^{\prime}}\) > 0.105 (walls with more column-like behavior), in rehabilitating strategies, the bottom portion of the wall was replaced entirely by HPFRC elements up to the height \({h}_{D}\). Damage was then estimated for rehabilitated scenarios in 3 different loading levels and demonstrated in Fig. S4 of the ESM. To better understand both rehabilitating and retrofitting strategies, a detailed schematic of both strategies is illustrated in Fig. S7 of the ESM. The damage estimations for the original, retrofitted, and rehabilitated scenarios were compared with each other to quantify the capability of each strategy. To this end, three different ratios, namely, damage ratio (\({\rho }_{D}\)), repair ratio (\({\rho }_{R}\)), and crushing ratio (\({\rho }_{C}\)) were defined:

$${\rho }_{D}={A}_{DI=0.1}/({h}_{w}\times {l}_{w})$$
(18)
$${\rho }_{R}={A}_{DI=0.2}/({h}_{w}\times {l}_{w})$$
(19)
$${\rho }_{C}={A}_{DI=0.4}/({h}_{w}\times {l}_{w})$$
(20)

where \({A}_{DI=0.1}\), \({A}_{DI=0.2}\), and \({A}_{DI=0.4}\), are the surface area of the wall surface displaying DI > 0.1 (i.e., overall damage), DI > 0.2 (i.e., potentially need to be repaired), and DI > 0.4 (i.e., crushed region), respectively. It is worth noting that for the regions with \(0.1<DI<0.4\), the damage severity spanned from ‘negligible damage’ to ‘not easily repairable damage’; the DI = 0.2 contour line, therefore, could be used to delimit the localized severe damage which most probably should be removed and replaced with new material. In Figure S4 of the ESM, the DI = 0.2 counter line is displayed by dotted lines.

Using the data in Fig. S4, \({\rho }_{D}\) for both \({f}_{se}/{f}_{y}\) = 0.35, and 0.75 (upper and lower bounds) were calculated as shown in Fig. 10. As it can be seen in the figure, \({\rho }_{D}\) significantly decreases by increasing \({f}_{se}/{f}_{y}\) in all three cases (original, retrofitting strategy, and rehabilitating strategies). Considering the \({\rho }_{D}\) trends, by increasing \({f}_{c}/{f}_{c}^{^{\prime}}\) (particularly within the range of 0.095–0.125) the overall damage accelerates significantly. The retrofitting strategy cannot decrease the overall damage, and only a marginal decrease in \({\rho }_{D}\) is observed using the retrofitting strategy. Although using rehabilitating strategies shows decreasing damage, this effect was less pronounced when increasing \({f}_{se}/{f}_{y}\).

Fig. 10
figure 10

Damage ratio (\({\rho }_{D}\)) for both \({f}_{se}/{f}_{y}\) = 0.35, and 0.75. Note: retrofitting strategy (RETS), and rehabilitating strategy (REHS)

Full size image

To further investigate the capability of retrofitting strategy and rehabilitating strategy, \({\rho }_{C}\) was estimated for various scenarios and graphically summarized in Fig. 11. As seen in the figure, \({\rho }_{C}\) follows similar trends for both the retrofitting strategy and the rehabilitating strategy. The values of \({\rho }_{C}\) in the retrofitting strategy were marginally smaller than in the rehabilitating strategy, particularly in scenarios with higher values of \({f}_{c}/{f}_{c}^{^{\prime}}\) (> 0.095). HPC has a higher strength and toughness compared with conventional confined concrete (i.e., before reaching the peak strength) [22,23,24,25]. Thus, HPC can bear greater axial stress/load and transmit more stress/load upward and, consequently, induce more damage by transferring loads upward. Using a larger HPC region (i.e., casting bottom portion with HPC), therefore, could result in marginally more extensive crushing above the toe regions. Generally, the extent of crushing decreases by more than 50% using either the retrofitting strategy or the rehabilitating strategy. Both \({\rho }_{C}\) and \({\rho }_{D}\) can provide an overall view of the structural damage but cannot reflect a reasonable estimation of the repair work. Therefore, using Eq. (19) the amount of repair work can be quantitatively compared for both the retrofitting strategy and the rehabilitating strategy.

Fig. 11
figure 11

Crushing ratio (\({\rho }_{C}\)) for both \({f}_{se}/{f}_{y}\) = 0.35, and 0.75. Note: retrofitting strategy (RETS), and rehabilitating strategy (REHS)

Full size image

The values of \({\rho }_{R}\) were estimated for both \({f}_{se}/{f}_{y}\) = 0.35, and 0.75 (Fig. 12). The ratio provides critical information to accurately examine the capability of the retrofitting strategy and the rehabilitating strategy and facilitate the estimation of the minimum required repair work. As it can be seen in Fig. 12, increasing \({f}_{se}/{f}_{y}\) decreases the amount of repair work, whereas, increasing \({f}_{c}/{f}_{c}^{^{\prime}}\) increases the repair work; the increment is more pronounced for scenarios with \({f}_{c}/{f}_{c}^{^{\prime}}\) > 0.105 using the retrofitting strategy. Both the retrofitting strategy and the rehabilitating strategy have comparable capabilities in decreasing the repair work for scenarios with \({f}_{c}/{f}_{c}^{^{\prime}} \le\) 0.095. Although both strategies can satisfactorily decrease the repair work, the retrofitting strategy seems less efficient when \({f}_{c}/{f}_{c}^{^{\prime}}\) > 0.095.

Fig. 12
figure 12

Repair ratio (\({\rho }_{R}\)) for both \({f}_{se}/{f}_{y}\) = 0.35, and 0.75. Note: retrofitting strategy (RETS), and rehabilitating strategy (REHS)

Full size image

7 Discussion

Comparing the drift corresponding to the concrete crushing (local crushing in the toe regions) and the one for tendons’ yielding, the former was noticeably less pronounced even for large \({f}_{se}/{f}_{y}\) ratios. In all the considered scenarios, concrete crushing happened earlier than tendon’s yielding. Furthermore, after concrete crushing, which is mainly local and concentrates at the walls’ toe regions, the walls’ response did not change. The tendons’ yielding, therefore, could be considered as a determinative factor of the walls’ failure mode/ultimate state factor. However, concrete crushing could be considered as a determinative factor of the walls’ nominal state.

Due to the rocking mechanism, damage is not expected to develop in the whole, bottom portion of SRWs, and applying the plastic hinge concept might yield unreliable results. To circumvent this issue, a linear strain distribution was assumed over the scenarios’ damaged length at their nominal limit state. As shown in Fig. 7, the modified plastic hinge concept yielded a more accurate estimation of \({\varepsilon }_{cu}\) at the wall-footing interface when compared with experimentally measured values of \({\varepsilon }_{cu}\). Both the experimental [6] and numerical results show that the concrete strain at the corner of SRWs exceed \({\varepsilon }_{cc}\), due to the rocking mechanism and strain measurement considerations. Furthermore, the increment of \({\varepsilon }_{cu}\) is more pronounced when decreasing \({f}_{c}/{f}_{c}^{^{\prime}}\) owing to the higher self-centering efficiency [3, 18] of scenarios with lower \({f}_{c}/{f}_{c}^{^{\prime}}\). The scenarios with lower \({f}_{c}/{f}_{c}^{^{\prime}}\) have more self-centering response and experience more stress concentration at the corner; whereas, increasing \({f}_{c}/{f}_{c}^{^{\prime}}\) changes the wall response to a column-like behavior and to a more uniform stress distribution at the bottom of the wall. Considering the wide range of both \({f}_{c}/{f}_{c}^{^{\prime}}\) and \({f}_{se}/{f}_{y}\), it could be expected that in SRWs, the strain at the wall’s corner could easily exceed 0.0055. Therefore, to design the toe region of SRWs, materials which are both tougher and more ductile (roughly within \({0.0055\le \varepsilon }_{cc}\le 0.01\)) are more favorable. To estimate the wall capacity, however, considering \({\varepsilon }_{cu}=0.0055\) seems the most rational choice.

Concrete crushing could prevent damage propagation from the corner in the toe regions of SRWs. Although increasing the hazard level significantly increases the extent of damage (\({A}_{DI=0.1}\)), the amount of crushing (\({A}_{DI=0.4}\)), and repair work (\({A}_{DI=0.2}\)) were found not to change noticeably (see Figure S4). Applying the modified plastic hinge concept, considering 1% as the nominal limit state rotation, assuming negligible damage propagation in the wall’s toe regions due to the rocking mechanism, and neglecting the effect of tendons’ yielding and concrete local collapse in toe regions at the wall-footing interface, Eqs. (15) and (17) were proposed to estimate both \({h}_{D}\) and \({h}_{C}\), respectively. The results obtained from this simplified approach were more consistent with the numerical results than any of the existing relationships for estimating \({h}_{C}\)/plastic hinge length [10, 49, 51]. The observed discrepancy between numerical results and Eq. (17), could be attributed to the premature yielding of the tendons, and simplifying assumptions on \({\varepsilon }_{c,BTC}(y)\).

The results for \({\rho }_{D}\), \({\rho }_{C}\), and \({\rho }_{R}\), for three different loading levels, show that the maximum value of \({f}_{c}/{f}_{c}^{^{\prime}}\) has to be limited. Increasing \({f}_{c}/{f}_{c}^{^{\prime}}\) can significantly exacerbate the overall damage both in SRWs’ toe regions as well as in the centerline. In scenarios with higher and lower values of \({f}_{c}/{f}_{c}^{^{\prime}}\) and \({f}_{se}/{f}_{y}\), respectively (i.e., \({f}_{c}/{f}_{c}^{^{\prime}}\ge 0.105\), and \({f}_{se}/{f}_{y}\le 0.45\)), SRWs act more like columns/shear walls and damage develops uniformly at their bottom part. As shown in Fig. S4 of the ESM, more column-like SRWs experience unexpected damage mostly due to the poor reinforcing in the centerline (see Fig. 1). To further prevent unexpected damage and provide higher self-centering efficiency, therefore, the values of 0.105 and 0.45 are recommended as the maximum value of \({f}_{c}/{f}_{c}^{^{\prime}}\) and the minimum value of \({f}_{se}/{f}_{y}\), respectively.

Since the areas with 0.1 < DI < 0.2 are considered as damaged region in the calculation of \({\rho }_{D}\), and this damage generally can be neglected in repair work, the value of \({\rho }_{D}\) cannot be considered as a key factor for selecting the appropriate strategy/repair work process. Therefore, the value of \({\rho }_{C}\) and \({\rho }_{R}\) can provide a better insight into the extent of repair work. Based on the calculated \({\rho }_{D}\), either using HPC toe blocks or casting the bottom part with HPC leads to a better performance than the retrofitting strategy. Moreover, similar trends for both \({\rho }_{C}\), and \({\rho }_{R}\) are observed for \({f}_{c}/{f}_{c}^{^{\prime}}\) > 0.095 (typical SRWs). This implies that either using HPFRC locally in  the retrofitting strategy or placing toe blocks/casting solution in the rehabilitating strategy is a sound approach in preventing damage of typical SRWs. Conversely, for column-like SRWs, the rehabilitating strategy appears to be a more reasonable design choice.

8 Conclusion

In this research, a parametric numerical study was performed, through a validated FE model, to investigate the feasibility of strengthening of SRWs using HPC. Both the axial stress ratio (\({f}_{c}/{f}_{c}^{^{\prime}}\)) and tendons’ prestressing ratio (\({f}_{se}/{f}_{y}\)) of SRWs were taken into consideration as design variables for this study. A modified version of the plastic hinge concept was proposed and applied to defined scenarios to obtain \({\varepsilon }_{cu}\) at the SRWs’ toe region in the wall-footing interface. Using the calibrated \({\varepsilon }_{cu}\), a simplified and practical approach was introduced to estimate both \({h}_{D}\) and \({h}_{C}\) as intended for repair intervention. Two different strategies, retrofitting and rehabilitating, were then considered for repair work. For retrofitting, based on the damage estimation results, the crushed regions were replaced by HPFRC. In the rehabilitating strategy, using the simplified approach, \({h}_{D}\) was calculated and repair work was considered by either placing HPFRC block (i.e., \({h}_{D}\times {l}_{c}\)) in the toe regions or casting the bottom part of wall up to \({h}_{D}\) with HPFRC. By applying the required structural changes, the capability of each strategy was quantitatively established and investigated. Under the given geometry, boundary and loading conditions, the following conclusions are drawn:

  • Increasing \({f}_{c}/{f}_{c}^{^{\prime}}\) significantly decreases \({\varepsilon }_{cu}\), whereas \({f}_{se}/{f}_{y}\) does not have an obvious effect on \({\varepsilon }_{cu}\).

  • In SRWs, applying the modified plastic hinge concept yields more realistic estimations of \({\varepsilon }_{cu}\). With respect to the capacity, the value of 0.0055 could be considered as more suitable/conservative; whereas, in typical SRWs, with respect to the demand, a significantly higher magnitude ought to be considered particularly at the wall-footing interface in the toe regions.

  • Increasing \({f}_{c}/{f}_{c}^{^{\prime}}\), changes the wall behavior from a typical SRW to a column-like structure. Increasing \({f}_{c}/{f}_{c}^{^{\prime}}\) also increases the extent and severity of damage, whereas increasing \({f}_{se}/{f}_{y}\) decreases them. The areas in need of repair (DI > 0.2) are mostly limited to the toe regions.

  • To provide better self-centering behavior and prevent severe damage, the maximum value of 0.105 and the minimum value of 0.45 are recommended for \({f}_{c}/{f}_{c}^{^{\prime}}\) and \({f}_{se}/{f}_{y}\), respectively.

  • The proposed approach can satisfactorily estimate both \({h}_{D}\) and \({h}_{C}\) in DBE and MCE hazard levels. Although the estimated \({h}_{D}\) and \({h}_{C}\) are slightly conservative, the approach can more accurately predict \({h}_{C}\) than any of the current relationships available in the literature. The obtained results for \({h}_{C}\), using the proposed approach, show an average of \({0.051h}_{w}\).

  • Both retrofitting and rehabilitating strategies are effective in preventing severe damage at DBE and MCE hazard levels. For typical SRWs, both strategies lead to similar efficiency levels. For more column-like SRWs, however, the rehabilitating strategy (casting the bottom part of SRWs with HPFRC) seems the optimum design solution.