1 Introduction

Reinforced Concrete (RC) structures in practice are rarely subjected to pure torsion. Typically, torsional moments are combined with a combination of bending moments, axial and/or shear forces. However, in order to gain a complete and comprehensive understanding of the phenomena governing the torsional behavior of RC members, the study of specimens subjected to pure torsion represents an important and unavoidable starting point. The latter becomes even more significant for practice when considering the high amount of transverse reinforcement required in beams subjected to low torsional moments.

The behavior of RC beams in pure torsion has been investigated for over a century. Following pioneering tests carried out by Mörsch [1] and Graf and Mörsch [2], many studies have been reported in the literature on the response of RC beams subjected to pure torsion, or in combination with other actions [3,4,5,6,7,8,9]. With the advent and increasing use of high-strength concretes in research and practice over the last two decades, tests on conventionally reinforced concretes with compressive strengths upward of 100 MPa have been reported [10,11,12]. Furthermore, the response of RC beams strengthened with innovative materials and subjected to torsion have recently been reported [13,14,15]. All these tests confirm that, after first cracking, the shear stresses that develop as a result of the induced torsion are unable to be resisted unless a suitable mechanism is formed, which enables the transfer of stress across a cracked section. One such a mechanism can be described by the space truss analogy first developed by Rausch [16] and later refined by Lampert [17] and Lampert and Collins [18]. These models usually consist of diagonal compressive struts and tie elements (i.e., stirrups and rebars), which are formed to redress equilibrium and enable stresses to be transferred within the cracked sections [19].

As initially pointed out by Leonhardt and Mönning [20] and then recommended by different structural codes [21, 22], a minimum amount of longitudinal and transverse reinforcement must be provided in structural concrete in order to prevent brittle failure modes at the onset of first cracking. Considering that the role of web (transverse) reinforcement in members reinforced to resist torsion is analogous to that of stirrups in beams subjected to shear, the experimental results reported by Choi et al. [23], Susetyo et al. [24], Minelli and Plizzari [25] and Facconi and Minelli [26] appear to be very promising to support the view of partially or totally replacing of the minimum transverse reinforcement required to resist torsion by including steel fibers within the concrete matrix. The use of randomly orientated and uniformly distributed steel fibers in concrete improves its post-cracking behavior. This leads to tensile strengths and post-cracking toughness greater than those typically exhibited by Plain Concrete (PC) (i.e., concrete without fibers). Experimental tests performed worldwide over the last three decades have shown that fibers can be successfully used in different typologies to enhance the resistance of flexural- and shear-critical members such as beams [27,28,29], tunnels linings [30,31,32], slabs [33,34,35], etc. On the contrary, much less research on the topic of SFRC (Steel Fiber Reinforced Concrete) members subjected to torsion can be found in the literature.

The potential effectiveness of relying on steel fibers to resist torsion was first recognized by Mansur and Paramasivam [36] and shortly thereafter by Narayanan and Kareem-Palanjian [37, 38]. These studies reported an increase of the ultimate torsional strength, toughness and ductility of concrete beams subjected to pure torsion due to the inclusion of the fibers. Similar results were reported by Mansur et al. [39] after testing beams with different reinforcement ratios and steel fiber contents higher than 0.5% by volume, ρf. Later, in 2003, those results were confirmed by Rao and Seshu [40], who observed a general improvement of the ultimate capacity, toughness and stiffness of beams subjected to pure torsion reinforced with fibers only. The authors concluded that a minimum fiber content of 0.9% is required to provide significant ductility to the torsional response. Chalioris and Karayannis [41] carried out 35 tests on rectangular and flanged beams containing both conventional reinforcement and relatively high contents of steel fibers (ρf = 1%–3%). Aside of the typical observations noted above (i.e. increase of post-cracking torsional behavior due to fiber addition), Chalioris and Karayannis demonstrated that fibers have the potential to replace stirrups only if a very high volume fraction (ρf = 3%) is supplied. Ultra-High Performance Fiber Reinforced Concrete (UHPFRC) beams subjected to pure torsion were tested by Yang et al. [42], who tested, among others, some beams without stirrups and characterized by varying longitudinal reinforcement ratios (i.e., ρl = 0.56%, 0.88%, 1.27%) and high contents (ρf = 1% and 2%) of high strength short steel fibers. In spite of the very high post-cracking strength and toughness exhibited by the uniaxial tensile constitutive laws for the different UHPFRCs adopted, all beams without stirrups were not able to increase the torsional strength after first cracking. However, as highlighted by other studies, a slight increase of the post-cracking resistance was generally observed for increasing values of longitudinal reinforcement ratio [43]. Amin and Bentz [44] recently carried out pure torsion tests on rectangular beams reinforced with 30 kg/m3 of steel fibers (ρf = 0.38%) combined with two different transverse reinforcement arrangements. The authors highlighted the ability of fibers to maintain the stress across cracks leading to an improved control of cover spalling.

The data inferred from the previous literature survey illustrates that a few studies were carried out on SFRC beams without stirrups and, moreover, most of those studies included specimens reinforced with fiber contents not lower than 0.6%. Such dosages of steel fibers may be economically deterring in practice.

In addition, several experimental tests have been performed on beams without longitudinal reinforcement; the consequence of which is that the well-known space truss torsional resisting mechanism cannot be fully established. Furthermore, specimens without longitudinal reinforcement are not representative of members constructed in practice.

Moreover, except for a few recently published studies, many research programs have not reported a complete mechanical characterization of the post-cracking tensile behavior of SFRC at the material level. Most of these studies generally provide an assessment of the tensile strength of the concrete matrix only, without any consideration for the residual tensile strength provided by the fibers for a particular SFRC rheology. Without this information, consideration on the torsional response of beams composed of SFRC cannot be fully exhaustive.

To bridge this lack of information, this paper presents a series of pure torsion tests on SFRC beams with longitudinal reinforcement and without stirrups alongside a full suite of material characterization tests. The two pairs of beams were supplied with the same longitudinal reinforcement (ρl = 1.13%) and two different dosages of steel fibers respectively equal to 25 kg/m3 (ρf = 0.32%) and 50 kg/m3 (ρf = 0.63%). Companion notched beams for characterizing the tensile post-cracking behavior of SFRC were cast and tested under three-point bending. In order to assess the suitability of SFRC beams without stirrups to replace minimum transverse reinforcement requirements, a control test was also performed on a conventional RC beam containing the minimum torsional reinforcement recommended by Eurocode 2 [21]. Finally, a RC beam without stirrups was also tested as a reference sample.

The main results of the tests will be presented and discussed, by including considerations on the torsional rigidity, the deformation energy and the evolution of the crack pattern. A comparison with other results found in the literature will be also reported and discussed.

2 Experimental program

2.1 Test specimens

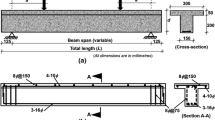
An experimental investigation was carried out on a total of six PC and SFRC beams subjected to pure torsion. All members were geometrically identical with an overall length of 2700 mm and a cross-section of 300 × 300 mm, typical of edge beams in reinforced concrete buildings. The specimens contained 18 mm diameter (Ø18) longitudinal deformed steel rebars located in each corner of the cross section. The longitudinal reinforcement was chosen to ensure its elastic response during the application of the torque. The specimen geometry and reinforcement detailing are illustrated in Fig. 1. Details of each specimen tested in this study are presented in Table 1. TB1-PC was a plain concrete (PC) beam and did not contain any transverse reinforcement. TB2-PC-ST was also a plain concrete specimen and contained 6 mm diameter deformed steel stirrups (Øst) spaced at 110 mm (sst) centers. Two identical SFRC beams (TB3-SFRC25, TB4-SFRC25) were reinforced with 25 kg/m3 of steel fibers and, lastly, other two identical SFRC beams (TB5-SFRC50, TB6-SFRC50) contained 50 kg/m3 of steel fibers. The hooked-end steel fibers used in this study were 30 mm long, had a diameter of 0.35 mm and a tensile strength of 2200 MPa. No transverse steel reinforcement was placed in the SFRC members. The transverse reinforcement arrangement of TB2-PC-ST fulfilled the following minimum requirements recommended by Eurocode 2 [21] (clause 9.2.3):

$$\rho _{{{\text{st}}}} = \frac{{{{A}}_{{{\text{sw}}}} }}{{{{s}}_{{{\text{st}}}} \cdot {b}}} = 0.17\% \ge \rho _{{\text{st,min}}} = 0.08 \cdot \frac{{\sqrt {{{f}}_{{{\text{ck}}}} } }}{{{{f}}_{{{\text{yk}}}} }} = 0.1\%$$
(1)
$${{s}}_{{{\text{st}}}} = 110\,{\text{ mm}} \le \,\min ({{p}}_{{\text{c}}} /8, 0.75\,{{d}}) = 150\,{\text{mm }}\& \,\min \left( {{{b}},{{h}}} \right) = 300\,{\text{ mm}}$$
(2)

where ρst and ρst,min are the actual and the minimum required transverse reinforcement ratios, respectively. In Eq. 1, fck = 31.7 MPa is the cylindrical characteristic compressive strength of the concrete used to manufacture the beam TB2-PC-ST; fyk = 450 MPa is the characteristic yielding strength of stirrups Ø6. In Eq. 2, b = h = 300 mm are the width and the height of the cross section, respectively; pc = 1200 mm is the perimeter of the cross section; Asw = 56.5 mm2 is the total area of transverse reinforcement; sst = 110 mm is the spacing of stirrups; and d = 265 mm is the effective depth of the section.

Fig. 1
figure 1

Geometry and reinforcement details of the test specimens (dimensions in mm)

Full size image
Table 1 Main properties of beam specimens
Full size table

Table 1 summarizes the basic properties of the specimens such as the longitudinal (ρl = Asl/Ac) and transverse (ρst) reinforcement ratios as well as the fiber volume fraction (ρf). Note that Ac = 9 × 104 mm2 is the area of the beam gross section.

All beams consisted of a monitored region, in which pure torsion was assumed to be completely developed, and two disturbed regions located at both ends of the member (refer to Fig. 1). To prevent torsional failure as well as local damages due to stress concentrations and to promote the full development of torsion in the middle portion of the beam (i.e., within the monitored region), the outer disturbed regions were provided with closely spaced (spacing = 50 mm) 10 mm diameter stirrups.

3 Materials

The concrete mix-design reported in Table 2 was adopted for all test specimens. After casting, the beams were stacked on the laboratory floor at room temperature up to the time of testing. To reduce the likelihood of any cracking due to shrinkage occurring, each specimen was covered with a polyethylene sheet and kept within the timber molds for at least 7 days after casting.

Table 2 Concrete composition and properties of steel fibers
Full size table

The average value of the fresh and hardened mechanical properties of the three concrete mixes and the corresponding coefficient of variation (percentage values within round brackets) are presented in Table 3. The consistency of fresh concrete was measured by a slump test (i.e., Abrams cone) according to EN 12350-2 [45]. Based on the results of the slump test, the slump classes (EN 206-1 (2006) [46]) reported in Table 3 show that the slump of the two SFRCs ranged between 160 and 200 mm (class S4) whereas PC showed a slump of 145 mm (class S3). This is due to the increase in superplasticizer supplied for the SFRC mixes. The mean uniaxial compressive strength (fcm,cube) of the mixes was assessed by testing 150 mm cubes after at least 28 days curing in a controlled environmental chamber having a constant temperature of 20°C and relative humidity of about 95%. The cylindrical mean compressive strength (fcm) was calculated as 0.83·fcm,cube. The mean tensile strength (fctm) and the mean secant elastic modulus (Ecm) of the concretes were both calculated according Eurocode 2 [21] as fctm = 0.3fck2/3 and Ecm = 22·(fcm/10)0.3.

Table 3 Concrete properties
Full size table

The fracture behavior of each mix was characterized by performing a series of 3-point bending tests (3PBTs) on 150 × 150 × 500 mm3 notched prisms tested in accordance to EN 14651 [47]. The tests provided the flexural tensile stress-CMOD (Crack Mouth Opening Displacement) curves depicted in Fig. 2, which allows determining the residual strength parameters required by the fib Model Code 2010 (MC2010) [48] to characterize the post-cracking behavior of SFRC. As summarized in Table 3, the aforementioned residual strength parameters include the limit of proportionality fL (i.e. the highest flexural tensile strength detected for CMOD ranging from 0 to 0.05 mm) and the residual strengths fR,1 (CMOD = 0.5 mm), fR,2 (CMOD = 1.5 mm), fR,3 (CMOD = 2.5 mm), and fR,4 (CMOD = 3.5 mm).

Fig. 2
figure 2

Flexural tensile stress-CMOD curves from three point bending tests according EN 14651 [47]

Full size image

The comparison between the PC and the SFRC curves of Fig. 2 shows, as expected, that the addition of fibers drastically increased the post-cracking strength and toughness of the concrete. It is seen that, considering the CMOD values ranging from 0.5 to 3.5 mm, the residual strengths for mix SFRC50 were 50–75% higher than those presented for mix SFRC25. Since short fibers (fiber length < 40 mm) were used, the maximum performance in tension of both SFRC materials was observed right after the localization of the crack in the notched section, when the CMOD was lower than 2 mm. Note the scatter in the post-cracking range of the results, particularly for mix SFRC25.

Both the stirrups and the longitudinal reinforcement were composed of conventional steel deformed bars (B450 C according to Eurocode 2 [21]) having the mechanical properties reported in Table 4. The latter were obtained by testing four samples for each bar typology according to the testing procedure described by ISO 15630-1[49].

Table 4 Properties of steel deformed rebars
Full size table

3.1 Test set-up and instrumentation

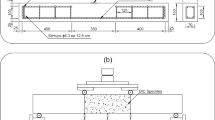
A state of pure torsion was applied to the specimens using the test rig illustrated in Fig. 3a. The specimens were supported at both ends by steel rollers that allowed free rotation about the longitudinal axis of the beam, without preventing extension or contraction due to deformation induced by the applied torsion. Each roller was aligned to the beam axis and welded to a bottom steel plate (plate (A) —Fig. 3a). A different steel plate (plate (B)—Fig. 3a) was laid on the roller to provide support to the bottom surface of the specimen. Four bolts were used to connect plate (B) to the steel cantilever placed on the top side of the specimen. The beam-to-plate (B) and the beam-to-steel cantilever interfaces were both filled with a thin layer of shrinkage compensating mortar to prevent contact problems pertaining to any possible uneven surfaces and to make specimen levelling operations much easier. Two equal counteracting torques were applied to the test beam by means of the steel cantilevers loaded by the spreader beam placed diagonally with respect to the longitudinal axis of the specimen. A stiff spreader beam was used to equally distribute the total vertical load (P) from the actuator to the two cantilevered ends, which provided the torsion arm (564 mm—see Fig. 3) of the twisting moment. The total load (P) acting on the center of the spreader beam was applied by the transversal loading beam which, in turn, was loaded by a couple of vertical Dywidag bars connected to a 1000 kN capacity electromechanical thrust jack. To continuously monitor the total load, two load cells were clamped between the Dywidag bars and the loading beam. Figure 3b shows the specimen TB3-SFRC25 prior to the application of load.

Fig. 3.
figure 3

Test set-up: 3D schematic view (a); top-view (b) and rear-view (c) schematics; actual view (d) (dimensions in mm)

Full size image

As shown in Fig. 3a, two potentiometers were located at each end of the monitored region in order to detect the horizontal displacement resulting from the rotation of the beam about its longitudinal axis. The following 4-index notation was used for labelling each horizontal sensor: first index, H for horizontal; second index, T for top side and B for bottom side of the beam; third index, F for front and R for rear side of the beam; the fourth digit refers to either the left (1) or the right (2) end section of the monitored region. To detect the potential growth of cracks, which were expected to have an inclination to the longitudinal axis of the specimens ranging from 30° to 50°, three potentiometers were installed on each of the four sides of the beam. A similar notation was chosen for these 12 sensors: first index, D for diagonal instrument; second index, T, R, F, B for top, rear, front and bottom side, respectively; the third index is used to number each of the three potentiometers, starting from the left side of the beam (Fig. 3a).

The load was monotonically increased at a constant speed so that the rate of change of the unit angle of twist of the beam was about 0.01 rad/(m s). This type of displacement control performed by the electromechanical actuator allowed to carefully control the post-peak softening response of the test beams. Data was detected and stored by a data acquisition system at constant intervals of 0.5 s.

4 Experimental results and discussion

Figure 4 and Table 5 present the Torque (T) versus twist (Ψ) response of each of the specimens and the key results of the tests, respectively. In Table 5, Kel,exp is the initial torsional rigidity, Tcr and Ψcr are the torque and the corresponding twist at first cracking, respectively and Tp and Ψp are the torque and the corresponding twist at peak load. Moreover, for each of the test beams, Table 5 reports the torque (T34) corresponding to the maximum twist (i.e., Ψ = 34 × 10–3 rad/m) achieved by specimen TB2-PC-ST at the conclusion of testing. It is worth remarking that the twist is here calculated as the ratio between the angle of rotations θ (i.e., the sum of the angles of rotation detected at both ends of the monitored region) and the length (L = 1.5 m) of the monitored region.

Fig. 4
figure 4

Torque versus twist experimental curves: overall response (a); focus on the initial branch (b)

Full size image
Table 5 Summary of main experimental results
Full size table

4.1 Overall torsional behavior of the specimens

Figure 4a compares the overall torsional response of the six specimens. The initial elastic branches of all curves presented in Fig. 4b displayed similar rigidities and consistent values for the torque and twist at first cracking. This is to be expected, as the contribution of fibers to concrete at the material constitutive level has minimal influence to the response prior to cracking. Only the beams TB2-PC-ST and TB5-SFRC50 presented a slightly different stiffness as compared to the other specimens. Averaging the data reported in Table 5, the mean torque and twist at first cracking results in 13.1 kNm and 0.9 × 10–3 rad/m, with a CV of 6% and 18%, respectively.

Cracking occurs when the maximum tensile stress due to torsion reaches the tensile strength of concrete. Different equations have been proposed to estimate the torque corresponding to first cracking. For instance, according to the classical de Saint–Venant’s (DSV) theory, the first cracking torque (Tcr,DSV) of a rectangular section results from the following equation:

$${{T}}_{{\text{cr, DSV}}} = {{f}}_{{{\text{ctm}}}} \cdot \frac{{{{b}} \cdot {{h}}^{2} }}{{3 + 1.8{{h}}/{{b}}}} = 16.88 - 19.13\,{\text{ kNm}}$$
(3)

where the minimum and maximum value of the torque have been calculated by considering respectively the lowest and the highest value of concrete tensile strength (fctm) reported in Table 3. Based on the “thin-walled tube theory” (WTT), as also reported in Collins and Mitchell [50], the cracking torque (Tcr,WTT) can be calculated as follows:

$${{T}}_{{\text{cr,WTT}}} = 0.33\sqrt {{{f}}_{{{\text{cm}}}} } \cdot \frac{{{{A}}_{{{c}}}^{2} }}{{{{p}}_{{\text{c}}} }} = 13.38 - 14.70 \,{\text{kNm}}$$
(4)

The two extreme values of the resisting torque presented in Eq. 4 are related to the minimum and the maximum value of the measured fcm (Table 3). Note that both the Eqs. 3 and 4 depend, directly or indirectly, on the tensile strength of concrete, whose value is independent of the fiber dosage. The average cracking torque provided by the present tests is very close to the one predicted by WTT and, at the same time, is more than 20% lower than the torque predicted by the de Saint Venant’s expression. However, considering several factors (e.g., pre-existing shrinkage tensile strains, variability of concrete tensile strength) that may affect the prediction of first cracking resistance of the member, the experimental values of Tcr observed herein appear very reasonable.

As expected, at first cracking, the beam without fibers and stirrups (TB1-PC) achieved its maximum torque (Tp = 16.18 kNm). After that, it started exhibiting a consistent softening response clearly governed by the post-cracking tensile behavior of PC. On the contrary, all the other specimens showed the ability to withstand increasing loads after first cracking because of the increased post-cracking tensile resistance provided by either the transverse reinforcement or steel fibers.

Regarding specimen TB2-PC-ST, the torque-twist response after cracking ( > 1.67 × 10–3 rad/m) reveals a sudden loss in stiffness which corresponded to a sudden increase of twist, typical of conventionally RC beams [19]. At this stage of testing, the ability of the beam to resist the applied load is closely related to the activation of the space truss mechanism, in which diagonal concrete compressive strains and steel tensile strains acting in the longitudinal and transverse rebars determine the twist angle. Since longitudinal rebars were designed to remain elastic for all test specimens, the maximum torque (Tp = 20.84 kNm) was considerably lower than that corresponding to yielding of longitudinal rebars. Therefore, failure was governed by yielding of transverse rebars. For safety reasons, the test was terminated after the first sharp reduction of torsional resistance during the post-peak response (i.e. prior to rupture of the transverse reinforcement).

The significant loss of torsional rigidity, which characterized the response of the beam TB2-PC-ST after cracking, was not observed for the four SFRC beams, whose post-cracking response was considerably much stiffer. As shown in Fig. 4, the applied torque continued to increase until the maximum capacity was reached. The latter ranged from a minimum of 22.94 kNm to a maximum 27.32 kNm, which were respectively 10% and 31% higher than the peak resistance of the beam TB2-PC-ST. Moreover, the angle Ψp of the SFRC beams was always more than 50% lower than that observed for the beam TB2-PC-ST. After the attainment of the maximum torque, an almost horizontal plateau followed by a descending branch was observed in all beams. It is worth noting that, irrespective of the adopted fiber content, steel fibers appeared to be effective in providing an overall stable and ductile response because of their ability to control the progression of cracking. Both the horizontal plateau and the gradual post-peak softening response described above represent clear evidence of the stability that characterizes the overall response of SFRC beams. As shown by the scatter of values corresponding to the torque T34 (Table 5), the descending branches exhibited by the SFRC beams after the plateau were considerably different in term of resisting torque and rotational capacity. As a matter of fact, the torque T34 achieved by the specimen TB3-SFRC25 was about 90% higher than that of the beam TB6-SFRC50.

4.2 Torsional rigidity

Table 5 indicates that the initial torsional rigidity (Kel,exp) varied from 12,850 kNm2/rad (TB2-PC-ST) to 19,630 kNm2/rad (TB5-SFRC50), with an average of 16,263 kNm2/rad and a CV of about 14%. Using the polar moment of inertia (Jt = bh3/[3 + 4.1(h/b)3/2]) of the cross section, the DSV theory defines elastic rigidity as follows:

$${{K}}_{{{\text{DSV}}}} = {{G}}_{{{\text{cm}}}} \cdot {{J}}_{{\text{t}}} = 15,830\,{\text{ kNm}}^{2} {\text{/rad}}$$
(5)

where Gcm = Ecm/[2(1 +  υ)] = 13.9 GPa is the shear modulus of concrete; υ  = 0.2 is the Poisson’s coefficient; Ecm = 33.3 GPa is obtained by averaging the elastic moduli of concrete reported in Table 3; Jt = 1.141 x 109 mm4. The rigidity provided by Eq. 5 is only 3% lower than the average value of Kel,exp but, on the contrary, it is 23% higher and 19% lower respectively than the minimum and maximum rigidity exhibited by SFRC specimens. However, considering the uncertainties that typically affect experimental results, one may conclude that the torsional rigidity experimentally observed is well predicted by the classical DSV theory.

As observed above, the SFRC specimens were not affected by the sharp reduction of the torsional stiffness presented by the specimen TB2-PC-ST at the onset of cracking (Fig. 4). To better estimate the actual improvement provided by fibers, the secant torsional rigidity (K) of the test beams was plotted against the normalized twist (Ψ/Ψcr). These results are presented in Fig. 5. Based on a similar approach used by Mc Mullen and El-Degwy [51] to define the cracked stiffness, the secant rigidity (Fig. 5) was calculated as the slope (i.e., (T2–T1)/(Ψ2–Ψ1)) of the line corresponding to a given range of twist values, whereas the normalized twist was defined as the actual twist (Ψ) to the first cracking twist (Ψcr) ratio. For example, Ψ/Ψcr = 1 at first cracking. For each beam, only a few ranges of values for the normalized twist were considered to estimate the rigidity. Each range was selected such that the secant line reasonably approximated the average slope of the torque-twist curve without considering local disturbances of the experimental curve. This simplification made the comparison of the five specimens much clearer.

Fig. 5
figure 5

Secant torsional rigidity versus normalized twist

Full size image

The curves of Fig. 5 allow appreciating the significant reduction of torsional stiffness that affected specimen TB2-PC-ST after cracking. In fact, once the normalized twist reached a value of 1.6, the stiffness of the beam TB2-PC-ST dropped to 260 kNm2/rad and then remained approximately constant up to the peak torsional resistance. Except for beam TB6-SFRC50, whose loss of rigidity within the normalized twist range 1–1.6 was as fast as that of TB2-PC-ST, all the other SFRC samples showed a more gradual reduction of rigidity, which however remained always higher than that of TB2-PC-ST. The highest decrement of rigidity after cracking occurred within the normalized twist range 1–2.4. After that, the SFRC beams presented almost constant rigidities that were 3.7–7.4 times higher than the minimum (260 kNm2/rad) exhibited by TB2-PC-ST. It is noteworthy that for normalized twists falling in the range 2.2–4.2, the rigidities of the SFRC beams varied from 915 kNm2/rad (TB4-SFRC25) to a maximum of 1850 kNm2/rad (TB3-SFRC25). Normalized twists higher than 4.2 led to a steady decrement of rigidity of the SFRC specimens that tended to approach the TB2-PC-ST curve. All the torsional rigidities became negligible once the normalized twist was over a value of 7.

4.3 Strain energy

The strain energy of each specimen was calculated by integrating the area bounded by the horizontal axis and the corresponding torque-twist curve shown in Fig. 4. The evolution of the cumulated energy is plotted in Fig. 6 as a function of the twist. As one may observe, the cumulated energy of all the SFRC beams is always greater than that exhibited by the specimen TB2-PC-ST.

Fig. 6
figure 6

Cumulated strain energy versus twist

Full size image

Considering a twist of 34·10–3 rad/m, which corresponded to the maximum rotation achieved by the beam TB2-PC-ST, the total energy absorption of the SFRC members ranged from 1055 kJ·rad (TB4-SFRC25) to 1218 kJ·rad (TB5-SFRC50). On the contrary, the maximum energy absorption of the beam TB2-PC-ST (977 kJ·rad) was 7% and 20% lower than the former ones, respectively. These results indicate that substituting stirrups for fibres can improve the performance of the beams both in terms of ultimate resistance and rotational capacity, leading to a higher energy absorption.

As expected, among the SFRC specimens, the TB3-SFRC25 and the TB4-SFRC25 recorded the highest and the lowest energy absorbing capacity, respectively.

4.4 Cracking evolution

Prior to testing, a careful examination of each surface of each beam was performed using a handheld digital microscope to determine whether any significant cracks due to shrinkage developed between casting and testing. No crack was detected with this regard.

During testing, the crack patterns were continuously monitored and manually recorded. The crack patterns detected at the end of the tests are presented in Fig. 7. For the purpose of reporting, the monitored region was divided into 3 segments of equal length (i.e., 500 mm). These are denoted as Segment 1, Segment 2 and Segment 3, as shown in Fig. 7.

Fig. 7
figure 7

Final crack patterns of beam specimens

Full size image

The crack pattern of the beam TB1-PC consisted of a main localized crack, having an inclination of about 40°–58°. This main crack began to localize within Segments 1 and 2 (see Fig. 3) at the onset of first cracking. As it is typical of PC, the main and the few secondary cracks rapidly propagated as the twist gradually increased. The brittle collapse of the beam was prevented by the displacement-controlled testing procedure.

Owing to its transverse reinforcement, TB2-PC-ST exhibited several cracks especially within Segments 2 and 3. At first cracking, few cracks started to form in the Segment 2. With increasing load, more cracks developed and each of these cracks subsequently widened. After peak load was attained, significant spalling of concrete cover was observed in an area between the rear and the bottom side of the beam (see Segment 2 in Fig. 3). The slope of the cracks detected after failure ranged from 30° to 51°.

In terms of damage evolution, the behavior of the four SFRC specimens was quite similar. More specifically the main cracks appeared on the surface of the beam before the onset of the post-peak descending branch of the torque vs. twist response (Fig. 4). As the torque decreased after the peak, the damage gradually localized in a single crack, whose width continued to increase till the end of the test. This was with exception for beam TB3-SFRC25, in which two major cracks developed and steadily progressed in width up to significant values, leading to a higher overall capacity. In addition, the crack pattern of the beam TB5-SFRC50 showed slightly more diffused cracks than in the specimen TB6-SFRC50. Note that crack inclination of the SFRC beams fell in the range 38°–50°, with a maximum slope of 60°–67° detected for very few cracks.

When the quasi-horizontal branch of the torque-twist response was attained, the crack pattern of the SFRC beams tended to stabilize and, therefore, the number of primary cracks remained almost constant up to the end of the test. Similar to the SFRC beams, the crack pattern of TB2-PC-ST remained stable as the torque decreased after the peak. In view of this, the mean crack width (wm) can be reasonably estimated by dividing the elongation of each diagonal potentiometer (see par. 2.3 and Fig. 3) by the number of cracks spanned by the instrument. The obtained width is an approximation of the actual value, as the potentiometers were not generally perpendicular to the direction of cracks. In view of future developments of analytical models able to accurately predict the torsional resistance of FRC members, a good estimation of the expected average crack width at peak torque for the dominant crack would be of paramount importance.

A summary of the crack widths detected in each segment and side of the specimens is reported in Table 6. The rows and columns of Table 6, named as “mean-segment” and “mean-side”, report the crack widths obtained by averaging those observed in every single segment and side of the beam, respectively. Moreover, the torque and the related twist reported for each beam in Table 6 were chosen so that the overall mean crack width (i.e. average of the mean values of each segment and side) was approximately equal to 0.3 mm. The latter is generally considered as a permissible (or maximum design) crack width for concrete structures under service loading conditions.

Table 6 Torque and twist corresponding to average crack widths (wm) of about 0.3 mm
Full size table

TB2-PC-ST exhibited cracks of about 0.3 mm when the twist and the corresponding torque were equal to 20 rad/m and 18.8 kNm. Compared to TB2-PC-ST, all SFRC beams recorded higher torques ranging from 22.5 kNm (TB4-SFRC25) to 27.3 kNm (TB3-SFRC25). As expected, the specimens characterized by the most diffused crack patterns (i.e., TB3-SFRC25 and TB5-SFRC50) presented the highest increment of resistance (i.e., 46% and 41%) with respect to the beam with stirrups. At the same time, the beam with the lowest number of cracks, i.e. TB4-SFRC25, experienced the lowest increment of resistance (i.e., 20%). The internal stress redistribution due to cracking affected the torsional resistance as well as the twist capacity of the specimen. In fact, looking at the behavior of the SFRC beams, it appears that the higher the number of cracks, the higher the twist leading to the same crack width level. Therefore, TB3-SFRC25 twisted 46% more than TB4-SFRC25 to reach a mean crack width value of 0.3 mm.

5 Discussion

The conventional reinforcement placed in the specimen TB2-PC-ST according Eurocode 2 [21] was able to ensure a reserve of capacity after cracking that prevented a brittle failure. As shown in Fig. 4, the resisting torque after cracking remained greater than Tcr and, in addition, Tp/Tcr (= 1.56) was adequately high (Table 5). Based on the space truss analogy [19, 20], one may further demonstrate that failure was governed by yielding of stirrups. In fact, the resisting torque related to tensile failure of stirrups (Tp,st) was significantly lower than those involving compression failure of the struts (Tp,str) and yielding of longitudinal reinforcement (Tp,sl):

$${{T}}_{{\text{p, st}}} = \frac{{{{A}}_{{{\text{sw}}}}^{{\prime }} }}{{{{s}}_{{{\text{st}}}} }} \cdot 2 \cdot {{A}}_{{\text{o}}} \cdot {{f}}_{{\text{y,st}}} \cdot \cot {{g}}\uptheta = 17.4\,{\text{ kNm}}$$
(6)
$${{T}}_{{\text{p, str}}} = 2 \cdot {{A}}_{{\text{o}}} \cdot {{t}}_{{\text{c}}} \cdot 0.5{{f}}_{{{\text{cm}}}} \cdot \frac{{\cot {{g}}\uptheta }}{{1 + \left( {\cot {{g}}\uptheta } \right)^{2} }} = 80.4\,{\text{ kNm}}$$
(7)
$${{T}}_{{\text{p, sl}}} = {{A}}_{{{{sl}}}} \cdot 2 \cdot \frac{{{{A}}_{{\text{o}}} }}{{{{p}}_{{\text{o}}} }} \cdot {{f}}_{{\text{y,sl}}} \cdot {{tg}}\theta = 64.0\,{\text{ kNm}}$$
(8)

In Eqs. 6–8, the inclination of the compressive struts (θ) is assumed equal to 40°. This corresponds to the mean inclination of the cracks detected for the beam TB2-PC-ST. In Eqs. 6–8, A'sw = 28.3 mm2 is the area of one leg of a stirrup; tc = Ac/pc = 75 mm is the thickness of the equivalent thin-walled tube according Eurocode 2 [21]; fcm = 36 MPa is the compressive strength of concrete (PC) without fibers (Table 3); fy,st = 485 MPa and fy,sl = 516 MPa are the yielding strengths of bars Ø6 and Ø 18, respectively (Table 4). Note that the prediction of Eq. 6 (17.4 kNm) is only 17% lower than the actual value observed in the test.

The results reported in the previous sections showed that fibers have the potential to replace the minimum required conventional transverse reinforcement to resist torsion. In fact, all the SFRC beams attained a torsional resistance 10–30% higher than TB2-PC-ST and, moreover, they experienced a twist capacity similar, or even higher, than that of TB2-PC-ST.

As typical of RC beams [3, 52], the beam TB2-PC-ST was affected by a substantial loss of torsional stiffness after cracking. This loss was significantly mitigated by fibers as the rigidity exhibited by SFRC beams right after first cracking was significantly higher. The ability of the fibers to control the torsional post-cracking stiffness of the members represents an important advantage for service loading conditions, as the reduced torsional deformation leads to much smaller crack widths. Beyond peak load, the beams containing fibers presented a stable and ductile behavior that was characterized by an almost constant torsional resistance for increasing rotations. The torsional resistance started to decrease once the twist achieved values slightly lower (18–20 rad/m), or even higher (30 rad/m for TB3-SFRC25 only), than the rotation at peak (24.35 rad/m) reached by TB2-PC-ST.

From the analysis of the experimental results reported herein it is premature to determine a definite relationship between the structural performance (i.e., resisting torque, deformation capacity, torsional stiffness, etc.) of the SFRC specimens and the corresponding fiber contents. Against expectations, the two beams containing the lowest amount of fibers (i.e., 25 kg/m3) were those that displayed the best (TB3-SFRC25) and the worst (TB4-SFRC25) behavior in terms of torsional capacity and toughness. An accurate study of the ultimate crack patterns can partly provide an explanation for the aforementioned responses. In fact, TB3-SFRC25 and TB4-SFRC25 were the beams with the most and the least diffused crack patterns at failure, respectively. Besides the quite consistent scatter of material tests reported in Table 3, the number of cracks developed during the test affected the ability of the specimens to redistribute internal stresses leading to differing structural performances. For the same reasons, the effect of the crack patterns of the two SFRC50 samples on their response was intermediate between those of the SFRC25 specimens. Other studies, including tests on beams having an overall length different from that adopted herein [53], reported a similar trend.

Table 7 provides a summary of selected data on pure torsion tests found in the literature. The beams reported in Table 2 are characterized by different longitudinal reinforcement ratios, varying from 0.25 to 1.57%, and different fiber volume fractions, ranging from 0.32 to 3%. All of the specimens experienced failure in tension (torsion-tension mechanism) as no stirrups were provided in any sample. The last column of Table 7 compares the fiber content of each beam with the minimum fiber volume fraction (i.e., 0.32%) adopted in the present study. As one may observe, the maximum increment of torsional resistance after cracking, i.e., Tp/Tcr = 2.0, is quite low if compared with the wide range of values ρf/ρf,min = ρf/0.32%, i.e., ρf/ρf,min = 2.0–9.4 (Table 7), that characterizes the increment of the fiber content. The same consideration can be stated for the increment of post-cracking twist (Ψp/Ψcr), which varied from 1.8 to 15.2. It is worth noting that, despite the low/moderate content of fibers adopted, the best performance was achieved by the beams tested in this research. This is probably due to the good tensile post-cracking behavior of the SFRC25 and SFRC 50, which contained steel fibers having geometrical and mechanical properties much better than those adopted by the other studies reported in Table 2. Unfortunately, the comparison is difficult since all other studies did not report any mechanical characterization of the SFRC.

Table 7 Comparison of different research studies
Full size table

Notwithstanding this, the results provided by the literature and reported in Table 7 represent an important reference point for the state of knowledge even though it remains an urgent need for new experimental research to improve the current knowledge about the torsional behavior of SFRC beams without stirrups.

6 Concluding remarks

The results of six large-scale beams subjected to pure torsion have been presented in this paper. Comparisons have been made between a sample with no stirrups nor fibers, one with the minimum classical reinforcement and the remaining four containing steel fibers. All specimens were longitudinally reinforced so that a space truss mechanism could be established. Based on the experiments and discussion reported herein, the following main conclusions can be drawn:

  • FRC with a post-cracking performance higher than class 2c, according MC2010, is able to completely substitute the minimum transverse reinforcement required for torsion.

  • FRC having performance class 2c was able to enhance the torsional behavior by increasing the torque at peak, the post-cracking torsional rigidity as well as the cumulative strain energy in comparison with the reference RC sample containing minimum conventional transverse reinforcement according Eurocode 2.

  • Steel fibers are able to promote a significantly higher post-cracking rigidity and a steadier development of the cracking phenomenon, compared to classical RC elements. This phenomenon provides an enhanced behavior at serviceability limit states.

  • From the discussion of the database of 14 experiments on SFRC specimens without torsional reinforcement, it seems that fibers enhance the torsional strength and, therefore, have the abilty to completing substituting transverse reinforcement required for torsion. Further specific studies are needed to validate this concept.