Abstract
The paper presents an experimental program carried out to check the load bearing capacity of a steel fibre reinforced concrete (SFRC) floor in northern Italy. The extensive mechanical characterization focused on the suitability of 3 non-standardized test methods for quality control and tensile constitutive curve assessment was performed, this consisting of: uniaxial tensile test (UTT), double edge wedge splitting test (DEWST) and double punching test (DPT) to characterize the post-cracking mechanical properties of the material. The joint experimental programme, carried out at the Politecnico di Milano and at the Universitat Politècnica de Catalunya, included the flexural characterization of four shallow beams (1.5 × 0.5 × 0.25 m3) and six standard notched beams (0.55 × 0.15 × 0.15 m3). All the samples were produced from the same batch and with the same SFRC mix which was applied for the floor. After that, 192 cores were drilled from the shallow beams and subjected to either UTTs, DEWSTs or DPTs. The stress level, the scatter and the constitutive curves derived from the non-standardized tests were identified and analysed. The calculated constitutive curves were used to predict the behaviour of the shallow beams.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Steel fibre-reinforced concrete (SFRC) is a well-established building material [1, 2] widely used for the construction of structures such as industrial pavements [3,4,5], sewer pipes [6,7,8], shotcrete linings [9, 10], precast segmental linings [11,12,13,14] and foundation slabs [15, 16] which are structurally redundant. SFRC is particularly attractive for such structures as it enables reinforcement and cross-sectional optimizations, simplification of the casting procedure, and durability improvement due to the enhanced crack opening control. In comparison with the consolidated applications mentioned, the use of steel fibres as the main reinforcement in elevated slabs has increased in the last 15 years, also because of the development of dedicated codes [17,18,19,20,21,22]. Successful examples of SFRC elevated slabs usually employ traditional steel high-bond bars in conjunction with steel fibres in critical regions to enhance robustness and to activate ductile failure mechanisms at the onset of collapse. The design philosophy foresees that the fibres are entrusted with the "average" values of bending moment acting on the elevated slab, while the peak stresses are entrusted to ordinary reinforcement in areas where a higher structural demand (bending moments) is expected. The addition of fibres in a reinforced concrete floor at the serviceability limit state allows reducing the crack opening and thus the stress levels in the steel bars in correspondence with the crack. This leads to a potential increase of durability of the structure. At the ultimate limit state, the addition of fibres allows increasing the ultimate bending capacity—the entire bending capacity in those sections without reinforcing bars—and ultimate shear capacity. SFRC slabs represent a competitive solution from both economic and technical viewpoints [23]. SFRC applications [24,25,26,27,28,29,30,31] generally entail the execution of tests as a first step to assess the post-cracking behaviour or constitutive equation [32,33,34] in terms of stress–strain (\(\sigma -\varepsilon\)) or stress–crack width (\(\sigma -w\)) relationships, which are used for the structural design or in the selection of a SFRC mix compliant with the structural design requirements. During construction, quality control tests have to be performed systematically to confirm the continued suitability of the SFRC mechanical performance. The uniaxial tensile test (UTT) is the most representative method to determine the uniaxial post-cracking behaviour of FRC as the results obtained can be directly translated into a uniaxial constitutive relationship. However, uniaxial tensile tests are prone to a number of execution challenges [2, 35] and present a high scatter in residual tensile strength and toughness (coefficients of variation above 30% according to Stroband [36]). For practical reasons, standards and codes recommend the use of flexural tests on prismatic specimens. The two best-known and widely used tests are the three-point bending test [37,38,39] and the four-point bending test [40, 41]. These tests are simple but also have a high scatter of the results, often above 20% [42, 43], which compromises their use for systematic quality control.
Simpler non-standardized methods have been used for material characterization, namely round determinate panel tests [44, 45] and the wedge-splitting tensile tests [46]. The latter was modified at the Politecnico di Milano by di Prisco et al. [47], who introduced a brasilian test with two-notched specimen leading to the proposal of the Double Edge Wedge Splitting test (DEWST) to obtain information about the uniaxial tensile behaviour as a result of a compression test, removing the interaction between compressive and tensile stresses in the softening response. Another idea related to the same aim is the double punch test formerly presented by Chen [48] to measure the tensile strength of plain concrete [49, 50]; the test was adapted at the Universitat Politècnica de Catalunya by Molins et al. [43] to assess the residual tensile strength and toughness of FRC, leading to the so-called Barcelona test or Double Punch Test (DPT). Experimental investigations [43, 49, 50] reported an average coefficient of variation lower than 13% in the DPT and Galeote et al. [51] suggested that such a low scatter could lend itself to the systematic control of FRC. Blanco et al. [52] proposed a formulation to derive the constitutive equation and Pujadas et al. [50] and Blanco et al. [53] showed that the DPT can be used to indirectly assess the influence of fibre orientation.
Both DEWST and DPT are shining examples of recent non-standardised methods that have the potential to improve the reliability of the characterisation of FRC while reducing sample size, waste and health and safety risks for technicians. However, no study in the literature reports an in-depth and balanced comparative assessment of the suitability of these tests for the determination of design parameters and the systematic quality control of FRC. This study is the first part of a larger study about the load bearing capacity of a SFRC elevated slab in a two-story (1 underground floor and 1 ground floor) family house built in northern Italy. The objective is to evaluate, in the context of the construction of this building, the suitability of 3 non-standardized test methods deployed in parallel for the quality control and tensile constitutive curve assessment: UTT, DEWST and DPT.
The building consisted of a SFRC foundation with a thickness of 400 mm and an area of 290 m2 that is covered by an SFRC elevated slab at ground level with a thickness of 250 mm and an area of 240 m2. Figure 1 shows a plan view of the SFRC elevated slab together with the supporting walls and columns. Due to the geometry and size of the slab, a one-way behaviour mainly characterizes the structural response. For this reason, both the terms SFRC floor and SFRC elevated slab are used along the paper to describe the structure. The joint experimental program conducted by the Politecnico di Milano and Universitat Politècnica de Catalunya included the flexural characterization of 4 shallow beams (1.5 × 0.5 × 0.25 m3) and 6 standard notched beams (0.55 × 0.15 × 0.15 m3), all of which were produced from the same batch and with the same SFRC mix applied for the elevated slab. After that, 192 cores were drilled from the shallow beams and subjected to either UTTs, DEWSTs or DPTs. From the total of 192 drilled cores, 24 were used for UTTs, 112 for the DEWSTs and 56 for DPTs.
The test results were used to evaluate residual flexural strengths (fR1k and fR3k) and to deduce the associated uniaxial tension constitutive relationships. The constitutive curves calculated were used to numerically simulate the behaviour of the shallow beams, evaluating the accuracy of the prediction provided by them. A closely-linked study [54] addresses the effects of fibre distribution and orientation on the flexural behaviour of the full-scale SFRC elevated slabs.
2 Experimental research
2.1 Material characteristics and mechanical characterization
Table 1 shows the SFRC composition adopted in the experimental programme and the production of the slabs. The composition was designed for a target compressive strength C28/35 (where 28 represents the cylindrical and 35 the cubic compressive strengths in MPa) and an S5 workability class according to the Italian code [55]. The steel reinforcement was provided by 35 kg/m3 (0.44% by volume) of a low-carbon cut-sheet indented steel fibre (60 mm long, 1 mm equivalent diameter and a tensile strength higher than 1200 MPa).
A fresh state control test was carried out according to [56] to determine the fibre content in seven concrete trucks during the slab casting. The average fibre content was 33 kg/m3 with a coefficient of variation (CV) equal to 20.7%. For each fibre content assessment at fresh state, one 150 mm cubic specimen was produced and characterised at 28 days for compressive strength, leading to an average of 55.6 MPa and CV equal to 4.78%. The SFRC had a density equal to 2358 kg/m3.
The post-cracking behaviour of the material was characterized according to [37] by means of three-point bending tests (3PBTs) on beams with a 25 mm deep notch and a span of 500 mm. The tests were performed in an electromechanical press (INSTRON 5867) with a maximum nominal capacity of 30 kN. The crack mouth opening displacement (CMOD) was measured by means of a clip gauge (having a range of measurement of \(\pm\) 5 mm and a sensitivity of 2.5 mV/V), positioned astride the notch at midspan. The tests were carried out considering the CMOD as a control parameter (up to 4.0 mm). A displacement rate of 0.05 mm/min was established up to a CMOD equal to 0.1 mm; from 0.1 to 4.0 mm of CMOD a displacement rate of 0.2 mm/min was set. Figure 2 shows the nominal stress \({\sigma }_{N}\)—CMOD from three-point bending tests together with the average result.
The limit of proportionality fLOP, the residual flexural tensile strengths fR1, fR2, fR3 and fR4 for a CMOD of 0.5, 1.5, 2.5 and 3.5 mm, respectively, were assessed for all the specimens. Table 2 shows the average values found. The characteristic fracture properties \({f}_{Rik}\) were calculated with the well–known expression given in [57] assuming a normal distribution:
The factor \({k}_{n}\) is a statistical coefficient that accounts for the number \({n}_{s}\) of test results of the sample (\({k}_{n}\) = 2.18 for \({n}_{s}=6\)). The characteristic fracture properties \({f}_{Rik}\) were also calculated by assuming a lognormal distribution following the approach proposed in [57]; the corresponding values are reported in Table 2. The FRC material was classified as “2.5c” according to fib Model Code 2010 specifications [58] with reference to the characteristic values.
2.2 Shallow beam: test set-up and loading protocol
Four nominally identical SFRC shallow beams were tested in a four–point bending test set–up (Fig. 3). The supports were 50 mm from the beam ends, while the shear span was equal to 500 mm (Fig. 3). The shallow beams—named A, B, E and F—were tested at the Politecnico di Milano using a hydraulic press (CONTROLS ADVANTEST 9) with a maximum load capacity of 300 kN. The tests were conducted under displacement control by using the machine crosshead displacement (stroke) as feedback parameter. The deflection at mid–span was measured with two (one at each side) Linear Variable Displacement Transducers (LVDTs). Four transducers were placed in the beam central zone (3 with a gauge length equal to 500 mm on the bottom surface and one with a gauge length equal to 200 mm on the top surface) to measure the crack opening displacement (COD). Three loading rates were adopted during the test: load control (6000 N/min) up to a load of 30 kN, stroke displacement control (50 μm/min) up to the post-peak phase and stroke displacement control at a rate of 150 μm/min up to the mean crack opening displacement (CODm) of 5.0 mm. All beams exhibited a single localized crack located in the constant moment region (Fig. 3).
2.3 Experimental procedure for the evaluation of non-standardized tests
UTTs were performed with rotating end-platens, while DEWSTs and DPTs followed the procedure defined in [43, 47], respectively. The tests’ configurations were intended to evaluate (a) the test representativeness as discussed later in this paper and (b) the effect of fibre distribution and orientation as discussed in the closely-linked study [54].
2.3.1 Core drilling strategy
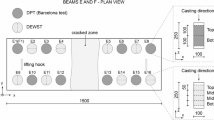
After the execution of the shallow beam tests, 48 cylinders with a diameter of 100 mm were drilled from the four beams along the x-, y- and z-directions (Fig. 4). Cylinders cored in beam thickness direction (z-direction) had a length of 250 mm while cylinders cored along the x- and y-directions had a length of 400 mm. The cores presented no visible cracks after the extraction process. Shallow beams E and F were cored in the z-direction (Fig. 4), and beams A and B were cored in the x- and y-directions (Fig. 4). Specimens for the UTTs were obtained by cutting cylinders cored in the x- and y-directions in three equal parts with a length of 100 mm. Specimens for the DPTs were obtained by cutting cylinders cored in the z-direction in two equal parts and in the x- and y-directions in three equal parts, all of which had a length of 100 mm. Specimens for the DEWSTs were obtained by cutting cylinders cored in the z-direction in four equal parts and cylinders cored in the x- and y-directions in six equal parts, so that all cylinders had a length of 50 mm. In total, 24 specimens (12 x–dir. + 12 y–dir.) were subjected to UTT, 112 specimens (24 x–dir. + 24 y–dir. + 64 z–dir.) were subjected to DEWST and 56 specimens (12 x–dir. + 12 y–dir. + 32 z–dir.) were subjected to DPT. Details on the univocal name assigned to the samples are given in [54], where the effects of fibre distribution and orientation are widely discussed.
2.3.2 UTT: test set-up and loading protocol
Figure 5 depicts the specimens’ geometries, sizes and notching details as well as the UTT set-up carried out at the Politecnico di Milano by means of an electromechanical press (Instron 8562) with a nominal capacity of 100 kN and a precision equal to 0.5%. The rotating end-platens solution was adopted to conduct the UTTs following the procedure described by [59] among others. With this solution, the specimens were bound to two rotating loading platens that can rotate with respect to the testing machine. The test procedure does not allow a uniform crack opening along the notched cracked cross–section. The upper and lower face of the specimen were glued to two 10 mm thick threaded steel plates of approximately the same diameter as the specimen using a commercial bi-component epoxy resin to guarantee a strong bond with the specimens. Once the glue hardened, the specimen was screwed by the top and bottom ends to two cylindrical pins, which were previously screwed onto the test machine.
UTTs were carried out under CODm control, obtained as the average COD from two LVDTs placed astride the notch, around the cylindrical specimen at 180° of each other. The two LVDTs were electrically connected in parallel to obtain an average signal used as the feedback parameter. Three additional LVDTs were placed radially at 120° astride the notch to fully register the specimen’s response. The LVDTs have a range of measurement of \(\pm\) 5 mm, a sensitivity of 80 mV/V (at full-scale), and a gauge length of 40 mm.
The tests were conducted at a displacement rate of 6 μm/min up to a CODm = 0.07 mm. After the snap-back phase of the crosshead displacement (stroke), tests continued under stroke control at rates that progressively increased from 12, 30, 60 to 300 μm/min until the total force applied was less than 5% of the maximum reached during the test.
2.3.3 DEWST: test set-up and loading protocol
Figure 5 shows the DEWST set-up, the specimen size and the notch. The DEWSTs were carried out at the Politecnico di Milano using an electromechanical press (Instron 5867) with a nominal capacity of 30 kN and a precision equal to 0.4%. Displacement control of the actuator at a speed ranging from 30 to 60 μm/min was applied depending on the crack propagating stage. The crack propagation was detected through two clip gauges placed at the mid–height of the specimen on front and rear sides. The gauges have a range of measurement of 10 mm, a characteristic tolerance of \(\pm\) 0.2%, a linearity deviation of \(\pm\) 0.2% and a sensitivity of 80 mV/V. Steel plates were glued to the groove edges and the contact surface was lubricated with graphite, having a friction coefficient (steel-steel) \(\mu =0.11\) and a splitting tensile force (resulting tensile force on ligament) \({F}_{SP}=0.80P\), where P is the applied vertical load.
2.3.4 DPT: test set-up and loading protocol
Figure 5 shows the DPT set-up and the specimen size. The DPTs were carried out at the Universitat Politècnica de Catalunya using a hydraulic press (Ibertest) and a circumferential chain to measure the total crack opening displacement (TCOD). They were performed by placing, two cylindrical steel punches (24 mm height and with a diameter of 35 mm) concentrically above and below the specimens. The DPTs were carried out under stroke control at a rate of 500 ± 50 μm/min. The test can also be carried out, with the same accuracy and representativeness, by exclusively controlling the vertical displacement of the actuator and avoiding the use of the circumferential chain [49, 51].
3 Structural test results
Figure 6 summarizes the response of the four shallow beams in terms of nominal stress (\({\sigma }_{N}\)) versus average crack opening displacement (CODm). The nominal stress is calculated as \({\sigma }_{N}=M/W\), M being the applied moment and W the section modulus. The CODm is calculated as the average of the three transducers located at the bottom surface of the beams. Shallow beams E and F were tested after a rotation of 180° along their longitudinal axis. This procedure was adopted to exclude the role of possible fibre segregation on the mechanical response of the beams. Notice that fibre segregation could positively affect the behaviour of structures subjected to positive bending since a higher concentration of fibres can be present in the lower layers.
The beam mechanical response was characterized by a large CV of about 40% for beams A and B, and 24% for beams E and F calculated at a COD equal to 2.5 mm. This trend was expected since the loading scheme of the beams is statically determinate with a limited possibility of stress redistribution. The average structural response of beams A and B and of beams E and F, are also included in Fig. 6 for comparison purposes. The slightly lower curves for beams E and F compared to beams A and B could indicate that fibre segregation played a role in the mechanical response but the data presented in this figure alone are not sufficient to confirm this conclusion. This aspect will be discussed in detail in the closely-linked study [54].
4 Material test results
In this section, the SFRC post–cracking tensile behaviour obtained in UTTs, DEWSTs and DPTs is presented and discussed. DEWST and DPT are indirect tensile tests where the tensile stresses are induced by applying a compressive vertical axial load to the specimen. In this regard, the UTT will act as a reference test to assess the advantages and disadvantages of indirect tensile tests. In this section, the results obtained for each type of test will be presented separately. A broad comparison of the various types of test is made in [54].
DEWST and DPT are attractive for their simplicity and straightforwardness of the identification procedure. Both have the peculiarity to use compact specimens, which can be even cored from existing structures. Moreover, in the DEWST a fracture plane can be a priori selected in the specimen thanks to the possibility of orienting the notch as required, so that the plane can be aligned to any required tensile direction, also with respect to the expected flow–induced fibre orientation. On the contrary, in DPT at least three radial cracked planes propagated allowing an isotropic measure of the toughness given by the nominal stress vs the average crack opening. The description of these experimental techniques as well as their advantages compared to direct tension and bending tests is widely discussed in [47] and [43], respectively.
The results of UTTs, DPTs and DEWSTs are then used to simulate the shallow beams' behaviour by a multi–layer plane sectional analysis which is discussed in Sect. 5. In order to better simulate the flexural behaviour of the beams, only the cores with a cracked plane orthogonal to the beam x–axis are considered here. In the closely-linked study [54], the other samples are considered with reference to the effect of fibre distribution and orientation. For the DPT specimens it is not possible to pre–assign a fracture plane as previously discussed; therefore, only the cylinders cored in y- and z-directions were considered.
4.1 UTT results
The experimental results of the notched specimens (see Fig. 5, left) tested under UTT are shown in Fig. 7 together with their average curve. For each sample, the COD reported in Fig. 7 is calculated as the average displacement measured from the five LVDTs connected to the specimen. Of the originally 12 drilled core samples with a cracked plane orthogonal to the beam x–axis, the figure reports the results of 7 specimens. In fact, several samples were lost at the beginning of the experimental campaign, mainly due to the use of a testing machine whose stiffness was not sufficient to ensure a stable test. This reflects the complexity behind the appropriate execution of a UTT. Furthermore, of the 7 curves shown in Fig. 7, 4 are complete (curves with solid line) while 3 are incomplete (curves with dashed line); for these last curves, the peak load and the unstable crack propagation phase linked to the matrix were lost whilst the fibre pull out phase was properly captured.
The post-cracking general trend can be grossly schematized as a bilinear behaviour. The first branch (COD smaller than about 0.1 mm) is characterized by a sudden initial load drop. The second branch (\(0.1\le \mathrm{COD}\le 2.5\) mm) displays a progressive decrease of the mechanical post-cracking stress with the COD increase. The mean tensile peak stress, affected by the notch intensity factor, \({f}_{ct}\) is 3.67 MPa (CV = 7.73%), while the residual strength evaluated at COD equal to 0.5 and 2.5 mm are respectively equal to \({f}_{tR,0.5}=1.49\) MPa (CV = 48.0%) and \({f}_{tR,2.5}=0.44\) MPa (CV = 34.2%).
4.2 DEWST results
Figure 8 presents the experimental results of the specimens tested under DEWSTs and the average curve. For each sample, the nominal stress is calculated as \({\sigma }_{N}={F}_{SP}/{A}_{n}\) where \({F}_{SP}\) is the splitting force (see Sect. 2.3.3) and \({A}_{n}\) is the net area along the notch, while the COD reported in Fig. 8 is calculated as the average displacement measured from the two clip gauges used to control the COD. Of the original 44 cores with cracked plane orthogonal to the beam x–axis, the figure reports the results of 30 specimens. Several samples were lost at the beginning of the experimental campaign before the optimization of the test set-up was obtained. The average curve (thick continuous line in Fig. 8) was calculated excluding results in which a loss of control occurred in the post-peak region. The thick dashed line indicates the region of the curve without any experimental valid data (from COD of 9.1 μm to COD of 47.6 μm).
The post-cracking general trend in Fig. 8 is similar to that previously obtained from UTTs, where a sudden initial load drop is followed by a small stress decrease at increasing COD. The average tensile peak stress, also affected by the two notches, \({f}_{ct}\) is 3.00 MPa (CV = 19.2%), while the residual tensile strengths evaluated at CODs equal to 0.5 and 2.5 mm are respectively equal to \({f}_{tR,0.5}=1.03\) MPa (CV = 47.9%) and \({f}_{tR,2.5}=0.71\) MPa (CV = 65.6%). The very high CV also is the result of the smallest cracked area of the different tests.
4.3 DPT results
It is worth noting that with the DPT technique the fracture planes do not follow a pre-defined plane. Instead, larger cracks tend to form perpendicular to the weakest plane and never perpendicular to the height of the specimen. Therefore, out of the 56 specimens extracted and tested, those parallel to the x-direction were not considered in the analysis, as they did not have a cracking plane orthogonal to the x-direction (12 in total). Of the original 44 specimens cored in y- and z-directions, Fig. 9 reports the results of 41 specimens in terms of nominal stress \({\sigma }_{N}\)—COD.
DPTs are characterized by three stages. In Stage 1 the load is initially applied and the radial stress generated inside the specimen is resisted by the concrete matrix. In this stage cracks are not observable. Stage 2 starts once the stress reaches the tensile strength of the material. During this stage upper and lower conical wedges are suddenly formed; at the same time between 2 and 4 major cracks appear, dividing the specimen in parts that are kept together by the fibres bridging the cracks. Stage 3 begins when the cracks are stabilized. During this stage a vertical displacement of the conical wedge can be observed which produces a lateral displacement of the fragments of the specimen and an increase of the total crack opening displacement (TCOD). The debonding and pull-out of the fibres fully characterize this stage and allow dissipating energy thus providing a significant increase in toughness. The alignment of the fibres due to the acting stresses (in the plane perpendicular to the load direction) improves the post-cracking response due to a greater number of effective fibres that cross the crack.
In order to allow a direct comparison with the other test methods (i.e. UTT and DEWST), the original data in terms of axial load versus the total crack opening displacement (not shown here for the sake of brevity) have been transformed into stress \({\sigma }_{N}\)—COD (Fig. 9) through the procedure described in Appendix 1. Figure 9 shows the \({\sigma }_{N}\)—COD curves for the DPTs, which yield an average tensile peak stress \({f}_{ct}\) equal to 3.15 MPa (CV = 5.07%), while the residual strength evaluated at COD equal to 0.5 and 2.5 mm are respectively equal to \({f}_{tR,0.5}=1.10\) MPa (CV = 24.6%) and \({f}_{tR,2.5}=0.38\) MPa (CV = 40.6%).
5 Identification of the constitutive law
It is interesting to observe that the cracked areas of the specimens selected are significantly different: in fact, we pass from a critical area of 18,750 mm2 for 3PBT, to 12,726 mm2 for DPT, 5026 mm2 for UTT and only 3000 for DEWST. Analysing the coefficients of variation, we pass for the two reference CODs (0.5 and 2.5 mm) from 0.21–0.19 for 3PBT respectively to, 0.25–0.41 for DPTs, 0.48–0.34 for UTTs, to 0.48–0.66 for DEWSTs. This means that, in terms of characteristic values of residual tensile strengths, UTT and DEWST specimens do not have a fracture area large enough to consider as homogeneous the mechanical behaviour identified by these tests. To overcome this problem, a simple yet effective way is to normalize the UTT and DEWST experimental data to the same fracture plane area as that of 3PBT. The fractured areas ratio between 3PBT and UTT is equal to 3.73:1, while between 3PBT and DEWST it is equal to 6.25:1. The normalization procedure carry out for UTTs and DEWSTs consists of:
-
(a)
The whole data set is randomly permuted and n values are selected (n = 4 for UTT and n = 6 for DEWST);
-
(b)
The mean value is calculated from this subset of n values;
-
(c)
Steps (a) and (b) are repeated to have a final set of ns curves which corresponds to the original set of specimens;
-
(d)
From the set created in Step (c), the characteristic value is calculated and is directly compared to the characteristic value from 3PBTs and DPTs.
This normalization procedure is equivalent to creating virtual samples of larger area (\({A}_{t}\)), which are composed of n smaller real samples of area A working like springs in parallel and combined by random permutation.
The uniaxial tension response obtained through UTTs, DEWSTs and DPTs is used to simulate the shallow beam tests using a multi–layer sectional approach [60] in terms of nominal stress versus COD. The cross–section is discretized into several layers assuming a linear distribution of the strains. The constitutive model is characterized by a parabola rectangular law in compression. In tension, a linear–elastic law in pre-peak and a linear–softening law in post-peak were adopted as suggested by fib Model Code 2010 [58]. Since no steel reinforcement was included in the shallow beams, the structural characteristic length (lcs) adopted corresponds to the beam height (h). The unfactored ultimate bending moment is computed by imposing both translational and rotational equilibrium of the cross–section and assuming that the ultimate crack opening (wu) is reached at the bottom layer. As proposed in [58], an ultimate crack opening equal to wu = 2.5 mm was chosen.
The two parameters fFts and fFtu, necessary to identify the tensile constitutive law and representing the uniaxial tensile residual strengths at serviceability and ultimate limit state conditions, respectively, are directly deduced considering the nominal stress at 0.5 and 2.5 mm of COD. Then, for the three test methods (UTT, DEWST and DPT), the stress measured at a COD of 0.5 mm has been linearly extended to a COD equal to zero for the construction of the constitutive law as suggested by [61]. The values of fFts and fFtu for the three test methods are reported in Table 3, while the constitutive laws for the four testing methods (including 3PBT) are compared in Fig. 10. The constitutive law for 3PBT has been derived in accordance to [61].
The experimental (average values for beams A and B and for beams E and F) and analytical beam responses are compared in Fig. 11 adopting the plane section approach for the characteristic values of the UTT, DEWST and DPT specimens. The numerical response obtained adopting the characteristic (assuming a normal distribution) and design (including the strength FRC class) results of the 3PBT tests are also included in Fig. 11 for comparison purpose. The characteristic 3PBT curve slightly underestimates the experimental mean response confirming the need of characteristic and design value adoption if a structure has a limited capacity to redistribute the stresses, as for the statically determinate shallow beams considered herein [62]. The selected UTT specimens provide results that slightly underestimate the mean experimental beam results. The numerical response obtained adopting the characteristic results from DEWSTs and DPTs underestimate the beam experimental results. The fracture area already discussed plays a role in this underestimation, but it should be also taken into account that the specimen has been cored and sliced, leading to a cut of some of the fibres and a consequent loss of anchorage. This means that, even with the same number of fibres, the performance measured in these tests (UTT, DEWST and DPT) could be lower than that obtained from 3PBT, where all the fibres are effective. It is worth noting that the characteristic curves shown in Fig. 10 are quite close, the lowest curve experimentally shown in Fig. 6 remaining in favour of safety. It is important to remark that for DPTs, the fracture planes are not necessarily perpendicular to the beam's x-axis.
6 Conclusions
A 240 m2 SFRC floor was designed and built in a two–storey family house in Erba (Italy). The flexural strength characterization of the SFRC on notched beam specimens according to EN 14651 led to a “2.5c” strength class. The fib Model Code 2010 approach was used to predict the behaviour of four bent shallow beams made of the same material and without any traditional reinforcement. With cores taken from the shallow beams, the tensile-strain constitutive models suggested by fib Model Code 2010 for tensile (pre- and post-cracking) were compared with those results derived from performing two other alternative characterization tests based on indirect tension: DEWST and DPT. The following conclusions are derived from the study.
-
Both, DEWST and DPT have revealed some advantages and limitations with respect to the traditional flexural test on prismatic specimens. In particular, their characteristic values approximate the design value obtained by the 3PBT. The significant differences in fracture areas between 3PBT and DEWST must be duly considered when calculating the characteristic value.
-
The post-cracking tensile strengths obtained from DPT and DEWST results are quite similar despite the different fracture mechanism associated with each of those. The main deviations of the average tensile stresses between both tests occur within the range from 0 to 0.5 mm crack opening, which is generally governed by the unstable crack propagation. In this regard, the post-cracking tensile strength obtained from DEWST tends to be lower compared to that derived from DPT. This variation is attributed to the complex fracture mechanism developed in the DPT sample; the analytical model is unable to consider the specific energy dissipated for the formation of conical wedges.
-
Conversely, dealing with the failure mechanism characterizing DEWST specimens, both cracks start from the opposite notches and these converge rectilinearly without involving additional frictional energy. Usually, the post-cracking behaviour shows, after initial cracking, a drop of load followed by a pull-out plateau.
References
di Prisco M, Plizzari G, Vandewalle L (2009) Fibre reinforced concrete: new design perspectives. Mater Struct 42:1261–1281. https://doi.org/10.1617/s11527-009-9529-4
Walraven JC (2009) High performance fiber reinforced concrete: progress in knowledge and design codes. Mater Struct 42:1247–1260. https://doi.org/10.1617/s11527-009-9538-3
Meda A, Plizzari GA, Riva P (2004) Fracture behavior of SFRC slabs on grade. Mater Struct 37:405–411. https://doi.org/10.1007/BF02479637
Meda A, Plizzari GA (2004) New design approach for steel fiber-reinforced concrete slabs-on-ground based on fracture mechanics. ACI Struct J 101:298–303. https://doi.org/10.14359/13089
Falkner H, Huang Z, Teutsch M (1995) Comparative study of plain and steel fiber reinforced concrete ground slabs. Concr Int 17:45–51
de la Fuente A, Escariz RC, De Figueiredo AD, Molins C, Aguado A (2012) A new design method for steel fibre reinforced concrete pipes. Constr Build Mater 30:547–555. https://doi.org/10.1016/j.conbuildmat.2011.12.015
de la Fuente A, Escariz RC, De Figueiredo AD, Aguado A (2013) Design of macro-synthetic fibre reinforced concrete pipes. Constr Build Mater 43:523–532. https://doi.org/10.1016/j.conbuildmat.2013.02.036
Monte R, de la Fuente A, De Figueiredo AD, Aguado A (2016) Barcelona test as an alternative method to control and design fiber-reinforced concrete pipes. ACI Struct J 113:1175–1184. https://doi.org/10.14359/51689018
Cengiz O, Turanli L (2004) Comparative evaluation of steel mesh, steel fibre and high-performance polypropylene fibre reinforced shotcrete in panel test. Cem Concr Res 34(8):1357–1364. https://doi.org/10.1016/j.cemconres.2003.12.024
Banthia N, Trottier JF, Beaupré D (1994) Steel-fiber-reinforced wet-mix shotcrete: comparisons with cast concrete. J Mater Civ Eng 6:430–437. https://doi.org/10.1061/(ASCE)0899-1561(1994)6:3(430)
fib Bulletin 83 (2017) Precast tunnel segments in fibre-reinforced concrete. Lausanne. https://doi.org/10.35789/fib.BULL.0083
Caratelli A, Meda A, Rinaldi Z (2012) Design according to MC2010 of a fibre-reinforced concrete tunnel in Monte Lirio, Panama. Struct Concr 13:166–173. https://doi.org/10.1002/suco.201100034
Plizzari GA, Tiberti G (2006) Steel fibers as reinforcement for precast tunnel segments. Tunn Undergr Sp Technol 21:438–439. https://doi.org/10.1016/j.tust.2005.12.079
Liao L, de la Fuente A, Cavalaro S, Aguado A (2016) Design procedure and experimental study on fibre reinforced concrete segmental rings for vertical shafts. Mater Des 92:590–601. https://doi.org/10.1016/j.matdes.2015.12.061
Buchta V, Mynarčík P (2014) Experimental testing of fiberconcrete foundation slab model. Appl Mech Mater 501–504:291–294. https://doi.org/10.4028/www.scientific.net/AMM.501-504.291
Čajka R, Vaskova J (2014) Fibre concrete foundation slab experiment and FEM analysis. Key Eng Mater 627:441–444. https://doi.org/10.4028/www.scientific.net/KEM.627.441
Mobasher B, Destree X (2010) Design and construction aspects of steel fiber-reinforced concrete elevated slabs. ACI Spec Publ 274:95–108
di Prisco M, Plizzari G, Vandewalle L (2014) Structural design according to fib MC 2010: comparison between RC and FRC elements. In: Charron JP, Massicotte B, Mobasher B, Plizzari G (eds) American concrete institute, ACI Special Publication, 2014-July (SP 310), pp 1–16
di Prisco M, Martinelli P, Parmentier B (2016) On the reliability of the design approach for FRC structures according to fib model code 2010: the case of elevated slabs. Struct Concr 17(4):588–602. https://doi.org/10.1002/suco.201500151
Pujadas P, Blanco A, Cavalaro S, de la Fuente A, Aguado A (2014) Fibre distribution in macro-plastic fibre reinforced concrete slab-panels. Constr Build Mater 64:496–503. https://doi.org/10.1016/j.conbuildmat.2014.04.067
Pujadas P, Blanco A, Cavalaro S, Aguado A (2014) Plastic fibres as the only reinforcement for flat suspended slabs: experimental investigation and numerical simulation. Constr Build Mater 57:92–104. https://doi.org/10.1016/j.conbuildmat.2014.01.082
Blanco A, Pujadas P, de la Fuente A, Cavalaro SHP, Aguado A (2016) Influence of the type of fiber on the structural response and design of FRC slabs. J Struct Eng (United States) 142:1–11. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001515
de la Fuente A, Casanovas-Rubio MDM, Pons O, Armengou J (2019) Sustainability of column-supported RC slabs: fiber reinforcement as an alternative. J Constr Eng Manag 145:1–12. https://doi.org/10.1061/(ASCE)CO.1943-7862.0001667
ACI. 544.6R-15 (2015) Report on design and construction of steel fiber-reinforced concrete elevated slabs
Døssland ÅL (2008) Fibre reinforcement in load carrying concrete structures: laboratory and field investigations compared with theory and finite element analysis. Norwegian University of Science and Technology, Trondheim
Ellouze A, Ouezdou MB, Karray MA (2010) Experimental study of steel fiber concrete slabs part I: behavior under uniformly distributed loads. Int J Concr Struct Mater 4:113–118. https://doi.org/10.4334/ijcsm.2010.4.2.113
Gödde L, Mark P (2015) Numerical simulation of the structural behaviour of SFRC slabs with or without rebar and prestressing. Mater Struct 48:1689–1701. https://doi.org/10.1617/s11527-014-0265-z
Gossla U (2005) Development of SFRC free suspended elevated flat slabs, test report. Aachen University of Applied Science, Aachen
Hedebratt J, Silfwerbrand J (2014) Full-scale test of a pile supported steel fibre concrete slab. Mater Struct 47:647–666. https://doi.org/10.1617/s11527-013-0086-5
Michels J, Waldmann D, Maas S, Zürbes A (2012) Steel fibers as only reinforcement for flat slab construction—experimental investigation and design. Constr Build Mater 26(1):145–155. https://doi.org/10.1016/j.conbuildmat.2011.06.004
Pujadas P, Blanco A, de la Fuente A, Aguado A (2012) Cracking behavior of FRC slabs with traditional reinforcement. Mater Struct 45:707–725. https://doi.org/10.1617/s11527-011-9791-0
Blanco A, Pujadas P, de la Fuente A, Cavalaro S, Aguado A (2013) Application of constitutive models in European codes to RC-FRC. Constr Build Mater 40:246–259. https://doi.org/10.1016/j.conbuildmat.2012.09.096
Blanco A, Cavalaro S, de la Fuente A, Grünewald S, Blom CBM, Walraven JC (2015) Application of FRC constitutive models to modelling of slabs. Mater Struct 48:2943–2959. https://doi.org/10.1617/s11527-014-0369-5
Mobasher B, Bakhshi M, Barsby C (2014) Backcalculation of residual tensile strength of regular and high performance fiber reinforced concrete from flexural tests. Constr Build Mater 40:243–253. https://doi.org/10.1016/j.conbuildmat.2014.07.037
Van Mier JGM, Van Vliet MRA (2001) Uniaxial tension test for the determination of fracture parameters of concrete: state of the art. Eng Fract Mech 69(2):235–247. https://doi.org/10.1016/S0013-7944(01)00087-X
Stroband J (1988) Standardisation of test methods for steel fibre reinforced concrete. Laboratory report no. 25.5.98-14, Delft University of Technology, Delft
EN 14651:2005+A1 (2007) Test method for metallic fibered concrete—measuring the flexural tensile strength (limit of proportionality (LOP), residual). European Committee for Standardization (CEN), Brussels
RILEM TC 162-TDF (2003) Final recommendation of RILEM TC 162-TDF: test and design methods for steel fibre reinforced concrete sigma-epsilon-design method. Mater Struct 36:560–567
ASTM C-1609/C1609M (2020) Standard test method for flexural performance of fiber-reinforced concrete (Using Beam With Third-Point Loading). ASTM International, West Conshohocken. https://doi.org/10.1520/C1609_C1609M-19A
UNI 11039 (2003) Steel fibre reinforced concrete – part I: definitions, classification specification and conformity. Part II: test method for measuring first crack strength and ductility indexes, UNI Ente Italiano di Normazione
NBN B 15–238 (1992) Test on fibre reinforced concrete—bending test on prismatic samples. Norme Belge, Institut Belge de Normalisation, Brussels
Parmentier B, De Grove E, Vandewalle L, Van Rickstal F (2008) Dispersion of the mechanical properties of FRC investigated by different bending tests. In: J.C. W, D. S, eds. Proc Int FIB Symp 2008—Tailor Made Concr Struct New Solut our Soc. Amsterdam: CRC Press/Balkema
Molins C, Aguado A, Saludes S (2009) Double punch test to control the energy dissipation in tension of FRC (Barcelona test). Mater Struct 42:415–425. https://doi.org/10.1617/s11527-008-9391-9
Bernard ES (2000) Behaviour of round steel fibre reinforced concrete panels under point loads. Mater Struct 33:181–188. https://doi.org/10.1007/bf02479412
ASTM C1550–12 (2012) Standard test method for flexural toughness of fibre reinforced concrete (Using Centrally Loaded Round Panel). ASTM International, West Conshohocken. https://doi.org/10.1520/C1550-12
Tschegg EK, Linsbauer HN (1986) Testing procedure for determination of fracture mechanics parameters. Patentschrift no. A-233/86
di Prisco M, Ferrara L, Lamperti MGL (2013) Double edge wedge splitting (DEWS): an indirect tension test to identify post-cracking behaviour of fibre reinforced cementitious composites. Mater Struct 46:1893–1918. https://doi.org/10.1617/s11527-013-0028-2
Chen WF (1970) Double punch test for tensile strength of concrete. J Am Concr Inst 67:993–995
Pujadas P, Blanco A, Cavalaro SHP, de la Fuente A, Aguado A (2013) New analytical model to generalize the Barcelona test using axial displacement. J Civ Eng Manag 19:259–271. https://doi.org/10.3846/13923730.2012.756425
Pujadas P, Blanco A, Cavalaro SHP, de la Fuente A, Aguado A (2014) Multidirectional double punch test to assess the post-cracking behaviour and fibre orientation of FRC. Constr Build Mater 58:214–224. https://doi.org/10.1016/j.conbuildmat.2014.02.023
Galeote E, Blanco A, Cavalaro SHP, de la Fuente A (2017) Correlation between the Barcelona test and the bending test in fibre reinforced concrete. Constr Build Mater 152:529–538. https://doi.org/10.1016/j.conbuildmat.2017.07.028
Blanco A, Pujadas P, Cavalaro S, de la Fuente A, Aguado A (2014) Constitutive model for fibre reinforced concrete based on the Barcelona test. Cem Concr Compos 53:327–340. https://doi.org/10.1016/j.cemconcomp.2014.07.017
Blanco A, Pujadas P, de la Fuente A, Cavalaro SHP, Aguado A (2015) Assessment of the fibre orientation factor in SFRC slabs. Compos Part B Eng 68:343–354. https://doi.org/10.1016/j.compositesb.2014.09.001
Martinelli P, Colombo M, Pujadas P, de la Fuente A, Cavalaro S, di Prisco M (2021) Characterization tests for predicting the mechanical performance of SFRC floors: identification of fibre distribution and orientation effects. Mater Struct. https://doi.org/10.1617/s11527-020-01593-7
Ministero delle Infrastrutture (2008) Nuove norme tecniche per le costruzioni. NTC 2008. Rome
BS EN 14721 (2005) Test method for metallic fibre concrete—measuring the fibre content in fresh and hardened concrete. BSI Standards Publication, London
EN 1990:2002+A1 (2005) Eurocode - basis of structural design. European Committee for Standardization (CEN), Brussels
fib (2013) fib Model Code for Concrete Structures (2010) fédération internationale du béton / International Federation for Structural Concrete (fib), Lausanne. https://doi.org/10.1002/9783433604090
Vervuurt A, Schlangen E, Van Mier JGM (1996) Tensile cracking in concrete and sandstone: part 1—basic instruments. Mater Struct 29:9–18. https://doi.org/10.1007/bf02486002
Hordijk D (1991) Local approach to fatigue of concrete. Delft University of Technology, Delft
di Prisco M, Colombo M, Dozio D (2013) Fibre-reinforced concrete in fib model code 2010: principles, models and test validation. Struct Concr 14:342–361. https://doi.org/10.1002/suco.201300021
di Prisco M, Martinelli P, Dozio D (2016) The structural redistribution coefficient KRd: a numerical approach to its evaluation. Struct Concr 17:390–407. https://doi.org/10.1002/suco.201500118
Acknowledgements
The authors are in debt with Prof. Roberto Felicetti for his help in conducting the uniaxial tensile tests. The authors thank also Matteo Tratta and Davide Trentini, who worked on the experimental DEWSTs and DPTs as a part of their M.Sc. thesis in Civil Engineering at the Politecnico di Milano. The authors thank DSC-Erba and Calcestruzzi Erbesi for the contribution in the preparation of the specimens investigated and in the sharing of both material and structural design detailing.
Funding
Open Access funding provided by Politecnico di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1: Derivation of \({{\varvec{\sigma}}}_{{\varvec{N}}}\)—COD law from the DPT
Appendix 1: Derivation of \({{\varvec{\sigma}}}_{{\varvec{N}}}\)—COD law from the DPT
This Appendix reports the derivation of the of \({\sigma }_{N}\)—COD law from the axial load (\({F}_{p}\))—TCOD result obtained through the DPT. In this regard, Blanco [52] developed a formulation to predict the tensile behaviour of FRC based on the results of the Barcelona test (see Figs.
Frontal and top views of the specimens after cracking [52]
12 and
a Forces at the conical wedge, b balance of forces at the conical wedge, c forces at the specimen and d balance of forces at the specimen [52]
13). COD was derived from dividing TCOD by the counted number of cracks (2–5). In those cases that COD does not reach the reference value of 2.5 mm, a linear approximation of the curve tail can be considered.
From imposing equilibrium and compatibility conditions in the force diagrams of Fig. 13, Eq. (2) can be derived.
Equation 2 relates Fp, at different displacements of the actuator (0.02, 0.75 and 4.00 mm), to the radial stress (σN) through a coefficient \(\omega\), which depends on the failure angle \(\beta\) and the static friction coefficient (\({\mu }_{k}\)). According to [52] and the results obtained in the experimental program carried out for this research, values of \(\beta =22^\circ\) and \({\mu }_{k}\) = 0.7 were found to be representative of the FRC tested.
A σ–ε diagram can be established by particularizing Eq. (2) for different levels of conical wedge vertical displacement (δp), which are related to specific values of TCOD and COD:
Equations 3–6 were derived in [52] by imposing compatibility and kinematic conditions of the fracture mechanism. A stands for the area involved in the mechanism and an equation based on geometric boundary conditions is also proposed in [52] to assess its magnitude.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Martinelli, P., Colombo, M., de la Fuente, A. et al. Characterization tests for predicting the mechanical performance of SFRC floors: design considerations. Mater Struct 54, 2 (2021). https://doi.org/10.1617/s11527-020-01598-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1617/s11527-020-01598-2