1 Introduction

The precise and reliable knowledge of tensile properties and constitutive laws of materials is most important for structural design and safety verification. This is particular so for tensile strain-hardening Ultra-High Performance Fiber Reinforced Cementitious Composites (UHPFRC), which exhibit relatively high elastic limit stress (≥ 8 MPa), high tensile strength (≥ 10 MPa) and significant deformation capacity with strain up to 5‰ at the end of hardening when subjected to uniaxial tension. Taking benefit from these properties, UHPFRC are generally used for thin slab-like structural elements, which provide the required resistance against bending, shear and fatigue even without ordinary steel reinforcement bars [1,2,3]. Typical structural applications include cast-in place UHPFRC layers for strengthening of reinforced concrete slabs [4, 5], slabs of new bridges and buildings as well as shells [6, 7]. These innovative applications are now spreading rapidly worldwide under the impulse of pioneering countries such as Switzerland [4, 5], China [8], Malaysia [9], France [6, 10], Japan [11] and others. Such structural UHPFRC systems are generally subjected to multiple-axial stresses [12], hereafter called equi-biaxial stresses, where different tensile properties may be expected compared to uniaxial stress condition. Thus, the equi-biaxial tensile response of UHPFRC needs to be known and characterized accurately.

It is well known that there is no unique tensile response for discontinuous fiber reinforced cementitious composites, especially for strain-hardening UHPFRC with relatively high fiber volume content (Vf ≥ 3.0%), which is influenced largely by the action of the fibrous skeleton in materials [13,14,15]. In the case of equi-biaxial tensile response, such influence may even be more significant, given that the effect of fiber distribution in different directions is involved. Swanepoe [16] conducted biaxial direct tensile tests (DTT) on strain-hardening cement-based composites (SHCC). The confinement effect was proven to occur due to the action of fibers in both directions, leading to different failure mechanism compared with that under uniaxial condition. Similar findings were observed by Yoo et al. [12, 17] for UHPFRC specimens under equi-biaxial flexure, where considerably higher flexural strength and normalized energy absorption capacity were observed under equi-biaxial stresses condition compared to those under uniaxial stress condition.

The DTT appears to be the most suitable and straightforward method to quantify the tensile behavior of materials. The uniaxial DTT has been applied extensively for characterization of the uniaxial tensile response of UHPFRC by different researchers [18,19,20,21]. However, few studies to characterize the biaxial tensile response of UHPFRC are available. This can be attributed to the various difficulties in preparing and performing biaxial DTT, since at least two actuators in both perpendicular directions and a large frame are generally necessary. In addition, many challenges pertaining to uniform load distribution, frictional effect, accurate boundary condition and load control need to be addressed carefully. Ple et al. [22] investigated experimentally and numerically the biaxial tensile behavior of Reactive Powder Concrete (RPC, one specific type of UHPFRC) using an original biaxial cruciform specimen under a systematic program. However, the strains measured from two orthogonal directions were not symmetrical despite symmetric loading, which could be attributed to the asymmetry of rigidity between the specimen and the machine. Besides, the study in [22] was restricted to the linear behavior.

On the other hand, the flexural test provides an easy-to-conduct method to derive indirectly the tensile response of materials based on the inverse analysis of test results. This method is generally performed by means of either analytical solutions or numerical approach through reproducing the flexural measurement results like force–deflection curves. Currently, various inverse analyses have been widely applied to characterize the uniaxial tensile properties of UHPFRC [13, 23,24,25,26,27] using four-point bending testing (4PBT), and some of them are even standardized in UHPFRC standards like SIA 2052 [28] and NF P18-470 [29].

In addition, a flexural test using circular slab specimen (circular slab test) was described as valuable alternative to the 4PBT and square slab test for fiber reinforced concrete (FRC) [30]. Based on a general theoretical approach considering the random fiber distribution and successive softening by fiber pullout, an effective flexural tensile strength and a fracture energy parameter were proposed to characterize the strength and toughness of FRC. Compared with the results from 4PBT and square slab test, the circular slab test provided more reliable results. This method is also standardized in the recommendation SIA 162/6 for FRC [31, 32].

More recently, the ring-on-ring test similar to the one used to characterize ceramics and glass according to ASTM C. 1499-05 [33], has been applied successfully to investigate the equi-biaxial flexural behavior of UHPFRC [17, 34]. A circular slab specimen is simply supported on a ring support and the external loading is uniformly distributed on a central loading ring from the top. Thus, the central part of the specimen is in pure bending condition, produced by a uniformly distributed moment according to the elastic slab bending theory [35]. Unfortunately, there is no study available in the literature concerning an inverse analysis from this test.

The principle objective of the present study is to determine the equi-biaxial tensile properties of strain-hardening UHPFRC based on an original inverse analysis method for the ring-on-ring test configuration. First, the analytical inverse analysis of the ring-on-ring test, extending from [13] for 4PBT, is developed based on the elastic slab bending and yield line theories. This method provides a new objective criterion for determining the elastic limit stress of strain-hardening UHPFRC, and a point-by-point inverse analysis is used to obtain the strain at the end of hardening of UHPFRC. Afterward, the inverse analysis results are validated against the experimental evidence, especially based on Digital Image Correlation (DIC) analysis. Moreover, the uniaxial tensile properties are derived from the inverse analysis of 4PBT results and compared with the equi-biaxial tensile properties as obtained from the proposed inverse analysis of ring-on-ring test results.

2 Proposed analytical inverse analysis method

2.1 Overview

In this section, the proposed analytical inverse analysis, following the approach from [13] using an uniaxial flexural test (4PBT), is developed first based on the force–deflection response from a equi-biaxial flexural test (ring-on-ring test). Figure 1 shows the typical force–deflection curve of UHPFRC specimen under flexure, where points A′ and C′ stand for the elastic limit and peak force of flexural response, respectively. It is well known that part of the UHPFRC material close to the tensile surface of the specimen is already in the strain softening domain at point C′. Thus, a damage localization point, hereafter referred as point B′ in Fig. 1, is expected between point A′ and C′, from which the softening response of UHPFRC specimen enters into play.

Fig. 1
figure 1

Typical force–deflection curve under flexure

Full size image

The principle of the proposed method is to convert pairs of measured force Fi and deflection δi at characteristic points under equi-biaxial flexure into corresponding pairs of equi-biaxial tensile stress and strain at the surface of the specimen in the constant moment zone under tension. This is achieved based on: (1) the hypotheses of the classic elastic slab bending theory [35], and (2) the equilibrium of moments and normal forces in a sectional analysis. In addition, the strain distribution in the sectional analysis is considered as linear; and the compressive behavior of UHPFRC is assumed to be linear elastic. The curvature in the constant moment zone is assumed to be identical in all directions.

2.2 Analytical basis

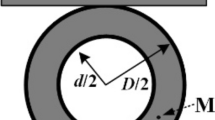
As for the ring-on-ring test, the circular slab is simply supported on a ring with radius of R, and the recorded force F as a result of the imposed vertical actuator displacement is uniformly distributed along a small ring with radius r from the top. The notations and sign conventions used in the analysis are shown in Fig. 2. Dividing the slab into two parts as shown in Fig. 2b, c, it may be seen that the inner portion of the slab is in the condition of pure bending produced by the uniformly distributed moment mi per unit length and that the outer part is bent by mi and the shearing force qi per unit length.

Fig. 2
figure 2

Schematic description of ring-on-ring test

Full size image

Based on the elastic slab bending theory [35], the uniformly distributed moment mi per unit length acting on the inner portion of slab is given by Eq. (1):

$$m_{i} = \frac{{F_{i} }}{8\pi }\left[ {\frac{{(1 - \nu )(R^{2} - r^{2} )}}{{R^{2} }} - 2(1 + \nu )\ln \frac{r}{R}} \right]$$
(1)

with the central deflection δi:

$$\delta_{i} = \frac{{F_{i} }}{8\pi D}\left[ {\frac{{(3 + \nu )(R^{2} - r^{2} )}}{2(1 + \nu )} + r^{2} \ln \frac{r}{R}} \right]$$
(2)

where ν is the Poisson’s ratio. The value of ν is assumed as a typical value of 0.2 for UHPFRC during elastic domain and set as 0 after elastic limit in present study. The value \(D = \frac{E}{{1 - \upsilon^{2} }}\frac{{h^{3} }}{12}\) is the elastic flexural stiffness of the slab.

2.3 Determination of equi-biaxial tensile elastic modulus and elastic limit stress

The determination of equi-biaxial tensile elastic modulus and elastic limit stress requires using the elastic limit point A′ under flexure. The point A′ generally corresponds to the loss of linearity in the force–deflection curve. However, point A′ is not easy to be obtained directly from the curve due to the high ductility of UHPFRC [13, 23], and thus, a reliable and representative criterion to determine the elastic limit is necessary. In this section, a criterion based on an irreversible decrease of the moving average elastic modulus Emi, same with the one defined for 4PBT in [13], is introduced. Similar criterion was applied for bending tests in [36].

Transformed from Eq. (2), the elastic modulus Ei for each pair of measured force and central deflection (Fi, δi) is:

$$E_{i} = \frac{{3(1 - \upsilon^{2} )}}{{2\pi h^{3} }}\frac{{(F_{i} - F_{0} )}}{{(\delta_{i} - \delta_{0} )}}\left[ {\frac{{(3 + \nu )(R^{2} - r^{2} )}}{2(1 + \nu )} + r^{2} \ln \frac{r}{R}} \right]$$
(3)

where (F0, δ0) is the reference point at the beginning of the force–deflection curve.

Then the moving average Emi is calculated from at least 10 values of Ei in the elastic domain after the initial domain of specimen response, and plotted as a function of the measured deflection δi. The point A′ (corresponding to force Fe and deflection δe) thus is determined when an 1% irreversible decrease of Emi is observed firstly, and the value of Ei given by Eq. (3) for Fe and δe is defined as the equi-biaxial tensile elastic modulus EU of the UHPFRC material. This methodology can considerably reduce the influence of noise from the measured points in the force–deflection curve since the average values of Emi is used.

As derived from linear elasticity theory [35, 37], the stress distribution in cross-section at point A′ is assumed according to Fig. 3a. Thus, the corresponding equi-biaxial tensile elastic limit stress fUte for Fe and δe is equal to

Fig. 3
figure 3

Stress and strain distribution of cross-section at: a elastic limit; b ultimate limit; c damage localization point

Full size image
$$f_{Ute} = \sigma_{Uti} = \frac{{3F_{e} }}{{2\pi h^{2} }}\left[ {\frac{{(1 - \nu )(R^{2} - r^{2} )}}{{2R^{2} }} - (1 + \nu )\ln \frac{r}{R}} \right]$$
(4)

2.4 Determination of equi-biaxial tensile strength

The ultimate limit point C′ characterizes the maximum force measured during the ring-on-ring test of the UHPFRC slab. As demonstrated by several researchers [7, 38,39,40], the flexural resistance Fp of a thin UHPFRC slab can be estimated using the yield line theory [41, 42]. Based on the boundary and loading conditions of UHPFRC circular slab under ring-on-ring test configuration, the crack pattern consisting of radial and tangential yield lines is assumed as shown in Fig. 4, which will then be verified against the actual failure modes as observed from the test results.

Fig. 4
figure 4

Assumed yield lines

Full size image

The external work done, giving the virtual displacement δp at Fp (point C′), is

$$W_{{\text{ext}}} = F_{p} \delta_{p}$$
(5)

and the internal work done is

$$W_{\text{int}} = 2\pi rm_{t}^{u} \varphi + 2\pi (R - r)m_{r}^{u} \varphi = 2\pi \delta_{p} \left( {m_{r}^{u} \frac{r}{R - r} + m_{t}^{u} } \right)$$
(6)

with

$$\varphi = \frac{{\delta_{p} }}{R - r}$$
(7)

where φ is the rotation angle of single segment, m ur and m ut are the ultimate resistance moments per unit length along the radial and tangential directions, respectively.

Considering energy balance, Wext = Wint, the flexural resistance Fp is determined:

$$F_{p} = 2\pi \left( {m_{r}^{u} \frac{r}{R - r} + m_{t}^{u} } \right)$$
(8)

At point C′, multiple fictitious cracks are largely developed with relatively small stress transfer between fictitious crack surfaces, and a considerable part of the tensile zone of UHPFRC enters into the softening domain. Following [13], the stress distribution in the cross-section can thus be assumed as illustrated in Fig. 3b, in which αph is the height of neutral axis. As reported by Baril et al. [38], the maximum plastic moment of the UHPFRC slab is similar to the one obtained from beam bending under 4PBT configuration. Thus, the value of αp is set as 0.82 at point C′, following [13, 14] based on non-linear finite element analysis. This assumption is expected to be reliable given that the large damage propagation appears only on one or several localized cracks in single direction at peak load (Fig. 7), suggesting the dominant effect of uniaxial tension. This leads to:

$$m_{r}^{u} = m_{t}^{u} = \frac{1}{2.3}h^{2} f_{Utu}$$
(9)

Combining Eqs. (8) and (9) allows to obtain the equi-biaxial tensile strength:

$$f_{Utu} = 1.15\frac{{F_{p} }}{{\pi h^{2} }}\frac{R - r}{R}$$
(10)

2.5 Determination of equi-biaxial strain at the end of hardening

The damage localization point B′ is required for the determination of equi-biaxial strain at the end of hardening. In present method, an additional criterion linked to the equi-biaxial tensile strength as determined using Eq. (10) is introduced. Noting that the inverse analysis is invalid beyond point B′.

In the central portion of UHPFRC slab under the force transmitting ring, considering the uniformly distributed moment mi per unit length, the values of curvature χi are given by Eq. (11); they are assumed to be identical in all directions.

$$\chi_{i} = \frac{{m_{i} }}{D(1 + \nu )}$$
(11)

Combined with Eqs. (1) and (3), the curvature χi from Eq. (11) in the central portion of slab is obtained for every pair of measured force and central deflection (Fi, δi) according to:

$$\chi_{i} = \frac{{2(1 - \nu )(R^{2} - r^{2} )/R^{2} - 4(1 + \nu )\ln \frac{r}{R}}}{{(3 + \nu )(R^{2} - r^{2} ) + 2r^{2} (1 + \nu )\ln \frac{r}{R}}}\delta_{i}$$
(12)

It should be noted that Eq. (12) is based on elastic structural mechanics and considered as reasonably valid for nonlinear behavior of UHPFRC in the strain-hardening domain, which can still be assumed as homogeneous material. Similar approach is adopted in [13, 26, 27].

For the points between the elastic and ultimate limits, the sectional stress and strain distribution in a section is determined according to Fig. 3c. This simplification is based on the proposal from [13] which was validated by numerous finite element simulations. By assuming that EU is constant in all directions, the stress is thus expressed as a function of depth z from the tensile surface, the yielding zone height αh and σUti

$$\sigma (z) = \left\{ {\begin{array}{*{20}l} {\sigma_{Uti} } \hfill & {{\text{if}}\;0 \le z \le \alpha h} \hfill \\ {\sigma_{Uti} + \frac{{(z - \alpha h)\chi_{i} E_{U} }}{1 - \nu }} \hfill & {{\text{if}}\;\alpha h \le z \le h} \hfill \\ \end{array} } \right.$$
(13)

Consequently, the distributed axial force Ni and moment mi per unit length in a section are obtained using Eq. (14) and Eq. (15), respectively:

$$N_{i} = h\sigma_{Uti} + \frac{1}{2}(1 - \alpha )^{2} h^{2} \frac{{\chi_{i} }}{1 - \nu }E_{U}$$
(14)
$$m_{i} = \frac{1}{2}h^{2} \sigma_{Uti} + \left( {\frac{1}{3} - \frac{\alpha }{2} + \frac{{\alpha^{3} }}{6}} \right)^{2} h^{3} \frac{{\chi_{i} }}{1 - \nu }E_{U}$$
(15)

Based on the equilibrium of forces in sectional analysis, namely Ni = 0:

$$2\alpha^{3} - 3\alpha^{2} + 1 - \frac{{12(1 - \nu )m_{i} }}{{h^{3} \chi_{i} E_{U} }} = 0$$
(16)

Based on the equilibrium of moments in sectional analysis, namely combining Eq. (16) with Eq. (1), the value of αi is determined. Subsequently, the equi-biaxial tensile stress \(\sigma_{Uti}\) and deformation \(\varepsilon_{Uti}\) at the tensile surface of the central part of slab are determined using Eqs. (17) and (18), respectively:

$$\sigma_{Uti} = \frac{1}{2}(1 - \alpha_{i} )^{2} h\frac{{\chi_{i} }}{1 - \nu }E_{U}$$
(17)
$$\varepsilon_{Uti} = \frac{{(1 - \nu )\sigma_{Uti} }}{{E_{U} }} + \alpha_{i} \chi_{i} h$$
(18)

The inverse analysis then is performed for a series of points evenly distributed between the force range of 0.50Fp to 0.80Fp, given that point B′ falls in this range based on preliminary study. The first point “j” for which the calculated stress σUtj is larger than the value of fUtu according to Eq. (10) gives an estimate of the equi-biaxial strain hardening value of the UHPFRC, namely εUtu = εUtj.

3 Results of inverse analyses

3.1 Experimental campaign

Two experimental campaigns are conducted to investigate the uniaxial and equi-biaxial flexural behavior of UHPFRC elements. A total of four circular slabs (diameter of 1200 mm, thickness of 50 mm) are used for the ring-on-ring test; the metallic support ring and force transmitting ring have a radius of R = 500 mm and r = 150 mm, respectively. Ten rectangular plates (length of 500, width of 100 mm and thickness of 50 mm), extracted from a circular slab of same fabrication, are used for 4PBT with a span of 420 mm. The real geometry, especially the thickness, of each specimen has been measured precisely before testing. It should be mentioned that the size effect between these two types of specimens is ignored in the present study, since its influence on the flexural response of UHPFRC, especially thin members, is negligible, as reported in [43,44,45]. Figure 5 shows the full test setups and instrumentations for both tests. The net central deflection under ring-on-ring test is determined by DIC analysis on the bottom surface, excluding the deformation of rubber pad measured from three LVDTs on the top surface. The net mid-span deflection under 4PBT is directly obtained from DIC analysis.

Fig. 5
figure 5

Schematic description of test setup and devices: a ring-on-ring test; b 4PBT

Full size image

The tested strain-hardening UHPFRC is an industrial premix containing 3.8% by volume of straight steel fibers with length of 13 mm and diameter of 0.175 mm. At 28 days, the UHPFRC has compressive strength of 185 MPa, measured using cylinders of 70 mm diameter and 140 mm height.

The experimental details are reported in [34]. Only the main testing results are summarized in the following.

3.2 Inverse analysis results from ring-on-ring test

3.2.1 Experimental results

The force versus central deflection (F–δ) curves of four UHPFRC circular slabs from the ring-on-ring test are presented in Fig. 6, where the thick curve refers to the average response. It should be mentioned that the variation of F–δ curves is mainly attributed to the thickness difference of different slabs [34]. Based on DIC analysis, Fig. 7 shows the fracture process observed on the bottom surface of slab S3 as an example (all the other slabs show a similar response), in which the white dashed circle marks the position of the force transmitting ring.

Fig. 6
figure 6

Force- central deflection (F–δ) curves from four quasi-static ring-on-ring tests

Full size image
Fig. 7
figure 7

Example of cracking and fracture process on the tensile surface of the UHPFRC slab under quasi-static ring-on-ring testing (S3)

Full size image

In general, the ring-on-ring test yields consistent equi-biaxial flexural response. Four characteristic domains in terms of F–δ curves can be distinguished, namely, the elastic domain (OA), quasi-elastic domain (AB), hardening domain (BC) and softening domain (CD), as marked with letters A–D in Fig. 7. Based on the DIC strain contours, the elastic limit (described by Fe, δe and we at point A) is determined when the first matrix discontinuity is detected, while the quasi-elastic limit (described by Fqe, δqe and wqe at point B) refers to the start of strain concentration on one or several matrix discontinuities, implying the formation of first fictitious cracks. Accordingly, Table 1 summarizes the characteristic parameters, including force, deflection and maximum opening, at the end of each domain (point A, B and C) and for all slabs.

Table 1 Equi-biaxial flexural parameters from ring-on-ring tests
Full size table

3.2.2 Inverse analysis results from ring-on-ring test

Figure 8 illustrates the determination of elastic limit (point A′) from specimen S3 as example. According to the description in Sect. 2.2, the evolution of moving average secant modulus Emi as a function of central deflection δi is calculated using Eq. (6). It should be noted that more than 50 pairs of measured force Fi and deflection δi are used for the plotting of Fig. 8a and assumed to be enough for an unequivocal determination of point A′ in the present study, although further investigation on the sensitivity of the interval of the used pairs is required for validation. Thus, following the 1% irreversible decrease criterion, the elastic limit is determined at a deflection of 0.46 mm and force of 28.77 kN, corresponding to equi-biaxial elastic limit stress of 9.17 MPa and elastic modulus of 57,500 MPa.

Fig. 8
figure 8

Example of determination of elastic limit: a elastic modulus as a function of deflection; b position of elastic limit

Full size image

Figure 9 shows the determination of damage localization point B′ from specimen S3. Considering that the experimentally determined quasi-elastic limit is at a force level of 0.55 Fp, a total of 20 interpolated points are selected between 0.50 Fp to 0.80Fp, as indicated by the red circles Fig. 9a. The corresponding values of stress and strain based on Eqs. (17) and (18) are given in Fig. 9b. The equi-biaxial strain at the end of hardening εUtu corresponding to the calculated equi-biaxial tensile strength (fUtu= 14.24 MPa) is determined to be 1.62‰.

Fig. 9
figure 9

Example of determination of damage localization point: a test results with interpolated points; b corresponding tensile properties

Full size image

Finally, all results from inverse analyses of the ring-on-ring tests are summarized in Table 2, where FA′ and FB′ refer to the force at elastic limit and at damage localization point as determined using the proposed inverse analysis method. In general, the equi-biaxial tensile properties are consistent within the four slab specimens, although a relatively low value of εUtu is observed for S4. The equi-biaxial elastic modulus is 59,000 MPa in average. It is noted that the determined elastic limit (point A′) agrees well with the experimental result (point A), where the first matrix discontinuity is observed from DIC analysis. Value FB′, corresponding to 0.63 Fp in average, is around 16% higher than the quasi-elastic limit (point B, Fqe) as determined experimentally. For direct comparison, the position of point B′ is marked in Fig. 7 for S3. The corresponding DIC strain contours at points B and B′ are given in Fig. 10 for each UHPFRC slab specimen. It is observed that at point B, a network of matrix discontinuities is formed in the central tensile area of the slab. Afterward, this network resists cooperatively the increasing load, although slight strain concentration (red lines in the DIC strain contours) is observed. Beyond point B′, the strain concentrates largely and locally to form several fictitious cracks. Therefore, point B′ as determined from inverse analysis matches well with the damage localization point as obtained from experiments.

Table 2 Equi-biaxial tensile properties from inverse analysis of ring-on-ring test
Full size table
Fig. 10
figure 10

Comparison between quasi-elastic limit (B) and fictitious crack localization point (B′) of slabs: a S1; b S2; c S3; d S4

Full size image

3.3 Inverse analysis results from 4PBT

3.3.1 Experimental results

The force–deflection curves from different UHPFRC plates under 4PBT are shown in Fig. 11, where a four-domain response can be identified. Based on DIC analysis, Fig. 12 shows the fracture process observed from plate B1 as representative example, in which the damage propagation on the bottom surface of the constant moment zone (between loading points) are presented.

Fig. 11
figure 11

Force–deflection responses from 4PBT

Full size image
Fig. 12
figure 12

Example of fracture process of UHPFRC plate under 4PBT (B1)

Full size image

The determination of corresponding uniaxial flexural parameters is based on the same methodology as for the ring-on-ring tests. In general, the flexural responses from different plates agree well until reaching the quasi-elastic limit, and afterward, varying in terms of force–deflection curve and cracking pattern with increase of deflection.

3.3.2 Uniaxial tensile properties from 4PBT

The inverse analysis is conducted individually based on the force–deflection response of each specimen under 4PBT condition, following the method proposed by Denarié et al. [13]. The inverse analysis results of 4PBT are summarized in Table 3. A considerable variation of uniaxial tensile properties, especially the uniaxial strain at the end of hardening, is observed. This is attributed to the fact that fiber distribution varies in different 4PBT specimens as they were extracted from different positions of the UHPFRC slab. Similar finding was reported in [1, 14, 15, 46].

Table 3 Uniaxial flexural parameters and uniaxial tensile properties from 4PBT
Full size table

Similar with the findings from the inverse analysis of the ring-on-ring test results (Sect. 3.2), point A′ corresponds well to the elastic limit, where the first matrix discontinuity exists. Point B′ represents the initiation of large damage concentration on single fictitious crack, as illustrated in Fig. 12 as an example.

4 Discussion

Based on the inverse analysis results obtained from the ring-on-ring test and 4PBT, the equi-biaxial and uniaxial tensile properties (in average) of strain-hardening UHPFRC are compared. It is found that under equi-biaxial stresses, the average elastic modulus is 59,000 MPa, approximately 24% higher than the one obtained under uniaxial stress, while the equi-biaxial elastic limit stress (9.14 MPa) is 18% smaller than the uniaxial elastic limit stress (11.16 MPa) in average. This may be attributed to the fact that a large zone of the UHPFRC slab specimen in ring-on-ring test configuration is under pure bending in all directions, while a relatively small zone of the rectangular plate in 4PBT is under pure bending in only one direction. Thus, it is plausible that the formation of first matrix discontinuity occurs at lower stress in the ring-on-ring test, given the stochastic nature and inherent variability of fiber distribution in the UHPFRC material. On the other hand, the relatively high value of equi-biaxial elastic modulus may be explained by the confinement effect due to multiple axial tension under ring-on-ring testing. The same effect was reported by Swanepoe [16] for SHCC under biaxial DTT. However, further investigation of this aspect is required.

As for the damage localization point B′ where the fictitious cracks start to propagate significantly, the corresponding force FB′ represents 90% of the flexural resistance (0.90 Fp) under 4PBT condition. This is slightly lower than values (FB′ ≥ 0.95 Fp) reported in the literature [23, 27], in which different strain-hardening UHPFRC mixes and specimen sizes were used. However, in the study of López et al. [23], point B′ was proposed empirically without experimental validation. In the study of Baby et al. [27], a pair of staggered LVDTs were installed on the tensile surface of the specimen, and the point B′ was identified at the bifurcation of deformation measurements from the two LVDTs. However, the result depends largely on the measuring length and position of LVDTs, given that the matrix discontinuities before point B′ are not distributed uniformly but are concentrated in specific zones in the constant moment length, as illustrated in Fig. 12. This implies that the apparent bifurcation is not determined accurately, leading to an overestimation of strain at the end of hardening [13]. The full-field strain measurements using the DIC technique in the present study allow to determine point B′ with high accuracy, the details can be found in [34].

On the other hand, point B′ from the ring-on-ring test corresponds to 0.63 Fp, which is much lower than the corresponding values obtained from the 4PBT. This is explained by the significant stress distribution since complex cracking pattern with large crack surfaces are observed (Fig. 7) beyond point B′ under the ring-on-ring test configuration, resulting in a considerable increase of the flexural resistance. Besides, the analytical equi-biaxial strain at the end of hardening is 1.27‰, while the uniaxial strain is as high as 4.50‰. This large difference can also be observed visually at point B′ from Figs. 7 and 10 for the ring-on-ring test and Fig. 12 for 4PBT, where more compact distribution and higher amount of matrix discontinues per unit surface are detected on the tensile surface for the 4PBT. This may be explained by inhomogeneous fiber distribution in one specific direction of the UHPFRC slab, where damage localizes early and then restrains further development of matrix discontinuities over the remaining part of the slab. Similar experimental results were reported in [22] using biaxial DTT, in which the biaxial strain at the end of hardening was determined to be 0.17‰, while the uniaxial strain was 0.25‰ for the same type of UHPFRC. Conversely, the equi-biaxial tensile strength (14.08 MPa) is almost equivalent to the uniaxial tensile strength (13.99 MPa). However, further experimental and analytical studies using different specimen sizes and UHPFRC types are necessary for understanding the mechanism and quantitatively

5 Conclusion

An original analytical inverse analysis method for determining the equi-biaxial tensile properties of strain-hardening UHPFRC from the ring-on-ring test is proposed based on elastic slab bending and yield line theories. The inverse analysis results are validated against experimental evidence obtained from DIC analysis. Moreover, the uniaxial tensile properties of the same UHPFRC are obtained from the inverse analysis of 4PBT, following the method proposed in [13]. Uniaxial and equi-biaxial tensile properties of strain-hardening UHPFRC are then compared.

The main conclusions are:

  1. (1)

    The proposed inverse analysis offers a simple method to determine the equi-biaxial tensile properties of strain-hardening UHPFRC based on the experimental force–deflection curves from the ring-on-ring test. The method does not require extensive iterative procedures and can be implemented in a ready-to-use spreadsheet.

  2. (2)

    The determination of elastic limit based on the criterion of 1% irreversible reduction of the moving average of the secant elastic modulus is proven to be objective, as validated experimentally based on DIC analysis. The corresponding equi-biaxial elastic limit stress (9.14 MPa) is 18% smaller than the uniaxial elastic limit stress (11.16 MPa), owing to the stochastic nature and inherent variability of fiber distribution in the UHPFRC material, while the equi-biaxial elastic modulus (59,000 MPa) is 24% higher than that under uniaxial stress, which can be explained by the confinement effect due to multiple axial tension under ring-on-ring testing.

  3. (3)

    The damage localization point corresponds to 63% of flexural maximum resistance under the ring-on-ring testing condition, while 90% under 4PBT condition. The corresponding equi-biaxial strain at the end of hardening is 1.27‰, which is only 28% of the uniaxial strain. This difference can also be observed visually on the DIC strain contours at point B′, where more compact distribution and higher amount of matrix discontinues per unit surface are detected on the tensile surface for 4PBT, compared with the corresponding findings from the ring-on-ring test.

  4. (4)

    The equi-biaxial tensile strength (14.08 MPa) is almost equivalent to the uniaxial tensile strength of cut-out of larger plates 4PBT strips (13.99 MPa) as determined by inverse analysis.