Abstract
Determining the mechanical properties of cross-laminated timber (CLT) panels is an important issue. A property that is particularly important for CLT used as shear walls in buildings is the in-plane shear modulus. In this study, a method to determine the in-plane shear modulus of 3- and 5-layer CLT panels was developed based on picture frame tests and a correction factor evaluated from finite element simulations. The picture frame test is a biaxial test where a panel is simultaneously compressed and tensioned. Two different testing methods are simulated by finite elements: theoretical pure shear models as a reference cases and picture frame models to simulate the picture frame test setup. An equation for calculating the shear modulus from the measured shear stiffnesses in the picture frame tests is developed by comparisons between tests and finite element simulations of the CLT panels. The results show that pure shear conditions are achieved in the central region of the panels. No influence from the size of the tested panels is observed in the finite element simulations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cross laminated timber (CLT) panels are normally used in the building industry [1] for walls and flooring. The popularity of CLT has increased due to its prefabrication potential, relatively high strength to weight ratio and reputation as an environmentally friendly building material. CLT is a plate-like material built up from boards in a crosswise arrangement in a number of layers. The number of layers is odd or even and at least three. The board material, the number and arrangement of layers and the layer thicknesses define the properties of CLT panels [2]. Since CLT is being a relatively new construction material, many of its properties are currently under investigation [3]. The in-plane shear properties of CLT panels may limit the possibility of constructing tall wooden buildings [4], rendering the investigation of the in-plane shear properties of CLT panels highly important.
The picture frame test (sometimes denoted as the direct shear test) is a biaxial test commonly used for determining the shear properties of textiles [5] but is used here for CLT panels. Earlier tests [6, 7] of textiles have reported issues of reproducing picture frame results due to difficulties in properly aligning the textile fibres with the frame. A reason for this was the problem of fixing the textile in the frame [7]. A size effect was observed for textiles, namely that the resulting values of shear stiffness for a textile depended on the specimen size [7]. This may, according to [7], be a textile related problem caused by the increased friction between the threads due to the increased textile area. For CLT, this frictional effect is not an issue since the deformation between boards and layers is mechanically different from the motion between threads in textiles.
Another testing method to simulate shear is the diagonal compression test. This method has been used for testing of non-isotropic materials such as wood and masonry walls, see [8] and [9]. The underlying problem with this test method is the nonhomogeneous stress state in the test sample, [10].
Numerous previous studies [11,12,13,14,15] have presented experimental results for CLT using the picture frame test. The main differences between the experimental setups were the transfer of load from the frame to the CLT panel: [11] used friction, [12] and [13] used glue while [14] and [15] used bolts. A motivation for using picture frame tests is that, according to [3], gross shear tests may be more appropriate than single node tests. However, using gross shear tests in favour of single node tests introduces potential difficulties, such as how to transfer the load to the CLT panel and how to assure a pure shear condition in the whole of the tested panel. There is no evidence that a CLT panel will perform in a similar way to a textile fabric in a picture frame test and none of the previous studies have investigated whether a CLT panel in a picture frame test is subjected to a pure shear condition. In addition, it has not been analysed whether a size effect for CLT exists for the picture frame test setup, e.g., using finite element (FE) simulations. A size effect would mean that the shear modulus obtained from a test would depend on the size of the tested CLT panel and this would be a serious shortcoming of the test method.
The purpose of this study is to confirm the applicability of the picture frame test for CLT by investigating whether a pure shear condition is achieved in the measured region. In addition, also to find the potential occurrence of a size effect. Finally, an equation is presented for the calculation of the shear modulus based on a picture frame test for CLT. The equation is based on FE simulations on a pure shear case and a picture frame case, and is believed to give more reliable values for the shear modulus compared to [14].
2 Materials and methods
2.1 Picture frame test
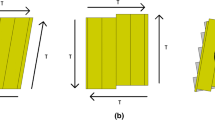
The test material and picture frame test setup were the same as in the study by Turesson et al. [15]. Fourteen 3-layer and eleven 5-layer panels were tested (Fig. 1). All panels were manufactured by a commercial CLT producer. CLT panels were constructed by multiple boards arranged side-by-side. Layers were crosswise directed, meaning that the main fibre direction was 0°, 90° and 0° for the 3-layer panels and 0°, 90°, 0°, 90° and 0° for the 5-layer panels. The board widths and thicknesses were 180 and 29 mm for the 3-layer panels and 156 and 20 mm for the 5-layer panels, respectively. The boards were glued on the flat sides (no edge gluing) with polyurethane glue. The dimensions of the CLT panels were 600 × 600 × 87 and 600 × 600 × 100 mm for the 3- and 5-layer panels, respectively. The average modulus of elasticity, El, for the boards was measured to be 10,714 and 10,863 MPa for the 3- and 5-layer panels, respectively. The moisture content was measured on cut-out clear wood samples to 8.6% and 7.4% for the 3- and 5-layer panels, respectively.
The picture frame was held at the bottom corner pin and the force was applied as tension in the upper corner pin, as shown in Fig. 1. The average shear stiffness values obtained from the measurements of deformations in the central region (Fig. 1) on sides 1 (s1, vertical direction) and 2 (s2, horizontal direction) were \(\bar{k}_{s1s2}\) = 181.9 and 232.9 kN/mm for the 3- and 5-layer panels, respectively. Please refer to Turesson et al. [15] for more details on the test procedure.
2.2 FE simulations
FE simulations were conducted with three-dimensional models in the FE software Abaqus 6.14 [16]. Two different testing methods were simulated. One simulated test method was of a CLT panel mounted in the steel picture frame (Fig. 2) and the other simulated test method was the CLT panel loaded in pure shear (Fig. 5). Contact between individual board surfaces was simulated using contact conditions. For flat side surfaces, slip between two surfaces in contact was prohibited and the surfaces were not allowed to penetrate or separate from each other. An adjustment zone of 1 mm was used to set the initial contact between the contact surfaces. For adjacent side edges, both conditions of no contact (no edge gluing) and conditions of contact (edge gluing) were used. In cases of edge gluing, the same contact conditions as presented for flat side surfaces were used. No contact conditions were applied in cases of no edge gluing. Edge gluing was applied between boards for reference comparisons between the picture frame and the pure shear cases. Second-order cuboid FEs (denoted C3D20R) were used with a global mesh size of 7.5 mm.
Both orthotropic and isotropic material properties were used in the FE simulations. Models with orthotropic material properties were used to represent wood and the models with isotropic material properties were used for comparisons between the picture frame and the pure shear FE simulations. The models with isotropic material properties had an elastic modulus of 300 MPa, a shear modulus of 120 MPa and a Poisson’s ratio of 0.25. The orthotropic material properties were setup according to SS-EN 338:2016 [17] (Table 1). The modulus of elasticity in the fibre direction, El, was set to the values described in Sect. 2.1. The Poisson’s ratios were set to zero, partly because of a lack of reliable data and partly because they were assumed to have a negligible effect on the results. Furthermore, the Swedish standard Eurocode 5 advises the use of a Poisson’s ratio of zero [18], as assumed in [19] and [20]. The moduli of elasticity in the radial, Er, and tangential, Et, directions were set as equal, as were the shear moduli in the fibre-radial, Glr, and fibre-tangential, Glt, planes. The rolling shear modulus is denoted as Grt.
2.2.1 FE simulation of picture frame test
The steel shear frame and the attached CLT plate were modelled as half models with a symmetry condition in the thickness direction, see Fig. 2. Four steel frame members with attached dowels transferred the load to the mounted CLT panel. Each steel frame member was modelled with attached load-transferring dowels and two holes, one hole in each end. A rigid pin was mounted in these holes. The force was applied vertically upwards on the top pin via a loading device, as shown in Fig. 2b. The bottom pin was fixed. All parts of the picture frame, except the rigid top pin, were assigned steel material properties with a modulus of elasticity of 200 GPa and a Poisson’s ratio of 0.25.
Contact conditions between the components of the picture frame were created by restricting the surfaces from penetrating and separating during the FE simulations. Movement between contact surfaces was controlled by a friction coefficient of 0.01. This contact condition was applied (Fig. 2) between the dowels of the steel frame members and the holes of the CLT panel, between the corner pins and the steel frame members and between the top corner pin and the loading device. The contacts between the steel frame members and the outer layer surfaces of the CLT panels were neglected.
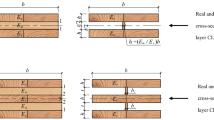
The geometry of the CLT panels is illustrated in Fig. 3. A cut-out of 60 × 60 mm was made in each corner for the corner pins. Displacements were measured at the “×”-marks in Fig. 3. CLT panels for the 3- and 5-layer models were created with two types of lay-ups based on board positions, a symmetrical or a non-symmetrical lay-up, as shown in Fig. 3.
An overview of all CLT picture frame FE simulations with orthotropic and isotropic material properties is presented in Table 2. The FE simulations were divided into symmetrical (Sy) and non-symmetrical (Ns) board lay-ups with either isotropic (Iso) or orthotropic (Ort) material properties. For the tested CLT panels, there was no control of the board positions within each layer. Only ten of sixteen possible combinations were considered relevant and used in the analysis.
2.2.2 Evaluation of shear modulus from picture frame tests and FE simulations
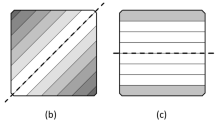
The size of the CLT panel was L × L with L = 600 mm. The size of the measured central region was predetermined to be a × a where a = 0.4L, as shown in Fig. 4. The in-plane shear modulus, G, for the picture frame tests and FE simulations was calculated as the shear stress τ divided by the shear strain γ. The shear strain was defined by using the cosine rule for describing the shear angle γ created in the central region (square a × a) due to a length increase/decrease Δ of the displacement transducer, with an initial length d, as shown in Fig. 4.
For small deformations sin(γ)≈ γ and Δ2≈0 we obtain
To remove the effects due to holes and cut-outs, a size of a fictious (smaller) panel Leff × Leff, without holes and cut-outs was defined. The force F was distributed on this smaller panel in order to calculate the shear stress as
where tclt is the total thickness of the panel and Leff is defined from
This means that if there was no effect of holes and cut-outs, then Leff was equal to L and the constant r should be equal to 0.4 (note that this was the case in [14] and [15]). If there was an effect of holes and cut-outs, then r would be > 0.4 and Leff would be < L. From Eqs. (2)–(4) the shear modulus G became
where k is the shear stiffness value taken from the slope of the load displacement F–Δ curves. The value of the constant r was unknown at first but later evaluated based on the results from several FE simulations and comparisons between calculated G values with Eq. (5) and calculated in-plane shear modulus, Gp, from the pure shear FE simulations. The least squares method (LSM) was used to find the optimum value for r and a coefficient of determination, R2, from several comparisons.
2.2.3 FE simulation of pure shear models
FE simulation models were created with the same board and outer dimensions as the panels in the picture frame tests and FE simulations, i.e., 600 × 600 mm. There were no holes and cut-outs in the models. Both symmetrical and non-symmetrical board lay-ups were used for both the 3- and 5-layer panels. See Table 2 for more information about the models. The CLT models were loaded with surface traction shear forces Fs on the four side edges of the panel (Fig. 5). The panels were kept in position by locking the movement of the first corner in the x and y directions, and the x direction for the fourth corner. A symmetry plane in the middle was used in the z direction (thickness direction of the panel) to reduce the calculation time and to prevent movement.
The pure shear modulus Gp was calculated as
where tclt is the total thickness of the panel and dy is the displacement in the y direction.
3 Result and discussion
Examples of results from the FE simulations of picture frame tests and pure shear models are shown in Fig. 6. Deformations near edges were influenced by individual board edges.
The results from the two simulated methods are presented in Table 3. The shear modulus Gp [Eq. (6)] from pure shear FE simulations is shown in the first column of Table 3 for ten combinations of symmetric and nonsymmetric, edge glued and non-edge glued, isotropic and orthotropic materials and 3 and 5 layer panel variants. Only ten of sixteen possible combinations (see Table 2) were considered relevant and used, as shown in Table 3. The second column shows shear stiffnesses k from picture frame FE simulations and the third column shows the corresponding shear modulus G [Eq. (5)] calculated with r = 0.475. This r value was determined by using LSM to fit values of G to values of Gp in the best possible way for the ten combinations shown in Table 3. This LSM resulted in r = 0.475 with a R2 value of 0.99, which means an efficient side length, Leff, of 505.3 mm. Interestingly, this Leff is approximately equal to the side length L minus the lengths of the two corner cut-outs, as shown in Fig. 4.
The corrected version of Eq. (5) for the shear modulus G became
The edge glued and isotropic models, 3EgSyIso and 5EgSyIso in Table 3 resulted in a Gp of 119.7 MPa, which was as expected based on the isotropic material data with a shear modulus of 120 MPa. This showed that there was a pure shear state in the pure shear FE simulations, as also confirmed visually in Fig. 6. The results for the orthotropic models (3EgSyOrt and 5EgSyOrt in Table 3) were as expected equal to the value of the shear modulus in fibre-radial Glr (and fibre-tangential Glt) directions. There was no difference in Gp between the symmetrical and non-symmetrical board lay-up models (3SyOrt versus 3NsOrt and 5SyOrt versus 5NsOrt).
The mean error of the least square fit was 1.7%. The largest error of − 13.0% was for the non-symmetrical model 3NsOrt. This large error occurred because the pure shear model was not sensitive to symmetrical or non-symmetrical board lay-up but the picture frame model was (see Gp and G for 3SyOrt and 3NsOrt in Table 3). The reduction of shear stiffness having a non-symmetrical board lay-up in the picture frame FE simulation was almost 20% for the 3-layer panels. This reduction was because the smallest board on one side was only connected to steel frame members on one side of the shear frame, not to two or three steel frame members as other boards in the panel, see boards in Fig. 3b. On that side, the result was that force transmission from the picture frame to the CLT panel was into the middle layer of the panel and not to the two outer layers. This gave stress concentrations and increased panel deformations and thus gave lower shear stiffness.
Figure 6 shows that a state of pure shear deformation dominated for the most part of the panel areas during the picture frame FE simulation. Only small parts of the areas at the side edges and corners deviated from a state of shear. This indicated that size effects due to edge influence were small and thus that size of the tested panels did not influence the results. This conclusion was also supported by the results for the edge glued isotropic models (3EgSyIso and 5EgSyIso) that resulted in a shear modulus G = ~120 MPa, as expected from the isotropic input material data.
The largest differences between the pure shear FE simulations and the picture frame FE simulations were how the load was transferred to the panels. The forces in the pure shear FE simulations were applied uniformly on each side edge of the panels. This force application method resulted in varying local displacements for each layer of the panel. The force in the picture frame FE simulations was not added uniformly to each layer, instead each layer was subjected to equal displacements (via the dowels). This resulted in an uneven force distribution between the layers of the CLT panels.
The results from practical picture frame tests on 3-layer and 5-layer panels are presented in Table 4. The shear stiffness results are taken from [15]. Equation (7) was used to calculate the shear modulus G shown in the third column. The corresponding FE simulations gave ~ 9% higher values for G. The reasons for discrepancies are the board lay-up, which was not controlled, material data variations, gluing quality variations and FE simulation model quality.
The shear modulus was 56.7 MPa higher for the 5-layer panels than the 3-layer panels. A similar 3-layer panel as the panel used in this study was earlier tested in [21] and the result was a shear modulus of 470 MPa compared to the result here of 497 MPa. In [21], the 3-layer panel had a board width of 160 mm compared to the board width of 180 mm in this study.
4 Conclusions
A picture frame test method was studied and found to be applicable for determination of the in-plane shear modulus of CLT panels. With this method, a single square CLT panel was mounted inside a shear frame. The CLT panel in the picture frame was simultaneously compressed and stretched by the picture frame in the horizontal and vertical diagonal directions, respectively. A pure shear condition was concluded by comparing the deformation pictures of a CLT panel tested in picture frame test and during a pure shear condition. The deformation pictures were created by using finite element (FE) simulations. A calculation of the in-plane shear modulus was conducted by measuring the applied force on the picture frame, by measuring the deformation in the middle (central region) of the panel and by use of an equation. The used equation was established based on FE simulations where pure shear model results were compared to picture frame FE simulations model results. The equation was applied with test data for 3- and 5-layer CLT panels and the in-plane shear modulus G was calculated to be 497 and 553 MPa, respectively. No influence from the size of tested panels was found.
References
Lukacs I, Björnfot A, Tomasi R (2019) Strength and stiffness of cross-laminated timber (CLT) shear walls: state-of-the-art of analytical approaches. Eng Struct 178(1):136–147. https://doi.org/10.1016/j.engstruct.2018.05.126
Brandner R, Flatscher G, Ringhofer A, Schickhofer G, Thiel A (2016) Cross laminated timber (CLT) overview and development. Eur J Wood Wood Prod 74(3):331–351. https://doi.org/10.1007/s00107-015-0999-5
Brandner R, Tomasi R, Moosbrugger T, Serrano E, Dietsch P (eds) (2018) Properties, testing and Design of Cross Laminated Timber: a state-of-the-art report by COST Action FP1402/WG 2. Shaker Verlag Aachen
Foster RM, Reynolds TP, Ramage MH (2016) Proposal for defining a tall timber building. J Struct Eng 142(12):02516001. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001615
Li L, Zhao Y, Vuong H, Chen Y, Yang J, Duan Y (2014) In-plane shear investigation of biaxial carbon non-crimp fabrics with experimental test and finite element modeling. Mater Des 63:757–765. https://doi.org/10.1016/j.matdes.2014.07.007
Wilks CE, Rudd CD, Long AC, Johnson CF (1999) Rate dependency during processing of glass/thermoplastic composites. In: Proceedings of 12th international conference on composite materials (ICCM-12), Paris, July 5–9
Lussier D, Chen J (2002) Material characterization of woven fabrics for thermoforming of composites. J Thermoplast Compos Mater 15(6):497–509. https://doi.org/10.1177/0892705702015006205
Dujic B, Klobcar S, Zarnic R (2007) Influence of openings on shear capacity of wooden walls. In: Proceedings of international council for research and innovation in building and construction, working commission W18—Timber structures (CIB-W18/40-15-6), Bled, 28–31 August
Anonymous (2002) ASTM: E519/E519M-15 Standard Test Method for Diagonal Tension (Shear) in Masonry Assemblages. ASTM international, West Conshohocken, PA, United States
Frocht MM (1931) Recent advances in photoelasticity and an investigation of the stress distribution in square blocks subjected to diagonal compression. Trans ASME 55:135–153
Bosl R (2002) Zum Nachweis des Trag- und Verformungsverhaltens von Wandscheiben aus Brettlagenholz. Military University Munich, Munich (in German)
Traetta G, Bogensperger T, Moosbrugger T, Schickhofer G (2006) Verformungsverhalten von Brettsperrholzplatten unter Schubbeanspruchung in der Ebene. In 5. GraHFT’06, Tagungsband, Brettsperrholz – Ein Blick auf Forschung und Entwicklung. p H1-H16 (in German)
Bogensperger T, Moosbrugger T, Schickhofer G (2007) New Test Configuration for CLT-Wall-Elements under Shear Load. In: Proceedings of international council for research and innovation in building and construction, working commission W18—Timber structures (CIB-W18/40-21-2), Bled, 28–31 August
Björnfot A, Boggian F, Steinsvik Nygård A, Tomasi R (2017) Strengthening of traditional buildings with slim panels of cross-laminated timber (CLT). In: Proceedings of the 4th international conference on structural health assessment of timber structures (SHATIS’17), Istanbul, 20–22 September
Turesson J, Björnfot A, Berg S, Ekevad M, Tomasi R (2019) Picture frame and diagonal compression testing of cross-laminated timber. Mater Struct 52:66. https://doi.org/10.1617/s11527-019-1372-7OAI
Anonymous, Simulia Abaqus 6.14-4, Abaqus/CAE User’s Guide
Anonymous (2016) Swedish standard: structural timber—strength classes. SS-EN 338:2016
Anonymous (2004) Swedish standard: Eurocode 5: design of timber structures—Part 2: bridges. SS-EN 1995-2:2004
Turesson J, Berg S, Ekevad M (2019) Impact of board width on in-plane shear stiffness of cross-laminated timber. Eng Struct 196:109249. https://doi.org/10.1016/j.engstruct.2019.05.090
Berg S, Turesson J, Ekevad M, Björnfot A (2019) In-plane shear modulus of cross-laminated timber by diagonal compression test. BioResources 14(3):5559–5572. https://doi.org/10.15376/biores.14.3.5559-5572
Brandner R, Dietsch P, Dröscher J, Schulte-Wrede M, Kreuzinger H, Sieder M (2017) Cross laminated timber (CLT) diaphragms under shear: test configuration, properties and design. Constr Build Mater 147:312–327. https://doi.org/10.1016/j.conbuildmat.2017.04.153
Acknowledgements
Open access funding provided by Lulea University of Technology. The experimental work presented in this paper was part of the EU-funded COST Action FP1402 working group and part of the Norwegian project “Increased use of wood in urban areas - WOOD/BE/BETTER”, funded by The Norwegian Research Council (Grant No. 416163) through the BIONÆR/BIONAER research program. The conducted research was also financed by the research and innovation project “Future CLT”, part of the European Union Interreg Nord (Grant No. NYPS 20200295) programme. The authors are indebted for their support. Special thanks goes to Anders Steinsvik Nygård for the brainstorming of ideas.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Turesson, J., Berg, S., Björnfot, A. et al. Shear modulus analysis of cross-laminated timber using picture frame tests and finite element simulations. Mater Struct 53, 112 (2020). https://doi.org/10.1617/s11527-020-01545-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1617/s11527-020-01545-1