Fire resistance of timber-concrete composite slabs

Abstract

The paper presents a simplified method for calculation of resistance of a TCC slab in fire conditions. Within the method the tensile and the compressive failure criteria in the outermost fibres of the cross-section are checked. The influence of the fire is applied through one-dimensional charring of the timber part of the cross-section in accordance with current standards on reduction of properties of materials. The concrete-timber connection is assumed to be ideal during the determination of resistant moment of the TCC cross-section. On the other hand, the calculation of the deflection of the TCC slab is conducted with the reduction of the connection’s rigidity. The ineffective zone of the timber as well as the cracked tensile zone of concrete part do not contribute to the effective stiffness of the TCC slab. The method is validated against the results of full sized fire tests of one way spanning TCC slabs form literature. Calculated and experimentally determined midspan deflections and failure times of the TCC slabs are compared and their considerable agreement is observed. Due to its convenience and accuracy, the present simplified method represents a useful tool for designers of TCC structures in fire conditions.

1 Introduction

Composite structural elements represent popular and, when properly designed, one of the most optimized structural bearing systems. They are used as a bearing system of new buildings and infrastructure as well as for rehabilitation and strengthening of existing ones. The latter can be achieved through the replacement of the entire damaged structural element with a composite one or through an application of an additional material layer to the existing element, which can increase its initial bearing capacity, stiffness and/or ductility. Other properties of the original element, such as sound and thermal insulation as well as fire resistance, can also be improved in the same way. Lately, there has been an increase in the usage of composite systems made of timber and concrete, mainly due to the favourable properties of timber. Timber, being a natural resource, is a renewable and recyclable material and it requires low energy for production compared to other widely used building materials such as concrete or steel. In principle, composite structures are assembled in such a way that each off the materials can be fully exploited. The upper layer of timber-concrete composite (TCC) systems is usually made of concrete due to the high compressive strength of the concrete. The lower layer is made of timber in order to exploit its relatively high tensile strength, low weight and, as already mentioned, to lower environmental impact. Currently, European standard for design of timber structures, Eurocode 5, gives some design rules, which can also be applied to TCC systems at ambient conditions, while no specific rules or design procedures for determination of fire resistance of TCC systems are given. Eurocode standards are currently also under the revision procedure and it was one of the goals of the European COST Action FP1404 on Fire safe use of bio-based building products to provide some rules for design of TCC systems in fire and harmonise them with already established design principles for timber and concrete structures in fire conditions. An extensive literature review of TCC structures in fire [1] revealed that, while there are already some analytical methods for calculation of fire resistance of TCC beams [2,3,4] available, there is no such method applicable to TCC slabs. Accordingly, this paper focuses on presentation of new analytical design procedure for TCC slabs in fire conditions, which employs some well-established design principles for timber and concrete structures in fire conditions.

The so called $\gamma$-method [5], which is a simplified approach for determination of effective bending stiffness and resistance of mechanically jointed beams with flexible elastic connection, is a method also proposed for design of TCC beams at ambient temperatures by Yeoh et al. [6]. Furthermore, each of aforementioned simplified methods for design of TCC beams in fire conditions [2,3,4] is based on the $\gamma$-method, however, the methods differ in consideration of reduction of strength and stiffness of timber and concrete at elevated temperatures as well as in the type of timber and timber-concrete connection. Frangi et al. [2] presented an analytical procedure for TCC beam which consists of a glulam beam, a thin timber board and a concrete slab. This method assumes that the temperature in concrete is low enough that no reduction of strength and stiffness of concrete occur. Hence, fire influenced only glulam beam and timber-concrete connection. The performance of the glulam beam in fire is determined with the reduced cross-section method given in EN 1995-1-2 [7] and influence of temperature on stiffness and strength of connection is accounted via the modification factors, which depend on the thickness of side cover. Method enables calculation of failure times and deflections of TCC beams in fire. In comparison to [2], Nežerka [3] upgraded the method by inclusion of the reduction of concrete compression strength with the modification factor for concrete strength according to EN 1992-1-2 [8]. Similar analytical method as in [2] was proposed by O’Neill [4] for calculation of the fire resistance of simply supported beam-type TCC floors with notched and screwed connections. This method is also based on reduced cross-section of timber beam, however, the gamma coefficient is calculated solely for the concrete part and slip modulus of the fastener itself is temperature dependent via charring rate.

In TCC beams (and beam-type floors), timber part represents the majority of height of the composite cross-section and it is at the same time much narrower than the concrete part. On the other hand, the timber part of a TCC slab (which is sometimes named also TCC slab-type floor) is often thinner than the concrete part, or at least the heights of both parts are of roughly the same magnitude, while widths of both parts are equal. Consequently, while there are practically no tensile stresses expected in concrete part of a TCC beam (i.e. neutral axis is expected to be in timber part of the composite cross-section), there can be a significant portion of the concrete part of the TCC slab, which is in tension (i.e. neutral axis is very likely to be in concrete part of the composite cross-section). This can result in cracking of concrete in tensile zone, which considerably alters the stiffness of the concrete part of TCC slab. The effective stiffness of the mechanically jointed cross-section and stress distribution can be determined with $\gamma$-method only if stiffnesses of both timber and concrete part of the cross-sections are known. As discussed above, stiffness of the concrete part of the cross-section of TCC slab depends on stress distribution. Therefore, stress distribution over cross-section of TCC slab need to be determined with different method.

The main objective of this paper is to present a novel simplified design method for the calculation of resistance of a TCC slab in fire conditions. Mechanical principles of the presented analytical method are based on principles at normal temperatures [9] and improved with consideration of additional failure criterion. Influence of high temperatures is accounted for, including reduced strength and stiffness of materials, the charring of timber and cracking of concrete in tension. Once stress distribution over cross-section is known, stiffness of each part (timber and concrete) can easily be determined. Effective stiffness of TCC slab is then calculated similar as in the Annex B of EN 1995-1-1 [10], which is one of the formulations of the $\gamma$-method and thus development of deflections over time can be determined. The presented method is applicable for one way spanning TCC slabs only, which is actually quite typical execution of TCC slabs [11]. However, due to this limitation, only timber parts made of solid timber, glued laminated timber (glulam) or laminated veneer lumber (LVL) can be considered, as they have approximately constant strength of material in the spanning direction of the slab. The method is therefore invalid for TCC slabs with timber part made of cross-laminated timber (CLT), as certain lamellas have very different strength in the spanning direction of the slab as the others. Also, different type of timber means different charring rates. Nevertheless, the modifications of the present method for considerations of CLT timber part are possible and will be considered in future research. Finally, validation of novel simplified design method for the calculation of resistance of a TCC slab in fire conditions is performed by comparing the analytical results with the experimental results from literature [11, 12].

2 Calculation of the fire resistance of a TCC slab

It is a common practice to upgrade a simplified method for calculation of certain structural element resistance at normal temperatures in a way to include reduction of material or geometric properties of this element due to fire conditions. Some of these methods, such as “500$^{\circ }{\rm C}$ isotherm method” for reinforced concrete cross-sections as well as “reduced cross-section method” and “reduced properties method” for timber cross-sections, are widely accepted and incorporated in standards [7, 8]. Furthermore, several simplified methods have been developed lately for determination of fire resistance of TCC beams [2,3,4], all of them on the basis of aforementioned methods for concrete and timber in combination with the so called $\gamma$-method [5].

The simplified method for determination of fire resistance of TCC slabs, presented in this paper, follows the same idea. Thus, mechanical principles of the method, which are the same for both normal and elevated temperatures, are outlined hereinafter, followed by description of modifications of the method inherent to the fire exposure.

2.1 Mechanical principles of the method

The resistance of TCC slab can be defined through a moment resistance of its cross-section. The procedure for determination of moment resistance in the present simplified method is adopted from [9], with one rather important difference. While Van der Linden [9] considers only a failure of TCC slab due to exceeded tensile strength of the timber, the present method adds another failure criterion regarding ultimate compressive strain in concrete. The following assumptions apply:

• (1) A contact between the timber and the concrete is ideal; connectors provide full-interaction between the two materials and does not allow either horizontal interlayer slip or any differences in vertical deflection of the timber and the concrete parts of the cross-section. Furthermore, the sufficient strength of the connection between timber and concrete at room temperature is assumed to be ascertained.

  Note, that the assumption of a fully rigid connection between timber and concrete parts is in reality achievable for glued connections only. Grooves (notches) with or without steel fastener can also be counted among almost rigid connections, while connections with screws, dowels or nail-plates are among less rigid ones [13].

• (2) Euler–Bernoulli beam theory applies; initially plane cross-sections remain plane at all times, shear deformations are not considered and strain distribution over the cross-section is linear.

• (3) TCC slabs are usually used as a simply supported one way spanning slabs [11]. Accordingly, the present simplified method considers only a rectangular cross-section of a TCC slab loaded with uni-axial bending moment.

• (4) Concrete is modelled with bilinear elastic-plastic stress–strain relationship without hardening in compression and linear elastic stress–strain relationship in tension. Compressive strength of concrete is denoted with $f_\mathrm {c,c}$, while $f_\mathrm {c,t}$ is its tensile strength and $E_\mathrm {c}$ is the elastic modulus of concrete. $\varepsilon _\mathrm {c,0}$ denotes strain at the beginning of plastification and $\varepsilon _\mathrm {c,u}$ is the ultimate compressive strain in the concrete.

• (5) Timber is modelled with linear elastic stress–strain relationship, where $f_\mathrm {t,m}$ and $E_\mathrm {t}$ represent its bending strength and elastic modulus, respectively.

• (6) Steel reinforcement is modelled with bilinear elastic-plastic stress–strain relationship without hardening, which is anti-symmetrical in compression and in tension. Reinforcement strength is denoted as $f_\mathrm {y}$ and elastic modulus of reinforcement is denoted as $E_\mathrm {s}$.

Cross-section of a TCC slab, distributions of strains, $\varepsilon$, and stresses, $\sigma$, in accordance with the above listed assumptions are depicted in Fig. 1. Note, that compressive strains and stresses have negative values. The height of the cross-section, h, is divided into the height of the timber part, $h_\mathrm {t}$, and the height of the concrete part, $h_\mathrm {c}$. The latter is further divided into the compressive plastic zone, $h_\mathrm {c,c,pl}$, compressive elastic zone, $h_\mathrm {c,c,el}$, tensile elastic zone, $h_\mathrm {c,t,el}$, and a zone where tensile strength is exceeded and the concrete has cracked, $h_\mathrm {c,t,cr}$. An initial height of the timber part previous to any fire exposure, $h_\mathrm {t,0}$, and the effective charring depth, $d_\mathrm {eff,j}$, which are introduced in Sect. 2.2, are also depicted in Fig. 1. The width of the timber part of the cross-section, $b_\mathrm {t}$ is equal to the width of the concrete part, $b_\mathrm {c}$. Tensile and compressive steel reinforcements have cross-sectional areas $A_\mathrm {s,t}$ and $A_\mathrm {s,c}$, and are positioned at distances $h_\mathrm {s,t}$ and $h_\mathrm {s,c}$ from the lowest timber fibre, respectively. Strains and stresses with the first index “c” belong to the concrete, and the ones with the first index “t” belong to the timber. Index “1” denotes the uppermost fibre, while index “3” denotes the bottom fibre of the cross-section. Index “2” indicates the point of contact between the timber and the concrete. Furthermore, resultant forces in the tensile and compressive reinforcement, $F_\mathrm {s,t}$ and $F_\mathrm {s,c}$, are schematically depicted on the stress distribution diagram. It can easily be concluded that the corresponding strains, $\varepsilon _\mathrm {s,t}$ and $\varepsilon _\mathrm {s,c}$, do not exceed values of $\varepsilon _\mathrm {c,u}$ in compression and $f_\mathrm {t,m}/E_\mathrm {t}$ in tension. Since those two boundaries are generally smaller than the ultimate strain of the ductile reinforcement, the omitting of any failure criterion regarding reinforcement in the present simplified method is justified.

Fig. 1

Cross-section of a TCC slab with distributions of strains and stresses

A tensile failure criterion, which defines a failure of a TCC slab when the bending strength of the timber is exceeded in its outermost fibre, where the tensile stresses are the greatest [9], can be written as

$$\begin{aligned} \sigma _\mathrm {t,3}\ge f_\mathrm {t,m}. \end{aligned}$$

(1)

Similarly, the assumed failure of the TCC slab in compression occurs, when ultimate compressive strain is exceeded in the uppermost fibre of the concrete part. Thus, the second, compressive failure criterion reads

$$\begin{aligned} \varepsilon _\mathrm {c,1}\le \varepsilon _\mathrm {c,u}. \end{aligned}$$

(2)

In order to determine the moment resistance of the TCC slab, stress at the timber’s outermost fibre $\sigma _\mathrm {t,3}$ is first set to $f_\mathrm {t,m}$ in accordance with the tensile failure criterion, which can also be expressed in terms of strains as $\varepsilon _\mathrm {t,3}=f_\mathrm {t,m}/E_\mathrm {t}$. The distribution of the remaining strains over the cross-section is obtained through an iterative process and must result in the equilibrium of the stresses.

$$\begin{aligned} f(\sigma _\mathrm {t,2,i})=|F_\mathrm {c}|-|F_\mathrm {t}|=0 \end{aligned}$$

(3)

Here, $F_\mathrm {c}$ is a compressive resultant force, which is a sum of resultant forces of stresses from the elastic and the plastic compressive zones of concrete, $F_\mathrm {c,c,el}$ and $F_\mathrm {c,c,pl}$, respectively, and from the compressive reinforcement, $F_\mathrm {s,c}$. Tensile resultant force, $F_\mathrm {t}$, is a sum of resultant forces of stresses from the non-cracked tensile concrete zone, $F_\mathrm {c,t}$, the tensile reinforcement, $F_\mathrm {s,t}$, and the timber, $F_\mathrm {t,t}$.

$$\begin{aligned} F_\mathrm {c}&=F_\mathrm {c,c,pl}+F_\mathrm {c,c,el}+F_\mathrm {s,c} \end{aligned}$$

(4)

$$\begin{aligned} F_\mathrm {t}&=F_\mathrm {c,t}+F_\mathrm {s,t}+F_\mathrm {t,t} \end{aligned}$$

(5)

$\sigma _\mathrm {t,2,i}$ is stress in timber at the contact of the two materials in ith iteration. In the first iteration, $\sigma _\mathrm {t,2,i}$ is chosen as an arbitrary value on the interval $[0,f_\mathrm {t,m})$. The resultant stresses are then calculated and $\sigma _\mathrm {t,2,i+1}$ is determined with the Newton–Raphson method as

$$\begin{aligned} \sigma _\mathrm {t,2,i+1}=\sigma _\mathrm {t,2,i}+\frac{f(\sigma _\mathrm {t,2,i})}{f'(\sigma _\mathrm {t,2,i})}. \end{aligned}$$

(6)

The iterations continue until the resultant forces are in equilibrium, i.e. until Eq. 3 is satisfied with the required accuracy.

This procedure can result in strains in the uppermost fibre of concrete, $\varepsilon _\mathrm {c,1}$, being greater than the ultimate compressive strain $\varepsilon _\mathrm {c,u}$ (in absolute terms). Since the concrete is actually crushed at this level of compressive strains, the resistant moment of TCC slab, calculated with current stress and strain distribution, would be overestimated.

Therefore, if the ultimate compressive strain in the uppermost fibre of the concrete is indeed exceeded, we proceed with the compressive failure criteria. Now, the strain in the concrete’s outermost fibre $\varepsilon _\mathrm {c,1}$ is set to $\varepsilon _\mathrm {c,u}$, while the remaining strains are again iteratively calculated until they result in the equilibrium of stresses. Equations (3–6) apply unchanged. Note, that the resultant forces are functions of $\sigma _\mathrm {t,2,i}$ and that they are different for the two failure criteria. For readers’ convenience, the resultant forces and their derivatives, as used in the Newton–Raphson method, are given in the “Appendix A” for the tensile failure criterion and in the “Appendix B” for the compressive failure criterion.

The check of the two failure criteria can also be executed in the reverse order. In that case, the check of the tensile failure criterion would be needed only if strains $\varepsilon _\mathrm {t,3}$, obtained through the compressive failure criterion, would be greater than $f_\mathrm {t,m}/E_\mathrm {t}$.

Once the appropriate limit strain and stress distributions have been established, the resistant moment, $M_\mathrm {R}$, of the cross-section of the TCC slab can be calculated as the sum of each resultant force times its distance to the neutral axis.

2.2 Modifications of the method due to fire conditions

The main assumption regarding the fire exposure of a TCC slab is, that only the bottom side of a TCC slab is subjected to fire. The exposure is uniform along the horizontal dimensions of the slab, which results in a one-dimensional charring of the timber part. This eliminates the “reduced properties method” as an option for consideration of the effect of high temperatures on the timber [7]. Instead, we employ the “reduced cross-section method” as specified by EN 1995-1-2 [7]. Accordingly, the initial height of the timber part of the TCC cross-section, $h_\mathrm {t,0}$, is reduced due to a completely charred layer and an additional ineffective, zero-strength layer of material. The remaining timber part, with its height being $h_\mathrm {t}$, has the same material properties as at normal temperatures.

The charring rate depends on the type of the structural timber and on the environmental temperature development during the fire. This paper focuses on a TCC slab with the timber part made of the LVL and with the environmental temperatures following the standard fire curve ISO 834 [14]. However, the method can be easily adapted for solid and glulam timber through the calculation of the depth of the zero-strength layer with the use of appropriate coefficients according to EN 1995-1-2 [7]. The adaptation of the method for the use with different fire curve would require knowledge on the development of the depth of the zero-strength layer with time for the considered fire curve.

The LVL timber part of a one way spanning TCC slab can be assembled from one or several equally oriented LVL plates. Here we assume, that an entire LVL plate fall off when it is completely charred, with none of the individual laminations falling off earlier. This way, the lower LVL plate(s) act as a temporary fire protection for the upper LVL plate(s).

The reduced height of the timber part of the TCC cross-section can be determined as

$$\begin{aligned} h_\mathrm {t}=h_\mathrm {t,0}-d_\mathrm {eff,j}, \end{aligned}$$

(7)

where $d_\mathrm {eff,j}$ is the effective charring depth, i.e. the depth of the charred and zero-strength layer together. Index “j” refers to the currently exposed LVL plate. The effective charring depth of initially the lowest plate, $d_\mathrm {eff,j=1}$ is easily determined as

$$\begin{aligned} d_\mathrm {eff,j=1}=\beta _\mathrm {0}t+k_\mathrm {0}d_\mathrm {0}. \end{aligned}$$

(8)

Due to the one-dimensional charring of the timber part, the one-dimensional charring rate, $\beta _\mathrm {0}$, is used in Eq. (8) with value of 0.65 mm/min for the LVL timber with density greater or equal to 480 kg/m$^{3}$ [7]. t is time of exposure to the standard fire in minutes, $d_\mathrm {0}$ with value of 7 mm is the depth of the fully developed zero-strength layer, while the coefficient $k_\mathrm {0}$ varies linearly from 0 to 1 in the first 20 min of the fire exposure and is constant afterwards [7]. The effective charring depth of the remaining, initially protected LVL plates, $d_\mathrm {eff,j>1}$, is

$$\begin{aligned} d_\mathrm {eff,j>1}=\left\{ \begin{array}{ll} \sum \limits _{i=1}^{j-1}h_\mathrm {t,0,i}+k_\mathrm {3}\beta _\mathrm {0}(t-t_\mathrm {f,j-1})+d_\mathrm {0}, & \ \ t<t_\mathrm {a} \\ \\ \sum \limits _{i=1}^{j-1}h_\mathrm {t,0,i}+k_\mathrm {3}\beta _\mathrm {0}(t_\mathrm {a}-t_\mathrm {f,j-1})+ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\beta _\mathrm {0}(t-t_\mathrm {a})+d_\mathrm {0}, & \ \ t>t_\mathrm {a}. \end{array}\right. \end{aligned}$$

(9)

$h_\mathrm {t,0,i}$ denotes the initial height of the already-charred-away LVL plates. Coefficient $k_\mathrm {3}$ with value 2 enables increased charring rate on the time interval between the time, when the previous LVL plate has fallen off, $t_\mathrm {f,j-1}$ and the time when the charred layer of the currently exposed LVL plate provides some thermal insulation, $t_\mathrm {a}$. The standard EN 1995-1-2 [7] provides equation for time $t_\mathrm {a}$, however, we introduce a simplification and assume, that t is always smaller than $t_\mathrm {a}$ (as in the first option in Eq. 9) and therefore the increased charring rate apply to the entire depth of the initially protected plate, due to the fact that the LVL plates in the TCC cross-sections are usually rather thin. Also, the depth of the zero-strength layer is herein assumed to be fully developed immediately after the loss of protection. These two minor deviations from the EN 1995-1-2 [7] specifications result in increased effective charring depth, which is therefore on the safe side. A reader might also be interested in a recent discussion on the depth of the zero-strength layer by Schmid et al. [15], where the EN 1995-1-2 specifications were characterized as non-conservative and in need of a revision.

In the present simplified method for calculation of the moment resistance of TCC slab in fire, the reduced height of the timber part from Eq. (7), $h_\mathrm {t}$, means also equally reduced height of the entire TCC cross-section, h, and the distances of the steel reinforcements from the bottom of the cross-section, $h_\mathrm {s,t}$ and $h_\mathrm {s,c}$.

The effects of elevated temperatures on the concrete are considered in accordance with the “500 $^{\circ }$C isotherm method” [8], where areas of the concrete part of the cross-section with temperatures above 500 $^{\circ }$C are considered as zero-strength areas and the ones with temperatures below 500 $^{\circ }$C have the material properties as at normal temperatures. In case of a TCC slab, the entire width of the concrete part is protected from a direct exposure to fire with the timber. Therefore, until the timber part is fully charred away, the temperature in the concrete clearly does not exceed the charring temperature, which is approximately 300 $^{\circ }$C [7]. When the entire timber part is charred away, however, the slab is no longer a composite of the two materials and the resistant moment of the cross-section can no longer be determined with the present method. Consequently, in the simplified method for calculation of the moment resistance of TCC slab in fire the material properties of the concrete are used with the same values as at normal temperatures. Regardless of the unchanged material properties of the concrete, the heights of the various zones in the concrete ($h_\mathrm {c,c,el}$, $h_\mathrm {c,c,pl}$, $h_\mathrm {c,t,el}$ and $h_\mathrm {c,t,cr}$) are adjusted at each time in order to satisfy the equilibrium of stresses, due to the modified height of the timber part.

The standard EN 1992-1-2 [8] prescribes a reduction of strength of the reinforcement only for temperatures higher than 350 $^{\circ }$C. Accordingly, the unreduced material properties of the reinforcement are used within the present simplified method.

The contact between the timber and the concrete is, concerning the determination of the resistant moment of a TCC cross-section in fire, assumed ideal regardless of the progress of charring and of the elevated temperatures. The assumption is based on the experimental research of TCC beams with screwed connections by Frangi et al. [2], which has shown, that the reduction of strength and slip modulus of the connections can be expressed through the remaining side cover of the connections. The side cover of the connections in TCC slab does not change during the fire, since only the bottom surface of the slab is exposed. Therefore, constant strength and slip modulus of the connections throughout the fire duration were assumed in the present method. Accordingly, the strength of the connection at room temperature should be verified previous to fire analysis. However, further experimental research is needed for validation of such assumption for various types of connections.

3 Vertical displacement

A proper estimation of an effective bending stiffness of the TCC cross-section is essential in calculation of a vertical displacement of the TCC slab either at normal or at elevated temperatures. Van der Linden [9] recommends a rough estimate of an effective bending stiffness, herein denoted as $EI_\mathrm {eff}^{*}$, which originates in the Euler–Bernoulli beam theory [16]

$$\begin{aligned} EI_\mathrm {eff}^{*}=\dfrac{M_\mathrm {R}}{\kappa }, \end{aligned}$$

(10)

with curvature, $\kappa$, determined from strains as

$$\begin{aligned} \kappa =\dfrac{\varepsilon _\mathrm {t,m} -\varepsilon _\mathrm {t,2}}{h_\mathrm {t}}. \end{aligned}$$

(11)

In case of fire exposure, both $M_\mathrm {R}$ and $\kappa$ are time dependent, and, consequently, so is $EI_\mathrm {eff}^{*}$.

Although the present simplified method assumes that initially plane cross-sections remain plane after loading, which is also one of the basic assumptions of the Euler–Bernoulli beam theory, the latter considers homogeneous, isotropic and linear elastic material. Since the composite cross-section of the TCC slab is, by definition, inhomogeneous and consists also of elastic-plastic materials, the effective bending stiffness $EI_\mathrm {eff}^{*}$ might prove to be inadequate.

Therefore we determine effective bending stiffness of the TCC slab, $EI_\mathrm {eff}$, similar as it is defined for mechanically jointed timber beams in the Annex B of EN 1995-1-1 [10], which represents one of the formulations of the $\gamma$-method [5].

$$\begin{aligned} EI_\mathrm {eff}=E_\mathrm {t}I_\mathrm {t}+E_\mathrm {c}I_\mathrm {c,*}+\gamma E_\mathrm {t}A_\mathrm {t}a_\mathrm {t}^2+\gamma E_\mathrm {c}A_\mathrm {c,*} a_\mathrm {c,*}^2. \end{aligned}$$

(12)

The influence of the reinforcement on the bending stiffness is neglected. We also assume that the cracked tensile zone of the concrete does not contribute to the bending stiffness of the TCC cross-section. Hence, $I_\mathrm {c,*}$ and $A_\mathrm {c,*}$ are the moment of inertia and the area of the concrete part of the TCC cross-section without the cracked tensile zone. Likewise, $I_\mathrm {t}$ and $A_\mathrm {t}$ are the moment of inertia and the area of the currently effective timber part of the TCC cross-section. Distances between the centre of gravity of the TCC cross-section to the centres of gravity of each part—$a_\mathrm {c,*}$ for the concrete and $a_\mathrm {t}$ for the timber part—are also determined with neglected cracked tensile zone of concrete. The height of the cracked zone of the concrete $h_\mathrm {c,t,cr}$ and the height of the timber part $h_\mathrm {t}$, determined from the equilibrium of stresses in limit state in Sect. 2, change during the fire exposure, which results in time dependent $EI_\mathrm {eff}=EI_\mathrm {eff}(t)$.

Coefficient $\gamma$ in Eq. (12) represents the influence of the rigidity of the concrete-timber connection. It depends on the type of the connection, more specifically on its highly variable slip modulus and spacing between the connectors, which makes it difficult to determine $\gamma$ for a general use [17]. The ideal contact, assumed during the calculation of the moment resistance in Sect. 2, implies totally rigid connection with $\gamma =1$, which is hereinafter denoted as $\gamma _1$. However, it has been experimentally proven that the rigidity of the connection decreases during fire exposure due to the increased temperatures and the loss of timber cover [2]. Furthermore, the horizontal slip between timber and concrete was reported to gradually increase during exposure of TCC slab to elevated temperatures, although the temperatures at the interface remained low [11]. In order to take into account the influence of exposure to fire, we propose another $\gamma$ in form of a quadratic function of the remaining timber height and denote it as $\gamma _2(t)$.

$$\begin{aligned} \gamma _\mathrm {2}(t)=1-\bigg (1 -\dfrac{h_\mathrm {t}(t)}{h_\mathrm {t,0}}\bigg )^2. \end{aligned}$$

(13)

Note, that this formulation of $\gamma _2(t)$ was chosen empirically with regard to test results of validation case 1, and was later-on used in unchanged form with validation case 2 (where, as it is shown in Sect. 4.2, the calculated and experimental results matched even better).

Once a time-history of the effective bending stiffness of the TCC cross-section during fire exposure is known, a development of the mid-span deflection of the TCC slab can be approximated through analytical equations for the deflection of a simply supported beam with length L under various loading conditions [16]. For example, a mid-span deflection due to a uniformly distributed load q reads

$$\begin{aligned} w_\mathrm {fi}(t)=\dfrac{5qL^4}{384EI_\mathrm {eff}(t)}. \end{aligned}$$

(14)

An ultimate load $q_\mathrm {lim}$ can be calculated at each time from previously determined $M_\mathrm {R}(t)$ in accordance with considered loading conditions. Therefore, a uniformly distributed ultimate load would be determined as

$$\begin{aligned} q_\mathrm {lim}(t)=\dfrac{8M_\mathrm {R}(t)}{L^2}. \end{aligned}$$

(15)

When the actual load on the TCC slab q equals $q_\mathrm {lim}(t)$, the resistant moment $M_\mathrm {R}(t)$ is reached and thus the TCC cross-section fails. A mid-span deflection of the slab due to $q_\mathrm {lim}(t)$ is denoted as $w_\mathrm {R,fi}(t)$.

4 Validation

4.1 Validation case 1

The present simplified method for calculation of the fire resistance of a TCC slab is hereinafter validated against the results of two full size fire tests described in the literature. The first fire test was conducted at the Institute of Structural Engineering of ETH Zurich and is described in their test report [11, 18, 19]. The loading of the slab during the test was constant and the temperature in the furnace followed the standard ISO 834 fire curve.

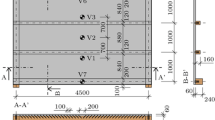
The tested TCC slab was made of two beech LVL plates, each with height of 4 cm, and 12 cm thick concrete plate. Grooves were used to ensure timber-concrete connection. Steel reinforcement consisted of two layers of shrinkage reinforcement, each with area of cross-section 1.7 cm$^2$/m. The clear length of the tested slab was 4.84 m, which is the span of the slab used in the calculation with the present method. The slab was, in addition to its self weight, $g=3.336$ kN/m, loaded with two equal concentrated forces, $P=16.761$ kN, positioned at 1.565 m from the supports [19]. We assessed the self-weight of the slab based on the given densities of the used materials; the density of the concrete was 2350 kg/m$^3$ [19] and the density of the beech LVL was 730 kg/m$^3$ [20]. After that, the concentrated loads have been calculated from the maximum applied bending moment in the fire test, which was 36 kNm/m [11]. The geometry and the loading of the TCC slab in validation case 1, as used in the calculation with the present simplified method, are depicted in Fig. 2.

Fig. 2

Validation case 1: the geometry and the loading of the TCC slab

Material properties of the C50/60 concrete are taken as determined in [11] with small scale tests. Compressive strength of the concrete $f_\mathrm {c,c}$ is 6.49 kN/cm$^2$ and its elastic modulus $E_\mathrm {c}$ is 3579 kN/cm$^2$. Tensile strength of the concrete $f_\mathrm {c,t}$, which is not given in [11], is considered with value 0.41 kN/cm$^2$ in accordance with [21], and so is the ultimate compressive strain $\varepsilon _\mathrm {c,u}=$ –3.5 ‰. The properties of beech LVL are taken from [20], where the same TCC slabs were considered at normal temperatures. The bending strength of the beech LVL $f_\mathrm {t,m}$ is 7.79 kN/cm$^2$ and its elastic modulus $E_\mathrm {t}$ is 1380 kN/cm$^2$. The shrinkage reinforcement is of B500B quality, with yield strength $f_\mathrm {y}=$ 50 kN/cm$^2$ and elastic modulus $E_\mathrm {s}=$ 20,000 kN/cm$^2$. The effective bending stiffness is considered according to Eq. 12, with rigidity of the concrete-timber connection being taken as $\gamma _2$, and is hereinafter denoted as $EI_\mathrm {eff,\gamma _{2}}$.

Klippel et al. [11] report that the first of the two LVL plates fell off after 50 to 60 min of fire exposure. The falling off of the first plate as assumed in the present method, with the one-dimensional charring rate for the LVL timber according to the EN 1995-1-2 [7], $\beta _0=$ 0.65 mm/min, would occur at 61.5 min, which correspond relatively good with the test report. The test [11] was stopped at 68 min due to rapid increase of mid-span deflection and the measured average charring rate of both LVL plates was 0.85 mm/min. According to the standard [7], the charring rate of the second, protected LVL plate in the simplified method should be 1.3 mm/min, which would result in the average charring rate 0.71 mm/min. In order to model experimental fire conditions in our calculations as accurately as possible, the coefficient $k_3$ in Eq. (9) was increased from 2 to 4.219, which resulted in the charring rate of the second LVL plate being 2.74 mm/min and the average charring rate of both LVL plates being the same as in the test.

Figure 3 shows development of mid-span deflections of the TCC slab during standard fire exposure from the experiment [11], $w_\mathrm {test}(t)$, and the ones calculated with the present simplified method, $w_\mathrm {fi}(t)$. The development of the mid-span displacement as it would be if the slab has been loaded with time dependent resistant moment $M_\mathrm {R}(t)$, $w_\mathrm {R,fi}(t)$, is also depicted. According to the simplified method the failure occurs when internal moment due to actual loading conditions equals $M_\mathrm {R}$, i.e. when $w_\mathrm {fi}$ equals $w_\mathrm {R,fi}$. For the slabs with very low percentage of reinforcement in the concrete part of the cross-section, which is often the case with TCC slabs, the failure can also occur when the timber part is completely charred. In the present case the internal moment at the mid-span cross-section is at all times lower then its resistant moment and therefore $w_\mathrm {fi}$ is smaller then $w_\mathrm {R,fi}$. Instead, the calculation stops at 71 min due to the completely charred timber part of the cross-section. The failure of the TCC slab can be assumed from rapid increase of $w_\mathrm {fi}$.

Fig. 3

Validation case 1: time history of the mid-span deflection of the TCC slab

Failure times of the slab determined with test and with simplified method are in fine agreement; the latter being overestimated for only 3 min. As already mentioned, the test was stopped because of a fast increase of displacements. The measured deflection at that time, $w_\mathrm {test}$(68 min), was 8.6 cm. The displacement determined with the simplified method at the same time, $w_\mathrm {fi}$(68 min), is 10 cm and has a higher increase rate. On the other hand, up to 67 min of fire exposure, the calculated deflections are lower then the experimentally determined ones. Possible reasons for the differences are the assumed charring rates, being slightly too small for the first LVL plate and consequently too high for the second one (as previously discussed), and also the assumed effective bending stiffness $EI_\mathrm {eff,\gamma _{2}}(t)$. However, the initial effective bending stiffness, $EI_\mathrm {eff,\gamma _{2}}$(0 min), appears to be estimated well, since the difference between $w_\mathrm {fi}$(0 min) and $w_\mathrm {test}$(0 min) is less than 0.5 mm.

A study of influence of different effective bending stiffnesses on the mid-span deflection of the TCC slab is presented in Fig. 4. The effective bending stiffness according to Euler–Bernoulli beam theory, $EI_\mathrm {eff}^{*}$, is clearly too small as it leads to a notable overestimation of the initial deflection. The effective bending stiffness according to Eq. 12 with fully rigid concrete-timber connection, $EI_\mathrm {eff,\gamma _{1}}$, naturally results in even smaller deflections than $EI_\mathrm {eff,\gamma _{2}}$. The differences become more prominent towards the end of the analysis with the increase of the charring rate.

Fig. 4

Validation case 1: time history of the effective bending stiffnesses and corresponding mid-span deflections of the TCC slab

For the effective bending stiffness $EI_\mathrm {eff,\gamma _{2}}$, which proves to be the most accurate for the present case, the strain and stress distributions over the mid-span cross section at the resistant moment $M_\mathrm {R}(t)$ are analysed. As can be seen from Fig. 5, the strains in the uppermost fibre of the cross-section, $\varepsilon _\mathrm {c,1}$, at $t=0$ min equal $\varepsilon _\mathrm {c,u}=$ –3.5 ‰, while at the same time the strains in the lowermost fibre, $\varepsilon _\mathrm {t,3}$, are smaller than $f_\mathrm {t,m}/E_\mathrm {t}=5.6$ ‰. This implies, that the governing failure mode at normal temperatures and at the beginning of fire exposure is the compressive failure of the concrete. At 29 min and after, however, the situation is overturned and $\varepsilon _\mathrm {t,3}$ equals 5.6 ‰, while $\varepsilon _\mathrm {c,1}$ is smaller than $\varepsilon _\mathrm {c,u}$ (in absolute terms), which means that the governing failure mode is the tensile failure of the LVL timber. Figure 5 also clearly shows an increase of the height of the cracked tensile zone of concrete, where the stresses equal zero, as well as a decrease of the height of the compressive plastic zone of concrete and of the effective timber height with time. As expected, the height of the tensile elastic zone of the concrete is very small at all times.

Fig. 5

Validation case 1: stress and strain distributions over the TCC cross-section at the mid-span of the slab at 0, 30 and 60 min of standard fire exposure

The development of resultant forces of the concrete and timber zones during standard fire exposure is shown in Fig. 6. The main contributions are from the elastic and plastic compressive concrete zones, $F_\mathrm {c,c,el}$ and $F_\mathrm {c,c,pl}$ and from the timber part $F_\mathrm {t,t}$. The resultant forces in either compressive or tensile reinforcement are small due to its small area of cross-section. The resultant force of the tensile elastic concrete zone is also negligible.

Fig. 6

Validation case 1: time history of the resultant forces in the cross-section at the mid-span of the TCC slab

4.2 Validation case 2

The second validation case is based on an experiment described in Dagenais et al. [12]. Here, the cross-section of the TCC slab consists of 13.3 cm high LVL timber plate and 8.9 cm high concrete plate. Concrete and timber part are connected with perpendicularly positioned lag screws. The laminations of the LVL timber are oriented in vertical direction, as shown in Fig. 7. Due to the orientation of the laminations, we consider entire timber part of the cross-section as one LVL plate. There were also some shrinkage reinforcement in the tested TCC slab, which we neglect in our calculations because of its unknown quality and quantity, as well as because of its negligible influence on the bending resistance of the TCC slab, as proven in the first validation case.

Fig. 7

Validation case 2: the geometry and the loading of the TCC slab

The model of the TCC slab is simply supported beam with length 4.8 m, loaded with uniformly distributed self-weight $g=10.02$ kN/m and imposed load $q=7.80$ kN/m. The densities of the materials are not given in the literature, thus the self-weight has been calculated for the density of the LVL being 730 kg/m$^3$ and for the density of the concrete being 2500 kg/m$^3$. Bending strength of the LVL, $f_\mathrm {t,m}=3.76$ kN/cm$^2$, its elastic modulus, $E_\mathrm {t}=1379$ kN/cm$^2$, compressive strength of concrete, $f_\mathrm {c,c}=3.59$ kN/cm$^2$, and elastic modulus of concrete, $E_\mathrm {c}=2694$ kN/cm$^2$, are taken as in [12] for their numerical model. The assumed tensile strength of concrete, $f_\mathrm {c,t}=0.29$ kN/cm$^2$, belongs to the strength class C30/37 [21]. The effective bending stiffness $EI_\mathrm {eff,\gamma _2}(t)$ is assumed.

The tested TCC slab was exposed to temperatures following the CAN/ULC-S101 fire curve [22], which is very similar to the ISO 834 fire curve [14]. The failure of the slab has been determined at 191 min with mid-span deflection being 13.7 cm because of the rapid increase of deflections. However, the test itself was stopped a few minutes later, at 197 min. The final mid-span deflection was 34.6 cm.

Due to the similar fire curves, the one-dimensional charring rate could be used according to EN 1995-1-2 [7], with value 0.65 mm/min. The charring rate, determined from the measured movement of isotherm 300 $^{\circ }$C, is 0.55 mm/min [23] and the charring rate of the used LVL timber as specified by the manufacturer is 0.59 mm/min [23]. In the fire analysis of the TCC slab with the present simplified method, we assume the charring rate $\beta _0$ with the intermediate of the three possible values listed above, i.e. $\beta _0=0.59$ mm/min.

The initial deflection of the tested slab was 1.5 mm [23] and the one obtained with the simplified method is 2 mm. Significant agreement of the measured and calculated mid-span deflections during the entire fire exposure, $w_\mathrm {test}(t)$ and $w_\mathrm {fi}(t)$, can be observed in Fig. 8. According to the present method, the fire resistance of the TCC slab is reached, when $w_\mathrm {fi}(t)$ equals $w_\mathrm {R,fi}(t)$, which occurs at 199 min, with mid-span deflection 29.1 cm. The governing failure mode is the tensile failure of the LVL timber. In fact, the tensile failure criterion would prevail during the entire fire exposure, since the resistant moment $M_\mathrm {R}(t)$ of this slab is always determined for $\varepsilon _\mathrm {c,u}$ smaller than $-3.5$ ‰ and $\varepsilon _\mathrm {t,3}=f_\mathrm {t,m}/E_\mathrm {t}=2.7$ ‰.

Fig. 8

Validation case 2: time history of the mid-span deflection of the TCC slab

5 Conclusions

A novel simplified method for calculation of resistance of a TCC slab in fire conditions was presented. Within the method two failure criteria are checked, namely the tensile failure criterion in the outermost timber fibre and the compressive failure criterion in the outermost concrete fibre. The influence of the elevated temperatures during fire is applied through the one-dimensional charring of the timber part of the cross-section and in accordance with widely accepted ways of reduction of properties of materials. The concrete-timber connection is considered perfect during the determination of resistant moment of the TCC cross-section, while during the calculation of the deflection of the TCC slab the reduction of the connection’s rigidity is taken into account. Furthermore, the cracked part of the concrete and the ineffective zone of the timber do not contribute to the effective stiffness of the TCC slab.

The method is applicable to one way spanning TCC slabs, therefore the fire resistance of the composite slab after the entire timber part has charred-away can not be determined through this method. Since it is usually the main purpose of the timber part to ensure tensile strength of the TCC slab, the concrete is often only sparsely reinforced with steel. Hence, the totally charred timber part in most cases also leads to a structural failure of the slab. In case of sufficient reinforcement in the concrete part, however, the analysis could be carried on as specified e.g. in [8] for reinforced concrete cross-sections.

Two full sized tests of TCC slabs exposed to standard fires [11, 12] were analysed with the present simplified method. The mid-span deflections and the failure times determined with the simplified method and experimentally are in considerable agreement in both validation cases. The study of differently defined effective stiffnesses of the TCC cross-section showed, that the reduction of the connection’s rigidity as well as the exclusion of ineffective parts of concrete and timber are necessary for adequate calculation of deflections. Note, that the applied reduction of the rigidity of the connection in these cases is an estimation only and that the proper knowledge on the connection’s properties would lead to even more accurate results. The analysis of the first validation case also showed, that the charring rate taken according to standards does not necessary represent the actual charring rate, which can result in either under- or over-estimation of the fire resistance of the TCC slab.

Among the two of the failure criteria considered in the present simplified method, the tensile failure criterion appears to prevail most of the time, at least in the analysed validation cases. However, the governing failure criterion cannot be predicted without analysis, since it depends on the configuration of TCC slab, which changes during fire duration. The order of checking of tensile and compressive failure criteria is irrelevant for the result of the calculation. Nevertheless, in order to optimize calculation time, it could be recommended to check the failure criteria in the same order as presented in Section 2.1, i.e. first the tensile failure criterion and then the compressive failure criteria only if it is applicable.

Although the method is currently limited to the use with one way spanning TCC slabs, it has a potential for being upgraded for the use with two way spanning TCC slab with timber part made of CLT. This, together with the uncomplicated calculation procedure and successful validation presented in the paper, indicates that the present simplified method could become a useful tool in fire design of TCC structures.

Appendices

Appendix A

Resultant forces as a function of stress in the uppermost fibre of timber, $\sigma _\mathrm {t,2,i}$, and their derivatives at the limit state of the cross-section according to the tensile failure criterion:

$$\begin{aligned}&F_\mathrm {c,c,pl}(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} 0, &{} \ \ \varepsilon _\mathrm {c,1}(\sigma _\mathrm {t,2,i})>\dfrac{f_\mathrm {c,c}}{E_\mathrm {c}} \\ f_\mathrm {c,c}b_\mathrm {c}h_\mathrm {c,c,pl}(\sigma _\mathrm {t,2,i}), &{} \ \ \varepsilon _\mathrm {c,1}(\sigma _\mathrm {t,2,i})\le \dfrac{f_\mathrm {c,c}}{E_\mathrm {c}}, \end{array}\right. \end{aligned}$$

(16)

$$\begin{aligned}&F_\mathrm {c,c,el}(\sigma _\mathrm {t,2,i}) =\left\{ \begin{array}{ll} \dfrac{1}{2}E_\mathrm {c}\varepsilon _\mathrm {c,1}(\sigma _\mathrm {t,2,i})b_\mathrm {c}h_\mathrm {c,c,el}(\sigma _\mathrm {t,2,i}),&{} \ \ \varepsilon _\mathrm {c,1}(\sigma _\mathrm {t,2,i})>\dfrac{f_\mathrm {c,c}}{E_\mathrm {c}} \\ \dfrac{1}{2}f_\mathrm {c,c}b_\mathrm {c}h_\mathrm {c,c,el}(\sigma _\mathrm {t,2,i}),&{} \ \ \varepsilon _\mathrm {c,1}(\sigma _\mathrm {t,2,i})\le \dfrac{f_\mathrm {c,c}}{E_\mathrm {c}}, \end{array}\right. \end{aligned}$$

(17)

$$\begin{aligned}&F_\mathrm {s,c}(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} f_\mathrm {s,c}A_\mathrm {s,c}, &{} \ \ |\varepsilon _\mathrm {s,c}(\sigma _\mathrm {t,2,i})|>\dfrac{|f_\mathrm {s,c}|}{E_\mathrm {s}} \\ E_\mathrm {s}\varepsilon _\mathrm {s,c}(\sigma _\mathrm {t,2,i})A_\mathrm {s,c}, &{} \ \ |\varepsilon _\mathrm {s,c}(\sigma _\mathrm {t,2,i})|\le \dfrac{|f_\mathrm {s,c}|}{E_\mathrm {s}}, \end{array}\right. \end{aligned}$$

(18)

$$\begin{aligned}&F_\mathrm {c,t}(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} \dfrac{1}{2}E_\mathrm {c}\bigg (\dfrac{\varepsilon _\mathrm {t,m}-\varepsilon _\mathrm {t,2}(\sigma _\mathrm {t,2,i})}{h_\mathrm {t}}h_\mathrm {c}+\varepsilon _\mathrm {c,1}(\sigma _\mathrm {t,2,i})\bigg )b_\mathrm {c}h_\mathrm {c,t}(\sigma _\mathrm {t,2,i}), \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \varepsilon _\mathrm {c,2}(\sigma _\mathrm {t,2,i})<\dfrac{f_\mathrm {c,t}}{E_\mathrm {c}} \\ \\ \dfrac{1}{2}f_\mathrm {c,t}b_\mathrm {c}h_\mathrm {c,t,el}(\sigma _\mathrm {t,2,i}), \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \varepsilon _\mathrm {c,2}(\sigma _\mathrm {t,2,i})\ge \dfrac{f_\mathrm {c,t}}{E_\mathrm {c}}, \end{array}\right. \end{aligned}$$

(19)

$$\begin{aligned}&F_\mathrm {s,t}(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} f_\mathrm {s,t}A_\mathrm {s,t}, &{} \ \ \varepsilon _\mathrm {s,t}(\sigma _\mathrm {t,2,i})>\dfrac{f_\mathrm {s,t}}{E_\mathrm {s}} \\ E_\mathrm {s}\varepsilon _\mathrm {s,t}(\sigma _\mathrm {t,2,i})A_\mathrm {s,t}, &{} \ \ \varepsilon _\mathrm {s,t}(\sigma _\mathrm {t,2,i})\le \dfrac{f_\mathrm {s,t}}{E_\mathrm {s}}, \end{array}\right. \end{aligned}$$

(20)

$$\begin{aligned}&F_\mathrm {t,t}(\sigma _\mathrm {t,2,i}) =(\sigma _\mathrm {t,2,i}+\dfrac{1}{2} (f_\mathrm {t,m}-\sigma _\mathrm {t,2,i}))b_\mathrm {t}h_\mathrm {t}, \end{aligned}$$

(21)

$$\begin{aligned}&F_\mathrm {c,c,pl}'(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} 0, &{} \ \ \varepsilon _\mathrm {c,1}(\sigma _\mathrm {t,2,i})>\dfrac{f_\mathrm {c,c}}{E_\mathrm {c}} \\ \dfrac{f_\mathrm {c,c}b_\mathrm {c}h_\mathrm {t}(E_\mathrm {t}f_\mathrm {c,c}-E_\mathrm {c}f_\mathrm {t,m})}{E_\mathrm {c}(f_\mathrm {t,m}-\sigma _\mathrm {t,2,i})^2}, &{} \ \ \varepsilon _\mathrm {c,1}(\sigma _\mathrm {t,2,i})\le \dfrac{f_\mathrm {c,c}}{E_\mathrm {c}}, \end{array}\right. \end{aligned}$$

(22)

$$\begin{aligned}&F_\mathrm {c,c,el}'(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} \dfrac{E_\mathrm {c}b_\mathrm {c}h^2}{2E_\mathrm {t}h_\mathrm {t}}-\dfrac{f_\mathrm {t,m}^2b_\mathrm {c}h_\mathrm {t}E_\mathrm {c}}{2E_\mathrm {t}(f_\mathrm {t,m}-\sigma _\mathrm {t,2,i})^2} ,&{} \ \ \varepsilon _\mathrm {c,1}(\sigma _\mathrm {t,2,i})>\dfrac{f_\mathrm {c,c}}{E_\mathrm {c}} \\ -\dfrac{f_\mathrm {c,c}^2b_\mathrm {c}h_\mathrm {t}E_\mathrm {t}}{2E_\mathrm {c}(f_\mathrm {t,m}-\sigma _\mathrm {t,2,i})^2},&{} \ \ \varepsilon _\mathrm {c,1}(\sigma _\mathrm {t,2,i})\le \dfrac{f_\mathrm {c,c}}{E_\mathrm {c}}, \end{array}\right. \end{aligned}$$

(23)

$$\begin{aligned}&F_\mathrm {s,c}'(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} 0, &{} \ \ |\varepsilon _\mathrm {s,c}(\sigma _\mathrm {t,2,i})|>\dfrac{|f_\mathrm {s,c}|}{E_\mathrm {s}} \\ E_\mathrm {s}A_\mathrm {s,c}\dfrac{h_\mathrm {s,c}}{h_\mathrm {t}E_\mathrm {t}}, &{} \ \ |\varepsilon _\mathrm {s,c}(\sigma _\mathrm {t,2,i})|\le \dfrac{|f_\mathrm {s,c}|}{E_\mathrm {s}}, \end{array}\right. \end{aligned}$$

(24)

$$\begin{aligned}&F_\mathrm {c,t}'(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} \dfrac{f_\mathrm {t,m}^2b_\mathrm {c}h_\mathrm {t}E_\mathrm {c}}{2E_\mathrm {t}(f_\mathrm {t,m}-\sigma _\mathrm {t,2,i})^2}- \dfrac{E_\mathrm {c}b_\mathrm {c}(f_\mathrm {t,m}h-f_\mathrm {t,m}h_\mathrm {c}-h\sigma _\mathrm {t,2,i}+h_\mathrm {c}\sigma _\mathrm {t,2,i})^2}{2E_\mathrm {t}h_\mathrm {t}(f_\mathrm {t,m}-\sigma _\mathrm {t,2,i})^2}, \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \varepsilon _\mathrm {c,2}(\sigma _\mathrm {t,2,i})<\dfrac{f_\mathrm {c,t}}{E_\mathrm {c}} \\ \\\dfrac{f_\mathrm {c,t}^2b_\mathrm {c}h_\mathrm {t}E_\mathrm {t}}{2E_\mathrm {c}(f_\mathrm {t,m}-\sigma _\mathrm {t,2,i})^2}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \varepsilon _\mathrm {c,2}(\sigma _\mathrm {t,2,i})\ge \dfrac{f_\mathrm {c,t}}{E_\mathrm {c}}, \end{array}\right. \end{aligned}$$

(25)

$$\begin{aligned}&F_\mathrm {s,t}'(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} 0, &{} \ \ \varepsilon _\mathrm {s,t}(\sigma _\mathrm {t,2,i})>\dfrac{f_\mathrm {s,t}}{E_\mathrm {s}} \\ E_\mathrm {s}A_\mathrm {s,t}\dfrac{h_\mathrm {s,t}}{h_\mathrm {t}E_\mathrm {t}}, &{} \ \ \varepsilon _\mathrm {s,t}(\sigma _\mathrm {t,2,i})\le \dfrac{f_\mathrm {s,t}}{E_\mathrm {s}}, \end{array}\right. \end{aligned}$$

(26)

$$\begin{aligned}&F_\mathrm {t,t}'(\sigma _\mathrm {t,2,i})= \dfrac{1}{2}b_\mathrm {t}h_\mathrm {t}. \end{aligned}$$

(27)

Heights of specific zones and strains as functions of $\sigma _\mathrm {t,2,i}$, which are present in Eqs. (16–27), can easily be determined on the basis of assumptions of the method, graphically presented in Fig. 1.

Appendix B

Resultant forces as a function of stress in the uppermost fibre of timber, $\sigma _\mathrm {t,2,i}$, and their derivatives at the limit state of the cross-section according to the compressive failure criterion:

$$\begin{aligned}&F_\mathrm {c,c,pl}(\sigma _\mathrm {t,2,i})= f_\mathrm {c,c}b_\mathrm {c}h_\mathrm {c,c,pl}(\sigma _\mathrm {t,2,i}), \end{aligned}$$

(28)

$$\begin{aligned}&F_\mathrm {c,c,el}(\sigma _\mathrm {t,2,i})= \dfrac{1}{2}f_\mathrm {c,c}b_\mathrm {c} h_\mathrm {c,c,el}(\sigma _\mathrm {t,2,i}), \end{aligned}$$

(29)

$$\begin{aligned}&F_\mathrm {s,c}(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} f_\mathrm {s,c}A_\mathrm {s,c}, &{} \ \ |\varepsilon _\mathrm {s,c}(\sigma _\mathrm {t,2,i})|>\dfrac{|f_\mathrm {s,c}|}{E_\mathrm {s}} \\ E_\mathrm {s}\varepsilon _\mathrm {s,c}(\sigma _\mathrm {t,2,i})A_\mathrm {s,c}, &{} \ \ |\varepsilon _\mathrm {s,c}(\sigma _\mathrm {t,2,i})|\le \dfrac{|f_\mathrm {s,c}|}{E_\mathrm {s}}, \end{array}\right. \end{aligned}$$

(30)

$$\begin{aligned}&F_\mathrm {c,t}(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} \dfrac{1}{2}E_\mathrm {c}\bigg (\dfrac{\varepsilon _\mathrm {t,m}-\varepsilon _\mathrm {t,2}(\sigma _\mathrm {t,2,i})}{h_\mathrm {t}}h_\mathrm {c}+\varepsilon _\mathrm {c,1}(\sigma _\mathrm {t,2,i})\bigg ) b_\mathrm {c}h_\mathrm {c,t}(\sigma _\mathrm {t,2,i}), \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \varepsilon _\mathrm {c,2}(\sigma _\mathrm {t,2,i})<\dfrac{f_\mathrm {c,t}}{E_\mathrm {c}} \\ \\\dfrac{1}{2}f_\mathrm {c,t}b_\mathrm {c}h_\mathrm {c,t,el}(\sigma _\mathrm {t,2,i}), \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \varepsilon _\mathrm {c,2}(\sigma _\mathrm {t,2,i})\ge \dfrac{f_\mathrm {c,t}}{E_\mathrm {c}}, \end{array}\right. \end{aligned}$$

(31)

$$\begin{aligned}&F_\mathrm {s,t}(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} f_\mathrm {s,t}A_\mathrm {s,t}, &{} \ \ \varepsilon _\mathrm {s,t}(\sigma _\mathrm {t,2,i})>\dfrac{f_\mathrm {s,t}}{E_\mathrm {s}} \\ E_\mathrm {s}\varepsilon _\mathrm {s,t}(\sigma _\mathrm {t,2,i})A_\mathrm {s,t}, &{} \ \ \varepsilon _\mathrm {s,t}(\sigma _\mathrm {t,2,i})\le \dfrac{f_\mathrm {s,t}}{E_\mathrm {s}}, \end{array}\right. \end{aligned}$$

(32)

$$\begin{aligned}&F_\mathrm {t,t}(\sigma _\mathrm {t,2,i})= \left( \sigma _\mathrm {t,2,i}+\dfrac{1}{2} (\sigma _\mathrm {t,3}(\sigma _\mathrm {t,2,i})-\sigma _\mathrm {t,2,i})\right) b_\mathrm {t}h_\mathrm {t}, \end{aligned}$$

(33)

$$\begin{aligned}&F_\mathrm {c,c,pl}'(\sigma _\mathrm {t,2,i})= \dfrac{f_\mathrm {c,c}b_\mathrm {c}h_\mathrm {c}E_\mathrm {t} (\varepsilon _\mathrm {c,1}E_\mathrm {c}-f_\mathrm {c,c})}{E_\mathrm {c} (-E_\mathrm {t}\varepsilon _\mathrm {c,1}+\sigma _\mathrm {t,2,i})^2}, \end{aligned}$$

(34)

$$\begin{aligned}&F_\mathrm {c,c,el}'(\sigma _\mathrm {t,2,i})=\dfrac{f_\mathrm {c,c}^2b_\mathrm {c} h_\mathrm {c}E_\mathrm {t}}{2E_\mathrm {c}(-E_\mathrm {t}\varepsilon _\mathrm {c,1} +\sigma _\mathrm {t,2,i})^2}, \end{aligned}$$

(35)

$$\begin{aligned}&F_\mathrm {s,c}'(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} 0, &{} \ \ |\varepsilon _\mathrm {s,c}(\sigma _\mathrm {t,2,i})|>\dfrac{|f_\mathrm {s,c}|}{E_\mathrm {s}} \\ E_\mathrm {s}A_\mathrm {s,c}\dfrac{h-h_\mathrm {s,c}}{h_\mathrm {c}E_\mathrm {t}}, &{} \ \ |\varepsilon _\mathrm {s,c}(\sigma _\mathrm {t,2,i})|\le \dfrac{|f_\mathrm {s,c}|}{E_\mathrm {s}}, \end{array}\right. \end{aligned}$$

(36)

$$\begin{aligned}&F_\mathrm {c,t}'(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} \dfrac{(-2E_\mathrm {t}^2\varepsilon _\mathrm {c,1}+2E_\mathrm {t}\sigma _\mathrm {t,2,i})2E_\mathrm {c}\sigma _\mathrm {t,2,i}b_\mathrm {c}h_\mathrm {c}}{(-2E_\mathrm {t}^2\varepsilon _\mathrm {c,1}+2E_\mathrm {t}\sigma _\mathrm {t,2,i})^2} -\dfrac{2E_\mathrm {c}E_\mathrm {t}\sigma _\mathrm {t,2,i}^2b_\mathrm {c}h_\mathrm {c}}{(-2E_\mathrm {t}^2\varepsilon _\mathrm {c,1}+2E_\mathrm {t}\sigma _\mathrm {t,2,i})^2},\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \varepsilon _\mathrm {c,2}(\sigma _\mathrm {t,2,i})<\dfrac{f_\mathrm {c,t}}{E_\mathrm {c}} \\ \\-\dfrac{f_\mathrm {c,t}^2b_\mathrm {c}h_\mathrm {c}E_\mathrm {t}}{2E_\mathrm {c}(-E_\mathrm {t}\varepsilon _\mathrm {c,1}+\sigma _\mathrm {t,2,i})^2},\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \varepsilon _\mathrm {c,2}(\sigma _\mathrm {t,2,i})\ge \dfrac{f_\mathrm {c,t}}{E_\mathrm {c}}, \end{array}\right. \end{aligned}$$

(37)

$$\begin{aligned}&F_\mathrm {s,t}'(\sigma _\mathrm {t,2,i})=\left\{ \begin{array}{ll} 0, &{} \ \ \varepsilon _\mathrm {s,t}(\sigma _\mathrm {t,2,i})>\dfrac{f_\mathrm {s,t}}{E_\mathrm {s}} \\ E_\mathrm {s}A_\mathrm {s,t}\dfrac{h-h_\mathrm {s,t}}{h_\mathrm {c}E_\mathrm {t}}, &{} \ \ \varepsilon _\mathrm {s,t}(\sigma _\mathrm {t,2,i})\le \dfrac{f_\mathrm {s,t}}{E_\mathrm {s}}, \end{array}\right. \end{aligned}$$

(38)

$$\begin{aligned}&F_\mathrm {t,t}'(\sigma _\mathrm {t,2,i})=\dfrac{b_\mathrm {t}h_\mathrm {t} (E_\mathrm {t}h_\mathrm {c}+h)}{2E_\mathrm {t}h_\mathrm {c}}. \end{aligned}$$

(39)

Note, that heights of specific zones and strains as functions of $\sigma _\mathrm {t,2,i}$, which are present in Eqs. (28–39), are different than those at the tensile failure criterion.