Abstract
The radiation-induced volumetric expansion (RIVE) of aggregate-forming minerals causes damage in concrete exposed to high levels of fast neutrons fluence (\(>\,\sim \,10^{19}\, \hbox {n}\,\hbox {cm}^{-2}\) at kinetics energy above 0.1 MeV). Historical post-irradiation RIVE and Young’s modulus data obtained in test reactors were revisited using a polycrystalline homogenization model (self-consistent scheme) accounting for the aggregates’ minerals content and the formation of voids/cracks during irradiation. It was found that the formation of extra voids/cracks can contribute to the aggregate expansion more substantially than the cumulated expansions of aggregate-forming minerals. The rate of void creation appears to be inversely correlated to the silica content, although aggregates of higher silicate contents exhibit higher RIVEs. The loss of Young’s modulus decreases exponentially with the aggregates’ expansion. At a comparable RIVE level, the relative loss of modulus is more significant in aggregates of higher silica content.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The prospect of extending operation of nuclear power plants beyond 60 years raises critical questions about the structural integrity of the concrete biological shield against prolonged neutron and gamma irradiation. Experimental evidence shows that the primary damage mechanism of irradiated concrete is caused by the radiation-induced volumetric expansion (RIVE) of the concrete aggregates [1,2,3,4,5]. Meso-scale analytical [6, 7] and numerical [8, 9] models were successfully applied to derive concrete RIVE in the past. However, these models require the irradiated properties of the aggregates as inputs, which dramatically vary with the nature and composition of the rocks [1, 4].
The high-energy ballistic collisions caused by neutrons, ions, or alpha-induced recoil irradiation lead to the formation of damage cascades in rock-forming minerals’ crystalline structures, causing change of coordination of the silicate tetrahedrons. This leads to atomic bonds stretching and eventually breaking [10, 11]. Cumulated defects result in macroscopic change of the physical [4, 12,13,14], chemical [15,16,17], and mechanical properties of irradiated minerals [18,19,20]. Most silicate-bearing minerals, metal-bearing oxides, and to a lesser extent, carbonated minerals of initial pristine crystalline structures experience RIVE as a density decrease caused by irradiation-induced amorphization, which is also called metamictization [21]. Amorphous glassy minerals such as obsidian or vitreous silica appear to undergo moderate irradiation-induced shrinkage [18, 22]. At a given irradiation exposure, silicate-bearing minerals are subject to varied expansion levels [22]. The maximum observed RIVE value is 17.8% for fully amorphized quartz, whereas feldspars exhibit a maximum RIVE of about 7–8% and carbonates, of less than \(\approx 1\%\) [22, 23]. Consequently, as rocks are complex assemblages of multiple minerals of varied shapes and sizes, they also experience change in physical properties: dimensional change, general expansion, [1, 2], thermal diffusivity [1], loss of mechanical properties such as Young’s modulus [1, 2], tensile strength [1], and compression strength [4]. In some cases [4], these changes are accompanied by a modification of the stress-strain curve (gradual hardening) which origin remains to be determined. The relationship between the nature and composition of the irradiated rocks and the change of density and mechanical properties remains to be established. This relationship is critical to the assessment of concrete’s tolerance of irradiation. The research described herein was focused on providing insights on the role of the mineralogical composition and the rocks’ nature regarding the loss of elastic properties in relation to irradiation-induced expansion. The proposed modeling approach relies on the homogenization theory of random crystalline mediums.
2 Neutron-irradiated rocks data
2.1 Nature and chemical composition
The experimental data used in this analysis are provided by the Russian literature collected by Denisov et al. [22]. 27 magmatic rocks and 8 silicate- or carbonate-bearing sedimentary rocks were irradiated in different Russian test reactors—identified as AM, BR-5, BR-10, and BOR-60—at varied fluence levels and irradiation temperatures. All fluence data were normalized by Denisov et al. to a threshold of 10 keV according to the different reactors’ neutron spectra. The compositions of the magmatic (or igneous) rocks (# 1–27) are provided in Table 4. Felsic igneous rock (with high contents of quartz and feldspars) compositions are plotted within the quartz, alkali feldspar, plagioclase, feldspathoid (QAPF) double-ternary diagram [24] presented in Fig. 1, including granites and granodiorites (# 1–7), quartzitic andesite (# 9), diorites (# 10–12), urtite (# 13), gabbros, diabases, and basalts (# 14–20). For the sake of a convenient representation, the two silicate-bearing sedimentary aggregates, laminated aleurolite (# 28) and sandstone (# 29), are of mineral composition comparable to irradiated magmatic rocks and were also incorporated in this figure. Mafic igneous rock compositions are represented in Fig. 2, including pyroxenite (# 22), dunites (# 23–24), and hornblendite (#27). The remaining rock samples (# 30–35) are classified as carbonates, including two high-calcite limestones (# 30–31) and a dolimitic limestone (32: 20% dolomite). The other three irradiated sedimentary carbonates correspond to magnesite (# 33), 10%-quartz siderite (# 34), and dolomite (# 35).
Classification of felsic irradiated aggregates based on the QAPF double-triangle diagram of the IUGS with mafic minerals < 90%. \(\mathrm {SiO_2} \ge 75\%\): ultra-acid; \(65\% \le \mathrm {SiO_2} < 75\%\): acid; \(52\% \le \mathrm {SiO_2} \ 65\%\): median; \(40\% \le \mathrm {SiO_2} < 52\%\): basic; \(\mathrm {SiO_2} < 40\%\): ultra-basic. \(^*\)Indicates sedimentary rocks plotted here for the purpose of comparison. Q, quartz; A, alkali feldspars; P, plagioclases; F, feldspathoids
Classification of mafic irradiated rocks based on the Px–Ol–Hbl (left) and Cpx–Ol–Opx (right) diagrams of the IUGS with mafic minerals \(\ge \) 90%. a Px–Ol–Hbl aggregate classification diagram. b Cpx-Ol-Opx aggregate classification diagram. \(40\% \le \mathrm {SiO_2} < 52\%\): basic; \(\mathrm {SiO_2} < 40\%\): ultra-basic. Ol: olivine. Hbl: hornblende. Px: pyroxene. Cpx: clinopyroxene. Opx: orthopyroxene
2.2 Radiation-induced volumetric expansion
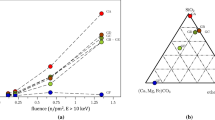
Denisov et al. gathered RIVE data for 132 aggregates provided in the form of RIVE-fluence plots with indications of the average irradiation temperatures. All plots have been digitized, and the extracted data were recorded in the irradiated minerals, aggregate and concrete (IMAC) database. The RIVE data are distributed as follows (numbers in parenthesis indicate the number of available RIVE data): granites (21), basalt (4), pyroxenites (3), sandstones (4) [25,26,27,28,29,30,31,32], granodiorites (5), liparite (3), quartzitic andesite (2), albatite (3), labradorite (10), urtite (3), diabases (13), peridotite (4), dunites (12), hornblendite (7) [28, 30,31,32], diorites (4), gabbros (10) [25, 27,28,29,30,31,32], magnesite (4), siderite (4) [30], and dolomite (2) [30, 33, 34]. The data cover a wide range of neutron fluences (\(<7\, \mathrm {n^{\tiny {E>10\;keV}}}\,\hbox {pm}^{-2}\)) and irradiation temperatures (\(<350\,^{\circ }\text {C}\))—Fig. 3.
a Irradiation exposures (fluence and temperature) corresponding to the 132 RIVE data available for this study [22]. Vertical bars indicate the irradiation temperature ranges. b The colors (red, blue, and green) are directly derived from \(\hbox {SiO}_{2}\) and –\(\hbox {CO}_3\) and the “other oxides” ternary diagram of the 35 tested aggregates. (Color figure online)
2.3 Elastic modulus
The dynamic elastic modulus of pristine and irradiated rocks were measured by ultrasonic pulse velocity and the data from a table extracted from Denisov’s work [22, Tab. 3.6.], which provides only a range of loss of mechanical properties for a given range of irradiation temperature and fluence for each rock. The hypothesis in this work is that the loss of modulus is governed by the rock-forming RIVE and the resulting mismatch strain between mineral grains of varied orientations and compositions. Hence, because of thermal annealing [12, 35, 36] in neutron-irradiated crystallin minerals, it was assumed that the maximum loss of elastic properties of irradiated rocks corresponds to the highest irradiation fluence at the lowest temperature and highest fluence, whereas the minimum loss occurs at the highest temperature and lowest fluence. Therefore, each given range of fluence and irradiation temperature provides two data points (numbers in parentheses indicate the number of available RIVE data): (i) Igneous rocks: granite (12), graniodorite (4), liparite (2), obsidian (2), diorite (4), quartzitic andesite (4), trachesite andeiste (4), albitite (2), labradorite (4), urtite (2), gabbro (2), diabase (6), basalt (8), pyroxenite (8), peridotite (2) hornblendite (2), olivinite (2) dunite (8), serpentinized dunite (4); (ii) Sedimentary rocks aleurolite (6), sandstone (2), quartzitic sandstone (4), calcium-bearing limestone (6), other limestones (4) dolomite (4), magnesite (4), siderite (4); (iii) Metamorphic rocks hornstone (2), serpentinite (6). Ores are not considered in this study. While the RIVE data distinguish between different rock compositions, the elastic modulus data do not. The loss of mechanical properties data is assumed to be relevant for all rocks belonging to the same class. The irradiation conditions corresponding to the irradiated aggregates’ Young’s modulus are presented in Fig. 4. The corresponding range of fluences and irradiation temperatures are comparable to the RIVE data.
3 Methodology
In this work, the interpretation of the RIVE and loss of elastic properties in irradiated rocks are derived using an upscaling approach. Only limited information about the rocks’ mineral compositions (volume fractions with an uncertainties estimated around \(\sim \pm \,5\%\)) and the average grain size are provided by Denisov et al. Hence, the proposed upscaling strategy is also limited to the homogenization theory of random polycrystallin mediums. Neutron-irradiation of rock-forming minerals causes the amorphization or metamictization of their pristine crystalline structures [12], which generally results in (1) a change of density [12, 22, 37], (2) the isotropization of its elastic tensor [18, 38], a change of apparent elastic modulus [18, 20, 38, 39], and (3) a change of chemical durability [15,16,17].
3.1 Minerals’ RIVE
The minerals’ tolerance against irradiation [21] and RIVE [22, 23] varies considerably with the chemical composition and the crystalline structures of the minerals. Details can be found in an article by Le Pape et al. [23]. In summary, at complete amorphization, carbonated minerals exhibit less RIVE (\(<\,\sim \,1\%\)) than metal oxides (\(<\,\sim \,5\%\)) and silicate-bearing minerals (\(<\,18\%\)). Important variations of RIVE are observed with silicated minerals: higher RIVEs are observed in highly percolated silicate structures (e.g., framework/tectosilicates such as quartz and feldspars) with higher silica content and Si–O bonds, whereas lower RIVEs occur when isolated \(\hbox {SiO}_{4}\) is present (e.g., island/orthosilicates), thus increasing the number of ionic bonds. The absence of highly covalent bonds in carbonated minerals is also the main reason for their low RIVEs [15]. Not only the final volumetric expansion varies with the mineralogy, but the expansion rate also varies and is a function of the cumulated fluence level and the irradiation temperature governing the annealing effects [36, 37]. In a previous work, Le Pape et al. [23] have established empirical RIVE models for different mineral groups, mathematically described in the form of \(\varepsilon ^*=\mathcal{F}(\Phi ,T)\), where \(\varepsilon ^*\) is the volumetric expansion, \(\Phi \) the cumulated fluence, and T is the average irradiation temperature. \(\mathcal{F}\) is a monotonic function of fluence, often sigmoidal, which expansion rate decreases with higher irradiation temperature. The details of the varied forms of \(\mathcal{F}\) can be found in section 2.1. of reference [23]. For each mineral group, the parameters governing \(\mathcal{F}\) were best-fitted on a set of nearly 400 data points collected originally by Denisov [22]. The possibility of nonuniform amorphization within a specific rock-forming mineral grain is not considered here. Mineral RIVE is assumed to produce isotropic dimensional change.
3.2 Elastic properties of minerals
The elastic properties of most common pristine rock-forming minerals are abundantly available in the public literature. The elastic constants are usually determined using acoustic wave propagation-based techniques such as the resonance frequency method. The number of independent elastic constants varies between 2 for an isotropic structure such as vitreous silica and 21 for a triclinic crystal such as albite. The corresponding elastic tensors for the minerals present in the aggregates reported in the Denisov study are reported in “Appendix 2”. The elastic properties of irradiated rock-forming minerals are insufficiently reported in the literature to develop a satisfactory model. Only the evolutions of the quartz elastic constants with fast neutron fluence have been comprehensively reported by Mayer and Lecomte [18], and partially by Zubov and Ivanov [38]. More recently, the apparent elastic properties of a chosen set of irradiated minerals were studied using molecular dynamics (MD) simulations [20]. The neutron irradiation primary knock-out mechanism was modeled by ejecting constitutive minerals’ atoms at high kinetic energy until full amorphization was obtained. The Young’s modulus of the isotropic disordered mineral was compared to the apparent modulus of the equivalent random-oriented polycrystallin mineral. The Krishnan et al.’ study found the following variations of Young modulus: albite (framework silicate, feldspar group, \(\hbox {NaAlSi}_3\hbox {O}_{8}\)), \(-18\%\), almandine (nesosilicate, garnet group, \(\hbox {Fe}_3\hbox {Al}_2\hbox {Si}_3\hbox {O}_{12}\)), \(-42\%\), anorthite (framework silicate, feldspar group, \(\hbox {CaAl}_2\hbox {Si}_2\hbox {O}_8\)), \(-\,5\%\), diopside (single-chain inosilicates, pyroxene group, \({\hbox {MgCaSi}_2\hbox {O}_6}\)), \(-\,46\%\), enstatite (single-chain inosilicates, pyroxene group, \({\hbox {MgSiO}_3}\)), \(-\,26\%\), jadeite (single-chain inosilicates, pyroxene group, \({\hbox {NaAlSi}_2\hbox {O}_6}\)), \(-\,57\%\), nepheline (framework silicate, feldspathoid group, \({\hbox {NaAlSiO}_4}\)) \(+\,12\%\), and quartz (framework silicate, \({\hbox {SiO}_2}\)), \(+\,22\%\). An important change in stiffness between the pristine state and the fully disordered state occurs, including hardening in monocrystallin structures. However, in this work, the elastic constants of irradiated minerals are assumed constant and equal to those of the pristine materials due to the lack of data to support a validated model accounting for the evolution of the elastic constants of the irradiated minerals of interest. This limitation is addressed in the discussion.
3.3 Aggregate’s microstructures
Due to a lack of petrographic data, morphological information is limited to the volume fraction of the constitutive minerals. It is assumed that all rocks can be modeled by an assemblage of mineral polycrystals randomly oriented and defects such as cracks or pores modeled as oblate shapes with an aspect ratio varying between 0 (no-volume penny-shaped crack) and 1 (spherical pore). Those defects are introduced in the model to account for (1) the creation of volume during irradiation that is not accounted for by the cumulated volume change of the constitutive minerals and (2) for the loss of mechanical properties reported after irradiation. The mechanisms that initiate and cause development of voids and/or cracking during irradiation remain to be characterized. In this study, it is hypothesized that cracking occurs at the minerals’ grain boundaries because of the mismatch strains [40] caused by the differential radiation-induced expansion (Fig. 5). Mismatch strains can result from a difference in crystal orientation or a difference in mineral composition and structure. The “nano-voids” caused by the irradiation-induced amorphization are included in the model by the change of density of the irradiated minerals: that is, by the RIVE, which is assumed to occur uniformly for any given mineral grain.
3.4 Micromechanical model
3.4.1 Irradiated aggregate morphological and volume fractions model
An aggregate is modeled as a polycrystalline assemblage of minerals. Each cell of the polycrystal is homogeneously constituted from a single mineral and can randomly differ from other cells by its crystal orientation or by its constitutive mineral. In the case of porous aggregates, for the sake of simplicity, porosity is simply considered as an additional phase without stiffness. During irradiation, minerals are subject to expansion (RIVE). Due to the heterogeneities of both local stiffness and local expansion, so-called defects (cracks, additional porosity) are created. In this work, intergranular defects are considered to be forming at the interfaces between the polycrystal’s adjacent cells. A generic microstructure before and after irradiation is illustrated in Fig. 5.
Modeling the full extent of microstructural changes during irradiation—including local incompatible expansions, cracking, and defect growth—would be a tedious challenge requiring sophisticated nonlinear numerical models. Such approaches are being developed [41] in the context of energetic materials [42] which share some similarities with aggregates. Microstructure-wise, these energetic materials are polycrystals made up of only one grain type, with a few percent of binder phase. When exposed to temperature elevation, the heterogeneity of the thermal expansion tensor causes cracking due to crystallographic orientation mismatches. The local strains at stake are much smaller than in the irradiated aggregates case, but a first model has been proposed [41] to show crack development in a 2D polycrystal subjected to temperature elevation.
Alternatively, the simplified approach proposed herein only considers the initial pristine and final post-irradiation states. Furthermore, the final microstructure is considered sufficiently damaged so that constitutive crystals can be considered free of any residual stresses which may have arisen as the result of incompatibilities of local expansions. The final microstructure can thus be described from volume balances, without any mechanical computation.
Each aggregate comprises N different types of minerals (each mineral occupies several cells of varied orientations) as denoted by the subscript \(i=1,\ldots ,N\). Subscripts a and d respectively denote the aggregate as a whole, as well as irradiation-induced defects. Volumes and volume fractions with respect to the aggregate are denoted as V and f. The superscript 0 represents the initial pristine state, whereas the absence of a superscript denotes the final state. The RIVE of each mineral (estimated from model described in Sect. 3.1) and of the aggregate (experimental measurement) are denoted as \(\varepsilon _i\) and \(\varepsilon ^*\):
The final volume of the constitutive minerals is as follows:
denoting \(\hat{\varepsilon }^*\) as the weighted (by initial volume fractions \(f^0_i\)) average of mineral RIVE \(\varepsilon _i\). The volume difference between the expanded aggregates and the expanded minerals is considered to be the irradiation-induced defects:
denoting \(\Delta \phi =\varepsilon ^* - \hat{\varepsilon }^*\) as the difference between the measured aggregate RIVE and the cumulated RIVE of minerals. The volume fraction of defects, \(f_\mathrm{d}\), in the final post-irradiation state is then obtained by dividing by the final aggregate volume:
The final volume fraction of each mineral is straightforwardly obtained from Eq. (1):
Volume fractions of minerals and defects in the irradiated aggregate can thus be estimated using these two equations, along with the volume fractions in the pristine aggregate and RIVE of minerals and \(\Delta \phi \). The latter can be deduced from the aggregate RIVE when it is known, or, following a more predictive approach, it can be estimated using the strategy described in Sect. 4.1.
The approach described above to estimate the amount of defects does not take into account the initial microstructure of aggregates, and does not model microstructural changes during irradiation. It is thus a simplified approach, which only yields an estimate of the volume fraction of defects. Modeling cracks and voids’ gradual development within the aggregates’ microstructure as irradiation proceeds would be a tedious challenge. However, the authors recognize that it would provide both refined estimates of the amount of irradiation-induced defects and valuable insights on their location.
3.4.2 Irradiated aggregate homogenization scheme
Estimating the effective post-irradiation stiffness of aggregates requires a so-called homogenization scheme. Among the available schemes, the self-consistent scheme [43,44,45] is the most suited to represent a polycrystalline assemblage. As only intergranular defects are considered, they are modeled at the same scale as the mineral cells, as an additional \((N+1)\)th phase. The self-consistent scheme is thus implemented following these assumptions: (1) each mineral cell is represented by a sphere, (2) each defect is represented by an oblate spheroid with a unique aspect ratio for all defects, (3) for each mineral phase, the distribution of the crystals’ orientations is assumed isotropic, (i.e., randomly distributed), and (4) the orientation of defects is also isotropically distributed. Thus, the effective stiffness of any aggregate is also isotropic. In summary, the effective elastic moduli of irradiated aggregates are derived by the self-consistent scheme as functions of the minerals’ stiffness tensors and the volume fractions of minerals and defects at the final state. “Appendix 1” provides the mathematical details of the micromechanical model. In particular, Eq. (19) presents the estimate of the elastic tensor of the irradiated aggregates in a compact form. To estimate the relative (irradiated with respect to pristine state) Young’s modulus, the initial Young’s modulus is computed by resorting to the same self-consistent scheme with the initial volume fractions of minerals and no defects (corresponding to the microstructure shown on the left in Fig. 5).
As the self-consistent scheme represents microstructure in an ”implicit” way, it is important to validate its estimates with respect to numerical computations on explicit microstructures. In the context of energetic materials, Gasnier et al. [46] recently developed a similar self-consistent scheme using penny-shaped cracks instead of oblate defects. The estimated effective stiffness has been compared [46, 47] to numerical computations on microstructures reconstructed from several morphological assumptions regarding cracks and grains. The self-consistent scheme is found to accurately estimate effective moduli in the cases of cracked materials with (1) isotropic grains [47] or (2) moderately anisotropic grains when cracks are either transgranular [46] or superimposed to the polycrystalline tessellation [47]. When cracks are intergranular (separating two grains), the self-consistent scheme is found to over-estimate the effective moduli computed numerically in the cases investigated by Gasnier et al. [46]. These comparisons support the concept that mean field techniques have difficulties imposing the specific locations of inhomogeneities, cracks between two grains, for example. Sevostianov and Kachanov [48] propose to modify the differential scheme in this respect, but their approach is limited to isotropic grains.
Nevertheless, the self-consistent scheme is used here in the context of irradiated aggregates for the sake of simplicity. Approximations introduced by this scheme must be considered with the approximations on input data and without knowledge of the precise microstructures of irradiated aggregates.
4 Results
4.1 Radiation-induced volumetric expansion of aggregates
The theoretical expansion of irradiated aggregates, \(\hat{\varepsilon }^*\), is first calculated accounting only for the cumulated contribution of the constitutive minerals’ RIVEs. The calculated expansions are then compared with the post-irradiation examination data, \(\varepsilon ^*\), provided by Denisov et al. [22] as presented in Fig. 6. Each mark corresponds to a specific irradiation experiment. The colors of the marks are based on the mineral composition using the ternary silica-carbonate-other oxide diagram: red, blue and green indicate high-silica, high carbonate, and high metallic oxide contents, respectively. The size of each mark indicates its average grain size. The number associated with a mark corresponds to the aggregate’s label in Table 5. The theoretical RIVEs range between 0 and \(\sim 9.5\%\), while the experimental RIVEs range between \(\sim \,-\,5\%\) and \(<\,25\%\). In general, the theoretical RIVEs tend to underestimate the experimental values, which supports the hypothesis of additional volume creation. For the sake of simplicity, the data can be subdivided into three groups: low-cracking (green shaded area), moderate cracking (yellow shaded area) high-cracking (pink shaded area). It is remarkable that the data points corresponding to high-cracking have a high content of silica, which confirms recent results obtained by Maruyama et al. [49]. It can be observed that the RIVEs of rich metal oxide-bearing aggregates do not exceed 10%, which is in agreement with the lower RIVEs of such minerals. The RIVEs of rocks with high content carbonate contents remains low, with the exception of aggregate #34, which contains nearly 10% quartz.
The additional void creation \(\Delta \phi =\varepsilon ^*-\hat{\varepsilon }^*\) is calculated for each irradiation experiment’s data. Based on the first interpretation of Fig. 6, the data set was subdivided into three different groups according to their respective silica contents: a high silica content of \(>\,65\%\), an intermediate silica content between 20% and 65% (relatively rich in metal oxides), and a low silica content of \(<\,20\%\), which corresponds to carbonated aggregates. Figures 7a, 8a and 9a show the additional void creation against the experimental RIVE for the three groups. It can be seen that \(\Delta \phi \) and \(\varepsilon ^*\) are linearly correlated. The corresponding equations are provided in the figures referenced above. The creation of defects (voids or cracks) occurs concurrently with the expansion of the aggregate-forming minerals. From a modeling perspective, the description of this process would need to be performed in the framework of nonlinear mechanics. In this work, the objective is focused on developing empirical models describing the final state following the irradiation experiment. Hence, alternatively, the void creation is estimated on an upper bound basis: \(\sup (\Delta \phi )\), derived directly from the theoretical expansion \(\hat{\varepsilon }^*\) of the uncracked aggregates. The analysis of the porosity increase against the theoretical expansion of the uncracked aggregates leads to postulation of the following linear relation: \(\sup (\Delta \phi )\sim \eta \hat{\varepsilon }^*\). The values of \(\eta \) for each aggregate group are 1.86 (Fig. 7b) for the high silica content group, 3.00, (Fig. 8b) for the intermediate silica content group, and 9.00 (Fig. 9b) for the low silica content group. The decrease of \(\eta \) with the increase of silica content may seem counterintuitive since higher RIVE is observed in minerals rich in silica, such as quartz. However, it can be hypothesized that the creation of voids results from the difference of RIVEs between the constitutive minerals causing crack formation. This crack formation is induced by mismatch strain occurring between minerals with different natures and crystal orientations [40]. This effect is illustrated by the aggregate #34 containing \(\sim 10\%\) of highly expansive (\(\sim 18\%\) at complete amorphization) quartz within a siderite matrix (\({\hbox {Fe}^{2+}\hbox {CO}_3}\)) with a very low expansion potential \(\sim 0.55\%-0.7\%\) [23].
4.2 Young’s modulus of irradiated aggregates
The void creation causes degradation of the mechanical properties of the irradiated aggregates. However, the loss of elastic properties depends not only on the volume fraction of voids, but also on the morphology of these voids, which are described by the oblate-shaped cracks governed by a unique aspect ratio.
The effective stiffness of exposed aggregate depends on the aspect ratio adopted to model the defects. To illustrate this dependence, 3 aggregates and exposure conditions are selected. The volume fraction of defects is evaluated according to (4) and is reported in Table 1. The influence of the defects’ aspect ratio on Young’s modulus reduction is plotted in Fig. 10. The residual Young’s modulus is smaller for flatter defects. As expected, the residual Young’s modulus is also smaller for higher volume fractions of defects.
For each aggregate group, an independent aspect ratio of defects is identified to reproduce the relation between the loss of modulus and the aggregate RIVE as closely as possible. Experimental data presented in Sect. 2.3 are used as reference. As these data are rather scattered, a straightforward decreasing exponential evolution is introduced:
where \(\varepsilon _\mathrm{ref}\) is a ”reference” characteristic aggregate RIVE.
For each aggregate group, the aspect ratio of defects is fit following this procedure:
-
A characteristic RIVE \(\varepsilon _\mathrm{ref}^\mathrm{exp}\) is identified based on reference experimental data (RIVE, relative Young’s modulus) as presented in Sect. 2.3.
-
For irradiated aggregates collected as described in Sect. 2.2, the upper bound on additional voids \(\Delta \phi = \eta \hat{\varepsilon }^*\) (see Sect. 4.1) is taken as an estimate. Note that the measured aggregate RIVE is not used here. Volume fractions of minerals and defects in the irradiated configuration are calculated according to Eqs. (5) and (4). The homogenization procedure described in Sect. 3.4.2 is then used to estimate the loss of Young’s modulus, depending on the defect’s aspect ratio. The aspect ratio is identified by minimizing the distance with respect to experimental data represented by Eq. (6), with \(\varepsilon _\mathrm{ref}=\varepsilon _\mathrm{ref}^\mathrm{exp}\).
-
For reference purposes, another characteristic RIVE \(\varepsilon _\mathrm{ref}^\mathrm{mod}\) is identified based on modeled data (RIVE, relative Young’s modulus).
Results are provided in Table 2. The identified aspect ratios are of the same order of magnitude and correspond to flat, crack-like defects. Finding the same order of magnitude for each aggregate group supports the fact that the main features of the irradiated morphology are similar. Differences lie in the volume fractions of defects, which depend on the specific constitutive minerals and the exposure conditions.
The loss of mechanical properties of irradiated aggregates is illustrated by the evolution of the relative Young’s modulus with the RIVE shown in Figs. 11, 12, and 13 for the three groups of rocks. The relative Young’s modulus exhibits an exponential-like decrease with the RIVE. Such behavior is qualitatively comparable to the loss of elastic properties caused by alkali-silica reaction-induced swelling [50]. This decreasing trend is fitted using the following mathematical expression: \(E^*/E_0\simeq \exp \left[ -\,\beta \left( \hat{\varepsilon }^*+\sup \Delta \phi \right) \right] \), where \(E^*\) is the Young’s modulus of the irradiated material, and \(E_0\) is its pristine value. The values of \(\beta \) increase when the silica-content decreases, indicating that for an equivalent expansion level, the extent of damage substantially increases for lower content silicate-bearing aggregates: \(\beta =47.1\) for \([\hbox {SiO}_2]>65\%\), \(\beta =53.1\) for \(25\%<[\hbox {SiO}_2]<65\%\), and \(\beta =79.3\) for \({[\hbox {SiO}_2]}<20\%\). This trend can be put in perspective, with the evolution of \(\eta \) supporting the hypothesis of higher damage development in aggregates formed with different minerals subjected to contrasted RIVEs.
5 Discussion
5.1 Contribution of the elastic tensors in irradiated minerals
Due to the lack of data, the assumption made in this study is that the elastic tensors of the irradiated minerals do not change with gradual amorphization. Based on the results, which were mainly obtained using first principle–based simulation on a limited set of silicates, the stiffness of the irradiated silicates at full amorphization appears to decrease in a range of \(-\,5\%\) to nearly \(-\,50\%\) except in two framework silicates, quartz and nepheline, in which stiffness increases by \(+\,20\%\) and \(+\,10\%\), respectively. It should be emphasized that these values are relevant for the final stage of the amorphization process, which corresponds to high RIVEs occurring at high levels of fluence. Tentatively, the amorphization index (\(\in [0;1]\)) is approached with the relative expansion to the maximum RIVE, \(\hat{\varepsilon }^*/\hat{\varepsilon }^*_\mathrm{max}\), as derived from the mineral contents of the aggregates. Figure 14 presents the evolution of the loss of Young’s modulus with the amorphization index. It can be observed that the calculated loss of Young’s modulus evolves differently with the aggregates’ silica content. The effective modulus of the poly-crystalline assemblage of minerals results from the contribution of (1) The evolution of the stiffness tensors of its constitutive minerals caused by irradiation-induced defects at the atomistic scale, and (2) The formation of defects at the meso-scale (e.g., at the grain boundary) caused by mismatch expansions between different minerals as proposed in our model. For high content of silica (\([\hbox {SiO}_2]\ge 65\%\)), it reaches its maximum value for relative expansion between about 20 and 40%. In that case, it can be hypothesized that early-stage mismatch expansions of the constitutive minerals causes substantial internal mechanical damage. The contribution of the irradiation-induced change of the minerals’ elastic constants to the Young’s modulus of aggregates with \([\hbox {SiO}_2]\ge 65\%\) is of lesser importance. As the silica content decreases, the rate of Young’s modulus loss with the amorphization index is not as sharp. For that type of aggregate (\(20\%\le [\hbox {SiO}_2]\le 65\%\)), it is possible that the changing irradiated minerals’ elastic properties interact with the RIVE-induced mismatch strains, causing damage, and contributing to the effective loss of stiffness in the aggregates. For carbonated aggregates, most data correspond to a state of complete amorphization, making it difficult to draw conclusions. Detailed examination and damage characterization of irradiated rocks are needed in the future to study this question further.
Loss of elastic modulus of aggregates with the amorphization index. The red, green, and blue solid lines correspond to the fitting curves using the expression \(E^*/E_0=\exp (-\lambda \varepsilon ^*/\varepsilon ^*_{\mathrm {max}})\), respectively for \([\hbox {SiO}_2]\ge 65\%\), \(20\%\le [\hbox {SiO}_2]\le 65\%\), and \([\hbox {SiO}_2]\le 20\%\). (Color figure online)
5.2 Role of the average grain size
While detailed information about the microstructures of the tested rocks is not available, the average grain size of each rock is provided by Denisov et al. Theoretically, the formation of misfit strain (\(\Delta \varepsilon \))-induced cracking onset at the grain boundary depends on the grain size l [40, 51]: \(\Delta \varepsilon \propto l^{-1/2}\). Figure 15 presents the estimated contribution of irradiation-induced void creation to the experimental RIVE, \(\Delta \Phi /\varepsilon ^*\), plotted as a function of the aggregates’ silica content \([\hbox {SiO}_2]\) and the aggregates’ average grain size for all the RIVE data available in this study. For aggregates of similar silica content, no clear trend regarding the role of the average grain size on the irradiation-induced void formation can be drawn. Once more, only thorough characterization of the irradiation-induced damage in rocks will make it possible to clearly understand the nature, scale and development of defects and voids in rocks of varied natures.
Estimated contribution of irradiation-induced void creation to the experimental RIVE, \(\Delta \Phi /\varepsilon ^*\), plotted as a function of the aggregates’ silica content \([\hbox {SiO}_2]\) and the aggregates’ average grain size. The diameter of the plot is proportional to the value of \(\Delta \Phi /\varepsilon ^*\). a Complete data set. b Reduced data set around irradiation condition of \(\sim \,1 \mathrm {n^{\tiny {E>10\;keV}}}.\hbox {pm}^{-2}\) and \(100\,^{\circ }\text {C}\). The same color chart representing the aggregates’ mineral composition as for the other figures is used here. (Color figure online)
5.3 Influence of the silica-content on irradiation-induced damage
The nature of irradiation-induced damage in concrete-forming aggregates varies with the observation scale.
At the atomistic scale, fast neutron-irradiation causes mainly ballistic effects in the form of cascading knock-on atoms. However, the impact of cumulated cascades on the effective physical and mechanical properties of irradiated aggregate-forming minerals vary with their crystalline structures. Covalent bonds are highly directional and rigid. Hence, the atoms surrounding knock-on position are subject to displacement caused by the crystals’ lattice deformation and broken bonds are unlikely to reform [10, 15]. Conversely, in the presence of less directional and rigid ionic bonds, knock-on atoms are displaced more independently of the surrounding crystal lattice and broken bonds are more likely to reform. In consequence, minerals RIVE increases with the number of covalent bonds and the silicates tetrahedrons structures. For example, this explains why quartz, a fully-covalent tecto-silicate exhibits a maximum RIVE one order of magnitude higher than olivine [22], a highly ionic ortho-silicate \(25\%\) of \(\hbox {Si}\)–\(\hbox {O}\) bonds [21]. Note that the silica content does not provide a good indication of the irradiation tolerance of silicates [21, 23].
At the meso-scale, aggregates can be described as a polycrystalline assemblage of varied minerals which exhibit varied RIVEs and mechanical properties. In this study, aggregates were classified by their oxides contents, and more specifically by their \(\hbox {SiO}_2\) content. At this scale, the irradiation-induced defects hypothetically correspond to the formation of voids, cracks and grains boundary debonding caused by mismatch strains between adjacent irradiated minerals. The defects are characterized by the loss of the effective elastic modulus. In this study, it is found that the silica-content acts differently on RIVE and on residual mechanical properties. High silica-content aggregates tends to exhibits higher expansions mainly because of a higher content of quartz, confirming Maruyama et al.’s findings [49]. However, and almost counterintuitively, the loss of elastic properties is sharper for lower silica-content aggregates than for higher silica-content aggregates at comparable RIVE. Without accessible data on post-irradiation examination of the aggregates, only hypothesis can be drawn. The authors’ assumption is that lower silica-content aggregates are subject to greater mismatch strain between the constitutive mineral phases as discussed in the previous section.
6 Conclusion
In this study, historical irradiation data of concrete-forming aggregates were revisited with the objective of analyzing the effects of neutron irradiation on their induced expansion and their loss of mechanical properties. The approach is derived from a polycrystalline micromechanical model (self-consistent scheme). To the authors’ knowledge, this is the first model ever developed for estimating the expansion and elastic properties of irradiated rocks based only on their mineral composition and their pristine Young’s moduli. From this analysis, it can be inferred that: (1) the post-irradiation expansion of aggregates is caused by the contribution of its rock-forming minerals and the formation of additional voids, the exact nature of which remains to be determined; (2) silicate-bearing aggregates are subjected to higher expansions than carbonate-bearing aggregates due to the higher inclination towards high RIVEs in tectosilicates such as quartz and feldspars; (3) however, it was found that, on average, the relative increase of defects was larger for aggregates of lower silica content at comparable theoretical expansions of the constitutive minerals; (4) the loss of Young’s modulus of irradiated aggregates is correlated to their RIVEs with a trend which can be represented by an exponential decrease; and (5) at comparable RIVEs, the loss of Young’s modulus is, on average, more important for aggregates with lower silica content. Hence, it is inferred that the irradiation-induced damage rate (void creation rate) is higher in aggregates with lower amounts of silica. It can be hypothesized that damage formation is driven by the strains’ mismatch between adjacent minerals. With that assumption, the highest damage rate would correspond to an aggregate containing quartz embedded in a carbonated mineral matrix. The practical implications of these findings are described here.
For operating light water reactors, the nature of the aggregates is critical regarding their tolerance against prolonged irradiation. In addition to the determination of the irradiation conditions (flux, fluence and temperature) using irradiation transport models, characterizing the mineralogy of the constitutive aggregates used for the construction of the biological shield is a necessary prerequisite to the sound assessment of the risk of degradation of the irradiated concrete shielding the reactor. For the construction of the biological shield of new reactors, it is recommended that carbonated rocks such as limestone or dolomite be used rather than igneous rocks such as granite, for example. However, even when using carbonated rocks, a careful characterization of the aggregates must be conducted to detect the presence of deleterious silicates such as quartz. The presence of more vitreous forms such as chert or flint is far less problematic because of their poorly crystallized structures causing less RIVE, if not moderate contractions.
Change history
24 March 2021
A Correction to this paper has been published: https://doi.org/10.1617/s11527-021-01655-4
References
Kelly BT, Brocklehurst JE, Mottershead D, McNearney S (1969) The effects of reactor radiation on concrete. In: Proceedings of the second information meeting on pre stress concrete and reactor pressure vessels and their thermal isolation, vol EUR-4531, Brussels, pp 237–265
Elleuch LF, Dubois F, Rappenau J (1971) Behavior of special shielding concretes and of their constituents under neutron irradiation, vol 7
Hilsdorf HK, Kropp J, Koch HJ (1978) The effects of nuclear radiation on the mechanical properties of concrete. Spec Publ Am Concr Inst 55:223–254
Seeberger J, Hilsdorf HK, von radioactiver Strahlung auf die Festogkeit Einfluß and von Beton Struktur (1982) Technical Report NR 2505, Institut für Massivbau and Baustofftechnologie, Universität Karlsruhe
Maruyama I, Ishikawa S, Yasukouchi J, Sawada S, Kurihara R, Takizawa M, Kontani O (2018) Impact of gamma-ray irradiation on hardened white portland cement pastes exposed to atmosphere. Cem Concr Res 108:59–71
Le Pape Y, Field KG, Remec I (2015) Radiation effects in concrete for nuclear power plants—part II: perspective from micromechanical modeling. Nucl Eng Des 282:144–157
Jing X, Xi Y (2017) Theoretical modeling of the effects of neutron irradiation on properties of concrete. J Eng Mech ASCE 143(12):04017137-1/14
Giorla A, Vaitová M, Le Pape Y, Štemberk P (2015) Meso-scale modeling of irradiated concrete in test reactor. Nucl Eng Des 295:59–73
Giorla A, Le Pape Y, Dunant C (2017) Computing creep-damage interactions in irradiated concrete. J Nanomech Micromech 04017001
Wang B, Yu Y, Pignatelli I, Sant GN, Bauchy M (2015) Nature of radiation-induced defects in quartz. J Chem Phys 143:024505
Wang B, Krishnan A, Yu Y, Wang M, Le Pape Y, Sant G, Bauchy M (2017) Irradiation-induced topological transition: structural signature of networks’ rigidity. J Noncryst Solids 463:25–30 Accepted
Primak W (1958) Fast-neutron-induced changes in quartz and vitreous silica. Phys Rev 110(6):1240–1254
Wittels MC (1957) Structural behavior of neutron irradiated quartz. Philos Mag 2:1445–1461
Wong CF (1974) Neutron radiation damage in some birefringent crystals. Phys Lett A 50(5):346
Pignatelli I, Kumar A, Field KG, Wang B, Yu Y, Le Pape Y, Bauchy M, Sant G (2016) Direct experimental evidence for differing reactivity alterations of minerals following irradiation: the case of calcite and quartz. Sci Rep Nat 6(20155):1–10
Hsiao Y-H, La Plante E, Krishnan NMA, Le Pape Y, Neithalath N, Bauchy M, Sant G (2017) The effects of irradiation on albite’s chemical durability. J Phys Chem A 121:7835–7845 submitted
Hsiao Y-H, Callagon La Plante E, Krishnan NMA, Dobbs HA, Le Pape Y, Neithalath N, Bauchy M, Israelachvili J, Sant G (2018) Role of the electrical surface potential and irradiation induced disordering on almandine’s dissolution kinetics. J Phys Chem C 122(30):17268–17277 Submitted
Mayer G, Lecomte M (1960) Effet des neutrons rapides sur le quartz cristallin et la silice vitreuse. J Phys Radium 21(12):846–852
Silva CM, Rosseel TM, Kirkegaard MC (2018) Radiation-induced changes in quartz, a mineral analog of nuclear power plant concrete aggregates. Inorg Chem 57:3329–3338
Krishnan ANP, Le Pape Y, Sant G, Bauchy M (2018) Effect of irradiation on silicate aggregates’ density and stiffness. J Nucl Mater 512:126–136
Eby RK, Ewing RC, Birtcher RC (1992) The amorphization of complex silicates by ion-beam irradiation. J Mater Res 7(11):3080–3102
Denisov AV, Dubrovskii VB, Solovyov VN (2012) Radiation resistance of mineral and polymer construction materials. ZAO MEI Publishing House (in Russian)
Le Pape Y, Alsaid MHF, Giorla AB (2018) Rock-forming minerals radiation-induced volumetric expansion—revisiting the literature data. J Adv Concr Technol 16:191–209
Le Maitre RW, Streckeisen A, Zanettin B, Le Bas MJ, Bonin B, Bateman P (eds) (2015) Igneous rocks: a classification and glossary of terms recommendations of the international union of geological sciences subcommission on the systematics of igneous rocks, 2nd edn. Cambridge University Press, Cambridge
Dubrovskii VB (1977) Radiation resistance of construction materials. Stroyizdat, Moscow
Dubrovskii VB, Lavdansky BK, Pergamenshchik VN, Solovyov VN (1973) Radiation resistance of materials. Atomizdat, Moscow
Dubrovskii VB, Korenevsky VC, Muzalevsky LL (1980) Radiation-resistant concreted from reactor protection. In: Radiation safety and protection of nuclear power plants, vol 2, Moscow, p 240
Dubrovskii VV, Korenevsky VV, Muzalevsky LP (1985) Effect of radiation on concrete fillers. Radiat Saf Prot Nucl Power Plants 9:242
Korenevsky VV (1974) Effect of irradiation on concrete and their components. PhD thesis, Moscow
Denisov AV (1986) Radiation changes in fillers of heavy concretes and method of their analytical determination. Candthesis, Moscow
Denisov AV, Dubrovskii VB, Korenevsky VV (1979) Effect of mineralogical composition on radiation resistance of concrete fillers. Issues of nuclear science and technology. Series of designing and construction, vol 4, p 41
Denisov AV, Dubrovskii VV, Korenevsky LP (1982) Radiation changes in magmatic filler rocks. Issue Nucl Sci Technol Ser Des Constr 11:12
Tucker DS, Zocco T, Kise CD, Kennedy JC (1986) Effects of neutron-irradiation on MgAl\(_2\)O\(_4\) and Al\(_2\)O\(_3\). J Nucl Mater 141–143:401–404
Denisov AV, Korenevsky VV, Muzalevsky LP (1978) Radiation changes in sedimentary rocks. Issue Nucl Sci Technol Ser Des Constr 2:102
Zubov VG, Ospova ND, ans Kundikova LP (1976) Annealing of radiation defects in fast neutron-irradiated quartz. Vestnik Moskovskogo universiteta. Seriia III, Fizika, astronomiia 17:628–629
Bykov VN, Denisov AV, Dubrovskii VB, Korenevskii VV, Krivokoneva GK, Muzalevskii LP (1981) Effect of irradiation temperature on the radiation expansion of quartz. Atomnaya Energiya 51(3):593–595
Zubov VG, Ivanov AT (1966) Expansion of quartz caused by irradiation with fast neutrons. Sov Phys Crystallogr 11(3):372–374
Zubov VG, Ivanov AT (1967) Elasticity of quartz irradiated with fast neutrons. Sov Phys Crystallogr 12(2):313–314
Mayer G, Gigon J (1956) Effets des neutrons rapides sur quelques constantes physiques du quartz cristallin et de la silice vitreuse. J Phys Radium 18:109–114
Clarke FJP (1964) Residual strain and fracture stress-grain size relationship in brittle solids. Acta Metall 12:139–143
Trumel H, Rabette F, Willot F, Brenner R, Ongari E, Biessy M, Picart D (2019) Understanding the thermomechanical behavior of a TATB-based explosive via microstructure-level simulations. Part i: microcracking and viscoelasticity. In: 44th International pyrotechnics seminar, Tours, France
Ambos A, Willot F, Jeulin D, Trumel H (2015) Numerical modeling of the thermal expansion of an energetic material. Int J Solids Struct 60–61:125–139
Hill R (1965) A self-consistent mechanics of composite materials. J Mech Phys Solids 13(4):213–222
Budiansky B (1965) On the elastic moduli of some heterogeneous materials. J Mech Phys Solids 13:223–227
Kröner E (1977) Bounds for effective elastic moduli of disordered materials. J Mech Phys Solids 25:137–155
Gasnier J-B, Willot F, Trumel H, Jeulin D, Biessy M, The case of jointed polycrystalline tatb (2018) Thermoelastic properties of microcracked polycrystals. Part ii. Int J Solids Struct 155:257–274
Willot F, Trumel H, Jeulin D (2019) The thermoelastic response of cracked polycrystals with hexagonal symmetry. Philos Mag 99(5):606–630
Sevostianov I, Kachanov M (2019) On the effective properties of polycrystals with intergranular cracks. Int J Solids Struct 156–157:243–250
Maruyama I, Kontani O, Takizawa M, Sawada S, Ishikawa S, Yasukouchi J, Sato O, Etoh J, Igari T (2017) Development of the soundness assessment procedure for concrete members affected by neutron and gamma-irradiation. J Adv Concr Technol 15:440–523
Jones AEK, Clark LA (1998) The effects of ASR on the properties of concrete and the implications for assessment. Eng Struct 20(9):785–791
Clarke FJP, Wilks RS, Bowen DH (1964) Mechanisms of irradiation-induced growth and cracking in beryllia. J Nucl Mater 14:205–207
Zaoui A (2002) Continuum micromechanics: survey. J Eng Mech 128(8):808–816
Dormieux L, Kondo D, Ulm F-J (2006) Microporomechanics. Wiley, New York
Eshelby JD (1957) The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc R Soc Lond Ser A Math Phys Sci 241(1226):376–396
Kaercher P, Militzer B, Wenk H-R (2014) Ab initio calculations of elastic constants of plagioclase feldspars. Am Mineral 99:2344–2352
Brown JM, Abramson EH, Angel RJ (2006) Triclinic elastic constants for low albite. Phys Chem Miner 33:256–265
Ryzhova TV (1964) Elastic properties of plagioclase. Bull Acad Sci USSR 7:633–635
Angel R, Brown JM, Abramson E, Johnson E (2006) Elasticity of plagioclase feldspars. In: Geological society of america annual meeting, vol 38 of 114, Philadelphia
Aleksandrov KS, Alchikov UV, Belikov BP, Zalavskii BI, Krupnyi A (1974) Velocities of elastic waves in minerals at atmospheric pressure and increasing precision of elastic constants by means of EVM. Bull Acad Sci USSR Geol Ser 10:15–24
Sanchez-Valle C, Sinogeikin SV, Lethbridge ZAD, Walton RI, Smith CW, Evans KE, Bass JD (2005) Brillouin scattering study on the single-crystal elastic properties of natrolite and analcime zeolites. J Appl Phys 98:053508-1–053508-6
Every AG, McCurdy AK (1992) The elastic constants of crystals. In: Nelson DF (ed) Landolt-Börnstein tables, vol III(29), vol III(29). Springer, Berlin, pp 1–634
Aleksandrov KS, Ryzhova TV, Belikov BP (1964) The elastic properties of pyroxenes. Sov Phys Crystallogr 8:589–591
Newnham RE, Yoon HS (1973) Elastic anisotropy in minerals. Mineral Mag 39:78–84
Aleksandrov KS, Ryzhova TV (1961) Elastic properties of rock-forming minerals: II layered silicates. Bull Acad Sci USSR Geol Ser 9:1165–1168
Cline CF, Dunegan HL, Henderson GW (1967) Elastic constants of hexagonal BeO, ZnS, and CdSe. J Appl Phys 38(4):1944–1948
Bentle GG (1966) Elastic constants of single-crystal BeO at room temperature. J Am Ceram Soc 49(3):125–128
Kumazawa M (1969) The elastic constants of single-crystal orthopyroxen. J Geophys Res 74(25):5973–5980
Ryzhova TV, Aleksandrov KS, Korobkova VM (1966) The elastic properties of rock-forming minerals, 5 additional data on silicates. Bull Acad Sci USSR 2:111–113
Dandekar DP (1968) Variation in the elastic constants of calcite with temperature. J Appl Phys 39:3694–3699
Hearmon RFS (1979) The elastic constants of crystals and other anisotropic materials. Springer, Berlin
Vo Thanh D, Lacam A (1984) Experimental study of the elasticity of single crystalline calcite under high pressure (the calcite I–calcite II transition at 14.6 kbar). Phys Earth Planet Inter 34:195–203
Chen CC, Lin CC, Liu LG, Sinogeikin S, Bass JD (2001) Elasticity of single-crystal calcite and rhodochrosite by brillouin spectroscopy. Am Mineral 86:1525–1529
Kaga H (1968) Third-order elastic constants of calcite. Phys Rev 172:900–919
Chang E, Graham EK (1975) The elastic constants of cassiterite \(\rm SnO_2\) and their pressure and temperature dependence. J Geophys Res 80:2595–2599
Mookherjee M, Mainprice D (2014) Unusually large shear wave anisotropy for chlorite in subduction zone settings. Geophys Res Lett 41:1506–1513
Toohill K, Siegesmind JD, Bass S (1999) Sound velocities and elasticity of cordierite and implications for deep crustal seismic anisotropy. Phys Chem Miner 26:333–343
Goto T, Anderson OL (1989) Elastic constants of corundum up to 1825 K. J Geophys Res 94:7588–7602
Gieske JH, Barsch GR (1968) Pressure dependence of the elastic constants of single crystalline aluminum oxide. Physica Status Solidi 29:121–131
Levien L, Weidner DJ, Prewitt CT (1979) Elasticity of diopside. Phys Chem Miner 4:105–113
Isaak DG, Ohno I (2003) Elastic constants of chrome-diopside: application of resonant ultrasound spectroscopy to moniclinic single-crystals. Phys Chem Miner 30:430–439
Humbert P, Plique F (1972) Propriétés élastiques de carbonates rhombohédriques monocristallines: calcite, magnésite, dolomie. C R Acad Sci 275:391–394
Pacalo REG, Weidner DJ (1997) Elasticity of majorite, \(\rm MgSiO_3\) tetragonal garnet. Phys Earth Planet Inter 99:145–154
Hearmon RFS (1984) The elastic constants of crystals and other anisotropic materials. Springer, Berlin
Sha Michael C, Li Zhuang, Bradt Richard C (1994) Single-crystal elastic constants of fluorapatite, \({{\rm Ca}}_5{{\rm F}}({{\rm PO}}_4)_3\). J Appl Phys 75:7784–7787
Yoneda A, Morioka M (1992) Pressure derivatives of elastic constants of single-crystal forsterite. In: Syono Y, Manghnani MH (eds) High pressure research: applications to earth and planetary sciences, vol 3. American Geophysical Union, Washington, DC, pp 207–214
Isaak DG, Anderson OL, Goto T (1989) Measured elasticity moduli of single-crystal MgO up to 1800 K. Phys Chem Miner 16:704–713
Suzuki I, Anderson OL, Sumino Y (1983) Elastic properties of a single-crystal forsterite \(\rm Mg_2SiO_4\) up to 1,200 K. Phys Chem Miner 10:38–46
Sumino Y, Nishizawa O, Goto T, Ohno I, Ozima M (1977) Temperature variation of elastic constant of single-crystal forsterite between \(-\) 190 and \(400\,^{\circ }\text{ C }\). J Phys Earth 25:377–392
Graham EK, Barsch GR (1969) Elastic constants of single-crystal forsterite as a function of temperature and pressure. J Geophys Res 74:5949–5960
Kumazawa M (1969) The elastic constant of polycrystalline rocks and noneleastic behavior inherent to them. J Geophys Res 74:5311–5320
Liebermann RC, Maasch KA (1986) Acoustic and static compression experiments on the elastic behavior of hematite. J Geophys Res 91(B5):4651–4656
Aleksandrov KS, Ryzhova TV (1962) Elastic properties of rock-forming minerals: III feldspars. Bull Acad Sci USSR Geol Ser 10:129–131
Auzende A-L, Pellenq RJ-M, Devouard B, Baronnet A, Grauby O (2006) Atomistic calculations of structural and elastic properties of serpentine minerals: the case of lizardite. Phys Chem Miner 33:266–275
Mookherjee M, Stixrude L (2009) Structure and elasticity of serpentine at high-pressure. Earth Planet Sci Lett 279:11–19
Sanchez-Valle Sujoy, Ghosh C, Rosa Angelika D (2011) Sound velocities of ferromagnesian carbonates and the seismic detection of carbonates in eclogites and the mantle. Geophys Res Lett 38:L24315
England AW (1970) Equations of state of oxides and silicates and new data on the elastic properties of spinel, magnetite, and cadmium oxide. PhD thesis, Massachusetts Institute of Technology, Cambridge, MA
Vaughan MT, Guggenheim S (1986) Elasticity of muscovite and its relationship to crystal structure. J Geophys Res 91:4657–4664
Clark Sydney P (1966) Handbook of physical constants. Memoir (Geological Society of America), vol 97. The Geological society of America, 231 East 46th Street, New York, New York 10017, rev. ed. A revised ed. of the handbook of physical constants, originally prepared by an editorial committee of the National Research Council. Includes bibliographies
Kaichi S, Makoto M, Tetsuya S, Hideyuki F (2013) Elastic properties of obsidian, vitreous SiO2, and vitreous GeO2 under high pressure up to 6 GPa, American Geophysical Union, pp 219–225
Waeselmann N, Brown JM, Angel RJ, Ross N, Zhao J, Kaminsky W (2016) The elastic tensor of monoclinic alkali feldspars. Am Mineral 101:1228–1231
Yoneda A (1990) Pressure derivatives of elastic constants of single crystal MgO and \({{\rm MgAl}}_2{{\rm O}}_4\). J Phys Earth 38(1):19–55
Isaak DG, Anderson OL, Goto T, Suzuki I (1989) Elasticity of single-crystal forsterite measured to 1700 K. J Geophys Res 94:5895–5906
Sumino Y, Anderson OL, Suzuki I (1983) Temperature coefficients of elastic constants of a single-crystal MgO between 80 and 1300 K. Phys Chem Miner 9:38–47
Jackson I, Niesler H (1982) The elasticity of periclase to 3 GPa and some geophysical implications. In: Akimoto S, Manghnani MH (eds) High-pressure research in geophysics: advances in earth and planetary sciences, vol 12. Center for Academic Publications, Tokyo, pp 93–113
Sumino Y, Ohno I, Goto T, Kumazawa M (1976) Measurement of elastic constants and internal frictions on single-crystal MgO by rectangular parallelepiped resonance. J Phys Earth 24:263–273
Spetzler H (1970) Equation of state of polycrystalline and single-crystal MgO to 8 kilobars and 800 K. J Geophys Res 11:2073–2087
Chang ZP, Barsch GR (1969) Pressure dependence of elastic constants of single-crystalline magnesium oxide. J Geophys Res 74(12):3291–3294
Anderson OL, Andreatch P Jr (1966) Pressure derivatives of elastic constants of single-crystal MgO at \(23^{\circ }\text{ C }\) and \(-195.9^{\circ }\text{ C }\). J Am Ceram Soc 49(8):404–409
Wenk H-R, Vasin RN, Kern H, Matthies S, Vogel SC, Ivankina TI (2012) Revisiting elastic anisotropy of biotite gneiss from the outokumpu scientific drill hole based on new texture measurements and texture-based velocity calculations. Tectonophysics 570–571:123–134
Chheda TD, Mookherjee M, Mainprice D, dos Santos AM, Molaison JJ, Chantel J, Manthilake G, Bassett WA (2014) Structure and elasticity of phlogopite under compression: geophysical implications. Phys Earth Planet Inter 233:1–12
O’Neill B, Bass JD, Rossman GR, Geiger CA, Langer K (1991) Elastic properties of pyrope. Phys Chem Miner 17:617–621
Ahrens Thomas J (ed) (1995) Mineral physics and crystallography: a handbook of physical constants. QE366.8.M55. American Geophysical Union, Washington, DC
Isaak DG, Carnes JD, Anderson OL, Cynn H, Hake E (1998) Elasticity of \(\rm TiO2\) rutile to 1800 K. Phys Chem Miner 26:31–43
Grimsditch MH, Ramdas AK (1976) Elastic and elasto-optic constants of rutile from Brillouin scattering study. Phys Rev B 14:1670–1682
Fritz IJ (1974) Pressure and temperature dependences of the elastic properties of rutile (\(\text{ TiO }_2\)). J Phys Chem Solids 35:817–826
Manghnani Murli H (1969) Elastic constants of single-crystal rutile under pressure to 7.5 kilobars. J Geophys Res 74(17):4317–4328
Haussühl S (1993) Thermoelastic properties of beryl, topaz, diaspore, sanidine and periclase. Z Kristallographie 204:67–76
Suzuki I, Ohno I, Anderson O (2000) Harmonic and anharmonic properties of spinel \(\rm MgAl_2O_4\). Am Mineral 85:304–311
Cynn H, Anderson O, Nicol M (1993) Effects of cation disordering in a natural \({{\rm MgAl}}_2{{\rm O}}_4\) spinel observed by rectangular parallelepiped ultrasonic resonance and raman measurements. Pure Appl Geophys 141:415–444
Askarpour V, Manghnani MH, Fassbender S, Yoneda A (1993) Elasticity of single-crystal \({{\rm MgAl}}_2O_4\) spinel up to 1273 K by Brillouin spectroscopy. Phys Chem Miner 19:511–519
Chang ZP, Barsch G (1973) Pressure dependence of single-crystal elastic constant and anharmonic properties of spinel. J Geophys Res 78:2418–2433
Liu HP, Schock RN, Anderson DL (1975) Temperature dependence of single crystal spinel elastic constants from 293 to 423 K measured by lightsound scattering in the raman-nath region. Geophys J R Astron Soc 42:217–250
O’Connell RJ, Graham EK (1971) Equation of state of stoichiometric spinel to 10 kbar and 800 K. Trans Am Geol Union 52:359
Lewis MF (1966) Elastic constants of magnesium aluminate spinel. J Acoust Soc Am 40:728–729
Ohno I (1995) Temperature variation of elastic properties of \(\alpha \)-quartz up to the \(\alpha -\beta \) transition. J Phys Earth 43:157–169
Ohno I (1990) Rectangular parallellepiped resonance method for piezoelectric crystals and elastic constants of alpha-quartz. Phys Chem Miner 17:371–378
McSkimin HJ, Andreatch P Jr, Thurston RN (1965) Elastic moduli of quartz versus hydrostatic pressure at \(25^{\circ }\) and \(-195.8^{\circ }{{\rm C}}\). J Appl Phys 36(5):1624–1632
Voigt W (1910) Lehrbuch der Kristallphysik. Teubner, BG, Leipzig
Lawson AW (1941) Comment on the elastic constants of alpha-quartz. Phys Rev 59:838
Bechmann R (1958) Elastic and piezoelectric constants of alpha-quartz. Phys Rev 110(5):1060–1061
James BJ (1987) Determination of the elastic and dielectric properties of quartz. PhD thesis, Dissertation, Royal Holloway and Bedford New College, University of London
Kushibiki J, Takanaga I, Nishiyama S (2002) Accurate measurements of the acoustical physical constants of synthetic \(\alpha \)-quartz for SAW devices. IEEE Trans Ultrason Ferroelectr Freq Control 49:125–135
Calderon E, Gauthier M, Decremps F, Hamel G, Syfosse G, Polian A (2007) Complete determination of the elastic moduli of \(\alpha \)-quartz under hydrostatic pressure up to 1 gpa: an ultrasonic study. J Phys Condens Matter 19(436228):13
Funding
This work is supported by the US Department of Energy Office of Nuclear Energy Light Water Reactor Sustainability Program under contract number DE-AC05-00OR22725.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Notice of Copyright This manuscript has been authored by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).
Notations The neutron fluence characterizing the number of particles crossing a unit’s surface is generally given in \(\hbox{n}\,\hbox{cm}^{-2}\). Since irradiation exposure in light water reactors and test reactors of concrete constituents reach fluence levels of \(\approx 10^{19}\)–\(10^{20}\hbox { n}\,\hbox { cm}^{-2}\), fluences are alternatively given in \(\hbox {n}\, \hbox{pm}^{-2}\). In this article, 1.0 n \(\hbox {pm}^{-2} =10^{20}\hbox { n}\,\hbox { cm}^{-2}\). Also, it is convenient to express fluence for a given energy threshold, or the neutron kinetic energy. In this article, both the usual notation and a specific compact notation are used: \(1.0\hbox { n}\,\hbox {pm}^{-2} (E>10\,\text {keV}\)) is equivalent to \(1.0\, \mathrm {n^{\tiny {E>10\;keV}}}\,\hbox {pm}^{-2}\)
The original online version of this article was revised: The original version of this article was revised due to a retrospective Open Access order.
Appendices
Appendix
1.1 Micromechanics equations
First, the general framework of homogenization of random media in linear elasticity is recalled. Then, the self-consistent scheme used to estimate irradiated aggregates stiffness is briefly derived. For more details, see Zaoui and Dormieux et al. [52, 53].
1.1.1 Introduction to homogenization of random media
A representative elementary volume (rev), occupying the domain \(\Omega \), of composite material is considered. Its local behavior is linear elastic with a heterogeneous stiffness tensor \({\mathbb {C}}(\underline{x})\):
An average macroscopic strain \({\varvec{E}}\) is imposed to this domain through kinematic uniform boundary conditions. More precisely, the displacement field \(\underline{\xi }(\underline{x})\) is prescribed on the boundary \(\partial \Omega \) of the rev, as:
These boundary conditions ensure that the average \(\left\langle {\varvec{\varepsilon }}(\underline{x}) \right\rangle _{}\) of the strain field arising in the rev is equal to \({\varvec{E}}\). This strain field linearly depends on the macroscopic strain due to the linearity of the equations defining the elastic problem:
Introducing the so-called strain localization tensor \({\mathbb {A}}(\underline{x})\), the macroscopic stress is then obtained by spatially averaging the microscopic stress:
The effective stiffness is then defined as the tensor relating the macroscopic stress \({\varvec{\Sigma }}\) to the macroscopic strain \({\varvec{E}}\):
When the composite material can be split into phases (domains in which the stiffness tensor is uniform), then this expression becomes:
i iterating over phases. Thus, the complete determination of the strain localization tensor field is not necessary: only averages over each phase are required. Starting from a statistical description of the morphology, these averages can be estimated by taking advantage of so-called homogenization schemes.
1.1.2 Derivation of the self-consistent scheme
The specific case of a polycrystalline material is now considered, with \(N+1\) phases. Each phase is characterized by a crystal shape and an anisotropic stiffness tensor. Each phase is present as many different crystals, differing only by crystallographic orientation, the orientation distribution being isotropic. The effective stiffness is thus isotropic.
For a given crystal of phase i whose crystallographic orientation is denoted or, the stiffness tensor is denoted \({\mathbb {C}}_{i,or}\). The average strain over all crystals of the same phase and having the same orientation in the rev is classically estimated as the strain arising in a single particle embedded into the sought effective medium (stiffness \({\mathbb {C}}^{SC}\)), with kinematic uniform boundary conditions \({\varvec{E}}^0\). This is the well-known Eshelby inhomogeneity problem [54], for which the solution is:
The Hill tensor \({\mathbb {P}}_{i,or}^{SC}\) depends on the embedding medium stiffness \({\mathbb {C}}^{SC}\) and on the shape of the particle representing orientation or and phase i. This shape is spherical for minerals (\(i=1..N\)) and oblate spheroidal for defects (\(i=N+1\)). In both cases, and with an isotropic stiffness \({\mathbb {C}}^{SC}\), the Hill tensor has an analytical expression, which can be found for example in [53]. These expressions are recalled in Sect. 1, for completeness purposes.
The average strain over all crystals of phase i is then obtained by angular average, considering the isotropic orientation distribution:
the averaging operator \(\left\langle \right\rangle _{or}\) being defined by:
with angles \(\theta ,\phi ,\) and \(\psi \) characterizing orientation of the crystal frame with respect to the reference frame (Fig. 16). Denoting \(T^u_{ijkl}\), the components (independent of \(\theta ,\phi ,\) and \(\psi \) by definition) of \({\mathbb {T}}\) tensor in crystallographic frame \((\underline{u}_1,\underline{u}_2,\underline{u}_3)\), the spherical and deviatoric components of the average tensor \(\left\langle {\mathbb {T}} \right\rangle _{or}=T_J {\mathbb {J}}+ T_K {\mathbb {K}}\), read:
The average strain over the whole rev is then evaluated through a second averaging operation over all phases:
Combining (13) with (18) yields the average strain localization tensor over phase i and orientation or. Then, Eq. (11) is used to derive the effective stiffness tensor:
This tensorial equation, projected over \({\mathbb {J}}\) and \({\mathbb {K}}\), yields two nonlinear equations, involving the effective bulk \(k^{SC}\) and shear \(\mu ^{SC}\) moduli.
1.1.3 Hill tensors expressions
The Hill tensor for a sphere in an isotropic elastic medium (Young’s modulus E and Poisson’s ratio \(\nu \)) is itself isotropic:
The Hill tensor for an oblate spheroid (aspect ratio \(\rho <1\)) in an isotropic elastic medium is transversely isotropic with major symmetry. In the frame associated to the spheroid axes (\(\underline{u}_3\) being the axis of revolution), its components in Mandel-Voigt notation are:
These 5 independent components are:
with:
Elastic tensors of rock-forming minerals
Table 3 summarizes the stiffness tensor data of the main rock-forming pristine minerals found in common rocks and used for this study. For each elastic constant, the mean value, the standard deviation, and the number of data available (in parenthesis) are provided. These data have either been obtained using experimental means (e.g., resonant frequency) or first principle–based simulations.
Irradiated rocks composition
The term felsic aggregates refers to igneous aggregates that contain relatively high amounts of quartz and feldspars, with mafic mineral content < 90%) and light chemical elements such as silicon, aluminum, sodium, and potassium, resulting in a light color and a specific gravity under 3. The 21 tested felsic rocks are subdivided as follows:
-
Seven gabbros, including two gabbros (# 14–15), a gabbro-porphyry (# 16), two diabase (# 17–18), a poikilitic diabase (# 19), and a basalt (# 20). The mineral compositions of these rocks are very similar (rich in plagioclase and low in quartz, P-corner of the double-triangle diagram). They contain a fraction of pyroxenes such as augite (clinopyroxene) and enstatite (orthopyroxene), and a minor amount of olivine.
-
Five granites, including syneo-granites (#1 and #4, 65-90% alkali feldspars content) and monzo-granites (# 2, 3, 7, 35–60% alkali feldspars content). Granites # 1–4 are composed of the same minerals (>20% quartz, alkali feldspars and a minor content of mafic minerals such as hornblende). The average grain size (a.g.s.) of granites # 1–4 ranges from medium to large except for the porphyry granite, which has a smaller grain size.
-
Three diorites: quartzic diorite (# 10), albatite (# 11, foid diorite), and labradiorite (# 12), composed primarily of plagioclases, pyroxenes, feldpathoids, micas, and small amounts of quartz. The mineral grain size of diorites here is small for both # 10 and # 11, and large for # 12.
-
Two granodiorites (# 5–6) of compositions comparable to those of granites except for a higher plagioclases content. Other minerals include hornblende, biotite, and augite.
-
Tonalite–Quartzitic andesite was the only silicate-felsic aggregate that was classified as tonalite. This class of rocks generally contains more than 20% quartz, plagioclases (mostly oligoclase and andesine), minor amounts of mafic minerals such as biotite, hornblende, or pyroxene, and usually \(< 10\%\) of alkali feldspars. The mineral grain size of tonalite is generally medium to fine.
-
Large-grain urtite (# 13, 80–90% nepheline and minor content of pyroxenes such as aegirine or augite).
-
Sandstone and laminated aleurolite were also classified with the other silicate-felsic aggregates here for the purpose of comparison. The mineral compositions of these two aggregates are very similar. The differences between sandstone and laminated aleurolite are that sandstone contains more quartz and less alkali feldspar than the laminated aleurolite. Moreover, laminated aleurolite contains a small amount of mica which was not clearly indicated in Denisov’s table [22]. The mineral grain size of sandstone is 0.3 mm, which is 10 times larger than laminated aleurolite.
Mafic aggregates are silicate aggregates that contain a large amount of mafic minerals (i.e., \(\ge \) 90%) such as olivine, pyroxene, hornblende, etc. Mafic minerals are rich with iron and magnesium. Therefore, they are dark in color and heavy in weight. Some mafic aggregates contain a minor amount of plagioclases. From this classification, six irradiated silicate aggregates fall into this classification. These include:
-
Dunite in Px-Ol-Hbl/Dunite in Cpx-Ol-Opx: Two irradiated silicate-mafic aggregates can be classified as dunite. These two aggregates are olivinite No. 23 and dunite No. 24. Dunite is usually rich with olivine mineral and contains minor amounts of clinopyroxene, orthopyroxene, spinel, and magnetite. Dunite No. 24 contains a small amount (10%) of orthopyroxene, 10% of serpentine, and the remainder is olivine, with fine grain size, while olivinite No. 23 contains mostly olivine and 5% of ore minerals, with a medium grain size.
-
OL-Pyroxene in Px-Ol-Hbl/OL-Orthopyroxene in Cpx-Ol-Opx: Pyroxenite irradiated silicate-mafic aggregate (No. 21) was classified in this work. This aggregate contains 50% of olivine mineral and 40% pyroxene (i.e., 40% clinopyroxene [enstatite]), and a minor amount of plagioclases (10%). The size of mineral grain of pyroxenite is 0.1 mm (fine).
-
Periodotite (# 22, 80% olivine, 15% orthopyroxene (15%), a.g.s.: 2 mm).
-
Hornblendite (#27, 100% hornblende, a.g.s.: 2 mm).
The remaining rock samples (# 30–35) are classified as carbonates, including two high-calcite limestones (# 30–31) and a dolimitic limestone (32: 20% dolomite), all of relatively fine grain structures \(<0.5 \hbox { mm}\). The other three irradiated sedimentary carbonates correspond to a porous fine magnesite (# 33, 99% magnesite 0.05 mm), a porous fine siderite (# 34) with a quartz content of 10 (a.g.s.: 0.04 mm), and dolomite (# 35) containing 5% siderite (a.g.s.: 2 mm).
While Table 4 is limited to silicate-bearing rocks and provides the necessary data to create Figs. 1, 2 and Table 5 provides the mineral contents of all the aggregates used to complete this study.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Le Pape, Y., Sanahuja, J. & Alsaid, M.H.F. Irradiation-induced damage in concrete-forming aggregates: revisiting literature data through micromechanics. Mater Struct 53, 62 (2020). https://doi.org/10.1617/s11527-020-01489-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1617/s11527-020-01489-6