Abstract
Aggregate segregation in asphalt mixture is a bothersome engineering issue during pavement construction. The practitioners have some measures to mitigate the segregation potential based on experiences which, however, can only reduce the risk to a certain extent. In this research, the authors aim to contribute to the discussion in a rational non-empirical way, by using novel experimental and numerical techniques. A case study is carried out to investigate the vibration-induced segregation in asphalt mixtures, corresponding to the circumstance arising during material transportation to the construction site. A novel experimental test is conducted for evaluating the segregation characteristics of asphalt mixtures under vertical vibration in laboratory conditions. A numerical investigation based on discrete element method is further performed to study the phenomenon from a micromechanical point of view. The obtained experimental and numerical results indicate that vibratory loading induces aggregate size segregation in asphalt mixtures, and the degree of segregation is influenced profoundly by the adhesive properties of bituminous binders and the aggregate gradation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Aggregate segregation in asphalt material commonly takes place in large flow situations, e.g., during truck loading, transporting, placing and paving. Without good control of these stages, inhomogeneous material properties (in terms of, e.g., air voids and stiffness) can be the consequence which, eventually, reduce the durability of pavements [1]. Practical experiences for reducing segregation potential, e.g. in [2, 3], are very helpful whereas theoretical inquiries are quite rare. Recently, some research studies have been found on quantitative evaluation of asphalt segregation in aggregate size and shape after compaction [4,5,6]. Such microstructural analyses contribute to the understanding of material properties of compacted asphalt mixtures, and therefore their performances in service. However, the governing mechanisms of aggregate segregation have received so far very limited attention. As a result, feasible tools which can assess or predict the segregation potential of asphalt mixtures are still lacking.
From a practical point of view, many factors could contribute to asphalt segregation, such as the material properties of the constituents, the device and operation parameters during handling, as well as the environmental conditions [7]. In order to unveil the causes and mechanisms from a mechanical point of view, carefully scrutinizing the flow of mixture in those large displacement situations prior to full compaction is needed. Generally, segregation in a particulate mixture is a very complex process. For instance, it has been pointed out in [8] that, driven by shear or vibration, granular materials are prone to segregate by size, shape, density and other material characteristics. In case of asphalt mixtures, the complexity of aggregate particle flow behaviour is further increased due to the lubricative and adhesive effects arising from bituminous binder.
Asphalt segregation during truck hauling from an mixing plant to the construction site is selected as the case scenario of this research. During hauling process, the possible factors which influence aggregate segregation include: (1) the temperature induced segregation after hauling, keeping in mind that normally the exterior part of material loses temperature faster than the interior part; (2) the way of truck unloading, such as end-lift dumping, belly-dumping or horizontal-push dumping; and (3) the material flow agitated by forces associated to truck vibrations due to pavement unevenness. The first two factors have been playing important roles, e.g. according to [3], whereas the effect from truck vibrations has barely been reported. The poor knowledge on vibration-induced segregation in asphalt mixtures can be largely due to the methodological difficulty of conducting a feasible measurement. Therefore, this work aims at contributing to the research by putting a prioritized focus on the vibration-induced segregation during truck hauling. The following specific objectives are formulated:
Experimental study of the particle size dependent segregation in a granular aggregate mixture caused by vertical vibration, via a relatively simple test under laboratory conditions.
Implementation of a discrete element (DE)-based numerical model to simulate asphalt flow under vibration, considering the major influences from vibratory loading parameters, material properties of aggregate and bituminous binder.
Quantitative analysis and experimental validation of the segregation caused by vertical vibration based on the microstructural information extracted from simulation, as well as gathering useful insights into the phenomenon of aggregate segregation in an asphalt mixture from those analyses.
2 Methodology
This section presents the experimental and numerical methods adopted for studying the vibration-induced aggregate segregation in both unbound mixture and hot mixed asphalt, at a small laboratory scale. In the experimental study, a customized test setup is utilized and a displacement-controlled vibration is applied. In numerical investigation, a DE model suitable for studying asphalt flow behaviour at a microstructural level is employed. The DE model used in this study is mainly based on the developments reported in [9]; it is further extended in this study to inquire the flow responses of unbound and asphalt mixtures under vibratory loading.
2.1 Experimental method and plan
Granular material has been used for the experimental study while, a customized experimental setup consisting of two separable cylindrical hollow moulds is utilized, as shown in in Fig. 1. The procedure of the proposed test method is as follows: firstly, aggregate particles are filled into a cylindrical steel container and along its depth, the loosely packed particles are separated from the middle and divided into two particle groups with equal volume, namely \(G_{\mathrm{upper}}\) and \(G_{\mathrm{bottom}}\); then, by manual sieving, the particle size distributions of \(G_{\mathrm{upper}}\) and \(G_{\mathrm{bottom}}\) before and after applying a vertical vibration are obtained and compared. Due to the difficulty in experimental handling, the effect of bituminous binder on mixture segregation is not introduced which, alternatively, will be investigated in the numerical study. The test procedure is presented below:
- 1.
Filling material Two batches of granular mixture with identical gradation and volume (1.7 kg) are prepared while, the volume of each at free packing state (i.e. without compaction) is approximate to the volume of the bottom mould. The vibration setup in Fig. 1 is assembled by fastening the moulds via fixtures on their outer wall. Thereafter, the material part of \(G_{\mathrm{bottom}}\) is slowly filled into the setup container; the other material part of \(G_{\mathrm{upper}}\) is subsequently filled on top of the first in a similar manner.
- 2.
Applying vibration A displacement-controlled sinusoidal load is vertically applied to vibrate the setup together with the mixture, at a fixed amplitude of 2 mm and frequency of 50 Hz. The vibration machine has a flexible control of vibration time, ranging from 0 to 60 min.
- 3.
Sieving analysis The molds are unfastened and by inserting a thin metallic plate in between, the particles are manually separated into two new parts of \(G_{\mathrm{upper}}\) and \(G_{\mathrm{bottom}}\). In that, a certain shear force needs to be overcome during pushing the plate. It was found easier to operate by holding the container horizontally and then inserting the plate from the top. The particle size distributions of \(G_{\mathrm{upper}}\) and \(G_{\mathrm{bottom}}\) after vibration are obtained by sieving and compared with that before vibration, giving thus an assessment of segregation.
A granular mixture made of crushed granite stones is selected for the study. The aggregate gradation curves used in experimental and numerical studies are reported in Fig. 2. For the purpose of studying the effect of vibration time on mixture’s segregation potential, a series of tests are carried out at vibration times of 0, 15, 60 min. Each test is repeated twice.
2.2 Simulation method and plan
DE method is a numerical method originally introduced by [10], which is to study the interactions among discrete elements using Newton’s second law and a force-displacement law. Asphalt mixture, nearly 90% of which is crushed stones, can also be taken as a granular system under certain assumptions. Thus, DE method shows its merit for studying the flow of uncompacted asphalt and, a number of research have been found on using the method to investigate asphalt compatibility, e.g. in [11,12,13,14]. When the unbound and asphalt mixtures are subjected to vibratory loading, several important factors could influence their flow behaviour: (1) the vibration condition, e.g., frequency, amplitude and time; (2) the material properties, e.g., gradation, shape, and density of particles; and (3) the contact interaction between particles, especially the adhesion effect from bituminous binder.
The DE modelling tool adopted for this study is based on the results of a previous study by the authors on the contact law type and parameters, particle shape, etc. [9]. The study plan is to: (1) simulate unbound and asphalt mixtures’ flow under vibration and, make a qualitative comparison with that of the experiment; (2) investigate the micromechanics of the mixture flow under vibration; (3) conduct a parametric study with respect to contact bond strength, so as to evaluate the flow and segregation at varied bitumen adhesion.
2.2.1 Model development
In a cylindrical container of 200 mm in diameter, rigid particles are randomly generated and loosely packed under action of gravity, as shown in Fig. 2. The size distribution of the particle system is identical to that in the experiment, which follows the gradation of a typical stone mastic asphalt (SMA) mixture. The aggregates’ nominal maximum size is 16 mm while, fine particles smaller than 4 mm are ignored in order to save computation time. Moreover, non-spherical particles are used to account for granular particle’s interlocking effect. As shown in Fig. 2 left, a single non-spherical particle is created by clumping five spherical pebbles of the same size. The whole particle system consists of 4603 non-spherical particles, and the piling height is approximately 10 cm. These particles are further classified into two groups based on their diametrical sizes: (1) ‘Small’ particle group with diameters ranging from 4–8 mm, taking up to 13.67% by mass; and (2) ‘Large’ particle group with diameters ranging from 8–16 mm, taking up to 86.33% by mass. As a result, aggregate segregation along the vibrational direction can be quantitatively assessed by monitoring and comparing the changes in positioning height of Small and Large particles.
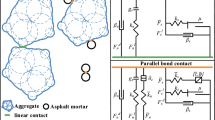
In the DE model of unbound material no binder exists and, 70/100 type neat bitumen with a content of 6.1% by weight is assumed in the asphalt mixture model. In the DE model of asphalt mixture, the bituminous coating is assumed to have a negligible thickness while its effect on particle interactions is governed by the selected contact models presented in Fig. 3. In the contact model, for both normal and shear directions, the contact force is resolved into a linear component and a dashpot component (\(\mathbf {F_c}=\mathbf {F^l}+\mathbf {F^d}\)). The linear component \(\mathbf {F^l}\) provides elastic, frictional and adhesion behaviour, while the dashpot component \(\mathbf {F^d}\) is a force imposed to account for viscous damping. When bonded, due to the adhesion force induced by bitumen, the contact behaviour is linearly elastic until the linear force exceeds the tensile or shear strength limit of the bond. After bond breakage, the behaviour is linearly elastic and the friction is accommodated by imposing a Coulomb-slip condition on the shear direction. The contact model parameters are listed in Table 1. The parameters have been calibrated based on a slump flow test in a previous work [9], except for the bond strengths \(St{_{n,s}}\). Alternatively, a parametric sensitivity study on \(St{_{n,s}}\) will be carried out based on the selected values in Table 1. Specifically, the simulation of unbound mixture flow is achieved by assigning contact bond strengths \(St{_{n,s}}\) with 0 Pa in the contact model; the simulation of asphalt flow at elevated bituminous adhesion is realized by increasing bond strengths \(St{_{n,s}}\), up to 40e3 Pa.
2.2.2 Vibration condition
In order to end up with reasonable computational times, the vibration is applied in an accelerated manner, which does not necessarily represent an actual field situation. Specifically, a displacement-controlled vibration i.e. \(\delta _v = sin(2\pi ft)\) is applied to the container with a vertical displacement amplitude \(\delta _v\) of 8 mm and a frequency f of 10 Hz. In order to investigate the effect of vibration time, continuous vibration is applied as a sequence of single loading groups, each consisting of a vibration phase of 0.5 s (i.e. 5 cycles) followed by a 0.5 s pause. In that, 0.5 s pause is the approximate time for the particles could settle down, as discussed later in Fig. 6a. The experimental test allows inquiring the long-term continuous vibration effect whereas, it can hardly be accomplished by the time-consuming numerical tool. Hence, as a compromise, the DE model simulates only a small amount of vibrations but with a high displacement amplitude.
3 Experimental test result and analysis
In order to check the capability of the approach as well as the suitability of the selected vibration condition, a pilot test was carried out. In particular, the granular particle system was initially created in a completely segregated state by filling first all Large particles (8–16mm) and subsequently placing all Small particles (4–8 mm) on top of the Large ones; thereafter, the completely segregated particle system was vibrated for 15 min. The top-views of particles’ appearance before and after vibrations are shown in Fig. 4. One can observe that due to the vibration, Large particles rise up and settle on top of Small ones. Hence, the pilot test qualitatively demonstrates the segregation phenomenon and, importantly, verifies that the selected vibration condition could affect mixture’s segregation state.
Results of segregation tests following the procedure described in Sect. 2.1 are reported below in Fig. 5. Shown in Fig. 5a, aggregate gradations of \(G_{\mathrm{upper}}\) and \(G_{\mathrm{bottom}}\) after 60 min of vibration are compared with that before vibration. One can observe that the passing rates below 11.2 mm increase in the \(G_{\mathrm{bottom}}\) mixture and, in comparison to that, a reverse trend is indicated in the \(G_{\mathrm{upper}}\) mixture. The results indicate that the particles smaller than 11.2 mm move downward by vibrating. Meanwhile, before vibration (i.e. at 0 min), the gradation curves in both \(G_{\mathrm{upper}}\) and \(G_{\mathrm{bottom}}\) groups deviate from the reference gradation curve (the one marked as ‘DE model’ in Fig. 2). The deviation is due to the error induced during material filling and plate inserting processes, as some small particles belonging to the upper part penetrate into the bottom part, resulting in a somewhat pre-segregated specimen.
In order to analyse segregation within the mixture, the mass ratio of small particles (4–8 mm) to large particles (8–16 mm) in \(G_{\mathrm{upper}}\) and \(G_{\mathrm{bottom}}\) are plotted with respect to vibration time in Fig. 5b. The mean values together with their standard errors are given in the figure plot, showing an acceptable repeatability of the test. Before vibration, in both \(G_{\mathrm{upper}}\) and \(G_{\mathrm{bottom}}\), the mass ratio of small/large particles should match with a reference value of 13.67%/86.33% =0.158 (according to Fig. 2). However, due to the pre-segregation induced during specimen filling and separation, the real measurements (0.126 in \(G_{\mathrm{upper}}\) and 0.186 in \(G_{\mathrm{bottom}}\)) deviate notably from the reference value. Under continuous vibration, the mass ratio in \(G_{\mathrm{upper}}\) decreases further while, in the long term, it tends to stabilize at a low level; correspondingly, a reversed trend of mass ratio change is indicated in \(G_{\mathrm{bottom}}\) of mixture. Therefore, though an initial pre-segregation is induced, segregation purely due to vibration is confirmed by the experiment and is non-linearly proportional to vibration time. The measurement indicates that a significant amount of small particles move downward due to the vibration whereas, the large particles are forced to rise up and settle on the top. This finding is believed to be tenable since, in general, when a graded particulate mixture is subjected to vertical vibration, large particles tend to rise and end up on top of the smaller ones, the phenomenon of which is known as Brazil Nut effect [15]. Another experimental finding is that segregation takes place further within the large particle group (8–16 mm), which is concluded by a comparison of the mass ratio of intermediate large particles (8–11.2 mm) to total large particles (8–16 mm), as shown in Fig. 5c. Similar to Fig. 5b, the trend in Fig. 5c indicates that, in an average sense, intermediate large particles with diameter of 8–11.2 mm tend to move down to the bottom while the largest particles (11.2–16 mm) settle in the upper region. Hence, the test furthermore demonstrates that, when a granular mixture is subjected to vertical vibration, the largest sized particles show greatest tendency to segregate with the surrounding smaller ones along the vibrational direction.
4 DE simulation results and analysis
By means of numerical simulation, this section presents further in-depth analysis of granular mixture’s flow and segregation under vertical vibration from a microstructural perspective and, importantly, with an extension to scrutinize the adhesive effect arising from bituminous binder.
4.1 Simulation analysis of flowability and segregation
Firstly, vertical vibration is continuously applied to the particle system of two mixtures, which are: (1) Unbound mixture, within which particle interactions are greatly influenced by sliding friction in shear direction of contact. (2) Asphalt mixture, in which particle interactions are affected by friction as well as the adhesion in normal and shear directions of the contact and, particularly, in the contact model, a low contact bond strength of 6e3 Pa is used to account for the small adhesion force of bitumen at high mixing temperature. The bond strength value of 6e3 Pa is determined based on a slump flow test on the same asphalt mixture, at a test temperature of 155 \(^{\circ }\)C [9]. In order to investigate the flow and segregation of the mixtures, the mean positioning heights of Small (4–8 mm) particles and Large (8–16 mm) particles along the vibrational direction are relied upon. In that, the positioning height of a particle is defined as the vertical distance from the centre of particle to the bottom of the container and in which, the radius of the particle is deducted in order to remove its effect. As plotted in Fig. 6a, the mean heights of small particles and large particles oscillate at a similar pace under continuous vibration. The response of unbound mixture is quite similar to that of asphalt mixture at high temperature. In order to conduct a comparison analysis with the experimental work, the unbound mixture in the simulation is further divided into an upper part and a bottom part, in a way similar to the experiment. The mass ratio of Small (4–8 mm) particles to Large (8–16 mm) particles in upper and bottom parts of the mixture are calculated and plotted versus vibration time (per vibration group) in Fig. 6b. Comparing Fig. 6b with Fig. 5b, a similar trend of mass ratio versus vibration time is observed. Therefore, vibration-induced segregation is found in the simulation and, importantly, the numerical result qualitatively agrees with the experiment. However, a quantitative agreement should not be expected, because the vibration conditions are not the same.
Based on the numerical results, an index defined as the ratio of mean positioning heights of all small particles to that of all large particles, namely \(H_{\mathrm{small}/\mathrm{large}}\), is further proposed, as it allows characterizing the segregation of the whole mixture in a more direct way. In that, \(H_{\mathrm{small}/\mathrm{large}}= 1\) indicates no segregation; \(H_{\mathrm{small}/\mathrm{large}}<1\) means segregation of large particles towards the top above the small ones (Brazil nut effect) and, \(H_{\mathrm{small}/\mathrm{large}} >1\) denotes an opposite trend of segregation. \(H_{\mathrm{small}/\mathrm{large}}\) of unbound and asphalt mixtures at the end of each vibration group are given in Fig. 6c. Obviously, the results of two mixtures are very close to each other. A relatively sharp decrease in \(H_{\mathrm{small}/\mathrm{large}}\) is noted at the beginning stage of vibration, which gradually approaches to be constant with further vibration. Hence, the simulation result of \(H_{\mathrm{small}/\mathrm{large}}\) quantitatively reveals that the vibration-induced aggregate segregation follows Brazil Nut effect, which is time dependent as well.
a Mean positioning heights of Small (4– 8 mm) and Large (8–16 mm) particles versus vibration time (s); b mass ratio of Small (4–8 mm) to Large (8–16 mm) particles versus vibration time [group], in unbound mixture; c\(H_{{\rm small}/{\rm large}}\), ratio of mean heights of Small particles to Large particles versus vibration time
In order to gain deeper insight into the mechanism of segregation, the spatial distribution of Small (4–8 mm) and Large (8–16 mm) particles after four vibration groups are virtually separated and presented in Fig. 7a, b, individually. In that, a representative cross-section volume of the specimen, obtained by a plane cut through the axis of symmetry of the cylindrical container, is shown. Since the two mixtures show nearly the same response, the plot is based on a representative cross-section volume of the whole asphalt specimen with 6e3 Pa bond strength. In that, the vertical displacements of the particles, i.e. the z-direction offset from the initial position, are also given by the contours in colour. Specifically, a positive value of z-displacement indicates that the particle has moved up after vibration while, a negative value indicates that the particle has moved down.
Figure 7 shows that along the vibrational direction, the Small (4–8 mm) and Large (8–16 mm) particles flow in a similar pattern. In that respect, the inner particles around the axisymmetric centre rise up to the top whereas the outer particles close to the wall move downward. Another contour plot of the particle’s displacement amplitude, i.e. the absolute offset distance from all directions, is depicted in Fig. 8 using arrows. The displacement amplitudes of the particles show a trend similar to the vertical displacements (Fig. 7), implying that the flow of the particles mainly occurs along the vibration direction. Furthermore, little inverse motion is observed between Small (4–8 mm) and Large (8–16 mm) particles. As a result, it is reasonable to assume that segregation is mainly driven by the difference in speed rather than the direction of the particles’ flow.
To sum up, several findings can be outlined from the above discussions: (1) Aggregate segregation along the vibrational direction is confirmed in the numerical simulation and, the analysis result quantitatively agrees with the experimental test result. (2) Both Small (4–8 mm) and Large (8–16 mm) particles produce a similar flow pattern, in which, the particles in the central area tend to rise up to the top while the ones closer to the wall of the container tend to move downward. (3) Little difference is observed between unbound mixture and asphalt mixture in a high mixing temperature environment, indicating that the small adhesion force from bitumen has a very limited influence under selected vibrating condition.
4.2 Effect of bitumen on flow and segregation
Slump tests in [9] have indicated that bitumen adhesion notably prevents aggregate particles from free flow, whereas the lubrication effect of bitumen (i.e. reduced friction) has much smaller influence. Hence, in this section, a parameter study focusing on the influence of bitumen adhesion on asphalt segregation is presented.
4.2.1 Effect of bitumen adhesion changes on flowability and segregation of asphalt mixture
Firstly, the flowability of a particle system is assessed using the total displacement of all particles, determined by summing up the individual ’flow’ distance of all particles. The ’flow’ of an individual particle is defined hereby as the displacement amplitude of the particle, i.e. the absolute offset distance from its initial position (as explained in Fig. 8). Accordingly, Fig. 9 presents the flowability (i.e. total displacement) of particle system versus vibration time at varying contact bond strength. The result displays that at different bond strength levels, the flowability is almost linearly proportional to vibration time, showing that the particle system flows at a nearly constant speed. Meanwhile, by progressively raising up contact bond strength from 6e3 Pa to 40e3 Pa, the flowability of the particle system decreases correspondingly. As a result, one can conclude that the adhesion of bitumen impedes particles from flowing under vibration. Additionally, in comparison to the asphalt mixture with very small bond strength of 6e3 Pa, slightly lower flowability is observed in the unbound mixture. Since friction dominates particle interactions within unbound mixture (not in asphalt mixture), the result confirms that shear friction prevents unbound particles from flow, but in a limited way. A similar conclusion can be found in a slump flow test in [9].
Figure 10a, b presents simulation results of \(H_{\mathrm{small}/\mathrm{large}}\) as a function of vibration time at varying contact bond strength, including the unbound and asphalt cases previously discussed in Fig. 6c. For zero to intermediate bond strength of 20e3 Pa, one can notice: (1) \(H_{\mathrm{small}/\mathrm{large}}\) decreases remarkably at first and then tends to saturate with increasing vibrating time, indicating its time dependence; and (2) \(H_{\mathrm{small}/\mathrm{large}}\) descends with raising contact bond strength, revealing that bitumen negatively contributes to the growth of segregation. At very high adhesion (bond strength \(\ge\) 30e3 Pa), asphalt flow is evoked at a delayed time, delaying also segregation. Comparing Fig. 9 with Fig. 10a, one can learn that a prerequisite for asphalt to segregate is that the particles in the mixture must have certain capability to flow. However, the segregation determined by \(H_{\mathrm{small}/\mathrm{large}}\) does not show any proportional relationship with bitumen adhesion and flowability of the mixture. This is also illustrated by replotting \(H_{\mathrm{small}/\mathrm{large}}\) versus contact bond strength, as shown in Fig. 10b. In that, \(H_{\mathrm{small}/\mathrm{large}}\) appears to be the lowest at bond strength of 20e3 Pa, indicating that the mixture shows highest degree of segregation at a medium level of bitumen adhesion. The finding can be indicated in a more intuitive way by plotting \(H_{\mathrm{small}/\mathrm{large}}\) versus bond strength at varied vibration groups, as shown in Fig. 10c. In order to have a better understanding of this, an in-depth discussion on the microstructural flow behaviour of the mixture will be made in the forthcoming subsection.
4.2.2 Micromechanics of vibration-induced flow
The mean heights of Small (4–8 mm) and Large (8–16 mm) particles, which have served as inputs for Fig. 10, are plotted in Fig. 11. These mean heights are determined by the individual flow of the particles, which are greatly influenced by their contact interactions. Hence, contact status within the particle system is examined and their evolution with vibration time is presented in Fig. 12, which includes: (a) total number of contacts; (b) percentage of the bonded contacts; (c) percentage of the contacts breaking in tension; and (d) percentage of the contacts breaking in shear. Figure12a shows that for all bond strength levels, the total number of contacts within the mixture vary little across the vibration process. Figure 12b displays that with continuous vibrations, the amount of bonded contacts gradually reduces, the reduction being greater in the mixture with a lower contact bond strength. This change corresponds to the increase in contact bond breakages in normal direction (Fig. 12c) and shear direction (Fig. 12d). Obviously, breakage especially happens in normal direction.
Based on the contact status results presented in Fig. 12, the mean height changes reported in Fig. 11 can be explained as follows:
- 1.
At very low contact bond strength (e.g., 6e3 Pa), most bonds break at very early stage of vibration and the majority of particles are allowed to flow readily; with continuous vibration, small particles flow and pass through the interspaces easier than large particles, thus causing to a notable decrease in the mean positioning height of small particles after settling down.
- 2.
At intermediate bond strength (e.g., 20e3 Pa), the flow behaviour of particles is becoming complex due to the increased adhesion at the contact points. As indicated in Fig. 11, at the initial stage of vibration, some particles are experiencing breakage or sliding while, at the same time, a considerable amount still has bonded contacts with neighbouring particles. Particles with little bonding force could flow under vibration, but are difficult to revert, especially the large ones. This can be due to the large forces imposed by the adjacent bonded particles, hindering particles from free flow after the removal of vibration. With further vibration, more bond breakages occur, which promote particles to flow and consequentially, a dense packing state is received again. This process corresponds to the change from increase to decrease in mean height of large particles, as well as mean height drop of small particles.
- 3.
At very high bond strength (e.g., 30e3 Pa and above), particles can hardly flow and the change in mean height is minor. However, as indicated in the plot, flow can still be agitated by continuous vibration and, followed by that, segregation occurs as well.
To summarize, the DE simulation study shows a possibility to estimate the vibration-induced aggregate segregation in an asphalt mixture by analysing the changes in the positioning heights of particles, as well as the micromechanical behaviours within the mixture. Particularly, the important influence of the bitumen adhesion on the flow and segregation of asphalt mixture is reasonably revealed.
5 Conclusions
By using novel experimental and numerical approaches, flow of asphalt and unbound mixtures under vertical vibrations have been investigated in this work. In the experimental study, vibration-induced segregation of unbound mixture has been studied. Firstly, a novel test method has been developed in order to evaluate vibration-induced particle segregation in granular-like mixture. Then, experimental case studies are further carried out and the results show that due to the imposed vertical vibration:
- 1.
Aggregates in granular mixture segregate in their sizes, with large particles rising up and settling on top of the smaller ones; likewise, the largest particles show the greatest tendency to segregate.
- 2.
The degree of segregation increases with vibration time, while the segregation rate is decreasing with vibration time.
A discrete element (DE) model for studying the flow of both unbound and asphalt mixtures under vibration has been further implemented for a numerical analysis. In that respect, advisable indexes are proposed to quantify the flow and segregation of the mixtures under vibration. The segregation observed numerically for the case of unbound mixture is in qualitative agreement with the experimental result, which validates the capability of the developed model. The influence of binder on asphalt mixture’s flow has been taken into account by modifying the contact law parameters in accordance with the previous study in [9]. In particular, the friction coefficient has been reduced and adhesive bond has been added to the contacts in order to account for the lubricative and adhesive effects from bitumen. From simulations of asphalt flow under vibration, it has been observed that:
- 1.
When the temperature is sufficiently high, the bitumen adhesion is too weak to significantly interfere with the mixture flow and, therefore, the flow characteristics observed numerically for the case of asphalt mixture is close to that of unbound granular mixture.
- 2.
An increase in bitumen adhesion (e.g. due to temperature drop) effectively prevents mixture flow and, accordingly, reduces the aggregate segregation.
- 3.
Segregation in an asphalt mixture is greatly influenced by its total flowability whereas, a clear correlation has not been established due to the complex microstructural activities involved within.
Furthermore, it has to be pointed out that the observations reported above apply only to the vibration conditions used in the present study. Their validity for other vibration amplitudes and frequencies still needs to be examined.
Abbreviations
- \(\mathbf {F_c}\) :
-
Contact force
- \(\mathbf {F^l}\) :
-
Linear force component
- \(\mathbf {F^d}\) :
-
Contact force component
- \(\mathrm{St}_{\mathrm{n},{\mathrm{s}}}\) :
-
Normal and shear strengths
- \(T_{\mathrm{F}}\) and \(S_{\mathrm{F}}\) :
-
Tensile force and shear force
- \(\beta _{\mathrm{s}}\) and \(\beta _{\mathrm{n}}\) :
-
Normal and shear critical damping ratios
- \(g_{\mathrm{s}}\) :
-
Surface gap
- \(g_{\mathrm{c}}\) :
-
Contact gap
- \(g_{\mathrm{r}}\) :
-
Reference gap
- \(\delta _{\mathrm{s}}\) :
-
Relative shear displacement
- \(k_{\mathrm{n}}\) and \(k_{\mathrm{s}}\) :
-
Contact normal and shear stiffness [force/length]
- \(F_{\mathrm{n}}^{\mathrm{l}}\) and \(F_\mathrm{s}^\mathrm{l}\) :
-
Normal and shear components of the linear force
- \(\mu\) :
-
Coefficient of sliding friction
- f :
-
Frequency (Hz)
- \(\delta _\mathrm{v}\) :
-
Vertical displacement of vibration (mm)
References
Kwon O, Choubane B, Hernando D (2019) Evaluation of the impact of asphalt mix segregation on pavement performance. Transp Res Record 2673(1):310–316
Kennedy TW, Tahmoressi M (1986) Segregation of asphalt mixtures–causes identification and cures. In: Austin, U.S.: American Association of State Highway and Transportation Officials
Stroup-Gardiner M (2015) Methods and practices on reduction and elimination of asphalt mix segregation. National Cooperative Highway Research program, Washington, DC
Williams RC, Duncan G Jr, White TD (1996) Hot-mix asphalt segregation: measurement and effects. Transp Res Rec 1543(1):97–105
Masad E, Tashman L, Somedavan N, Little D (2002) Micromechanics-based analysis of stiffness anisotropy in asphalt mixtures. J Mater Civ Eng 14(5):374–383
Zhang Y, Luo R, Lytton RL (2011) Microstructure-based inherent anisotropy of asphalt mixtures. J Mater Civ Eng 23(10):1473–1482
Tang P, Puri VM (2004) Methods for minimizing segregation: a review. Part Sci Technol 22(4):321–337
May LBH, Golick LA, Phillips KC, Shearer M, Daniels KE (2010) Shear-driven size segregation of granular materials: modeling and experiment. Phys Rev E 81(5):051301
Chen F, Jelagin D, Partl MN (2019) Experimental and numerical analysis of asphalt flow in a slump test. Road Mater Pavement Des 20:S446–461
Cundall PA, Strack ODL (1979) A discrete numerical model for granular assemblies. Geotechnique 29(1):47–65
Chen J, Huang B, Shu X, Hu C (2014) DEM simulation of laboratory compaction of asphalt mixtures using an open source code. J Mater Civ Eng 27(3):04014130
Roozbahany EG, Partl MN (2016) A new test to study the flow of mixtures at early stages of compaction. Mater Struct 49(9):3547–3558
Gong F, Liu Y, Zhou X, You Z (2018) Lab assessment and discrete element modeling of asphalt mixture during compaction with elongated and flat coarse aggregates. Constr Build Mater 182:573–579
Erik O, Denis J, Partl Manfred N (2019) New discrete element framework for modelling asphalt compaction. Road Mater Pavement Des 20(sup2):1–13
Möbius ME, Lauderdale BE, Nagel SR, Jaeger HM (2001) Brazil-nut effect: size separation of granular particles. Nature 414(6861):270
Acknowledgements
Open access funding provided by Royal Institute of Technology. The authors would like to acknowledge the financial support from Swedish Research Council under FORMAS with Project Grant No. 2012-1349.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Human and animal rights
This article does not contain any studies with human or animal subjects.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, F., Jelagin, D. & Partl, M.N. Vibration-induced aggregate segregation in asphalt mixtures. Mater Struct 53, 27 (2020). https://doi.org/10.1617/s11527-020-01459-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1617/s11527-020-01459-y