1 Introduction

Macroscopically, concrete is a linear-viscoelastic, age- and stress-stiffening material that shrinks in environments with relative humidity less than 96–98%. It exhibits creep under sustained stresses in sealed condition and additional drying creep in environments with relative humidity less than 96–98%. Following the traditional definition of concrete creep, a majority of researchers have performed their experimental studies on creep under sustained compressive stresses, although concrete structures during their service life [1, 2] are rarely subjected to them. But, load variations with rather low up to very high repetition rates with the notion of fatigue effects [3, 4] dominate.

Nowadays, experimental and theoretical investigations of the concrete’s viscoelasticity are often focused on specific concrete types like high-strength [5], steel fibre [6], lightweight [7], high-volume fly ash [8] and recycled aggregate concrete [9] or on various types of stresses like creep under tension [10,11,12], flexure [12] or torsion [13].

In the past, investigations of the reversibility of creep attracted wide attention, and as a result, it was confirmed that only a part of creep is recoverable. However, understanding of the creep reversibility under frequently repeating stresses is still incomplete.

Groups of researchers in Europe [14,15,16,17] and in the United States [18] have made successful efforts to experimentally investigate and describe concrete creep under variable stresses. However, keeping in mind that their aim was to check the principle of superposition and not to simulate the real variations of the working loads (which are repeatable in nature), they have created stepwise stress histories (e.g. “staircase” increasing loads, “staircase” decreasing loads or combination of both). Therefore, all conclusions concerning creep and its reversibility under variable loads, as well as its mathematical modeling, are based on these results.

One part of these experimental investigations leads to qualitative conclusions concerning reversibility of creep under variable stresses, like the influence of load histories [19,20,21], stress levels [19, 20] and concrete strength [19] on the final value and time development of creep recovery. Experimental results by Mullick [20], Mei [21], Yue and Taerwe [19], Freudenthal and Roll [22] and Chai [23] indicate that the recoverable part of creep increases with the age of first loading, while it decreases if the duration under load increases. Experimental investigations of Yue and Taerwe [19] suggest linear relations between creep recovery and stress levels, with a minor influence of the concrete’s strength. Rossi [24] came up to similar conclusions while analysing creep and creep recovery behavior of sealed and unsealed specimens subjected to various stress levels (30%, 50% and 70% of fc). Among them, only Mullick [20] considered load histories including more than one loading and unloading cycle. However, the histories cannot be considered as repeating ones.

Another part of experiments is focused on the quantitative conclusions of the creep recovery, expressed either as a fraction of the experienced creep [23, 26] or as a fraction of the instantaneous elastic strain [17, 25]. Chai’s tests [23] indicate that for concrete initially loaded at a relatively early age (12 to 28 days), recovery of 10 to 20% of the creep can be expected. Gamble and Parrott [26] arrived at similar conclusions investigating the effect of variable stresses and variable moisture history on creep and creep recovery. They concluded that basic and drying creep are recoverable to the same extent, but to only 20% to 25% of the original creep. On the other hand, Gardner and Tsuruta [27] found out while studying the validity of superposition principle for all three hygral conditions (drying before loading, loading before drying and sealed condition) that creep recovery corresponds to 70 to 80% of the creep of previously never loaded concrete for loads applied at the same age as the recovery.

Recently, the recovery behavior was investigated at a microscopic level and the influence of the cement paste porosity as well as of the volume fractions of solid phases was studied [28].

In the view of the majority of the above-mentioned researchers, only delayed elasticity is a recoverable component of creep. But, Freudenthal and Roll [22] additionally consider the influence of sustained load durations as well as the influence of environmental conditions on the reversibility. According to them, at the removal of the applied load, there is an instantaneous recovery, always followed by a delayed elastic recovery. Additionally, the deformation due to the flow of the absorbed water from cement gel (creep deformation) may be completely recoverable, partly recoverable, or irrecoverable, depending on the environmental conditions and the duration of the sustained load.

Apparently, there are plenty of experimental investigations regarding creep recovery of concrete under different loading histories. However, investigations of the reversibility and irreversibility of concrete creep under repeating loads have received minor attention.

From a practical perspective, tests including repeating loads are of particular interest since many concrete structures are typically subjected to similar loading pattern. Traffic passing over bridges, cars in traffic areas of parking garages, storage material in warehouses and other comparable loading scenarios create loading periods followed by unloading ones.

This paper investigates the reversibility of creep under repeating stresses by testing concrete specimens under different loading and drying conditions. To replicate the real field conditions, the study involves different stress levels (test series 1) as well as different hygral states of concrete (test series 2), considered within two independent experimental studies.

A special emphasis is placed on the ratio between recoverable and total creep in each subsequent loading and unloading cycle for different stress and drying histories. Investigation of this ratio deserves special attention as the irrecoverable creep strain acts cumulative under repeating loads which largely contributes to the over- or underestimations of the predicted total creep strains.

The tests will serve to clarify the structural behaviour under frequent, but still longer-term loadings and unloadings.

The paper is organized into five sections. A brief introduction and literature review on the reversibility phenomenon is presented in the first section, after which a detailed overview on the time-dependent strain components follows (Sect. 2). Section 3 presents the experimental program along with the developed setups. Finally, the test results and the effects of stress levels and drying conditions on the recovery phenomenon are discussed (Sect. 4). Moreover, selected outcomes from recalculations of tests are given and compared to the experimental results.

2 Decomposition of time-dependent strains

At a time t, under constant stress and temperature, the total concrete strain εc(t) consists of: instantaneous strain εi(t0), creep strain εcc(t,t0) and shrinkage strain εcs(t,ts). They can be roughly divided into time-dependent and time-independent, stress-induced and stress-free, and finally, recoverable and irrecoverable components. Part of the initial instantaneous strain εi(t0) is perfectly elastic εe(t0) and the other part, mostly resulting from microcracking, is inelastic εip(t0). At the removal of applied loads, a distinction should be made between instantaneous recovery εe(te), generally very close in absolute value to the instantaneous strain at the same age, and the total recovery εrec.tot., which is defined by the difference between the strain measured after unloading εres and the strain that would have been recorded at the same age if there had been no unloading εc(t) [29] (Eq. 1).

$$\varepsilon_{\mathrm{rec. tot.}} = \varepsilon_{\mathrm{e}} + \varepsilon_{\mathrm{cr.rec.}} = \varepsilon_{\mathrm{c}} - \varepsilon_{{\mathrm{res}}} = \varepsilon_{\mathrm{c}} - \varepsilon_{{\mathrm{cs}}} - \varepsilon_{{\mathrm{cr.f}}}$$
(1)

The creep recovery εcr.rec. can accordingly be defined as:

$$\varepsilon_{{\mathrm{cr.rec.}}} = \varepsilon_{\mathrm{c}} - \varepsilon_{\mathrm{e}} - \varepsilon_{{\mathrm{cs}}} - \varepsilon_{{\mathrm{cr.f}}}$$
(2)

The recoverable part of creep is often referred to as the delayed elastic strain εcr.d(t)–a consequence of the interaction between predominantly viscous cement paste and predominantly elastic aggregates [15]. The major share of the creep strain is irreversible and often referred to as the flow εcr.f(t). There are several explanations about the flow mechanism. Among the most accepted are the ones explaining it through the role of the water and its redistribution within the porous cement paste. Two different sources are responsible for short-term (reversible) and long-term (irreversible) creep, both compatible with the water mobility. The short-term creep mechanism is related to the stress-induced water movement in the capillary pores. The long-term creep is caused by mechanism that is more associated with the sliding of the viscous sheets in the cement gel between the layers of absorbed water [30]. The latter mechanism is extensively studied and supported by various experimental and theoretical (micromechanics-based) studies [31].

The flow component of creep is sometimes subdivided into rapid initial flow εcr.fi(t) and remaining flow εcr.f(t). The remaining flow can be further divided into basic flow εcr.fb(t) and drying flow εcr.fd(t) (Fig. 1) [29].

Fig. 1
figure 1

Time-dependent strain components (top) and drying conditions’ analogy (bottom)

Full size image

In structural analysis, it is unusual to subdivide the creep component into all of these sub-components. However, consideration of the recoverable and irrecoverable components of creep becomes necessary, if concrete is subjected to time-varying stress histories [29].

Concrete creep within an element of a cross-section is non-uniform with respect to moisture. For instance, at the initial state when the load is applied for the first time, the concrete has not yet lost much of its initial moisture [15] and therefore, creeps in sealed conditions. Later and near the surface of a member, creep takes place in a drying environment and develops different from the creep in the regions remote from a drying surface [32].

Therefore, where a more fundamental approach is warranted, a distinction should be made between concrete creep under different hygral states. The basic testing of creep and shrinkage considering the drying conditions deals with two simple cases: the case without moisture exchange with the environment, in which the specimen is sealed, and the case of drying in a stable environment typical for practical situations (in which the specimen is unsealed). The former case is relevant to mass concrete and also to the core of thicker cross sections, like in large bridges, supertall building columns, tunnels and dams. The latter case typifies thin cross sections, but it is also relevant for the behavior of a surface layer in thick cross sections (Fig. 1). In the first case, the loaded specimen exhibits a hygral equilibrium with the ambient medium (i.e. no drying) and only time-dependent, stress-induced strains known as basic creep appear. In the second case, additional creep shares occur, known as drying creep [32].

The total longitudinal strain of sealed specimens εtotsealed consists of the instantaneous elastic strain εe, the rapid initial strain εcr.fi, the basic creep strain εcr.fb and the autogenous shrinkage strain εas yielding:

$$\varepsilon_{{\text{sealed}}}^{{\text{tot}}} = \varepsilon_{\text{e}} + \varepsilon_{{\text{cr.fi}}} + \varepsilon_{{\text{cr.fb}}} + \varepsilon_{{\text{as}}}$$
(3)

I.e. the load-induced strain in sealed specimen reads:

$$\varepsilon_{{\text{sealed}}}^{{\text{tot}}} - \varepsilon_{{\text{as}}} = \varepsilon_{\text{e}} + \varepsilon_{{\text{cr.fi}}} + \varepsilon_{{\text{cr.fb}}}$$
(4)

In case of unsealed specimens the total longitudinal strain εtotunsealed consists of two shares more, namely the drying creep strain εcr.fd and the drying shrinkage εds:

$$\varepsilon_{{\text{unsealed}}}^{{\text{tot}}} = \varepsilon_{\text{e}} + \varepsilon_{{\text{cr.fi}}} + \varepsilon_{{\text{cr.fb}}} + \varepsilon_{{\text{cr.fd}}} + \varepsilon_{{\text{as}}} + \varepsilon_{{\text{ds}}}$$
(5)

The load-induced strains in unsealed specimens can then be obtained similar to (4), where εds expands the left side of the equation:

$$\varepsilon_{{\text{unsealed}}}^{{\text{tot}}} - \varepsilon_{{\text{as}}} - \varepsilon_{{\text{ds}}} = \varepsilon_{\text{e}} + \varepsilon_{{\text{cr.fi}}} + \varepsilon_{{\text{cr.fb}}} + \varepsilon_{{\text{cr.fd}}}$$
(6)

This decomposition is based on the assumption of the additive composition of the strain component, although not strictly correct [29]. Consequently, the combined autogenous and drying shrinkage strain in a loaded specimen is assumed to comply with the one in a load-free specimen, as well as basic creep strains are assumed to be of same extents in sealed and unsealed specimens [33].

3 Experimental investigation

Over a one-year period, two independent experiments were organized to provide a better understanding of the reversibility of concrete creep under different repeating stress histories and drying conditions. They are performed in the Structural Testing Laboratory at Ruhr University Bochum (Germany).

The aim of the first series of experiments was to assess the influence of different stress/strength ratios R = σc/fc on the reversibility of creep in each loading/unloading cycle, while the second series aimed to assess the influence of different drying conditions.

Table 1 gives an overview on the test setups, specimens types, curing conditions, stress to strength ratios and loading histories to yield the specific aims. Denotations and subscripts are defined at the bottom of the table.

Table 1 Overview of the experimental program
Full size table

Variables in the first test series were stress to strength ratios at loading RL and unloading RU. All specimens were kept under the same conditions and were allowed to dry during the entire test. Conversely, variables within the second test series were drying conditions as well as the type of a stress history. Specimens with two different drying conditions (sealed and unsealed) were studied under the same repeating and sustained stress histories. Here, the constant stress tests were performed to study the influence of the loading history on the total creep extent and the final residual strain.

The stress levels in both experiments were chosen between 30 and 45% of the compressive strength fc to stay in linear ranges and comparable to practical applications. The duration of the loading to unloading cycles (8 h/16 h and 12 h/12 h) was chosen to replicate typical live load variations in daily used concrete structures.

The studied concrete in both experiments was chosen to a standard C30/37 with no additives. Its mix design is given in Table 2.

Table 2 Concrete mix (per m3 of concrete) and results of pretests
Full size table

Cylindrical specimens d/H = 150/300 [mm], corresponding to the specimens used for the creep tests, were produced to test the compressive strength and the modulus of elasticity. After aging of 24 h, the specimens were demoulded and cured in 20 °C water until the start of the tests to prevent them from self-desiccation. Short time tests were performed on 6 samples at the concrete age at which the creep tests begin, in accordance to the specifications provided by the ASTM C 39/C 39M [34] and the ASTM C 469 [35].

Table 2 summarizes the results of the pretests together with their statistical parameters (mean value μ, standard deviation σ and coefficient of variation COV).

3.1 Test series 1 (Variables: stress level; unloading level)

Series 1 was carried out with a duration of 43 days. Five standard cylinders in total were involved. Two of them (SH1) were tested under repeated stresses consisting of cycles of 8 h loading followed by 16 h of full unloading. One of them (SH1_1) was subjected to a ratio RL of 45% of fc, while the other (SH1_2) was subjected to RL = 0.30. Another two specimens (Series SH2) exhibit a partial unloading. The level of unloading was chosen to the half of the corresponding loading level, so 0.225 fc in case of RL = 0.45 and 0.15 fc for RL = 0.30. The pattern of cycling remained the same. All creep specimens were loaded at the age of 24 days. The last specimen (SH0) was used as a companion specimen to observe the load-free strains of concrete (e.g. shrinkage strains, strains due to temperature and moisture variations, etc.). It should be noted however, that a part of the initial shrinkage (drying as well as autogenous one) during the equipping process, remained unrecorded.

Strains were measured by three strain gauges for each sample attached uniformly around the specimen’s periphery (0°, 120°, 240°) in the central portion of the specimen’s height. The chosen gauge length of 100 mm corresponds to the ASTM Standard C512/C512M [36], where a length not less than three times of the maximum aggregate size (dmax = 16 mm) is recommended. Strain data were recorded each second (1 Hz) to provide a precise measurement of the instantaneous strain and the initial rapid creep.

The duration of the loading and unloading sequences of SH1 and its complete unloading process, enabled to use only one hydraulic testing machine for an alternate testing of both specimens, SH1_1 (0.45 fc) and SH1_2 (0.30 fc). During the unloading of SH1_1, SH1_2 was stressed and vice versa.

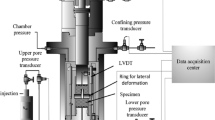
For SH2, a special test setup (Fig. 2 left) was developed to allow for a simultaneous testing of two specimens with different stress to strength ratios.

Fig. 2
figure 2

Setup for simultaneous loading and partial unloading of two specimens (SH2-test series 1) (left); Testing setup for sustained compressive test (specimens B-test series 2) (right)

Full size image

Introducing a single span steel girder and adjusting the lever arms to the stress ratio, the required stress level in both specimens was achieved.

Two calottes (d/H = 200/100 [mm]) were placed between the specimens and the girder’s surface to avoid a bending effect.

3.2 Test series 2 (Variables: drying conditions; stress history)

Series 2 was carried out with a duration of 16 days and involved 8 creep and shrinkage specimens. Two of them belong to series A (A1-sealed and A2-unsealed) and were subjected to identical repeated stress pattern. The stress pattern consisted of cycles of 12 h of loading (RL = 0.40) followed by 12 h of full (RU = 0) and partial (RU = 0.20) unloading (column 5 of Table 1). Two other specimens (B1-sealed and B2-unsealed) with identical drying conditions and loading age (t0 = 28 days) as those in series A, were exposed to sustained stress with a ratio RL of 0.40.

Series C and D consist of unstressed sealed and unsealed specimens, respectively. They were used to establish the shrinkage strains (autogenous and drying one) under identical atmospheric conditions.

All specimens were casted, prepared and equipped in an identical way to the specimens from test series 1.

Strains in the case of cyclic creep and shrinkage tests were recorded by strain gauges, while a portable extensometer was used in the case of constant creep tests. To prevent loss of moisture by evaporation, all specimens intended for autogenous shrinkage (C1 and C2) and basic creep (A1 and B1) were sealed immediately after their equipment with the measuring devices. The sealing was done by confining the specimens with a butyl-caoutchouc aluminium self-adhesive foil complying with the provisions in the ASTM C512/C512M [36] and the RILEM Recommendation [37]. The end faces of the basic creep specimens were sealed by means of liquid sealant that was a three-millimetre-thick layer of two-component epoxy.

For the specimens devoted to creep and shrinkage tests in unsealed conditions, the age of an exposure to drying was chosen corresponding to the age of first loading (t0 = ts = 28 days).

For simultaneous loading with repeated histories, the sealed (A1) and the unsealed (A2) specimens were mounted on top of each other in a hydraulic testing machine (type SCHENCK). Two calottes were placed to minimize a possible bending effect.

For the purpose of testing creep under sustained compressive loads, a spring-loaded frame capable of applying and maintaining a required load was constructed (Fig. 2 right). This rigid steel frame allows for a simultaneous loading of two specimens. It consists of: upper and lower loading plates; a middle plate-spacer; a load maintaining element-spring and threaded rods to connect the loading plates and take the reaction of the loading system.

A set of six springs arranged as shown in Fig. 2 (right) was used as a load maintaining element. After applying the initial compression with the hydraulic testing machine, the four nuts on the threaded rods were tightened. Periodic measurements of the applied load were performed through a permanent monitoring of the springs’ deformation change in order to verify that the force in the frame remained almost constant. In accordance to ASTM C512/C512M [36] and the RILEM Recommendation [37], each time a 2% loss of force was observed, the load in the frame was readjusted to the required value.

4 Results and discussion

4.1 Influence of stress history under uniform drying conditions

The experimental results of test series 1 are summarized in Figs. 3 and 4. They include the stress-induced strain evolution over time for the specimens SH1 and SH2 as well as the stress-free strains recorded on the companion specimen SH0.

Fig. 3
figure 3

Stress-induced and stress-free strain evolutions versus time for the specimens SH1 and SH0

Full size image
Fig. 4
figure 4

Stress-induced and stress-free strain evolutions versus time for the specimens SH2 and SH0

Full size image

The two fluctuating curves of Fig. 3 exhibit the expected steplike pattern of loading and unloading showing the daily change with breaks at weekends as well as creeping and recovery increments. They alternate in time due to the chosen interactive loading regime that loads one specimen while the other one recovers.

In the case of specimens SH2 (Fig. 4) loading and unloading go hand in hand due to the beam concept and unloading as well as recoveries become less pronounced due to the residual loading of one half of its maximum. It should be mentioned that the specimens SH2 exhibit an unintended unloading in the first cycle due to a disconnection of the machines. However, further results remain almost unaffected.

Test series 1 focuses on obtaining qualitative data on the amount of creep and creep recovery under repeated stresses with different loading (0.30 fc and 0.45 fc) and unloading (full and partial) levels.

The creep (black dots) and the recovery increments (grey dots) in each loading/unloading cycle of SH1_1 and SH1_2 are plotted in Figs. 5 and 6, respectively. Each individual increment is determined as a difference between the measured strains for two subsequent load changes. Thus, the creep increment here refers to the deformation gain within the loading cycle, while the recovery increment is considered as the deformation reduction in the unloading cycle.

Fig. 5
figure 5

Creep increments (black dots), recovery increments (grey dots) and their ratio over time for SH1_1 (0.45 fc)

Full size image
Fig. 6
figure 6

Creep increments (black dots), recovery increments (grey dots) and their ratio over time for SH1_2 (0.30 fc)

Full size image

For both stress levels, the results demonstrate a reduction in the creep response in each subsequent loading cycle. It is especially pronounced within the first cycles and gradually stabilizes in the later ones. This reduction has already been observed by Mullick [20] for variable, non-cyclic stress histories. It has been explained as a result of stabilization of microstructural changes in the cement paste caused by the previous stress history. Bažant considers it similarly in [18], emphasizing the markedly stiffer response to subsequent load increments caused by previous sustained stresses of low levels.

The creep reduction in each loading cycle for SH1_1 and SH1_2 is satisfactorily described by a power law (R2 = 0.89 − 0.95), using the nonlinear least squared method.

It is remarkable to note that the reduction of the recovery within the loading cycles is not as pronounced as in the case of creep, especially for the first few cycles (Figs. 5 and 6). One explanation might arise from the fact that the recoverable creep is ascribed in a great measure to a delayed elasticity which under the same loading and unloading durations depends exclusively on the instantaneous strain [15]. Hence, the observed small recovery variation with a decreasing tendency in each loading cycle is expectable to a certain extent. The change of creep recovery in each cycle is described here by a linear function, although not as satisfactorily as for the creep (R2 = 0.61−0.65).

The insets in the Figs. 5 and 6 present the developed creep-recovery/creep ratio in each loading/unloading cycle over the considered time. Regardless of the stress level, this ratio increases over time with a tendency to approach unity. It means that after a sufficient number of loading/unloading cycles, the whole creep share in the loading cycle will be fully recovered in the following unloading one. In the view of several authors [18, 39], it also indicates that the hydration process is over and that no more new bonds are developed to restrict the process of reversibility. The obtained results fall in line with the previous experience in [20, 21] where it was found that the more mature the concrete is at the time of reloading, the higher turns out the creep recovery. Mullick’s results [20, 39] indirectly reveal a similar trend. They show that the proportion of the irreversible creep decreases with increasing the ratio of the concrete strength at loading and unloading. This ratio can increase either when the load is applied at mature concrete, or when the loading cycle is of short duration. This partly explains the high proportion of the creep recovery in the later cycles of the repeated stress histories considered here.

The comparison between the specific creep (creep per unit stress) under both stress levels, 45% (SH1_1) and 30% (SH1_2) of fc, is shown in Fig. 7. In addition, the actual creep increments are presented in the inset of the same figure.

Fig. 7
figure 7

Specific and actual creep in each cycle for SH1_1 (0.45 fc) and SH1_2 (0.30 fc)

Full size image

The results demonstrate a similar specific creep for both stress levels, however, slightly higher for the level of 0.45 fc (11% in average/max 28%). This might be caused by a certain share of non-linearity due to first microcracking at the stress level of 45% of fc, that exceeds a linear creep threshold (cp. e.g. [38]).

To better analyse the influence of the stress level on the recovery behavior, specific recovery increments are compared (Fig. 8). Similar to the specific creep, somewhat higher specific recovery is observed for a higher stress level at loading. Similar conclusions can be found in [12, 20, 24, 32] for the specific strain components, however under sustained stresses.

Fig. 8
figure 8

Specific and actual recovery in each cycle for SH1_1 (0.45 fc) and SH1_2 (0.30 fc)

Full size image

The creep-recovery/creep ratio is plotted over time for the specimens subjected to partial unloading (SH2_1 and SH2_2) (Fig. 9). It should be emphasized that it does not present a ratio between the total creep recovery and the creep, as it was the case with the specimens exhibiting complete unloading (SH1). Here, a pronounced residual stress persists.

Fig. 9
figure 9

Creep-recovery/creep ratio for SH2_1 (0.45 fc) and SH2_2 (0.30 fc)

Full size image

Due to the partial unloading, the measured strain in this sequence presents a sum of two opposite time-dependent strains, namely creep recovery due to the removal of the stress and ongoing creep due to the remained stress.

The time development of this ratio can be described by a power law (R2 = 0.87−0.90), similarly to the case with a full unloading. During the entire test period, the creep-recovery/creep ratio is slightly higher for the stress level of 45% of fc. At the end of the test, it reaches a maximum value of 0.80 (neglecting the out-layer from SH2_1) regardless of the stress level.

The creep increments in each loading cycle for all specimens involved in the study are shown in Fig. 10.

Fig. 10
figure 10

Creep increments over time for SH1_1 versus SH2_1 and SH1_2 versus SH2_2

Full size image

Although the specimens SH1_1 and SH2_1 (as well as SH1_2 and SH2_2) are subjected to the same stress levels during the loading, they creep differently in that sequence.

The creep increments are continuously higher for the stress history containing full unloading. This may suggest that under repeated stresses, the creep ability in the loading sequence is affected by the stress level from which the load is reapplied.

4.2 Influence of stress history under different drying conditions

The aim of test series 2 was to observe the influence of the drying conditions and the type of stress history on the recoverable part of the creep.

The stress-induced (specimens A and B) and the stress-free strain evolutions (specimens C and D) over time are summarized in Fig. 11.

Fig. 11
figure 11

Stress-induced and stress-free strain evolutions versus time for the specimens A, B, C and D

Full size image

For all specimens involved in the tests, comparisons between the following strain components are tabularly arranged, namely: (1) final residual strain, (2) initial instantaneous strain, (3) instantaneous recovery strain, (4) total stress-induced strain (instantaneous plus creep), (5) sum of creep increments and (6,7) sum of recovery increments (see Fig. 11 and Table 3).

Table 3 Comparison of the stress-induced strain components of series A and B
Full size table

Regardless of the type of the stress history, larger residual strains (1) recorded at the end of the tests were observed for the specimens allowed to dry during the loading (A2 and B2). The reason is evident. In unsealed specimens, the basic creep component is accompanied by additional drying creep, which–according to results in the literature [39, 40]–participates with 56 to 68% in the total recorded creep.

For all specimens, the instantaneous elastic strain recovered upon removal of the sustained stress (3) is less than the initial instantaneous strain that occurs when the stress is applied for the first time (2). Permanent changes in the concrete structure due to the sustained load and the time-dependence of the modulus of elasticity are probably responsible for such differences.

The stress-induced strains before the final unloading (4) are 0.6 to 3.5% higher for specimens subjected to constant stresses. Therefore, the differences between the creep ratios φ determined for the repeated and the constant stresses are negligible (2.6–7.1%).

Under repeated stresses, the influence of the drying conditions on the creep behavior is evidently large, while in the case of recovery it is less pronounced. The sum of all creep increments within the repeated stress history is 35% bigger for the unsealed (A2) than for the sealed (A1) specimen. On the other hand, both specimens show similar amounts of recoverable creep (difference of 7%). This minor difference in the recovery behavior for both drying conditions suggests that creep recovery is modestly affected by the hygral exchange conditions of the specimen.

The creep-recovery/creep ratio shows that concrete exhibits higher reversibility in sealed conditions regardless of the type of stress history.

The high recovery/creep ratio (0.84) in the case of repeated stresses and sealed conditions reveals that a major share of the basic creep is reversible under these circumstances.

To better clarify the different extents of irreversible creep within the specimens subjected to frequently repeated stresses, two aspects have to be considered simultaneously, namely, environmental (drying) conditions and the duration of the sustained load. In environments with 100% humidity (i.e. sealed conditions) the expelled water on the concrete surface due to a sustained load can return to the pore spaces upon unloading and cause almost full creep recovery [22]. However, if the concrete environment is of lower humidity (i.e. unsealed conditions), the expelled water will evaporate during the sustained load. The amount of the evaporable water will depend on the sustained load duration before unloading. Partial evaporation before removal of a load results in a partial recovery of the developed creep and therefore in a higher irreversibility of the experienced creep.

4.3 Recalculation of selected test results

The strain development of specimen SH2_2 (test series 1) was recalculated using well-established methods in the literature, namely the principle of superposition and the so-called two-function method. The aim was to check whether their application can be extended to frequently repeated stress histories.

The direct principle of superposition does not allow a separate modeling of the creep and the recovery phenomena, i.e. it considers the recovery as a negative creep. Thus, the total strain εc at a time t results to:

$$\varepsilon_{\text{c}} (t,t_{\text{0}} ) = J(t,t_{0} ) \times \sigma_{\text{c}} (t_{0} ) + \sum\nolimits_{{\text{i} = \text{1}}}^{\text{n}} {J(t,t_{\text{i}} ) \times \Delta \sigma_{\text{c}} (t_{\text{i}} )}$$
(7)

where: J(t,t0) is the creep compliance function, σc(t0) is the initial stress value and Δσc(ti) is the stress variation at the time instant ti.

Unlike the principle of superposition, the two-function method accepts an incorporation of separate functions for describing creep and recovery phenomena. Equation 8 [19] was applied to predict the stress-induced strains due to one cycle of loading followed by single, partial unloading:

$$\begin{aligned} \varepsilon_{\text{c}} (t,t_{0} ) = & J(t_{1} ,t_{0} ) \times \sigma_{\text{c}} (t_{0} ) + [J(t,t_{0} ) - J(t_{1} ,t_{0} )] \times [\sigma_{\text{c}} (t_{0} ) - \Delta \sigma_{\text{c}} (t_{1} )] \\ & \quad - J_{{\text{rec}}} (t,t_{0} ,t_{1} ) \times \Delta \sigma_{\text{c}} (t_{1} ) \\ \end{aligned}$$
(8)

The total strain follows from summing up the single shares.

For the creep recovery compliance function Jrec, the model of the delayed elasticity from CEB-FIP Model Code 1978 [41] was used:

$$J_{{\text{rec}}} (t,t_{0} ,t_{1} ) = \frac{1}{{E(t_{1} )}} + \frac{1}{{E_{28} }} \times \varphi_{{\text{cr}}} (t_{0} ,t_{1} ) \times \left( {\frac{{t - t_{1} }}{{t - t_{1} + 328}}} \right)^{{\frac{1}{4.2}}}$$
(9)

where t1 is the concrete age at unloading, E(t1) is the time-dependent modulus of elasticity, E28 is the modulus of elasticity at 28 days and φcr is the ultimate value of the creep recovery coefficient.

Comparisons between the experimental and the analytical results were performed for the total stress-dependent strains (Fig. 12 top) and additionally for the creep and the recovery increments in the individual cycles (Fig. 12 bottom).

Fig. 12
figure 12

Results from the recalculation of the stress-induced strains (top) and the creep (recovery) increments (bottom) of specimen SH2_2 with available methods

Full size image

Results indicate that although the principle of superposition with the Model Code 1990 [42] formulations shows a fine agreement with the total measured strains, the creep and the recovery increments (dashed line) are overestimated during the entire test period. Conversely, the superposition with the Model Code 2010 [43] formulations better describes the local effects (solid line), but underestimates the global behavior.

The results obtained with the two-function method show reasonable fitting of both, the creep and the recovery increments (dotted line) and seemingly good capturing of the global behavior for the duration of the test. However, if the analysis is prolonged for a period longer than the experiment’s duration, a calculative decrease of strains will occur. The reason lies in the applied recovery model itself. In its original form (Eq. 9), it depends on the duration of the unloading sequence, disregarding the concrete age at unloading. Since the duration of the unloading sequences is constant (ΔtU = 16 h) within the considered stress history, the pure recovery increment will remain identical within each unloading cycle. After a sufficient number of loading/unloading cycles, the contribution of the recovery increments will dominate over the creep increments. Consequently, total deformations start to decrease.

The comparison between the tests and the predictions reveals certain limitations of the considered methods when applied to frequently repeated stress histories and motivates for further expansions of the methods in a futural research.

5 Conclusions

The paper presents experiments on the creep reversibility of normal strength concrete under repeating loading types. Based on the analysis of the results, the following conclusions are drawn:

  • Under repeating loading followed by full unloading, the creep response in the loading cycle continuously reduces. A stress-stiffening occurs due to the sustained stress in the previous cycle. Unlike the creep, the recovery reduces in a less pronounced way. It thus does not seem to be affected by the creep developed prior to it. The small variations observed in the creep recovery within the loading cycles appear acceptable, if the recovery phenomenon is ascribed mainly to a delayed elasticity. Under such loading pattern, the latter exclusively depends on the instantaneous deformation.

  • Regardless of the stress level, the creep-recovery to creep ratio increases from cycle to cycle. It finally tends to approach unity. After a sufficient number of loading and unloading cycles, the creep becomes completely recoverable. This–most likely–is due to the stabilization of the changes in the cement paste.

  • Both, specific creep and specific recovery are slightly higher for the stress level of 0.45 fc compared to 0.30 fc. Obviously, a certain nonlinearity caused by micro cracking arises under high service stress levels.

  • In repeated stress histories containing the same stress level upon loading and different levels of unloading, creep abilities in the single cycle differ. Namely, the lower the unloading level, the higher turns out the ability to creep.

  • The creep recovery seems unaffected by the hygral exchange conditions of the specimens. On the other hand, the influence of the drying and the hygral conditions on the irreversible proportion of the creep in each cycle is of remarkable extent.

  • Under sealed conditions, the major share of the creep strains in each cycle is reversible. This fact, as well as the fact that the creep recovery for sealed and unsealed specimens slightly differ, suggests that only the basic creep component is recoverable to some extent.

  • Results from recalculations of the experiments with well-established theoretical models show that they are not directly transmissible to predict variable loading scenarios. This motivates to elaborate the models for these loading types.