1 Introduction

Masonry arch bridges form an integral part of the European railway and highway infrastructure. These old structures are still in service and their condition varies with a tendency to deteriorate fast due to the increased vehicle loads and speeds that they carry. It is therefore necessary to assess the load carrying capacity of masonry arch bridges and to investigate the effect of cyclic loading to avoid premature deterioration and increased maintenance costs. Also masonry towers and pillars are often subjected to high alternating stress levels due to thermal fluctuations or wind.The rate of fatigue deterioration and changes in the materialproperties for masonry is therefore of great importance for improved assessmentand for planning maintenance works.A number of research studies have been performed in the past to evaluate the fatigue characteristics of masonry. However, the majority of these studies have been restricted to determining the relation between the applied stress and the fatigue life and developing SN (stress–number of cycles) curves. Experimental data on the strain evolution during the fatigue life of masonry are limited and no mathematical model has been developed to relate the total longitudinal strain with the loading cycles.

The only available experimental data on the deformation evolution of masonry under low-cycle fatigue loading in literature was presented by Abrams et al. [1]. The results indicated that the maximum recorded strain increases for decreased induced stress and that the accumulation of deformation is more rapid for prisms made with a stronger type mortar. However, Abrams et al. [1] presented a limited number of curves and did not comment on the different stages of fatigue indicated.

Carpinteri et al. [2], performed a series of quasi-static and cyclic tests on masonry specimens and walls. A typical ε − N curve was obtained for masonry under fatigue based on which three stages of fatigue were detected. Stage I during which the deformations increase rapidly for the first 10% of the fatigue life, Stage II where the deformations increase at a constant rate (10–80% of the total number of loading cycles) and Stage III which is characterised by rapid increase up to failure.

The authors Carpinteri et al. [2] proposed an equation to relate the rate of variation of the vertical deformation during Stage II, dεv/dn, and the number of cycles at fatigue failure Nf (Eq. 1).

$$N_{\text{f}} = a\left( {\frac{{{\text{d}}\varepsilon_{v} }}{{{\text{d}}n}}} \right)^{b}$$
(1)

The parameters a and b, which are material constants, can be evaluated by applying a number of loading cycles up to the point that the deformations start growing at a constant rate.

Tomor et al. [3] tested brick masonry prisms under cyclic compression and shear. Based on the acoustic emission recordings of the tests three distinct stages of the fatigue life of masonry were identified. Stage I, during which reduction in the emission was observed, occupies the range between 0 and 32% of the total loading cycles for compression and 0–58% for shear. The emission is stabilised during the second stage (32–67% for compression, not evident in shear) and finally rapid increase is characterised the third stage (67–100% for compression, 58–100% shear) which leads to failure.

In fatigue tests of concrete under compression a strong correlation was found between secondary creep and the life of a specimen. Sparks and Menzies [4], suggested that the fatigue life can be predicted from deformations early in the life of the structure. Similar conclusion were drawn by Taliercio and Gobbi [5, 6] for concrete under triaxial conditions who claim that secondary creep rate is a reliable parameter for predicting the fatigue life also in triaxial conditions.

Holmen [7], based on experimental data on the fatigue behaviour of concrete cubes and cylinders under constant amplitude loading, proposed expressions for the total maximum strain variation during the first and second stage of fatigue life. However, Zanuy [8] analysed available data using the relations proposed by Holmen [7] and indicated the existence of some drawbacks of the suggested equations. Apart from not providing an expression for the third stage of the ε − N curve, Zanuy [8] suggested that the slopes of the two equations do not coincide at the intersection point (N/Nf = 0.10), therefore, introducing gaps.

Zanuy [8], using information from the model proposed by Holmen [7], developed three new expressions, one for each stage of the fatigue life, to describe the ε − N evolution law. For the first and last stage the model involved a second order parabola, while for the second stage where the deformation increases steadily, a linear equation was established.

During this research, experimental tests were conducted on brick-masonry prisms under cyclic compressive loading to evaluate the fatigue stages for masonry. Then based on the concept developed by Zanuy [8, 9] and on the experimental data collected, a model was developed to express the strain evolution law for masonry in fatigue.

2 Materials and experimental test data

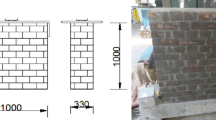
Brick masonry prisms were tested under compressive cyclic loading at different maximum stress levels until failure. The test specimens comprised stack-bond brick prisms built from full-size bricks and mortar joints according to the ASTM standards [10]. The total dimensions of the prisms were 210 × 100 × 357 mm3 (five B1 bricks and four 8 mm mortar joints). The tests were performed using a 250 kN capacity servo-controlled hydraulic actuator able to operate in either static or long-term fatigue loading.

The prisms were built using B1 handmade low-strength solid clay (210 × 100 × 65 mm3) Michelmersh bricks having an average compressive strength of 4.86 N/mm2 according to BS EN 772-1, 2011 (Standard Deviation 1.19 N/mm2) and 1823 kg/m3 gross dry density, while M01 lime-mortar with 0: 1: 2 cement: lime (NHL3.5): sand (3 mm sharp washed) by volume composition was selected for the joints (according to BS EN 1015-11, 1999). The mean compressive strength of B1M01 masonry was 2.94 N/mm2 (0.10 N/mm2 Standard Deviation), according to (BS EN 1052-1, 1999).

The tests were conducted at 2 Hz frequency (i.e. 2 cycles per second) to represent the flow of traffic at ca. 40–50 km/h speed over the bridge [11] adopting a sinusoidal load configuration. Before commencing the fatigue tests, load was applied quasi-statically up to the mean fatigue load. Subsequently, the load was alternated between a minimum and a maximum stress level defined as percentages of the mean compressive strength of masonry. The minimum stress level aiming to represent the dead load of the structure was set equal to 10% of the compressive strength for all the tests. The maximum stress level represents the live loading (e.g. due to traffic over a masonry arch bridge) and varied between 80 and 55% of the compressive strength of masonry. The number of loading cycles until ultimate fatigue fracture of the prisms (Table 1) was recorded for each test. Tests that sustained over 106 loading cycles were terminated. Failure patterns were similar to those under quasi-static loading. All specimens failed by developing vertical cracks through the bricks and mortar joints, causing splitting of the prisms. Major cracks developed along the narrow sides and swelling of the specimens was observed. The experimental procedures and results are presented in detail in Koltsida et al. [12].

Table 1 Fatigue tests in compression on B1M01 type prisms
Full size table

The fatigue data exhibit large scatter as indicated by the large coefficient of variation values. The phenomenon of scatter for fatigue test data under the same loading conditions is well known and attributed to differences in the microstructure for different specimens [13]. Potential sources of scatter could be the specimen production and surface quality, accuracy of testing equipment, laboratory environment and skill of laboratory technicians [14].

The number of loading cycles to failure were recorded and used by Koltsida et al. [15] to develop a probability based mathematical expression for the prediction of the fatigue life of masonry. The proposed model provides a set of curves for stress level-cycles to failure-probability of survival (S–N–P) to allow the fatigue life of masonry to be predicted for any desired confidence level. The prediction curves were compared with the test data and proposed expressions from the literature and proved to be suitable to predict the fatigue life of masonry.

The evolution of the maximum and minimum longitudinal strains (εmin, εmax) with the loading cycles was recorded for each prism. The ε − N curve exhibits an S shape (Fig. 1) based on which, three distinct stages can be identified. Stage I: strain grows at a high rate in the first 10% of the total life of the specimen due to initiation of micro-cracks. Stage II: this stage is the dominant and is characterised by gradual increase of strain at a constant rate. This stage occupies approximately 80–85% of the total loading cycles during which the micro-cracks grow steadily. Stage III: rapid increase of strain due to coalition of micro-cracks into macro-cracks, leading to ultimate fracture of the specimen is observed in the last 5–10% of the ε − N curve.

Fig. 1
figure 1

Typical maximum and minimum strain evolution curves

Full size image

Comparing the resulting graphs, it was observed that the higher the maximum stress applied on the specimen, the steeper the second stage is becoming. However, even for prisms subjected to the same maximum stress, the curve becomes steeper for decreased sustained loading cycles.

The rate of strain development during stage II is compared against the loading cycles to failure in Fig. 2 for different maximum stress levels. Each set of data is coupled with the logarithmic interpolation curve [5]. The strain development rate decreases for increased loading cycles to failure. The decrease is, however, larger for loading cycles below 10,000. For higher loading cycles the strain development rate seems to stabilise between 0.002 and 0.003.

Fig. 2
figure 2

Strain rate of stage II with loading cycles to failure for 55%, 60%, 68% and 80% maximum stress (n = 30)

Full size image

The duration of the three fatigue stages was calculated for each prism. For prisms B1M1-50 and B1M1-56 no data were recorded for the early and late stages of fatigue life, due to early failure of the specimens and, therefore, the durations of the different stages could not be calculated.

The average duration of Stage I of fatigue is 9.46% of the total loading cycles (SD 2.41%), while the average duration of Stage II is 76.68% (SD 4.90%) of the total loading cycles. There is no clear indication that the total loading cycles or the maximum stress level influences the duration of each of the three stages of fatigue.

The relationship between the normalised total maximum longitudinal strain ratio (i.e. the strain recorded after a specific number of loading cycles over the initially recorded strain at the beginning of the test) and the total loading cycles sustained until failure is presented in Fig. 3 at the end of Stage I, II and III. Strain at failure increases up to 5.25 times the strain recorded after the first cycle, ε0. The total maximum strain appears to get larger with the loading cycles at all stages of fatigue, that is likely to be caused by the increased effects of creep induced with higher numbers of fatigue cycles. For higher loading cycles the total test time is extended and creep damage is accumulated during the relatively longer time spent near the peak stress of each cycle [16].

Fig. 3
figure 3

Normalised strain at the end of Stage I, Stage II and Stage III against the total number of cycles

Full size image

3 Strain evolution law

Based on the same principles followed by Holmen [7] and Zanuy [8] to describe the strain evolution over the fatigue life of concrete, three equations have been generated to predict each stage of the ε − N curve for brick masonry. The first and third stage are characterised by second order parabolic equations, while a linear equation was adopted to reproduce the steady increase of strain during the second stage. To simplify calculations, durations of stage I, II and III will be considered 0–10%, 10–90% and 90–100%, respectively. The analysis for the derivation of each equation is as follows.

3.1 Stage I (Second order parabola)

The equation that characterises the strain evolution during the first stage of the fatigue life is a second order parabola of the type:

$$f\left( x \right) = ax^{2} + bx + c$$

Substituting x = N/Nf and f(x) = εmax/ε0 the following relationship is obtained (Eq. 2).

$$\frac{{\varepsilon_{\hbox{max} } }}{{\varepsilon_{0} }} = a\left( {\frac{N}{{N_{\text{f}} }}} \right)^{2} + b\frac{N}{{N_{\text{f}} }} + c,\;\;\frac{N}{{N_{\text{f}} }} < 0.1$$
(2)

The strain rate ε* during stage I (Eq. 3) is the tangent of the ε − N curve and can be evaluated from the first derivative of Eq. (2).

$$\varepsilon^{*} = \frac{{d\frac{{\varepsilon_{\hbox{max} } }}{{\varepsilon_{0} }}}}{{d\frac{N}{{N_{\text{f}} }}}} = 2a\left( {\frac{N}{{N_{\text{f}} }}} \right) + b$$
(3)

In order to evaluate the parameters a, b and c certain assumptions were considered. For N/Nf = 0 εmax/ε0 = 1 and, therefore, c = 1. For N/Nf = 0.10 \(\frac{{\varepsilon_{\hbox{max} } }}{{\varepsilon_{0} }}\left( {\frac{N}{{N_{\text{f}} }} = 0.10} \right) = \varepsilon_{1 - 2}\) (ε1–2 is the deformation at the intersection point between stage I and stage II) and the strain rate is \(\frac{{d\frac{{\varepsilon_{\hbox{max} } }}{{\varepsilon_{0} }}}}{{d\frac{N}{{N_{\text{f}} }}}}\left( {\frac{N}{{N_{\text{f}} }} = 0.10} \right) = \varepsilon_{2}^{*}\) (ε2* is the strain rate during the second stage). The second assumption suggests that the equations for stage I and II provide the same arithmetic value and the same derivative for N/Nf = 0.1 and ensures that there is no gap at the intersection points between the two stages in terms of curvature.

To evaluate the ε1–2 and ε2* relationships with the maximum applied stress, the experimental data were plotted against the stress level and curve fitting was performed (Figs. 4, 5). The following expressions were identified for ε1–2 and ε2* (Eqs. 3, 4).

$$\varepsilon_{1 - 2} = - 4.256\left( {S_{\hbox{max} } } \right)^{2} + 4.80S_{\hbox{max} } + 0.1369$$
(4)
$$\varepsilon_{2}^{*} = 12.23\left( {S_{\hbox{max} } } \right)^{2} - 15.58S_{\hbox{max} } + 6.081$$
(5)
Fig. 4
figure 4

Experimental data and curve fitting for the strain at the intersection point between Stage I and II of the fatigue life against the maximum stress level

Full size image
Fig. 5
figure 5

Experimental data and curve fitting for the strain rate during the second stage of the fatigue life against the maximum stress level

Full size image

After solving the resulting system of equations, parameters a, b and c were calculated and Eq. (2) can be rewritten accordingly:

$$\begin{aligned} a & = 547.9S_{\hbox{max} }^{2} - 635.8S_{\hbox{max} } + 147.12 \\ b & = - 97.35S_{\hbox{max} }^{2} + 111.58S_{\hbox{max} } - 23.343 \\ c & = 1 \\ \end{aligned}$$

3.2 Stage II (Linear)

The equation that characterises the strain evolution during the second stage of the fatigue life is linear of the type:

$$f\left( x \right) = ax + b$$

Substituting \(x = N/N_{\text{f}} \;\;{\text{and}}\;\;f\left( x \right) = \frac{{\varepsilon_{\hbox{max} } }}{{\varepsilon_{0} }}\) the equation can be rewritten in the format of Eq. (6) and the strain rate during stage II is given by Eq. (7).

$$\frac{{\varepsilon_{\hbox{max} } }}{{\varepsilon_{0} }} = a\frac{N}{{N_{\text{f}} }} + b$$
(6)
$$\varepsilon_{2}^{*} = \frac{{d\frac{{\varepsilon_{\hbox{max} } }}{{\varepsilon_{0} }}}}{{d\frac{N}{{N_{\text{f}} }}}} = a$$
(7)

As mentioned before, for \(\frac{N}{{N_{\text{f}} }} = 0.10\) the strain is \(\frac{{\varepsilon_{\hbox{max} } }}{{\varepsilon_{0} }}\left( {\frac{N}{{N_{\text{f}} }} = 0.10} \right) = \varepsilon_{1 - 2}\) (avoid gaps at intersection points) and the strain rate for \(0.10 < \frac{N}{{N_{\text{f}} }} < 0.90\) is ε2*. Using Eqs. 4 and 5 parameters a and b were calculated and Eq. (6) was fully defined.

$$a = \varepsilon_{2}^{*} = 12.23\left( {S_{\hbox{max} } } \right)^{2} - 15.58S_{\hbox{max} } + 6.081$$
$$b = - 5.479S_{\hbox{max} }^{2} + 6.358S_{\hbox{max} } - 0.4712$$

3.3 Stage III (Second order parabola)

The ε − N curve during the third stage of the fatigue life is again of a second order parabolic type. To avoid discontinuity between stage II and stage III for \(\frac{N}{{N_{\text{f}} }} = 0.90\), the strain is \(\frac{{\varepsilon_{\hbox{max} } }}{{\varepsilon_{0} }}\left( {\frac{N}{{N_{\text{f}} }} = 0.90 } \right) = \varepsilon_{2 - 3}\) as calculated from Eq. (6) and the strain rate is ε2* as calculated from Eq. (5). The resulting strain at the intersection point between stage II and stage III \(\varepsilon_{2 - 3}\) is:

$$\varepsilon_{2 - 3} = 5.528S_{\hbox{max} }^{2} - 7.664S_{\hbox{max} } + 5.002$$
(8)

It was also considered that for \(\frac{N}{{N_{\text{f}} }} = 1.00\) the strain is equal to the strain recorded at failure, εf. For the evaluation of the relation of the strain at failure εf with \(\frac{{S_{\hbox{max} } }}{{S_{u} }}\) the maximum applied stress ratio, the experimental data were plotted against the stress ratio (Fig. 6) and curve fitting was performed (Eq. 9).

$$\varepsilon_{\text{f}} = 14.57S_{\hbox{max} }^{2} - 24.11S_{\hbox{max} } + 12.88$$
(9)
Fig. 6
figure 6

Experimental data and curve fitting for the strain at failure against the maximum applied stress ratio

Full size image

Substituting the identified values for stain and strain rate in the second order parabolic equation, a system of equations is obtained. Solving the system, parameters a, b and c were calculated and the following expression was obtained for the strain evolution during the third stage of the fatigue life:

$$\frac{{\varepsilon_{\hbox{max} } }}{{\varepsilon_{0} }} = a\left( {\frac{N}{{N_{\text{f}} }}} \right)^{2} + b\frac{N}{{N_{\text{f}} }} + 1,\;\;0.90 < \frac{N}{{N_{\text{f}} }} < 1$$
(10)

where

$$\begin{aligned} a & = 781.9S_{\hbox{max} }^{2} - 1488.8S_{\hbox{max} } + 727.02, \\ b & = - 1395.19S_{\hbox{max} }^{2} + 2664.26S_{\hbox{max} } - 1302.555 \\ \end{aligned}$$

and

$$c = 627.86S_{\hbox{max} }^{2} - 1199.57S_{\hbox{max} } + 588.415$$

In Fig. 7a–d the experimentally recorded strain variation during the fatigue life of masonry is juxtaposed with the analytical model developed above. The graphs are grouped according to the maximum stress levels applied during the tests (55%, 60%, 68% and 80%).

Fig. 7
figure 7

Total longitudinal experimental strain variation and analytical prediction with the cycle ratio for a 55% maximum stress, b 60% maximum stress, c 68% maximum stress and d 80% maximum stress

Full size image

Good correlation of the analytical expression with the experimental data can be observed. The curve corresponding to Stage I of the fatigue life starts from ε/ε0 = 1 for N/Nf = 0 and has a curvature that fits the actual experimental data. The inclination of the line that is proposed to predict Stage II seems to be a good representation of the mean inclination at any stress level. However, at 68% maximum stress level, the initial part of the curve seems to be underestimating the experimental results. The curvature of the final part of the model provides a good approximation of the experimental data for higher stress levels. For Smax 55% and 60% the curve is steeper than the real behaviour. However, the start and end of this curve, corresponds to the mean strain at the respective points.

At the intersection points between adjoining stages, the slopes of the curves, as well as the arithmetic values coincide. These two facts are shaping a continuous differentiable function avoiding points at which the rate of strain development would have to be infinite.

4 Discussion and conclusions

Experimental data collected from fatigue tests on brick masonry prisms were analysed and a model to describe the deformation evolution with the loading cycles, during different stages of fatigue was developed. Three different equations were proposed to reproduce the behaviour of masonry during the respective three stages of fatigue.

The comparison of the proposed model with the experimental data proved that the model is appropriate to predict the strain evolution of B1M01 type masonry at any maximum stress level. No gaps exist at the intersection points between subsequent stages (accuracy of at least ten decimals was achieved) and the slopes of the curves coincide at these points resulting to a differentiable function.

Nevertheless, the validity of the equation for different types of masonry is still to be investigated since the analysis was based on experimental data on low-strength brick masonry prisms. Other possible influencing factors need to be considered (frequency, minimum induced stress, loading type etc.).

For structural engineers the process of progressive, irreversible damage in a material under cyclic loading is of great importance. The structural changes are associated with progressive growth of internal micro-cracks, which leads to significant growth of plastic strain. At a macro-level this process leads to changes in the mechanical properties of the material [17]. Therefore, a time-dependant model able to predict the mechanical changes of masonry with the number of cycles is necessary to study the influence of fatigue on the structural behaviour of masonry. Changes to the rate of growth of deformation during long term monitoring of masonry arch bridges under traffic can be associated with different stages of fatigue. The proposed prediction model for the law of evolution for the total longitudinal strain with the number of cycles could be adopted to evaluate the remaining service life. Maintenance works could be planned based on the analysis results to minimise life-cycle costs and prevent premature failures and replacement costs.