Abstract
Currently, no appropriate standard exists that describes how to determine the in-plane shear stiffness for cross-laminated timber (CLT) panels, meaning that, there is a lack of appropriate and reliable test methods. In this paper, two gross shear test methods are evaluated: a picture frame test and a diagonal compression test, which are intended to measure the shear stiffness of a whole CLT panel. This evaluation aimed to compare the shear modulus, the amount of compression/tension in the diagonal directions of the panels and the deformations of both sides of the panels. The picture frame test and diagonal compression test provides a bi- and uniaxial pre-stress, respectively. A total of 30 non-edge glued CLT panels were tested, 17 3-layer and 13 5-layer panels. The shear modulus for the 3- and 5-layer non-edge-glued panels were measured as 418 and 466 MPa, respectively, in the picture frame test. In the diagonal compression test, the shear modulus was measured to substantially higher values of 530 and 626 MPa for the 3- and 5-layer panels, respectively. In the picture frame test, panels were equally stretched along one of the diagonals as they were compressed along the other diagonal, which was not the case for panels in the diagonal compression test. The test results also showed that measuring only one side incurs a risk of over- or under-estimating the in-plane shear modulus. Compared with results from the literature, the picture frame test seems to be a more reliable test method than the diagonal compression test.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cross-laminated timber (CLT) was introduced to central Europe more than two decades ago. CLT is a laminar plate-like structural element, typically consisting of three to seven layers. Each layer is composed of boards placed side by side, and these layers are usually arranged perpendicular to each other [1]. CLT elements are commonly used for floors, loaded perpendicular to their plane (plate action), and for diaphragms and shear walls, loaded in-plane (panel action) (see e.g. [2]). Due to its thickness, CLT can be used as a stand-alone structural element with high strength and stiffness properties. The properties of the final product depend on the strength and stiffness of the input material, the number and thickness of the layers and their arrangement [1]. The derivation of design parameters and test configurations for correctly determining these parameters is an important issue [3].
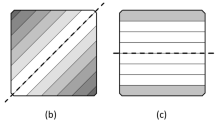
The shear characteristics of CLT diaphragms can be expressed by three failure modes and corresponding stiffness values: gross shear, net shear and torsional shear [4] (Fig. 1). Gross shear failure involves a constant distribution of shear stresses over the whole cross section of the panel, meaning that shear failure may occur parallel to the grain in all layers. For this mechanism to take place, shear stresses need to be transferred between adjacent boards via edge gluing, and no cracks should exist between the layers. In net shear failure, the longitudinal (transversal) layers fail in shear along a failure plane between the longitudinal (transversal) layers, coinciding with the gaps (either non-edge-glued gaps or cracks at the glued edges) in the transversal (longitudinal) layers [5]. For a single lamination, this shear stress represents longitudinal-transverse shear [3]. A torsional shear failure of the glued interface area between a longitudinal and a transversal layer involves both longitudinal and rolling shear failure mechanisms.
Currently, no appropriate standard exists that describes how to determine the shear stiffness of CLT panels. Testing standard EN 408 [6] mainly deals with conventional elements involving test setups that are not ideal for testing of panels [3]. Some individual CLT panel properties can be obtained from EN 789 [7]. However, test results show that neither the strength nor stiffness properties derived from four-point bending tests are appropriate for assessing the respective properties of the original panels [3]. EN 16351:2015 [8] describes typical single-node test configurations for net and torsional shear that are specific to CLT, providing more relevant material properties.
According to [3], the single-node test setups of EN 16351:2015 are not well-suited to determining gross shear strength. In addition, the relevance of single-node test methods is doubtful in terms of producing a well-defined stress state that is relevant for e.g. wall elements. It is also possible that some of the single-node test methods introduce torsional shear after the initiation of some local failure. In addition, the use of single-node tests for net shear is questionable, as they require correction parameters to cater for system effects. Consequently, the test setup and the size of the test specimens used is crucial in order to fully and correctly assess the shear properties of CLT [3]. The in-plane shear test method proposed by Kreuzinger and Sieder [9], which uses a column-like compressive specimen of CLT cut at 45° from the main directions, is increasingly becoming accepted as the most appropriate gross shear test setup for CLT. Although gross shear test setups may appear to be more appropriate than single-node alternatives, they introduce several challenges related to load introduction, failure modes other than shear failure, and the issue of ensuring a pure state of shear stress [3].
For textile fabrics, the picture frame test has emerged as a popular method for measuring pure states of shear stress [10]. According to [11], the picture frame test allows the application of biaxial pre-stress by clamping the shear specimen along its edges, which subjects the specimen to a uniform deformation resulting in a homogenous state of pure shear for a straightforward definition of the shear stiffness. A method similar to the picture frame test, albeit slightly more complex, can be found in [12]; in the process of verifying the modified compression-field theory for reinforced concrete, the authors developed a membrane element tester. This tester allowed any combination of membrane shear, compression and tension by coupling hydraulic jacks to shear keys cast into the edges of the concrete specimen.
Since the anchoring used by this proposed membrane element tester is not directly applicable to CLT elements, [13] proposed a picture frame test method, in the paper called the direct shear test method, with continuous bonding along the edges to a hinged steel frame. Initial tests with this picture frame were presented in [4] and showed promising results with low coefficients of variation. In addition, the shear modulus evaluated in this way correlated well with expected theoretical values, indicating that a state of pure shear was probably obtained in the middle of the CLT panel. The studies in [14,15,16] proposed similar test setups for measuring the in-plane shear stiffness of CLT panels. The main difference among methods was in the way of transferring the load from the frame to the panel: the work in [14] used friction, [15, 16] used glue while [4] used bolts.
The diagonal compression test [17, 18] seems more straight forward to measure the in-plane shear stiffness. This method is similar to the picture frame test, although only one diagonal is compressed. The method assumes that by compressing one diagonal, the other diagonal will become stretched. The work in [17] and [18] used this test method, albeit with different calculation methods to evaluate the in-plane shear stiffness; while [17] used a basic equation based on a uniform pure shear stress in the panel, [18] used an equation based on different stress–strain states in the active loaded and passive panel directions.
Neither the authors of the picture frame (direct shear) test method nor the papers on the diagonal compression test method performed an in-depth analysis of the applicability of these test methods for the evaluation of the shear modulus. The present paper is a continuation of the research in [4, 18], presenting and evaluating the two gross shear test methods for CLT: the picture frame test and the diagonal compression method. The primary aim of this paper is to investigate whether these two test methods result in equal and reliable values for the in-plane shear modulus. The secondary aim is to evaluate whether the panels are equally compressed and tensioned, as would be expected in a pure shear condition.
2 Materials and methods
2.1 Cross-laminated panels
Two types of CLT panels were used in this study: a 3-layer and a 5-layer panel, with properties as shown in Table 1. All panels were manufactured by a commercial CLT producer. The panels were built of wood lamellas classified as C24 according to SS-EN 338 [19] and glued on the flat side only using polyurethane glue (i.e. no edge-gluing). The mean modulus of elasticity (E-modulus) was determined using 587 clear wood samples from three of the 3-layer and from three of the 5-layer panels, according to EN 408 [6]. The coefficient of variation (COV) for the E-modulus is presented in Table 1. The same clear wood samples were then used to determine the moisture content (MC).
To ensure that the CLT panels fitted into the picture frame, holes were drilled around the border using a CNC machine (see Fig. 2). To analyse the effect of these drilled holes in the diagonal compression test, three of the 3-layer and two of the 5-layer panels were not CNC machined and instead used as reference panels (Table 1). Thus, 14 of the 3-layer and 11 of the 5-layer panels were tested in the picture frame and in diagonal compression, while the five reference panels were tested only in diagonal compression.
Exploded view of the picture frame with all parts attached to the CLT panel. A front view (side 1) is shown in Fig. 3
2.2 Picture frame test
The steel shear frame distributing the load to the CLT panel (Fig. 2) was designed according to [4]. Some parts of the fixture, such as the dowels, the mounting of the L-shaped beams (see Fig. 2) and bushings, were improved in this setup compared to the earlier experimental study [4]. The picture frame was built using eight L-shaped steel beams, four per side of the CLT panel. The steel used in the L-shaped beams was S235JRG2 with dimensions of 60 × 60 × 10 mm.
Transfer of the load from the picture frame to the CLT panel was achieved via 28 dowels and eight bolts, each with a diameter of 12 mm. The bolts were placed near the corner pins to prevent the frame from separating during testing. A tolerance of 1 mm was used to prevent the dowels and bolts from becoming stuck during the mounting and demounting of the CLT panel. The corner pins had a tight fit and were assembled in bushings, allowing free rotation with low friction in the corners. The dowels and corner pins were manufactured from steel of quality S355, and the bolts were classified as strength class 8.8.
Four Vishay HS25 displacement transducers (0.05 mm accuracy) were used to measure displacements at fixed coordinates on the CLT panel, see Fig. 3a. The transducers were applied along the two diagonal directions on both sides of the panel. They covered the central region, representing 40% of the original size of the panel, in which the effects of the boundary conditions could be neglected [4, 18]. To measure the load, a Omegadyne LC412-75 K load cell with an accuracy of 200 N was used. The transducers acting parallel to the force vector were denoted as active transducers, while those transducers acting orthogonally to the force vector were denoted as passive transducers, see Fig. 3b. Each side (sides 1 and 2) of the panel had one active and one passive transducer. The values of the active and passive directed transducers were positive and negative, representing tension and compression, respectively.
The picture frame was fixed at the bottom corner pin, and the force was applied as tension to the upper corner pin (see Fig. 3a, b).
Based on experience from the previous experimental study in [4], the load was applied at a speed of 5 mm per minute in three equal and subsequent load cycles, from 0 to 150 kN for the 3-layer panels. For the 5-layer panels, the load was applied in three equal and subsequent cycles, from 0 to 180 kN. No panels were tested to failure, since the main focus was on measuring the stiffness of the panels. The purpose of the first cycle was to allow the panel to settle in the frame, and the stiffness value k was then measured in the second and third cycles as a gradient of the load displacement curve in the linear elastic range of 60–80 kN.
The stiffness ki was calculated based on different transducer displacements, in order to compare the behaviour in compression and tension, to evaluate transducer uniformity and variation (as explained below), and to discover possible material variations. Index i denotes the transducers used to measure the stiffness k, and k is the stiffness based on the displacement Δ obtained from the transducers, as further described in the results section below. To evaluate any difference between the active and passive loading directions, two random 5-layer panels were tested in both directions, i.e. first in the initial position and then rotated by 90°, meaning that the compressed direction became tensioned and vice versa.
2.3 Calculation of shear modulus in the picture frame test
The in-plane shear modulus GPF, s1s2 for the picture frame test was calculated as the pure shear stress τpu divided by the shear strain γ. The index PF refers to picture frame and s1s2 refers to the use of transducer values from sides 1 and 2. In a similar way to [4], τpu was assumed to be constant throughout the central region representing 40% of the panel. In this region, the shear strain γ was evaluated using the cosine rule (Eq. 1) with each side of length a (0.4 l), diagonal length d and the mean change in length for both diagonals Δ (see Fig. 4).
Considering small displacements \(\left[ {\cos \left( {90 - \gamma } \right) = \sin \gamma \approx \gamma ; \Delta^{2} \approx 0} \right]\) gives
The pure shear stress τpu can then be written as:
where F is the force applied through the hydraulic jack. This results in an equation describing the modulus of shear
where tclt is the thickness of the CLT panel.
2.4 Diagonal compression test
The diagonal compression test was conducted by compressing the panel in the diagonal direction, i.e. compressing two opposite corners, and measuring the resulting displacement in the active and passive directions of the panel (Fig. 5a, b).
A Omegadyne LC412-100 K load cell with an accuracy of 200 N was used for the diagonal compression test. For information about transducers, active and passive directions, please refer to earlier description for the picture frame test (Chapter 2.2).
The load was applied in three cycles; from 0 to 50 kN, from 0 to 100 kN and finally from 0 to rupture for the 3-layer panels and from 0 to 100 kN, 0 to 150 kN and 0 to rupture for the 5-layer panels. The load was applied in steps, due to the uncertainty in the maximum strength of the panel, and to allow the panel to settle during loading in the first cycle. All panels were tested to obtain a linear elastic zone in the force versus displacement curve.
Four panels (two 3- and two 5-layer panels) were tested in both diagonal directions, first in the initial position and then rotated by 90°. The tests in the alternating perpendicular directions aimed to detect whether there was a difference between the two diagonal directions. The four panels were subjected to the first load cycle in one diagonal direction, and were then subjected to three load cycles along the other diagonal.
k was calculated as a mean value based on loading in the second and third load cycles in the linear elastic range of 60–80 kN for all tested panels. For the four panels tested in both diagonal directions, k was calculated for the first diagonal direction in the linear elastic range of 45–50 kN and 60–80 kN for the 3- and 5-layer panels, respectively.
The testing procedure for the diagonal compression test is summarised in Fig. 6.
2.5 Calculation of shear modulus in the diagonal compression test
The in-plane shear modulus GDC, i was calculated as the shear stress τ divided by the shear angle γ. The index DC refers to diagonal compression and i denotes the transducers used to measure k (a for the transducers in the active direction only, or s1s2 for all transducers on both sides). The approach outlined here was first presented in [18]. A similar approach to the picture frame test was used to calculate the shear strain γ (see Eqs. 2, 3). Based on [20], Andreolli et al. [18] defined a parameter \(\bar{C}_{i}\) that takes into account the non-uniform shear stresses occurring in the diagonal compressed panel:
\(\bar{C}_{i}\) is the ratio of the estimated τ occurring in the central region divided by τpu. In [20], the compression and tension stresses are described at specific points along the diagonals of a diagonally compressed square. According to [18], by using Mohr’s circle and calculating a ratio τ/τpu (denoted C) for these points, an estimate of τ for the panel can be obtained. A mean value of C at the points on the diagonals between the measuring points was calculated. This mean value was denoted \(\bar{C}_{i}\) where i denoted the used transducer (chosen measuring points). This means that \(\bar{C}_{i}\) depends on the ratio a/l and chosen transducers. In this case \(\bar{C}_{i}\) was equal to 1.431 for i = s1s2 and 1.611 for i = a.
2.6 Data analysis
The stiffnesses from the picture frame and diagonal compression tests were analysed. This to check whether uniform compression and tension behaviour was present in the panels and to detect any material variations. Stiffness values were evaluated as mean values, standard deviations and coefficient of variation (COV).
Variations in stiffness in CLT panels were analysed by calculating the difference between the stiffness values in third loading cycle (kcycle III) and the second loading cycle (kcycle II) divided by the mean stiffness \((\bar{k}_{\text{mean}} )\) obtained from the two cycles.
Based on \(v_{m,n}\) values from both 3- and 5-layer panels, a mean value denoted \(\bar{v}\) was calculated for each test method. The panels that were tested twice in the picture frame test (firstly in the initial position and then rotated 90°) are represented twice in \(\bar{v}\), one \(v_{m,n}\) for each position. For the panels tested twice in the diagonal compression test, \(v_{m,n}\) was calculated only in the 90° rotated position. The reference panels \(v_{m,n}\) was also included in \(\bar{v}\) for the diagonal compression test.
3 Results and analysis
3.1 Picture frame test
The measured mean stiffness \(\bar{k}_{i}\) and mean shear modulus \(\bar{G}_{PF, i}\), based on different transducer combinations i, are shown in Table 2. The \(\bar{v}\) (Eq. 7) was calculated to − 1.3%.
The differences in COV for the active and passive transducers for both 3- and 5-layer panels are negligible (Table 2). A higher absolute value of stiffness was seen in the passive direction (\(\bar{k}_{p}\)) for both 3- and 5-layer panels. The absolute value of \(\bar{k}_{p}\) was 5.0 and 13.4 kN/mm higher than \(\bar{k}_{a}\) for the 3- and 5-layer panels, respectively. The same behaviour was also observed for the panels that were tested in both loading directions (see Table 3). The reason for this may be some form of flexibility in the picture frame. However, for one panel, the diagonal tested as active reduced in stiffness when tested as passive (224.2 compared to 220.0 kN/mm in Table 3).
The results for \(\bar{k}_{s1}\) and \(\bar{k}_{s2}\) in Table 2 show a difference between the two sides, indicating a difference in the material properties or some form of non-uniform loading in the thickness direction. A lower stiffness was measured on side 2 compared to side 1 of the 5-layer panels. The difference of 34.8 kN/mm (250.3 kN/mm vs. 215.5 kN/mm) between \(\bar{k}_{s1}\) and \(\bar{k}_{s2}\) seems large; however, as shown in the load displacement curves for the second and third loading cycles for all 5-layer panels (Fig. 7), a large spread was observed between curves, without any clear grouping of stiffness values for sides 1 and 2.
The mean shear modulus \(\bar{G}_{{{\text{PF}},s1s2}}\) for the 3-layer panels was 418.1 MPa, and the mean shear modulus \(\bar{G}_{{{\text{PF}},s1s2}}\) for the 5-layer panel was 465.8 MPa.
3.2 Diagonal compression test
The measured mean stiffness \(\bar{k}_{i}\) and mean shear modulus \(\bar{G}_{{{\text{DC}}, i}}\), based on different transducer combinations i, for all diagonally compressed panels are shown in Table 4. The \(\bar{v}\) was calculated to 2.5%. This increase may be due to local failures in the panel during the loading cycles. The \(\left| {\bar{k}_{p} } \right|\) was much higher than \(\bar{k}_{a}\) for all tested panel types; meaning that the panels were compressed more in the active direction than they were tensioned in the passive direction (refer to Fig. 5).
The differences between the COV for \(\bar{k}_{a}\) and \(\bar{k}_{p}\) were negligible for all panels (Table 4). The COV for the two reference groups were excluded, due to the low number of panels tested. Grouping of the active and |passive| transducers are visible (see Fig. 8) for all 5-layer panels with holes in the force versus displacement curves for the second and third loading cycles. The same behaviour was observed for the panels tested in both loading directions (Table 5). A slight curve of the lines can also be seen in Fig. 8. This indicates that there is not a clear elastic zone during the complete load cycles.
The \(\bar{G}_{{{\text{DC}}, s1s2}}\) and \(\bar{G}_{{{\text{DC}}, a}}\) for the reference panels were higher than for the panels with drilled holes and cut corners (see Table 4). By excluding the passive directed transducers from calculations, the shear modulus was reduced by 19.0 MPa, 12.4 MPa, 30.4 MPa and 6.3 MPa for the 3-layer, 3-layer reference, 5-layer and 5-layer reference panel, respectively (see Table 4).
The largest differences between \(\bar{k}_{s1}\) and \(\bar{k}_{s2}\) were obtained for the 5-layer panels. In this case, \(\bar{k}_{s1}\) was higher than \(\bar{k}_{s2}\). Based on loading cycles one and two, Fig. 9 shows the individual \(k_{s1}\) and \(k_{s2}\) for all 5-layer panels with holes.
All tested panels had a higher \(k_{s1}\) than \(k_{s2}\), indicating a non-uniform loading in the thickness direction which results in bending of the panels.
According to Table 4, \(\bar{k}_{s1s2}\) for the 5-layer panels was 62.3 kN/mm higher than for the 3-layer panels (229.2 vs. 166.9 kN/mm). The 3-layer panels had a COV value of 16.0%, which was higher than for the 5-layer panels (9.6%).
The differences between ka and kp in the two loading directions (initial and 90° rotated position) for the four panels tested in this way are shown in Table 5. The mean increase in the stiffness, ka (active diagonal) tested as kp (active diagonal 90° rotated), was 48.6 and 56.4 kN/mm for the 3- and 5-layer panels, respectively. The corresponding stiffness difference taken from Table 4 were similar: 47.6 kN/mm and 70.1 kN/mm for the 3- and 5-layer panels, respectively.
4 Discussion
4.1 Picture frame test
Operating the picture frame was simple, however, the disassembly of dowels and bolts after testing turned out to be slightly more difficult. The dowels and bolts closest to the corner pins tended to become stuck in the panels. This indicated that the load transfer from the frame to the panels was highest in the corners, and not uniformly distributed along the frame. However, use of the picture frame test resulted in a uniform deformation of the CLT panels in the active and passive directions (equal absolute values) as intended (see Fig. 4).
Stiffness differences between side 1 and 2 of the panels were measured (see Table 2). The reasons for this are that there may be a variation in the CLT properties or non-uniform loading in the thickness direction.
The equation used for evaluating the shear modulus in the picture frame test is also used for other materials, such as fabrics. In that case, the threads of the fabric are parallel to each other and remain parallel during loading. In CLT, the situation may be different but due to the large variation of \(\bar{G}_{{{\text{PF}},s1s2}}\) and the small measured displacements, this effect may be negligible.
4.2 Diagonal compression test
There were no difficulties to operate the diagonal compression set-up. The panels were not stretched across the loading direction (passive) as much as they were compressed in the loading direction (active). If the contact area between the panel and the supports increase (refer to Fig. 5), the stiffness in the passive direction would likely increase. The supports would also prevent any deformation in the passive direction. The parameter \(\bar{C}_{i}\) [20] offers a way of quantifying the non-uniform shear stresses occurring during diagonal compression. However, this constant does not take into account the deformation issue in the passive direction.
The test results show that the absolute values of the stiffnesses are not equal in the active and passive directions; consequently, the deformation figure used to derive the shear strain (Fig. 4) is unsuitable in this case, and another assumption is recommended for future work. For this study, it seems better to exclude the deformations in the passive directions altogether and to only rely solely on the active direction when calculating the shear modulus. This also means that \(\bar{C}_{i}\) would change, with unknown implications at this stage.
4.3 Comparison between the methods
By using the picture frame test rather than diagonal compression test, the \(\bar{k}_{s1s2}\) increased by 15.0 kN/mm and 3.7 kN/mm for the 3-layer and 5-layer panels, respectively. A higher stiffness measured in the picture frame test is required in order to give the same shear modulus (Eq. 4) as in the diagonal compression test (Eq. 6). These two equations only differ in terms of the coefficient \(\bar{C}_{i}\). For the picture frame test, the stiffness \(\bar{k}_{s1s2}\) should be 1.43 (or 1.61 for G based on only ka) times higher than the stiffness measured in the diagonal compression test to give the same modulus of shear.
Consequently, there are only two possibilities: either the stiffnesses measured in the diagonal compression tests are too high, or those measured in the picture frame tests are too low.
It is possible that the stiffness measured in the diagonal compression tests are too high, due to the holes drilled in the panel. The holes will create local deformations close to the supports, which probably decreases measured displacements. This explanation is more likely than the possibility that the picture frame test provides stiffness values that are too low.
In the literature, the shear modulus for 3-layer panels differs depending on panel composition. In [21], the value for a similar 3-layer panel was reported as 470 MPa, and in [17] the value for a 3-layer panel was measured from 500 to 700 MPa. The present study resulted in values of 418 and 530 MPa for the 3-layer panel in the picture frame test and diagonal compression test, respectively.
The COV for the picture frame test were lower than for the diagonal compression test. The COV obtained in this study are similar to those in previous studies. For example, in [21], the COV was as high as 14.2% and in [14], the COV even exceeded 35%. The tests performed in [15] gave a COV of 10.2% while the COV for using a previous version of the picture frame was 4.1% [4].
In general, the difference between the picture frame test and the diagonal compression test was relatively large for the same panel. Since the picture frame compressed and stretched the panel equally, the theoretical assumption of pure shear was verified. Due to a better approximation for the real shear behaviour and a straightforward calculation of the in-plane shear modulus, the results from the picture frame test are deemed to be more reliable than those obtained from diagonal compression.
5 Conclusions
The picture frame test and diagonal compression test were used for determining the shear modulus of CLT panels. The main difference between these two methods is how the shear load is applied and therefore the way in which the panels deform.
The picture frame test uses a steel frame to transfer the load to the panels. This method gives a uniform shear deformation. In the diagonal compression test, only one diagonal was compressed, creating a non-uniform shear deformation of the panels.
The picture frame test is believed to give more reliable results than the diagonal compression tests due to the uniform loading of the panels and the straightforward and simple equations for calculating the shear modulus. In the diagonal compression test, there is non-uniform shear deformation of the panels, which complicates evaluation of the shear modulus.
The mean shear modulus measured in the picture frame test was 418.1 and 465.8 MPa for the 3- and 5-layer panels, respectively. The diagonal compression test gave values for the shear modulus of 530.1 and 625.8 MPa for the 3- and 5-layer panels respectively. The higher shear modulus in the diagonal compression test is the result of the \(\bar{C}_{i}\) parameter, which is used to compensate for the non-uniform shear stresses. It was possible to decrease the shear modulus measured in the diagonal compression test by 6–32 MPa by excluding the transducers in passive directions.
However, there is also some uncertainty if transducers should be excluded when calculating the in-plane shear modulus. CLT is a new material, meaning that reliable and established values for non-edge-glued CLT are lacking.
References
Brandner R, Flatscher G, Ringhofer A, Schickhofer G, Thiel A (2016) Cross laminated timber (CLT) overview and development. Eur J Wood Wood Prod 74(3):331–351. https://doi.org/10.1007/s00107-015-0999-5
Lukacs I, Björnfot A, Tomasi R (2019) Strength and stiffness of cross-laminated timber (CLT) shear walls: state-of-the-art of analytical approaches. Eng Struct 178(1):136–147. https://doi.org/10.1016/j.engstruct.2018.05.126
Brandner R, Tomasi R, Moosbrugger T, Serrano E, Dietsch P (eds) (2018) Properties, testing and design of cross laminated timber: a state-of-the-art report by COST action FP1402/WG 2. Shaker Verlag, Aachen
Bjørnfot A, Boggian F, Steinsvik Nygård A, Tomasi R (2017) Strengthening of traditional buildings with slim panels of cross-laminated timber (CLT). In: Proceedings of the 4th international conference on structural health assessment of timber structures (SHATIS’17), Istanbul, 20–22 September
Danielsson H, Serrano E (2018) Cross laminated timber at in-plane beam loading—prediction of shear stresses in crossing areas. Eng Struct 171:921–927. https://doi.org/10.1016/j.engstruct.2018.03.018
Swedish Institute for Standards (2012) Swedish standard: timber structures—structural timber and glued laminated timber—determination of some physical and mechanical properties. SS-EN 408:2010+A1:2012
Swedish Institute for Standards (2004) Swedish standard: timber structures—test methods—determination of mechanical properties of wood based panels. SS-EN 789:2004
Swedish Institute for Standards (2015) Swedish standard: timber structures—cross laminated timber—requirements. SS-EN 16351:2015
Kreuzinger H, Sieder M (2013) Einfaches Prufverfahren zur Bewertung der Schubfestigkeit von Kreuzlagenholz/Brettsperrholz. Bautechnik 90(5):314–316. https://doi.org/10.1002/bate.201300024 (in German)
Li L, Zhao Y, Vuong H, Chen Y, Yang J, Duan Y (2014) In-plane shear investigation of biaxial carbon non-crimp fabrics with experimental test and finite element modeling. Mater Des 63:757–765. https://doi.org/10.1016/j.matdes.2014.07.007
Colman AG, Bridgens BN, Gosling PD, Jou GT, Hsu XY (2014) Shear behaviour of architectural fabrics subjected to biaxial tensile loads. Compos A Appl Sci Manuf 66:163–174. https://doi.org/10.1016/j.compositesa.2014.07.015
Vecchio FJ, Collins MP (1986) The modified compression-field theory for reinforced concrete elements subjected to shear. ACI Struct J 83(2):219–231
Nygård A, Björnfot A, Tsalkatidis T, Tomasi R (2016) Test method for determining the in-plane shear strength and stiffness of cross laminated timber (CLT). In: Proceedings of WCTE 2016—world conference on timber engineering, Vienna, 22–25 August
Bosl R (2002) Zum Nachweis des Trag- und Verformungsverhaltens von Wandscheiben aus Brettlagenholz. Dissertation Military University Munich, Munich (in German)
Traetta G, Bogensperger T, Moosbrugger T, Schickhofer G (2006) Verformungsverhalten von Brettsperrholzplatten unter Schubbeanspruchung in der Ebene. In: 5. GraHFT’06, Tagungsband, Brettsperrholz—Ein Blick auf Forschung und Entwicklung, p H1–H16 (in German)
Bogensperger T, Moosbrugger T, Schickhofer G (2007) New test configuration for CLT-wall-elements under shear load. In: Proceedings of international council for research and innovation in building and construction, working commission W18—timber structures (CIB-W18/40-21-2). Bled, 28–31 August
Dujic B, Klobcar S, Zarnic R (2007) Influence of openings on shear capacity of wooden walls. In: Proceedings of international council for research and innovation in building and construction, working commission W18—timber structures (CIB-W18/40-15-6). Bled, 28–31 August
Andreolli M, Rigamonti MA, Tomasi R (2014) Diagonal compression test on cross laminated timber panels. In: Proceedings of the 13th world conference on timber engineering (WCTE 2014). Quebec, 10–14 August
Swedish Institute for Standards (2016) Swedish standard: structural timber—strength classes. SS-EN 338:2016
Frocht MM (1931) Recent advances in photoelasticity and an investigation of the stress distribution in square blocks subjected to diagonal compression. Trans ASME 55:135–153
Brandner R, Dietsch P, Dröscher J, Schulte-Wrede M, Kreuzinger H, Sieder M (2017) Cross laminated timber (CLT) diaphragms under shear: test configuration, properties and design. Constr Build Mater 147:312–327. https://doi.org/10.1016/j.conbuildmat.2017.04.153
Acknowledgements
The experimental project presented in this paper is part of the EU-funded COST Action FP1402 working group and part of the Norwegian project “Increased use of wood in urban areas—WOOD/BE/BETTER”, funded by The Norwegian Research Council through the BIONÆR/BIONAER research programme. The research conducted was also financed by the research and innovation project “Future CLT” as part of the European Union Interreg Nord programme. The authors are grateful for their support. Special thanks also go to Anders Steinsvik Nygård for his dedication in developing the picture frame test setup.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Turesson, J., Björnfot, A., Berg, S. et al. Picture frame and diagonal compression testing of cross-laminated timber. Mater Struct 52, 66 (2019). https://doi.org/10.1617/s11527-019-1372-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1617/s11527-019-1372-7