1 Introduction

Nowadays, environmental and economical requirements are pushing the development of eco-friendly and low-energy road paving materials. In this regard, bitumen emulsion mixtures play an important role because they are manufactured at ambient temperature and therefore, significantly reduce carbon dioxide emissions and energy consumption, with respect to hot and warm bituminous mixtures [1, 2]. Bitumen emulsion mixtures are also widely used in cold recycling. Cold recycled mixtures can incorporate up to 100% reclaimed asphalt (RA), further reducing disposal cost and consumption of natural aggregates [3].

In contrast to hot mixtures, water is used in cold mixtures to reduce bitumen viscosity (through emulsification), facilitate mixing and enhance compaction. The dosage of the residual bituminous binder from emulsion is generally between 2 and 6%, with respect to the dry aggregate mass, whereas the total water content may vary between 3 and 10% [4].

Ordinary Portland cement (OPC), composite cements or other supplementary cementitious materials (fly ash, silica fume, ground granulated blast furnace slag) may be added to bitumen emulsion mixtures [5,6,7]. In this paper, the term bitumen emulsion-cement (BEC) mixture identifies a broad family of cold paving mixtures in which the hydraulic binders, generally dosed between 1.5 and 5% (by mass), play a key role in determining short- and long-term mixture performance. BEC mixtures are temperature-sensitive and prone to fatigue cracking [8]. Compared to hot-mix asphalt (HMA) mixtures, they are characterised by a higher stiffness at high temperatures [9, 10] and by a lower rutting potential [7].

BEC mixtures require a certain curing time after construction to achieve suitable engineering properties [11]. Curing is characterised by the gradual reduction of water content, the breaking and setting of emulsion and the hydration of cementitious materials. Thus, the physical structure of the mixtures evolves, and their mechanical properties improve [12,13,14]. As water evaporation proceeds, the air voids of BEC mixtures increase and normally exceed the air voids of HMA mixtures. Notwithstanding their benefits, the higher air voids content and the slower curing process can reduce durability and mechanical performance of BEC mixtures with respect to HMA, thus limiting their use.

Besides the above-mentioned differences, both HMA and BEC mixtures are multiphase materials and, at different length scales, can be described as composites consisting of a homogeneous interconnected region, also called the matrix, with particulate inclusions [15]. For HMA, four scales of interest are commonly identified: bitumen, mastic, mortar and mixture [16,17,18]. In particular, the mortar can be described as a mastic matrix (filler sized particles dispersed in a continuous bitumen phase) with fine aggregate inclusions. At the mixture scale, the mortar represents the matrix phase that exists between the coarse aggregate particles [19, 20].

Mortar scale composites, also known as fine aggregate matrix (FAM) materials [21], are interesting because they are only one scale smaller than mixtures. If their composition is adequately defined, they can show viscoelastic and failure properties similar to mixtures [22]. Important phenomena, such as fatigue cracking, healing and moisture damage can be studied at the FAM scale [23,24,25]. Table 1 summarises the main approaches for the definition of the FAM material composition in terms of maximum aggregate dimension (upper sieve size), grading curve, bitumen dosage and air voids content.

Table 1 Summary of the approaches proposed for defining FAM composition
Full size table

In comparison to HMA, relatively few works investigated the composition of BEC mortars and related their behaviour to that of BEC mixtures. Fu et al. [29, 30] used fine element models to evaluate the behaviour of BEC mixtures. In these models, coarse aggregates were identified by a minimum dimension of 2 mm, the mortar matrix included mastic and fine particles, and air voids were considered as a separate phase in the mixture. Miljković et al. [31,32,33] proposed to use a standard mortar to characterise the influence of bitumen emulsion on cold asphalt mixture performance. The grading distribution of the mortar was derived from the standard sand used in Europe to evaluate cement properties [34]. The residual bitumen content was 6.6%, and the cement content was 1.5%. Godenzoni et al. [35] also used mortars prepared with natural sand (upper sieve size was 0.5 mm) to compare different mineral additions (Portland cement, calcium carbonate and hydrated lime). They used the same content of residual bitumen and cement (10%) and a total water content between 8 and 9%.

The literature review suggests that testing BEC mortars rather than BEC mixtures offers attractive perspectives. Mortars may be used as model systems to predict mixture behaviour (saving laboratory time and material with respect to BEC mixtures) or to study bitumen emulsion properties and interaction between bitumen emulsion and cementitious materials (eliminating inhomogeneities due to large aggregate particles). Moreover, a detailed study of the properties of the mortar phase can support the development of more realistic computational models for BEC mixtures (for example in finite element modelling).

Based on this background, the objectives of this study are to identify the composition of BEC mortars that closely describes the fine matrix of BEC mixtures and to compare the mechanical behaviour of mixtures and mortars throughout the curing process.

In the first part of the study, the mortar composition was investigated, focusing on the effect of water and air voids content on the mortar strength at a fixed curing time (1 day). In the second part, the effect of curing on the behaviour of mixtures and mortars with fixed composition was evaluated, considering strength, stiffness and moisture loss by evaporation.

2 Materials and methods

2.1 Materials

The BEC composites investigated in this research were composed of RA aggregate, virgin fine aggregate, mineral filler, bitumen emulsion, cement and additional water.

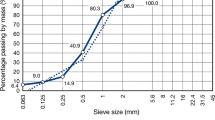
The RA aggregate, supplied by Società Cooperativa Braccianti Riminese from Rimini (Italy), was initially crushed and screened at the production plant to eliminate large asphalt lumps and to obtain a material with an upper sieve size of 20 mm (RA20). The sample was further sieved in the laboratory to separate the fraction with an upper sieve size of 2 mm (RA2). The fine aggregate was a crushed limestone sand with an upper sieve size of 2 mm (FA2) and the filler was a finely ground limestone powder. Table 2 summarises the main physical properties of aggregates, according to European specifications. Their gradation curves are reported in Fig. 1.

Table 2 Physical properties of granular materials
Full size table
Fig. 1
figure 1

Gradation curves of aggregates, BEC mixtures and BEC mortars

Full size image

The bituminous binder was a commercial cationic over-stabilised bitumen emulsion supplied by Valli Zabban S.p.A. Its residual bitumen content was 60% and its designation was C60B10 (EN 13808 [36]). The cement, supplied by Italcementi S.p.A., from Bergamo (Italy) was a Portland limestone cement type II/B-LL with strength class 32.5R (EN 197-1 [37]). Its main physical properties are: maximum dimension of 90 μm, particle density of 3.02 Mg/m3, Blaine surface area of 3800 cm2/g (EN 196-6 [38]).

2.2 Mixture and mortar composition

The aggregate blend of the mixtures was composed of 80% RA20, 17% FA2 and 3% filler (by dry mass). A gradation close to the maximum density curve with upper sieve size of 16 mm was obtained (Fig. 1). The emulsion dosage was 3.3% (by dry aggregate mass) corresponding to 2% of residual bitumen. Two cement dosages were used, 1.5% and 2.5% (by dry aggregate mass) and the corresponding mixtures were identified using the residual bitumen to cement ratio: B/C = 1.3 and B/C = 0.8. The total water content of both mixtures was W tot = 4.67% (by dry aggregate mass), it was determined following the procedure described in [13]. Finally, a target value of voids in the mixture V m = 11% was selected for the compacted specimens. As explained in Sect. 2.3, V m indicates the percentage of total mixture volume that is occupied by air and intergranular water (not absorbed by aggregates).

The starting point for this study was that BEC mixtures are two-phase composite materials, where BEC mortar is the continuous matrix phase and coarse aggregate particles are the inclusions. Thus, a reference mortar was adopted, including all cement, residual bitumen, water and air voids of the mixture. Following the prevailing practice for FAM (Table 1), an upper sieve size of 2 mm was selected. Removing the volume of all coarser particles from the mixture allowed the determination of the composition of the reference mortar (Table 3) and its grading distribution (Fig. 1). The bitumen emulsion dosage in the mortar was 7.8% (by dry aggregate mass), corresponding to 4.7% of residual bitumen. The two cement dosages were 3.5% and 5.9%, corresponding to 1.5% and 2.5% in the mixture, respectively. As can be observed, mixtures and mortars are characterised by the same B/C ratio.

Table 3 Composition of BEC mixtures and mortars with respect to total volume (v/v) and total mass (m/m)
Full size table

As regards the water content of the mortar, two further conditions were selected reducing the water content of the reference composition. In total, three values of water content, with respect to dry aggregate mass of the mortar, were considered:

  • W 1 = 9.4%;

  • W 2 = W 1 − 1.25% = 8.15%;

  • W 3 = W 1 − 2.5% = 6.9%.

The first value refers to the reference mortar composition (all the mixture’s water is included in the mortar), while the second and third values imply that part of the water content of the mixture is not included in the mortar and thus forms the third phase of the mixture, along with mortar and coarse aggregate.

Similarly, two further conditions were selected reducing the air content of the reference mortar. In total, three values of air content, with respect to the total mortar volume, were considered:

  • V A,1 = 7.6%;

  • V A,2 = 0.5 V A,1;

  • V A,3 = 0.0%.

The first value refers to the reference mortar composition (all the mixture’s air is included in the mortar), while the second and third conditions imply that part of the air content of the mixture is not included in the mortar and thus forms the fourth phase of the mixture, along with mortar, coarse aggregate and water. In particular, in the third condition, all mortar pores are filled with water (saturated mortar).

In summary, nine trial mortar compositions were tested (Fig. 2): one deriving from considering the mixture as a two-phase composite (reference composition), and eight obtained considering the mixture as a three- or a four-phase composite.

2.3 Specimen preparation

For manufacturing mixtures and mortars, aggregates were first dried until reaching constant mass, at 105 ± 2 °C for FA2 and at 40 ± 2 °C for RA. A water amount related to the aggregate absorption was added to the dry aggregate blend, and the wet samples were stored in a sealed plastic bag for 12 h at room temperature. Next, cement, water and bitumen emulsion were gradually added and mixed in this sequence to the aggregate blend. Water was added 8 min after cement, bitumen emulsion 3 min after water. The whole process required about 15 min. Mixing was carried out by means of a mechanical mixer to guarantee a good particle coating (checked by visual examination). Three specimens were obtained from each batch of mixed material (about 9 kg for mixtures and 3 kg for mortars).

Specimens were compacted with a shear gyratory compactor, adopting the following protocol: constant pressure of 600 kPa, gyration speed of 30 rpm and angle of inclination of 1.25°. Moulds with diameter of 150 mm and 100 mm were employed for the compaction of mixtures and mortars, respectively. The height of the specimens was measured at each gyration, allowing monitoring of the air voids content (\(V_{\text{A}}\)), the voids in the mixture (\(V_{\text{m}}\)), and the voids filled with liquids (VFL), which are calculated as follows [39, 40]:

$$V_{\text{A}} = \frac{{V_{{{\text{V}},{\text{A}}}} }}{V} = \frac{{V - (V_{\text{S}} + V_{{{\text{B}},{\text{E}}}} + V_{{{\text{W}},{\text{F}}}} )}}{V}$$
(1)
$$V_{\text{m}} = \frac{{V_{{{\text{V}},{\text{A}}}} + V_{{{\text{W}},{\text{F}}}} }}{V} = \frac{{V - (V_{\text{S}} + V_{{{\text{B}},{\text{E}}}} )}}{V}$$
(2)
$${\text{VFL}} = \frac{{V_{{{\text{B}},{\text{E}}}} + V_{{{\text{W}},{\text{F}}}} }}{{V_{{{\text{V}},{\text{A}}}} + V_{{{\text{B}},{\text{E}}}} + V_{{{\text{W}},{\text{F}}}} }} = \frac{{V_{{{\text{B}},{\text{E}}}} + V_{{{\text{W}},{\text{F}}}} }}{{V - V_{\text{S}} }}$$
(3)

where \(V\) is the geometric volume of the specimen (based on its height and diameter), \(V_{\text{S}}\) is the volume of solids (aggregates and unreacted cement), \(V_{{{\text{B}},{\text{E}}}}\) is the volume of residual bitumen, \(V_{{{\text{W}},{\text{F}}}}\) is the volume of intergranular water and \(V_{{{\text{V}},{\text{A}}}}\) is the volume of intergranular air voids. It is important to note that \(V_{\text{S}}\), \(V_{{{\text{B}},{\text{E}}}}\) and \(V_{{{\text{W}},{\text{F}}}}\) are calculated using the initial mass of the materials and their density, whereas \(V_{{{\text{V}},{\text{A}}}}\) is calculated based on the total volume of the specimen \(V\) (Eq. 1). Clearly, Eqs. (1) to (3) are accurate only if material loss during compaction is negligible. To check material loss, each specimen was weighed immediately after extraction from the mould.

To obtain the target content of voids, the final heights of the specimens were fixed. Moreover, the total masses of the specimens, 2800 g for mixtures and 770 g for mortars, were adjusted to ensure the same height to diameter ratio.

Mixture and mortar specimens were cured in a climatic chamber at 25 ± 2 °C and 70 ± 5% relative humidity. Two curing conditions were adopted: unsealed (U) and sealed inside a small plastic bag (S). In unsealed condition, water evaporation is not restricted and thus gives an important contribution to emulsion breaking [41]. This contribution is minimum for sealed specimen where relative humidity is very close to 100%. Hence, it is expected that bituminous bonds will be more developed in unsealed specimen, whereas cementitious bonds will be more developed in sealed specimens.

Different curing times were adopted with the aim of monitoring the development of physical and mechanical properties. In particular, 1, 3, 7 and 28 days for mixtures, and 6 h, 1, 3, 7 and 28 days for mortars.

2.4 Testing methods and program

The indirect tensile stiffness modulus (ITSM) was measured using a servo-pneumatic equipment following the procedure described by the standard EN 12697-26 (Annex C) [42]. The test is performed applying consecutive load pulses with a rise time of 124 ms and a period of 3.0 s. The peak load is adjusted using a closed-loop control system in order to achieve a peak horizontal deformation of 2 microns. ITSM measurements were repeated along two diameters, and the average value was calculated for each specimen.

The indirect tensile strength (ITS) was measured using a mechanical equipment following the procedure described by the standard EN 12697-23 [43]. The test is performed applying a constant rate of deformation of 50 ± 2 mm/min until specimen failure. Both ITSM and ITS tests were carried out at 25 °C therefore, specimens did not need further temperature conditioning after curing.

All specimens were weighed before mechanical testing. The normalised moisture loss by evaporation (DW), was calculated as follows:

$${\text{DW}} = \frac{{m_{o} - m_{t,i} }}{{m_{\text{W}} }} \cdot 100$$
(4)

where \(m_{o}\) is the mass of the specimen immediately after compaction, \(m_{t,i}\) is its mass measured at curing time \(t_{i}\) (before mechanical testing) and \(m_{\text{W}}\) is the initial mass of water within the specimen.

Table 4 summarizes the details of the testing program. In particular, the ITS after 1 day of curing was used to evaluate mortar composition, whereas DW, ITS and ITSM were used to compare mixtures and mortar throughout the curing process.

Table 4 Summary of the testing program
Full size table

2.5 Modelling of curing effects

To model the evolution of physical and mechanical properties as a function of curing time, the following regression equation was adopted:

$$y\left( t \right) = y_{1} + \left( {y_{a} - y_{1} } \right)\frac{t - 1}{{(h_{y} - 1) + (t - 1)}}$$
(5)

where \(t\) (days) is the curing time, \(y(t)\) is the property under investigation (DW, ITS or ITSM), \(y_{1}\) is an intercept term, \(y_{a}\) is the long-term asymptotic value of \(y\left( t \right)\) and \(h_{y}\) (days) is a parameter representing a specific curing time.

Equation (5) is a modified version of the Michaelis–Menten asymptotic model that was previously applied to analyse the curing process of cold recycled bitumen emulsion mixtures [13, 44]. The main change is the introduction of the intercept term in order to improve the fitting capability of the model. The time delay \((t - 1)\) is a simple reparametrization that allows the value \(y_{1} = y\left( 1 \right)\) to be used directly as model parameter.

The parameter \(y_{1}\) can also be interpreted as the average rate of evolution of material properties during the first curing day. As regards \(h_{y}\), from Eq. (5) it can be observed that \(y\left( {h_{y} } \right) = y_{1} + \left( {y_{a} - y_{1} } \right)/2\). Thus, the ratio \(r_{2} = \left( {y_{a} - y_{1} } \right)/\left[ {2(h_{y} - 1)} \right]\) can be interpreted as the average rate of evolution of material properties from \(y_{1}\) to \(y\left( {h_{y} } \right)\).

The values of the best-fit regression parameters were estimated using the classical least-squares method. Goodness of fit was evaluated using the residual standard error, which provides a measure of the average distance between the measured data and the fitted regression model.

3 Results and discussion

3.1 Study of mortar composition

Figure 3 reports the average ITS after one curing day of the two mixtures and the corresponding eighteen mortar compositions (Fig. 2). The ratio between the ITS of mortar (ITSm) and the ITS of mixture (ITSM) is reported on the y-axis (ITSM was 0.26 MPa and 0.28 MPa, for B/C = 1.3 and B/C = 0.8, respectively). Similarly, the ratio between the air voids content of the mortars (V A,m) and the air voids content of the mixtures (V A,M) is reported on the x-axis (V A,M was 7.6% and 7.7%, for B/C = 1.3 and B/C = 0.8, respectively).

Fig. 2
figure 2

Comparison of mixture and mortar proportions related to the 9 mortar compositions tested

Full size image

In Fig. 3, the bottom-right points show the results for the reference mortar. For both B/C ratios, this composition resulted in the lowest ITSm/ITSM values, 0.47 and 0.48 for B/C = 1.3 and B/C = 0.8, respectively. Thus, when the mortar specimens were manufactured including all the mixture’s water and air voids, their ITS after 1 day of curing was less than one half the ITS of the mixture. Figure 3 shows that reducing water and air voids content of the mortars, according to the scheme depicted in Fig. 2, resulted in an increase of their ITS. In a few cases, the mortar strength exceeded the mixture strength (ITSm/ITSM > 1).

Fig. 3
figure 3

Mortar-to-mixture ITS ratio versus mortar-to-mixture air content ratio

Full size image

In general, the strength of matrix-particle composites may be higher or lower with respect to the strength of the matrix, depending on the volume fraction of the inclusions, their dimension and shape, the matrix-particle interfacial adhesion and the presence of interfacial defects [45, 46]. The results reported in Fig. 3 confirm this general behaviour and do not indicate an optimal or “more realistic” mortar composition.

Therefore, to study the effect of curing, mortars having short-term ITS value close to that of the mixtures (ITSm/ITSM ≈ 1) were selected. Among the mortars that satisfy this condition, those characterised by V A,m/V A,M ≈ 0 (saturated mortar) were excluded. In fact, removing all the air voids from the mortar, and thus leaving only a separated air phase within the mixture, does not appear realistic. Finally, the mortar characterised by the lower content of water (W 3) and containing 50% of the total air voids existing in the mixture (V A,2) was selected. As shown in Fig. 3, this “design” composition (Table 3) is characterised by ITSm/ITSM equal to 0.88 and 1.15, for B/C = 1.3 and B/C = 0.8, respectively.

3.2 Study of curing effect

3.2.1 Volumetric properties of the specimens

The specimens of mixture and design mortar were prepared according to the composition reported in Table 3. Gyratory compaction stopped when the height of the specimens reached the value corresponding to the target values of V m of 11% and 14.1%, for mixture and mortar, respectively.

Figure 4 shows the upper and lower limits of the compaction curves obtained for all specimens. The two envelopes allow the variability of the compaction process to be estimated. Simultaneously, VFL increased until reaching the final values of 74.8% and 83.5% for mixtures and mortars, respectively. Figure 4 also shows that the number of gyrations required to reach the target V m of mixture and mortar was very similar. This indicates that the energy per unit volume necessary to compact mixture and mortar specimens was practically the same.

Fig. 4
figure 4

Upper and lower limits of the compaction curves (mortar and mixture specimens for studying the curing effect)

Full size image

Figure 5 shows the empirical density distribution functions of the mass loss of all the specimens, measured at the end of compaction. As can be observed, the loss of material (water and fines) was less than 0.1% and 0.3% for mixtures and mortars, respectively. This is consistent with the final values of VFL and confirms that the volumetric composition of the specimens is actually the one reported in Table 3.

Fig. 5
figure 5

Density distributions for the mass loss during compaction (mortar and mixture specimens for the study of the curing effect)

Full size image

3.2.2 Moisture loss

Figure 6 shows the evolution of DW as a function of curing time for specimens cured in unsealed conditions (unrestricted evaporation). The experimental results were fitted using Eq. (5) and the estimated values of \(y_{1}\), \(y_{a}\), \(h_{y}\), \(r_{2}\) along with the residual standard error are reported in Table 5.

Fig. 6
figure 6

Evolution of moisture loss versus curing time in unsealed curing conditions

Full size image
Table 5 Regression parameters for Eq. (5 )
Full size table

The results show that the long-term behaviour of mortars and mixtures was similar. Decreasing the B/C ratio from 1.3 to 0.8, the asymptotic value \(y_{\text{a}}\) decreased from 88.4 to 80.5% and from 82.1 to 76.0% for mixtures and mortars, respectively. For the mixtures, the non-evaporated water contents (with respect to dry mass of aggregates), were 0.55% and 0.92% for B/C of 1.3 and 0.8, respectively. For the mortars, the non-evaporated water contents were 1.24% and 1.66% for B/C of 1.3 and 0.8, respectively. These values are proportional to the actual cement dosages of the composites (the average ratio between non-evaporated water and cement is 0.35). This suggests that, in the long term, all non-evaporated water is chemically and physically bound by cement [47, 48] and that unsealed curing condition did not limit the complete hydration of cement.

3.2.3 Indirect tensile strength

Figure 7 shows the evolution of ITS as a function of curing time for mortars and mixtures with B/C = 0.8 (unsealed and sealed specimens). The evolution of ITS for mortars and mixtures with B/C = 1.3 followed a similar trend. In particular, the ITS measured after unsealed curing always exceeded the ITS measured after sealed curing. This confirms that unsealed curing favours the development of bituminous bonds, without penalising cementitious bonds. The experimental results were fitted using Eq. (5), and the estimated values of the regression parameters are reported in Table 5.

Fig. 7
figure 7

Evolution of ITS versus curing time for mortars and mixtures with B/C = 0.8 (unsealed and sealed curing condition)

Full size image

Figure 7 shows that the ITS of mixtures and mortars after 1 day of curing at 25 °C was very similar. This follows from the selection of the mortar design composition described in Sect. 3.1. After 1 day, the ITS of mixtures and mortars improved with different rates. As shown by the values of \(r_{2}\), in this phase, the curing rate of mortars was two to three times higher than the curing rate of mixtures. In the long term, the ITS of mixtures and mortars tend to be very close, as shown by the asymptotic values \(y_{\text{a}}\). This indicates that bituminous and cementitious bonds are developing in a different way within mortar and mixture, even though the two materials are characterised by the same B/C ratio.

For specimens cured in sealed conditions, decreasing the B/C ratio from 1.3 to 0.8 (i.e. increasing cement dosage) produced a clear increase of ITS in both the short (\(y_{1}\)) and the long-term (\(y_{\text{a}}\)). Specifically, \(y_{\text{a}}\) increased from 0.33 to 0.53 MPa (+ 60%) and from 0.33 to 0.49 MPa (+ 49%) for mixtures and mortars, respectively. This confirms that the cement dosage controls the strength of sealed specimens. On the other hand, after unsealed curing, the increase of cement dosage did not lead to an ITS increase for mixtures (\(y_{\text{a}}\) = 0.61 MPa). For mortars \(y_{\text{a}}\) increased from 0.54 to 0.64 MPa (+ 18%). Thus, in unsealed specimens, the increase of strength due to the increase of cement dosage is less marked because of the presence of a higher volume of bituminous bonds.

3.2.4 Indirect tensile stiffness modulus

Figure 8 shows the evolution of ITSM as a function of curing time for mortars and mixtures with B/C = 1.3 (unsealed and sealed specimens). The evolution of ITSM for mortars and mixtures with B/C = 0.8 followed a similar trend. The experimental data were fitted using Eq. 5 and the estimated values of the regression parameters are reported in Table 5.

Fig. 8
figure 8

Evolution of ITSM versus curing time for mortars and mixtures with B/C = 1.3 (unsealed and sealed curing condition)

Full size image

Different from ITS, ITSM of mixtures always exceeded ITSM of mortars. In the short-term, considering the values of \(y_{1}\), the average increase of ITSM from mortars to mixtures was 56%. In the long term, considering the values of \(y_{\text{a}}\), the average increase was 26%. In fact, after the first curing day, the rate of ITSM increase (\(r_{2}\)) for mortars was about two times that of mixtures. In summary, including coarse aggregates into the mortar resulted in a stiffness increase, even though most of the inclusions were RA particles. Moreover, since the stiffness of the mortar matrix increases with curing time, the stiffening effect of the RA particles progressively reduces.

Decreasing the B/C ratio from 1.3 to 0.8 (i.e. increasing cement dosage) led to a clear increase of both \(y_{1}\) and \(y_{\text{a}}\) (short- and long-term stiffness). Specifically, the average increase of \(y_{\text{a}}\) was 28% after unsealed curing and 36% after sealed curing.

The effect of curing conditions on the long-term value of ITSM is different from the effect on ITS. At the lower cement content (B/C = 1.3), changing from sealed to unsealed curing, \(y_{\text{a}}\) decreased from 6719 to 6463 MPa (− 4%) for mixtures and increased from 4963  to 5326 MPa (+ 7%) for mortars. Similarly, at the higher cement content (B/C = 0.8), \(y_{\text{a}}\) decreased from 8878 to 8246 MPa (− 7%) for mixtures and from 6952 to 6889 MPa (− 1%) for mortars.

In summary, the change of ITSM due to the change of curing condition (from unrestricted to restricted evaporation) is low. Thus, different from strength, the effect of curing on stiffness does not appear practically significant.

3.3 Relation between mixture and mortar behaviour

In terms of ITS and ITSM, BEC mixtures and design mortars showed a similar sensitivity during the curing process (Figs. 7, 8). This experimental evidence suggests that a study aimed at comparing different BEC mixtures can be performed using BEC mortars.

Figure 9 compares the average values of ITS and ITSM of mixtures and design mortars. As can be observed, unique relationships exist between mortar and mixture properties regardless of B/C ratio, curing time and curing condition:

Fig. 9
figure 9

Mechanical properties of mixtures as a function of mechanical properties of mortars, a indirect tensile strength (ITS), b indirect tensile stiffness modulus (ITSM)

Full size image
$${\text{ITS}}_{\text{Mixture}} = 0.804 \cdot {\text{ITS}}_{\text{mortar}} + 0.04$$
(6a)
$${\text{ITSM}}_{\text{Mixture}} = 0.995 \cdot {\text{ITSM}}_{\text{mortar}} + 832\quad$$
(6b)

where ITS and ITSM are in MPa. In other words, properly designed BEC mortars can be used to predict the behaviour of BEC mixtures throughout the curing process.

Figure 9 also shows that the BEC mortars slightly overestimated the mixture strength and underestimated the mixture stiffness. Both effects clearly depend on the criterion adopted for selecting the mortar design composition, and thus on the presence in the mixture of separate water and air phases. This suggests the idea that adjusting mortar composition to obtain the same properties of the mixtures is possible. For example, this could be achieved by changing the binders content or the B/C ratio.

4 Conclusions

The composition and the mechanical behaviour of BEC mortars closely describing the fine matrix of BEC mixtures was investigated. Based on the experimental results the following conclusions can be drawn:

  • Mortars produced including all bitumen, cement, water and air of the mixture, had an ITS which was about one half the ITS of mixtures, after 1 day of curing at 25 °C. However, reducing the water and air voids contents, the ITS of mortars increased and exceeded the ITS of mixtures.

  • Mortar produced including about 75% of mixture water and 50% of mixture air voids can be used to simulate the effect of curing on mixtures, in terms of water loss, ITS and ITSM.

  • ITS and ITSM of both mixtures and mortars increased when cement content was increased.

  • When curing conditions were changed from sealed to unsealed, ITS of both mixtures and mortars increased, whereas the effect of curing on ITSM did not appear practically significant.

  • Unique relationships relating ITS and ITSM of mixtures and mortars were identified regardless of B/C ratio, curing time and curing condition.

The study of BEC mortar composition is a promising subject. It can be developed analysing different choices of upper sieve sizes, B/C ratios, water dosages and air voids contents. In principle, the mortar composition could be adjusted based on the final goals of the study. The latter could be, for example, to predict mixture behaviour, to compare emulsion properties or to support the development of mechanical models.