Experimental investigation of the axial strength of glued-in rods in cross laminated timber

Abstract

This paper presents results from an experimental assessment of glued-in rods in cross laminated timber (CLT). For the purposes of the study more than 60 pull–pull tests were performed, where the specimens varied in terms of bonded-in length (from 80 to 400 mm), rod diameter (16–24 mm) and rod-to-grain angle (parallel and perpendicular). Several different failure modes that are not common for other applications of glued-in rods (e.g., a failure between CLT layers) were obtained for the analysed CLT specimens. It was found that these failure mechanisms can substantially influence the obtained ultimate tension loads. At the end, the experimental results were compared with empirical and semi-empirical equations for estimating the pull-out strength of glued-in rods in structural timber and glulam. The comparison showed that most of the existing equations overestimate the ultimate tension loads for specimens with the rod parallel to the grain and underestimate the ultimate tension load for specimens with the rod perpendicular to the grain. The results vary because the possible CLT failure modes were not included in previous studies. Further studies are proposed to improve the equations for glued-in rods in CLT.

Introduction

Glued-in rods in timber elements can be considered as hybrid connections, since they involve three different elements: the timber, the rod connector and the adhesive [1]. In many cases these joints outperform dowel-type mechanical fasteners. For example, they usually exhibit a higher load-carrying capacity per unit of connected cross-sectional area as well as a significantly higher stiffness [2]. Apart from the enhanced mechanical performance, there are several other benefits of this type of joint: good fire resistance, adaptability from the architectural point of view, a relatively low overall cost and the possibility of an automated production process. Glued-in rods can also be efficiently used with CLT elements. One of the possibilities is to connect two CLT walls, where the rods can be placed parallel to the axis of the walls or with an inclination. Furthermore, glued-in rods are also appropriate to connect the CLT with other structural elements of different materials (e.g., vertical joints between CLT walls and steel beams, joints between CLT walls and concrete elements, etc.). In this way glued-in rods can be a solution for connecting different structural elements into hybrid structural systems. Research covering glued-in rods in CLT is therefore necessary to address the growing interest for constructing mid- to high-rise structures, where hybrid structural systems are frequently being used.

Glued-in rods have been experimentally investigated primarily for cases of solid structural timber [3, 4], glulam [5, 6] and, most recently, laminated veneer lumber (LVL) [7, 8]. Usually, joints with single rods under axial tensile loading are investigated (e.g., pull–pull, pull–compression and one-sided pull tests). Using these tests the influence of different parameters on the mechanical performance of the joint were investigated [9, 10]. A few studies have also involved investigating joints with multiple rods [11, 12], and some studies have tried to develop design equations based on analytical or numerical models. More information about the existing analytical models can be obtained from [9, 10, 13, 14]. Most studies conclude that the behaviour of a glued-in rod is similar to a lap joint [15] and focus on predicting the pull-out strength of the rod [16, 17], although other failure modes also need to be accounted for, e.g., by prescribing the minimum edge distances to avoid splitting. The primary objective of this research was to analyse the mechanical behaviour of glued-in rods in CLT and how it differs from the behaviour of glued-in rods in structural timber, glulam and LVL.

Previous studies on solid structural timber, glulam and LVL demonstrated that increasing the anchorage length, increases the axial load-carrying capacity, but the non-uniform distribution of the shear stresses along the anchorage length leads to a decrease in the nominal shear strength [5]. The rod diameter and the bond-line thickness are other commonly investigated parameters as they are directly related to the joint’s load-carrying capacity [14]. Thicker bond-lines increase the net surface area between the rod and the wood and therefore should cause a more uniform stress distribution (commonly applied bond-line thicknesses range from 1 to 3 mm) [2, 3]. In [3] it was concluded that the glue line thickness is an important parameter, since it affects the performance of the joint by offering different strength and compatibility with the wood (e.g., making full use of the rheology of the adhesives and optimizing the stress transfer from the timber to the rod). In addition, the slenderness ratio (the ratio between the bonded-in length and the rod diameter: $\lambda = l_{\text{a}} /d$) and rod spacing are also often considered. With slenderness the combined influence of the anchorage length and the rod diameter is described. It was shown that the total pull-out force increases at higher slenderness values [6]. The investigation of the rod spacing and the edge distances showed that a decrease in the total load-carrying capacity could occur when the spacing is less than 5 times the rod diameter and the edge distance is less than 2.5 times the rod diameter [11, 18].

Information about glued-in rods for CLT is scarce, especially compared to the large number of publications available for glued-in rods in solid structural timber or glulam. In [19], glued-in rods for CLT were studied experimentally and numerically with a pull–pull test. The failure modes and the pull-out strength of 12 different specimen types with epoxy adhesive were studied; however, only three repetitions were made for each type. In [20] the glued-in rods in CLT were analysed with a pull–compression test. In that study a polyurethane (PUR) adhesive and different rod-to-grain angles were considered; however, there was no variation in the glued-in length and the rod diameter. Some conclusions related to the glued-in rods in CLT can also be drawn from [21], where screwed-in rods in CLT were analysed. The response of the screwed-in rods is in many ways similar to the glued-in rods.

On the basis of the above-mentioned research a different response of the glued-in rods in CLT can be anticipated for the following reasons; (1) Since CLT is cross-wise laminated, the effective axial stiffness and the strength of the timber (in the pull direction) are dependent on the distribution and thickness of the layers; this could significantly influence the pull-out response of the glued-in rod. (2) The angle of the rod relative to the orientation of the grain might influence the behaviour/capacity of the connection. (3) The effect of the glued-in length, which was studied for the structural timber and the glulam, could change significantly with a different position of the rod in relation to the CLT layers. The rod can be glued in the middle of a single layer, in between two neighbouring layers, next to the border of the CLT layer or even close to the CLT edge. These different positions directly mean that the rod can be glued into layers with a different grain orientation and consequently influence the pull-out response. (4) Different failure modes might occur (e.g., splitting or tearing of the CLT), which are not observed in solid structural timber, LVL or glulam. (5) The different influence of the spacing (when multiple rods are used in the same CLT cross-section) and edge thickness on the pull-out response, etc.

In this paper the behaviour of glued-in rods in CLT was further analysed. Firstly, several tests were performed and a wider range of bonded-in rod lengths was analysed compared to previous research. Secondly, the performed research demonstrated the differences of the glued-in rods in the CLT compared to the glued-in rods in solid structural timber, glulam or LVL, by analysing the failure modes and comparing the results based on existing equations.

Description of the test specimens and the laboratory testing

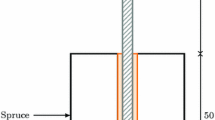
The glued-in rods in CLT were investigated using a “pull–pull” test configuration (Fig. 1). The specimens were prepared with glued-in rods on both sides. To avoid failure of the supporting rod, the threaded rod was increased in terms of diameter and bonded-in length compared to the rod at the tested end. The monotonic tension tests were performed using a Zwick Z2500Y testing machine under displacement control. The velocity of the test was 1 mm/min until the failure occurred; thereafter the velocity was increased to 25 mm/min. The displacements were measured with optical extensometers. In addition, a HD camera (resolution 720p, 30fps) was used to record the failure modes.

Fig. 1

Test specimen and test set-up [19]

The specimens varied in terms of the bonded-in length (l _a), rod diameter (d) and rod-to-grain angle (Table 1). For each bonded-in length, at least five specimens were tested with the force parallel to the grain and at least five with the force perpendicular to the grain configuration. Altogether 60 tests were made. The basic dimensions of the CLT specimens are shown in Table 1. The CLT was glued with melamine urea formaldehyde adhesive (MUF: type I according to EN 301) between the layers, while the lamination edges were not glued. CLT consisting of five layers (33/20/34/20/33 mm) with a cross-section of 14 × 30 cm × L was used (L represents the bonded-in length—see Table 1), where the quality of the laminations was C24. The rod was glued into the centre of the middle layer with a brittle epoxy adhesive HILTI RE500 V3 [22]. To prevent yielding of the rod, threaded rods made from high-grade steel (10.9) were used.

Table 1 Basic characteristics of the specimens used in the experiments

Results and discussion

The experiments showed that the behaviour of the joints varies greatly depending on the bonded-in length and the rod diameter. Therefore, the results are dealt with separately in two sections. In Sect. 3.1, only the specimens with shorter bonded-in lengths (l _a ≤ 240 mm) and smaller rod diameters (d = 16 mm) are presented. In Sect. 3.2, the longer bonded-in lengths (l _a ≥ 320 mm) and larger rod diameters (d = 24 mm) are shown. A summary of the experimental results and the failure modes is then given in Sects. 3.3 and 3.4.

Bonded-in lengths 80–240 mm

In the case of the short bonded-in lengths and the smaller rod diameter, significantly different failure modes were observed for the specimens with different rod-to-grain angles (Fig. 2). The typical failure for a specimen with the rod parallel to the grain (0° specimen) was rod pull-out (Fig. 2a). This type of failure is typically characterized by a failure at the interface between the timber and the adhesive. In some cases failure of the timber next to the adhesive occurred, as shown in Fig. 2a (change in the fibre direction due to the knot). There were only a few examples where failure occurred between the adhesive and the CLT layers.

Fig. 2

Typical response of the specimens with l _a = 80 mm: a rod parallel to the grain and b rod perpendicular to the grain of the middle CLT layer

Unlike the specimens with a parallel rod-to-grain orientation, the failure modes of the specimens with the perpendicular rod-to-grain orientation (the 90° specimens) were associated with the failure of the CLT. In most cases the failure occurred due to edge-lamination tear out of the core CLT layer, which enabled the rod pull-out (Fig. 2b). The lamination typically failed while bending after the failure of the adhesive between the CLT layers. In some cases, a complete tear-out of the edge lamination was also observed. However, such failure modes were more common in the case of the longer bonded-in lengths and the larger rod diameters (see Sect. 3.2).

As discussed above, the failure modes of the 0° specimens can be described as a combination of rod and wood pull-out, with different amounts of wood being attached to the rod. Despite the variation in failure type, the load capacity was similar in all cases and the variability in the ultimate load was relatively small (Fig. 3). Nevertheless, a thorough comparison shows that the highest values of the load capacity were achieved for specimens where the rod pull-out was the governing mode of failure.

Fig. 3

Results for specimens with: a l _a = 80 mm, b l _a = 160 mm and c l _a = 240 mm

Comparing the results for 0° and 90° specimens reveals a great difference in the ductility of the response. In the case of the 0° specimens the failure is relatively brittle, while the 90° specimens have a much more ductile response. This difference is also reflected in the variability of the load capacity. Due to the brittle nature of the failure, the ultimate load capacity of the 0° specimens is more unpredictable (coefficient of variation—COV) compared to the 90° specimens. As a result, the COV of the load-carrying capacity of the 90° specimens is even lower, i.e., below 10% (Fig. 3).

For the 90° specimens with l _a = 80 mm the only failure mode was the edge lamination tear-out. In contrast, for the specimens with l _a = 160 mm and l _a = 240 mm, two different failure modes were observed: (1) edge lamination tear-out and (2) complete lamination tear-out. A slightly higher load-carrying capacity was observed in the cases when the edge-lamination tear-out occurs. The failure mode of complete lamination tear-out only occurs if the width of the edge lamination in the core layer (dimension parallel to the rod) does not exceed the bonded-in length (l _a). The ultimate load-carrying capacity of the 90° specimens is therefore greatly dependent on the CLT geometry. The complete lamination tear-out can be observed on the force–displacement curve as a sudden drop in the load-bearing capacity (see Fig. 3b).

Bonded-in lengths 320 and 400 mm

Figure 4 shows the typical failures of specimens with longer bonded-in lengths (l _a ≥ 320 mm) and a larger rod diameter (d = 24 mm). As in the case of the shorter bonded-in lengths, different failure modes were observed for different rod-to-grain angles. The failure mode for the 0° specimens is a combination of rod pull-out and the failure of the CLT (Fig. 4a). The general observation is that the load-bearing capacity of the adhesive layer between the CLT laminations becomes critical due to: (1) the larger anchorage resistance of the longer and thicker bonded-in rods and (2) the shorter distance to the edge of the lamination (the hole diameter is almost equal to the lamination thickness). In some cases the rod was glued next to the edges of two laminations. In these cases the failure occurs along the non-glued edge (Fig. 4a).

Fig. 4

Typical response of the specimens with l _a = 320 mm: a rod parallel to the grain and b rod perpendicular to the grain of the middle CLT layer

Figure 4b presents the failure of a specimen with the rod perpendicular to the grain. In all cases the complete tear-out of the CLT was observed. The laminations in the core CLT layer were pulled-out completely, together with the rod. The latter indicates that the maximum strength of the adhesive layer along the rod was not reached. The ultimate load capacity is hence largely dependent on the capacity of the CLT.

It should be noted that the failure mode described above (Fig. 4b) occurred because the tested CLT panels were relatively narrow. In practice such cases could occur when the rod is glued close to the edge of the CLT panel. If the width of the specimens had been larger, different failure modes would have occurred and the ultimate load-carrying capacity of the glued-in rod would have been higher. Such a case could be tested using a pull–compression test set-up. With this type of test, the failure mode of the complete lamination tear-out is avoided.

For the 0° specimens (Fig. 5) the COV of the ultimate load equals 16.5% (the same value applies for the l _a = 320 and l _a = 400 mm specimens) and is therefore much larger than in the case of the specimens with the short bonded-in lengths (Sect. 3.1). The larger COV value is a direct consequence of several possible failure modes, which are dependent on the position of the rod relative to the CLT layout and also on the bearing capacity of the analysed CLT. The lowest load capacity of the glued-in rod was observed when most of the failure took place at the bondline between the CLT layers (shear failure of adhesive) due to the unfavorable layout of the laminations in the CLT cross-section.

Fig. 5

Results for specimens with: a l _a = 320 mm and b l _a = 400 mm

Since the failure mode of the 90° specimens was similar in all cases, the COV was also lower (Fig. 5). The response of the 90° specimens is more ductile compared to the 0° specimens. However, the difference in ductility between the two specimen types (0° and 90°) is not that large as in the case of short bonded-in lengths (Sect. 3.1). On the other hand, there is a larger difference in terms of load capacity: with a larger bonded-in length the ratio between the load-carrying capacity of the 90° specimens and the 0° specimens is significantly larger.

Overview of the results

In Table 2 the average results are presented for the 0° and 90° specimens. The characteristic values of the ultimate load were also calculated and are based on [23]. From Table 2 several conclusions can be drawn:

Table 2 The average results obtained from the 0° and 90° specimens

• 1. The mean maximum tensile force (F _ax,mean) is monotonically increasing with a larger bonded-in length.

• 2. In general, F _ax,90,mean is higher than F _ax,0,mean (assuming the same l _a). The difference is the largest in the case of the longest bonded-in rod (l _a = 400 mm). For l _a = 80 mm the capacity is slightly in favour of the 0° specimen (approximately 20% larger).

• 3. The differences between the 0° and 90° specimens are even larger when the characteristic tensile forces are compared (F _ax,char.). This is expected since the coefficients of variation were, in general, larger for the 0° specimens.

• 4. The displacement at the maximum tensile force (δ) is significantly (approximately two times) larger for the 90° specimens than for the 0° specimens. The differences in ductility can be explained by different modes of failure (Sects. 3.1, 3.2).

• 5. The effective global stiffness k _eff,0 is mostly dependent on the rod diameter and not on the bonded-in length. The same applies for the k _eff,90 with some exceptions (l _a = 80). The k _eff,0 is larger than k _eff,90 for all the tested bonded-in lengths. The differences between k _eff,0 and k _eff,90 are below 20% (except in the case l _a = 80 mm).

• 6. The average shear strength in the bondline along the threaded rod (f _v,0,mean) can only be estimated for the 0° specimens, which are characterized by the pull-out failure mechanism. For the 90° specimens, the failure in the CLT was critical. Therefore, in these cases only τ _mean can be estimated, which represents the stress at the maximum tensile force.

• 7. The average shear stress in the bondline along the threaded rod (τ _mean) is monotonically decreasing for the 0° specimens. For the 90° specimens, no specific pattern that would describe the influence of the bonded-in length on the shear stress (τ _mean) could be determined. This is expected, since most of the failures for the 90° specimens were due to the failure in the CLT. If the width of the specimens had been larger, different failure modes would probably occur (e.g., edge lamination tear-out or rod pull-out) that would result in larger shear stresses.

Description of the failure modes

Based on the results of the analysed specimens all the possible failure modes of the glued-in rods in CLT were documented. The connections with glued-in rods are usually designed to achieve a ductile failure through the yielding of the rod. However, for the purposes of this study, the rod was prevented from yielding in order to analyse the other possible types of failure. This approach was adopted to determine the weak points and the upper strength capacity of the CLT and the timber-adhesive interface. In this study the failure in the timber was the result of the high strength of the rod and the epoxy adhesive.

The possible failure modes were divided into the main groups that describe the global failure (denoted by numbers). Each of the main groups is then further divided into subgroups (denoted by capital letters), which distinguish between the different local failures (denoted by lower-case letters). The failure modes can be described with the following list:

• 0. Rod failure

  • (A) Yielding of the rod

  • (B) Buckling of the rod

• 1. Rod pull-out

  • (A) Adhesion failure (steel-adhesive bondline)

  • (B) Failure at the timber-adhesive interface

    • (a) Adhesion failure (timber-adhesive bondline)

    • (b) Cohesive failure of timber

  • (C) Cohesive failure of adhesive

• 2. Wood pull-out (rod along the grain of the core lamination)

  • (A) Shear failure in timber

    • (a) Reduction of strength characteristic for timber (e.g., failure due to the knot, changes in fibre direction)

    • (b) Failure due to the rolling shear effect

    • (c) Failure along the grain

  • (B) Lamination bond failure

    • (a) Adhesive (shear) failure in the bondline between CLT layers

    • (b) Non-edge bonded timber lamination pull-out

    • (c) Adhesive failure of the edge-bonded timber laminations

• 3. Wood pull-out (rod perpendicular to the grain of the core lamination)

  • (A) Edge lamination tear-out (bending of the core lamination)

  • (B) Multiple lamination tear-out (complete tear-out, CLT splitting)

    • (a) Adhesive (shear) failure in the bondline between CLT layers

    • (b) Shear failure in the core lamination–rolling shear effect

In most of our experiments multiple failure modes were combined within a single test specimen. In such cases a primary failure mode should be defined based on the governing failure. The failure modes of the specimens in Figs. 2 and 4 could be classified according to the proposed list as follows: (1) primary failure, 2B-a, and secondary failure, 1B-b (specimen in Fig. 2a); (2) primary failure, 3A, (specimen in Fig. 2b); (3) primary failure, 2A-c, and secondary failure, 2B-a (specimen in Fig. 4a); and (4) primary failure, 3B-a (specimen in Fig. 4b).

The large variety of the failure modes indicates the complexity of the response of the connections with glued-in rods in CLT. In order to correctly predict the bearing capacity of the glued-in rods in CLT several important variables should be considered, such as (1) glued-in length, (2) rod diameter, (3) adhesive thickness, (4) angle of the rod in relation to the grain angle of the CLT lamination, (5) position of the rod in relation to the CLT cross-section (rod bonded in the middle of the lamination, rod bonded on the border between the two CLT laminations, rod bonded next to the non-glued edge between two laminations in the same CLT layer, etc.), (6) CLT dimensions (width of the CLT, lamination thickness, etc.), (7) distance of the rod from the edge of the CLT panel, (8) ratio between the hole diameter and the lamination thickness, (9) width of the crosswise edge lamination in relation to the glued-in length (largely influences the failure mode for the 90° specimens), (10) multiple glued-in rods in the CLT cross-section, and (11) edge bonding of the CLT laminations, etc.

Due to the large number of possible influencing parameters it is difficult to predict the strength of the analysed connection. The experimentally obtained values were compared with previously proposed design equations in Sect. 4. An assessment was made to see whether the existing equations, which were originally derived for other glued-in rod applications, could also be applied to the glued-in rods in CLT.

Comparison of the experimental data with the design equations

There have been many experimental and numerical studies analysing the glued-in rods in solid structural timber, glulam and LVL. However, the research related to glued-in rods in CLT is scarce. The main purpose of this section is to compare the existing design equations with the experimental data obtained on CLT. The comparison is made in Fig. 6 for the 0° specimens and in Fig. 7 for the 90° specimens. When the different design equations are compared it is necessary to consider their assumptions and the conditions of the derivation (e.g., all of the analysed equation proposals were based on specimens where the failure mode described as rod pull-out occurred). These assumptions are described in Sects. 4.1, 4.2, 4.3, 4.4, 4.5 and 4.6.

Fig. 6

Comparison of pull-out strength equations with experimental data for the 0° specimens: a d _h = 20 mm, and b d _h = 28 mm

Fig. 7

Comparison of pull-out strength equations with experimental data for the 90° specimens

Feligioni et al. proposal

Feligioni et al. experimentally investigated the influence of different types of adhesives (brittle and ductile) on the pull-out strength of glued-in rods in structural timber (specimens from spruce wood) [3]. The tests confirmed that a ductile adhesive leads to a higher pull-out strength, since the ductility of the adhesive ensures a uniform load transfer from the rod to the timber. Hence, a design equation for the axial pull-out strength of the rod parallel to the grain was proposed that takes into account the type of adhesive:

$$F_{{{\text{ax}},0}} = \pi \cdot l_{\text{a}} \cdot \left( {f_{{{\text{v}},{\text{k}}}} \cdot d_{\text{equ}} + k \cdot \left( {d + e} \right) \cdot e} \right)\cdot a$$

(1)

$$f_{{{\text{v}},{\text{k}}}} = 1.2 \cdot 10^{ - 3} \cdot d_{\text{equ}}^{ - 0.2} \cdot \rho^{1.5}$$

(2)

where F _ax,0 is the axial pull-out strength, f _v,k is the characteristic shear strength of the adhesive-timber interface, k is an adhesive strength parameter found to be 0.086 for brittle and 1.213 and ductile adhesives, e is the thickness of the adhesive, ρ is the density of the wood and d _equ is the equivalent diameter (d _equ = min(d _h, 1.25 d)).

The following values were assumed for the CLT specimens in this study: k = 0.086, e = 2 mm and ρ = 450 kg/m³. The values l _a, d _h and d were those listed in Table 2.

The GIROD project proposal

The GIROD (Glued-In Rods) proposal for the design equation is presented in [14]. The model for the estimation was developed based on glulam specimens with thin bondlines between the rod and the timber (0.5 mm or less). The proposed equation was derived assuming a pull–compression set-up, with the aim of applying this to all situations as a simplification on the safe side. The axial pull-out strength of the rod parallel to the grain is determined by the geometry of the joint and by two empirical parameters describing the bondline and the material properties:

$$F_{{{\text{ax}},0}} = \tau_{\text{f}} \cdot \pi \cdot d \cdot l_{\text{a}} \cdot \left( {\tanh \omega /\omega } \right)$$

(3)

where τ _f is the local bondline shear strength (characteristic value) and ω is the stiffness ratio of the joint (described in [14]). The stiffness ratio is dependent on the fracture energy (G _f), the area of the rod (A _r), the modulus of elasticity (MOE) of the rod (E _r), the area of the wood (A _w), and the MOE of the wood (E _w).

In this paper the GIROD equation was used for the CLT specimens and a glue line thickness of 2 mm, which does not fit exactly with the original assumptions of the GIROD study (e.g., test data with thin bondlines and glulam specimens). Since the axial pull-out strength from CLT with different orientations of the glued layers is calculated, the stiffness of the wood was defined as a combination of the properties in the parallel and perpendicular directions (E _w·A _w = E _w,0·A _w,0 + E _w,90·A _w,90). The following values were assumed for the CLT specimens in this study: τ _f = 9.6 MPa, G _f = 1750 Nm/m², E _r = 210 GPa, A _w,0 = 140 cm², A _w,90 = 56 cm², E _w,0 = 11 GPa and E _w,90 = 0.4 GPa.

Steiger, Widmann and Gehri proposal

Steiger et al. [10] conducted tests on threaded rods glued in glulam (GL24 h) parallel to the grain by means of an epoxy-type adhesive. A total of 48 tests of specimens with varying density and slenderness ratio were performed. Based on these assumptions, the following empirical pull-out strength model was proposed:

$$F_{{{\text{ax}},0,{\text{mean}}}} = f_{{{\text{v}},0,{\text{mean}}}} \cdot \pi \cdot d_{\text{h}} \cdot l_{\text{a}}$$

(4)

$$f_{{{\text{v}},0,{\text{mean}}}} = 7.8 \cdot \left( {{{\lambda_{\text{h}} } \mathord{\left/ {\vphantom {{\lambda_{\text{h}} } {10}}} \right. \kern-0pt} {10}}} \right)^{ - 1/3} \cdot \left( {{\rho \mathord{\left/ {\vphantom {\rho {480}}} \right. \kern-0pt} {480}}} \right)^{0.6}$$

(5)

where f _v,0,mean is the nominal shear strength of a single axially loaded rod parallel to the grain, dependent on the slenderness of the hole (λ _h = l _a/d _h) and the density of the wood (ρ).

A similar strength model was developed by Widmann et al. [24], who conducted 86 tests on threaded rods glued in glulam (GL24 h) perpendicular to the grain (the rod was bonded-in through several glulam layers) using an epoxy-type adhesive. The following equation was proposed:

$$F_{{{\text{ax}},90,{\text{mean}}}} = 0.045\cdot\left( {\pi \cdot d_{\text{h}} \cdot l_{\text{a}} } \right)^{0.8}$$

(6)

New Zealand design guide

The New Zealand Design Guide [25] provides an equation to predict the axial pull-out strength of a rod parallel to the grain. The equation was derived based on experimental and theoretical studies of epoxy-bonded steel connections in glued laminated timber. The proposed equation:

$$F_{{{\text{ax}},0,{\text{char}} .}} = 6.73\cdot k_{\text{b}} \cdot k_{\text{e}} \cdot k_{\text{m}} \cdot \, \left( {{{l_{\text{a}} } \mathord{\left/ {\vphantom {{l_{\text{a}} } d}} \right. \kern-0pt} d}} \right)^{0.86} \cdot \left( {{d \mathord{\left/ {\vphantom {d {20}}} \right. \kern-0pt} {20}}} \right)^{1.62} \cdot \left( {{{d_{\text{h}} } \mathord{\left/ {\vphantom {{d_{\text{h}} } d}} \right. \kern-0pt} d}} \right)^{0.5} \cdot \left( {{{e^{{\prime }} } \mathord{\left/ {\vphantom {{e^{{\prime }} } d}} \right. \kern-0pt} d}} \right)^{0.5}$$

(7)

takes into account the embedment length (l _a), bar diameter (d), edge distance (e′), hole diameter (d _h), moisture content (k _m), steel bar type (k _b) and epoxy type (k _e). In this study: k _m = k _b = k _e = 1.0 and e′ = 70 mm 0.086. The values l _a, d _h and d were taken from Table 2.

Rossignon and Espion proposal

Rossignon and Espion [6] investigated rods that were glued in manually drilled holes of glulam with a thick bondline. The failures in their tests occurred mainly due to splitting of the timber element along the anchorage length. Based on their research the F _ax,0,mean is calculated according to Eq. 4, where the mean nominal shear strength of a single axially loaded rod set parallel to the grain is given by the semi-empirical equation:

$$f_{{{\text{v}},0,{\text{mean}}}} = 5.8\cdot\left( {{{\lambda_{\text{h}} } \mathord{\left/ {\vphantom {{\lambda_{\text{h}} } {10}}} \right. \kern-0pt} {10}}} \right)^{ - 0.44}$$

(8)

Yeboah et al. proposal

Yeboah et al. [26] estimated the structural capacity of bonded-in Basalt Fibre Reinforced Polymer (BFRP) rods loaded perpendicular to the glulam lamellas. A two-component-epoxy gap-filling (thickness 2–12 mm) adhesive was used for the experiment. The axial pull-out strength of the rod perpendicular to the grain was estimated as:

$$F_{{{\text{ax}},90,{\text{mean}}}} = f_{{{\text{v}},90,{\text{mean}}}} \cdot \pi \cdot d_{\text{h}} \cdot l_{\text{a}}$$

(9)

where f _v,90,mean = 5.7 MPa.

According to [26] the design equation should only be used for l _a < 15 · d _h, since no strength improvement was observed beyond this bonded-in length.

Comparison with existing models

The design equations described above are compared to the experimental results using CLT specimens in Fig. 6. Since almost all the equations for the 0° specimens take into account the influence of the rod (hole) diameter, the results are shown separately for: (a) d _h = 20 mm (Fig. 6a) and (b) d _h = 28 mm (Fig. 6b). The experimental results are represented with a square (mean values) and a rhombus (characteristic values) indicator. The design equations are shown with blue (mean values) and red (characteristic values) curves.

From a comparison of the experiments with the design equations the following conclusions can be drawn:

• 1. The design equations predict relatively well the ultimate tension force of the glued-in rod with small d _h and l _a (Fig. 6a). However, at higher values of d _h and l _a (Fig. 6b) the difference between the experiments and the design equations is much larger. The reason for this is that the specimens with large values of d _h and l _a exhibit different failure modes, which were not considered in the existing design Eqs. 

• 2. Most of the design equations (for both the characteristic and mean values) prove to be insufficient for a conservative estimation of the ultimate tension force of the glued-in rod (the result is overestimated in almost all cases).

• 3. The best estimation for the ultimate tension force of the glued-in rod in CLT is the GIROD equation, as it more-or-less matches the experimental data, but in most cases it is still overestimating the ultimate tension force. This equation is not linear, it reduces the bondline strength for longer l _a, and takes into the account the grain orientation of the wood (parallel and perpendicular). This makes it the most suitable approximation for an estimation of the capacity of glued-in rods in CLT.

• 4. On the basis of the experiments with the 0° specimens it is difficult to propose a general equation due to the large number of influencing parameters and the different failure modes obtained. Therefore, a parametric numerical study should be performed to estimate the effect of a large number of parameters that influence the failure modes and hence the load capacity of glued-in rods in CLT.

For the 90° specimens it is even more difficult to find design equations that would be directly comparable to the research performed in this paper. The design equations in [24, 26] were proposed for bonded-in rods in glulam perpendicular to the grain (the rods were bonded through several glulam layers) and therefore have a different global effective stiffness and different characteristic failure modes. This should be taken into account when evaluating the results.

Figure 7 shows only the results of the specimens with a small diameter (d _h = 20 mm) and small bonded-in lengths (l _a ≤ 240 mm). The results for the specimens with larger values of d _h and l _a are not given, since these results were strongly dependent on the CLT width (the main failure mode was splitting of the CLT). The existing design equations are therefore significantly different for larger d _h and l _a and are not comparable with the experimental data.

In contrast to Fig. 6, where most of the existing design equations overestimate the maximum tensile load, the two design equations in Fig. 7 mostly underestimate the mean experimental results. Similar to the case of the 0° specimens, there are many parameters influencing the failure mode and, consequently, the bearing capacity of the 90° specimens. Therefore, new equations should also be derived for the rods glued in CLT perpendicular to the grain.

Conclusions

From the obtained experimental results the following conclusions can be drawn:

• 1. As expected, the ultimate tension force of the glued-in rod in CLT is increased for larger rod diameters and larger bonded-in lengths. However, on the basis of the 60 tested specimens it is still difficult to predict the general response of the connections with glued-in rods in CLT, since there are a variety of possible influencing parameters that were not analysed.

• 2. The difference in the ultimate tension loads between the 0° and 90° specimens is smallest for the shortest bonded-in rod (up to 20% difference for the mean values) and largest for the longest bonded-in rod (up to 48% difference for the mean values).

• 3. The connections with the rod perpendicular to the grain have a more ductile response than the connections with the rod parallel to the grain. The displacement at the maximum tensile force (δ) is approximately two times larger in the case of the 0° specimens. The differences in δ could be additionally explained by the largest load-bearing capacity of the 90° specimens.

• 4. The effective global stiffness k _eff,0 is mostly dependent on the rod diameter and not on the bonded-in length. The k _eff,0 is larger than k _eff,90 for all the tested bonded-in lengths. The differences between k _eff,0 and k _eff,90 are, in most cases, below 20%, when the same bonded-in lengths were compared.

• 5. The average shear strength in the bondline along the threaded rod (f _v,0,mean) is monotonically decreasing with the increased bonded-in length in the case of the 0° specimens. However, for the 90° specimens, no specific pattern could be obtained for the shear stress level in the bondline along the rod. This was mainly due to the failure between the CLT layers for the specimens with longer bonded-in lengths and larger diameters.

• 6. The comparison of the experimental results with the existing design equations showed that these estimations are, in most cases, not appropriate for glued-in rods in CLT. The equations could potentially be used only for connections where there is no failure of the CLT cross connections [connection with the rod parallel to the grain and in the middle of the CLT layer, a small rod diameter (d _h ≤ 12 mm) and a short bonded-in length (l _a ≤ 120 mm)]. An extensive parametric study should therefore be performed to reliably estimate the response and propose new design equations for glued-in rods in CLT (taking into account the different possible configurations of the connection).