Evaluation of surface cracks of bending concrete using a fully non-contact air-coupled nonlinear ultrasonic technique

Abstract

In this paper, a fully non-contact second harmonic generation (SHG) technique using a pair of air-coupled ultrasonic transducers is developed and the feasibility of the technique is investigated through the evaluation of surface cracks of concrete beams subjected to the bending load. The reliability of developed technique is subsequently validated by comparing the non-contact nonlinear ultrasonic measurements with measurement results based on contact-type sensors, where the coefficient of variation of non-contact measurements is averagely about 46% of the contact measurements. The defined nonlinear parameter is found to have a monotonically increasing trend with the growth of concrete crack, and the nonlinear parameter corresponding to the largest crack increases about 7 times from its initial value corresponding to the sample in intact state. In contrast, the increase of linear parameter namely the time-of-flight of surface wave is only about 40%. The difference as high as one order of magnitude verifies the high sensitivity of developed air-coupled SHG technique. With consideration of the easily removable characteristic of air-coupled ultrasonic measurements, the developed SHG technique could be promising for the large scale quality control of concrete structures in engineering practice.

Introduction

The evaluation of health condition of aged concrete structures is of importance for the service security. Various nondestructive evaluation (NDE) techniques have been attempted to assess the damage of concrete structures and experimental techniques based on the ultrasonic wave propagation are the most commonly used in academia and industry [1,2,3,4,5]. Particularly in recent years, a new group of ultrasonic methods in the light of nonlinear ultrasonic theory have gain substantial attentions due to their highly sensitive response to the structural defects in a variety of materials [6,7,8,9].

There exist several types of nonlinear ultrasonic techniques according to the different ultrasonic phenomena. The first method is based on the investigation of higher order harmonic of primary signal, which could be excited due to the existence of structural damage. For example, Nucera and Lanza di Scalea [10] used the second harmonic generation technique to monitor load levels in multi-wire steel strands in concrete. The second method is based on the examination of extra sidebands due to wave modulation phenomena when a low-frequency and high-frequency signal interact with each other. Wu et al. [11] and Chen et al. [12] employed the impact vibration signal and continuous harmonic signal as the low-frequency source to modulate the high-frequency wave for the damage characterization of concrete samples. The third method is the analysis of resonance frequency shift when the self-resonance of structures is excited by the external trigger. Payan et al. [13] and Chen et al. [14] developed the nonlinear ultrasonic resonance spectroscopy and nonlinear impact resonance acoustic spectroscopy to investigate the thermal and mechanical damage of concrete. Although these nonlinear ultrasonic techniques showed the excellent feasibility for damage assessment of concrete in different application cases, the experimental set up was mainly dependent of contact-type sensors and the coupling condition between sensors and sample surface has a significant influence on the reliability of signal measurements. The reliability problem of ultrasonic methods using contact-type sensors greatly limit their applications in engineering practice, where the large-scale inspection area of concrete structures inevitably requires the reinstallation of sensors at different inspection locations.

To reduce the effect of contact coupling and improve the measurement reliability, researchers began to explore the application possibility of air-coupled transducers in the nonlinear ultrasonic techniques. Thiele et al. [15] developed a half non-contact SHG technique for the material damage assessment where a wedged regular transducer is used as the signal transmitter and an air-coupled transducer is used as the receiver. Kim et al. [16, 17] further evaluated the variation of internal porosity of concrete due to the effect of carbonation and shrinkage using the developed half non-contact SHG technique. In et al. [18] developed a fully non-contact ultrasonic setup to measure the linear transmission coefficient of surface wave across a surface breaking crack in concrete. In addition, Maier [19] proposed a noncontact nonlinear resonance ultrasound spectroscopy for the analysis of microscopic damage of small metallic samples. However, it has to be noted that the hysteresis nonlinearity is measured in the nonlinear resonance ultrasound spectroscopy and is different from the quadratic nonlinearity measured in the air-coupled SHG technique.

In this paper, a fully non-contact experimental setup is developed as a further progress of the half non-contact SHG method, where both transmitting and receiving transducers are air-coupled sensors. The fully non-contact SHG technique is used to characterize the concentrated crack of reinforced concrete beam subjected to the bending load. The feasibility of the proposed experimental technique is firstly validated by checking the proportional relationship between the second harmonic amplitude and square of the primary signal amplitude. The measurement reliability is then examined by a comparison of coefficient of variation of multiple measurements based on the contact sensors and non-contact sensors. Finally, the variation of nonlinear parameter corresponding to different bending cracks is investigated and compared with the linear parameter such as the time-of-flight (TOF) of surface waves for the validation of sensitivity of the developed technique.

Theoretical background of nonlinear parameter measurements

As described by the nonlinear acoustic theory [20], the cracks of concrete could produce both the classical nonlinearity expressed by the power series of the strain and the nonclassical hysteresis nonlinearity containing the term of strain rate. The even harmonic is only caused by the classical nonlinearity and the odd harmonic is caused by both the classical and nonclassical nonlinearity [20]. Since only the second harmonic is measured in this work, the material nonlinearity is assumed to solely come from the quadratic order of strain in the constitutive relationship [21, 22]. The measurement of quadratic nonlinear parameter is thus the key step for the nonlinear ultrasonic characterization of material defects. As follows, the theoretical background of nonlinear parameter measurements based on the Rayleigh surface wave is concisely presented and more details can be referred to previous publications [23,24,25,26].

First, the Rayleigh wave is assumed to propagate along the x axis of an isotropic, macroscopically homogeneous, and nonlinear elastic half space and z axis refers to the distance to the surface.

Because of the existence of the shear and longitudinal wave, the linear displacement in z axis can be expressed as [23]

$$u_{z} (\omega ) = iA_{1} \frac{{b_{1} }}{{k_{R} }}\left( {e^{{b_{1} z}} - \frac{{2k_{R}^{2} }}{{k_{R}^{2} + b_{2}^{2} }}e^{{b_{2} z}} } \right)e^{{i\left\{ {k_{R} (x - C_{R} t)} \right\}}}$$

(1)

where C _R is the speed of the Rayleigh wave, ω = C _R k _R is the fundamental frequency, $b_{1} = \sqrt {k_{R}^{2} - k_{L}^{2} }$ and $b_{2} = \sqrt {k_{R}^{2} - k_{S}^{2} }$. k _L , k _S and k _R are the wave numbers of the longitudinal wave, the shear wave and the Rayleigh wave.

Analogously, we can calculate the displacement of the second harmonic as [22, 23]

$$u_{z} (2\omega ) = iA_{2} \frac{{b_{1} }}{{k_{R} }}\left( {e^{{b_{1} z}} - \frac{{2k_{R}^{2} }}{{k_{R}^{2} + b_{2}^{2} }}e^{{b_{2} z}} } \right)e^{{i\left\{ {k_{R} (x - C_{R} t)} \right\}}}$$

(2)

It has been demonstrated that the quadratic nonlinear parameter is related to the out-of-plane displacement of the Rayleigh waves at the surface (z = 0) as shown in Eq. (3) [22]

$$\beta = \frac{{u_{z} (2\omega )\left| {_{z = 0} } \right.}}{{u_{z}^{2} (\omega )\left| {_{z = 0} } \right.}}\frac{{8b_{i} i}}{{k_{1}^{2} k_{R} x}}\left( {1 - \frac{{2k_{R}^{2} }}{{k_{R}^{2} + b_{2}^{2} }}} \right)$$

(3)

Combine Eqs. (1), (2) and (3), then simplify the equation, the relationship of A ₁, A ₂ and β can be obtained as follows [17]

$$\beta \propto \frac{{A_{2} x}}{{A_{1}^{2} }}$$

(4)

Since the propagating distance x is constant in the SHG measurements of this work, the nonlinear parameter β used in this work is expressed as

$$\beta = \frac{{A_{2} }}{{A_{1}^{2} }}$$

(5)

Experimental procedure

Specimen

A reinforced concrete specimen (100 × 100 × 400 mm) was prepared for the experiment. River gravel (maximum size of 20 mm) as coarse aggregate, ordinary sand (maximum size of 2 mm) as fine aggregate, Type P•O42.5 (ordinary Portland cement with a nominal strength of 42.5 MPa) and water were used for the cast of concrete specimen, and a water-to-cement ratio (w/c) of 0.45 was designed in the mixing. Two steel bars with a diameter of 8 mm were placed near the bottom of specimen to mitigate the brittle failure during the bending tests. Table 1 shows the detailed mix proportion of the concrete sample. The specimen was cured in a standard curing chamber (23 °C and 95% relative humidity) for 28 days after demolding.

Table 1 Mixture proportioning of concrete sample (kg/m³)

Bending test of the concrete beam

The concrete damage was induced by the three-point bending test, where the sample was placed on a universal loading machine and an increased bending load was applied on the middle spot of the top surface of concrete sample. For each loading level, the sample was pull out from the loading frame for the ultrasonic experiments and crack width measurements. A crack detector was installed near the middle spot of bottom surface to record the images of bending crack. The image of cracks at different loading stage is shown in Fig. 1, where a clear growth of crack width due to the increasing bending load is seen while the crack length keeps the same.

Fig. 1

Image of cracks at the different bending load

Experimental setup of air-coupled SHG measurements

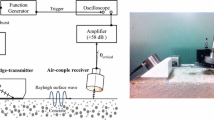
The experimental setup of air-coupled SHG measurements is shown in Fig. 2. A tone-burst signal at a frequency of 50 kHz is first generated by a digital function generator (Rigol DG1022). A power amplifier (Krohn-Hite 7500) is then used to amplify the signal by a gain of 40 dB which is then fed into an air-coupled transducer (Ultran NCG50-D50) having a central frequency of 50 kHz. The Rayleigh wave transmits through the concrete specimen and is picked up by the second air-coupled transducer (Ultran NCG100-D50) having a central frequency of 100 kHz. The peak-to-peak voltage of the signal changes from 15 V to 20 V with a step of 0.5 V. The received signal is averaged 64 times and eventually recorded by a digital oscilloscope (Tektronix MDO3012).

Fig. 2

Experimental setup of fully air-coupled SHG measurements

The phase velocity of the Rayleigh wave in the concrete specimen is needed for the determination of incidence angel of transducers, and it is measured using a high power pulser-reciever (Olympus 5077PR) in experiments. A pair of regular ultrasonic transducers were glued to wedges made of Teflon and firmly attached with the specimen surface for the measurement of traveling time of different propagation distance, and the phase velocity can be calculated accordingly. With knowing the phase velocity, the critical incidence angle for the Rayleigh wave θ (i.e., the tilted angle of the central axis of the air-coupled transducer from the plane perpendicular to the concrete surface) is calculated according to Snell’s law, which is set to be 11° in experiments. The vertical distance between the central location of air-coupled transducers and the concrete surface (the lift-off distance) is designed to be 15 mm to ensure a satisfactory signal strength.

Results and discussion

Determination of nonlinear parameter

Figure 3 shows a time-domain signal obtained in experiments, which may contain multiple reflections since the length of tone burst signal is larger than the sample length. As theoretically proved in one author’s recent work [27], the defined nonlinear parameter β originally for a propagating wave can be measured also from the second harmonic generation in standing waves. A Hanning window is applied on the time-domain signal and the selection criterion of window size and location is to get the steady part of propagating wave. The same window size and location is kept for all ultrasonic signals and thus the relative comparison of nonlinear parameter will not be affected by the window selection. The spectra of the windowed signals with the increased input amplitude are obtained in Fig. 4 using the fast Fourier transform (FFT). The FFT magnitudes of primary signal and second harmonic in the spectra of Fig. 4 are defined as M ₁ and M ₂ respectively and are used to represent the amplitude A ₁ and A ₂ in Eq. (5) since the frequency-domain magnitude is proportional to the time-domain amplitude. The nonlinear parameter $\beta^{{\prime }}$ is then calculated by the slope of linear relationship between M ²₁ and M ₂ as shown in Fig. 5.

Fig. 3

Time-domain signal of fully air-coupled SHG measurements

Fig. 4

Frequency-domain signal of fully air-coupled SHG measurements

Fig. 5

Nonlinear parameter β′ obtained from the linear relationship of M ²₁ and M ₂

In addition, it has to be noted that the instruments themselves may generate spurious nonlinearity to affect the nonlinearity measurement of concrete sample. To further validate the instrument nonlinearity negligible, a known linear sample—a PMMA plate is used in the air-coupled second harmonic experiments. The experimental setup and procedure is exactly the same as for the concrete sample. The nonlinear parameter of the PMMA plate calculated is only 4.6% of the value of intact concrete. Thus, the instrumentation nonlinearity is demonstrated to have little influence compared to crack nonlinearity.

Results of phase velocity of Rayleigh wave

The phase velocity of Rayleigh wave is considered as a typical parameter to characterize the structure defects and is thus used here for a comparison with the nonlinear parameter of SHG measurements. The variation of phase velocity of Rayleigh wave is plotted in Fig. 6. It is seen the phase velocity generally has a decreasing trend with the development of bending crack and the maximal decrease corresponding to the largest crack width is about 27%. However, the velocity does not present a substantial change when the crack is tiny. The decrease of velocity from the intact state to the crack width of 0.11, 0.13 and 0.28 mm is about 1.2, 7.9 and 11.0%, respectively. The results in Fig. 6 indicate that the phase velocity of Rayleigh wave is not very sensitive to the early phase of bending crack development, which is consistent with previous experimental observations based on bulk waves [28].

Fig. 6

Variation trend of phase velocity of Rayleigh wave with respect to average crack width

Nonlinear SHG measurements

The SHG measurements were conducted after each loading and the nonlinear quadratic parameter was calculated following the procedure described above. The linear relationship between M ₂ and M ²₁ at different crack width is shown in Fig. 7, where the values of both axis were normalized to make all data distribute in the similar range. An excellent coefficient of correlation is generally seen for each line and the slope has a clear increasing trend. The results in Fig. 7 indicate that the SHG measurements based on air-coupled transducers can well characterize the material nonlinearity due to bending crack. The normalized nonlinear parameter is plotted in Fig. 8, where a rapid growth is seen throughout the entire course of bending test. For instance, the nonlinear parameter of the crack width of 0.13 mm increases about 72% from the intact state of specimen, and the nonlinear parameter further grows about 2.7 times when the crack develops to a width of 0.30 mm. The error bars in Fig. 8 refer to the standard deviation arising from the three measurements where the transducers were re-located at the same spot for each time.

Fig. 7

Variation of M ²₁ and M ₂ of concrete specimen with increased crack width

Fig. 8

Variation trend of nonlinear parameter β′ with respect to average crack width in the case of non-contact SHG measurements

Reliability and sensitivity analysis

To validate the reliability of SHG measurements using air-coupled transducers, the contact-type SHG measurements were conducted simultaneously for the same specimen, where two wedged ultrasonic transducers were used. The measurements for each crack width were repeated three times where the wedges were removed and reattached to the same locations of the specimen. The normalized nonlinear parameter of the contact-type SHG measurements is plotted in Fig. 9. Through a comparison of Figs. 8 and 9, it is seen that the nonlinear parameters from contact measurements and non-contact measurements have an excellent linear correlation where the coefficient of correlation is as high as 0.986. Furthermore, the coefficient of variation of contact measurements and non-contact measurements for each crack state is compared in Fig. 10. The average level of coefficient of variation of non-contact measurements is about 46% of that of contact measurements, showing that the reliability of air-coupled SHG measurements is better than the contact SHG measurements.

Fig. 9

Variation trend of nonlinear parameter β′ with respect to average crack width in the case of contact SHG measurements

Fig. 10

Comparison of coefficient of variation for non-contact and contact SHG measurements

Since the phase velocity decreases with the crack growth and this trend is opposite to the variation of nonlinear parameter, it is necessary to convert the phase velocity to a physical parameter having the increasing trend for the better demonstration of sensitivity comparison between SHG measurements and linear measurements. With consideration that the propagating distance of surface wave is known, the TOF of surface wave calculated by dividing the propagating distance by the phase velocity is used to compare with the nonlinear parameter. The variations of TOF of surface wave and nonlinear parameter are plotted in Fig. 11. The increase of nonlinear parameter shows a very large distinction from the increase of TOF of surface wave during the entire course of crack occurrence and growth. The maximal increase of TOF of surface wave corresponding the largest crack is about 40% while the maximal increase of nonlinear parameter is about 700%. The sensitivity of SHG measurements based on air-coupled transducers is thus validated.

Fig. 11

Comparison of increasing trend of nonlinear parameter and linear parameters

Conclusion

A fully non-contact SHG technique based on both air-coupled transmitting and receiving transducers is developed in this paper and is applied for the crack evaluation of the reinforced concrete beam subjected to the bending load. The conclusions of this paper are as follows:

• 1. The fully air-coupled SHG technique is feasible for the detection of bending crack in the concrete specimen. Pronounced second harmonics are generated with the propagating Rayleigh wave across the crack and the variation of second harmonic amplitude with respect to the square of primary signal amplitude conforms to the linear trend predicted by the theoretical derivation of nonlinear ultrasonic theory.

• 2. The developed experimental technique has a better reliability compared to contact-type SHG method. The coefficient of variation of multiple measurements using air-coupled transducers is about 46% of the coefficient of variation of SHG measurements using contact transducers.

• 3. The developed technique has a better sensitivity in terms of crack detection compared to the conventional phase velocity method. The nonlinear parameter has a relative increase as high as 700% from the intact state of concrete specimen while the change of TOF of surface wave is about 40%.

Based on the current finding of this work, the fully non-contact SHG technique demonstrates to be an effective method for the crack characterization of concrete owing to its feasibility, stability and sensitivity. Furthermore, the non-contact characteristic of this technique make it convenient for the repeatable measurements on a large scale area since no reinstallation of transducers is needed. Combing with the automatic moving and relocating system, the developed technique is promising for the rapid quality control of large concrete structures on site.