1 Introduction

Unfired crude (untreated) earth is a hygroscopic porous material that contains generally a small quantity of active clay minerals. Currently, considering the context of sustainable construction, reduction of energy consumption and greenhouse gas emission, it is regarded as a promising non-industrial construction material. Several construction technics using earthen materials have been invented, leading to monolithic walls, like rammed earth and cob, or to masonry units, like adobe or compressed earth blocks [1]. After constructions, earthen buildings being always subject to atmospheric conditions possess relatively low water contents and high suction which impact significantly on their mechanical behaviour.

In order to study the behaviour of unsaturated earthen materials, a series of large-scale laboratory tests were carried out by several researchers [2,3,4,5]. The main conclusion drawn from all these experiments is that the mechanical properties of earthen materials, whatever their origin and their implementation technic, are strongly influenced by their water content: even a small increase of the latter leads to a significant reduction of both the failure strength and Young’s modulus E, while the irreversible plastic strain is increased. Apart from plastic deformations and suction effects, a progressive but non-negligible degradation of Young’s modulus E with increasing stress level were observed in recent study [6, 7]. This stiffness reduction is conjectured to be a consequence of damage induced by initiation and development of micro-cracks. The above experimental observations motivate the development of a new constitutive model which can simulate the poroplastic behaviour of earthen materials while accounting for damage effects.

To begin with, the main drawback of classic elastoplastic models is their erroneous prediction of a sharp transition at yield from elastic to elastic–plastic behaviour (jump of apparent stiffness), as well as their difficulty to reproduce realistic volumetric behavior (typically a smooth transition from contractancy to dilatancy). Models developed using the Bounding Surface Plasticity (BSP) theory can overcome these limitations. This theory, firstly proposed by Mroz [8] and Dafalias et al. [9, 10] to simulate metal behaviors, was successively applied by Bardet [11] on saturated sands and later on followed by Gajo and Muirwood [12] as well as by Yu and Khong [13]. BSP theory was later extended to partially saturated materials in order to describe suction effects [14,15,16,17,18,19]. In addition, BSP theory is also applied on geomaterials other than soils due to its versatility, such as rockfills and clay-fouled ballast [20, 21].

In parallel, there have been extensive studies on the development of coupled elastoplastic damage models [22,23,24,25,26]. However, most of them are devoted to modeling dry materials without considering coupled hydromechanical interactions, not to mention the capillarity effects due to partial saturation. In recent years, several researchers have attempted to couple damage with hydromechanical interactions. For instance, a coupled poro-elastoplastic damage model is proposed by Shao et al. [27] and extended to partially saturated conditions in order to study coupled hydromechanical damageable behaviours in drying–wetting processes. Zhang et al. [28] developed a unified elastic–viscoplastic damage model to describe long-term hydromechanical behavior of argillites under unsaturated condition. Bui et al. presented a new constitutive model accounting simultaneously for the impact of damage on hydraulic and mechanical properties of unsaturated poroplastic geomaterials, by means of the thermodynamic framework for partially saturated media [29]. The present work follows a similar path of this last reference.

After a summary of experimental investigations showing the main trends on the mechanical behaviour of earthen materials, a new constitutive model is presented for unsaturated earthen materials. It is based on the BSP theory and the effective stress concept. It adopts a non-associative flow rule and a simple radial mapping rule, and takes into account an isotropic damage variable. Plastic straining and damage evolution occur as two coupled processes. The influence of suction on plastic straining and damage evolution is taken into account. Finally, the performance of this model is investigated by comparing the numerical simulation with a series of triaxial tests results on compacted earth samples at different hydraulic conditions and confining pressures.

2 Summary of experimental investigations

The raw earth materials used in this study came from Limonest, in the south-eastern part of France and will here-after be refered to as Lim. It possesses a natural clay content of 35%. To study the impact of clay content on the hydromechanical behaviour, sand is added to obtain two other materials, refered to as Mix1 and Mix2 with clay contents respectively of 17 and 26%. The optimum condition of the Lim earth from proctor test was used to prepare specimens. Besides, in order to make the comparison of different soils meaningful and easily interpretable, the optimum condition (12.5%, 1.95 g/cm3) is also applied to Mix1 and Mix2. Cylindrical samples (3,5 cm diameter and 7 cm high) were fabricated using a home-made mold which allows a double compaction (compression applied simultaneously at both ends of the sample) of the raw earth at controlled displacement rate. After fabrication, samples were cured at three different relative humidity conditions (23, 75, and 97%) at 23 °C until reaching equilibrium. The total suctions, denoted by \(s_{\text{t}}\), corresponding to the three values of relative humidity (RH) can be calculated by Kelvin’s law:

$$s_{\text{t}} = - \frac{{\rho_{\text{w}} {\text{RT}}}}{{M_{\text{w}} }}\ln {\text{RH}}$$
(1)

where \(\rho_{\text{w}}\) and \(M_{\text{w}}\) are the density and the molar mass of water, \(R\) the perfect gas constant and \(T\) the absolute temperature. Since distilled water was used in the tests, the solute concentration is expected to be very low; hence, the osmotic suction should be negligible. The total suction in the above relation is therefore reduced to matric suction s. In the rest of this paper, the term ‘suction’ will therefore refer to ‘matric suction’. The matric suctions corresponding to the three values of RH (23, 75, and 97%) imposed at 23 °C are 201, 39 and 4 MPa respectively.

A series of drained triaxial compression tests were performed at three confinement pressures (0, 100 and 600 kPa). Non-contact sensors were installed to measure the axial and radial strains. Two types of mechanical loadings were applied at constant relative humidity conditions. More details on the experimental device can be found in the paper [7]. The first loading type is classic in triaxial tests: axial load is applied at a constant displacement rate until failure. After measuring the maximum deviator stress at failure (noted f c) for one particular specimen using this type-1 loading, the second loading type consisting of loading–unloading cycles at prescribed stress levels, respectively 20, 40, 60 and finally 80% of f c was conducted on two other specimens prepared under identical conditions. The second loading–unloading cycle was used to estimate the evolution of Young’s modulus E with the level of axial stress applied, assuming unloading is reversible. Young’s modulus E is therefore computed from the following equation:

$$E = \frac{{\Delta \sigma_{xx}^{\text{cycle}} }}{{\Delta \varepsilon_{xx}^{\text{cycle}} }}$$
(2)

where \(\Delta \sigma_{xx}^{\text{cycle}} ,\Delta \varepsilon_{xx}^{\text{cycle}}\) are the differences respectively of the axial stress and axial strain between the maximal and minimal of a load cycle. The loadings were applied by imposing a constant axial displacement rate of 0.002 mm/s (corresponding to 0.003%/s) in loading and unloading.

Figure 1 illustrates the typical stress–strain behaviour (Mix1 at 100 kPa confining pressure) extracted from the results of a series of triaxial compression tests at 3 different relative humidities. Firstly, all tests exhibit a smooth stress–strain behaviour from the beginning to the end, with non linearity appearing practically from the beginning. Secondly, large residual strains are systematically observed after unloading for all type-II tests. These observations indicate the appearance of plastic (irreversible) strains even at low stress levels. In addition, a post-peak softening behaviour is captured for the case of low relative humidity (e.g. RH = 23%). Last but not the least, the typical stress–strain behaviour of earthen materials is sensitive to relative humidity conditions, including the amplitudes of residual strain and f c. All the remarks mentioned above are also observed for Lim and Mix2.

Fig. 1
figure 1

Stress-strain curves on Mix1 at three different hydraulic states (RH = 23%, RH = 75% and RH = 97%) at 100 kPa confining pressure

Full size image

Figure 2a shows values of Young’s modulus E measured during the unloading–reloading cycle at 20% f c and the evolution with relative humidity. Young’s modulus decreases drastically with the rise of relative humidity. Results presented in Fig. 2b on the evolution of Young’s modulus E versus stress level indicate that there is a progressive and significant degradation of the material stiffness when the stress increases. This degradation of stiffness is faster at low stress and slower at high stress. Consistently with the stiffness degradation, macro-cracks oriented in the direction of major principal stress appeared during the compression test.

Fig. 2
figure 2

Evolution of Young’s modulus versus: a relative humidity and b applied stress level

Full size image

To summarize, results of our experimental investigation indicate that the basic mechanical behaviour of unsaturated earthen materials can be characterized by irreversible plastic straining and stiffness degradation. The first behaviour is commonly modelled using classic elastoplasticity theory, despite its unrealistically prediction of a stiffness-discontinuity on the stress–strain curve at yield. To improve this, it is proposed to adopt the approach of Bounding Surface Plasticity (BSP). The stiffness degradation due to microcracks has not been considered in the literaure on earthen materials constructions. To address this issue, it is proposed to follow the approach of continuum damage mechanics.

3 A poro-elastoplastoplastic damageable constitutive model

As mentionned in the previous section, the construction of the new constitutive model requires to address two mechanisms: a poroplastic mechanism capable of simulating the suction-dependent plastic straining and a damage mechanism to capture the stiffness degradation. The poroplastic mechanism in this new model follows the same approach as the CASMNS model developed by Lai et al. [19] for unsaturated soils. The formulation is based on the concepts of effective stress and bounding surface plasticity theory. To accurately simulate volume changes (e.g. transition from compressibility to dilatancy), a state-dependent non-associative flow rule is used, by adopting the plastic potential of Yu [30]. The starting point is the definition of an effective stress to account for effects of partial saturation.

3.1 Partial saturation and effective stress

There are two main classical modelling approaches on partially saturated soils. All of them need two independent stress variables. The classic BBM model is based on net stress and suction whereas a few others use an effective stress and suction [14, 15, 31]. Some recently appeared models proposed to use the degree of saturation instead of suction as a generalised stress variable [32,33,34]. This new approach seems to be promising, but the feedback is still limited. In this paper, we follow the approach based on an effective stress and suction.

At partially saturated states, the effective stress tensor \(\sigma_{ij}^{'}\) can be expressed as [35]:

$$\sigma_{ij}^{ '} = (\sigma_{ij} - u_{\text{a}} \delta_{ij} ) + \chi s\delta_{ij}$$
(3)

where \(\sigma_{ij}\) is the total stress tensor, \(u_{\text{a}}\) is the pore air pressure, s is the difference between pore air and pore water pressure (\(u_{\text{a}} - u_{\text{w}}\)), referred as suction, \(\delta_{ij}\) is the second order identity tensor, and χ is defined as the effective stress parameter and generally is state dependent. In all the following, a prime (‘) above a stress variable will denote the effective stress counterpart. In many practical cases, air pressure can be identified as the atmospheric pressure, taken as the reference datum for stresses and fluid pressures, hence, Eq. (3) can be simplified to:

$$\sigma_{ij}^{ '} = \sigma_{ij} + \chi s\delta_{ij}$$
(4)

In this paper, only the configuration of conventional triaxial tests is of concern, exhibiting cylindrical symmetry, hence axial and radial directions are always the directions of principal stresses and strains. Let \(\sigma_{1}\) denotes the total axial stress, \(\sigma_{2} = \sigma_{3}\) the total radial stress, \(\varepsilon_{1}\) the axial strain and \(\varepsilon_{2} = \varepsilon_{3}\) the radial strain. This cylindrical symmetry allows to work with bi-vectors instead of 3-vectors; however, the various transformation and stiffness matrices lose their symmetry. The classical notation \(\left( {p, q} \right)\) is used to denote the mean and equivalent deviatoric stresses. It is evident that:

$$p^{\prime} = p + \chi s;\quad q = q^{\prime},$$
(5)

hence, we only need to refer to \(q\) in future.

Several definitions for χ have been proposed in the existing literature: some researchers identified the effective stress parameter with degree of saturation \(S_{\text{r}}\) [5, 36]; while others argued that \(\chi\) should be a function of suction [37]. In this study, the functional form (9) below firstly proposed by Khalili and Khabbaz [38] has been adopted:

$$\chi = \left\{ {\begin{array}{*{20}c} {\left( {\frac{{s_{\text{e}} }}{s}} \right)^{\alpha } } & {{\text{if }}\,s > s_{\text{e}} } \\ 1 & {{\text{if }}\,s \le s_{\text{e}} } \\ \end{array} } \right.$$
(6)

where α is a material constant and \(s_{\text{e}}\) represents the air-entry suction which can be determined from water retention measurements.

It is a classic result that when the failure stress states are plotted in the stress space \(\left( {p',q} \right)\), with an adequately chosen function \(\chi\) to be applied in the translation (4), they lie approximately on a unique line. Khalili and Khabbaz showed that this result is obtained for a large class of unsaturated soils for the functional form Eq. (6) with \(\alpha = 0.55\) [38]. Based on our experimental results on compacted earth samples, the particular value \(\alpha = 0.85\) appears to lead to the same result for the three different earths studied, as illustrated in Fig. 3 for the case of Lim. This value of \(\alpha\) was adopted in the subsequent numerical studies.

Fig. 3
figure 3

Failure states for Lim at different suctions and confining pressures before and after the translation using Eqs. (5) and (6), with \(\alpha = 0.85\), demonstrating the unique failure line in the (\(p^{\prime}\)–\(q\)) plane

Full size image

For future manipulations, it is useful to introduce the following concise vectorial notations to denote axial/radial (i.e. principal) components and mean/deviatoric components:

$$\varvec{\sigma^{\prime}} = \left[ {\begin{array}{*{20}c} {p^{\prime}} \\ q \\ \end{array} } \right] ;\,{\mathbf{\varSigma^{\prime}}} = \left[ {\begin{array}{*{20}c} {\sigma_{1}^{ '} } \\ {\sigma_{3}^{ '} } \\ \end{array} } \right] ;\,\varvec{\varepsilon}= \left[ {\begin{array}{*{20}c} {\varepsilon_{v} } \\ {\varepsilon_{q} } \\ \end{array} } \right] ;\,\varvec{E} = \left[ {\begin{array}{*{20}c} {\varepsilon_{1} } \\ {\varepsilon_{3} } \\ \end{array} } \right]$$
(7)

where \(\varepsilon_{v}\) is the volumetric strain and \(\varepsilon_{q}\) is the deviatoric strain.

The mean/deviatoric effective stresses are linked to their axial/radial counterparts by the following relations (which evidently also holds for total stresses):

$$\varvec{\sigma^{\prime}} = {\mathbb{A}}{\mathbf{\varSigma^{\prime}}};\text{ }\quad {\mathbb{A}} = \left[ {\begin{array}{*{20}c} {\frac{1}{3}} & {\frac{2}{3}} \\ 1 & { - 1} \\ \end{array} } \right]$$
(8)

The following equation holds for the conjugate strain components:

$$\varvec{\varepsilon}= {\mathbb{B}}\varvec{E};\text{ }\quad {\mathbb{B}} = \left[ {\begin{array}{*{20}c} 1 & 2 \\ {\frac{2}{3}} & { - \frac{2}{3}} \\ \end{array} } \right]$$
(9)

Within the framework of elastoplasticity, strains are supposed to be decomposable as the sum of an elastic (superscripts e) and a plastic component (superscripts p):

$$\varvec{\varepsilon}=\varvec{\varepsilon}^{\varvec{e}} +\varvec{\varepsilon}^{\varvec{p}} ; \,\varvec{\varepsilon}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {\varepsilon_{v}^{e} } \\ {\varepsilon_{q}^{e} } \\ \end{array} } \right] ;\,\varvec{\varepsilon}^{\varvec{p}} = \left[ {\begin{array}{*{20}c} {\varepsilon_{v}^{p} } \\ {\varepsilon_{q}^{p} } \\ \end{array} } \right];\,\varvec{E} = \varvec{E}^{e} + \varvec{E}^{p}$$
(10)

For the damage mechanism, a damage variable D is introduced as an internal variable to simulate the effects of microcracks. For the sake of simplicity, only isotropic damage is considered here and \(D \in \left( {0,1} \right)\) is a scalar variable.

3.2 General concept of bounding surface plasticity

The concept of bounding surface plasticity (BSP), also known as two-surface plasticity, was first originated by Mroz [8] and Dafalias et al. [9, 10], and applied by Bardet [11] and Yu et al. [13] to soils. Russell and Khalili [39] appear to be the first who applied the BSP theory to model unsaturated soils. Similar to the bounding surface models, sub-loading surface models are also widely used for modelling complicated plasticity behaviour for soils. Based on Hashiguchi’s initial framework [40], Yao et al. proposed a simple but very useful unified hardening equation [41] and corresponding models to consider complicated soil behaviour like hardening behaviour related to thermal effects [42] and hardening behaviour related to unsaturation [43].

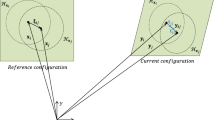
The major advantage of bounding surface plasticity (BSP) theory is the ability to reproduce a progressive appearance of irreversible strains hence a smooth stress–strain behaviour at increasing loads, thereby avoiding an abrupt change predicted by classical elastoplastic models when yielding occurs. For this purpose, two surfaces are introduced generally: a Loading Surface (LS) \(f = 0\) containing the current stress point \(\varvec{\sigma^{\prime}}\) and a bounding surface (BS)\(F = 0\). As loading increases so that the current stress point advances in the direction of the BS, inducing additional plastic strains, the BS itself evolves through a hardening mechanism that depends on the accumulated plastic strains. The central idea of BSP is that the plastic strain rate, which governs the rate of hardening hence the movement of the BS, depends on the distance separating the current and image stress point and the BS. The plastic strain rate is designed to be small at large distances from the BS and increases when approaching the latter. In order to define this “distance”, it is necessary to define an image stress point \(\bar{\varvec{\sigma }}^{\varvec{'}}\) on the BS. The “distance” in question will then be the one separating \(\varvec{\sigma^{\prime}}\) and \(\bar{\varvec{\sigma }}^{\varvec{'}}\). Among those mapping rules (giving \(\bar{\varvec{\sigma }}^{\varvec{'}}\) as a function of \(\varvec{\sigma^{\prime}}\)), one frequently used is called “radial mapping” introduced by Dafalias due to its simplicity [9]. It consists of extrapolating the position vector linking the origin to the current stress until it intersects the image stress on the Bounding Surface as illustrated in Fig. 4.

Fig. 4
figure 4

Bounding surface, Loading surface, and the radial mapping method

Full size image

3.3 Elastic mechanism accounting for damage

It is assumed that the loading surface always lies inside the bounding surface and that there is no “elastic domain” such that strain increments contain generally an elastic and a plastic component. To simplify, an isotropic elastic mechanism is adopted, commonly used in other constitutive models [14,15,16]:

$$d\varvec{\varepsilon}^{\varvec{e}} = {\mathbb{C}}^{e} d\varvec{\sigma^{\prime}}$$
(11)

\({\mathbb{C}}^{\varvec{e}}\) is the elastic compliance matrix which is usually expressed in terms of the bulk and shear moduli K and G. To account for the effects of damage on the stress-dependent elastic properties, the following expressions are adopted based on the previous results of [23, 27, 29]:

$${\mathbb{C}}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {\frac{1}{{K\left( {1 - D} \right)}}} & 0 \\ 0 & {\frac{1}{{3G\left( {1 - D} \right)}}} \\ \end{array} } \right];\quad K = \frac{{1 + e_{0} }}{\kappa } p^{\prime} ;G = \frac{{3\left( {1 - \nu } \right)}}{{2\left( {1 + \nu } \right)}}K$$
(12)

where D is the isotropic damage variable, \(\nu\) the Poisson ratio, \(\kappa\) a material constant, and \(e_{0}\) the initial void ratio.

3.4 Bounding surface, loading surface and hardening mechanism

In this model, a whale-head shaped bounding surface (BS) is adopted. It writes:

$$F\left( {\bar{p}^{ '} ,\bar{q},p_{\pi } } \right) = \left( {\frac{{\bar{q}}}{{M\bar{p}^{ '} }}} \right)^{n} + \frac{1}{\ln r}{ \ln }\left( {\frac{{\bar{p}^{ '} }}{{p_{\pi } }}} \right) = 0$$
(13)

In the above equation, M represents the slope of critical state line (CSL) in \(p' - q\) plane, while \(n\) and \(r\) are two other model constants. The first constant \(n\) specifies the shape of the bounding surface and the second constant \(r\) is a space ratio used to control the intersection point of the CSL with the BS. \(p_{\pi }\) is a variable analogue to the preconsolidation pressure in the classic Cam Clay model that determines the current size and position of the bounding surface. For simplicity, the loading surface (LS) is defined simply by homotheticity relative to the BS, as illustrated in Fig. 4:

$$f\left( {p ',q,p_{\pi } } \right) = \left( {\frac{q}{{Mp^{ '} }}} \right)^{n} + \frac{1}{\ln r}{ \ln }\left( {\frac{p '}{{\beta p_{\pi } }}} \right) = 0$$
(14)

After some simple manipulations, we obtain:

$$q = \beta \bar{q};\,p^{\prime} = \beta \bar{p}^{ '} ;\, \beta = \frac{{p^{\prime}}}{{p_{\pi } }} r^{{\left( {\frac{\eta }{M}} \right)^{n} }} ;\,\eta = \frac{q}{p '} = \frac{{\bar{q}}}{{\bar{p}^{ '} }}$$
(15)

where \(\beta\) is the scale factor between the BS and the LS, \(\beta \in \left( {0,1} \right)\), and \(\eta\) is the stress ratio.

An isotropic hardening mechanism based on the Cam Clay model is applied here. In the presence of suction and damage effects, the preconsolidation pressure, noted \(p_{\pi }\), is assumed to take the following form, inspired from previous work [27, 31]:

$$p_{\pi } (\varepsilon_{v}^{p} ,s, D) = \left( {1 - D} \right)\left( {1 + k_{1} \times l\left( s \right)} \right)p_{0} (\varepsilon_{v}^{p} )$$
(16)

In the above relation, \(\left( {1 - D} \right)\) represents a softening effect due to damage, whereas the other factor \(\left( {1 + k_{1} \times l\left( s \right)} \right)\) accounts for suction-hardening, \(k_{1}\) being a model constant and the function \(l\left( s \right)\) is defined in Eq. (19) here-below. At positive suction, the pre-consolidation pressure at full saturation \(p_{0}\) is supposed to vary with the plastic volumetric strain according to the following relation:

$$dp_{0} = \frac{{1 + e_{0} }}{\lambda \left( s \right) - \kappa }p_{0} d\varepsilon_{v}^{p}$$
(17)

The suction-dependent coefficient of virgin (i.e. elastoplastic) compressibility \(\lambda \left( s \right)\) is assumed to take the following form:

$$\lambda \left( s \right) = \lambda_{0} - k_{2} \times l\left( s \right)$$
(18)

here \(\lambda_{0}\) is the limiting value of \(\lambda \left( s \right)\) at full saturation, and \(\kappa\) is the elastic coefficient of compressibility (applicable for unloading), assumed suction-independent. The function \(l\left( s \right)\) plays an important role here and must be chosen properly, ensuring continuity at full saturation and the capacity to simulate wetting collapse. The following form for \(l\left( s \right)\) is adopted in this work:

$$l\left( s \right) = \left\{ {\begin{array}{*{20}c} {\frac{s}{{s_{\text{e}} }}\chi - 1 } & { {\text{if}}\,s > s_{\text{e}} } \\ 0 & {{\text{if}}\,s \le s_{\text{e}} } \\ \end{array} } \right.$$
(19)

where the suction-dependent effective stress parameter \(\chi\) is defined in Eq. (6).

3.5 Plastic potential, non-associative flow rule and plastic modulus

The dilatancy, defined as the ratio between the plastic volumetric strain increment and the equivalent plastic deviatoric strain increment, has an important bearing on the soil behaviour. This state-dependent parameter can be incorporated in the definition of the plastic potential. In the present model, the following stress-dependent relation proposed by Yu is adopted [30]:

$$\frac{{d\varepsilon_{v}^{p} }}{{d\varepsilon_{q}^{p} }} = \frac{{M^{n} - \eta^{n} }}{{m\eta^{n - 1} }}$$
(20)

In the above equation, m is another model constant which governs the plastic potential, whereas constants M and n as well as the stress ratio \(\eta\) have already been defined. This equation implies the dilatancy depends only on the stress ratio and becomes zero at the critical stress ratio \(\eta = M\). A plastic flow rule which satisfies the above dilatance ratio can be written as:

$$d\varvec{\varepsilon}^{p} {\mathop{=}^{\text{def}}}\,\left( {\begin{array}{*{20}c} {d\varepsilon_{v}^{p} } \\ {d\varepsilon_{q}^{p} } \\ \end{array} } \right) = d\lambda \varvec{m} = d\lambda \left( {\begin{array}{*{20}c} {m_{p} } \\ {m_{q} } \\ \end{array} } \right)$$
(21)

where \(\varvec{m}\) is a unit vector with components obtained from Eq. (20):

$$m_{p} = \frac{{M^{n} - \eta^{n} }}{{\sqrt {\left( {M^{n} - \eta^{n} } \right)^{2} + \left( {m\eta^{n - 1} } \right)^{2} } }} ; m_{q} = \frac{{m\eta^{n - 1} }}{{\sqrt {\left( {M^{n} - \eta^{n} } \right)^{2} + \left( {m\eta^{n - 1} } \right)^{2} } }} ;$$
(22)

and \(d\lambda\) is the plastic multiplier to be determined from the consistency condition.

In this study, plastic flow is coupled with damage evolution under a general loading condition. Therefore, the plastic strain rate and damage evolution rate have to be determined simultaneously. The consistency condition on the bounding surface requires:

$$dF = \frac{\partial F}{{\partial \bar{p}^{ '} }}d\bar{p}^{ '} + \frac{\partial F}{{\partial \bar{q}}}d\bar{q} + \frac{\partial F}{{\partial \varepsilon_{v}^{p} }}d\varepsilon_{v}^{p} + \frac{1}{{\sigma_{0} }}\frac{\partial F}{\partial D}\left( {\sigma_{0} dD} \right) + \frac{\partial F}{\partial s}ds = 0$$
(23)

The reference stress \(\sigma_{0} = 1\, {\text{MPa}}\) has been added to make the dimension of different terms homogeneous. The plastic volumetric strain rate have already been defined in Eq. (21) and the damage evolution rate \(dD\) will be defined in Eq. (34). The above equation can be recast into a slightly more compact form by normalising the pseudo-gradient of the BS. The following notation is introduced:

$$\tilde{\nabla }F = \left( {\frac{\partial F}{{\partial \bar{p}^{ '} }},\frac{\partial F}{{\partial \bar{q}}},\frac{\partial F}{\partial s},\frac{1}{{\sigma_{0} }}\frac{\partial F}{\partial D}} \right)^{\text{T}} ; {\bar{\mathbf{n}}} = \left( {{\bar{\text{n}}}_{p} ,{\bar{\text{n}}}_{q} ,{\bar{\text{n}}}_{s} ,{\bar{\text{n}}}_{D} } \right)^{\text{T}} = \frac{{\tilde{\nabla }F}}{{||\tilde{\nabla }F||}}$$
(24)

where \(\tilde{\nabla }\) is a pseudo-gradient operator and \(||.||\) represents the classic Euclidean norm of a vector. Similarly, the pseudo-gradient and the associated unit vector for the LS can be defined:

$$\tilde{\nabla }f = \left( {\frac{\partial f}{\partial p '},\frac{\partial f}{{\partial {\text{q}}}},\frac{\partial f}{\partial s},\frac{1}{{\sigma_{0} }}\frac{\partial f}{\partial D}} \right)^{\text{T}} ; {\mathbf{n}} = \left( {{\text{n}}_{p} ,{\text{n}}_{q} ,{\text{n}}_{s} ,{\text{n}}_{D} } \right)^{\text{T}} = \frac{{\tilde{\nabla }f}}{{||\tilde{\nabla }f||}}$$
(25)

The classic assumption that stress increments at the current stress point and at the image stress point give the same plastic multiplier allows to write [9]:

$$d\lambda = \frac{{{\text{n}}_{p} dp^{\prime} + {\text{n}}_{q} dq + {\text{n}}_{D} \sigma_{0} dD + {\text{n}}_{s} dS}}{H} = \frac{{{\bar{\text{n}}}_{p} d\bar{p}^{ '} + {\bar{\text{n}}}_{q} d\bar{q} + {\bar{\text{n}}}_{D} \sigma_{0} dD + {\bar{\text{n}}}_{s} ds}}{{H_{\rm b} }}$$
(26)

where \(H\) is plastic modulus on the loading surface, and \(H_{\text{b}}\) the plastic modulus on the bounding surface.

When the current stress point is on the BS, hence coinciding with its image stress point, the combination of the Eqs. (21), (23), (24) and (26) leads to the following expression of the plastic modulus:

$$H_{\text{b}} = - \frac{1}{{||\tilde{\nabla }F||}}\frac{\partial F}{{\partial \varepsilon_{v}^{p} }}m_{p} = - \frac{1}{{||\tilde{\nabla }F||}}\frac{\partial F}{{\partial p_{\pi } }}\frac{{\partial p_{\pi } }}{{\partial p_{0} }}\frac{{\partial p_{0} }}{{\partial \varepsilon_{v}^{p} }}m_{p}$$
(27)

At this point, we will introduce the simplifying assumption that suction will remain constant, \(ds = 0\), which corresponds to the experimental conditions. Combining Eqs. (13), (16), (17) and (22) with (27), the hardening modulus at the image point can be further developed to:

$$H_{\rm b} = \frac{{\left( {1 + e_{0} } \right)m_{p} }}{{\left( {\lambda \left( s \right) - \kappa } \right)\ln r}}\left[ {\left( {\frac{1}{{\bar{p}^{'} \ln r}} - \left( {\frac{\eta }{M}} \right)^{n} \frac{n}{{\bar{p}^{'} }}} \right)^{2} + \left( {\left( {\frac{\eta }{M}} \right)^{n - 1} \frac{n}{{M\bar{p}^{'} }}} \right)^{2} + \left( {\frac{{k_{1} \left( {1 + \alpha } \right)\chi }}{{s_{e} \left( {1 + k_{1} l\left( s \right)} \right)\ln r}}} \right)^{2} + \left( {\frac{1}{{\left( {1 - D} \right)\sigma_{0} \ln r}}} \right)^{2} } \right]^{{ - \frac{1}{2}}}$$
(28)

In the more general case when current stress point lies strictly inside the bounding surface, the plastic modulus \(H\) is the sum of \(H_{\text{b}}\) and another term, denoted by \(H_{\delta }\). This additive term depends in some way on the distance \(\delta\) between \(\varvec{\sigma^{\prime}}\) and \(\bar{\varvec{\sigma }}^{\varvec{'}}\). In this present model, \(H_{\delta }\) is postulated to be a function of the scale factor \(\beta\) defined in Eq. (15), inspired from the previous work of Bardet and Morvan et al. [11, 15]. The final form of the plastic modulus \(H\) is written as follows:

$$H = H_{\text{b}} + H_{\delta } ; \quad H_{\delta } = \frac{{1 + e_{0} }}{{\left( {\lambda \left( s \right) - \kappa } \right)}}\frac{1 - \beta }{\beta }\frac{h}{||\nabla F||}$$
(29)

in which \(h\) is a material constant. Note that the above expression of the plastic modulus satisfies the following two conditions:

$$H = \left\{ {\begin{array}{*{20}c} {H_{\text{b}} } & {{\text{when}}\,\beta = 1} \\ { + \infty } & {{\text{when }}\,\beta = 0 } \\ \end{array} } \right.$$
(30)

corresponding respectively to the two limiting cases when the current stress lies on the BS and when it is far from the BS.

3.6 Damage mechanism

Similar to the case of plasticity, damage kinetics is controlled by a pseudo-potential of dissipation. It is often described by a scalar-valued damage criterion function which depends on the damage variable D and/or the conjugate damage force \(Y_{D}\). Although the latter can be derived directly from the framework of thermodynamics, this usually leads to overly complex expressions. An alternative simpler family of damage evolution laws, which has been successfully applied to concrete and rocks under compressive deviatoric stresses is based on the tensile part of principal strains. Following the approach of Mazars [23], the tensile part of the principal strain, noted \(\varepsilon_{i}^{ + }\), is defined by:

$$\varepsilon_{i}^{ + } = \left\{ {\begin{array}{*{20}c} 0 & {{\text{if}}\, \varepsilon_{i} \ge 0 } \\ { - \varepsilon_{i} } & {{\text{if}}\, \varepsilon_{i} < 0} \\ \end{array} } \right.$$
(31)

Note that the above definition is consistent with the sign convention of positive compressive strains. Moreover, in conventional triaxial compression tests, the axial compressive strain \(\varepsilon_{1}\) is positive while the radial tensile strain \(\varepsilon_{3}\) is negative.

The damage force \(Y_{D}\) is assumed to depend on the tensile parts of principal strains defined above and a simple damage criterion is proposed in the following form based on [26, 28, 29]:

$$f_{D} \left( {Y_{D} ,D,s} \right) = Y_{D} - r\left( {D,s} \right) \le 0$$
(32)
$$Y_{D} = \sqrt {\mathop \sum \limits_{i} \left( {\varepsilon_{i}^{ + } } \right)^{2} } ;\,r\left( {D,s} \right) = r_{0} + r_{1} \left( s \right)D;\,r_{1} \left( s \right) = k_{3} \chi \left( s \right)$$
(33)

The function \(r\left( {D,s} \right)\) represents the damage threshold which depends on the current values of damage and suction. More specifically, \(r_{0}\) defines the initial damage threshold and \(r_{1} \left( s \right)D\) accounts for the drift due to damage evolution and suction, with the parameters \(k_{3}\) controlling the suction-dependent sensitivity. The damage evolution rate is determined through the classic “flow” rule:

$$dD = d\lambda_{D} \frac{{\partial f_{D} }}{{\partial Y_{D} }}$$
(34)

in which the damage multiplier \(d\lambda_{D}\) should be determined from the consistency condition of damage criterion, fulfilling the Kuhn–Tucker condition:

$$f_{D} \left( {Y_{D} ,D,s} \right) = 0;\,df_{D} \ge 0;\,f_{D} \left( {Y_{D} ,D,s} \right)df_{D} = 0$$
(35)

Specifically, in the case of conventional triaxial tests at constant suction \(ds = 0\), the damage evolution rate can be deduced as the following expression:

$$dD = - \sqrt 2 \frac{{d\varepsilon_{3} }}{{r_{1} \left( s \right)}}$$
(36)

3.7 Elastoplastic compliance matrix accounting for damage

For the particular case of constant suction (the only case considered in this paper) \(ds = 0\), the plastic strain rate in Eq. (21), on account of Eq. (26), can be rewritten in matrix form:

$$d\varvec{\varepsilon}^{p} - \frac{{n_{D} }}{H}\sigma_{0}dD\,\varvec{m} = {\mathbb{C}}^{p} d\varvec{\sigma^{\prime}} ; \,{\mathbb{C}}^{p} = \frac{1}{H}\left[ {\begin{array}{*{20}c} {m_{p} n_{p} } & {m_{p} n_{q} } \\ {m_{q} n_{p} } & {m_{q} n_{q} } \\ \end{array} } \right]$$
(37)

where \(\varvec{ }{\mathbb{C}}^{p}\) is the plastic compliance matrix. Summation of Eqs. (11) and (37) leads us to:

$$d\varvec{\varepsilon}- \frac{{n_{D} }}{H}\sigma_{0} dD\,\varvec{m} = ({\mathbb{C}}^{e} + {\mathbb{C}}^{p} ) d\varvec{\sigma^{\prime}}$$
(38)

Taking into account the damage evolution rate \(dD\) deduced from Eq. (36) and combining with Eqs. (8) and (9), the following relationship between principle strain and stress increments is obtained after some simple manipulations:

$$d\varvec{E} = {\mathbb{C}}^{epD} d{\varvec{\Sigma}}$$
(39)

with:

$${\mathbb{C}}^{epD} = {\mathbb{Q}}^{ - 1} ({\mathbb{C}}^{e} + {\mathbb{C}}^{p} ) {\mathbb{A}};\text{ }\quad {\mathbb{Q}} = \left[ {\begin{array}{*{20}c} 1 & {2 + \frac{1}{H}\frac{{\sqrt 2 {\text{n}}_{D} \sigma_{0} {\text{m}}_{p} }}{{r_{1} \left( s \right)}}} \\ {\frac{2}{3}} & { - \left( {\frac{2}{3} - \frac{1}{H}\frac{{\sqrt 2 {\text{n}}_{D} \sigma_{0} {\text{m}}_{q} }}{{r_{1} \left( s \right)}}} \right)} \\ \end{array} } \right]$$
(40)

where \({\mathbb{C}}^{epD}\) represents the elastoplastic compliance matrix accounting for damage. The above equations define completely the relation between strain and stress increments.

4 Model validation against experimental data and discussion

4.1 Determination of model parameters

The proposed bounding surface plastic damage model requires 14 parameters for its complete definition. They characterize particular aspects of material behaviour: (1) \(\nu\) and \(\kappa\) to describe the elastic behaviour. (2) Seven constants on the plastic behaviour: \(\lambda_{0}\) and \(\varGamma\) define the position of critical state line (CSL) in the \(e - \ln p'\) plane while M defines the slope of CSL in \(p^{\prime} - q\) plane; \(n\) and \(r\) specify the shape of bounding surface; \(h\) controls the hardening modulus; and m controls the stress-dilatancy. (3) Another four model parameters are needed to account for suction effects: \(s_{e}\) and \(\alpha\) define the effective stress used in this model, \(k_{1}\) and \(k_{2}\) account for suction effects on hardening and volumetric deformability respectively. (4) Finally, the constant \(k_{3}\) controls damage evolution.

The above model parameters can be determined from a few classic tests in the laboratory. \(\nu\), \(\kappa\) and \(\lambda_{0}\) can be obtained from classic oedometric and triaxial consolidation tests at full saturation under drained conditions: \(\kappa\) is based on the slope of elastic unloading–reloading line on \(e - \ln p^{\prime}\) plane, \(\nu\) is the Poisson’s ratio (can be determined from axial vs radial strain rates during elastic unloading) and \(\lambda_{0}\) is detemined from the loading part of the isotropic triaxial consolidation tests expressed in \(e - \ln p^{\prime}\) plane. \(\varGamma\) and M associated with the definition of critical state line can be deduced using triaxial tests at different controlled suctions. The parameter \(k_{2}\) defining the reduction of volumetric deformability \(\lambda \left( s \right)\) with suction can be assessed by carrying out virgin oedometric compression tests at different controlled suctions. \(s_{\text{e}}\) is identified as air-entry suction determined from the classical water retention curve and a unique value \(\alpha = 0.85\) was adopted for the three different soils as mentioned in the Sect. 3.1. The remaining parameters: \(h, m, n, r,\) \(k_{1}\) and \(k_{3}\) have to be determined by trial and error using experimental results.

4.2 Model implementation

To implement the constitutive model proposed in this paper, a simple computer program was developed under Matlab environment. The performance of this model was investigated by comparing the numerical simulation with a series of triaxial tests results for earthen materials (Lim and Mix1), at different hydraulic conditions (23, 75, and 97% relative humidity) and two confining pressure conditions (100 and 600 kPa). The parameters used for the study are presented in Table 1.

Table 1 Model parameters adopted in simulation for Lim and Mix1
Full size table

4.3 Stress–strain behaviour and volumetric evolution

Figure 5 presents the results of triaxial compression tests and model simulations on Lim at three different hydraulic states (RH = 23%, RH = 75% and RH = 97%), at 100 kPa confining pressure. The comparison shows a good agreement between experiments and simulations in \(q\)–\(\varepsilon_{1}\) plane. From Fig. 5a, it can be seen the constitutive model is able to describe correctly the basic features of the unsaturated earthen materials behaviour: damage softening, plastic and suction induced hardenings. Most notably, the smooth stress–strain behaviour (always observed in experiments) and transitions from pre-peak hardening to post-peak softening were also well simulated.

Fig. 5
figure 5

Triaxial compression tests on Lim at three different hydraulic states at 100 kPa confining pressure: a \(q\)–\(\varepsilon_{1}\) plot and b \(\varepsilon_{v}\)–\(\varepsilon_{1}\) plot

Full size image

As shown in Fig. 5b, the volumetric strain versus axial strain \(\varepsilon_{v}\)–\(\varepsilon_{1}\) as predicted by this model is also in good agreement with the experimental data. This confirms that the model can indeed reproduce the complex volumetric behaviour: transition from contraction to dilation state. The model also captures the suppressed dilation induced by the increasing relative humidity (suction decreasing).

At lower hydraulic state RH = 23%, some deviations are observed both in stress strain curve and volumetric evolution, especially for the post-peaking stage. One possible explanations is that some form of localization may appear, which cannot be simulated by a purely continuous modelling approach. Note that this kind of deviation is also faced with in previous modelling work [27, 29].

Figure 6a, b shows the results of triaxial compression tests and model simulations of Lim at 600 kPa confining pressure. In \(q\)–\(\varepsilon_{1}\) plane, the results predicted by the model are quitredicted by this model is alson \(\varepsilon_{v}\)–\(\varepsilon_{1}\) plot, it is seen the dilatancy reproduced by the model is overestimated compared with the test results especially for the RH = 23% case. To improve the model’s performance, a suction-dependency plastic potential is considered to use in the future work.

Fig. 6
figure 6

Triaxial compression tests on Lim at three different hydraulic states at 600 kPa confining pressure: a \(q\)–\(\varepsilon_{1}\) plot and b \(\varepsilon_{v}\)–\(\varepsilon_{1}\) plot

Full size image

By making a comparison between Figs. 5 and 6, it is worth noting that the model also captures the increased deviator stress and overall reduced dilation with an increase in confining pressure. As confining pressure increases, particle crushing begins to dominate plastic deformation, resulting in a reducing tendency for a peak in the shear resistance and for a volumetric expansion.

Triaxial compression tests on Mix1 at three different hydraulic states (RH = 23%, RH = 75% and RH = 97%) and at 100 kPa confining pressure were conducted in the laboratory. A good agreement is obtained between numerical simulation and experimental data as illustrated in Fig. 7.

Fig. 7
figure 7

Triaxial compression tests on Mix1 at three different hydraulic states at 100 kPa confining pressure: a \(q\)–\(\varepsilon_{1}\) plot and b \(\varepsilon_{v}\)–\(\varepsilon_{1}\) plot

Full size image

4.4 Degradation of elastic property

Figure 8 presents evolutions of Young’s modulus versus radial strain during triaxial tests on Mix1 at confining pressure of 100 kPa and two relative humidity conditions (RH = 75% and RH = 97%). There is an acceptable agreement between numerical predictions and experimental data, indicating the developed model qualitatively describes the general trend observed in test data: elastic modulus decreases with the damage induced by the radial strain. Considering there is only an additive parameter \({\text{k}}_{3}\) to describe the damage evolution rate, the simulation results is acceptable.

Fig. 8
figure 8

Evolutions of Young’s modulus versus radial strain during triaxial tests on Mix1 at confining pressure of 100 kPa. a RH = 75%, b RH = 97%

Full size image

In addition, it is worth noticing the degradation rate of Young’s modulus at RH = 75% (higher suction, lower water content) is higher than that at RH = 97% (lower suction, higher water content), which is conform to the physical intuition that higher water content should result in higher ductility.

Finally, in order to illustrate the effects of damage on the stress–strain behaviour, numerical simulations with different values of \(k_{3}\) are presented for Mix1 at 75% RH and 100 kPa confining pressure (Fig. 9). With decreasing of \(k_{3}\), the damage evolution rate becomes higher. From the simulation results, it could be observed that the response of compacted earthen materials becomes more and more brittle when the effect of damage on plastic flow is stronger.

Fig. 9
figure 9

Influence of \(k_{3}\) on the stress–strain behaviour for Mix1 at 75% RH and 100 kPa confining pressure

Full size image

5 Conclusions

A new constitutive model for unsaturated earthen materials is proposed accounting simultaneously for the impact of suction and confining pressure on mechanical properties. This model is formulated using the concept of effective stress and bounding surface plasticity (BSP) theory under a critical state framework. It adopts an whale-head shaped loading and bounding surfaces, a simple radial mapping rule, a non-associative flow rule which generally gives a better description on volumetric behaviour, and suction-dependent hardening controlled by plastic volumetric strains. At the present stage of development, only isotropic damage is considered. Damage evolution rate is assumed to be driven by tensile strain and restrained by suction. Plastic flow and damage evolution occur as coupled processes.

The model has been used to simulate the triaxial compression tests subjected to different relative humidities and confining pressures. Good agreement is generally obtained between model predictions and experimental data. Of fundamental importance in practice, this model only requires 14 independent soil parameters for its definition and makes it ideally suited for engineering applications. Despite the minimal number of parameters, the model is able to reproduce the essential trends in the behaviour of partially saturated earthen materials: suction-induced hardening and stiffening, smooth stress–strain behaviour, post-peak softening ae well as contractancy-dilatancy transition.

Furthermore, the present model qualitatively describes a degradation of elastic properties observed in experimental data. The model in its current form is intended for monotonic loading, an extension of this model to cyclic loading will be the subject of future work.