Influence of moisture condition on chloride diffusion in partially saturated ordinary Portland cement mortar

Abstract

Experiments have been carried out to study the influence of moisture condition, including moisture content and its distribution, on the chloride diffusion in partially saturated ordinary Portland cement mortar. The mortar samples with water-to-cement (w/c) ratios of 0.4, 0.5 and 0.6, cured for 1 year, were preconditioned to uniform water saturations ranging from 18 to 100%. The interior relative humidities of these partially saturated cement mortars, i.e. water vapour desorption isotherm (WVDI), were measured. The WVDI results in relation to the pore structures obtained from the mercury intrusion porosimetry tests of paste samples with the same w/c ratios were analyzed, which provided a basic insight into the moisture distribution in the non-saturated cement mortars. The relative chloride diffusion coefficients of cement mortars at various water saturations were determined based on the Nernst-Einstein equation and conductivity technique. It is found that the relative chloride diffusion coefficient D_rc depends on the degree of water saturation S_w and WVDI. At a given S_w level, the D_rc is larger for a higher w/c ratio. The role of the w/c ratio in the D_rc–S_w relation, however, becomes less pronounced with increasing w/c ratio. There exists a critical saturation, below which the water-filled capillary pores are discontinuous and the D_rc-value tends towards infinitely small. An increase of the w/c ratio results in a decrease of the critical saturation level.

1 Introduction

Chloride-induced corrosion is nowadays the main durability concern for the reinforced concrete structures in marine environment. Whenever the chloride concentration at the steel surface reaches a critical level, along with enough oxygen and moisture, steel corrosion may take place, resulting in cracking and spalling of the cover concrete and hence shortening the service life of the concrete structures [1].

Current durability design, e.g. DuraCrete [2], relies on the chloride diffusion coefficient of saturated concrete. In reality, however, concrete is often partially saturated. The interior relative humidity of concrete, as a result of self-desiccation, can be as low as 80% [3]. The concretes exposed to the atmospheric and tidal marine conditions undergo variations in moisture distribution with time. Even for an underwater concrete, splitting it longitudinally, only the outer few centimeters have a wet look while the interior part is rather dry [4]. The propagation of the saturation front in the concrete depends on the pore size and elapsed time after contact with water [5]. In the absence of sufficient knowledge about the effect of non-saturated state on chloride diffusion, the service life prediction based on the chloride diffusion coefficient of saturated concretes may give rise to misjudgement of the actual serviceability of reinforced concrete structures. In this regards a critical understanding of the non-saturated chloride diffusion is meaningful.

Chloride diffusion occurs only if water is present. In saturated concrete, the connected pores are responsible for the ionic transport. In partially saturated concrete, the connected water-filled pores provide the main pathways for the ionic transport. It is well known that the water phase is inclined to fill the small pores in the form of capillary condensed water, which allows for chloride diffusion. The gas phase, on the contrary, tends to fill the central region of the large pores and forms the gas phase clusters, which can block the passage of chloride diffusion [6]. The water content and its distribution in the pore structure are the key factors that influence the chloride diffusion in partially saturated concrete.

Since early in this century increasing attention has been given to study the chloride diffusion in non-saturated cementitious materials, yet up to date only a limited amount of experimental investigations can be found in the literature. These investigations were based on either direct diffusion tests or conductivity technique. For the direct diffusion tests, a chloride source can be imposed on the outer surface of unsaturated concretes through gaseous hydrogen chloride [7], chloride-containing solution [8] or solid crystal (sodium chloride) [9]. After a certain period of test, the chloride profiles were obtained by grinding successive parallel layers and quantifying the chloride content in each layer with potentiometric titration [10]. The Fick’s 2nd law was then applied to quantify the non-saturated chloride diffusion with and without chloride binding considerations [7, 8]. It is worthwhile to note that imposing the different chloride sources into unsaturated concretes may lead to unwanted moisture redistribution and/or microstructural alteration in the concretes. The conductivity technique, combined with the Nernst-Einstein equation, is an alternative approach to determine the chloride diffusion coefficient in the non-saturated cementitious materials [11,12,13,14,15,16]. Compared to direct diffusion tests, conductivity measurements are fast and easy to perform. Nevertheless, the conductivity technique is unable to consider the chloride binding effect.

So far the effect of non-saturated state on the chloride diffusion in cementitious materials remains a pending issue. The published results with respect to the relationship between chloride diffusion coefficient and moisture content show a large scatter [6]. The role of water-to-cement (w/c) ratio in the non-saturated chloride diffusion is still a point of controversy in view of the existing research works [7, 13, 17]. The moisture distribution in the pore structure and its effect on the non-saturated chloride diffusion are not clear.

The present work aims to experimentally study the influence of moisture condition, including moisture content and its distribution, on the chloride diffusion in the partially saturated ordinary Portland cement mortar. The mortar samples with w/c ratios of 0.4, 0.5 and 0.6, cured for 1 year, are preconditioned in an oven at 50 °C to reach uniform water saturations ranging from 18 to 100%. The relative humidities of the mortar samples at different water saturation levels, i.e. water vapour desorption isotherm (WVDI), are measured. The effects of w/c ratio on the pore structure, measured from mercury intrusion porosimetry tests, and on the WVDI are analyzed. The conductivities of the partially saturated cement mortars and their pore solutions are derived based on experiments and, by using the Nernst–Einstein equation, the relative chloride diffusion coefficient D_rc is subsequently expressed as a function of the degree of water saturation S_w. Finally, the roles of the moisture distribution and the w/c ratio in the D_rc–S_w relation are discussed in detail.

2 Experimental program

2.1 Materials and sample preparation

Ordinary Portland cement CEM I 42.5 N (OPC) was used to cast cement pastes and mortars. The mean particle size, measured by laser diffraction, was 24.1 µm for the cement powders.

The cement pastes were prepared for pore structure measurements. The cement powders and distilled water were mixed with a HOBART mixer at low speed for 1 min and at high speed for 2 min. The fresh pastes were poured into plastic bottles. The bottles were shaken continuously to remove air bubbles and sealed with lids thereafter. In order to avoid bleeding, the paste samples were rotated for 1 day before placing them in the curing room at 20 ± 0.1 °C. After the age of 370 days, the hardened paste samples were taken out of the plastic bottles and crushed into small pieces (around 1 cm³). The paste pieces were immersed in liquid nitrogen at − 195 °C for 5 min, and then placed in a freeze-dryer with − 24 °C and under vacuum at 0.1 Pa. Until the water loss was below 0.01% per day, the paste pieces can be ready for pore structure measurements.

The cement mortars were prepared for water vapour desorption tests and resistivity tests. The mortar samples were made with the same amount of siliceous sand (according to EN 196-1), but with different w/c ratios of 0.4, 0.5 and 0.6. The particle size of the siliceous sand was in the range of 0.125–2 mm. The cement binder to sand ratio was 1:3 by weight. Cylindrical mortars (ϕ100 × 80 mm) were cast. After wet-cured at 20 ± 0.1 °C for 370 days, the top and bottom surfaces of the mortar samples with thickness of 15 mm were cut off. The middle part of each mortar sample was stored in lime water for 1 week, followed by the sample preconditioning procedures as will be described in Sect. 2.2.

For the sake of description, the paste samples with w/c ratios of 0.4, 0.5 and 0.6 are abbreviated as P4, P5 and P6, respectively; the mortar samples with w/c ratios of 0.4, 0.5 and 0.6 are abbreviated as M4, M5 and M6, respectively.

2.2 Sample preconditioning for desired moisture content

At present, “RH” (relative humidity) preconditioning and “SD” (saturation degree) preconditioning are the main approaches for preparing partially saturated cementitious samples [6]. In both approaches the samples are usually wet-cured until a high maturity, followed by a series of drying procedures to reach desired moisture contents. For “RH” preconditioning, the sample (often saturated) is dried step-by-step under drier humidity circumstances until the sample is in equilibrium to the target humidity level, i.e. water loss < 0.02 g/week [13]. The different humidity circumstances can be controlled by saturated salt solutions [18]. For “SD” preconditioning, the sample (often saturated) is firstly dried in an oven at a relatively high temperature to get a preassigned loss of water and then conducted with a moisture redistribution step in order to gain homogeneous moisture distribution [19].

The two approaches were evaluated at the beginning of the sample preconditioning. The “RH” preconditioning approach was found to be time-consuming, and it was difficult to reach the equilibrium moisture contents for the low humidity circumstances because of the low moisture diffusivity of the samples. The “SD” preconditioning approach, on the contrary, was convenient and fast. In the present work, all mortar samples with desired moisture contents were obtained from the “SD” preconditioning approach.

Degree of water saturation, S_w, was used to quantify the moisture content of the mortar samples. The S_w-value is defined as the ratio of the volume of pore water over the total pore volume in the sample, as shown in Eq. (1a). The water absorption, A_b, is expressed in Eq. (1b).

$$S_{\text{w}} = \frac{{m_{\text{h}} - m_{\text{d}} }}{{m_{\text{s}} - m_{\text{d}} }}$$

(1a)

$$A_{\text{b}} = \frac{{m_{\text{s}} - m_{\text{d}} }}{{m_{\text{d}} }}$$

(1b)

where m_h [g] is the mass of the sample at a particular saturation state, m_s [g] is the mass of the sample at saturated state and m_d [g] is the mass of the dried sample. The parameters A_b, m_s, m_d and m_h were all determined by following the procedures described in Ref. [19].

The sample mass, m_h, corresponding to a particular saturation S_w level can be deduced from Eq. (1a–1b).

$$m_{\text{h}} = m_{\text{s}} \frac{{1 + A_{\text{b}} \cdot S_{\text{w}} }}{{1 + A_{\text{b}} }}$$

(2)

The sample preconditioning of the present work, which was similar to that used in Ref. [19], proceeded with three steps. The details will be described in the following.

Step one: drying each sample at 50 °C to reach its desired S_w-value

• 1. The lateral and bottom sides of the mortar sample (50-mm thick) were sealed with electric isolating tape to avoid any multi-directional moisture transfer. Only the top side of the sample was left as the drying surface.

• 2. The mortar sample was moved into a ventilated oven, which was heated gradually at a rate of 5 °C per hour up to 50 °C. A CO₂ absorbent (sodium hydroxide) was placed in the oven to minimize the carbonation effect.

• 3. The oven was vacuumed until the pressure was below 50 Pa. The low pressure circumstance enables to dry the sample to a low S_w level in a relatively short period.

• 4. The mass loss was recorded at frequent intervals during the first 6 h, followed by one measurement per day later on.

Step two: monitoring moisture homogeneity by a moisture redistribution procedure

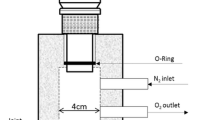
Once the sample mass m_h corresponding to a particular saturation S_w level reaches its desired value, there may still be a moisture gradient from the bottom to the top of the mortar sample. A moisture redistribution procedure is required so far as the homogeneous moisture distribution is concerned. To this end, all the surfaces (top, bottom and lateral) of the sample were tightly sealed with isolating tape. The sample was then stored in a plastic bag at 50 °C for a certain period, i.e. 7–45 days, depending on the saturation S_w level of the sample. The storage period was longer for the sample with a lower S_w level. At this stage, a great deal of moisture was transferred from the bottom to the top of the sample. Next, the sample was gradually cooled down to 30 ± 0.1 °C. A novel set-up shown in Fig. 1 was established to monitor the moisture homogeneity by measuring the RH of both surfaces (top and bottom) of the sample. A similar method for monitoring the moisture homogeneity of cylindrical samples has been previously used in Ref. [20].

Fig. 1

Set-up for monitoring the moisture homogeneity of mortar sample (ϕ100 × 50 mm)

• 1. The isolating tape on the top and bottom surfaces of the mortar sample was removed. The lateral surface of the mortar sample was still sealed.

• 2. The mortar sample was placed in a cylindrical chamber. The chamber was sealed with lid and maintained a constant temperature of 30 ± 0.1 °C. The time-related RH changes at the top and bottom surfaces of the sample were monitored with the same type of hygrometer. As expected, the RH-value on the top surface was increasing while that on the bottom surface was decreasing. Once the RH-values on both surfaces approached the same value (difference less than 1%), the moisture distribution inside the sample was considered homogeneous.

• 3. The sample was cooled down slowly with 5 °C per hour to room temperature (20 ± 0.1 °C).

• 4. The sample was removed from the chamber. All the surfaces (top, bottom and lateral) of the sample were tightly sealed with isolating tape. The sample was then stored in a plastic bag to keep its specific water saturation level.

Step three: evaluation on the preconditioned samples

An evaluation step was performed on the preconditioned samples in order to check the efficiency of the preconditioning approach introduced in this work.

Firstly, drying at 50 °C may influence the phase mineralogy and the pore structure of the mortar sample and, therefore, can affect the calculated water saturation level of the sample when Eq. (2) is applied for the calculation. The details will be given in Sect. 4.1 in this respect.

Secondly, the preconditioned mortar samples were examined under an optical microscope (×100). No micro-cracking was observed in this magnification. The possibility of crack initiation was minimized due to two reasons: (a) no large moisture or temperature gradient occurred at any time of a series of preconditioning procedures; (b) the moisture moved towards only one direction in the whole sample preconditioning process.

All mortar samples, preconditioned with desired water saturation levels, were ready for the resistivity measurements. The details will be given in Sect. 2.5.2.

2.3 Pore structure of cement paste

In partially saturated pore systems the ionic diffusion primarily depends on the water-filled pores. The water-filled pores are usually small. A deep insight into the pore structure, especially the structure of the small capillary pores, becomes a prerequisite for capturing the non-saturated ionic diffusion.

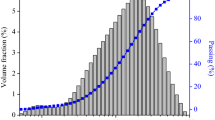
Mercury intrusion porosimetry (MIP) is a technique commonly used to characterize the pore structure of cementitious materials [21]. It is known that the 1st intrusion of MIP test, due to the ink-bottle effect, is considered inappropriate to identify the real pore size distribution [22]. The 2nd intrusion, however, has little ink-bottle effect and provides a more truthful size distribution of the small capillary pores in cement paste [23].

An example of the cumulative intrusion volume with applied pressure is shown in Fig. 2, in which the extrusion curves in the 1st and 2nd cycles are almost overlapped. It is clear that the 1st intrusion-extrusion cycle shows a serious ink-bottle effect, as indicated by the ink-bottle porosity, but there is little ink-bottle effect in the 2nd intrusion-extrusion cycle. In this work, the 2nd intrusion was applied to characterize the pore size distribution of the cement pastes with various w/c ratios.

Fig. 2

An example of the cumulative intrusion volume obtained from MIP in the 1st and 2nd intrusion-extrusion cycles

The relationship between pore diameter d [μm] and applied pressure P [MPa] is determined by the Washburn equation [24]:

$$d = - \frac{{4\gamma_{\text{Hg}} \cos \theta_{\text{m}} }}{P}$$

(3)

where $\gamma_{\text{Hg}}$ is the surface tension of mercury (0.48 kN/m); $\theta_{\text{m}}$ is the contact angle between mercury and cement paste (139° for mercury intrusion).

Pore connectivity is a key parameter that influences the transport properties of cementitious materials. It is often expressed as the ratio between the volume of the continuous pores and the total pore volume. The pore connectivity $\eta_{\text{p}}$ can be deduced from the MIP test [25], and calculated as the quotient of the effective porosity $\phi_{\text{e}}$ over the total porosity $\phi_{\text{t}}$.

$$\eta_{\text{p}} = \frac{{ \phi_{\text{e}} }}{{ \phi_{\text{t}} }} \times 100\%$$

(4)

2.4 Water vapour desorption isotherm of cement mortar

Water vapour desorption isotherm (WVDI) illustrates the changes of the interior relative humidity RH with different degrees of water saturation S_w. According to the Kelvin law, each RH level corresponds to a particular pore diameter. Below this diameter all the pores are considered filled with water. These water-filled pores constitute a major contribution to the ionic transport. The relationship between WVDI (RH vs. S_w) and pore structure will be analyzed based on the Kelvin law in order to examine the moisture distribution and ionic transport in the non-saturated cement mortars.

2.4.1 RH–S _w relationship

The RH of the mortar sample at a particular saturation S_w level was recorded when the sample exhibited homogenous moisture distribution at 20 ± 0.1 °C, as illustrated in Fig. 1. The water vapour desorption isotherms (RH vs. S_w) in the cement mortars with w/c ratios of 0.4, 0.5 and 0.6 were determined.

This RH–S_w relationship is not valid, in theory, for the very surface-near parts of the specimens since they have been dried and rewetted. Those parts follow instead a scanning-curve. The effect of this should, however, be minor since the surfaces are somewhat wetted when a wet sponge is applied when the conductivity measurements are done.

2.4.2 Evaluation of moisture distribution

The interior RH of cementitious material is mainly associated with the meniscus formed above the water-filled pores. The Kelvin equation [26] gives:

$${ \ln }\left( {\text{RH}} \right) = - \frac{{2\gamma_{\text{w}} V_{\text{m}} \cos \theta_{\text{w}} }}{{r_{\text{k}} RT}}$$

(5)

where $\gamma_{\text{w}}$ is the surface tension of water (0.072 N/m in pure water); $V_{\text{m}}$ is the molar volume of water [m³/mol]; $\theta_{\text{w}}$ [°] is the contact angle between water and solids (it is assumed to be zero for water); R is the ideal gas constant (8.314 J/mol K); T is the absolute temperature [K]; $r_{\text{k}}$ is the meniscus radius [m]. The Kelvin equation is able to provide a valid estimation for the menisci with radius $r_{\text{k}}$ as low as 4 nm, with a discrepancy of ± 6% when the radius is within 4–20 nm [27].

If the adsorbed water film is taken into account, as illustrated in Fig. 3, the Kelvin equation is replaced by the Kelvin–Cohan equation [28], as:

$$\ln \left( {\text{RH}} \right) = - \frac{{2\gamma_{\text{w}} V_{\text{m}} \cos \theta_{\text{w}} }}{{\left( {r_{\text{p}} - t} \right)RT}}$$

(6)

where $r_{\text{p}}$ is the radius [m] of the pores in which the meniscus surface is formed. $d_{\text{p}}$ $(d_{\text{p}} = 2r_{\text{p}} )$ is considered as the smallest drained pore diameter in a partially saturated specimen; herein, a pore is defined as drained when the pore is only covered with the nano-scale water film. t [m] is the thickness of the water film, which is a function of the interior RH [29]:

Fig. 3

Meniscus curvature and adsorbed water film in the capillary pores

$$t = \left[ {0.385 - 0.189 \cdot \ln \left( { - \ln \left( {\text{RH}} \right)} \right)} \right] \times 10^{ - 9} \;\;\left( {1\% \, \le {\text{RH}} \le \, 95\% } \right)$$

(7)

2.5 Conductivity of cement mortar at different water saturations

2.5.1 Diffusion coefficient and conductivity: Nernst–Einstein equation

When a cementitious material is considered a solid electrolyte, the chloride diffusion coefficient of the cementitious material can be related to its electrical conductivity [30, 31]. Cementitious material is a three-phase system consisting of pore solution phase, solid phase and vapour phase. The conductivity of the pore solution phase is usually many orders of magnitude higher than that of the solid phase and vapour phase [32]. The Nernst–Einstein equation shows that the ratio of conductivity $\sigma_{0}$ [S/m] of the pore solution to conductivity $\sigma$ of the cementitious material is equal to the ratio of chloride diffusion coefficient D₀ [m²/s] in the pore solution to chloride diffusion coefficient D in the cementitious material.

$$\frac{{\sigma_{0} }}{\sigma } = \frac{{D_{0} }}{D}$$

(8)

The coefficient D ₀ is around 1.5 × 10⁻⁹ m²/s at room temperature when the chloride concentration is within 0.1–1.0 mol/l [33]. The $\sigma_{0}$-value relies on the pore solution chemistry. The conductivity $\sigma$ of cementitious material is the inverse of its resistivity $\rho_{e}$ [Ωm], which is a function of the electrical resistance $R_{\text{mat}}$ of the material, as:

$$\sigma = \frac{1}{{\rho_{\text{e}} }} = \frac{mL}{A} \cdot \frac{1}{{R_{\text{mat}} }}$$

(9)

where m is the geometry factor (m = 1 for cylindrical specimen); L [m] is the length of the specimen; A [m²] is the cross sectional area of the specimen.

2.5.2 Resistivity measurement of cement mortar

Figure 4 shows the experimental set-up for resistivity measurement (under direct current) on a partially saturated mortar specimen. For the principles of the resistivity measurement reference is made to Polder [34]. In the present work the resistivity measurements were performed at room temperature (20 ± 0.1 °C). The top and bottom sides of the specimen were exposed as the measuring surfaces, with the lateral side sealed. The electrical resistance $R_{\text{mat}}$ of the specimen (ϕ100 × 50 mm) was measured with one stainless steel electrode covering each end of the specimen. A wet sponge was applied between specimen surface and each electrode to ensure the whole surface specimen under current flow. During the test, the measured resistance $R_{\text{mat}}$ was found to decrease with time. This was caused by the moisture transfer from the wet sponge into the specimen. To minimize this effect, the result obtained from the first measurement was adopted. The adoption of the first measurement was based on two considerations. First, the top, middle and bottom parts of the specimen can exhibit almost the same moisture level when the whole specimen was tightly sealed with isolating tape. After the isolating tape on the top and bottom surfaces of the specimen was removed, wetting the surface specimen by using the wet sponge was considered an instantaneous process. Second, the measured $R_{\text{mat}}$ value showed a gradually decreasing trend with time. If wetting the surface specimen with the wet sponge was not an instantaneous process, an abruptly sharp drop of the $R_{\text{mat}}$ value will occur in a few seconds after the first measurement. However, such abruptly sharp drop was not found in the present study.

Fig. 4

Resistivity measurement on a cylindrical specimen under direct current (DC)

Each specimen has been weighed before and after the resistivity test. The weight increase of each tested specimen was less than 0.2 g, due to the use of wet sponge, which led to a change of the water saturation S_w inside the specimen of around 0.2%. This minor amount was negligible.

2.5.3 Relative chloride diffusion coefficient of cement mortar

Based on the resistivity measurements, and using Eqs. (8) and (9), the chloride diffusion coefficients of the cement mortars at various water saturations were obtained. Relative chloride diffusion coefficient (D_rc) is expressed as the ratio of chloride diffusion coefficient at a particular saturation S_w level ($D_{{S_{w} }}$) to that at saturated state (D _Sat ), as:

$$D_{\text{rc}} = \frac{{D_{{S_{\text{w}} }} }}{{D_{\text{Sat}} }} = \frac{{\sigma_{{S_{\text{w}} }} }}{{\sigma_{\text{Sat}} }} \cdot \frac{{\sigma_{{0,{\text{Sat}}}} }}{{\sigma_{{0,S_{\text{w}} }} }}$$

(10)

For each mortar mixture, $\sigma_{{S_{\text{w}} }}$ and $\sigma_{\text{Sat}}$ are the conductivities of cement mortar at a particular saturation S_w and at saturated state, respectively. The both can be obtained directly from the resistivity tests. $\sigma_{{0,S_{\text{w}} }}$ and $\sigma_{{0,{\text{Sat}}}}$ are the conductivities of pore solutions when the cement mortar is at a particular saturation S_w and at saturated state, respectively. The determination of $\sigma_{{0,S_{\text{w}} }}$ and $\sigma_{{0,{\text{Sat}}}}$ is rather complex, which will be discussed in detail in Sect. 4.2.

3 Experimental results

3.1 Pore size distribution of cement pastes

The pore structures of the 1-year-old cement pastes were measured by the MIP tests. As introduced in Sect. 2.3, each MIP test consisted of a 1st intrusion and a 2nd intrusion. Figure 5a shows the results of the differential pore size distribution (PSD) obtained from the 1st intrusion. These PSD curves exhibit intersections, and it is not easy to identify the role of the w/c ratio in the truthful size distribution of the small pores (< 200 nm). This can be ascribed to the presence of ink-bottle pores, whose volumes have been included in the PSD results obtained from the 1st intrusion.

Fig. 5

Differential pore size distributions of the 1-year-old cement pastes: a from the 1st intrusion of MIP; b from the 2nd intrusion of MIP; d_cr and d_th are marked for the cement paste P6 as critical diameter and threshold diameter, respectively

Figure 5b shows the PSD curves obtained from the 2nd intrusion. Since the volumes of ink-bottle pores are excluded, the role of the w/c ratio in the small pore sizes can be revealed more clearly. Each curve shows a main peak. The pore diameters corresponding to the top and the onset of the main peak are defined as critical diameter d_cr and threshold diameter d_th, respectively. In the cement pastes P4, P5 and P6, the d_cr-values are determined as 26.2 nm, 34.6 nm and 34.6 nm, and the d_th-values are 79.5, 112.6 and 225.7 nm, respectively. Obviously, the w/c ratio greatly alters the capillary pore size range from d_cr to d_th. The PSD curves of pastes P5 and P6 are more close to each other (especially for the pores < 20 nm), but they are very different from the PSD curve of paste P4 in both size and shape.

3.2 Water vapour desorption isotherm of cement mortars

Figure 6 shows the water vapour desorption isotherms in the cement mortars with w/c ratios of 0.4, 0.5 and 0.6. In general, the interior RH decreases with decreasing water saturation S_w level. The RH decrease, however, is much less pronounced in the cement mortar with a higher w/c ratio. Take mortar M6 (w/c = 0.6) for an example, a significant decrease of the S_w from 95 to 65% results in a small decrease of the RH from 98 to 90%. In contrast, a much larger decrease of the RH from 98 to 70% is observed for mortar M4 (w/c = 0.4) when the S_w decreases in the same range. It is worth noting that in the range of 50–90% RH, corresponding to the smallest drained pore diameter d _p of 4.0–21.8 nm, almost linear RH–S_w patterns can be observed for all the w/c ratios, but that these linear relationships vary with different w/c ratios. For a given water saturation an increase of the w/c ratio results in an increase of the RH. This agrees with previous results from Parrott [35]. The RH–S_w curves for M5 and M6 are closer, compared to that of M4. For instance, at RH = 60%, the S_w-values are 54, 31 and 27% for the mortars M4, M5 and M6, respectively.

Fig. 6

Water vapour desorption isotherms in the 1-year-old cement mortars with varying w/c ratios

The interior RH is primarily controlled by the meniscus formed above the water-filled pores. With decreasing water saturation S_w, the water loss occurs preferably from large pores to small pores. The specimen with a higher w/c ratio, e.g. M6, contains more large pores and thus can maintain a high interior RH even at a relatively low S_w level. In contrast, for the specimen with a lower w/c ratio (e.g. M4), the interior RH is more sensitive to the water content and the RH-value falls off rapidly as soon as the S_w starts to decrease from saturated state. The closer RH–S_w curves for mortars M5 and M6, as shown in Fig. 6, are attributable to the similar pore structures of their paste matrixes, as already described in Sect. 3.1.

3.3 Relative chloride diffusion coefficient of cement mortars

Based on Eq. (10), the relative chloride diffusion coefficient D_rc was expressed as a function of the degree of water saturation S_w. It should be mentioned that at very low saturation levels the conductivities of the mortar specimens were infinitely small. In these specimens the water-filled capillary pores were assumed discontinuous. The term critical saturation is introduced to describe the water saturation level, below which the water-filled capillary pores are unable to form a continuous path for ionic diffusion.

Figure 7 shows the D_rc–S_w relations in the cement mortars with various w/c ratios. In general, the D_rc–value decreases with decreasing S_w. The D_rc–S_w relation can be divided into three stages. Take mortar M6 as an example, when the S_w decreases from saturated state, the D_rc-value shows a slight decrease (stage I). There is a sharp drop in the D_rc-value when the S_w reduces from 90 to 60% (stage II), followed by a slight decline (stage III). An increase of the w/c ratio results in an increase of the D_rc-value. For example, at S_w = 80%, the D_rc-value is 0.34 for mortar M4, compared to D_rc = 0.58 and D_rc = 0.67 for mortars M5 and M6, respectively. The D_rc–S_w curves for M5 and M6 are closer compared to that for M4. It indicates that the role of the w/c ratio in the D_rc–S_w relation becomes less pronounced with increasing w/c ratio. The same finding has been reported in a previous simulation work as presented in [17].

Fig. 7

Relative chloride diffusion coefficient D_rc as a function of water saturation S_w in the 1-year-old cement mortars with varying w/c ratios

Once the water saturation S_w is lower than the critical saturation S_cr level, the D_rc-value tends towards infinitely small. In this work the critical saturation S_cr of each mortar was estimated based on the changes of the electrical resistance R_mat when the water saturation S_w decreases in the stage III. An example for determining the critical saturation S_cr is given in Fig. 8, where the plots (R_mat vs. S_w) for mortar M6 are presented. To better assess the relationship (R_mat vs. S_w), schematic representations of the moisture distribution in the cementitious system at water saturation S_w above/below the critical saturation S_cr are inserted in Fig. 8. There are capillary pores (diameters d ₁  > d ₂ ) and interlayer (gel) pores in the porous system.

Fig. 8

Moisture distribution and electrical resistance R_mat at water saturation S_w levels above/below the critical saturation S_cr. The resistances R_mat were measured from resistivity tests performed on the mortar specimens (M6: w/c = 0.6, size $\phi$ 100 × 50 mm) at low saturation levels (S_w = 18–60%)

• At S_cr < S_w ≤ 60%, the capillary pores d ₁ are partially water-filled, and the capillary pores d ₂ are fully water-filled. The capillary water can form a continuous path that dominates the ion conduction/diffusion in the system. A decrease of the S_w level results in an increase of the resistance R_mat.

• At S_w = S_cr, the capillary pores d ₁ are drained (only thin water film is present). The fully water-filled capillary pores d ₂ become discontinuous. In this case, the interlayer (gel) water in the C–S–H gel is responsible for the ion conduction/diffusion. The resistance R_mat is very high, and the ionic diffusion coefficient is infinitely small.

• At S_w < S_cr, the capillary pores d ₁ are drained, and the capillary pores d ₂ become partially water-filled. The interlayer (gel) water in the C–S–H gel dominates the ion conduction/diffusion. The resistance R_mat is much higher than that in the case of S_w > S_cr. In addition, the increase of the resistance R_mat with decreasing S_w is more pronounced, compared to that in the case of S_w > S_cr.

As indicated in Fig. 8, the increase of the resistance R_mat with decreasing S_w can be categorized into two groups according to the S_w above or below the critical saturation S_cr. Each group tends to present an approximately linear relationship (R_mat vs. S_w). The S_w level corresponding to the intersection of the two lines is estimated as the critical saturation S_cr. On this basis, the critical saturations S_cr are found to be approximately 37, 28 and 22% for the cement mortars with w/c ratios of 0.4, 0.5 and 0.6, respectively. The accuracy of the obtained S_cr-values is expected to be higher in the case when more specimens at low saturation levels (S_w = 18–60%) were prepared for the resistivity measurements.

4 Discussion

4.1 Influence of sample preconditioning on the microstructure of cementitious samples

In order to obtain desired saturation levels, in this study the samples were pre-treated by drying in an oven. This process is a quick method to obtain cementitious samples with less water content. However, oven-drying at a relatively high temperature and the resultant declining RH can affect the thermodynamic stability of the hydration products. As a result, the porosity and associated water saturation S_w inside the preconditioned samples may be influenced.

4.1.1 Effect of temperature on microstructure

The hydration products show different sensitivities to the exposure temperature. Calcium hydroxide (CH) is relatively stable, which decomposes at a temperature higher than 440 °C [36]. The decomposition temperature of the main hydrates, i.e. calcium-silicate-hydrate (C–S–H), is not well established, but it is considered that C–S–H may lose a considerable amount of non-evaporable water at 105 °C [37]. Crack initiation has also been reported at this temperature [38]. The AFm phases, i.e. a family of hydrated calcium aluminates, can be decomposed in a wide range of temperature, i.e. 75–250 °C [39]. The dehydration of gypsum starts at approximately 80 °C [40]. The decomposition of ettringite (AFt) commences at around 60 °C [41].

It is evident that drying at elevated temperatures makes the water loss faster but may result in more severe microstructural alterations. For the hardened cement paste oven-dried at 50 °C after 4 weeks, the pores larger than 8 nm were found to be increased and the pores smaller than 8 nm decreased, while the total pore volume remained unchanged [42]. 50 °C is recommended as the most efficient drying temperature for cementitious materials, because it costs the least time meanwhile the minimum microstructural alterations [43]. Given all these aspects, 50 °C was selected for the oven drying temperature in this work.

4.1.2 Effect of relative humidity on microstructure

The change of interior RH influences various hydrates to different extents. At 25 °C, the monosulfoaluminate (Ms) starts to dehydrate at RH = 97%; its volume is reduced by 8% at RH = 50%, and by 15% when the RH is as low as 8% [44]. Hydroxy-AFm is found until RH = 97%, and it is completely dehydrated from OH19-AFm into OH13-AFm at RH = 83%, and further into OH11-AFm at RH < 23%. The volume of the hydroxy-AFm decreases by around 27% when the interior RH reduces from 97 to 50% [44]. In contrast, the carboaluminate is stable along a wide range of exposure RH conditions (25–97% RH). The AFt phase is very robust against the interior RH, and only one water molecule is lost when the RH drops from 97 to 8% [44].

4.1.3 Evaluation on the change of porosity

The mortar samples were made with a constant cement binder-to-sand ratio (1:3 by weight). The specific gravity was 3.12 × 10³ kg/m³ for the cement and 2.65 × 10³ kg/m³ for the sand. Taking the mortar sample M5 as an example, the volume ratio of the paste matrix over the mortar was estimated as 32.58%. The interior RH of all the preconditioned samples was above 50%, which primarily resulted in the volume of the AFm phases (Ms and OH-AFm) reducing by 8–27%. With the assumption that the solid AFm phases constitute 15% by volume of the paste matrix [45], the interior RH reducing from 100 to 50% would result in the change of porosity of the sample M5 by 15% × 32.58% × (8–27) % = (0.39–1.32) %. This minor porosity change, which has little influence on the water saturation level of the preconditioned sample, was not taken into account in this study.

4.2 Conductivity of pore solution at various saturations

The chloride diffusion coefficients of cement mortars at various water saturations were calculated by using the Nernst–Einstein equation, where the conductivities of the pore solutions, viz. $\sigma_{0}$-values, have to be determined. According to Snyder et al. [46], the $\sigma_{0}$-value is mainly determined by the concentrations of ions, viz. hydroxide (OH⁻) and alkalis (Na⁺, K⁺), in the pore solution.

4.2.1 Ionic concentrations at various saturations

For the cement mortars with w/c ratios of 0.4, 0.5 and 0.6, the pore solutions at S_w = 100% were squeezed out from the 1-year cured saturated mortar specimens. The concentrations of the alkalis (Na⁺, K⁺) in these pore solutions were measured by means of inductively coupled plasma optical emission spectrometry (ICP-OES). The concentration of OH⁻ was considered as equal as the sum of alkalis (Na⁺, K⁺) concentrations [47].

In principle, the alkalis (Na⁺, K⁺) released during cement hydration are either bound by hydrates (mainly C–S–H) or freely present in the pore solution [47]. The relationship between bound and free alkalis is dependent on the mass of C–S–H [48]. At a particular saturation (S_w < 100%), the concentrations of the alkalis (Na⁺, K⁺) can be predicted according to the method developed by Chen and Brouwers [48]:

$$C_{\text{Na}} = \frac{{n_{\text{Na}}^{r} }}{{V_{\text{w}} + Rd \cdot m_{{{\text{C}} - {\text{S}} - {\text{H}}}} }}$$

(11)

$$C_{\text{K}} \cdot V_{\text{w}} + K_{\text{f}} \cdot \left( {C_{\text{K}} } \right)^{0.24} \cdot m_{{{\text{C}} - {\text{S}} - {\text{H}}}} = n_{\text{K}}^{\text{r}}$$

(12)

Various parameters are described as follows:

• (a) ${\text{Rd}}$ is the distribution ratio (${\text{Rd}}$ = 0.45 × 10⁻³ L/g); $K_{\text{f}}$ is the adsorption coefficient ($K_{\text{f}}$ = 0.20 × 10⁻³ L/g); $V_{\text{w}}$ is the volume (L) of the pore solution, which depends on the total porosity and water saturation level of the specimen. The $V_{\text{w}}$-value was determined as 0.0726 L for the mortar specimen M4 (ϕ100 × 50 mm) at S_w = 100%.

• (b) $m_{{{\text{C}} - {\text{S}} - {\text{H}}}}$ is the mass of C–S–H, which is simplified as the composition of C_1.7SH₄ in the OPC mortars. The value of $m_{{{\text{C}} - {\text{S}} - {\text{H}}}}$ was estimated by Thermogravimetric analysis (TGA/DSC) with the assumption that the released water was from the thermal decomposition of C–S–H (105–1100 °C) and CH (400–550 °C) [49]. For the mortar specimen M4, $m_{{{\text{C}} - {\text{S}} - {\text{H}}}}$ was calculated as 100.67 g.

• (c) $C_{\text{Na}}$ and $C_{\text{K}}$ represent the concentrations (mol/L) of alkalis Na⁺ and K⁺, respectively. From the ICP-OES tests, $C_{\text{Na}}$ and $C_{\text{K}}$ for the mortar specimen M4 at S_w = 100% were determined as 0.176 and 0.341 mol/L, respectively.

• (d) $n_{\text{Na}}^{\text{r}}$ and $n_{\text{K}}^{\text{r}}$ refer to the moles of the alkalis, viz. Na⁺ and K⁺, released during cement hydration. Substituting the values of the parameters ($V_{\text{w}}$, $m_{{{\text{C}} - {\text{S}} - {\text{H}}}}$, ${\text{Rd}}$, $C_{\text{Na}}$ and $C_{K}$) at S_w = 100% into Eqs. (11) and (12) allows for determining the values of $n_{\text{Na}}^{\text{r}}$ and $n_{\text{K}}^{\text{r}}$, which were equal to $n_{\text{Na}}^{\text{r}}$ = 0.0207 mol and $n_{\text{K}}^{\text{r}}$ = 0.0403 mol for the mortar specimen M4.

In Eqs. (11) and (12), the parameters ($n_{\text{Na}}^{\text{r}}$, $n_{\text{K}}^{\text{r}}$, $Rd$, $K_{\text{f}}$ and $m_{{{\text{C}} - {\text{S}} - {\text{H}}}}$) are considered to be independent of the water saturation S_w level except the $V_{\text{w}}$-value that is linearly proportional to the S_w level. On this basis, the alkalis concentrations ($C_{\text{Na}}$ and $C_{\text{K}}$) can be determined as a function of the S_w level.

4.2.2 $\sigma_{0}$-values at various saturations

Synthetic solutions were prepared by mixing the solids (NaOH, KOH) with distilled water in proper proportions in accordance to $C_{\text{Na}}$ and $C_{\text{K}}$ at each water saturation level. The conductivities of the pore solution at various saturations, viz. $\sigma_{0}$-values, were obtained through the conductivity measurements performed on these synthetic solutions. Figure 9a presents an example of the calculated ionic concentrations in the mortar M4. Figure 9b shows the measured $\sigma_{0}$-values in the mortars M4, M5 and M6. The conductivity of pore solution, $\sigma_{0}$, is almost two times larger when the water saturation decreases from 100 to 30%.

Fig. 9

a Ionic concentration as a function of water saturation level in the cement mortar M4 (1 year old, w/c = 0.4); b Conductivity $\sigma_{0}$ of pore solution as a function of water saturation level in the cement mortars (1 year old) with w/c ratios of 0.4, 0.5 and 0.6

4.3 Moisture distribution in partially saturated cement mortars

Figure 6 showed that the interior RH strongly depends on the water saturation S_w. At a particular RH, there is a smallest drained pore diameter d _p (d _p  = 2r _p ) by following Eq. (6). The pores below the diameter d _p are filled with water allowing for ionic transport. The d _p –S_w plots are used to describe the moisture distribution in the non-saturated cement mortars.

Based on the d _p -RH relation, the RH–S_w plots (Fig. 6) were transformed into the d _p –S_w plots, as presented in Fig. 10. With a decrease of water saturation S_w the d _p -value shows three-stage change, especially for the specimen at a high w/c ratio, viz. M6. The d _p -value falls off significantly in the high saturation range (e.g. S_w > 60%), whereas decreases much slowly in the low saturation range (e.g. S_w < 60%). A decrease of the w/c ratio results in the d _p -value to drop more rapidly. The d _p –S_w plots of M5 (w/c = 0.5) and M6 (w/c = 0.6) are closer, compared to that of M4 (w/c = 0.4).

Fig. 10

Moisture distribution, i.e. d _p –S_w plots, estimated from the water vapour desorption isotherm tests of cement mortars (1 year old). d _p (d _p  = 2r _p ) is the smallest drained pore diameter determined by Eq. (6)

The decrease of the d _p -value results in a lower amount of the water-filled pores and hence affects the ionic transport. In this respect more details will be given in the following Sects. 4.4 and 4.5.

4.4 Relationship between relative chloride diffusion coefficient and water saturation

4.4.1 Comparison of D _rc–S _w relationship between this study and previous studies

The available data (D_rc vs. S_w) from the literature are also plotted in Fig. 7 for a comparative analysis. Based on the Nernst–Einstein equation and conductivity technique, Olsson et al. [13] determined the D_rc–S_w relations in the cement mortars with w/c ratios of 0.38 and 0.53. Between the study of Olsson et al. and this study, the data are not very different for high saturation S_w levels, whereas disagreements arise for low saturation levels. In contrast to this study, Olsson et al. [13] concluded that the w/c ratio had little effect on the D_rc–S_w relation in the OPC mortars. The different conclusions, drawn from different experimental results, might possibly be ascribed to two aspects: (1) the size and the age of the samples prior to the sample preconditioning procedures were different between the study of Olsson et al. and this study, and (2) the sample preconditioning approaches used were different, i.e. “RH” preconditioning was used by Olsson et al. while “SD” preconditioning was used in this study. Note that it is increasingly difficult for the “RH” preconditioning approach to prepare a sample with lower equilibrium moisture content. Therefore for low saturation levels, the moisture distributions of the samples obtained from the “RH” preconditioning approach may exhibit great differences from those of the samples obtained from the “SD” preconditioning approach.

Besides the OPC binder, three blended binders were also prepared by Olsson et al. [13] to study the ionic diffusion under non-saturated state. The topic on the effect of various blended materials on the D_rc–S_w relation is beyond the scope of this work. The details will be discussed in a separate paper.

The values of critical saturation S_cr from the literature are compared with those derived in this study. Martys [50] simulated the non-saturated ionic diffusion in wetting fluid by means of lattice Boltzmann method. He found that a connected water-filled path can be formed allowing for ionic diffusion only when the water saturation was above 0.33. Based on the diffusion tests, de Vera et al. [51] measured the chloride diffusion coefficients of the cement concretes with interior RH of 54, 75, 86 and > 95%. It was found that a lower w/c ratio resulted in a higher S_cr-value, a similar trend as presented in this study. On the other hand, de Vera et al. [51] reported critical saturations S_cr = 0.4 and S_cr = 0.33 for the cement concretes with w/c = 0.5 and w/c = 0.6, respectively. The S_cr-values from de Vera et al. are higher than those derived in this study. This possibly results from the fact that de Vera et al. applied the “RH” preconditioning approach to prepare concrete samples, while in this study the “SD” preconditioning approach was used to prepare mortar samples.

4.4.2 D _rc –S _w relationship and moisture distribution

Figure 7 has shown that the relative chloride diffusion coefficient D_rc is highly dependent on the degree of water saturation S_w. The decrease of the D_rc-value with decreasing S_w can be ascribed primarily to three aspects: (1) the amount of water available for the chloride diffusion is less; (2) the number of transport channels, where continuous water-filled paths are present, becomes less; (3) the interaction forces between chloride ions and cement paste are increased due to the decreased thickness of the water layers adsorbed on the pore walls [52].

The three aspects mentioned above are, in essence, related to the moisture state in the pores. In a partially saturated porous system, there are three typical moisture states in a pore: saturated, partially saturated or drained (only adsorbed water film is present). It is sensible to assume that the saturated pores play a major role in the ionic transport. The moisture state in the entire capillary pores, i.e. moisture distribution, governs the relationship between D_rc and S_w.

For the sake of describing the moisture distribution, two pore parameters are introduced: threshold diameter and critical diameter [53]. Both are the key parameters influencing the pore connectivity. The threshold diameter (d_th) corresponds to the pore size, above which there is comparably little mercury intrusion, immediately below which significantly intruded mercury is detected. The critical diameter (d_cr) corresponds to the pore size, at which the mercury can fill the bulk of the specimen. Based on the pore size distribution obtained from the MIP test, the pore size can be categorized into three groups (Fig. 11): (1) macro pores, with diameter d > d_th; (2) meso pores, d_th ≥ d ≥ d_cr; (3) micro pores, d < d_cr.

Fig. 11

Illustration of three pore size groups based on the pore size distribution of cement paste (1 year old, w/c = 0.5) obtained from the MIP test. d_th and d_cr refer to threshold diameter and critical diameter, respectively

The macro pores refer to the large void space present in the surface specimen, which will be filled with mercury at the beginning of the MIP test. When a threshold pressure corresponding to the threshold diameter d_th is applied, the mercury starts to fill the small void space present in the surface specimen and penetrate rapidly into the specimen with increasing pressure. Once the critical pores (diameter d_cr) are filled, a connected pore network forms and the mercury fills the bulk specimen. The meso pores, which are in the size range between d_th and d_cr, control the percolation of the pore structure, and they represent the void space within the clusters of the loosely packed hydrates. With further increase of the applied pressure the mercury penetrates the micro pores, which account for the void space within the clusters of the densely packed hydrates.

On basis of the mercury penetration in the microstructure of hydrated cementitious system, a simple pore network as shown in Fig. 12 can be extracted. The micro pores and macro pores are both connected through the meso pores. When the pore system is partially saturated, the meso pores provide the main pathways for moisture transfer, and the moisture loss in meso pores will significantly influence the continuity of water-filled pores. According to the Kelvin law, with a decrease of water saturation the water in the pore network gradually loses from the macro pores to the micro pores. Water loses in a pore until the pore is only adsorbed with a thin water film [29]. Impedance spectroscopy measurements, conducted by Sánchez et al. [54], confirmed that all the pores kept at least a thin layer of electrolyte covering their walls, regardless of the saturation levels (S_w = 18–100%).

Fig. 12

Schematic representations of the moisture distribution and ionic diffusion in the pore network with decreasing water saturation level

The three-stage D_rc–S_w relationship (see Fig. 7) can be explained by the three-stage change of the moisture state in the meso pores (see Fig. 12):

• Stage I All the meso pores are saturated. When the S_w starts to decrease from fully saturated state, the macro pores lose water. The main pathways for ionic diffusion, viz. meso pores, remain filled with water. The D_rc-value is not much influenced and quite close to that in the saturated condition.

• Stage II With further decrease of the S_w level, the meso pores start to lose water and become partially saturated. In the meantime the meso pores are gradually occupied with the gas phase, which can hinder the ionic diffusion to a great extent. As a result, the D_rc-value drops rapidly.

• Stage III Once the S_w is lower than a certain level, nearly all the meso pores are drained but only adsorbed with the nano-scale layers, which are composed of water molecules and chemical compounds, e.g. Ca(OH)₂. In this stage, the water loss commences in the micro pores. The ionic diffusion tends to be quite slow and the D_rc-value decreases less obviously.

4.5 Role of w / c ratio in relative chloride diffusion coefficient

The role of the w/c ratio in the D_rc–S_w relation is a result of its effect on the moisture distribution in the pore structure. The moisture distribution, in essence, determines the number of transport channels, where the water-filled pores are connected and ionic diffusion can take place. At a particular water saturation S_w, the amount of water-filled pores and their continuity can be altered with varying w/c ratios. The term water continuity is introduced to quantify the effect of moisture distribution on the number of transport channels.

4.5.1 Definition of water continuity

The water continuity $\eta_{\text{w}}$ indicates the continuity of water-filled pores in a porous system. A channel that consists of continuous water-filled pores allows for ionic transport. The water continuity is expressed as: $\eta_{\text{w}} = N_{\text{w}} /N_{\text{Sat}}$, where $N_{\text{w}}$ and $N_{\text{Sat}}$ represent the number of transport channels available for ionic transport when the porous system is at a particular water saturation level and at saturated state, respectively. At saturated state, all the connected pores are filled with water allowing for ionic transport, i.e. $N_{\text{w}}$ = $N_{\text{Sat}}$ and $\eta_{\text{w}}$ = 1. A decrease of the water saturation leads to a decrease of the $N_{\text{w}}$-value and hence a decrease of the $\eta_{\text{w}}$-value. When the water saturation is lower than a critical level, there is no continuous water-filled path allowing for ionic transport, i.e. $N_{\text{w}}$ = 0 and $\eta_{\text{w}}$ = 0. A decrease of the water continuity $\eta_{\text{w}}$ results in a decrease of the relative chloride diffusion coefficient D_rc.

4.5.2 Role of w/c ratio in water continuity

The role of the w/c ratio in water continuity can be evaluated by two different ways. One way is based on the water vapour desorption isotherm (i.e. d _p –S_w plots, see Fig. 10), and the other way is based on the pore connectivity of the specimen.

In partially saturated specimens, the transport channels are constituted mainly by the water-filled pores (with diameter d ≤ d _p ). A decrease of the water saturation S_w results in a decrease of the d _p -value. For the cement mortar with a lower w/c ratio, the d _p -value decreases more rapidly with the decreasing water saturation (see Fig. 10). In principle, a greater decrease in the d _p -value leads to a greater decrease in the number of transport channels ($N_{\text{w}}$-value). It is considered, therefore, that at the same water saturation level the water continuity $\eta_{\text{w}}$ and associated D_rc-value can be smallest in the mortar M4, followed by M5 and M6 in a larger order. The closer d _p –S_w plots of M5 and M6, as seen from Fig. 10, provide an evidence for their similar $\eta_{\text{w}}$-values. All these are in good agreement with the D_rc–S_w relations shown in Fig. 7.

Alternatively, the water continuity $\eta_{\text{w}}$ is evaluated from the pore connectivity point of view. With declining water saturation S_w, the continuity $\eta_{\text{w}}$ of water-filled pores will be less severely influenced in the specimen with higher pore connectivity [55]. In this work the pore connectivity was estimated from the MIP tests, and it was determined as 44.2, 56.5 and 62.5% for the cement pastes with w/c ratios of 0.4, 0.5 and 0.6, respectively. Obviously, the pore connectivities at w/c = 0.5 and w/c = 0.6 differ a little, but both are much higher than the pore connectivity at w/c = 0.4. In this sense, for a given saturation S_w level, the water continuities $\eta_{\text{w}}$ between M5 and M6 are more similar but both are much higher than that of M4. This provides a further evidence for the role of the w/c ratio in the D_rc–S_w relations as presented in Fig. 7.

5 Conclusions

From the findings of this study, the following main conclusions can be drawn:

• 1. At a particular degree of water saturation S_w, the cement mortar with a higher w/c ratio shows a higher RH level. In the range of 50–90% RH, linear RH–S_w relationships are observed for all the w/c ratios of 0.4, 0.5 and 0.6.

• 2. The change of relative chloride diffusion coefficient D_rc with decreasing saturation S_w level can be divided into three stages, i.e. a slight decrease (stage I), a sharp drop (stage II) and another slight decline (stage III).

• 3. The w/c ratio plays an important role in both water vapour desorption isotherm and D_rc–S_w relationship. This indicates that the D_rc in unsaturated cementitious material strongly depends on the microstructure of the material. At a particular water saturation S_w, the D_rc is larger for a higher w/c ratio. However, the role of the w/c ratio in the D_rc–S_w relation becomes less pronounced with increasing w/c ratio.

• 4. There exists a critical saturation level, below which the water-filled capillary pores are unable to form a continuous path to allow for ionic diffusion. The w/c ratio has a great influence on the critical saturation. The critical saturation levels for the 370-day OPC mortars with w/c ratios of 0.4, 0.5 and 0.6 are found to be 37, 28 and 22%, respectively.

• 5. A finer pore size distribution or lower pore connectivity tends to result in a smaller relative chloride diffusion coefficient D_rc.