1 Introduction

Roads paved using asphalt mixtures based on soft bitumens (graded by viscosity at 60 °C), constitutes a relatively large and important part of the low-volume road network in Sweden and other northern countries: more than 10,000 km in Sweden [1]. The deterioration of such soft bitumen pavements are, in contrast to the more familiar penetration grade bitumen on high-volume roads, primarily the result of climatic factors, including uneven deformations due to frost heave and thawing, and low-temperature cracking. Consequently, flexibility to withstand deformations and temperature fluctuations represent a highly desired rheological property of both the binder and the final pavement. At the same time, there is a balance between flexibility and providing sufficient stiffness to carry traffic. While technical quality is of great importance, it is also desirable to continuously increase the sustainability of the asphalt industry by providing incentives and means to manufacturing asphalt mixtures and pavement layers using ever higher amounts of reclaimed asphalt pavement materials (RAP).

Since it is well-known that RAP shows dramatic effect on binder and mixture viscosity, due to the often stiff and oxidized bitumen, it is of interest to investigate and quantify this effect on the technical quality of asphalt paving materials based on soft bitumen. Among the questions often referred to in the industry is whether RAP is too oxidized and stiff to be incorporated at elevated ratios as it is feared that either a too stiff asphalt concrete or insufficient mixing of the old and new bitumen, is obtained. One way of reducing the risk of the asphalt being too stiff is to use a softer binder, than required for the final mix, when using elevated ratios of recycled asphalt.

The mixing of old and new virgin binder is complex but can conceptually be described to be largely governed by three factors: (1) distribution (i.e., how the added binder is physically distributed), (2) mechanical mixing and (3) diffusion. While the two first factors probably occur almost instantaneously during asphalt mixing, diffusion represents a time-dependent process affected by material properties, temperature and binder layer thicknesses.

The main purpose of the current study is to investigate whether RAP can be utilized in soft bitumen asphalt mixtures in such a way that the mixture produced exhibits similar mechanical properties as a corresponding pavement produced using virgin materials. In particular, three questions are investigated:

  • will old binder from the RAP and new virgin binder mix?

  • how rapidly will the mixing occur?

  • can the mechanical properties of the mixed binder be predicted?

In order to investigate these questions, the present study comprises laboratory testing on mixtures of different soft bitumens and recovered binder from RAP, and asphalt mixtures using recycled and virgin materials. Pure binder testing include viscosity and diffusion rate and asphalt concrete is characterized by stiffness modulus and resistance to permanent deformation. It was deemed important that testing on pure binder model systems is supported by measurements on asphalt concrete.

Basic binder mixability (old and new) is studied on pure binder systems. In these cases it is assumed that full mixing is achieved by mechanical mixing and the results are compared and fitted to well-known mixing models. The hypothesis in this case is that the binders can be mixed and if results concur with the mixing models this is a strong indication that the binders are mixed by mechanical mixing. In addition, diffusion experiments are performed with the intent of studying if there actually is a diffusion process and if steady-state rheology concurs with predictions based on mechanical mixing.

In addition to pure binder model systems, we design an experimental plan to support these findings by testing asphalt concrete samples. RAP and virgin binder mixing dynamics in asphalt mixtures is a complex matter and inherently difficult to study in minute detail without introducing artefacts and creating simplified and artificial model systems. In this study we chose an indirect way to investigate if soft bitumen asphalt could be produced using RAP and virgin material. If the mixtures made from RAP and virgin material show similar mechanical behavior as the virgin material only Reference mixture, this suggests that the binders actually do mix, at least from a macro-mechanical point of view. Furthermore, by studying development by time we can make inferences on when the mixtures have reached steady-state i.e., indicate whether there is a time-dependent mixing that could be due to diffusion.

To summarize the experimental plan:

  • study binder mixing and diffusion on pure binder systems

  • based on the binder results (mixing models) design asphalt mixtures with predicted similar mechanical behavior using virgin material only mixtures and mixtures containing calculated amounts of RAP.

Based on results and analysis we make step-wise inferences regarding mixability, adding a practical perspective e.g., we might see statistical differences that are too small to have any large influence on asphalt production.

2 Previous findings

In general, there are many previous studies concerning viscosity and diffusion of binary liquids. However, when it comes to road construction materials, bitumen and asphalt mixtures, the number of publications is more limited, especially concerning diffusion. One of the key issues when mixing liquids is to predict (i.e., modelling) the rheology. In practical road construction that commonly means viscosity of virgin bitumen mixed with old RAP-binder. In the case of asphalt concrete manufacturing using recycled asphalt, the main issue concerns admixing soft virgin bitumen, or rejuvenators of even lower viscosity. Although, a clear distinction between these two soft liquids is difficult to make, since both normally are oil derivatives, the common denominator is that they should counteract the stiffening effect from the RAP-binder in order to have a final asphalt mixture with rheology corresponding to a given virgin asphalt mixture.

In many cases, and for practical purposes, the viscosity of bituminous (or bitumen-like) binder mixtures can be predicted using relatively simple models. Some of the more recent findings can be noted. Chen et al. [2] defined a model based on Arrhenius (c.f. Sect. 3.1.1 below) but with an additional interaction term added (i.e., comparable to the model suggested by Grunberg–Nissan, 1948) and noted that, with the exception of admixed fuel oil, the model was able to predict viscosities. In addition, Lin et al. [3] showed that a mixture of aged bitumen and synthetic rejuvenator can deviate considerably from predictions using Arrhenius-based models. Technical specifications, e.g., ASTM D4487 [4] and Swedish Transport Administration [5] are commonly based on simple ratios. Generalizing previous findings, mixing of bitumens can be predicted with reasonable accuracy using simple fraction based models, the more different the two liquids are, the larger deviation from a strictly fraction based model.

The rationale for the common restrictive use of RAP in asphalt mixtures is often based on the difficulty of characterizing any relationship between RAP and virgin binder added and final mixture characteristics. Further complexity has been added to the question by a phenomenon commonly referred to as black rock [6], which conceptually illustrate severely aged, hard and inert binders that hardly mix with virgin binder; the binder part of recycled material does not mix with virgin binder and added RAP is considered merely as aggregate. A number of studies have been performed on this issue of which a few are summarized here to serve as illustration of the complexity of the issue and heterogeneity of findings. McDaniel et al. [7] reach the conclusion, based on an elaborate laboratory campaign, that RAP does not act as black rock and binder properties can be estimated using mixing charts. Several other studies have indicated that mixing of old and new bitumen generally is good. Chen et al. [2] also offers support to the conclusion by McDaniels et al. [7] i.e., new and old binder do mix. On the other hand, Oliver [8] found indications of incomplete mixing; he noted a softer response for the asphalt concrete based on virgin material and RAP, than for the virgin binder only mix.

Diffusion of bituminous binders has been studied to some extent. Oliver [9] tried to improve the performance of oxidized pavements by treating the surface with a thin layer of new binder, or oil that with time would mix with the aged binder by diffusion. A conclusion from the study was that the process takes relatively long time, probably months, without mechanical mixing. Later studies, e.g., Carpenter and Wolosick [10] and Huang et al. [11] performed stagewise binder extraction from rejuvenated asphalt mixtures, the hypothesis being that subsequent solvent extraction will uniformly and stepwise solve the binder film inwards. In both of these investigations, they found increasing stiffness by increasing stages thus indicating incomplete mixing of the softer binder in the outer layer and the old recycled inner binder layer. More recently, to reduce the influence of procedural artefacts during stage extraction, Zhao et al. [12] performed a number of experiments using various solvents. They concluded that the stage extraction technique provides reliable information regarding virgin and recycled binder mixing. They also concluded that, after a rapid asphalt mixing procedure, there is a binder stiffness gradient through the binder film. Karlsson and Isacsson [13–15] studied diffusion processes in binary mixtures of aged bitumen and soft additives using infra-red spectroscopy. They concluded that there is diffusion and it can be characterized using Fick’s law where the rate of diffusion was strongly temperature dependent but only marginally affected by the degree of aging for a given binder.

To study diffusion processes in asphalt concrete appears more complex than the study of binder-only mixtures. In order to calculate the time for the binders to reach steady-state, i.e., full mixing, during a simulated plant process, Zaumanis and Mallick [16] defined a numerical model of the diffusion process. The main conclusion was that at a specific temperature (145 °C) a steady-state could be reached within 1 min of plant mixing, depending on rejuvenator type. However, no empirical support for the results or the validity of the model is provided. Mallick et al. [17] used a similar model to estimate mixing of rejuvenators and RAP during in situ paving operations (remixing). In their study it was concluded that diffusion is strongly temperature-dependent and that only limited diffusion occurs below 100 °C. This last study also comprised empirical investigations on laboratory samples: rejuvenator was mixed into aged asphalt material where after the stiffness increase by time was analyzed. The results showed that the stiffness continuously increased during the 65 days investigated: between 35 and 100 % depending on sample manufacturing temperature (between 90 and 150 °C). The specimens were stored at 60 °C. Hence, the laboratory results indicate diffusion processes below the 100 °C concluded from the numerical study.

3 Experimental

Laboratory work was performed on pure binders to investigate mixing and diffusion. These results were subsequently used to design asphalt mixtures using RAP and a softer grade bitumen in which the predicted all-binder viscosity is equal to the virgin reference bitumen viscosity.

3.1 Binder

The binder viscosity testing was performed using a rotational viscometer (Brookfield). Diffusion rates were determined based on rheological testing of a two-layered system: recovered binder from RAP and virgin soft bitumen.

Three types of soft bitumens were used [18]:

  • V1500

  • V3000

  • V6000

denoted by nominal kinematic viscosity (mm2/s, capillary method) at 60 °C. RAP was obtained from a local pile and binder was reclaimed for further testing: penetration at 25 °C was 21 dmm and softening point 64.2 °C.

3.1.1 Viscosity

The viscosity of the binders (virgin, RAP and mixtures) were measured by rotational viscosimetry (Brookfield). The testing was performed at three temperatures: 60, 80 and 100 °C, and at six different mixing ratios: 0, 20, 40, 60, 80 and 100 % binder from RAP.

In general, viscosity is not independent of test parameters such as temperature and shear rate. To simplify analysis, we want to reduce the shear rate dependence. In order to establish a common basis for viscosity comparison, testing can either be performed at the same constant shear rate or in the so-called Newtonian state, where viscosity is independent of shear rate. The binders covered by the investigation exhibits a very wide range of viscosities and the capacity of the instrument does not allow for testing at a single shear rate because of rate and torque limitations. Hence, measures to normalize and reduce procedural influence were undertaken. Viscosity testing was performed at three torque levels within the range of the equipment: around 5, 50 and 75 % of maximum capacity. Thereafter, a reference viscosity was calculated according to three different models: linear extrapolation to zero shear viscosity (η zero), mean of measurements (η mean), and slope of the shear stress vs shear rate (η slope). The three different models were analyzed to reduce any bias possibly induced by the testing circumstances.

The primary purpose of determining the viscosity is to establish a specific model to predict the viscosity of bitumen mixtures. In this case, the most basic binary model was used by Arrhenius [19]:

$$ \eta = A^{x} \cdot B^{y} $$
(1)

where η is the mixture viscosity, A and B is the viscosity of each component, and, finally, x and y their relative amount, respectively. Although this model provides adequate predictions in many cases, the model can be insufficient in other cases where some kind of interaction between the two fluids can be observed. Accordingly, Grunberg and Nissan [20] suggested an extension of Arrhenius’ model:

$$ \log \eta_{s} = N_{1} \log \eta_{1} + N_{2} \log \eta_{2} + N_{1} N_{2} d $$
(2)

where η s is mixture viscosity, η 1 and η 2 the viscosity of each component and N 1 and N 2 their relative amount, respectively. The factor d is a mixture specific constant taking any interaction between the components into account.

For more complex mixtures, adequate descriptions may need even more elaborated models. However, in the current study it is argued that sufficient adequacy is obtained using the model proposed by Grunberg and Nissan. Figure 1 shows typical results fitted to the two models, respectively.

Fig. 1
figure 1

Viscosity mixing models: typical results and fitted models (V1500 at 60 °C, each point represents one mixture i.e., six mixtures in total)

Full size image

3.1.2 Diffusion

In the case of asphalt mixing, it is possible to distinguish between two main modes of binder mixing: (1) mechanical mixing and (2) diffusion. In the case that mixing extends after the immediate mechanical mixing is discontinued, the process probably involves diffusion. This second process depends on concentration differences between the two fluids.

Diffusion caused by concentration differences between the two fluids can be characterized using Fick’s (second) law [21]:

$$ \frac{\partial y}{\partial t} = - k\frac{{\partial^{2} y}}{{\partial x^{2} }} $$
(3)

where y is concentration, t is time, k is the diffusion coefficient and x is length. The left-hand side of the equation represents the change in concentration with time which is a function of the concentration gradient and the diffusion coefficient.

The main testing and analysis procedure has been described elsewhere [22] but specific details are given below. In essence, the measurement of rate of diffusion is based on complex shear modulus testing for a two-layer system (virgin binder and bitumen recovered from RAP). The test geometry was parallel plates with a diameter of 25 mm and the total sample thickness was approximately 0.75 mm. For practical reasons and increased testing resolution, the upper 2/3 contained binder from recycled asphalt while the remaining 1/3 was virgin soft bitumen. Diffusion measurements were performed at 60, 80 and 100 °C.

The assumption is that, when the parallel plates are brought in contact, the two discrete layers start to mix mainly by diffusion. Rheological measurements were performed at 10 rad/s and intermittently at increasing time intervals. Dynamic viscosity (η′) is obtained as:

$$ \eta^{\prime} = \frac{{G^{\prime\prime}}}{\omega } $$
(4)

where G″ is loss modulus and ω is angular velocity.

At the onset of testing, the composite sample consists of two distinct layers: one stiff and one soft. The apparent viscosity (η meas) of this two-phase system is mainly determined by the softer binder. However, with time, as the diffusion process progresses, the mixing causes a successively higher viscosity. The increase in viscosity can be characterized using Fick’s law, and suitable boundary conditions, and a mixing model for viscosity. Figure 2 illustrates some of the basic definitions for two binders (A, B).

Fig. 2
figure 2

Conceptual description of geometry and coordinate system for diffusion analysis >L thickness, x distance, ∝ relative amount of A

Full size image

Diffusion in terms of concentration (c) can be determined by solving Eq. 3 (Fick’s law) and three boundary conditions [15]:

$$ c(x,t) = (1 - \alpha )c_{0} - \frac{{2c_{0} }}{\pi }\sum\limits_{n = 1}^{\infty } {\frac{\sin (\alpha n\pi )}{n}} \cos \left( {\frac{xn\pi }{L}} \right)e^{{ - \left( {\frac{n\pi }{L}} \right)^{2} Dt}} $$
(5)

where the concentration (c) of binder B is a function of height (x) and time (t) and:

  • α is relative amount of binder A

  • L is total sample thickness

  • n is number of elements in the Fourier series (in this case 20)

  • D is the diffusion coefficient.

The estimated maximum relative error of α is 5 % and approximately 1 % regarding thickness.

Figure 3 illustrates a mixing process according to Eq. 5 at a temperature of 100 °C.

Fig. 3
figure 3

Illustration of diffusion during testing (100 °C). Black color indicates stiff RAP binder while white indicates virgin soft bitumen

Full size image

As indicated in the figure, at time 0 the sample constitutes two separate layers, while mixing can be observed after 1 min. After 30 min the entire virgin binder has been affected by the diffusion process. According to the model, the two binders have essentially been completely mixed after 2 h.

However, Fig. 3 only concerns concentration, while what actually is measured during the experiment is apparent viscosity. Assuming an Arrhenius-type model, the mixture viscosity (η mix) is obtained as:

$$ \eta_{\text{mix}} = \frac{{\eta_{A}^{\alpha } \eta_{B} }}{{\eta_{B}^{\alpha } }} $$
(6)

where η A and η B is viscosity for binder A and B, respectively, and α is fraction of binder A.

In order to numerically analyze the sample illustrated in Fig. 2, the sample is theoretically divided into 25 layers of equal thickness (approximately 30 µm). In addition, the shear stress (τ) is assumed constant throughout all of the 25 layers. The shear strain of the sample (γ) (or each of the theoretical layers), is obtained as:

$$ \gamma = \frac{\tau }{{\eta_{\text{mix}} }} $$
(7)

What is measured during testing is the total displacement (d tot), which is the sum of all displacements in the 25 layers:

$$ d_{\text{tot}} = \sum\limits_{i = 1}^{25} {\gamma_{i} L_{i} } $$
(8)

where γ i is shear strain of an individual layer and L i the corresponding thickness.

Furthermore, the total displacement (d tot) corresponds to the product of measured strain (γ tot) and total sample thickness L:

$$ d_{tot} = \gamma_{tot} \cdot L $$
(9)

By combining Eqs. 8 and 9 we get:

$$ \gamma_{\text{tot}} \cdot L = \sum\limits_{i = 1}^{25} {\gamma_{i} L_{i} } $$
(10)

The shear strains (γ tot and γ i ) in Eq. 10 are substituted with the strain of the entire sample and the individual layers according to Eq. 7 and the final equation for sample viscosity (η app) becomes:

$$ \eta_{\text{app}} = \frac{{L\eta_{B} }}{{\sum\limits_{i = 1}^{25} {\left( {\frac{{\eta_{B} }}{{\eta_{A} }}} \right)^{{c(x_{i} ,t)}} \cdot L_{i} } }} $$
(11)

For every layer (i) and at each time (t) the concentration c(x i , t) is calculated, according to Eq. 5.

In order to compensate for the unknown absolute viscosity, due to inability to accurately measure sample geometry during testing, the nonlinear optimization is based on the relative increase (compared to the initial measurement) in viscosity. The fit is achieved by relating the calculated relative viscosity (η app) to the measurement (η meas) as indicated in Fig. 4

Fig. 4
figure 4

Fit of measurement data to model according to Eq. 11 (V1500 and RAP binder at 80 °C)

Full size image

One test per virgin binder (V1500, V3000) and temperature was carried out. At the termination of each test the mixed sample was adjusted to a known geometry whereafter the absolute viscosity was determined.

3.2 Asphalt concrete

In addition to the binder evaluation, tests on laboratory-manufactured asphalt concrete samples were carried out to estimate the degree of binder mixing by studying mechanical properties and their development with time. RAP-mixtures were designed to show similar response compared to a Reference mixture, by using a softer grade bitumen compared to the required grade. In addition to this, mixtures just adding RAP were investigated to add information on the general effect of using RAP in soft bitumen asphalt production.

In order to provide a more general view of the mixing process, measurements were performed at two different rheological states: a relatively rapid excitation at low temperature and a slower excitation at elevated temperature. The test methods chosen in the study do not necessarily correspond to what is utilized in practice for this particular mixture type, they are mainly used to indicate the influence of soft and hard binders on asphalt mixtures: e.g., resistance to permanent deformation is not necessarily an important feature of this pavement type but the testing represents a rheological state used to indicate binder mixing dynamics.

3.2.1 Asphalt mixture

Altogether testing comprised five different mixtures. The basic idea was to investigate the effect of mixing virgin and recycled material compared to a reference material, asphalt concrete using only virgin soft bitumen (V6000) and aggregates. Using softer binder than required for the final mix, the amount of RAP that could be added so that fully mixed binders equaled V6000 in terms of viscosity, was calculated. The amounts of RAP were determined based on Arrhenius` model. In addition two mixtures were manufactured where 20 and 40 % RAP, respectively, was added to the reference mixture. The complete schedule is summarized in Table 1.

Table 1 Pavement materials: proportions and predicted binder viscosity
Full size table

All pavement materials investigated had a nominal binder content of 4.0 % by weight. The nominal aggregate size distributions are given in Fig. 5. As indicated in the figure, only minor deviations could be noted between the different materials.

Fig. 5
figure 5

Aggregate size distribution of pavement materials investigated (mixture types in order at 0.063 mm)

Full size image

Prior to mixing all materials were pre-heated to 100 °C for about 4 h. Mixing and subsequent compaction was performed at 100 °C and within approximately 1 h. The asphalt concrete samples were manufactured using the traditional Marshall procedure.

3.2.2 Stiffness modulus

The fast-load testing was obtained by indirect tensile stiffness modulus testing at 5 °C (basically according to EN 12697-26 [23], annex c). The specimens had a diameter of 100 mm and a thickness of around 60 mm. The length of loading was 250 ms (124 ms rise time) and the applied force was chosen so the total sample deformation would be close to 5 µm.

One of the most critical aspects of the test schedule was to perform measurements at specified times. Each sample tested was manufactured on the afternoon day 0. After ambient cooling, approximately 1 h, the sample was placed in a climate chamber at 5 °C to be tested the following day. The first test was conducted after slightly less than 24 h.

The experimental schedule was formed in such a way that the samples were tested after 1, 2, 4, 7, 16 and, as shortest, 38 days. Between tests, the samples were stored at 20 °C until the day before the actual test and then conditioned at 5 °C during night. Each test series consisted of 4 samples.

3.2.3 Accumulated deformation

The performance of the pavement material during repetitive loading was investigated using uniaxial cyclic creep testing (basically according to EN 12697-25 [24] method A). However, some deviations from the standard procedure were applied: the sample size was chosen to be 100 mm in diameter and testing temperature was 20 °C. The loading was applied by a 100 mm diameter plate, 1 s square-shaped pulse (100 kPa) followed by 1 s unloading. The performance of the material was evaluated by measuring the vertical deformation of the sample with number of load applications.

Sample manufacturing and storage were similar to that of the stiffness testing with the exception that both testing and storage temperature was 20 °C. Measurements were carried out after 1, 2, 4, 7, 17 and 30 days and comprised two samples per occasion and mixture series.

4 Results and analysis

In the statistical analysis, the chosen level of significance (α) is 5 %, i.e., the null hypothesis is rejected if p < 0.05.

4.1 Binder

4.1.1 Viscosity

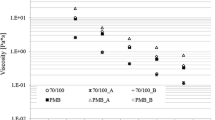
The viscosity was measured at three temperatures using rotational viscometry. In order to obtain comparable results, the viscosity was evaluated using three different approaches. Figure 6 summarizes the results from the virgin binders and recovered RAP binder. For each of the 4 binders, the figure also indicates the effect of the three different models to determine viscosities (η mean , η zero , η slope) previously described: all of the calculated viscosities are given in Fig. 6.

Fig. 6
figure 6

Viscosity for the different binders and methods used to determine viscosity (η mean, η zero, η slope)

Full size image

Concerning the three different viscosity models, it can be noted in Fig. 6, that there are visual differences only for V6000. To further examine any differences, means and standard deviations of the logarithm of viscosity were calculated. The determined coefficient of variance was generally very low, around 1 %, and in no case larger than 4 %. In conclusion, this indicates that there is only minor variance due to algorithmical differences. This, in turn, implies that the viscosity measurements are fairly insensitive to shear rate differences within the range used. It seems viscosities are comparable even within the very broad range of viscosities measured (nearly a factor 20,000). In the remaining part, the analysis is based on zero-shear viscosity (η zero).

We can now proceed to analyze mixtures of virgin and recycled binder and evaluate the different mixing models. As previously described, each soft bitumen was tested at five different levels of recycled binder admixing and measurements were performed at three temperatures. Obtained results were fitted to the two mixing models: Arrhenius and Grunberg–Nissan. In Fig. 7, results are summarized as predicted viscosity versus measured. For reference, the line of equality, 1:1, is also shown.

Fig. 7
figure 7

Comparison between predicted, using Arrhenius’ and Grunberg–Nissan’s models, and measured viscosities for all mixtures studied

Full size image

Both models provide, at least visually, fair predictions. A statistical analysis based on extra-sum-of-squares was performed. The basis of this procedure is to estimate whether the extra parameter (the interaction) provides a statistically significant improvement in describing the data. Table 2 summarize d-values determined for the different combinations and also indicate statistical significance of the interaction parameter.

Table 2 Grunberg–Nissan interaction (d) for the different bitumens and temperatures (italicized indicates statistical significance)
Full size table

From Table 2, it can be observed that in most cases there is a significant interaction and that d is negative in all cases.

4.1.2 Diffusion

The diffusion coefficient of the different binary binder combinations were obtained from testing of a two-layer system in a dynamic shear rheometer and the determined diffusion coefficients are given in Fig. 8

Fig. 8
figure 8

Diffusion coefficient as a function of temperature. For reference, results from a previous study are also given [22]

Full size image

The diffusion experiments lasted for about 5 h at 100 °C and slightly more than 2 days at 60 °C. Given prevailing measurement and calculation uncertainties, all results are considered as coherent and there does not appear to be any large differences between the bitumens investigated. The logarithm of the diffusion coefficient seems to be a linear function of temperature: the diffusion rate is doubled every 6th °C.

The diffusion experiments did not allow for a strict control of sample geometry during the actual testing. However, at the end of the test sequence sample geometry was adjusted and a viscosity measurement could be performed. To estimate whether the two binders had fully mixed by diffusion, the final viscosity measurement can be compared to predictions based on the previously fitted mixing models (Arrhenius and Grunberg–Nissan). The excitation during dsr testing was, in contrast to the rotational viscometry previous utilized, applied sinusoidally. Cox-Merz rule [25] provides a comparison among different test modes where viscosity from rotational viscometry is equal to the norm of complex viscosity |η*| obtained from dynamic modulus testing, if the shear rate is equal to the corresponding angular frequency. This empirical rule was used in the current study to compare the final viscosity of the diffusion tests to estimates from the mixing models. A measure of the conformity (∆) between diffusion results and rotational predictions is defined as:

$$ \Delta = \frac{{\eta_{\text{dsr}} - \bar{\eta }_{{{\text{Arrhenius}}\_{\text{G - N}}}} }}{{\eta_{\text{Arrhenius}} - \eta_{\text{G - N}} }} $$
(12)

where η dsr is viscosity obtained from shear rheometry measurements, \( \bar{\eta }_{{{\text{Arrhenius}}\_{\text{G - N}}}} \) is the mean value of predictions according to the two mixing models, and η Arrhenius and η G-N are predicted viscosity from each model. A ∆-value between −1 and 1 means that the difference between the two modes of testing is smaller than the difference between predicted viscosities according to the two mixing models. Table 3 summarizes the results from the shear rheometer testing and predicted rotational viscosity from previously given mixing models.

Table 3 Comparison between measured viscosity from dsr and predicted according to each mixing model (Pas)
Full size table

In each case, except for V1500 at 60 °C, the difference between oscillating sinusoidal and continuous rotational loading was smaller than between predictions from the two models. This indicates that the final viscosity of the diffusion investigation largely agrees with the results from the tests of mechanically mixed samples, which in turn suggests that the two layers tested actually mix by diffusion and that the mixing process, in the end, has been completed. However, some caution is advised since the empirical evidence is limited. No obvious explanation to the apparent anomaly for V1500 at 60 °C could be found.

4.2 Asphalt concrete

The basic methodology was to add RAP to the asphalt mixture and measure mechanical response as a function of time. Achieved results are analyzed in relation to what could be expected from the binder evaluation. Furthermore, evolution over time is studied, the hypothesis being that if we can determine a stiffening trend the binders were incompletely mixed at the onset of mechanical testing.

4.2.1 Stiffness modulus

Stiffness modulus at 5 °C is summarized in Fig. 9 as a function of time after specimen manufacturing. Results are mainly given as mean values but to visualize typical sample variance, individual results for the stiffest mixture is included. The relative variance is similar for the other mixtures.

Fig. 9
figure 9

Stiffness modulus (mean values, 5 °C and loading time 0.25 s) as function of time after sample manufacturing for each asphalt concrete studied. For the stiffest mixture (40 % RAP) individual test results are given to indicate sample variability (note the logarithmic y-scale)

Full size image

There is a clear difference between the asphalt concrete mixtures at elevated amounts of RAP compared to the three mixtures composed to have the same binder viscosity equaling virgin V6000 bitumen. Comparing mean values, the 20 and 40 % mixtures are significantly stiffer compared to the equiviscous mixtures, which in turn cannot be statistically separated, i.e., any differences between the equiviscous mixtures (Reference, V3000 + RAP and V1500 + RAP) can be due to random error. Stiffness testing cannot unequivocally indicate whether the RAP and virgin binder have mixed on a molecular level, but concerning asphalt concrete stiffness they behave as if the binders in the different mixtures, have equal viscosity, which in turn indicates that RAP and virgin binder have mixed. The pronounced stiffening effect of just adding RAP (i.e., V6000 + RAP) can be clearly seen. For all the mixtures tested, there is a strong linear relationship (R 2 = 1.00) between stiffness and binder viscosity i.e., the mechanical response clearly depends on binder viscosity.

As indicated in Fig. 9, no obvious effect of time on stiffness can be observed. In order to determine whether any stiffness evolution can be considered as statistically significant, the data illustrated in Fig. 9 were analyzed using three regression models: (1) linear (2) linear stiffness versus logarithmic time and (3) logarithmic stiffness versus logarithmic time. The statistical significance of change, i.e., slope, is summarized in Table 4.

Table 4 Statistical significance of slope for stiffness with time using three regression models: 1 indicates statistical significance
Full size table

As indicated Table 4 in most results do not provide any significance of changing stiffness with time. In the few cases any statistical significance of change in stiffness was observed, the increase was only very limited. It should also be noted that a large number of statistical tests are summarized in Table 4. If the level of significance (α) is adjusted for multiple comparisons (Bonferroni) only 1 of the slopes is significant (model 1, V6000 + 20 % RAP). Furthermore, from a practical point of view this stiffening is only very small and probably inconsequential in an asphalt production setting.

Results presented in Fig. 9 indicate that the stiffness levels for the equiviscous RAP-mixtures are similar to the Reference mixture and Table 4 shows essentially no indication of a time-dependent stiffening. Consequently, the overall results suggest that binder mixing has essentially been completed before the first measurement.

4.2.2 Accumulated deformation

In addition to the non-destructive stiffness and relatively high frequency modulus testing, the mechanical investigation also comprised destructive testing at relatively high stress repetitive loading. The relative deformation after 1000 load applications for each pavement material studied are given as function of time after manufacturing in Fig. 10. Results are given as mean values at each storage time and a linear regression line is also shown. For clarity, results are divided in two diagrams: one with equiviscous mixtures and the other with high-RAP mixtures compared to the Reference. The hypothesis is that if RAP and virgin binder mix, the equiviscous mixtures should show similar mechanical response while we expect a stiffer response for the high-RAP mixtures.

Fig. 10
figure 10

Accumulated deformation, mean values, as a function of number of days after sample manufacture: to the left equiviscous mixtures and elevated RAP to the right

Full size image

As in the case of stiffness modulus testing, neither does the accumulated deformation show any clear dependence on time. The results from deformation testing were also statistically analyzed. In no case was any slope (change in deformation with respect to time) statistically significant. In the case of total deformation accumulated, the reference pavement mixture comprising V6000 binder appeared slightly more prone to deformation compared to the mixtures containing RAP and V1500 and V3000 mixtures. However, it should be noted that this result was not statistically significant and may be explained by random error. The results are in strong concurrence with stiffness modulus testing i.e., the equiviscous mixtures cannot be statistically separated and the high-RAP mixtures are more deformation resistant. Furthermore, there is no significant evolution by time.

Compared to previous experience of the precision of this method [26], measurements performed in this investigation seems to be in statistical control, i.e., the sample variance was similar.

5 Discussion and conclusions

The scope of this research was limited to, in a practical way using research methodology, indicate means of how to accommodate for using RAP in the production of soft bitumen asphalt. More detailed aspects of old and new binder mixing, especially in the complex asphalt concrete mixture matrix were not studied. Interesting recent research includes studies on clustering effects [27] and atomic force microscopy of the old and new binder interface [28], among others.

The main purpose of this study was to investigate whether RAP can be utilized in soft bitumen asphalt concrete in such a way that the final mixture is similar to asphalt produced using virgin materials. In particular, three questions were investigated:

  • Will old binder from the RAP and new virgin binder mix?

  • How rapidly will the mixing occur?

  • Can the mechanical properties be predicted?

Although, the final answer to the overall question whether RAP can be used, must be given from actual in-service pavement behavior, a number of obstacles make this difficult to investigate under field conditions e.g., lack of reliable test methods, measurement difficulties, confounding mechanisms and an extended time frame needed. In lieu of in-service pavement behavior we use laboratory testing as a proxy. Basic mechanisms such as mixability and diffusion are more easily studied on pure binder systems. Nevertheless, at the end pavement behavior is more decisive. Therefore, it was deemed important that binder tests were supplemented with asphalt concrete testing to support or reject findings based on pure binder analysis.

The results from the rheological testing show that virgin bitumen actually mixes with binder from RAP. Furthermore, the final viscosity of the mixture can be predicted using relatively simple models such as those of Arrhenius, and Grunberg and Nissan. The analysis indicated the presence of an interaction effect between the binders. However, although statistically significant, the effect is considered as relatively small. In essence, a prediction based on the Arrhenius model would slightly over predict mixture viscosity, i.e., a softer mixture is obtained, but considering bitumen specification limits the error can be considered minor: the error will be in the same range as viscosity specification tolerances.

The analysis of the diffusion tests indicate that mixing occurs also without mechanical mixing, and that the process can be characterized reasonably well using Fick’s law. However, the experimental part was demanding due to measurement artefacts such as sensitivity to sample geometry and temperature susceptibility. Although, effort has been made to compensate for these artefacts, it is probably difficult to completely eliminate sources of error, wherefore test results may still be associated with uncertainties. The purpose of the diffusion experiments in this investigation was not to provide a detailed diffusion characterization per se, but more of a means to indicate whether diffusion actually occurs and if the process is fully completed. More details on diffusion can be found elsewhere, e.g., the extensive and thorough investigation by Kriz [29].

Based on results on pure binders, it seemed plausible that they actually do mix, either by mechanical mixing or by diffusion, and the viscosity can be predicted using well-known and relatively simple mixing models. We can now proceed to investigate whether these findings also are supported by testing on asphalt concrete mixtures. Using binder mixture viscosity predictions (Arrhenius’ relationship) asphalt concrete mixtures using RAP and a softer grade bitumen were designed to have the same overall binder viscosity as the Reference mixture, made from virgin materials only. If these equiviscous mixtures show similar mechanical behavior, this indicates binder mixing. Molecular level binder mixing details cannot be inferred from these tests, but from a practical point of view it seems reasonable to assume that mixing occurs and the mechanical behavior of the asphalt concrete can be predicted from binder properties and mixing models. As mentioned previously, the intention of the experimental plan was that three asphalt mixtures would be similar in terms of mechanical properties: the reference containing solely virgin V6000 bitumen, and V1500 and V3000 mixtures admixed with RAP. The mechanical testing was carried out at two different rheological conditions (time and temperature combinations). Both stiffness modulus and uniaxial cyclic compression testing resulted in only relatively small, statistically insignificant, differences between the three materials: for stiffness modulus a slightly softer response and regarding creep a slightly stiffer response for the RAP-mixtures compared to the virgin mix. For all practical purposes the mixtures are similar, which indicates that the binders are mixed. The small differences observed can be due to random error. In the case of time to reach steady-state properties, the results from the mechanical testing suggest that the essential mixing between RAP and virgin bitumen occurs rapidly, already before the first test after 1 day was conducted. Since both mechanical and diffusional mixing are strongly temperature dependent, it is fair to assume that the essential mixing occurred during the ca. 1 h sample preparation. In reality, asphalt mixing and subsequent paving is normally a more extended exercise.

Based on the findings in this investigation the following conclusions can be drawn.

Concerning pure binder:

  • virgin soft bitumen and binder from RAP can be mixed

  • the viscosity of the binder mixture can be predicted with high accuracy based on the Grunberg–Nissan model, and in many cases with adequate accuracy using Arrhenius’ model

  • soft bitumen and RAP fully mix both by mechanical mixing and diffusion

  • diffusion can be characterized using Fick’s law and regarding asphalt concrete:

  • the mechanical properties of asphalt mixtures correspond to what would be expected for a complete mixture between virgin binder and RAP: the same absolute levels in terms of stiffness and resistance to permanent deformation is reached for the equiviscous mixtures

  • the mixing between new and old binder probably occurs essentially during asphalt mixing and hot storage: in general, no evolution by time after manufacturing can be noted.

Given the conclusions presented above, the overall result from the current study suggests that it is possible to produce asphalt concrete using either a specified virgin binder of nominal viscosity or a relatively softer virgin binder and adding RAP, and obtain similar mechanical properties.