Changes in rheology of self-consolidating concrete induced by pumping

Abstract

Pumping is an easy and flexible process to place concrete inside a formwork. Many studies have recently been performed to understand and optimize the pumping process and identify the main differences between pumping of conventional vibrated concrete and self-consolidating concrete (SCC). However, due to pumping, changes in fresh concrete properties and the air-void system have been noticed. This paper describes the consequences of pumping on the fresh properties of SCC by means of two experimental pumping campaigns. In many cases, the concrete undergoes a large shear rate in the pipe, thus (re-)dispersing cement particles. This is expected to be the main cause of the observed decrease in plastic viscosity, V-Funnel flow time and pumping pressure resulting from increased flow rate or pumping time. The changes in yield stress or slump flow are anticipated to be influenced by the same phenomenon, but the final outcome is assumed to depend on the availability of residual superplasticizer in the mixing water. Pumping can cause a stable SCC to become segregating if both the yield stress and plastic viscosity decrease, or it can provoke a significant loss in filling ability, passing ability and self-consolidation of the concrete if the yield stress increases dramatically.

Introduction

Pumping of concrete is the fastest and most efficient way to place concrete inside a formwork. In the past, several practical guidelines were developed to optimize concrete mix designs, to predict pumping pressure or to optimize the layout of pumping circuits [1–3]. More recently, scientific studies have contributed to understanding the flow process of concrete inside a pipe. These studies included the evaluation of tribology [4–10] as well as the assessment of the thickness of the lubrication layer [11–13]. Different models are now available to predict pumping pressure, based on the applied flow rate, length and radius of the pipeline, the rheological properties of the concrete, and the properties of the lubrication layer. The properties of the lubrication layer are measured through tribology carried out on concrete [8, 14], or are assumed to be the rheological properties of a wet-screened mortar [11–13].

It is also well known that the concrete properties can alter during the pumping operation. Losses in slump consistency and changes in air-void systems are the most commonly reported [15, 16]. Some recent studies have attempted to investigate separately the influence of pressure and shearing on concrete rheology [17–19]. The main conclusion from these studies is that the shearing action may be the most important effect influencing the concrete properties. As previously stated by the authors in [20], for self-consolidating concrete (SCC), shear rate values could reach 30–60 s⁻¹ during pumping, in the bulk concrete. Assuming the lubrication layer has 10 times lower viscosity, the shear rate in this layer would be several 100 s⁻¹. As shearing can significantly affect concrete rheology, SCC properties should be largely affected by pumping.

A second effect that influences the rheology of concrete during pumping is the change in air content and air-void system. Typically in concrete, increasing the air content would lead to a decrease in plastic viscosity [21–23]. In the case of yield stress, the effect depends on the size of the air bubbles [22–24]. Increasing the amount of sufficiently small air bubbles will increase the yield stress, as the bubbles remain spherical and act similarly to solid inclusions [22–24]. Larger air bubbles deform and would result in a decrease in yield stress. More details on the influence of air on rheology can be found in [24].

Previous pumping experiments on SCC, have led to the conclusion that the pressure loss (Δp)—flow rate (Q) relationship is in agreement with the (non-)linearity in the rheological behavior of the concrete: i.e., if the flow is Bingham, the Δp − Q relationship is straight, and if the SCC shows shear-thickening behavior, the pumping curve is also non-linear [20]. However, due to a limited number of data points in some of the experiments, or a negligible presence of shear-thickening in other cases, shear-thickening is not taken into account in this paper.

In this paper, the results of two series of full-scale pumping tests carried out on SCC mixtures with different compositions and rheological properties are described. The changes in rheological properties, workability and pumping pressure observed with increased pumping time or flow rate are described and analyzed.

Experimental setup

The results in this paper are from two different testing campaigns: one carried out at Ghent University in Belgium [20, 25] and the other one at the Université de Sherbrooke in Quebec, Canada [7, 8, 14, 26]. The two test setups are described in the sections below.

Pumping circuits

Circuit at Ghent University

The concrete pump used for the experiments at Ghent University was a truck-mounted piston pump (Schwing P2023), capable of delivering a maximum pressure of 95 bar, or a maximum flow rate of 41.5 l/s. The working action of the pump is as follows: two cylinders with a volume of 83.1 l each alternately pull concrete from the hopper and push concrete inside the pumping circuit.

Behind the pump, a loop circuit was installed with 100 mm diameter pipes, allowing the concrete to flow back inside the hopper of the pump. The circuit was 103 m long for SCC A and B, and 81 m long for SCC C and D (Fig. 1). It consisted of five horizontal straight sections, connected by 180° bends, while a 6^th final straight section was inclined to complete the loop. Pressure sensors were installed flush in the last straight horizontal section, with a separation distance of 13 and 10 m in the 103 and 81 m circuit, respectively (Fig. 1). A set of three strain gauges was attached to the outer pipe wall, acting as a back-up for in case the pressure sensors would fail [20, 25]. All sensors were connected to a data acquisition system registering data at a frequency of 10 Hz [25].

Fig. 1

Lay-out of 103 and 81 m long pumping circuits at Ghent University. The arrows define the measurement sections in which pressure losses were registered: these are the last straight horizontal sections in the circuit [25]

The flow rate was determined by measuring the time needed to complete a certain number of pumping strokes. A calibration procedure has revealed, in this case, that the correction needed for the incomplete filling of the cylinders was compensated for by the correction imposed by the dead time of the pumping stroke. As a result, the flow rate estimated by determining the time was equal to the real flow rate during which pressure was registered [20, 25].

Pumping circuit at the Université de Sherbrooke

The pump used at the Université de Sherbrooke was a Schwing BPL 900 truck-mounted piston pump. The maximum pressure that the pump can deliver is 60 bar, while the maximum flow rate is 25 l/s. The volume of one pumping cylinder is 68.1 l. Behind the pump, a 30 m long loop circuit was installed. The first horizontal straight section was constructed with 100 mm diameter pipes. After making a 180° turn and enlarging the diameter, a second straight horizontal section in 125 mm pipes was installed, followed by a vertical part enabling the concrete to flow back inside the reservoir of the pump (Fig. 2) [8, 14, 26]. Both straight sections, with 100 and 125 mm diameter pipes, were equipped with pressure sensors spaced 10 m apart, and strain gauges acting as back-up [8]. All data were registered at a frequency of 10 Hz, which was similar to the experiments at Ghent University.

Fig. 2

Lay-out of pumping circuit at the Universite de Sherbrooke [8, 14, 26]

The flow rate was assessed using the same strategy done at Ghent University, but the calibration procedure has revealed that a correction factor was necessary for each concrete mixture pumped [8].

Testing procedures

Two different testing procedures were employed, as described below.

Testing procedure at Ghent University

The procedure employed was specifically designed to investigate the effect of pumping on fresh concrete properties (Fig. 3). Flow rates could be varied in discrete steps by the pumping operator. The procedure consisted of:

• Bringing the concrete to its “reference state” at each flow rate [27], meaning that equilibrium in pressure was awaited for.

• Taking a sample of the pumped concrete

• Stepwise decreasing the flow rate from the current step to the lowest step.

Fig. 3

Testing procedure for SCC A–D. Starting at the lowest flow rate step of the pump (1), flow rate was maintained until pressure achieved equilibrium, followed by taking a sample and a quick stepwise decrease in flow rate, not exceeding the maximum flow rate already applied (except for step 1, where there is no descending curve). For SCC A, B (first test) and C, flow rate step 5 was not achieved

The lowest flow rate was first examined (around 4 l/s), and logically, there was no decreasing curve. The flow rate was then increased to around 7 l/s, equilibrium in pressure was awaited for and the down-curve (7 and 4 l/s) was determined. The down-curve consisted of minimum five strokes or 60 s at each flow rate. Consecutively, this procedure was repeated for flow rates around 10, 14 and 16–18 l/s (if time and pressure allowed for the latter one). As a result, for each imposed flow rate (except the 4 l/s), an equilibrium value for the pressure loss was obtained. The pressure loss at each previous flow rate was also determined. Connecting the equilibrium Δp − Q points could be considered as the upper part of a loop curve, while the quick stepwise decrease in Q delivers different lower parts of a loop curve.

After reaching equilibrium at each flow rate, a sample of the concrete was taken to assess the fresh properties: slump flow, V-Funnel flow time, density and air content as well as the rheological properties using a Tattersall Mk-II rheometer [28].

Testing procedure at the Université de Sherbrooke

This testing procedure aimed at studying the influence of rheology and mix design on pumping pressure [8, 14]. It consisted of awaiting equilibrium at the highest flow rate (between 10 and 18 l/s, dependent on the pressure generated by the pump), and decreasing the flow rate in six or seven steps, maintaining each step for five strokes or 45 s maximum [8, 26]. Figure 4 shows the results for the pressure measurements in the 100 mm diameter section for one test [8]. Such test generally took 5 min and was repeated four or five times at 30 min intervals. After each pumping test, a sample of the concrete was characterized by means of slump flow, V-Funnel, density and air content, sieve stability, rheology (by means of the ICAR) and tribology [7, 8]. A sample of concrete was kept aside and tested once before all pumping tests and once before the last pumping test. This sample served as reference to determine the loss of workability of the concrete and was manually re-agitated prior to testing. By comparing the successive rheological results of the pumped samples, and subtracting the workability loss, assuming yield stress and viscosity evolve linearly with time, the effect of pumping on the rheology can be isolated.

Fig. 4

Testing procedure at the Universite de Sherbrooke [8, 14]. This test was repeated every 30 min

Rheometers

As mentioned before, two different rheometers were used, both based on the principle of the coaxial cylinders. The inner cylinder of the Tattersall Mk-II consists of an interrupted helicoidal screw. The maximum distance between the edges of the blades of the screw was 160 mm in horizontal direction and 140 mm in vertical direction [28]. The diameter of the container was 250 mm, measured between the outer sides of the ribs, which were installed to prevent the formation of a lubrication layer. The testing procedure in the Tattersall Mk-II consisted of pre-shearing the concrete at approximately 75 rpm. Once equilibrium was achieved, the rotational velocity was decreased in 11 steps of 5 s each. Torque and rotational velocity were registered at the inner cylinder and averaged for the last 4 s of each step.

A correction procedure to obtain reliable rheological measurements was employed [29], and a comparative study revealed that the results from the Tattersall Mk-II are similar to those of the ConTec Viscometer 5, except for very fluid SCC mixtures [30]. Furthermore, most of the mixtures tested with the Tattersall Mk-II rheometer at Ghent University showed important shear-thickening behavior [25, 31, 32], requiring the application of a non-linear rheological model. The modified Bingham model [33] was chosen. The rheological properties obtained with the Tattersall Mk-II rheometer reported in this paper are the modified Bingham yield stress, and the differential viscosity at a shear rate of 5 s⁻¹. This represents the slope of the rheological curve at this shear rate. If the material was too fluid (e.g. SCC D, see further), no reliable rheological properties could be obtained. As this has occurred in this research work, the equilibrium torque at maximum rotational velocity (=ca. 75 rpm) was also reported as an indication of flow resistance.

The ICAR rheometer is based on the same principle, but the inner cylinder is a 4-blade vane [34]. The inner cylinder has a radius of 63.5 mm and a height of 127 mm. The outer radius, measured between the ribs of the container, is 143 mm. Both in horizontal and vertical direction, the gap between the vane and the bucket is at least 80 mm, allowing a maximum aggregate size up to 20 mm. The testing procedure consisted of pre-shearing the concrete at 0.5 rps for 20 s, followed by a stepwise decrease of the rotational velocity from 0.5 to 0.025 rps in 10 steps of 5 s each. Torque and rotational velocity are measured at the inner cylinder and are averaged for the last 4 s of each step, provided the torque was in equilibrium. The Reiner-Riwlin equation was used to calculate yield stress and plastic viscosity according to the linear Bingham model [35]. A correction for plug flow was employed if necessary [36]. Finally, based on a comparative test between the ConTec Viscometer 5 and the ICAR rheometer [37], the values were transformed to “as if obtained with the ConTec rheometer”. The specific reasons for this transformation are described in [8]. For some tests: SCC 2, test 5; SCC 12, test 4 and SCC 19, test 5, the yield stress value is quite elevated, and the rheological values could be doubtful due to inaccuracies in the measurements. However, qualitatively, these three measurements represent concrete with a high yield stress value.

Concrete mixtures

Tests at Ghent University

Four different SCC mixtures were tested at Ghent University. The mixtures were produced in 3.25 m³ batches at a ready-mix plant located about 30 min away from the laboratory. Table 1 shows the mixture proportioning of SCC A and C. SCC B and D are commercial products of the ready-mix company. The main difference between SCC A and C resides in the amount of water in the mixture, while mixtures B and D were identical, except for a slightly higher superplasticizer (SP) dosage in the latter concrete. All mixtures were made with ordinary Portland cement (CEM I 52.5 N), limestone filler, river sand and a mixture of two gravels with nominal maximum aggregate sizes of 8 and 16 mm. The SP employed was a commercially available polycarboxyl-ether, able to maintain workability for up to 2 h, according to the manufacturer. No air-entraining agents or viscosity-modifying agents were used. Results on fresh concrete kept aside during the test indicate that even after 3.5 h, no large changes in slump flow and V-Funnel flow time can be observed.

Table 1 Mixture proportionings of SCC pumped at Ghent University

The insertion of the concrete in the pipes took, especially for SCC A and SCC C, approximately 1 h due to many blockages during pumping start-up. For SCC B and D, as the previous concrete was kept in the pipes, the start-up had a significantly shorter duration (±5 min). The mixtures underwent the testing procedure as follows: SCC A underwent four steps with 12.6 l/s as maximum flow rate, for SCC B, the test was performed twice with a maximum flow rate of 13.1 l/s (four steps) and 16.4 l/s (five steps) respectively, SCC C and D had a maximum flow of 13.9 l/s (four steps) and 18.5 l/s (five steps) respectively.

Tests at the Université de Sherbrooke

In total, 18 different SCC mixtures were delivered in 1.25 or 1.5 m³ batches during this testing campaign. All mixtures were produced in a nearby ready-mix plant. The blended cement employed was a mixture of 92 % GU (Portland) cement and 8 % silica fume (GUbSF). All mixtures, except SCC 5 having an extra replacement of cement with class C fly ash, contained no other binder. The sand was a river sand, while the coarse aggregates were a combination of 80 % 5–10 mm and 20 % 10–20 mm crushed aggregates. For SCC 18 and 19, in an attempt to improve the compressive strength, the source of the coarse aggregates was varied, but the grain-size distribution was maintained. Two different types of polycarboxyl-ether based superplasticizers were used, one with long workability retention (SP-L), added at the plant and resulting in a slump flow of approximately 350–450 mm at delivery, and another one with short workability retention (SP-S) added in the laboratory to fine-tune the consistency of the mixture.

The reference mixture was produced with 600 kg of blended cement per m³, w/cm equal to 0.295, a paste volume of 37.5 % (excluding air) and a sand-to-total aggregate ratio (s/a), by mass, of 0.53. The SP-S dosage was adjusted to obtain a target slump flow of approximately 700 mm. SCC 1, 4, 10 and 15 were considered as reference mixtures. For SCC 2 and 3, the SP-S dosage was varied to change the initial slump flow. SCC 5 contained fly ash, SCC 8, 9 and 19 have different w/cm, varying between 0.22 and 0.34. SCC 11 and 12 have different paste volumes, while for SCC 16 and 17, s/a was reduced. SCC 13 was the only mixture that was air-entrained. SCC 14 contained a very small dosage of VMA. All mixtures were produced during winter in Canada, requiring heated water. This has led to some anomalies, as SCC 7 may have lost a part of its paste sticking to the frozen drum of the concrete truck, and SCC 14 is likely to have higher water content than requested as chunks of ice were present in the coarse aggregates. SCC 6 is not reported in this paper as it showed severe segregation and the results could not be used. The mix designs are displayed in Table 2.

Table 2 Mixture proportionings of SCC pumped at the Universite de Sherbrooke

Table 3 Evolution of fresh and rheological properties for mixtures SCC A-D, evaluated after achieving equilibrium at each flow rate

Observations

Influence of reference state on pumping pressure, rheology and workability

As mentioned above, for every SCC pumped at Ghent University, a new reference state was imposed at each flow rate step, as pumping was continued until equilibrium was achieved in the pressure registrations, and the flow rate was then increased during the test (see Fig. 3 for testing procedure). As a result, a some-how loop curve with very discrete points is obtained for the pressure loss (Δp, in kPa/m) versus flow rate (Q, in l/s) relationship. The up curve consists of connecting all equilibrium points at each flow rate (Equilibrium line in Fig. 5). The down curves are the quick descending curves, determined after equilibrium was achieved at each flow rate (Down from Q − x, where x represents the flow rate step). As can be seen, the pressure loss at a certain flow rate decreases when the maximum flow rate applied before was more elevated. This behavior was observed for SCC A, B (first test), C and D. Figure 5 shows the result for SCC D.

Fig. 5

The results on SCC D show that all descending Δp − Q curves are below the equilibrium curve. All descending curves show lower pressure losses with increasing maximum applied flow rate

The second test on SCC B shows a different pattern (Fig. 6). Almost all curves are overlapping, except the last curve determined during the test: the decreasing curve at 16.4 l/s maximum flow rate. This latter curve is slightly higher than the others, which could be attributed to the workability loss. It should be noted that at that time, the test was performed 3.5 h after water addition, and that the concrete was in circulation for 2 h, almost continuously. The curves are also overlapping with the last pressure loss – flow rate curve from the first time the test was performed (down from Q-4 previous, dashed line and hollow dots in Fig. 6). The overlapping of the Δp − Q curves during test 2 on SCC B indicate that the concrete did not undergo changes in rheological properties since the execution of “down from Q-4” in test 1. The reason for this observation is explained in Sect. 4.1.1.

Fig. 6

The second test on SCC B shows a different pattern: all curves are almost equal, except for the down from Q-5 curve, which may be influenced by workability loss. The dashed line is the last descending curve of the first test on SCC B

Table 4 shows all results for the peak pressure loss values (maximum measured at each flow rate), the equilibrium pressure loss values and the pressure loss—flow rate data for each down-curve. Fresh concrete data almost consistently indicate a decrease in V-Funnel flow time and a slight decrease in slump flow, except for SCC B, test 2, where the decrease in slump flow was more notable (see Table 3). Except for SCC A, an increase in air content was also noticed. The rheometer results show a clear general decrease in viscosity, or torque at maximum rotational velocity with increasing imposed flow rate (Table 3), while the results for the yield stress are more variable.

Table 4 Peak and equilibrium pressure loss for each flow rate for SCC A-D. The down curve displays the pressure loss (Δp)—flow rate (Q) data established after reaching equilibrium. The testing procedure is presented in Fig. 4

Influence of consecutive pumping tests on rheology

The pumping tests carried out at the Université de Sherbrooke indicate similar results as from the previous section: the longer the concrete was pumped, the lower the pressure loss was observed for each flow rate. Figures 7 and 8 show the evolution of the rheological properties as a function of the product of flow rate and time (Qt). This Qt product is representative for the amount of shearing the concrete has undergone during the test, as it represents the volume of concrete that was pumped. The evolution of the rheological properties of the non-pumped concrete mixtures was also recorded. A linear evolution of yield stress and plastic viscosity with time is assumed. Although it has been demonstrated that yield stress and plastic viscosity show more of an exponential increase with time [38, 39], the assumption of a linear profile can be justified if the elapsed time is not too large compared to the duration of the dormant period of cement hydration. The relative plastic viscosity is calculated according to Eq. 1.

$$\mu_{{{\text{p}},{\text{rel}}}} = \frac{{\mu_{{{\text{p}},x}} - \left( {\mu_{{{\text{p}},a}} - \mu_{{{\text{p}},b}} } \right)\frac{{t_{x} - t_{b} }}{{t_{a} - t_{b} }}}}{{\mu_{{{\text{p}},b}} }}$$

(1)

where μ _p = plastic viscosity (Pa s), t = time (min) and the indices rel = relative, x = considered test, b = non-pumped sample at the beginning, a = non-pumped sample after tests.

Fig. 7

The relative plastic viscosity is calculated as the plastic viscosity divided by its value measured before pumping, and corrected for the workability loss based on a linear evolution between the two tests before and after pumping (Eq. 1). For the reference SCC mixtures SCC 1, 4, 10 and 15, a repeatable decreasing trend in relative plastic viscosity versus the flow rate x time was observed (trendline only shown for SCC 4). For mixtures with different w/cm, larger differences are observed)

Fig. 8

The relative yield stress, calculated in a similar way as the relative plastic viscosity, shows no clear pattern: it can decrease (SCC 9), remain approximately constant (SCC 10, 15) or increase dramatically (SCC 3)

Using this equation, a deviation of the relative plastic viscosity from unity means that the concrete viscosity undergoes an evolution different than the one caused by the workability loss. For all mixtures, the relative plastic viscosity decreases with increased product of pumping time and pumping flow rate. Figure 7 shows the relative plastic viscosity for reference mixtures SCC 1, 4, 10 and 15, showing a consistent exponential decrease which is quite repeatable. Other mixtures showed similar trends although the magnitude of the decrease was variable.

Figure 8 shows the same principle for the relative yield stress. However, no clear pattern can be observed; for some mixtures, the yield stress decreased, provoking segregation; for other mixtures, the yield stress showed a slight variation and for some mixtures, a dramatic increase in yield stress was noticed. Detailed results on fresh and rheological properties can be found in Table 5.

Table 5 Evolution of fresh and rheological properties of SCC 1-19 with increasing number of tests. The pumping pressure—flow rates can be found in [8]

V-Funnel and slump/slump flow measurements confirm the trends of the rheological measurements (Table 5). In contrast to SCC B-D, the mixtures pumped at the Université de Sherbrooke did not show significant variations in air content, except in the case of the air-entrained mixture (SCC 13).

Physical effects influencing rheology during pumping

Shearing

Mechanism

The shear stress in a circular pipe evolves linearly from zero at the center to the maximum value at the wall [40]. Due to the presence of a yield stress in concrete, a zone around the center is not sheared. The magnitude of this zone increases with increasing yield stress. For conventional vibrated concrete, it can occur that the yield stress is significantly high causing only the lubrication layer to be sheared [41]. For SCC, however, the yield stress is sufficiently low to shear a significant portion of the bulk concrete in the pipe. Shear rates in the bulk concrete can reach values of 30–60 s⁻¹ [20]. Furthermore, as a pipe is circular, a larger volume of concrete is subjected to high shear rates compared to the volume subjected to low or zero shear rates. As a consequence, a large portion of concrete is exposed to a high shear rate for a relatively long time. For example, in the Université de Sherbrooke circuit, approximately 300 liter is continuously in the pipes. Pumping concrete at a flow rate of 15 l/s leads to a time of 20 s during which the concrete is subject to shearing. This duration is similar to the time typically employed during the pre-shearing in a rheological measurement to eliminate the effect of thixotropy [36, 42, 43]. The shear rates imposed on concrete are in most cases significantly higher than the shear rate in a concrete truck or a regular concrete mixer [44]. Some high-performance concrete mixers are able to introduce an enhanced shear rate on the concrete for a prolonged time. In this case, the conclusions are likely to be altered [45].

As mentioned in Sect. 3.1 for the procedure at Ghent University (Fig. 3), with each increase in flow rate step, a new reference state, corresponding to the applied shear rate, is imposed. As a normal batching plant was used to mix the concrete, the applied shear rate at each flow rate step is expected to be the highest shear rate the concrete has underwent at that time. As equilibrium is awaited for, the imposition of the higher flow rate eliminates the importance of the shear history before the application of this flow rate. Also, with each increase in flow rate, more cement(-itious) particles are (re-)dispersed. This leads to a decrease in plastic viscosity of the mixture. This is confirmed by the rheological and V-Funnel measurements and pressure loss. It has been shown, especially for SCC, that pressure loss is well related to viscosity of the concrete [14, 20, 25]. As viscosity is decreased with each increase in flow rate step, the pressure loss should also decrease. This is observed in Fig. 5 and in Table 4, as the pressure loss at a certain flow rate decreased with increasing maximum flow rate applied before. For example (see Fig. 5 and Table 4 for SCC D), the pressure loss at approximately 4 l/s was 8.7 kPa/m in equilibrium, while it decreased to 6.6 kPa/m (at 4 l/s flow rate) when the flow rate applied before was 6.9 l/s; 5.1 kPa/m (at 4 l/s) with a maximum flow rate of 11.4 l/s applied before, and around 4.0 kPa/m if even higher flow rates were imposed before.

The second test on SCC B confirms the effect of shearing, as no further decrease in pressure loss was observed after the concrete was sheared at a flow rate of 13.1 l/s for the first time. Indeed, as the highest flow rate applied before the second test on SCC B was 13.1 l/s, the reference state corresponding to this flow rate was imposed and maintained. During test 2, the imposed flow rates were lower than or equal to 13.1 l/s, except for step 5, meaning that no new reference state was introduced. As the internal structure needs a lot more time to rebuild than the time needed to break it down, one can assume that the reference state remains approximately constant for the duration of test 2, although some stiffening occurred near the end of the test. As no higher shear rate is applied since step 4 of test 1, no additional dispersion of cement particles is expected and no decrease in viscosity, V-Funnel flow time and pressure loss is observed. However, for step 5 in test 2, such a decrease is expected, but is probably hidden due to the stiffening of the concrete at that time.

This can be explained by means of the PFI theory developed by Wallevik [46]. Cement particles can be connected in two ways: by means of physical attraction forces (causing thixotropy), or by means of chemical bonds caused by the initial hydration (causing structural breakdown, as defined by Tattersall [47]). The thixotropic forces only act on the “smaller” particles and are fully reversible: the connections can be broken when increasing the shear rate while at lower shear rates, they build back up. The chemical links though are easily broken down due to shearing, but they take a longer time to build up. Monitoring the workability loss gives a good indication on the evolution of the chemical links over time. Important to know is that some connections, whether physical or chemical, can be considered permanent, or impossible to break. However, this depends on the amount of work put in the system, which depends on the shear rate applied. Permanent connections at a specific shear rate can be broken at higher shear rates, leading to more dispersion.

In both testing campaigns, after mixing the concrete at the plant, it took 15 to 45 min to transport it to the job site. Once on site, the concrete is remixed in the truck, but typically, shear rates in a truck are not elevated, and the time the concrete is exposed to this shear rate is not long either, as the highest shear rates occur in very distinct areas. Some of the thixotropic connections which have formed during transport are broken down, but not all of them. Exposing the concrete to the high shear rates in the pipes could further break down the thixotropic connections, thus re-dispersing the cement particles.

However, as the mixer at both batching plants is not expected to deliver very high shear rates for prolonged times, the shear rate in the pipes can cause additional dispersion of cement particles, whether they were connected via thixotropic bonds or chemical links, and each increase in shear rate could cause more of the “permanent” connections to break down, thus further fluidifying the concrete.

For the mixtures pumped at the Université de Sherbrooke, a decrease in relative plastic viscosity, with increased product of flow rate and time was observed. The fact that the viscosity still decreased after the first tests is probably due to the fact that perfect equilibrium was not achieved during the first test. Equilibrium was judged visually based on the pressure values displayed on the screen of the data acquisition system.

An additional confirmation that the concrete is sheared can be found in the compressive strength measurements after 28 days of moist curing of the mixtures pumped at the Université de Sherbrooke. Three cylinders were taken for each mixture from the initial delivery, and three others were produced with pumped concrete after the last pumping test. In general, compressive strength increased due to pumping, between 2 and 20 % (Table 6). The change in compressive strength can be attributed to an increase in surface area of the cement particles due to dispersion, thus provoking better cement hydration [48]. Mixtures SCC 2 and 3 showed a decrease in compressive strength, but this could be due to inadequate self-consolidation as these mixtures showed a significant increase in yield stress and no mechanical consolidation was applied in preparing the cylinders, as all mixtures were considered self-consolidating. SCC 12 and SCC 19 showed similar decreases in self-consolidation and a reduction of compressive strength can be expected. However, as described below, SCC 12 and SCC 19 are the mixtures with the largest decrease in viscosity, and are thus expected to show a large dispersion due to pumping. The increase in compressive strength is not large however, which could indicate the combination of the dispersion and the lack of self-consolidation.

Table 6 Compressive strength determined on three moist cured cylinders at 28 days shows in most cases an increase due to pumping

Most influential parameters

The two main mix design parameters which influence the change in viscosity due to pumping are the w/cm and the paste volume. Decreasing the w/cm and decreasing the paste volume can lead to a greater level of decrease in viscosity with increasing product of flow rate and pumping time. Figure 7 shows the relative plastic viscosity as a function of Qt, for SCC 9 (w/cm = 0.34), Reference SCC 1, 4, 10 and 15 (w/cm = 0.30), SCC 8 (w/cm = 0.25) and SCC 19 (w/cm = 0.22). In general, decreasing the w/cm results in a more important decrease in relative plastic viscosity, despite the results of SCC 8. A reduction in w/cm makes it more difficult to disperse cement particles in the concrete mixer, as the relative particle fraction (volumetric concentration of solids divided their maximum packing density) is increased in the cement paste [49, 50]. This leads to an enhancement of the inter-particle forces, an increase in the yield stress (when keeping the admixture dosage constant), requiring more energy to disperse the particles. As the energy of the pumping action is expected to be larger than the energy delivered by the mixer, more dispersion would occur during pumping. Furthermore, a lower w/cm is also the cause of a faster thixotropic re-build [51, 52], which could result in more re-dispersion of cement particles during pumping.

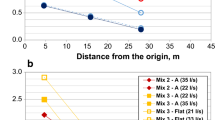
Figure 9 shows the effect of paste volume for SCC 12 (paste volume = 35 %), SCC 4 (paste volume = 37.5 %) and SCC 11 (paste volume = 40 %). Decreasing the paste volume from 37.5 to 35 % led to a more substantial decrease in relative plastic viscosity. This can be attributed to the higher shear rate in the cement paste at constant flow rate in the concrete. However, increasing the paste volume has not significantly altered the decrease in relative plastic viscosity, up to a point at which the relative plastic viscosity is increased with increased pumping action. SCC 11 is the only concrete where this important increase has been observed (the increase in plastic viscosity due to pumping is larger than the increase due to workability loss for test 5: see hollow points in Fig. 9). The reason for this behavior is currently unknown.

Fig. 9

Reducing paste volume causes the relative plastic viscosity to decrease faster, while an increase in paste volume does not have a significant effect initially, but causes a dramatic increase in viscosity after extended pumping operations. The hollow points indicate the increase in viscosity due to pumping for SCC 11 which have been excluded from the regression

Influence of shear-thickening?

Shear-thickening is not expected to influence the changes in viscosity and yield stress, as it is caused by a different mechanism. As stated in [32], shear-thickening of SCC is thought to be caused by the formation of hydroclusters of small cement(-itious) particles when subjected to a high shear rate. This means that the forces induced by the flow push small cement particles (or small agglomerates) sufficiently close together to create a temporary cluster. Slowing down the flow releases the particles from this cluster, and the “viscosity” decreases with decreasing shear rate. Furthermore, large agglomerates of particles are less likely to form clusters than individual particles or small agglomerates. In fact, this means, roughly stated, that the breakdown of the connections must happen before shear-thickening can occur. Therefore, it is expected that shear-thickening does not affect the dispersion process caused by the pumping.

Shearing combined with superplasticizer content

The significant shearing during pumping of concrete explains well the observed effect on viscosity, V-Funnel flow time and pressure loss. The effect of pumping on slump flow or yield stress is not straightforward to explain. During mixing, shearing causes (re-)dispersion of cement particles, but if after shearing, and if these particles are not prevented to re-coagulate (by means of superplasticizers), the yield stress of concrete can become rather high. If sufficient superplasticizer is available, the particles can be prevented to re-coagulate, and a low yield stress is observed [53].

It is expected that a similar process influences the yield stress during pumping. The additional shearing in a pipe causes additional dispersion and re-dispersion of cement particles. If residual superplasticizer is still available in the mixing water, the influence of the dispersion can be limited, or can even be counteracted if the superplasticizer is highly dosed, or even overdosed. In the latter case, a decrease in viscosity and yield stress can cause segregation of the SCC, as is observed for SCC 5 and SCC 9 from the Université de Sherbrooke data set.

On the other hand, if the amount of residual superplasticizer is limited, the dispersion of cement particles can enhance the yield stress due to the increase in available surface for re-coagulation.

Changes in air-void system

Changes in the air-void system, namely an increase or decrease in total air content, or a change in air-void distribution can significantly affect the rheological properties of concrete [21–23]. Increasing the air content should decrease the viscosity and enhance the effect air has on the yield stress. The latter effect depends on the capillary number, which depends on the air-void size [24]. However, as variations in rheological properties are observed for the pumped mixtures at the Université de Sherbrooke, which did not show a significant change in air content, it is most likely that changes in air content and air-void distribution are not the main factor influencing the rheology of concrete.

Consequences for practice

In practice, SCC will usually not be exposed to these long-time pumping operations. The changes of rheological properties in practice would not be as elevated as demonstrated in this research work. However, for large scale projects which require long pumping lines, the changes in rheological properties may become important and preliminary evaluation of the mix designs is recommended.

In any case, the stability of SCC mixtures should be closely monitored as the viscosity of the mixture decreases due to pumping. In this research work, this has been especially observed for the mixture with fly ash (SCC 5) and the mixture with an increased w/cm (SCC 9) and to a lesser extent SCC 14 (with an accidentally increased w/cm). For these mixtures, both yield stress and viscosity values decreased, leading to instability. Sieve stability values increased from 13.2 % before pumping for SCC 5 to 25.1 % after the first test, and higher than 30 % for the consecutive tests. Similar observations have been made for SCC 9 where the sieve stability value increased from 13.1 % before pumping to 15.5 % and higher from test 2 on. For SCC 14, the sieve stability value slightly increased from 14.8 % before pumping to 16.1 % at tests 3 and 4.

On the other hand, a significant increase in yield stress can occur during pumping. Based on the results, there is no clear distinction in which cases the yield stress increases significantly, although SCC 12 (less paste) and SCC 19 (lowest w/cm) show an important increase. However, SCC 8 (also a lower w/cm) and SCC 11 (higher paste volume) contradict the above statements. The difference between SCC 1 (almost no increase in yield stress), SCC 2 and 3 (significant increase in yield stress) could be related to the ratio of SP-L and SP-S (see Table 2), but a real explanation cannot be provided by the authors. A significant increase in yield stress can however lead to a loss in self-consolidation, eliminating all advantages of using SCC.

The mix design of SCC is though mostly controlled by the specified performance and availability of materials. The room for variations to optimize the mix in view of the results described in this paper is rather restricted. Instead, the following actions could reduce the significance of the changes in rheology due to pumping:

• Use intensive shearing concrete mixers, as the main cause of changes in SCC rheology is attributed to dispersion of cement particles. Having initially good dispersion will reduce the effect of additional dispersion, and hence reduce the changes in yield stress and viscosity. Using the delivery truck as mixer for SCC would most likely lead to the largest changes in rheological properties.

• Pump at low flow rates, as the applied flow rate, and thus shear rate, directly influences the amount of dispersion. As shown in Fig. 5, each increase in flow rate applied increases the dispersion and provokes an additional decrease in viscosity.

• Use larger pipes. The same flow rate can be obtained, but the shear rate is going to be smaller, reducing the importance of the dispersing effects. Furthermore, larger pipes have the advantage of reducing significantly the pressure losses [14].

Conclusions

Full-scale pumping tests on SCC at Ghent University in Belgium and the Université de Sherbrooke in Quebec, Canada, have revealed that pumping can have significant influences on the rheological properties of SCC. From the results and analysis, it can be concluded that:

• The viscosity of the concrete decreases substantially with increasing pumping time and increasing flow rate. This effect is attributed to the additional shearing that the concrete undergoes during pumping, which can lead to re-dispersion and additional dispersion of cement particles. The results have been confirmed based on rheometer measurements, V-Funnel flow times and pressure loss registrations. From the data, it appears that decreasing w/cm and decreasing the paste volume have the largest effect on the change in viscosity. Compressive strength of cylinders sampled before and after pumping show an increase due to pumping, thus supporting the above statement of greater cement dispersion during pumping.

• For the yield stress, no uniform conclusion can be drawn. Yield stress can decrease, remain relatively constant or even increase dramatically due to pumping. It is expected that the (un-)availability of superplasticizer molecules in solution in the concrete may play an important role in maintaining (re-)dispersion of cement particles, or not. A decrease in yield stress and plastic viscosity may cause segregation of SCC, even if the concrete was stable before pumping. With a significant increase in yield stress, filling ability, passing ability and self-consolidation may be compromised, thus eliminating all advantages of using SCC.

• All SCC mixtures, except one, did not contain any air-entraining agent. The change in air content of the mixtures due to pumping is not constant. Except for SCC A, a significant increase in air content was observed for the mixtures pumped at Ghent University. However no important changes in air content were noted for the mixtures pumped at the Université de Sherbrooke. As a consequence, the air content cannot be the major cause of the variations in yield stress and plastic viscosity observed.