Abstract
The aim of the presented research programme was to investigate the flexural behaviour of steel fibre reinforced self-compacting concrete beams. The tested beams were reinforced with two types of crimped steel fibres. Fibres were added in volumes of 0.5, 1.0 and 1.5 %. The experimental tests were conducted on specimens cut from 1.2 m long elements. Before destructive mechanical testing the specimens were subjected to medical X-ray computed tomography (XCT) procedures. Results of XCT allowed to determine the distribution of fibres. The flexural behaviour of the beams was tested according to the RILEM TC 162-TDF recommendation. A comparison of non-destructive results and mechanical behaviour of tested specimens proved a very strong dependence. XCT also made it possible to assess the uniformity of fibre distribution throughout the tested elements. The influence of the location of concrete casting on fibre distribution was determined. The influence of mixture flow on fibre orientation was also analysed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Modern steel fibre reinforced concrete (SFRC) was officially developed in the USA in 1969 when US Patent 3429094 was issued to J.P. Romualdi. It was initially produced by the Battelle Development Corporation of Columbus located in Ohio and followed by several other producers of chopped steel fibres [1, 5]. Originally SFRC was mainly used to cast flat slabs, pavements and tunnel linings. It was also applied for various repair applications [4, 46]. Currently SFRC is recognized as a cement composite characterized by a high toughness in tension and bending and it is commonly used in construction industry. Its resistance to all types of dynamic loading (including blast and projectile loads) is also utilized in many types of modern concrete structures. From the very beginning of SFRC, fibre distribution was the most important technological problem significantly hindering its application and development of standards. Fibre distribution is influenced by numerous factors including particle size of aggregate, type and volume of used fibres, method of adding fibres, mixing procedure, casting sequence and compaction method. For the last 45 years there has been huge research efforts focused on SFRC which solved the majority of these technological problems. The following was defined: limits of fibre additions, best types of steel fibres for specific applications, ordinary concrete mixes compatible with specific fibre reinforcement, best mixing, casting and compaction practices. All these valuable achievements were based on two conditions: the matrix concrete has a non-self-compacting consistency and there was no suitable or accurate non-destructive method of assessing fibre distribution. Although the correlation between fibre distribution, and properties of fresh and hardened SFRC was pointed out by many researchers [6, 13, 20, 22] this topic deserves a much deeper investigation. The newest trend in technology of SFRC is to use self-compacting concrete (SCC) as a matrix. This material known as steel fibre reinforced self-compacting concrete (SFR-SCC) has a wide range of potential applications in construction industry. Previously unknown possibilities in creating a concrete structure, including new types of thin-wall elements, is within reach for this material. The main obstacle in successful implementation of SFR-SCC in civil engineering is the lack of thorough analysis of fibre distribution (especially when considering thin elements [8, 23]). The results of a few research programmes dealing with SFR-SCC [6, 7, 24, 26, 37] prove that fibre distribution in such structural elements varies due to the type of casting process, the flow rate, the wall effect, the location of concrete casting point (CCP), the thickness of elements and the proximity to the bottom of moulds. Variations in fibre distribution in case of SFR-SCC can be higher compared to traditional SFRC. The knowledge about rules governing fibre distribution in SFRC is less meaningful in case of SFR-SCC. So far, it was difficult to assess fibre distribution in SFR-SCC without undertaking traditional destructive or sophisticated and difficult to use non-destructive testing [10, 30, 31, 45, 47, 49, 50]. As an alternative the magnetic method is being developed by Italian [15] and Spanish [29] research groups. Keeping in mind all previous technological experience with SFR-SCC, the authors decided to apply X-ray computed tomography (XCT) as a non-destructive method to assess its fibre distribution. XCT also proved to be an efficient and flexible non-destructive method of high-resolution microstructural characterization of different materials [24, 25, 37, 39, 40, 48, 49]. The main aim of the research programme was to denominate the correlation between the location of CCP, fibre distribution and mechanical properties of hardened SFR-SCC beams.
2 Materials and mixture composition
Two types of crimped steel fibres were used in this research programme. Both fibre types are characterized by a cross-section with a shape of a segment of a circle, a tensile strength equal to 800 MPa and modulus of elasticity of 201 GPa. Basic geometric properties of the fibres are presented in Table 1. The choice of the fibres was based on previous research experience of the authors and other researchers with SFRC and SCC mixes [33–35, 37]. The commercial availability and number of civil engineering applications of specific fibre types were also studied and taken into consideration [22].
Cement CEM I 42.5R was used as a binder. The specific gravity of the cement is equal to 3.1 g/cm3 and its fineness is equal to 3400 cm2/g. This cement is characterized by an initial setting time of 170 min and a final setting time of 250 min. Compressive strengths after 2, 7 and 28 days are equal to 24 ± 2, 41 ± 2 and 52 ± 3 MPa, respectively. The chemical composition of the cement is presented in Table 2.
The aggregates used for the mixes were of natural origin. Natural fine aggregate was sand characterized by the maximum diameter of 2 mm and median diameter of 0.435 mm [21]. Coarse aggregate was in a form of crushed basalt gravel characterized by the maximum diameter of 8 mm. Admixtures utilized to compose SFR-SCC were chosen according to rules defined in [9]. The selected superplasticizer was characterized by a density of 1.07 g/cm3 and was based on polycarboxylate-ether (concentration 20 %). The base constituent of the selected stabilizer was a synthetic co-polymer. The density of the stabilizer was equal to 1.01 g/cm3. The mixes were prepared using a relatively high content of cement (490 kg/m3). Similar cement contents in SCC was investigated and successfully applied by several researchers [15, 32, 44]. The dosage of fine and coarse aggregates were both equal to 800 kg/m3. In order to maintain a water/cement ratio of 0.41, tap water was added in a volume of 201 kg/m3. Superplasticizer was added to the fresh mix in order to achieve the slump flow range of 720 ÷ 800 mm of SCCs modified by fibre. The amount of 3.5 % (17.2 kg/m3) of superplasticizer proved to be sufficient to achieve the slump flow of 830 mm for unreinforced SCC. Stabilizer was added in the amount of 1.96 kg/m3. The described mixture was modified by 0.5, 1.0 and 1.5 vol% of steel fibres. The described mix proportions were achieved using mix proportioning system proposed by Okamura and Ozawa [28]. This system was successfully developed in Japan and applied for in situ applications and prefabrication. The aggregate contents are fixed. The self-compatibility is achieved only by adjusting the water-powder ratio and superplasticizer dosage [11, 28]. The utilized mixing procedure is presented in Table 3. The mix design has not been adjusted (as proposed by Ferrara et al. [14]) to account for the incorporation of larger volumes of fibre. In this way the compliance with previous research programmes [36–38, 43] was maintained and full comparison of achieved results is enabled.
3 Cast specimens and research programme
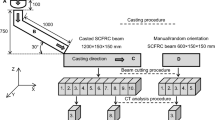
The research programme was divided in two stages. The first stage focused on non-destructive testing of cast specimens. During this stage, 13 SFR-SCC specimens in the form of beams (1200 mm × 150 mm × 150 mm) were cast. The slump-flow test was utilized to check the flowability of the mixes, according to RILEM TC 145-WSM [41]. The slump-flow diameter (SFD), and time to reach the 500 mm spread (T 50) of the fresh mix were measured. Density and air content in the fresh mix were also investigated.
The cast beams were differentiated by fibre type and fibre volume. Six specimens were cast with Fibre 35; six specimens were produced with Fibre 50 and one specimen without fibres. The CCP was located near one end of a beam (see Fig. 1). After hardening, the beams were cut into two specimens (BEAM I and BEAM II) having dimensions of 600 mm × 150 mm × 150 mm each. 24 specimens (12 BEAM I and 12 BEAM II) were cured for 14 days and then they were subjected to XCT imaging using a 64-row medical scanner GE Discovery 690. The penetration factor was an X-ray beam with parameters of acquisition protocol not less than a cathode voltage of 140 kV, X-ray tube current of 400 mA using helical mode. After tomography reconstruction volumetric images of size 512 × 512 × 1500 (voxel size 0.47; 0.47; 0.4 mm) were obtained. This protocol was described in detail in an earlier publication [37]. The thickness of a series of reconstructed native CT scan was 0.625 mm. The examined surface of each layer of concrete was 150 mm × 150 mm. For each specimen the result consisted of a native series written in Digital Imaging and Communications in Medicine (DICOM) format with 12-bit gray-scale intensity with at least 950 images. Voxel intensity was expressed in Hounsfield Units (HU). The reconstructed series consisted of at least 1500 images (taking into account the interval in the range 50 ÷ 80 % of the thickness of the native layer). The acquired CT volumetric images were processed by in-house written software using C++ libraries for medical image processing “The Insight Toolkit” [17]. Using this data, spherical histograms were generated following the procedure used in previous research programmes by Rudzki et al. [43] and by Ponikiewski et al. [37], which completed the first stage of the research programme.
The second stage of the research programme focused on mechanical properties of SFR-SCC. After additional 14 days of curing three-point bending tests were conducted on notched specimens. The tests were performed according to the general guidelines of RILEM TC 162-TDF [42] and EN 14651-2005 [12] measuring the load—CMOD (crack mouth opening displacement) response. During the tests the mid-span deflection of the specimen increased at a constant rate of 0.2 mm/min. The tests were performed until the beam reached a deflection of 5 mm. The deflection of the two opposite sides of the specimen was measured in the centre of the specimen by a LVDT sensor placed on a steel frame. The steel frame was supported at the top and on both sides of the specimen. The steel frame was used to avoid deformations in overall deflection coming from the subsidence or rotation of the specimen on the supports, which was widely investigated by Banthia and Trottier [3]. The CMOD was measured, simultaneously with the beam deflection, with a clip gauge attached at the knife-edge. The acceptable error level for the CMOD was chosen according to [2]. After execution of the three-point bending tests, the beams were cut into 150 mm × 150 mm × 150 mm cubes and their compressive strength was tested, which completed the second stage of the research programme.
4 Test results
The results achieved during the first stage of the research programme are summarized in Table 4. The value of the SFD ranged from 720 ÷ 830 mm. The smallest value of SFD was achieved for both SFR-SCC modified by the maximum (1.5 %) volume of steel fibres. The largest SFD was achieved for the cement matrix without fibres. The time to reach 500 mm spread varied from 1.5 ÷ 2.5 s. T 50 was equal to 1.5 s for the matrix without fibres. Five SFR-SCC mixes were characterized by T 50 = 2.0 s, and seven mixes were characterized by T 50 = 2.5 s. There are no official requirements for properties of fresh SFR-SCC mixes, thus the properties of the fresh mixes were compared with requirements given by EFNARC for non-reinforced SCC [11]. All composites in question fulfilled the criteria for properties of fresh non-reinforced mix to be classified as SCC. The density (ρ m) and air content of the fresh (A cm) mixtures were determined for quality control and to check the homogeneity of the mixtures. The mixture without fibres was characterized by the lowest density ρ m = 2317 kg/m3. Along with increasing the volume of fibre the density of composites increased; the density was 2425 kg/m3 for V f = 1.5 % (fibre F35). The air contents of the SFR-SCCs were in the range of A cm = 2.45 ± 0.35 %, while the A cm of the matrix was equal to 1.6 %.
The compressive strength of matrix was about 62.0 MPa. The addition of randomly distributed short steel fibres influenced the compressive strength of the tested composites. For the maximum volume of added fibres, the compressive strength reached 80 MPa. It means that the value of compressive strength was increased by almost 30 %.
The results achieved during the second stage of the research programme allowed to calculate flexural tensile strength (for limit of proportionality—LOP) for notched beams (f L). The LOP strength was determined by interpolation of the elastic part of the test. The applied equation [1, 19] is as follows:
where f L is the load corresponding to the LOP; l, b, h are the span, width and depth of a beam; a 0 is the height of notch.
The values of residual flexural strengths were also determined: f R,1, f R,2, f R,3 and f R,4 determined for CMOD equal to 0.5, 1.5, 2.5 and 3.5 mm, respectively. The equations defining these strengths are given in [32, 42]. Strengths f R,1 and f R,3 are considered as significant for service and ultimate conditions, respectively. The strength f L represents the nominal strength class in the fib classification [16] and strength ratio f R,3/f R,1 represents the softening or hardening of composite behaviour. Conventional reinforcement substitution is possible when at the ultimate limit state the following conditions are met:
The values of residual flexural strength of all tested composites with assigned strength class are presented in Table 5. The strength interval ranges from 1.5 to 9. Sixteen composites are characterized by class b, four by class a, three by class c and one by class d of residual strength ratio. All SFR-SCCs fulfil the requirements for enabling conventional reinforcement substitution. The graphical representation of all five residual strengths (f R,1, f R,2, f R,3, f R,4 and f L) with corresponding equations are shown in Figs. 2 and 3. The largest deflection at the maximum load (F MAX), equal to 0.83 mm, was noted for specimens modified by 1.5 % of F50 fibres.
In Fig. 4 selected 2D- and 3D-XCT images of steel fibres in tested SFR-SCCs are shown. 2D-images are basically the fracture surfaces. 3D-images show the central area (200 mm long) of beams. The images show composites modified by different volumes of fibres F50. In case of 2D-images there is a characteristic picture deformation at the edges. This phenomenon is associated with the internal structure of the concrete as a result of the mix flowing during casting. There are no large clusters of fibres in the matrix. The arrangement of fibres during casting is parallel to the direction of the flow. There are only few fibres arranged perpendicularly to the direction of flow. Apart from assessing general fibre spacing and spacing uniformity the XCT images allowed to calculate the density of fibre spacing (ρ F). This parameter is basically the number of fibres identified in a particular cross-section of a specimen using XCT images. The density of fibre spacing was expressed in 1/cm2 and summarized in Table 6.
5 Discussion
As expected, for both types of steel fibres, the beams reinforced by higher fibre volumes are characterized by higher flexural tensile strengths. Fibre F50 seems to be more effective in improving the flexural tensile strength of tested SFR-SCC than fibre F35. The distance from CCP strongly influences the f L of SFR-SCC. This phenomenon, is the most visible, in case of the maximum addition of fibre F50. However, this dependency was more pronounced for fibre dosages higher than 1.0 %. The observed increase of the flexural tensile strength is almost linear, thus the authors decided to use the formula proposed by Akcay [1]. This formula based on the research of Naaman and Reinhardt [27], allows to calculate the flexural strength of SFRC in a very straightforward way:
where L is the length of steel fibres, d is the diameter of steel fibre, σ mu is flexural strength of matrix; V f is the volume of steel fibres; k 1, k 2 are the coefficients.
In case of the studied composites, the value of k 1 is equal to 1.0. The same value of k 1 was obtained by other researchers [1, 18, 19]. On the basis of the test results of this research programme, the value of k 2 was ranging from 0.18 to 0.19 and from 0.19 to 0.23 for F35 and F50 fibres, respectively (see Fig. 2). These values are similar to the ones presented by Akcay [1] and Kang [19].
Residual tensile strengths f R,1, f R,2, f R,3, f R,4 presented in Fig. 3, differ dependent on the fibre type and location of CCP. The highest values of the strength were obtained for specimens reinforced by F50 and located far from the CCP (Beam II). Specimens cut from where CCP was located are characterized for this beam by much smaller values of residual tensile strengths. The larger the volume of fibre, the larger the difference between mechanical characteristic of Beam I and Beam II. In case of composites modified by F35, strength characteristics of both types of specimen (located close to the CCP—Beam I, and located far from the CCP—Beam II) are very similar. All relations presented in Figs. 2 and 3 are prepared using V f on horizontal axis. In this method of preparing charts the amount of added fibre is assumed to be fixed and uniform throughout the whole volume of concrete. The consistency of SFR-SCC and associated with it a different way of casting the mix significantly influence fibre distribution. Usually (depending on mix design and rheological characteristics) fibre distribution of SFR-SCC is impaired on a much greater scale than in ordinary SFRC. This phenomenon was noted and described in previous publications [36, 38] dealing with SFR-SCC slab and wall elements. To get accurate relationship between fibre volume and mechanical parameters of a given SFR-SCC element, XCT procedures were used to calculate the density of fibres (ρ F) for each fracture surface. The influence of density of fibre spacing of the fracture surface (expressed in 1/cm2) on LOP tensile strength f L of tested SFR-SCC is presented in Fig. 5. In the same way all four residual flexural strengths are presented in Fig. 6.
On the basis of the comparison of Figs. 2 and 3 with Figs. 5 and 6 it can be stated that the general shape and slopes of all relationships are similar. Differences are noticeable for f L and f R,1 characteristics. When using ρ F for f L and f R,1 characteristics instead of V f, larger differences between F35—Beam I and F35—Beam II can be observed. Both f L and f R,1 characteristics are vital for classification of the post-cracking strength of SFR-SCC. Using either V f or ρ F for the prediction of strengths characteristics can influence the strength classification according to “fib Model Code 2010” and possible reinforcement substitution associated with it.
6 Conclusions
The following conclusions can be drawn, based on the conducted research programme:
-
The location of CCP influences the fibre distribution in SFR-SCC beams.
-
SFR-SCC mixes with longer steel fibre are much more susceptible to the location of CCP, than the same mixes with shorter steel fibre.
-
The length of steel fibres significantly influences mechanical characteristics of SFR-SCC.
-
A formula describing the flexural strength of SFRC proposed by Akcay is valid for SFR-SCC notched beams with crimped steel fibres. The calculated correction factors are similar to those published by Akcay.
-
Medical XCT method can be used for assessing the fibre distribution in SFR-SCC elements.
-
Differences in strength characteristics based on V f and ρ F were observed and are
-
A dedicated image processing software for analysis of concrete, allowing fully automatic fibres and air pore segmentation (providing data on their position, orientation and shape properties), should be developed.
-
The research programme should be conducted using multiple types of fibre and geometric shapes of cast beams.
References
Akcay B, Tasdemir MA (2012) Mechanical behaviour and fibre dispersion of hybrid steel fibre reinforced self-compacting concrete. Constr Build Mater 28:287–293
Baar BIG, Lee MK (2003) Round-robin analysis of the RILEM TC 162-TDF beam—bending test: Part 2—approximation of d from the CMOD response. Mater Struct 36:621–630
Banthia N, Trottier J-F (1995) Test methods for flexural toughness characterization of fiber reinforced concrete: some concerns and a propositions. ACI Mater J 92(1):48–57
Bentur A, Mindess S (2007) Fibre reinforced cementitious composites, 2nd edn. Taylor & Francis, London
Brandt AM (2009) Cement-based composites. Materials, mechanical properties and performance. Taylor & Francis, London
Bui VK, Geiker MR, Shah SP (2003) Rheology of fiber reinforced cementitious materials. In: Naaman AE, Reinhardt HW (eds) Proceedings of HPFRCC4 workshop, Ann Arbor. RILEM Publications, Cachan, pp 221–231
Bywalski C, Kamiński M (2011) Estimation of the bending stiffness of rectangular reinforced concrete beams made of steel fibre reinforced concrete. Arch Civ Mech Eng 11(3):553–571
Corinaldesi V, Moriconi G (2011) Characterization of self-compacting concretes prepared with different fibers and mineral additions. Cem Concr Compos 33(5):596–601
Deeb R, Karihaloo BL, Kulasegaram S (2014) Reorientation of short steel fibres during the flow of self-compacting concrete mix and determination of the fibre orientation factor. Cem Concr Res 56:112–120
Eberhardt C, Clarke A (2001) Fibre-orientation measurements in short-glass-fibre composites. Part I: automated, high angular-resolution measurement by confocal microscopy. Compos Sci Technol 61:1389–1400
EFNARC (2002) Specification and guidelines for self-compacting concrete, English edn. European Federation for Specialist Construction Chemicals and Concrete Systems, Norfolk, February 2002
EN 14651:2005+A1:2007(E). Test method for metallic fibre concrete—measuring the flexural tensile strength (limit of proportionality (LOP), residual). CEN European Commit-439 tee for Standardization 440
Ferrara L, Meda A (2006) Relationships between fibre distribution, workability and the mechanical properties of SFRC applied to precast roof elements. Mater Struct 39:411–420
Ferrara L, Park Y-D, Shah SP (2007) A method for mix-design of fiber-reinforced self-compacting concrete. Cem Concr Res 37:957–971
Ferrara L, Bamonte P, Caverzan A, Musa A, Sanal I (2012) A comprehensive methodology to test the performance of steel fibre reinforced self-compacting concrete (SFR-SCC). Constr Build Mater 37:406–424
fib Model Code for Concrete Structures (2010) Ernst & Sohn, 2013. ISBN: 978-3-433-03061-5
Ibáñez L, Schroeder W, Ng L, Cates J (2005) The ITK Software Guide. Kitware. http://www.itk.org/ItkSoftwareGuide.pdf
Kang ST, Kim JK (2011) Investigation on the flexural behavior of UHPCC considering the effect of fiber orientation distribution. Constr Build Mater 28:57–65
Kang ST, Lee Y, Park YD, Kim JK (2010) Tensile fracture properties of an Ultra High Performance Fiber Reinforced Concrete (UHPRFC) with steel fiber. Compos Struct 92:61–71
Katzer J (2008) Properties of precast SFRCC beams under harmonic load. Sci Eng Compos Mater 15(2):107–120
Katzer J (2012) Median diameter as a grading characteristic for fine aggregate cement composite designing. Constr Build Mater 35:884–887
Katzer J, Domski J (2012) Quality and mechanical properties of engineered steel fibres used as reinforcement for concrete. Constr Build Mater 34:243–248
Khayat KH, Manai K, Trudel A (1997) In situ mechanical properties of wall elements cast using self-consolidating concrete. ACI Mater J 94(6):491–500
Kim KY, Yun TS, Choo J, Kang DH, Shin HS (2012) Determination of air-void parameters of hardened cement-based materials using X-ray computed tomography. Constr Build Mater 37:93–101
Liu JP, Li CF, Liu JZ, Cui G, Yang Z (2013) Study on 3D spatial distribution of steel fibers in fiber reinforced cementitious composites through micro-CT technique. Constr Build Mater 48:656–661
Martinie L, Roussel N (2011) Simple tools for fiber orientation prediction in industrial practice. Cem Concr Res 41:993–1000
Namman AE, Reinhardt HW (2006) Proposed classification of FRC composites based on their tensile response. Mater Struct 39(5):547–555
Okamura H, Ozawa K (1995) Mix design for self-compacting concrete. Concr Lib JSCE 25:107–120
Orbe A, Cuadrado J, Losada R, Rojí E (2012) Framework for the design and analysis of steel fiber reinforced self-compacting concrete structures. Constr Build Mater 35:676–686
Ozyurt N, Woo LY, Mason TO, Shah SP (2006) Monitoring fiber dispersion in fiber reinforced cementitious materials: comparison of AC-impedance spectroscopy and image analysis. ACI Mater J 103(5):340–347
Ozyurt N, Mason TO, Shah SP (2006) Non-destructive monitoring of fiber orientation using AC-IS: an industrial-scale application. Cem Concr Res 36:1653–1660
Pająk M, Ponikiewski T (2013) Flexural behavior of self-compacting concrete reinforced with different types of steel fibers. Constr Build Mater 47:397–408
Ponikiewski T (2012) The rheological and mechanical properties of steel fibres reinforced self-compacting concrete. Cement Wapno Beton 79:301–309
Ponikiewski T, Gołaszewski J (2012) The new approach to the study of random distribution of fibres in high performance self-compacting concrete. Cement Wapno Beton 79:165–176
Ponikiewski T, Gołaszewski J (2013) The effect of casting by local moulds filling on the steel fibres distribution of self-compacting concrete beams and their strength. Cement Wapno Beton 80:91–99
Ponikiewski T, Katzer J, Bugdol M, Rudzki M (2014) Steel fibre spacing in self-compacting concrete precast walls by X-ray computed tomography. Mater Struct. doi:10.1617/s11527-014-0444-y
Ponikiewski T, Gołaszewski J, Rudzki M, Bugdol M (2015) Determination of steel fibres distribution in self-compacting concrete beams using X-ray computed tomography. Arch Civ Mech Eng 15:558–568
Ponikiewski T, Katzer J, Bugdol M, Rudzki M (2015) X-ray computed tomography harnessed to determine 3D spacing of steel fibres in self-compacting concrete (SCC) slabs. Constr Build Mater 74(15):102–108
Pradhan AK, Das D, Chattopadhyay R, Singh SN (2012) Effect of 3D fiber orientation distribution on transverse air permeability of fibrous porous media. Powder Technol 221:101–104
Promentilla MAB, Sugiyama T, Shimura K (2008) Three dimensional characterization of air void system in cement-based materials. In: Third Asian concrete federation (ACF) international conference, Ho Chi Minh, pp 940–947
RILEM TC 145-WSM (2002) Workability and rheology of fresh concrete: compendium of tests. In: Bartos PJM, Sonebi M, Tamimi AK (eds) Report of RILEM technical committee TC 145-WSM workability of special concretes. RILEM Publications, Cachan
RILEM TC 162-TDF (2002) Test and design methods for steel fibre reinforced concrete, final recommendations. Mater Struct 35(9):579–582
Rudzki M, Bugdol M, Ponikiewski T (2013) Determination of steel fibers orientation in SCC using computed tomography and digital image analysis methods. Cement Wapno Beton 80:257–263
Sahmaran M, Yurtseven A, Yaman IO (2005) Workability of hybrid fiber reinforced self-compacting concrete. Build Environ 40:1672–1677
Şanal İ, Ozyurt N (2013) To what extent does the fiber orientation affect mechanical performance? Constr Build Mater 44:671–681
Swamy RN (1975) Fibre reinforcement of cement and concrete. Mater Struct 8(45):235–254
Torrents JM, Blanco A, Pujadas P, Aguado A, Juan-Garcίa P, Sánchez-Moragues MÁ (2012) Inductive method for assessing the amount and orientation of steel fibers in concrete. Mater Struct 45:1577–1592
Vavrik D, Jandejsek I, Fila T, Vesely V (2013) Radiographic observation and semi-analytical reconstruction of fracture process zone in silicate composite specimen. Acta Technica CSAV (Ceskoslovensk Akademie Ved) 58(3):315–326
Wong RCK, Chau KT (2005) Estimation of air void and aggregate spatial distributions in concrete under uniaxial compression using computer tomography scanning. Cem Concr Res 35(8):1566–1576
Zerbino R, Tobes JM, Bossio ME, Giaccio G (2012) On the orientation of fibres in structural members fabricated with self-compacting fibre reinforced concrete. Cem Concr Compos 34:191–200
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ponikiewski, T., Katzer, J. X-ray computed tomography of fibre reinforced self-compacting concrete as a tool of assessing its flexural behaviour. Mater Struct 49, 2131–2140 (2016). https://doi.org/10.1617/s11527-015-0638-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1617/s11527-015-0638-y