Introduction

The need for systems with enhanced energy and power density has driven research into perovskite-filled polymer-matrix nanocomposites [1,2,3]. Barium titanate (BTO) is a ferroelectric perovskite with the chemical formula BaTiO3. BTO exhibits a tetragonal lattice structure that demonstrates exceptional electrical polarizability [4, 5]. The dielectric properties of BTO have made it an attractive material for high-energy density systems. For example, multilayer ceramic capacitors (MLCCs) are widely used in electronic devices that require high-performance capacitors with micrometer-scale dimensions [4, 6,7,8]. MLCCs are composed of several hundred dielectric layers, which makes the use of nanoparticles in these capacitors advantageous [9]. Previous studies have shown that the dielectric constant of BTO particles is maximized at a diameter of ~ 1 μm and exponentially decreases at smaller diameters [10, 11]. However, several studies of BTO nanoparticles have observed narrow but high-magnitude peaks in BTO dielectric constant at diameters between 70 and 140 nm [12, 13]. Therefore, understanding the role of BTO nanoparticle diameter with respect to BTO dielectric constant requires further study.

In this work, we present the impact of BTO nanoparticle diameter on the dielectric constant of the perovskite through the fabrication and characterization of nanocomposites consisting of BTO nanoparticles in an acrylonitrile butadiene styrene (ABS) matrix. Polymer-matrix nanocomposites are particularly relevant given the increased demand for embedded passive components, such as capacitors [13,14,15,16]. The method that was utilized to determine the dielectric constant of BTO nanoparticles in this study is detailed in Fig. 1. BTO nanoparticles with diameters ranging between 50 and 500 nm were incorporated into ABS and subsequently injection molded into nanocomposite discs. The discs were sputtered with gold to create parallel plate capacitors, which enabled the dielectric constants of the nanocomposites to be measured. Dielectric constants of BTO nanoparticles were determined by comparing experimentally measured nanocomposite dielectric constants with results from COMSOL finite element analysis (FEA) simulations of the nanocomposites.

Fig. 1
figure 1

Method of extracting the dielectric constants of BTO nanoparticles through experimental measurements and computational simulations of nanocomposites using COMSOL

Full size image

Materials and methods

Fabricating and measuring BTO–ABS nanocomposites

The method of fabricating BTO-filled ABS-matrix nanocomposites is shown in Fig. 2a. BTO nanoparticles that were produced through a hydrothermal synthesis process with diameters of 50 nm, 100 nm, 200 nm, 300 nm, and 500 nm were provided by Sakai Chemical Industry Co., Ltd., (Japan). As-received BTO powders were de-agglomerated through a surfactant-assisted ball milling process [17, 18] using tert-Butylphosphonic acid (tBuPA) as a surfactant, which has been shown to limit the re-agglomeration of BTO nanoparticles after ball milling [19]. Similar BTO nanoparticles have been extensively characterized using Fourier transform infrared spectroscopy (FTIR) [20], x-ray diffraction (XRD) [21], Raman spectroscopy [21], solid-state nuclear magnetic resonance [20], and transmission electron microscopy (TEM) [20, 22]. A Bruker D2 Phaser diffractometer was used to obtain an XRD pattern of tBuPA-functionalized BTO nanoparticles (Fig. S1), which exhibits peaks that are characteristic of BTO. A Retsch PM100 ball mill with an yttrium-stabilized zirconium oxide grinding jar and yttrium-stabilized zirconium oxide grinding balls (0.8 mm diameter, Inframat 4039GM-S008) were used in the ball milling process. As shown in Sect. 2 in Supplementary Information, tBuPA was added in a 1:1 surface area ratio with the BTO nanoparticles. The surfactant was first ball milled for 30 min at 150 rpm to evenly distribute tBuPA in the ball milling jar. BTO was then added to the ball milling jar and milled at 150 rpm for an additional 4 h.

Fig. 2
figure 2

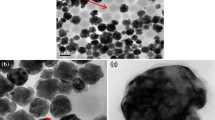
a Fabrication process of ABS-matrix nanocomposites containing de-agglomerated and functionalized BTO. b Image of a fabricated BTO–ABS nanocomposite sputtered with gold. c TEM image of BTO nanoparticles with an average nanoparticle diameter of 50 nm incorporated into an ABS matrix. Scale bar is 200 nm

Full size image

ABS was selected as the polymer matrix because it readily dissolves in acetone at ambient conditions, which enables dispersing and incorporating nanoparticles into the polymer. BTO nanoparticles functionalized with tBuPA were dispersed into a solution of ABS dissolved in acetone (0.3 g of ABS per mL of acetone) using an overhead mechanical mixer (XZBELEC DX-120D) at 450 rpm for 1 h. Solutions consisting of ABS, BTO, and acetone were deposited onto silicone trays, which were then placed in a fume hood for 10 h to evaporate the acetone. BTO–ABS nanocomposite sheets were then shredded and pelletized using a FilaBot Reclaimer. The resulting BTO–ABS pellets were further dried in a vacuum oven at 80 °C for 2 h. Dried pellets were fed into a LNS Technologies 150A injection molding apparatus operating at a barrel temperature of 260 °C. Nanocomposite specimens were created by injection molding melted pellets into a disc-shaped mold with a diameter of 40 mm and thickness of 2.5 mm. The mold was kept at an elevated temperature during injection molding using a hot plate. A hot plate temperature of 107 °C was found to enable melted ABS containing solid BTO nanoparticles to flow into the mold at each of the nanoparticle sizes studied. A Sartorius YDK03 density determination kit and Sartorius Entris 224-1S analytical balance were used to determine the experimental densities of the fabricated nanocomposites by the Archimedes principle [23, 24]. Using techniques reported in literature [23, 24], the measured densities of fabricated specimens were compared to theoretical nanocomposite densities, which confirmed the BTO vol% in the specimens. The fabrication process described herein enabled ABS-matrix nanocomposites with a maximum BTO loading of 40 vol% to be fabricated for BTO nanoparticles with diameters of 300 nm and 500 nm. However, the highest BTO loading that could be achieved for BTO nanoparticles with diameters of 50 nm, 100 nm, and 200 nm was 35 vol%. The differences in maximum BTO loading are believed to be the result of a constant amount of ABS interfacing with BTO nanoparticles that had increasing total surface areas with decreasing diameters. Therefore, this study focused on fabricating ABS-BTO nanocomposites with a filler loading of 35 vol% for all the nanoparticle sizes that were investigated. The average loading of BTO nanoparticles in ABS for the specimens produced in this work was 34.9 ± 2.2 vol%.

Disc-shaped nanocomposites were sputtered with a layer of gold with a thickness of 100 nm using an EMS 150RS sputter coater (Fig. 2b). Capacitance measurements were taken using an ECG CX-920A capacitance meter at the 200 pF level inside a Faraday cage using the setup shown in Fig. S2 in the Supplementary Information. Between three to five specimens were measured in triplicate for each nanoparticle size. The dielectric constant of each nanocomposite was calculated from capacitance measurements using Equations S1 and S2 in Supplementary Information. TEM specimens of the nanocomposites were prepared using a Leica EM UC7 Ultramicrotome. The dispersion of BTO nanoparticles in ABS was characterized using a JEOL Tecnai F30 transmission electron microscope. A TEM image of 50 nm BTO nanoparticles in an ABS matrix is shown in Fig. 2c. Additional TEM images of 50 nm, 200 nm, and 500 nm BTO nanoparticles in ABS are shown in Fig. S3 in Supplementary Information.

Computational simulations of BTO–ABS nanocomposites

The impact of the dielectric constants of BTO nanoparticles on the dielectric constants of BTO–ABS nanocomposites was determined using a combination of Python, MATLAB, and COMSOL Multiphysics FEA software. Nanocomposite models were created using two-dimensional representations of nanoparticles in ABS, which were based on TEM images of fabricated nanocomposites (Fig. 2c). Using techniques reported by Ferro et al. [25], two-dimensional representations of nanoparticles in ABS were processed using Python’s OpenCV image processing packages, which created a text file containing the geometric and spatial parameters of the nanoparticles within the polymer matrix (Fig. 3). MATLAB LiveLink was used to import the Python text files containing nanoparticle parameters into COMSOL, where nanocomposites with a finite number of BTO nanoparticles dispersed in a matrix were created. The matrix material was set to ABS and gold electrodes were located on the top and bottom faces of the matrix, which had the shape of a rectangular prism. The relative dielectric constants for gold and ABS were assumed to be 1 and 3.194 [26], respectively. BTO nanoparticles were assumed to be spherical and equally sized within the ABS polymer matrix to generate nanocomposites with a BTO loading of 34.9 vol%. Based on twenty TEM images of BTO–ABS nanocomposites containing BTO with diameters of 50 nm, 200 nm, and 500 nm, the spherical morphology of BTO nanoparticles was assumed to be appropriate for each of the BTO nanoparticle sizes that were investigated in this study. Following techniques that were previously reported by Kaufmann et al. [27], FEA was performed on modeled nanocomposites using COMSOL and its AC/DC module, which enables electrostatics modeling. Nanocomposite dielectric constants were obtained in COMSOL using a volumetric internal energy calculation, which is shown in Sect. 5 in Supplementary Information. The dielectric constant that was calculated for each nanocomposite model was then compared to the experimentally measured dielectric constant for each nanocomposite specimen. As summarized in Fig. 3, the dielectric constants of BTO nanoparticles were extracted by determining the values of BTO dielectric constants that resulted in matches between the dielectric constants of modeled nanocomposites and fabricated nanocomposites.

Fig. 3
figure 3

Process of modeling ABS-matrix nanocomposites filled with BTO nanoparticles to extract dielectric constants of BTO nanoparticles

Full size image

Results and discussion

The average dielectric constants of fabricated nanocomposites at each BTO nanoparticle size are shown in Fig. 4a, which reveals a relationship between nanoparticle diameter and nanocomposite dielectric constant. Specimens containing nanoparticles with diameters greater than 200 nm were found to have higher average nanocomposite dielectric constants relative to specimens containing BTO with diameters of 100 nm and 50 nm. Some sample-to-sample variation in BTO loading in the fabricated nanocomposites was observed and is tabulated in Table S1 of Sect. 6 in Supplementary Information. However, a two-way analysis of variance (ANOVA) on the data with nanoparticle size and volume percent as independent variables revealed that the observed variations in BTO loading did not have a significant effect on the nanocomposite dielectric constants for the specimens in this study (see Sect. 7 in Supplementary Information). The ANOVA results therefore indicate that the nanocomposite dielectric constants were influenced by the sizes of the BTO nanoparticles.

Fig. 4
figure 4

a Measured dielectric constants of BTO–ABS nanocomposites across nanoparticle diameters. Mean and error of one standard deviation are shown. Sample sizes range between 3 and 5. b Relationship between BTO nanoparticle dielectric constant and BTO–ABS nanocomposite dielectric constant (computed). c BTO dielectric constant at each nanoparticle size. Mean and error of one standard deviation are shown

Full size image

Figure 4b shows the relationship between the dielectric constants of BTO nanoparticles and the dielectric constants of BTO–ABS nanocomposites that were determined using COMSOL. Based on the ANOVA results, the assumption of a BTO loading of 34.9 vol% was justified in the COMSOL models of the fabricated nanocomposites. The range of nanoparticle dielectric constants was chosen based on the values of BTO dielectric constants reported in literature [10, 11]. COMSOL simulations revealed that the BTO–ABS nanocomposite dielectric constant increases sharply as the BTO dielectric constant increases but eventually plateaus at a nanocomposite dielectric constant of ~ 24. This behavior, which is shown in Fig. 4b, is consistent with trends previously observed in COMSOL simulations of BTO nanoparticles in an epoxy matrix [27], which suggests that the dielectric constants of nanocomposites containing BTO have an upper limit in polymer matrices.

Figure 4c shows how the dielectric constant of BTO depends on nanoparticle diameter, which was obtained by combining the experimental results (Fig. 4a) with the COMSOL results (Fig. 4b). BTO nanoparticles with diameters between 200 and 500 nm in ABS demonstrated the highest dielectric constant values of the nanoparticle sizes that were investigated. Slight variations in dielectric constants were observed for nanoparticle diameters between 200 and 500 nm, but the regions of uncertainty for nanoparticle sizes in this range overlap, which indicates that this variation may not be significant. There was a considerable decrease in dielectric constant for nanoparticles smaller than 200 nm. Nanoparticles with a diameter of 50 nm had the lowest dielectric constant. The rate of decrease in dielectric constant is greatest for nanoparticle diameters between 100 and 50 nm. BTO nanoparticles with diameters of 100 nm demonstrated an average dielectric constant more than four times larger than the 50-nm nanoparticles, while the mean dielectric constant value of 500-nm nanoparticles was found to be more than eight times greater than the mean dielectric constant of 50-nm nanoparticles. The considerable decline in dielectric constant at smaller BTO grain sizes has been previously observed in studies of BTO thin films [11]. However, the maximum dielectric constant of BTO reported by Aygün et al. is larger than the values found through the methods described in this study [11]. Aygün et al. studied spin-casted BTO deposited on copper plates, whereas this study focused on BTO produced through hydrothermal synthesis and incorporated in ABS. This difference between studies indicates that processing parameters have a significant impact on BTO dielectric constant [11]. It should be noted that the prominent spikes in dielectric constant that have been reported in some literature [9, 12, 13, 28] were not observed in any of the nanoparticle diameters investigated in this study. Particle size has also been shown to have an effect on the lattice parameters of BTO [29]. Previous reports have found that either the cubic or orthorhombic phases of BTO is favored at room temperature with grain size reduction [21, 30]. As the dielectric properties of BTO are directly related to its tetragonal lattice structure, the results shown in Fig. 4c could be a result of changes to the lattice structure of BTO at nanoparticle diameters below 200 nm.

Conclusion

Here we have demonstrated an experimentally and computationally paired study of the influence of size on the dielectric constant of BTO nanoparticles in ABS. BTO nanoparticles between 200 and 500 nm in diameter were found to exhibit dielectric constants between 2000 and 3000. The dielectric constant of BTO declined sharply at nanoparticle diameters below 200 nm. These findings advance the understanding of the effect of particle size on the dielectric properties of BTO. However, the impact of BTO loadings greater than 34.9 vol% in ABS on the dielectric properties of BTO–ABS nanocomposites should be investigated, which will require modifications to the nanocomposite fabrication process used in this study. Additionally, more advanced modeling methods should be developed to understand the effects of non-uniform nanoparticle arrangements, various degrees of nanoparticle agglomeration, and different nanoparticle orientations on BTO dielectric properties. These advanced modeling methods will require further characterization of BTO–ABS nanocomposites by techniques, such as TEM, scanning electron microscopy, FTIR, and XRD. Developing advanced energy storage and power conditioning systems will require a better understanding of perovskites and nanomaterials with high dielectric constants.