Introduction

The sport of surfing is rapidly growing in number of participants and was introduced as an Olympic sport at the Tokyo Olympics [1, 2]. Surfboards are fitted with fins to give the surfer control and manoeuvrability while riding waves. It is well known that experienced surfers change their fins depending on the wave conditions to enhance their surfing performance. During surfing manoeuvres, fins will experience a lift and drag forces that act perpendicularly and parallel, respectively, to the flow of water around their fins. The magnitude of these lift and drag forces depends on the shape of the fins and the angle of attack (between fin and flow of water). The manoeuvrability and, in turn performance, of the surfers are influenced by the magnitude and ratio of the lift and drag forces generated on surfboard fin [3]. Developing fins which can optimise surfing performance, therefore, requires cooperation between surfers, fin manufacturers, and surfboard manufacturers [4].

It is well known from aerodynamic studies on airplane wings that performance can be enhanced by increasing lift and/or decreasing drag, resulting in an increased lift-to-drag ratio. The same principle can be applied to the lift and drag experienced by fins in surfboards. Several researchers have studied the hydrodynamic performance of three- and four-fin configurations using computational fluid dynamics (CFD) [3, 5,6,7,8,9,10]. It has been shown that the maximum lift for three-fin configurations occurred at smaller angle of attached compared to four-fin configurations [6].

Recently, a CFD study has evaluated the performance of a variety of conventional fin designs and used the results to design a fin for a specific ocean wave (WinkiPop in Australia) [10]. The research team demonstrated that variations in rake showed the biggest impact on the turbulence intensity at angles of attack larger than 20 degrees. It was shown that variations in base length resulted in greater lift at small angle of attack values, but significant lift losses at high angles of attack [10].

Investigation of the hydrodynamic performances of whale flippers has demonstrated that modifying the leading-edge shape could enhance performance and manoeuvrability [11]. These studies showed that introducing tubercles to the leading edge significantly improved in the drag (reduction of 11%) and lift-to-drag ratio (increase of 18%) at an angle of attack of 10 degrees compared to a section with no tubercles [11].

Herein, we describe a CFD performance analysis of conventional surfing fins and fins with a modified leading-edge shape (so-called grooved fins) to determine whether the grooved edge improved the lift-to-drag ratio.

Materials and methods

Fin design

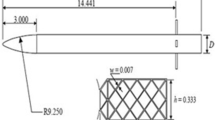
A conventional surfing fin was designed based on the National Advisory Committee for Aeronautics (NACA) airfoils, with fin dimensions similar to those of medium-sized commercial fins (Fig. 1A and B). The main fin dimensions of the conventional fin were rake (29 degrees), base (111 mm), and depth (115 mm). A second fin was designed with a modified leading edge and grooves, hereafter referred to as a “grooved fin” (Fig. 1C and D). The main dimensions of the grooved fin were similar to the conventional fin (Fig. 1A and B) but included 6 grooves that were 60 mm in length with a separation of 6 mm between each grooves (Fig. 1C and D). All fins were designed using computer-aided design (CAD, Solidworks, see Fig. 1).

Fig. 1
figure 1

Fin designs. A Dimensions of conventional fin. B Leading edge of conventional fin. C Dimensions of grooved fin, arrows indicate position of grooves with length 60 mm and separation of 6 mm. D Leading edge of grooved fin. All fins are shown with FCS2 bases

Full size image

Computational domain

The flow domain resembled the shape of a cube, with side of 700 cm and a height of 350 cm (Fig. 2A). The fins were attached to an idealised surfboard of 6 feet (186 cm) in length and 20 inches (50 cm) in width in a twin-fin configuration.

Fig. 2
figure 2

Validation of CFD model. A Flow domain and boundary conditions. B Section of mesh of the surfboard with base of the fins. C Mesh of conventional fin. D Mesh of the surfboard with fins

Full size image

Two inlet boundary conditions (front and left-hand side) were used to define the angle of attack from the boundaries. Two outlet boundary conditions were used as shown in Fig. 1A. The underside of the surfboard and the fins boundaries were set as walls with free slip conditions to eliminate the influence of turbulence on the flow around the fins). The inlet velocity at the boundary was introduced as a function of the angle of attack which is the amount of rotation around the vertical axis (and is commonly known as yaw).

Mesh generation

The mesh was generated using ANSYS Workbench meshing software. The domain was sliced into several blocks to ease the process of grid generation and to control the element size. Both structured and unstructured meshes were used. The element size range used for the CFD simulations of both fins was 1–5 mm, whereas the element size for the fins and surfboard was kept below 1 mm. An inflation layer was applied around the fin regions in order to capture the boundary layer effects. The details of meshing for the whole domain, at the surfboard and on the fins are shown in Fig. 1B to D. The simulation consisted of 5,833,940 elements.

Model setup

All simulations used water as the working fluid with a 3D CFX solver employed to solve the incompressible Reynolds-averaged Navier–Stokes (RANS) equations. To account for the effect of turbulent flow, the shear stress transport SST k-ω turbulence model was used in this simulation because this approach is suitable for both internal and external flow regimes and is suitable for separating flows and adverse pressure gradients [12]. The convergence criteria were set to be 10–6 for all cases. The inlet flow velocity used in the simulation was set at a surfing relevant value of 5.6 m/s (20 km/h) and was informed by experimental data of surfers on waves [13].

Results and discussion

CFD simulations are beneficial to understanding the fluid mechanics and modifying complex geometries. In this study, we considered the effect of turbulent flow conditions around both conventional and grooved fins, and analysed the resulting hydrodynamic forces (lift and drag). The first step was to establish the CFD model and perform CFD simulations for the conventional fins under angles of attack up to 45°. In the second step, the grooved fins were analysed under the same model conditions and angles of attack.

A mesh independence study was conducted using three meshes with an element size range of 1–3 mm (very fine), 1–5 mm (fine), and 3–10 mm (coarse). The resulting number of elements for these three meshes was 6,900,000, 5,834,000, and 1,900,000, respectively. Convergence was attained in the first 100 iterations for all three meshes. The results (data not shown) indicate that a mesh element size range 3–10 mm resulted in drag force values that were similar to those found for the finer mesh ranges. However, the values for the lift force for the coarse mesh showed a larger variation compared to the corresponding values for the fine and very fine meshes. As a result, the fine mesh setting was used in all cases because it was considered accurate enough to obtain valid lift and drag values.

Pressure contours around fins for both the conventional and grooved fin cases, which are located close to the fin base, are shown in Fig. 3A and B, respectively. The highest pressure is observed for the leading edge and outside surface of the right fin and the inside surface of the left fin (see Fig. 1D for labelling of fins). Note that in our simulation, the inlet boundary conditions were imposed on the front and the right-hand side of the idealised surfboard, the flow of the water was directed at the outside surface of the right fin (and inside of the left fin) as the angle of attack was increased. Therefore, lift was mainly generated by the right fin following the well-known air foil theory in generating lift. The pressure contours would be reversed if the flow of water was directed at the outside surface of the left fin.

Fig. 3
figure 3

Pressure contours, lift, and drag. A Pressure contours around conventional fins at 0 mm below the base in water flow of 20 km/h under angle of attack of 20 degrees. B Pressure contours around grooved fins at 0 mm below the base in water flow of 20 km/h under angle of attack of 20 degrees. C Pressure contours around conventional fins at 85 mm below the base in water flow of 20 km/h under angle of attack of 20 degrees. D Pressure contours around grooved fins at 85 mm below the base in water flow of 20 km/h under angle of attack of 20 degrees. Arrows in (A–D) show direction of water flow. E and F Drag and Lift forces as a function of angle of attack for conventional (spheres) and grooved (squares) fins, respectively

Full size image

The results show that higher pressures contours were observed around the conventional fins compared to the grooved fins. Figure 3C and D shows that incorporating of a bumpy-leading edge (and grooves) resulted in a clear reduction in the pressure distribution. This result suggests that the grooved fins will experience lower drag forces compared to the conventional fins under the same flow conditions.

A comparison of the lift and drag forces generated for the conventional fins compared to the grooved fins is shown in Fig. 3E and F, and Table 1. For angles of attack below 15 degrees, there are minor differences in the lift and drag forces experienced by the two fin types. At all these angles of attack, however, the lift and drag forces were always smaller for the grooved fins compared to the conventional fins. At the stall angle (30 degrees), the drag forces on the grooved fins were reduced by 13 ± 1% compared to the conventional fins, although this was coupled with a small reduction in lift (3.8 ± 0.5%). This larger reduction in drag indicates that the grooves are beneficial and likely improve surfing performance (e.g. speed and manoeuvrability) of the fins.

Table 1 Summary of lift force (Lift), drag force (Drag), and Lift-to-Drag (L-to-D) ratio values for conventional (C-Fin) and grooved (G-Fin) fins
Full size table

The coefficients of drag (CD) and lift (CL) can be calculated using information about the fluid density, fluid velocity relative to the fin, and a fin reference area. Assuming that the reference areas of the conventional and grooved fins are similar, the lift-to-drag ratio can be obtained from the ratio of the drag and lift forces. For all angles of attack, the lift-to-drag ratio of the grooved fins is always outperformed the ratio observed for the conventional fins. At the stall angle (30 degrees) where the fins exhibit the largest amount of lift force, the lift-to-drag ratio of the grooved fins shows an improvement in performance of 11 ± 1% compared to the conventional fins (see Table 1).

Conclusions

A conventional surfboard fin and a surfboard fin with a bumpy-leading edge and grooves were designed using CAD. CFD simulation (ANSYS CFX) was used to compare the performance of the grooved fin (with a bumpy-leading edge) to conventional surfboard fins at a surfing relevant fluid velocity and angles of attack up to 45 degrees.

Introducing grooves and bumpy-leading edge to the fin design resulted in a relatively large reduction in drag forces with only a small decrease in lift and, in turn, an increased lift-to-drag ratio, indicating improved fin performance for surfing applications.

This paper contributes to the use of CFD simulation as a tool for evaluating and validating performance improving changes to the designs of surfboard fins before field testing fins in a surfing environment.