High-throughput prediction of stress–strain curves of thermoplastic elastomer model block copolymers by combining hierarchical simulation and deep learning

Abstract

We achieved high-throughput prediction of the stress–strain (S–S) curves of thermoplastic elastomers by combining hierarchical simulation and deep learning. ABA triblock copolymer with a phase-separated structure was used as a thermoplastic elastomer model. The S–S curves of the ABA triblock copolymers were calculated from the hierarchical simulation of self-consistent field theory calculations and coarse-grained molecular dynamics simulations. Because such hierarchical simulations require considerable computational resources, we applied a deep learning technique to accelerate the prediction. Sets of phase-separated structures and the S–S curves obtained from the hierarchical simulation were used to train a 3D convolutional neural network. Using the trained network, we confirmed that the predicted S–S curves of the untrained structures accurately reproduced the simulation results. These results will enable us to design novel polymers and phase-separated structures with desired S–S curves by high-throughput screening of a wide variety of structures.

Graphic abstract

Introduction

Thermoplastic elastomers (TPEs) are typical industrial products, in which the process of microphase separation of block copolymer is utilized [1, 2]. The products have many applications in daily life—e.g., elastic fibers, films, and adhesives. Dynamic properties such as non-linear stress–strain (S–S) behaviors are key to the design of such industrial products. Phase-separated structures and polymer chain structures affect S–S behaviors. However, industrial products often have complicated metastable structures, and it is difficult to determine the relationship between such phase-separated structures and S–S behavior.

Aoyagi et al. [3, 4] have proposed hierarchical simulations to study the mechanical properties of ABA triblock copolymers such as those found in TPEs. The simulations combine self-consistent field theory (SCFT) calculations and coarse-grained molecular dynamics (CGMD) simulations. They constructed the spherical phase of the ABA triblock copolymers for CGMD simulations from the segment distribution obtained from the SCFT calculations. Using the initial structure, CGMD simulations were conducted and S–S curves were obtained under tensile deformation. This approach can be extended to study the S–S behavior of metastable structures. However, considerable computational resources are required to cover a wide variety of structures.

Recently, machine learning has been widely used in materials science, including in the study of polymeric materials [5,6,7]. With regard to polymeric materials, higher-order structures such as phase-separated structures in addition to chemical structures must be considered if structure–property relationships are to be determined by machine learning. The convolutional neural network (CNN) [8] is one of the most popular deep neural networks and widely employed for 2D image recognition. CNN methods can be extended to 3D images (3DCNN) [9], and the 3DCNN is potentially useful for the study of higher-order structure–property relationships [10,11,12].

In the present study, we introduce the high-throughput prediction of S–S curves of ABA triblock copolymers by combining hierarchical simulation and 3DCNN.

Materials and methods

Hierarchical simulation

Figure 1 is an overview of the hierarchical simulation used to obtain the S–S curves of the block copolymers.

Fig. 1

Overview of hierarchical simulation. (1) Phase-separated structures of block copolymers are obtained by self-consistent field theory (SCFT) calculations. (2) Initial configurations for coarse-grained molecular dynamics (CGMD) are generated by density biased Monte Carlo (DBMC). (3) Tensile deformations are conducted by CGMD

The following is a brief description of the method; the details are available in the literature [3, 4]. In the first step, SCFT calculations are conducted to obtain the phase-separated structures of the block copolymers. Next, the chain configurations for the CGMD simulations are generated by the density biased Monte Carlo algorithm (DBMC) proposed by Aoyagi et al. [13]. The generated structures were relaxed with the NVT ensemble followed by the NPT ensemble. The temperature T was set to 0.3 [ε/k_B], which is below the glass transition temperature of the glassy A domain (ε is the energy unit of the Lennard–Jones potential). The pressure for NPT was set to maintain the density at approximately 0.85 [m/σ³], where m is the mass of the bead and σ is the length unit of the Lennard–Jones potential.

The system was subjected to tensile deformation to elucidate its elastic behavior. The unit cell was elongated in one direction with constant deformation speed. We used the Parrinello–Rahman constant stress algorithm with fixing the cell angles to control the stress in the directions perpendicular to the deformation. The deformation speed was set so that the initial deformation rate was 1.0 × 10⁻⁴ [τ⁻¹], where τ is a time unit of the system, and deformation continued up to a strain of 3.0.

All calculations were conducted using the OCTA system [14], which is a platform for the simulation of soft material. The SUSHI [15] and COGNAC [13] programs within the OCTA system were used for SCFT calculations and CGMD simulations respectively.

Deep learning

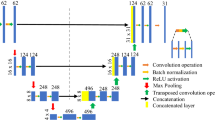
Figure 2 shows the 3DCNN architecture used in the present study. The training data were sets of the local volume fractions of the A segment f_A(r) in each 64 × 64 × 64 grid point (obtained from the SCFT calculations) and the array of stress at strains from 0 to 3.0 at intervals of 0.03 (a total of 101 points). Four convolutional layers and two max-pooling layers were followed by flatten and dense layers. A rectified linear unit (ReLU) function was used to activate each layer except the last one. Dropout with a 0.5 drop rate was applied after each of the two max pooling layers and the first dense layer to avoid overfitting.

Fig. 2

The three-dimensional convolutional neural network (3DCNN) architecture used in the present study

The 3DCNN was implemented using TensorFlow 2.3.0 [16]. We assigned 80% and 20% of all the data for training and validation, respectively. The training step was executed for 1000 epochs with a batch size of 32.

Polymer models

This study focuses on the elastic property of TPEs, in which the glassy (A) segments are minor components, and phase-separated structures are observed. The total volume fractions of the A segments f_A of the ABA copolymers were set at values between 0.15 and 0.50 with intervals of 0.05. The χNs for the SCFT calculations were set to 80 for f_A values less than or equal to 0.2, and to 40 for the remaining f_A values. The chain length N for CGMD simulations was set to 80, and the numbers of A and B segments in a chain are determined from the f_A. The total number of chains was set to 2970.

The physical properties and miscibility were controlled by the cutoff distances of the Lennard–Jones potential. The cutoff distances between the A-A and B-B segments were set to 2.5 and 2^1/6 σ to demonstrate glassy and rubbery properties, respectively. The cutoff distance between A and B was set to maintain phase-separated structures. Twenty phase-separated structures were obtained for each f_A with different initial random seeds for the SCFT calculations. Tensile deformation was applied to the x-, y-, and z-directions, and three S–S curves were obtained from one structure. A total of 480 sets of structures and S–S curves were prepared.

Results and discussion

Figure 3 shows examples of phase-separated structures obtained from the SCFT calculations. Normally, SCFT calculations with homogeneous initial state produce various metastable structures depending on the initial random seeds.

Fig. 3

Examples of phase-separated structures. Each structure is metastable structure obtained from different volume fraction and initial random seed for the SCFT calculations. Isodensity surfaces of f_A(r) = 0.5 are shown

Figure 4 shows the S–S curves for all the samples. The figure includes 480 plots. Although the plots with the same f_A values are bundled together and separated from those with different f_A values, the S–S curves also depend on the phase-separated structures.

Fig. 4

Stress–strain (S–S) curves of all the samples obtained by coarse-grained molecular dynamics (CGMD) simulations

We trained the 3DCNN using these phase-separated structures and S–S curves. After training, the S–S curves were predicted from the untrained phase-separated structures. Mean square errors of stress for both trained and untrained data were less than 0.001, and no obvious overfitting was observed. Figure 5 shows the S–S curves of some of the untrained samples. The predicted S–S curves agreed very well with those obtained by CGMD simulations, and we confirmed that the dependency of a phase-separated structure on the S–S curve was reproduced. The prediction by trained 3DCNN was completed in a second, whereas the hierarchical simulation required more than 1 week of computational time using a single CPU with eight cores.

Fig. 5

Stress–strain (S–S) curves of untrained samples. Blue: coarse-grained molecular dynamics (CGMD) results; red: three-dimensional convolutional neural network (3DCNN) predictions. The figure shows arbitrary chosen 48 plots out of 96 untrained samples

Conclusion

We performed high-throughput prediction of the S–S curves of TPEs by combining hierarchical simulation and 3DCNN. We produced the S–S curves of an ABA triblock copolymer—which served as a model TPE—by the hierarchical simulation of SCFT calculations and CGMD simulations. The 3DCNN was trained using sets of phase-separated structures and S–S curves, and the trained 3DCNN was able to accurately predict the S–S curves of untrained phase-separated structures.

This is a promising result for the study of higher-order structure–property relationships, and the technique enables the rapid screening of the physical properties of polymeric materials with various structures and morphologies. In this report, only phase-separated structures were used for the training of deep neural network. We are studying to include the polymer chain structure for the training set. With this extension, polymers with desired structures, morphologies, and properties can be designed by optimization using the trained neural networks.