Introduction

Manufacturing is facing the development of novel processes and advanced materials, including innovative composites and coatings, to meet the demands of customers for enhanced performance and customisation, which are further challenged by the call for the green transition [1]. Among several product properties, characterising technological surfaces is critical for controlling the manufacturing process and engineering the product [2, 3]. Thus, coatings and nano-structuring of surfaces are being extensively studied to enhance technological surface properties for various applications. Innovative Ge-coatings enhance the efficiency of solar photovoltaic panels [4]; surface nano-structuring is core for energy harvesting and power creation by nanodevices [5], as well as for battery electrodes efficiency and duration, critical requirements to enable the uptake of e-mobility [6]. Composites and multilayer coatings improve the precision of machining and service life of cutting tools [7] and surface treatments are designed to enhance the fatigue life of components [8, 9]. In fact, the mechanical properties of technological surfaces are of interest as they ultimately affect tribological, wear and fatigue behaviour.

Those applications require flexible, fast and highly informative quality inspections that rely on thorough, accurate, and precise characterisation methods [2, 10] to enable zero-defect and zero-waste manufacturing [11, 12]. Instrumented indentation test (IIT) is one of the most appealing mechanical characterisation techniques as it is a depth-sensing, semi-destructive, non-conventional hardness test that can be performed on the final product and allows for a thorough multiscale mechanical characterisation, including Young’s modulus, hardness, creep and relaxation and stress–strain behaviour [13]. This technique finds application in characterising micro- and nano-structures [14, 15], multilayer materials [16], estimating residual stresses [17] and when applied in the macro-range, it is a sustainable alternative to conventional destructive tests [18].

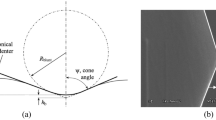
IIT requires applying a force-controlled loading-holding-unloading cycle on a test sample by an indenter of known geometry [19]. The applied force F and the indenter penetration depth h in the material are measured throughout the test, resulting in an indentation curve [see Fig. 1(a)].

Figure 1
figure 1

(a) Example of indentation curve F(h), highlighting the maximum force, the maximum penetration depth and the measured contact stiffness. (b) Vickers and (c) Berkovich indenter geometry. For Berkovich α is either 65.03° or 65.27°, for regular or modified geometry, respectively [20].

Full size image

Indentation curve analysis allows the evaluation of mechanical properties in terms of, e.g., indentation hardness HIT, indentation modulus EIT, which estimates the Young modulus, and reduced modulus Er:

$${H}_{\mathrm{IT}}=\frac{F}{{A}_{p}({h}_{c})}$$
(1)
$${E}_{\mathrm{IT}}= \frac{1-{\nu }_{s}^{2}}{\frac{2\sqrt{{A}_{p}\left({h}_{c,\mathrm{max}}\right)}}{S\sqrt{\pi }}-\frac{1-{\nu }_{i}^{2}}{{E}_{i}}}$$
(2)
$${E}_{r}=\frac{\sqrt{\pi }}{2\left({C}_{\mathrm{tot}}-{C}_{f}\right)\sqrt{{A}_{p}({h}_{c})}}$$
(3)
$${h}_{c}=h-{h}_{0}-\varepsilon \frac{F}{S}-{C}_{f}F$$
(4)
$${C}_{\mathrm{tot}}=\frac{1}{{S}_{m}}={\left({\left.\frac{\partial F}{\partial h}\right|}_{{h}_{\mathrm{max}}}\right)}^{-1}={C}_{f}+\frac{1}{S}$$
(5)

where νs and νi are the sample and the indenter’s Poisson modulus, Ei is the indenter’s Young modulus, hc is the corrected indenter penetration, \({A}_{p}\) is the area of the surface of contact between the indenter and the sample projected on the ideal horizontal plane of the sample surface, and Sm is the measured contact stiffness. The penetration depth is corrected, as per Eq. (4), for the zero-contact point (h0), the elastic deformation of the sample (\(\varepsilon \frac{F}{S}\), proportional to the force by a coefficient dependent on the indenter geometry and the sample stiffness S), and the elastic deformation of the indentation platform frame (\({C}_{f}F\), proportional to the force by the frame compliance \({C}_{f}\)) [19, 21]. The projected contact area \({A}_{p}\) typically is a polynomial function of hc, i.e., the area shape function \({A}_{p}({h}_{c})\) [19, 22].

Traceability is essential to provide end users with confidence in the obtained results, to allow comparing results and metrological performances of different indentation platforms, and ultimately enable IIT exploitation for specification and quality verification. Traceability is obtained by calibrating the force and displacement scale, the frame compliance and the area shape function [20]. The literature shows that the main contributors to measurement uncertainty and bias of mechanical characterisation are the Cf and Ap(hc) at the macro- and nano-range, respectively [22,23,24,25,26]. Current standard ISO 14577-2:2015 [20] presents several methods for their calibration in the Annex D. Area shape function [27] can be either directly calibrated by indenter tip measurement with AFM [28, 29] or indirectly, relying on iterative calibration methods [30] described in the standard as method 2 (ISO M2) and method 4 (ISO M4). The frame compliance can be calibrated based on iterative approaches either requiring direct calibration of the Ap(hc), i.e., standard method 2 (ISO M2) and method 3 (ISO M3), or exploiting ISO M2 or ISO M4. However, the current calibration framework presents several shortcomings. Direct calibration of Ap(hc) requires metrological AFM [31]. Thus, it is extremely expensive, complex and, consequently, is not applied at industrial level [28, 32]. Indirect approaches introduce a strong correlation between the Ap(hc) and the Cf, liable for transforming the parameters in adjusting factors, are highly sensitive to experimental conditions [25, 32], and, despite requiring only indentations on reference materials to be performed, their iterative nature makes them convoluted and hard-to-manage [26].

Therefore, to improve the usability of direct calibration methods while reducing costs and simplifying the empirical framework, this work proposes an innovative approach to directly calibrate indenter tip geometry based on optical surface topography measuring instruments [33]. Sparse attempts to evaluate the geometrical properties of indenters based on topographical measurements have been attempted in the literature [27, 34]. However, these focus only on main geometrical characteristics and neglect the area shape function evaluation (thus making the approach suitable only for microhardness applications). Furthermore, they tend to degrade the information collected by surface topography measuring instruments, exploiting only few profiles and not the whole topography [27, 34]. Innovatively, this work will present a holistic approach to calibrate geometrical properties and area shape function of indenter tips, including the measurement uncertainty evaluation. "Tip direct calibration by surface topography measurements" section will present the methodology, "Results and discussion" section will apply the proposed approach on micro and macro IIT platforms and compare performances with currently standardised methods, and “Conclusion” section will draw conclusions.

Tip direct calibration by surface topography measurements

This work will focus on the direct calibration of Vickers and Berkovich indenters [see Fig. 1(b, c)]. Calibration requires the evaluation of the area shape function ("Area shape function calibration" section) and of geometrical quantities ("Geometry calibration" section), that are the dihedral angle α and, for the Vickers indenter, the tip offset t. The tip offset is defined as the line of conjunction between opposite faces of the pyramid at the apex. The methodology for the calibration will be discussed depending on the indenter geometry in the following. The present work considers a Vickers indenter for macro IIT manufactured by AFFRI and calibrated by UKAS, and a modified Berkovich indenter by Anton Paar. Calibrated values will be reported in the text whenever necessary and are summarised in the supplementary material in Table S1.

Once the area shape function is calibrated, performances will be evaluated on the mechanical characterisation of calibrated reference materials sample [35] with state-of-the-art indentation platforms. In particular, for the macro-IIT, an AXIOTEK ISRHU09 will be considered. For the micro-IIT, an Anton Paar STeP6 equipped with an MCT3 indentation platform. Calibrated values of reference materials are available in the supplementary material in Table S2. Metrological characteristics of the considered indentation platforms are reported in the supplementary material Table S3.

However, to achieve mechanical characterisation, frame compliance requires calibration. The methodology to calibrate the Cf is reported in "Frame compliance calibration" section.

Last, performances will be compared with state-of-the-art standardised calibration methods within a metrological framework, considering measurement uncertainty propagation. "Standard methods for performance comparison" section presents the considered methods for the comparison, whilst "Measurement uncertainty evaluation" section discusses the uncertainty propagation.

Direct indenter tip measurement setup

Vickers and Berkovich indenters are out of diamond, which is highly reflective and transparent. Therefore, among the several surface topography measuring instruments [33], coherence scanning interferometry (CSI) [36] allows one of the most convenient tradeoff between the capability of measuring such materials and metrological characteristics [37]. In fact, compared to alternatives, CSI not only has very low noise and flatness deviation [37], but it can manage measuring transparent and highly reflective materials more easily than confocal microscopes and definitively better than focus variation, which, when used to measure high reflective surfaces, results in several non-measured points [33]. In this work, a state-of-the-art CSI Zygo NewView 9000 hosted in the facility of the Mind4Lab at Politecnico di Torino was used. Measurements were performed with a 50 × Mirau objective, with a squared pixel of (170 × 170) nm, numerical aperture of 0.55 and field-of-view of (1000 × 1000) pixel, i.e., (170 × 170) µm. The indenter has to be mounted in a holder with a slight tilt between the indenter tip stem and the microscope objective (see Fig. 2) to cope with high reflectivity. Measurement setup and execution take less than 10 min, which is significantly more convenient than AFM alternatives.

Figure 2
figure 2

Direct indenter tip measurement setup: notice the slight tilt to allow light reflection in the objective.

Full size image

Geometry calibration

Dihedral angle and tip offset (only for the Vickers indenter) can be evaluated based on linear algebra. Surface topography measurements result in a set of points z = z(x,y). Let’s assume, for the sake of simplicity, that the pyramid apex lies in the origin of the coordinate system. Indenter faces lie on planes \({p}_{f}\), where f identifies the pyramid face and ranges from 1 to the number of faces, i.e., 4 for the Vickers and 3 for the Berkovich. The plane is normal to the vector \(\overrightarrow{{n}_{f}}\) [see Fig. 3(a, b)]:

Figure 3
figure 3

Indication of vectors normal to the plane identified by each plane and related edges in the case of (a) Vickers and (b) Berkovich geometry. (c) Depiction of elements necessary to identify Berkovich tip height. (d, e) Tip offset possible configurations.

Full size image
$${p}_{f}={a}_{f}x+{b}_{f}y+{c}_{f}z+{d}_{f}=0$$
(6.1)
$$\overrightarrow{{n}_{f}}=\left({a}_{f},{b}_{f},{c}_{f}\right)$$
(6.2)

Parameters of the planes, i.e., \({a}_{f}\), \({b}_{f}\), \({c}_{f}\), \({d}_{f}\), can be obtained by least square regression of the measured points.

Edges of the pyramid are the intersection of adjacent faces [see Fig. 3(a, c)]. The vector describing an edge direction can be evaluated as the cross product of the vectors normal to the intersecting planes:

$${e}_{f,l}={p}_{f}\cap {p}_{l};$$
(7.1)
$$\overrightarrow{{e}_{f,l}}=\overrightarrow{{n}_{f}}\times \overrightarrow{{n}_{l}}$$
(7.2)

with f ≠ l and f,l range from 1 to the number of faces.

Vickers indenter

Tip offset t is a geometrical defect due to the poor intersection of four planes not into a point but rather along a line, which can identify the two conditions reported in Fig. 3(d, e). It is evaluated as the maximum distance between the edges’ intersection points, as in Eq. (8.1), where the operator \(\cap\) entails solving the system of linear equations of the planes, and the operator \(\Vert \Vert\) indicates the Euclidean norm.

$$t=max\{{t}_{\mathrm{1,2}},{t}_{3,4}\}$$
(8.1)
$${t}_{\mathrm{1,2}}=\Vert \overrightarrow{{P}_{1}}-\overrightarrow{{P}_{2}}\Vert$$
(8.2)
$${t}_{\mathrm{3,4}}=\Vert \overrightarrow{{P}_{3}}-\overrightarrow{{P}_{4}}\Vert$$
(8.3)
$${P}_{1}={e}_{\mathrm{1,2}}\cap {e}_{\mathrm{1,4}}=\left({p}_{1}\cap {p}_{2}\right)\cap \left({p}_{1}\cap {p}_{4}\right)={p}_{1}\cap {p}_{2}\cap {p}_{4}$$
(8.4)
$${P}_{2}={e}_{\mathrm{3,4}}\cap {e}_{\mathrm{2,3}}=\left({p}_{3}\cap {p}_{4}\right)\cap \left({p}_{2}\cap {p}_{3}\right)={p}_{3}\cap {p}_{2}\cap {p}_{4}$$
(8.5)
$${P}_{3}={e}_{\mathrm{1,2}}\cap {e}_{2,3}=\left({p}_{1}\cap {p}_{2}\right)\cap \left({p}_{2}\cap {p}_{3}\right)={p}_{1}\cap {p}_{2}\cap {p}_{3}$$
(8.6)
$${P}_{4}={e}_{\mathrm{3,4}}\cap {e}_{4,1}=\left({p}_{3}\cap {p}_{4}\right)\cap \left({p}_{4}\cap {p}_{1}\right)={p}_{3}\cap {p}_{4}\cap {p}_{1}$$
(8.7)

Once the tip offset is evaluated, the dihedral angle results as the angle between the faces joining along it:

$$\left\{\begin{array}{c}2\alpha =acos\left(\frac{\Vert \overrightarrow{{n}_{2}}\cdot \overrightarrow{{n}_{4}}\Vert }{\Vert \overrightarrow{{n}_{2}}\Vert \cdot \Vert \overrightarrow{{n}_{4}}\Vert }\right), if t={t}_{\mathrm{1,2}}\\ 2\alpha =acos\left(\frac{\Vert \overrightarrow{{n}_{1}}\cdot \overrightarrow{{n}_{3}}\Vert }{\Vert \overrightarrow{{n}_{1}}\Vert \cdot \Vert \overrightarrow{{n}_{3}}\Vert }\right), if t={t}_{3,4}\end{array}\right.$$
(9)

where the dot product indicates the internal product of the vectors.

Berkovich indenter

The evaluation of the dihedral angle for the Berkovich tip requires the identification of the pyramid height \(\overrightarrow{h}\), which is also the direction along which the penetration depth is measured. The pyramid height can be evaluated [see Fig. 3(c)] by first identifying the projection \(\overrightarrow{{t}_{f}}\) of the edge \(\overrightarrow{{e}_{m,l}}\) (m,l ≠ f and range from 1 to 3) on the opposite face normal to \(\overrightarrow{{n}_{f}}\), i.e.,

$$\overrightarrow{{t}_{f}}=\frac{\overrightarrow{{n}_{f}}\times (\overrightarrow{{e}_{m,l}}\times \overrightarrow{{n}_{f}})}{{\Vert \overrightarrow{{n}_{f}}\Vert }^{2}}$$
(10)

Then, the three planes through an edge and its projection can be identified by their normal \(\overrightarrow{{n}_{f,f}}\):

$$\overrightarrow{{n}_{f,f}}=\overrightarrow{{e}_{m,l}}\times \overrightarrow{{t}_{f}}$$
(11)

and the height results as the pair-wise intersection of such planes as:

$$\overrightarrow{{h}_{f}}=\overrightarrow{{n}_{m,m}}\times \overrightarrow{{n}_{l,l}}$$
(12)

Eventually, the dihedral angle can be evaluated by its geometrical definition [see Fig. 1(b, c)] as:

$${\alpha }_{f}=acos\left(\frac{\Vert \overrightarrow{{n}_{f}}\cdot \overrightarrow{{h}_{f}}\Vert }{\Vert \overrightarrow{{n}_{f}}\Vert \cdot \Vert \overrightarrow{{h}_{f}}\Vert }\right)$$
(13.1)
$${\alpha }_{Berkovich}=\overline{{\alpha }_{f}}=\frac{\sum_{f=1}^{3}{\alpha }_{f}}{3}$$
(13.2)

Area shape function calibration

In the case of nominal ideal Vickers and Berkovich geometries, the area shape function can be written as a simple quadratic function of the corrected penetration depths:

$${A}_{p}\left({h}_{c}\right)=4{\left(\mathrm{tan}\alpha \right)}^{2}{h}_{c}^{2}$$
(14)

which is, however, modified to cater for geometrical errors, such as the tip offset and tip rounding. Several alternatives are available, depending on the indenter geometry and the application force range [18, 19, 22].

Vickers indenter

Typically, Vickers indenters are used for large micro and macro IIT, ranges at which nano-defects are considered negligible. Thus, the area shape function can be written catering only for the tip offset as:

$${A}_{p}\left({h}_{c}\right)=4{\left(\mathrm{tan}\alpha \right)}^{2}{h}_{c}^{2}+2\left(\mathrm{tan}\alpha \right)t\cdot {h}_{c}$$
(15)

Berkovich indenter

Berkovich indenters are used for nano and low microhardness tests due to the higher precision of their geometry. Therefore, a more accurate and flexible area shape function is resorted to [19, 22, 32], i.e.,

$${A}_{p}\left({h}_{c}\right)={C}_{2}{h}_{c}^{2}+{C}_{1}{h}_{c}+{C}_{0}$$
(16)

whose parameters Ci can be identified by least square linear regression.

The proposed approach estimates the empirical values of the \({A}_{p}\left({h}_{c}\right)\) by thresholding the measured indenter surface at increasing distances from the pyramid vertex and evaluating the projected cross-section numerically as:

$${A}_{p}\left({h}_{c}\right)=n\cdot {p}_{xy}^{2}$$
(17)

where n is the number of pixels in the projected cross-section and \({p}_{xy}^{2}\) is the area of the pixel (with the presented experimental setup is 2.89e4 nm2). The evaluation is performed by using state-of-the-art software for topographical analysis MountainsLab v8.2 [38]. The regressor \({h}_{c}\) for the linear regression is taken as the thresholding distance from the tip vertex. However, preliminarily, the measured indenter surface height, \(\overrightarrow{h}\), has to be aligned to the z-axis to compensate for the misalignment necessary to perform the measurement (see "Direct indenter tip measurement setup" section).

Let the versor of the z-axis be \(\overrightarrow{k}=(\mathrm{0,0},1)\), and ϑ the rotation that is needed in a local coordinate reference system \(\langle \overrightarrow{h},\overrightarrow{k},\overrightarrow{w}\rangle\), then:

$$\overrightarrow{{w}_{f}}=\widehat{\overrightarrow{{h}_{f}}\times \overrightarrow{k}}=\frac{\overrightarrow{{h}_{f}}\times \overrightarrow{k}}{\Vert \overrightarrow{{h}_{f}}\times \overrightarrow{k}\Vert }=\left(\begin{array}{c}{w}_{f,x}\\ {w}_{f,y}\\ {w}_{f,z}\end{array}\right)$$
(18)
$$\vartheta_{f} = {\text{acos}}\left( {\frac{{\left\| {\overrightarrow {{h_{f}^{\prime } }} \cdot \vec{k}} \right\|}}{{\left\| {\overrightarrow {{h_{f} }} } \right\| \cdot \left\| {\vec{k}} \right\|}}} \right)$$
(19)
$$\overrightarrow{k}=\left[{R}_{\mathrm{\vartheta }}\right]\overrightarrow{h}$$
(20.1)
$${R}_{\mathrm{\vartheta },f}=\mathrm{cos}{\vartheta }_{f}{I}_{3}+\mathrm{sin}\vartheta \left[\begin{array}{ccc}0& -{w}_{f,z}& {w}_{f,y}\\ {w}_{f,z}& 0& -{w}_{f,x}\\ -{w}_{f,y}& {w}_{f,x}& 0\end{array}\right]+\left(1-\mathrm{cos}{\vartheta }_{f}\right)\left(\overrightarrow{{w}_{f}}\cdot {\overrightarrow{{w}_{f}}}^{^{\prime}}\right)$$
(20.2)

where \(\left[{R}_{\mathrm{\vartheta }}\right]\) is the well-known roto-translation matrix [39]. However, such representation is unpractical. Conversely, it is more convenient to express it in the conventional base of \({\mathbb{R}}^{3}\), i.e., \(\langle \overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\rangle\), for an angle \({\varphi }_{f}=\left[\begin{array}{c}{\varphi }_{f,x}\\ {\varphi }_{f,y}\\ {\varphi }_{f,z}\end{array}\right]\). Considering Eq. (20), and the fact that \(\overrightarrow{k}=\left[{R}_{\vartheta }\right]\overrightarrow{h}=\left[{R}_{\varphi }\right]\overrightarrow{h}\), it follows:

$${\varphi }_{f}=\left[\begin{array}{c}\mathrm{atan}2\left({w}_{f,y}{w}_{f,z}\left(1-\mathrm{cos}\vartheta \right)+{w}_{f,x}\mathrm{sin}{\vartheta }_{f},\mathrm{cos}{\vartheta }_{f}+{w}_{f,z}^{2}\left(1-\mathrm{cos}{\vartheta }_{f}\right)\right)\\ \mathrm{asin}\left(-{w}_{f,x}{w}_{f,z}\left(1-\mathrm{cos}{\vartheta }_{f}\right)-{w}_{f,y}\mathrm{sin}{\vartheta }_{f}\right)\\ \mathrm{atan}2\left({w}_{f,x}{w}_{f,y}\left(1-\mathrm{cos}{\vartheta }_{f}\right)+{w}_{f,z}\mathrm{sin}{\vartheta }_{f},\mathrm{cos}{\vartheta }_{f}+{w}_{f,x}^{2}\left(1-\mathrm{cos}{\vartheta }_{f}\right)\right)\end{array}\right]$$
(21.1)
$$\varphi =\overline{{\varphi }_{f}}$$
(21.2)

Therefore, the correction of the projected area, catering for the misalignment bias correction, is:

$$A^{\prime}_{p} = \overrightarrow {{A_{p} }} \cdot \vec{k} = A_{p} \frac{{\vec{h}}}{{\vec{h}}} \cdot \vec{k} = A_{p} \frac{{\left[ {R_{ - \varphi } } \right] \cdot \vec{k}}}{{\left[ {R_{ - \varphi } } \right] \cdot \vec{k}}} \cdot \vec{k} = = A_{p} \left( {\begin{array}{*{20}c} {\cos \varphi_{x} \cos \varphi_{z} \sin \varphi_{y} + \sin \varphi_{x} \sin \varphi_{z} } \\ {\cos \varphi_{x} \sin \varphi_{y} \sin \varphi_{z} - \sin \varphi_{x} \cos \varphi_{z} } \\ {\cos \varphi_{y} \cos \varphi_{x} } \\ \end{array} } \right)^{T} \cdot \left( {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right)$$
(22.1)
$${R}_{\varphi }=\left[\begin{array}{ccc}\mathrm{cos}{\varphi }_{z}& -\mathrm{sin}{\varphi }_{z}& 0\\ \mathrm{sin}{\varphi }_{z}& \mathrm{cos}{\varphi }_{z}& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}\mathrm{cos}{\varphi }_{y}& 0& \mathrm{sin}{\varphi }_{y}\\ 0& 1& 0\\ -\mathrm{sin}{\varphi }_{y}& 0& \mathrm{cos}{\varphi }_{y}\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& \mathrm{cos}{\varphi }_{x}& -\mathrm{sin}{\varphi }_{x}\\ 0& \mathrm{sin}{\varphi }_{x}& \mathrm{cos}{\varphi }_{x}\end{array}\right]$$
(22.2)
$${A}_{p}^{^{\prime}}={A}_{p}\mathrm{cos}{\varphi }_{y}\mathrm{cos}{\varphi }_{x}$$
(22.3)

where Eq. (22.1) is obtained by exploiting the inversion property of the rotation matrix, and Eq. (22.3) shows that, accordingly to the system physics, the correction of the misalignment is proportional to the cosine of the rotation error.

Frame compliance calibration

The calibration of frame compliance is essential to correct the measured penetration depth and achieve accurate mechanical characterisation. Different approaches are available in the literature, catering for the force range and the data availability.

Macro IIT indentation platform

In the case of the macro IIT indentation platform, AXIOTEK ISRHU09, which will mount the Vickers indenter, the frame compliance is known to be strongly non-linear [40], and methods to calibrate it have been recently developed in the literature to overcome limitations of the current standards. Calibration has been performed based on [35, 40], yielding results as shown in Fig. 4(a).

Figure 4
figure 4

(a) Calibrated frame compliance for the macro IIT testing platform AIXOTEK ISRHU09: notice the strong nonlinearity [35]. (b) Anton Paar MCT3 frame compliance calibration with ISO iterative method n°4, and the method presented in "Micro IIT indentation platform" section based on the direct area calibration. Error bars represent expanded uncertainty with a 95% confidence level.

Full size image

Micro IIT indentation platform

The frame compliance nonlinearity is less significant in the micro- and nano-range, and the current standard framework presents several alternatives to calibrate it. However, as mentioned in "Introduction" section, the literature has shown several limitations of the current state of the art, for it relies on an iterative procedure highly sensitive to experimental conditions. Therefore, in this work, a closed-form solution is proposed, relying on the direct calibration of the indenter area shape function achieved in "Vickers indenter" section. In particular, by rearranging Eqs. 3, 4 and 16, the system is obtained:

$$\left\{\begin{array}{c}{E}_{r}=\frac{\sqrt{\pi }}{2\left({C}_{\mathrm{tot}}-{C}_{f}\right)\sqrt{{A}_{p}\left({h}_{c}\right)}}\\ {h}_{c}=h-{h}_{0}-\varepsilon \frac{F}{S}-{C}_{f}F\\ {A}_{p}\left({h}_{c}\right)={C}_{2}{h}_{c}^{2}+{C}_{1}{h}_{c}+{C}_{0}\end{array}\right.\to \left\{\begin{array}{c}{C}_{2}{h}_{c}^{2}+{C}_{1}{h}_{c}+{C}_{0}-\frac{\pi }{{4E}_{r}^{2}{\left({C}_{\mathrm{tot}}-{C}_{f}\right)}^{2}}=0 \left(A\right)\\ {h}_{c}=h-{h}_{0}-\varepsilon \left({C}_{\mathrm{tot}}-{C}_{f}\right)F-{C}_{f}F \left(B\right)\end{array}\right.$$
(23)

Substituting Eq. (23.B) in Eq. (23.A), a 4th-order polynomial in \(\left({C}_{\mathrm{tot}}-{C}_{f}\right)\) is obtained, as in Eq. (24), with coefficients only dependent on either calibrated, i.e., \({C}_{2}\), \({C}_{1}\), \({C}_{0}\), \({E}_{r}\), or measured quantities, i.e., F, h, h0, Sm.

$$\left\{\begin{array}{c}{c}_{4}^{2}{\left({C}_{\mathrm{tot}}-{C}_{f}\right)}^{4}+{c}_{7}{\left({C}_{\mathrm{tot}}-{C}_{f}\right)}^{3}+{c}_{6}{\left({C}_{\mathrm{tot}}-{C}_{f}\right)}^{2}-{c}_{8}=0 \, \\ {c}_{4}=2{a}_{2}(1-\varepsilon ){F}_{\mathrm{max}}\\ \begin{array}{c}{c}_{6}={\left(2{a}_{2}\left({h}_{\mathrm{max}}+\frac{{F}_{\mathrm{max}}}{{S}_{m}}\right)+{a}_{1}\right)}^{2}-{a}_{1}^{2}+4{a}_{2}{a}_{0}\\ \begin{array}{c}{c}_{7}=4{a}_{2}(1-\varepsilon ){F}_{\mathrm{max}}\left[2{a}_{2}\left({h}_{\mathrm{max}}-\frac{{F}_{\mathrm{max}}}{{S}_{m}}\right)+{a}_{1}\right]\\ {c}_{8}=\frac{\pi {a}_{2}}{{E}_{r}^{2}}\end{array}\end{array}\end{array}\right.$$
(24)

Finding the roots \(x=\left({C}_{\mathrm{tot}}-{C}_{f}\right)\) of the polynomial, and considering only the physically meaningful solution (two roots are complex, and between the two real roots, only one has a reasonable order of magnitude, given the parameters and the measured quantities ranges), the frame compliance is obtained as:

$${C}_{f}=\left({C}_{\mathrm{tot}}-min\left\{x:x\in {\mathbb{R}}\right\}\right)$$
(25)

Measured quantities are obtained, exploiting current state-of-the-art [20], by performing replicated indentations on a calibrated reference tungsten (W) sample at different maximum force levels within the range to be calibrated [32]. In this work, 15 replications at six force levels, i.e., (80, 100, 150, 200, 300, 390) mN, were performed.

Standard methods for performance comparison

Macro IIT

Benchmark will be performed against conventional contact direct calibration of the tip performed at accredited and national metrological institutes. The comparison will tackle both geometry characterisation, area shape function and mechanical characterisation. As far as the mechanical characterisation is concerned, a set of 10 replicated tests will be performed on the calibrated reference Aluminium sample at (100, 150, 200, 250, 300, 400, 500, 600, 700, 800, 900, 1000) N. The frame compliance is calibrated and corrected as per "Macro IIT indentation platform" section. The results will be only assessed in terms of HIT, for simplicity.

Micro IIT

The results and performances of the proposed direct calibration method discussed in "Berkovich indenter" section and "Micro IIT indentation platform" section will be assessed against the most widely and commonly adopted standard and state-of-the-art calibration method, i.e., ISO M4. The conventional method indirectly calibrates the area shape function by an iterative procedure. In this work, a data set is collected on calibrated BK7 and W reference materials, gathering 15 replicated indentations at (80, 100, 150, 200, 300, 390) mN.

Results will be compared in terms of accuracy and precision of the calibrated quantities (tip geometry, area shape function and frame compliance) and mechanical characteristics (HIT, EIT and Er) of the BK7 and W.

Measurement uncertainty evaluation

The measurement uncertainty is reported at 95% confidence level evaluating the standard uncertainty by the law of uncertainty propagation, as per the guide to the expression of uncertainty in measurement (GUM) [41]:

$$u\left(y\right)=\sqrt{\sum_{j=1}^{n}{c}_{j}^{2}{u}_{{x}_{j}}^{2}}=\sqrt{\sum_{j=1}^{n}{\left({\left.\frac{\partial y({\varvec{x}})}{\partial {x}_{j}}\right|}_{x=\overline{{x }_{j}}}\right)}^{2}{u}_{{x}_{j}}^{2}}$$
(26.1)
$$U\left(y\right)=2u\left(y\right)$$
(26.2)

where y is the output quantity whose uncertainty U(y) has to be evaluated, and which depends on a certain function y(x) on a set of independent variables x.

Indenter-related calibrated quantities

Uncertainty evaluation according to GUM is applied to the closed-formula evaluation of the directly calibrated indenter geometric quantities (α and t) and area shape function, as per Eqs. 8.1, 9, 13, 15 and 16. According to the method proposed in this paper, the input quantities are the plane parameters obtained from regression, see Eq. (6).

Additionally, in the case of the Berkovich dihedral angle, a contribution to cater for the variability of the measurement due to the possible pair-wise plane intersection is included, i.e.,

$$u\left({\alpha }_{\mathrm{Berkovich}}\right)=\sqrt{\sum_{j=1}^{n}{c}_{j}^{2}{u}_{{x}_{j}}^{2}+\frac{\sum_{f=1}^{3}{\left({\alpha }_{f}-{\alpha }_{\mathrm{Berkovich}}\right)}^{2}}{3-1}}$$
(27)

Similarly, in the case of the area shape function direct calibration for the Berkovich, obtained by the regression model in Eq. (16), the resolution contribution of the objective is added and propagated assuming a uniform distribution [37, 41]:

$$u\left( {A_{p} } \right) = \sqrt {\mathop \sum \limits_{j = 1}^{n} c_{j}^{2} u_{{x_{j} }}^{2} + \frac{{\left( {\frac{1}{2}p_{xy}^{2} } \right)^{2} }}{3}}$$
(28)

In the case of the area shape function for the Berkovich indenter, it is also interesting to present the explicit formula to highlight the contribution of the correction of the bias introduced by rotation:

$${u}_{{A}_{p}^{^{\prime}}}^{2}= {u}_{{A}_{p}}^{2}{\left(\mathit{cos}{\varphi }_{y}\mathit{cos}{\varphi }_{x}\right)}^{2}+{u}_{{\varphi }_{x}}^{2}{\left({A}_{p}\mathit{cos}{\varphi }_{y}\mathit{sin}{\varphi }_{x}\right)}^{2}+{u}_{{\varphi }_{y}}^{2}{\left({A}_{p}\mathit{cos}{\varphi }_{x}\mathit{sin}{\varphi }_{y}\right)}^{2}$$
(29)

Frame compliance

Uncertainty of the frame compliance is evaluated in the macro-range (See "Macro IIT indentation platform" section) according to the literature [35, 40].

In the case of the micro-range (see "Micro IIT indentation platform" section), the law of variance propagation is applied to Eq. (25), including the contributions of accuracy, reproducibility and resolution of the measured quantities [26, 35, 40]. Conversely, In the case of the ISO M4 method, a simulative nonparametric approach has to be applied because of its iterative nature to estimate the uncertainty of the calibrated frame compliance and area shape function parameters [22, 25, 26].

Mechanical characterisation

Uncertainty of the characterised HIT, EIT and Er is evaluated according to GUM considering their definition in Eqs. 1, 2 and 3, propagating the contribution of the calibrated quantities (see "Indenter-related calibrated quantities" and "Frame compliance" sections) and of the measured quantities [18, 23].

Results and discussion

CSI measurement of surface topographies of Vickers and Berkovich indenters brings to the results shown in Fig. 5. An extensive measurement range results, enabling characterisation well beyond the current minimum requirement of 6 µm from the tip [20], with a limited number of non-measured points and details of micro- and nano-geometrical defects on the surface.

Figure 5
figure 5

Measurement results from CSI of (a) Vickers indenter and (b) Berkovich indenter. Notice that with a single measurement, a depth of field larger than 40 µm is obtained.

Full size image

Macro IIT Vickers indenter calibration

The methodology presented in "Vickers indenter" section is applied, resulting in the calibration of the geometrical quantities reported in Table 1. Direct calibration based on CSI achieves results that are much more precise (uncertainty is reduced of two orders of magnitude for the dihedral angle) and resolute.

TABLE 1 Results of direct calibration of Vickers indenter.
Full size table

From the geometrical quantities and relying on the frame compliance calibration (see "Macro IIT indentation platform" section [35, 40]), the area shape function describing the projected area can be evaluated according to Eq. (15) and consequently achieve mechanical characterisation. Figure 6(a) shows that the resulting area evaluated from the proposed optical direct calibration methods and the current standard approach are compatible (error bars overlap), but the proposed approach is more precise, i.e., achieves a 4% reduction of uncertainty. As far as the mechanical characterisation is concerned, good agreement is shown with both the conventional calibration and the reference values in Fig. 6(b). In particular, more accurate results are obtained, and when evaluating the accuracy as the RMSE of the mechanical characterisation [average of error bars in Fig. 6(b)] with respect to the calibrated reference value [see Table S2 in the supplementary material or the average of black dashed lines in Fig. 6(b)], the proposed optical calibration method yields a reduction of 62%. Such accuracy improvement can also be justified considering that the calibrated dihedral angle shows a systematic difference considering the two methods, namely, the standard and the proposed direct calibration.

Figure 6
figure 6

Red: optical direct calibration based on CSI, black: contact conventional calibration. Error bars represent expanded uncertainty (95% confidence level). (a) Area shape function and (b) HIT, black dashed lines represent expanded uncertainty of the calibrated value.

Full size image

Micro-IIT Berkovich indenter calibration

Geometrical calibration was performed according to the method described in "Berkovich indenter" section, resulting in a dihedral angle α of (65.035 ± 0.792)°, compliant with the nominal geometry of a modified Berkovich indenter, i.e., (65.3 ± 0.3)°.

Area shape function is evaluated according to the methodology presented in "Berkovich indenter" section, by preliminarily correcting the rotation angle \({\varphi }_{x}=\left(0.97\pm 2e-7\right)^\circ\) and \({\varphi }_{y}=\left(1.25\pm 0.11\right)^\circ\). Figure 7 shows calibration results, highlighting good representativeness and robustness of the model (R2 of 99.9%) and that the normality of the residuals cannot be rejected either with a qualitative investigation (normal probability plot) or with quantitative goodness of fit test (Anderson–Darling test). Uncertainty propagation shows a negligible contribution of both the surface topography resolution and rotation correction, whose contribution, i.e., \({u}_{{\varphi }_{x}}^{2}{\left({A}_{p}\mathrm{cos}{\varphi }_{y}\mathrm{sin}{\varphi }_{x}\right)}^{2}+{u}_{{\varphi }_{y}}^{2}{\left({A}_{p}\mathrm{cos}{\varphi }_{x}\mathrm{sin}{\varphi }_{y}\right)}^{2}\) as per Eq. (29), weighs less than 0.5% on the variance, in the worst case, that is at the maximum depth.

Figure 7
figure 7

Results of the area shape function calibration from CSI topographical results: (a) calibrated trend (b) NPP of residuals showing not significant deviation from normality.

Full size image

The frame compliance is calibrated by the methodology presented in "Micro-IIT indentation platform" section, and mechanical characterisation is subsequently achieved. Results are compared against the standard state-of-the-art calibration method ISO M4, as detailed in "Micro IIT" section.

Figure 4(b) shows the calibration results of frame compliance. As it can be appreciated, the two methods are compatible, and no systematic differences, at a risk of error of 5%, can be highlighted with a t-test, neither between the methods nor with the ideal value (0 mm/N). In particular, this entails a great system stiffness that makes potentially negligible the effect of frame compliance in the investigated range, i.e., from 80 to 400 mN.

Once the frame compliance and the area shape function parameters are calibrated, the projected area can be evaluated as a function of the maximum corrected depth hc,max. Figure 8(a) shows that the two calibration methods yield compatible results. The direct calibration of the area achieves a reduction of the relative expanded uncertainty from 50 to 22%, which, additionally, is now independent from the load. Similar results are obtained considering the indentation hardness [see Fig. 8(b)], with a reduction from 50 to 28%, the reduced modulus [see Fig. 8(c)], with a reduction from 26 to 10%, and the indentation modulus [see Fig. 8(d)], with a reduction from 36 to 14%. Calibrated quantities (Er and EIT) show good agreement with the calibrated reference value (see Table S2 in supplementary material), indicating a lack of systematic bias. The evaluation of the accuracy as the RMSE with respect to the calibrated reference value (as done in "Macro IIT Vickers indenter calibration" section) shows an increase of 2% when the direct calibration is used. This slight worsening in the random contribution of accuracy can be explained considering that the ISO M4 relies on two materials, whilst the direct calibration exploits only calibrated W for the frame compliance.

Figure 8
figure 8

Comparison of mechanical characterisation on calibrated reference materials, BK7 and W, on the Micro IIT platform. Black: standard iterative indirect method ISO n°4, red: direct calibration of area based on CSI measurement and consequent calibration of frame compliance as per the proposed method in this paper (see "Berkovich indenter" and "Micro IIT indentation platform" sections). (a) Area shape function, (b) HIT, (c) Er and (d) EIT. Error bars represent expanded uncertainty with a 95% confidence level. Notice the significant improvement of precision and accuracy (with respect to reference calibrated values, i.e., blue dashed lines, in the case of Er and EIT).

Full size image

Conclusion

This work proposed a method to directly calibrate the indenter tip geometry based on optical surface topography measuring instruments. The proposed method shows definitive improvement in terms of resolution, accuracy (up to 62% in the macro range) and precision (up to halving) both in terms of calibrated quantities and the mechanical characterisation results and throughout different force scales.

The proposed direct calibration method based on optical surface topography measurement of the indenter tip is easier and cheaper than other direct calibration methods based on AFM. In fact, the measurement setup and execution are reduced to a few minutes rather than hours, with benefits in terms of the required amount of operators’ training and measurement flexibility.

Considering indirect calibration methods, the proposed direct calibration approach firstly allows improved traceability, for it directly calibrates the geometry and decouples the calibration of area shape function parameters from the frame compliance, eliminating risks of introducing compensation and adjustment effects amongst the calibrated quantities. From the perspective of implementation, indeed, the proposed direct calibration approach, with respect to indirect calibrations, is more expensive (two order of magnitudes for equipment), but it is faster.

Last, the proposed approach allows more straightforward management and propagation of the measurement uncertainty, not requiring complex simulative procedures.

Future work will apply the method in the nano range showing applicability and consistency of obtained results, to improve the standard framework and support improved traceability also for industry. Comparison with AFM-based approaches will be considered, as well as the implementation to other indenter geometries, e.g., spherical indenters.