Introduction

The development of novel optical sources finds vast number of applications in fields related to material processing, biological material imaging, medical therapy, and industrial applications. Such innovations also accompanied the studies on optical sensors as well, which are used in computers, alarm systems, xerox machines, synchros for photographic flashes, and light fixtures that automatically turn on in the dark and systems that are capable of detecting the presence of objects [1]. The necessity of protecting optical sensors from intense, harmful light radiations will prevail as long as these devices loose practical applicability, which is however impossible in modern technological scenario. In many cases, dealing with intense laser beams are inevitable which ascertains the need for proper and efficient optical limiters that can clamp the increased incident light intensity when the corresponding transmitted light reaches a threshold value. As far as optical limiting is concerned, the process of nonlinear absorption, being the one that involves attenuation of a laser beam, is of utmost importance since it determines whether the material will exhibit good optical limiting properties. Hence, an effective setup to determine the nonlinear absorption is required and Z-scan technique well serves the purpose.

As semiconductors are capable of emitting and detecting radiation efficiently as well as optical and electro-optical manipulation of signals is possible with them, they attracted much attention in optical technologies. They are also popular candidates in the development of nonlinear optical (NLO) devices by virtue of the large and fast optical nonlinear characteristics of such materials. Nano-semiconductors have also been recently proven to be worthy as optical limiters, for example, metal nanoparticles exhibit such useful optical limiting properties under nanosecond laser pulses [2].

The n-type semiconductor metal oxide SnO2 with a wide energy band gap of 3.6 eV has been attractive in applications, such as photodetectors [3], photocatalysis [4], rechargeable batteries [5], gas sensors [6], and heavy metal ion detection [7]. It is an interesting metal oxide which can be synthesized in the form of nanofilms using different physical and chemical deposition techniques. Spray pyrolysis deposition technique is a better choice in this regard as it facilitates large area deposition without the use of vacuum chamber. As it involves simultaneous heat supply to the film substrate during deposition, better crystalline films can be obtained. It is well known that the use of dopants greatly helps to tune the optical and electronic characteristics of semiconductor materials which play integral role in the fabrication of modern integrated devices [8]. In this direction also, spray pyrolysis is advantageous as it offers easy incorporation of dopants to give the final product.

The Rare-Earth (RE) ions, by virtue of their assured luminescent characteristics, have already proven to be promising dopants in the metal oxides for the fabrication of photoluminescent, electroluminescent, and other optical devices. As the characteristic red/orange emission of Eu3+ is sensitive to its local environment, it can expose the dopant location and distribution of the doping material within the lattice of SnO2 [9]. The oxygen vacancies which arises from the charge compensation process remain either in the neighbourhood or distant from the dopant Eu, respectively. These can lead to the presence of Eu-defect associates or substitutional isolated centres that may take part in the possible luminescence process. The optical limiting property is influenced by a number of states induced by defects, which enhance nonlinear absorption, which causes diminution of the intensity of laser at higher incident fluencies. Incorporation of Eu into the host matrix is expected to influence the defect density in the films, thereby affecting the optical limiting behaviour. Several studies on the role of Eu incorporation on the optical limiting behaviour of different glass systems like borate glasses are available, but such studies are very scarce in the area of metal oxides [10].

Only very few reports are available on the preparation of Sn1−xEuxO2 films and the dependence of Eu concentration on different characteristics of these films. Park et al. [11] reported magnetron-sputtered SnO2 thin films doped with Eu for transparent conductive phosphor layer application. They observed that the increase in Eu concentration increased the resistivity of the SnO2 film. They obtained PL excitation and emission signals peaking at 300 and 588 nm, respectively. It was noticed that above 1.0-atom % Eu concentration, the photoluminescence and cathodoluminescence intensity decreased due to the concentration quenching. Morais et al. [12] prepared dip-coated Eu:SnO2 films to study the properties of rare-earth centres and electron trapping mechanism. A distortion in the lattice of the films was assessed using the Rietveld refinements and was established by Raman spectra. In the case of thin film of Eu-doped SnO2 made via metal organic decomposition, Sawahata et al. [13] reported that the 5D0 → 7F1 emission was more intense in the samples with Eu content between 4.3 and 8.1 at.%. They observed no secondary phases peaks even at 12.7 at.% of Eu in the XRD spectra, but the intensity of all peaks was found to be lesser. The doped samples possessed larger peak widths than that of pure film. The optimal Eu concentration for 5D0 → 7F1 PL emission was found to be around 7.2 at.%, which is significantly higher than previous report (~ 0.5 at.%) in the case of sol–gel-synthesized Eu-doped SnO2 nanoparticles. The observed reduction of PL intensity at increased doping may be the result of the effect of concentration quenching. Park et al. [14] fabricated spray pyrolysis p-type Eu-doped SnO2 thin films. They observed successful incorporation of Eu3+ ions to the host crystal by replacing the Sn4+ sites. The Eu doping maintained the visible region film transmittance between 70 and 80% and Burstein–Moss effect caused broadening of band gap. A rise in the charge carrier concentration of the Eu-doped films with the increment of the molar content of the Eu was observed. Vinod et al. [15] studied influence of Eu doping on spray-pyrolyzed tin oxide films for nonlinear optical properties. They observed an additional peak related to Eu2O3 crystalline phase that was observed in the XRD spectra for 5-wt% Eu-doped sample. Eu doping increased the optical transmittance of the samples and the band gap showed only a nominal variation. The near band edge emission and defects due to oxygen vacancies gave rise to PL signals in ultraviolet and red region. The 5% Eu-doped sample showed maximum nonlinear absorption coefficient.

Despite the few available studies, some are incomprehensive or contradictory results associated with optical and transport properties are only available in literature, thus necessitating the need for in depth analysis. Hence, the present study aims at depositing highly transparent Sn1−xEuxO2 thin films and exploring the influence of Eu concentration on structure, morphological, linear, and nonlinear optical properties of tin oxide thin films.

Results and discussion

Structural properties

The effect of Eu concentration on the structural characteristics of Sn1–xEuxO2 films examined using patterns derived from X-ray diffraction is depicted in Fig. 1(a). The observed peaks were in line with the data in the JCPDS card No: 00-041-1445 and it was thus confirmed that the prepared Sn1–xEuxO2 films belongs to cassiterite structure possessing tetragonal lattice constants a = b = 4.7382 Å, c = 3.1871 Å belonging to space group P42/mnm. However, on closer analysis, it is revealed that higher concentration of doping (> 8 at.%) produced a peak at ~ 32.93 corresponding to the (4 0 0) plane of the cubic Eu2O3 (JCPDS 00-034-0392) [Fig. 1(b)]. Similar to this, for Eu3+-doped SnO2 phosphor, Chen et al. [16] report the appearance of second phase of cubic Eu2O3 upon increasing the doping concentration to 8 at.%. Tian et al. [17] also reported that Eu3+ concentration exceeding 2.0 mol% give rise to the presence of cubic phase Eu2Sn2O7 in Eu-doped SnO2 phosphor. Similarly, in SnO2:Eu3+ microspheres, Das et al. [18] that above 1.0 mol% of Eu3+, an Eu2Sn2O7 impurity phase was found to coexist with SnO2. The authors attributed this to the possibility that the solubility limit of this dopant might has exceeded in SnO2 matrix and also to the mismatch in the ionic charge between the ions of the dopant Eu3+ and host Sn4+. The Eu3+ ion radius of 0.947 Å is higher than that of Sn4+ ion (0.69 Å) so that when this dopant ion tends to replace Sn4+, it results in a disturbance in the host lattice. Thus, some of Eu3+ occupy the locations of Sn4+ favouring the formation of a stable solid solution. This also introduces point defects and stoichiometric changes due to charge imbalance. Also, when doping exceeds the solubility limit, the excess dopant ions have a propensity for segregating at the surface of nano-crystallite. It was noticed that all the deposits presented a preferred peak orientation along (1 1 0) plane, irrespective of the dopant concentration. Kolesnikov et al. [19] also reported the same plane to be prominent in the case of 5, 15, and 25-at.% Eu-doped SnO2 having cubic and spherical structure. However, Zhao et al. [20] obtained (1 0 1) as prominent plane in the case of methanol-sensing SnO2 nanorod array via hydrothermal route. Whereas, Vinod et al. [15] observed change in the prominent plane from (1 1 0) to (2 1 1) for Eu:SnO2 thin films upon introducing 5 wt% of Eu into SnO2.

Figure 1
figure 1

(a) X-ray diffractogram and (b) shift of major plane corresponding to the peaks of Sn1−xEuxO2 (x = 0 to 0.1) films.

Full size image

It can be observed from the diffractogram that a gradual decrease in the intensity of the peaks corresponding to prominent planes with the increase in the Eu content is clear from the diffractogram. Simultaneously, the full width at half maximum (FWHM) of the signals broadened; however, after 3 at.% of Eu doping, the trend reversed till 8 at.%. This shows that the Eu incorporation has influenced the extend of crystallinity of the host lattice. This suggests that the incorporated RE dopant ions suppressed the extend of crystallization in the film, producing lesser crystallite sizes than that of the pure sample. In order to gain insight into this, the average crystallite size (D) of Sn1−xEuxO2 deposits was estimated from the following Scherrer formula employed to the prominent peak [21]:

$$D=\frac{0.9\lambda }{\beta \mathrm{cos}\theta },$$
(1)

where λ is the wavelength of X-ray used, β in radians is the peak FWHM, and θ is the Bragg diffraction angle. Table 1 displays the values of the crystallite size (D) of the Sn1−xEuxO2 films. A reduction in D occurred at lower concentration of Eu incorporation. The crystallite size which was about 18.17 nm in the case of pure SnO2 film reduced to a minimum of 4.85 nm upon incorporation of 3-at.% Eu. This decrease in crystallite size may be due to the grain growth inhibition typical of RE doping. Beyond 3 at.% of Eu doping, the crystallite size gradually increased (Table 1). Beyond 8-at.% Eu doping the crystallite size value of the samples reduced. Further incorporation of dopant reduced the crystallite size which may be due to the secondary phase segregation. A shift of the peak related to major plane (1 1 0) to higher angle side for the Eu-doped samples when compared with undoped sample was observed. This is indicative of the Eu incorporation into the lattice and the presence of compressive strain. This also clued that inclusion of Eu3+ into lattice of the host occurred which produces imperfection in crystals and deviation from the lattice parameters of the pure SnO2 sample [22]. Contradictory to this observation, Tian et al. [17] observed shifting of the diffraction peak (1 1 0) to low angle direction with more Eu3+ addition. This indicated a likely replacement of Sn4+ ion by the incorporated Eu3+ ions, leading to crystal lattice expansion. However, similar to the present observation in the Eu-doped thin films, Bhosale et al. [22] also obtained higher angle-shifted diffraction peaks due to the addition of Eu3+ into the SnO2 which also led to formation of crystal imperfections. From Bragg’s law, nλ = 2dsinθ, it follows that, upon doping, the 2θ values increased, which indicated a reduction in the interplanar distance (d) due to the aforementioned ionic radii mismatch [13]. This also led to the observation that, increasing the dopant concentration favoured a slight increment in the lattice parameter values of the host, indicating the occupancy of Eu3++ in the lattice sites of Sn4. The lattice constants possessed by the samples were calculated from the following equation [23]:

TABLE 1 Structural parameters of Sn1−xEuxO2 (x = 0 to 0.1) films.
Full size table
$$\frac{1}{{d}^{2}}=\frac{({h}^{2}+{k}^{2})}{{a}^{2}}+\frac{{l}^{2}}{{c}^{2}}.$$
(2)

It was observed that the lattice parameters initially increased due to doping at lower Eu concentrations (Table 1). One reason for this observation may the lattice distortion. The other parameters denoting the structural features such as dislocation density (δ) and strain (ε) were estimated using the equations δ = 1/D2 and ε = βcosθ/4, respectively [24]. It was observed that the dislocation density was maximum for the 3-at.% Eu-doped sample and minimum for the 8-at.% Eu-doped sample (Table 1). Strain also followed the same trend as that of δ. The Williamson–Hall (W–H) method, used as alternative for estimating the crystallite size and strain (ε) of the sample, is plotted with the help of the given equation, considering the contribution of strain in the crystallite size [25]:

$$\beta \mathrm{cos}\theta =\left(\frac{k\lambda }{D}\right)+4\varepsilon \mathrm{sin}\theta.$$
(3)

The slope of the resulting βcosθ vs. 4sinθ plot denotes the strain and the y intercept helps calculating the crystallite size (D = kλ/y intercept) (supplementary figure S1). Crystallite size and strain obtained using this method also showed similar trend as obtained using Scherrer and strain equation (Table 1).

Morphological and compositional features

The SEM images of Sn1−xEuxO2 thin films are shown in Fig. 2 to analyse the effect of Eu concentration on the surface morphology of the deposits. Undoped SnO2 films showed fibrous morphology, whereas the Eu incorporation completely changed the surface features. This change in the surface morphology upon doping is accounted to the differences in the ionic radii and the electronegativity between dopant and host ions. In general, the Sn1−xEuxO2 samples showed evenly distributed dense grains with a shape resembling the tetragonal trapezohedron or bipyramidal structures, which are especially clear in the case of 2-at.% and 8-at.% Eu-doped samples showing well-defined grains and distinct grain boundaries. Similar morphology was observed by Anjana et al. [15] in spray-pyrolyzed Eu:SnO2 films. Due to the appearance of secondary phase, 10-at.% Sn1-xEuxO2 samples showed aggregation of grains. Compositional analysis using EDAX is provided in supplementary file as note 2 and figure S2.

Figure 2
figure 2figure 2

SEM micrograms of Sn1−xEuxO2 (x = 0 to 0.1) films.

Full size image

The XPS analysis was carried out in order to have insight into the chemical composition of the film. The survey spectra obtained for the Sn0.92Eu 0.08O2 sample after the carbon correction are shown in Fig. 3(a) in which peaks corresponding to C 1s, O 1s, Sn 3d, and Sn 4 s, Eu 4d, and Eu 3d are visible. Further, the presence of tin element in the “4+” oxidation state is evident from the binding energy (BE) values in the detailed scan [Fig. 3(b)]. The BE of the peak corresponding to Sn 3d3/2 and Sn 3d5/2 were ~ 495 and ~ 486 eV, respectively. The presence of lattice oxygen and oxygen vacancies were also found from the deconvoluted peak of O 1s at ~ 530 and ~ 531 eV, respectively [Fig. 3(c)]. Figure 3(d) displays the scan of Eu, wherein due to the significant spin orbit coupling at the Eu 3d core level, the spectrum is split into two groups, Eu 3d5/2 and Eu 3d3/2. The peaks observed at ~ 1133 and ~ 1164 eV correspond to “3+” oxidation state of Eu. However, the stronger peak at ~ 1155 eV represents the presence of divalent Eu also. Eu is inserted into the cell in an oxidized environment, as evidenced by the presence of two oxidation states of Eu [26]. Some authors have reported that the peak at 1154.2 eV is due to the shake-down satellite of Eu3+ 3d5/2 [27]. According to Armelao et al. [28] the core-level photoemission spectra of the light rare-earth compounds also show a distinctive satellite structure that has primarily been attributed to final state effects and/or charge transfer co-excitations, particularly from O2p to RE4f for lanthanide cations with a partially occupied 4f subshell. However, in the present sample, this peak is more intense, which may be due to the high amount of Eu incorporation that would eventually lead to secondary phase formation, as seen in the case of XRD for 9- and 10-at.% Eu-doped films. Yet another possibility is that the divalent surface layer is thought to be the cause of the divalent signals in the core-level spectra of trivalent compounds [29].

Figure 3
figure 3

(a) XPS survey spectra and detailed scan of (b) Sn 3d, (c) O 1s, and (d) Eu 3d Sn0.92Eu 0.08O2 film.

Full size image

Optical properties

The visible region transmittance plot shown by Sn1-xEuxO2 films [Fig. 4(a)] indicated that the presence of Eu in the host SnO2 lattice leads to overall reduction of the transmittance. Amongst the transmittance of doped films, 3-at.% Eu-doped film showed maximum (> 80%). The factors such as surface roughness, oxygen deficiency, and impurity centres may decrease the transmittance suggesting the dopant substitution in the host matrix [30]. The surface roughness of the films which are polycrystalline will be a major factor in influencing their transmittance and reflectance [31]. Also, doping might have increased the scattering of photons that influences the transmittance [32]. When dopant was added, the transmittance plot clearly demonstrated the change in absorption edge of the films. The band to band electron transition energy depends on the energy gap, direct or indirect gap, of the materials, which can also explain the observed dramatic drop in transmittance edge of the samples [33]. This abrupt decrease in transmittance close to the absorption edge denotes the direct band gap nature and crystallinity of the deposits [34]. Doping caused a noticeable shifting in the absorption edge of the films towards the longer wavelength region. This also suggests a potential narrowing of the films’ optical band gap following doping. This also indicates the possible narrowing of band gap of the films after doping. The absorption coefficient (α) was used to assess the deposits’ energy band gap Eg of the deposits using the given equation [35]:

$${\left(\alpha h\nu \right)}^{2}=A \left(h\nu -{E}_{\mathrm{g}}\right),$$
(4)

where A denotes a constant. The absorbance (a) and film thickness (t) were used to determine α = (2.303a)/t. Using Tauc’s plot [Fig. 4(b)], the Eg is calculated by extrapolating the linear part of the (αhν)2 vs. hν plot towards (αhν)2 = 0. It was observed that doped samples possessed smaller Eg than that of the pure film (supplementary table S1). Amongst the doped films, the maximum Eg was exhibited by Sn0.97Eu0.03O2 sample (3.90 eV). Doping can introduce new energy levels within the band gap of the material. These intermediate energy levels can act as traps for electrons and holes, allowing them to be easily excited and contributing to the electrical conductivity of the material. The presence of these intermediate energy levels reduces the effective band gap of the material. Doping can also create defects or vacancies in the material. These defects can act as energy levels within the band gap and contribute to the electrical conductivity of the material. Again, the presence of these defect states reduces the effective band gap of the material. When dopants are introduced at high concentrations, they can form impurity bands that lie within the band gap of the host material. These impurity bands can interact with the host material’s valence and conduction bands, reducing the effective band gap of the material. Thus, the presence of Eu ions in substitutional sites within the host material led to the development of more empty electron states near the edge of the conduction band, resulting in the shrinkage of the band gap after doping. Additionally, the doping-induced introduction of a large number of defect states with varying intensities could disrupt the band structure, as evident from the PL emission spectra also. However, additional band tail states may appear upon further doping which eventually shrink the band gap. Whereas, Bhosale et al. [22] obtained comparatively lesser Eg of 3.1, 3.08, and 3.0 eV for pure SnO2 and Eu-doped SnO2 (0.075 and 0.1 mol%), respectively. They attributed the narrowing of band gap with rise in Eu content to the substitution of Eu3+ ions in the lattice which resulted in the introduction of electron states into the band gap of SnO2 to form the lowermost unoccupied molecular orbital. In contrast to present observation, Kaur et al. [36] and Tian et al. [17] found monotonous increase of band gap beyond 4 eV with increase in Eu concentration.

Figure 4
figure 4

(a) Transmittance spectra, (b) Tauc’s plot, (c) ln(α) vs hν plots of Sn1−xEuxO2 (x = 0 to 0.1) films, and (d) dependence of energy band gap and Urbach energy on doping concentration x.

Full size image

The Urbach energy, a region of exponential behaviour in the absorption spectra close to the band edge in the films, is used to quantify the band tailing phenomena. Urbach energy (Eu) was calculated using the lnα vs. hν plot [Fig. 4(c)] employing \(\frac{1}{{E}_{\mathrm{U}}}=\frac{d\left(\mathrm{ln}\left(\alpha \right)\right)}{d\left(h\nu \right)}.\). The Eg and Eu showed inverse relation between them [Fig. 4(d)]. The Urbach effect has several root sources, including possible structural disorders, carrier–phonon interaction, and carrier impurities. Such films which also exhibit electrical conductivity are useful for the development of light-transmitting electrodes and surface layers in electroluminescent applications. The plot of extinction coefficient of the films is added in the supplementary file as note 3 and figure S3.

Photoluminescence spectra analysis

Excitation spectra

The emission wavelength of 614 nm that corresponded to the prominent transition 5D0–7F2 was used to extract the excitation spectra of Sn1−xEuxO2 films [Fig. 5(a)]. Only if such level can populate the emitting level and cause the formation of luminescence is it likely to be observed in the excitation spectrum. Hence, the absence of an energy level therein denotes that this level is inefficient for absorption of the excitation light and thus unable to populate the emitting level. The energy levels of the sensitizing ion may also be observed in addition to those of the emitting ions [37]. In case of Eu3+-doped phosphors, usually the excitation spectrum contains three different regions: charge transfer transition, band to band absorption, and f–f transitions [38]. The band corresponding to charge transfer is commonly observed in 220–300 nm range in the case of different hosts. However, no such band was seen in the current Sn1−xEuxO2 films, indicating that, between the activator and host there was no effective radiative energy transfer, that is, there was no exciton-mediated energy transfer from SnO2 to Eu3+ [39]. In the SnO2 host, the weak covalency between Eu3+ and O2 is another possible explanation for this [38]. The SnO2 host absorption is responsible for the band seen at 318 nm [40]. The ground state to the excited state 7F0 → 5L6 transition of Eu3+ represents the peak at 394 nm [16]. As reported by Chen et al. [16] at 466 nm and at 470 by Bazargan et al. [41], the one at 484 nm may be caused by direct excitation of the f–f transitions in Eu3+ ions, that is, to the excited states of 5D2 from the ground state of 7F0 in the Eu3+ ions. The small peaks at 337, 364, and 375 could also be observed. Similar to this, a band at 330 nm was detected by Bazargan et al. [41] and at 361 nm by Wang et al. [42].

Figure 5
figure 5

(a) PL excitation spectra of Sn0.95Eu 0.05O2 film, (b) PL emission spectra of Sn1−xEuxO2 (x = 0 to 0.1) films at an excitation of 265 nm, (c) Gaussian deconvoluted PL emission spectra of Sn0.92Eu 0.08O2 film, and (d) CIE chromaticity diagram of Sn1−xEuxO (x = 0–0.10) films.

Full size image

Emission spectra

The emission spectra of Sn1−xEuxO2 was obtained under UV excitation of 265 nm that corresponds to an energy of 4.67 eV, which exceeds the band gap of Sn1−xEuxO2 is displayed in Fig. 5(b). Both the host lattice and the f–f transitions pertaining to the rare-earth dopant Eu contributed to the PL signals comprised from. As a result, in the current system, the emission spectrum contained both the distinctive f–f lines and intrinsic band because the RE ions have a tendency to compete with the luminescence centres linked to the defects for the available exciting energy. Though Eu ions are present in the lattice, the emissions corresponding to them were observed to be broad and less intense than the emission related to the host SnO2. The magnetic dipole transitions corresponding to the 5D0–7F1 transition was observed at about 590 nm, corresponding to an energy of 2.10 eV. At about 613 nm, the 5D0–7F2 emission peak corresponding to the electric dipole transitions was also present with varying intensities according to the amount of dopant added. The peak corresponding to the magnetic dipolar transition is sharper than the one representing the electric dipolar transition. Usually in SnO2, the influence of crystal field leads to the splitting of 7F1 state to three distinct signals for 5D0–7F1 transition and the 5D0–7F2 lines split into two. However, in the present report, the splitting was not that much pronounced, which may be because of the lack of post-deposition heat treatment given to the samples. Other speculation in this regard is that the extend of broadening of the emission bands is also indicative of the structural distortions within the nanocrystals. Such a presence of distortions may be due to different reasons: one is due to the comparatively low synthesis temperature, so that the sample is prone to greater density of defects compared to bulk material prepared using treatments involving high temperature. In the present case, the films have been synthesized on substrates that cannot withstand such high temperature, which limited the synthesis temperature to less than 500 °C. The small size of the particles presents an additional possibility, as it has been found in other systems that size reduction may result in crystal lattice distortions due to the influence of the surface. It is possible to measure the Eu3+ ion site’s change in the inversion symmetry by comparing the intensities of the electric and magnetic dipole luminescence transitions. Compared to the PL signal of pure SnO2, the overall PL strength of all the samples with Eu was observed to be low except for 8 at.%. The 3-at.% Eu-doped sample showed the least intense PL curve. Beyond 3 at.% of doping, the intensity increased as the doping increased till 8 at.% of Eu incorporation, which may be indicative of the transfer of energy between the SnO2 and Eu3+ ions. The concentration quenching comes into picture as the concentration reached 8 at%.

Only the magnetic dipolar transitions favour to take place if the incorporated Eu3+ is centrosymmetric in the lattice. The stringent prohibition on the electric dipolar transitions would be relaxed if such inversion symmetry is absence and can produce corresponding PL signals. The pure SnO2 PL signals in the UV and visible region correlate with the crystalline defects arising from the difference in method adapted for film synthesis. The deconvoluted PL emission spectra of pure SnO2 comprised five peaks around ~ 359, 398, 458, 494, and 573 nm (supplementary figure S4). Figure 5(c) shows the typical Gaussian deconvoluted PL emission spectra of Sn0.92Eu 0.08O2 film. Since the energies of all the obtained peaks were lower than that of the films, the possibility of emission resulting from direct recombination of the holes in the VB with the electrons in the CB is disregarded in this case. These peaks are attributed to donor–acceptor recombination, defects in the conduction band, oxygen vacancies Vo+ that are singly charged, Vo++ electrons recombining with the photo-excited holes in the VB, and thermally stable deeper defect energy level, respectively [43]. Other small characteristic peaks which were not present in pure SnO2 film were also observed at about 467 nm and 505 are attributed to oxygen vacancies which are speculated to be the effect of charge compensation due to Eu incorporation [44, 45]. From a proposed modal relatable to RE ions in 11-VI compounds, a cation substitutional site is assumed for the Eu3+ ion with any associated defects situating local or remote sites for the purpose of compensating charge. The further discussion on the photoluminescence properties of the films (the possible defects in SnO2 and effects of charge compensation) are given in supplementary information as Note 4.

CIE diagram

The Commission Internationale de I׳Eclairage (CIE) colour co-ordinates for Sn1−xEuxO films under an excitation of 265 nm is displayed in Fig. 5(d) and the chromaticity co-ordinates are given in supplementary table S2. It was be noticed that till a 3 at.% of Eu incorporation, the co-ordinates are located in the intermediate region of a blue and white area, whereas further increase in the doping concentration made them come closer to a region tending more to white light emission, i.e. from the light co-ordinates meant for standard white (0.33, 0.33). The Sn0.92Eu 0.08O2 is nearer to the white light region with (x,y) of (0.309010, 0.299403). This shows the possible near white light emission via modulation of Eu concentration in sprayed SnO2 films.

Third-order nonlinear optical properties

Nonlinear absorption

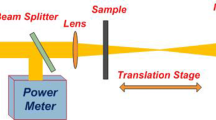
The OA curves were captured as a function of z in relation to the lens’s focus. By mathematically fitting the OA data obtained from the following equation to the normalized transmittance plot, the nonlinear absorption coefficient was determined [7]:

$${T}_{\mathrm{OA}}(z)=1\pm \frac{\beta {I}_{0}{L}_{\mathrm{eff}}}{2\surd 2(1+\frac{{z}^{2}}{{z}_{0}^{2}})},$$
(5)

where z is the distance from sample to focus and the distance between the waist to the point where the area of cross-section of the incident beam becomes double along the beam propagating direction is the Rayleigh range (z0), which is given by \(\frac{\pi {{w}_{0}}^{2}}{\lambda }\), where \({w}_{0}=\frac{4\lambda f}{\pi d}\) is the waist length. The intensity of radiation at the focus is \({I}_{0}=\frac{2P}{\pi {{w}_{0}}^{2}}\) and \({L}_{\mathrm{eff}}=\frac{\left(1-{e}^{\left(-\alpha L\right)}\right)}{\alpha }\). It stands for the effective length of the sample, where L and α are the sample’s length and linear absorption coefficient at the wavelength of the light incident on it, respectively. (A brief description on nonlinear optics and Z-scan experiment is included in supplementary information as note 6 and figure S5.)

The OA signatures of prepared Sn1−xEuxO2 films are given in Fig. 6. The OA curves in a Z-scan experiment provide details on absorptive nonlinearities, like SA (negative nonlinear absorption), RSA (positive nonlinear absorption), or a flip of one to the other. The curve exhibiting a normalized valley at the focus shows RSA (increase of input energy causes decrease of transmittance); on the other hand, transmittance peak at the focus is attributed to SA (increase of transmittance with the increase of input energy) [46]. Two photon absorption (TPA), free carrier absorption (FCA), excited state absorption (ESA), nonlinear scattering, or a combination of them are a few underlying reasons for the occurrence of RSA. Whilst the cross-section of absorption of the ground state is lower than that of the excited states, a nonlinear ground state absorption of a medium results in SA. The TPA in semiconductors is permitted if the energy of the incident light is less than that of the energy band gap (Eg) of the material and greater than that of Eg/2. If hν < Eg the NLO response contains virtual processes and the one-photon process is weaker than TPA [47]. TPA is a useful for centrosymmetric 4f systems with strong symmetry because the two-photon transition mechanism permits the 4f–4f transitions in RE ions. TPA has the effect of causing luminescence at a wavelength that is longer than the absorbed light and as a result, anti-Stokes emission. TPA can take place either through a real energy level (5D0) or a virtual excited state. In the event of a virtually excited state, the Eu3+ ion can be stimulated using a near-infrared light source [37].

Figure 6
figure 6

OA curves of Sn1−xEuxO2 (x = 0 to 0.1) films.

Full size image

In the present case, an apparent increase in the βeff of RSA films could be noticed with higher doping concentration. As presently the Eg is larger than the photon energy, the NLO response is owing to the third-order nonlinear optical property resulting from TPA and bound electronic effects [48]. It can also be observed that the introduction of the dopant in trace amounts has changed the nonlinear absorption behaviour of the film to SA from RSA. After 3 at.% of Eu incorporation, a switching back to RSA was noticed which remained throughout till 10 at.% of Eu doping into SnO2. It has been already observed that higher concentration of Eu in SnO2 narrowed the band gap and maximized the Urbach energy, peaking for 8-at.% Eu-doped film. This could have led to more probability of mechanisms responsible for TPA and OPA, hence the highest βeff exhibited by Sn0.92La0.08O2 may be owing to the mentioned behaviours [49]. In semiconductors, lowering of the Fermi energy level may happen due to heating which results in the increase of carriers within CB. When the samples are exposed to continuous wave laser illumination, the thermal effect due to local heating comes into picture. This affects the energy level of the nonlinear material, which is responsible for the observed nonlinear absorption and refractive index changes. The ground level thus gets depleted which induce bleaching effect in the ground state absorption and caused RSA to SA switching. Several authors have observed switching of SA to RSA or vice versa in different materials which they attribute to reasons like influence of doping concentration, annealing or laser parameters like input energy, and intensity. Albin et al. [46] observed electron beam-induced RSA to SA switching in FZO thin films. Changeover from SA to RSA according to change in input energy of MoS2 nanoflake array films has been observed by Ouyang et al. [50]. In semiconductors, saturable absorption is imperative for applications like up-conversion lasing, mode locking, and Q-switching [51]. Presently, the observation of RSA for Eu-doped SnO2 thin films is favourable for their application as good optical limiters, which is discussed further in the later section.

Optical limiting

Devices that require eye and sensor shielding include direct viewing devices, night vision systems, and focal plane arrays, such as telescopes and gunsights, remain one of the most demanded area where optical limiters find application.

The use of an appropriate optical limiter in the system prior to the sensor in a device aids in enhancing the dynamic range of the sensor and permits operation in extreme environments as well. Different nonlinear optical mechanisms including TPA, FCA, ESA, photo-refraction, induced refraction, self-defocusing, self-focusing, induced scattering, and induced aberration contribute to optical limiting [52]. The limiting threshold (LT), which is the input fluence where the linear transmittance value is cut in half, is used to measure the optical limiting capability of NLO materials. This can be derived using the data obtained from OA Z-scan experiment, using the laser fluence equation, ωz = ω0[1 + (z/z0)2]1/2 substituted to \({I}_{0}= 2P/\pi {\omega }_{z}^{2}\), where P is the power of laser which is input [53]. Lesser the LT, better is the performance of the material in terms of optical limiting.

The OL plots are displayed in Fig. 7. In the present work, LT values were obtained between ~ 1 and ~ 8 kJ/cm2 (Table 2) which is comparable with the report on Dy-doped tin oxide films by Shkir et al. [54]. It is believed that RSA is majorly contributing to the nonlinear mechanism in the prepared Sn1−xEuxO2 films. The laser absorption-induced heating is pointed out as a chief cause for the variations in the absorption coefficient and optical limiting behaviour [52]. It was already noticed that the increase of Eu to higher doping concentration culminated in the increase of size of crystallites in the samples, which is speculated to have enhanced the optical limiting behaviour of the 8-at.% doped films. Large particle size led to greater nonlinear absorption, according to the optical power limiting investigations by Nagaraja et al. [52] in ZnO films upon illumination with CW laser source. However, the LT is minimum for the undoped film itself, which may be due to differences in their linear optical parameters. Thus, Sn1−xEuxO2 (x = 0.04 to 0.10) films in spray-pyrolyzed thin-film form can be employed as optical limiters in suitable sensor protection devices.

Figure 7
figure 7

Optical limiting threshold of Sn1−xEuxO2 (x = 0 to 0.10) films.

Full size image
TABLE 2 Third-order NLO attributes of Sn1−xEuxO2 (x = 0 to 0.1) films.
Full size table

Nonlinear refraction

The Z-scan experiment was performed in CA configuration to measure n2 by finding Δϕ, the nonlinear phase shift. The \({n}_{2}=\frac{\Delta \phi }{k{L}_{\mathrm{eff}}{I}_{0}}\) (k = 2π/λ denotes wave vector here) is estimated from the equation using theoretical fit of the CA data [55]:

$${T}_{\mathrm{CA}}(z)=1\pm \frac{4\Delta \phi \left(\frac{z}{{z}_{0}}\right)}{[(1+{(\frac{z}{{z}_{0}})}^{2})+(9+{(\frac{z}{{z}_{0}})}^{2})}.$$
(6)

In the CA plots of the Sn1−xEuxO2 films, it is worth noticing that the doping concentration has influenced the nature of nonlinear refraction of the films as shown in Fig. 8. In Table 2, it can be noticed that n2 is between 10–6 and 10–5 cm2/W. A pre-focal peak followed by a post-focal valley shows negative nonlinear behaviour and self-defocusing lensing effect. On the other hand, a pre-focal valley followed by a post-focal peak denotes positive nonlinearity characteristic of the self-focusing nature. In the present case, switching between the self-focussing and self-defocussing nature could be noticed. Shaik et al. [56] has obtained similar results wherein RSA-showing films showed switching between negative and positive nonlinear refraction in thin films of ZnO with dissimilar micro- and nano-structured morphology. They attributed this behaviour to band gaps and TPA-related excited state population. Similar previous work on NLO properties of La-doped SnO2 and ZnO films also reported, such a switching behaviour [43, 57].

Figure 8
figure 8

CA curves of Sn1−xEuxO2 (x = 0 to 0.10) films.

Full size image

Electronic polarization, molecular reorientation effect, nonlinear scattering, free carrier absorption, and thermal effect are important factors that influence n2 values. If the separation from the peak to valley obeys the Δz > 1.7 z0 condition, it affirms that the third-order nonlinearity results from thermal effects [58]. The contribution from effect that is of thermal nature may be prominent in present films as the excitation was from a CW laser source. Excitation at 532 nm using CW laser may produce a localized heating in the films, leading to change in refractive index. Thermal nonlinearity effect like this comes into picture because of localized increase in temperature from absorption of the incident energy. Here, it is likely that the defect sites that behave like centres that trap-excited electrons (that dominates the photo-induced recombination of electron–hole pair) associated with the nano-Sn1−xEuxO2 films absorb a small amount of energy from the illumination, effecting the optical characteristics of the samples. As seen in the PL curves, increasing the amount of Eu in SnO2 increased the PL intensity. This indicated that the influence from defects becomes more prominent. This gives rise to more local heating owing to the thermal agitation of the system resulting in modification in refraction, thus influencing the nonlinear behaviour of the films. Thus, it is advantageous that optical nonlinearity can be tailored via appropriate amount of Eu dopant addition.

Third-order nonlinear susceptibility

The range of third-order nonlinear susceptibility χ(3) in various materials reported span around 15 orders of magnitude, which affirms that third-order optical nonlinearity cover a wide area in nonlinear optics. The survey of existing related literature shows that β and n2 depend on the method of processing also, which may be one cause of the wide range in the values of these coefficients, since microstructural evolution is typically process dependent in thin films. The real and imaginary parts of χ(3) are associated to n2 and β, respectively, as specified by the following equations [55]:

$$\mathrm{Re} {\chi }^{\left(3\right)}(\mathrm{esu})={10}^{-4}\frac{{\varepsilon }_{0}{c}^{2}{n}_{0 }^{2}}{\pi }{n}_{2}\left(\frac{{\mathrm{cm}}^{2}}{W}\right),$$
(7)
$$\mathrm{Im} {\chi }^{\left(3\right)}(\mathrm{esu})={10}^{-2}\frac{{\varepsilon }_{0}{c}^{2}{n}_{0}^{2}\lambda }{4{\pi }^{2}}\beta \left(\frac{\mathrm{cm}}{W}\right).$$
(8)

Magnitude of

$${\chi }^{\left(3\right)}=\sqrt{{{ \left(\mathrm{Im} {\chi }^{(3)}\right)}^{2 }+ \left(\mathrm{Re} {\chi }^{(3)}\right)}^{2}},$$
(9)

where c and ε0 assume their usual meanings. The linear refractive index (n0) at 532 nm is estimated using n = [H + (H2 − S2)1/2]1/2, where \(H=\frac{4{S}^{2}}{\left({S}^{2}+1\right){T}^{2}}-\frac{\left({S}^{2}+1\right)}{2}\). Here, S and T are, respectively, the substrate’s refractive index and transmittance of the films at 532 nm [59]. The variation of χ(3) of SnO2 films with Eu doping concentration is provided in Table 2. It shows χ(3) values in the range of 10–3–10–2 esu. It is seen that higher doping of 8-at.% Eu favoured the increase of χ(3). This increase may be a consequence of enhancement in the observed crystallite size and variation in the density of defects upon increasing doping concentration. Priyadarshini et al. [60] reported that the third-order χ(3) increased, whilst Eg reduced, in the present work observed that the higher concentration of doping has led to decrease in band gap. In most of the cases, Re χ(3) was larger than the Im χ(3), indicating that nonlinear refractive behaviour dominates the observed nonlinearity [61].

The literature on comprehensive NLO behaviour of RE-doped SnO2 system, Eu in particular, is very scarce for a direct comparison of the observed β, n2, and χ(3) values. Nevertheless, there are reports on Z-scan studies on anatase TiO2:Eu nanospheres and Eu3+:TiO2 nanoparticles, TiO2 being tetragonal in structure and also is a transparent conducting oxide, like SnO2. The former by Ghosh et al. [62] observed that third-order nonlinearity occurred in anatase TiO2 by the TPA process and that the nonlinearity increased due to the Eu doping. They speculated that the nonlinear transmittance is influenced by the oscillatory interaction between the bound excitons developed and trapped in the host lattice. The mechanism they proposed showed that the electron–hole pair formed by photoexcitation are bound excitons and these bound excitons are trapped in the lattice and Eu, which enable the effective trapping of excited electron, pointing out that photonic interactions in anatase TiO2 can be enhanced by Eu doping. The latter work by Basma et al. [63] observed an increase in n2 with an rise in Eu+3 amount, peaking for a doping of 2.3% of Eu (3.01 × 10–10 cm2/mw), whereas β decreased after doping, from 1.02 × 10–5 to 0.40 cm/mw which is somewhat in line with the trend in β and n2, we have obtained when compared to the values of pure SnO2 films. Shkir et al. [54] observed that the NLO parameters lessened with Dy concentration increase for Dy:SnO2 thin films. A comparison of third-order nonlinear absorption coefficient, refractive index, susceptibility, and limiting threshold of Sn1−xEuxO2 thin films with earlier literature on metal oxides doped with RE is given in supplementary table S3.

Conclusion

Nano-crystalline and transparent Sn1−xEuxO2 films were prepared using the spray pyrolysis method at different concentration of Eu to analyse the effect of Eu concentration on different structural and optical properties of the films. The structural studies confirmed that the prepared Sn1−xEuxO2 films belonged to cassiterite structure possessing tetragonal lattice constants. The crystallite size of the films was found to decrease till Eu concentration is up to 3 at.% and then increased to a maximum value of 20.53 nm for a doping of 8 at.%. It was also observed that beyond 8 at.% of doping produced a peak of cubic Eu2O3. An initial increase in the lattice parameter values was observed due to doping at lower Eu concentrations. The dislocation density and strain were maximum for the 3-at.% Eu-doped sample and minimum for the 8-at.% Eu-doped sample. In general, the Sn1-xEuxO2 samples showed evenly distributed dense grains with a shape resembling the tetragonal trapezohedron or bipyramidal structures. The presence of Eu in the host SnO2 lattice led to reduction of the transmittance of the films. Amongst the doped films, 3-at.% Eu-doped film showed the maximum transmittance (> 80%). The reduction of energy band gap of host film was observed with inclusion of Eu3+ in the lattice. However, the maximum Eg was noticed for Sn0.97Eu0.03O2 sample. The increase in extinction coefficient according to dopant amount was noticed due to the increased light absorption which was attributed to grain boundary scattering effect and change in grain size. The Urbach energy showed inverse relation with the energy band gap values. The excitation spectra contained no band corresponding to the charge transfer indicating that no efficient radiative energy transfer occurred between activator and host, that is, exciton-mediated energy transfer from SnO2 to Eu3+ was absent. Both the host lattice and the transitions pertaining to the rare-earth dopant Eu contributed to the overall PL emission of the films. The observed nonlinear behaviour was identified to be of third order through the Z-scan measurement analysis. It was observed that the introduction of the dopant in trace amounts brought changed the nonlinear absorption behaviour of the film to SA from RSA. After 3 at.% of Eu incorporation, a switching back to RSA was noticed which remained throughout till 10 at.% of Eu doping into SnO2. The films showing RSA exhibited good optical limiting behaviour with limiting threshold in the range of ~ 1 to ~ 8 kJ/cm2. The nonlinear refractive index was obtained in the range of 10–6–10–5 cm2/W with a switching over from self-focusing to self-defocusing and vice versa. The magnitude of third-order nonlinear susceptibility χ(3) was in the range of 10–3–10–2 esu and a higher doping of 8 at.% of Eu favoured the increase of χ(3).

Experimental procedures

Film deposition

The precursor solution was prepared from Stannous chloride (SnCl2·2H2O) dissolved in equal proportions of ethanol and double distilled water added with conc. HCl drops. The mass required to make up 0.1-M Europium Chloride (EuCl3·6H2O) solution was dissolved in distilled water. Proper mixing of the solutions was carried out in order to obtain the desired doping levels. The involved spray conditions were optimized for maintaining film thickness in 500 to 550 nm range. A spray rate of 2 ml/min and pressure of 0.4 bar were maintained during spray process. The deposition temperature was fixed as 450 °C and the spray nozzle was placed 12 cm apart from the substrate. The deposition process was carried out using computer-automated HO-TH-04 Holmarc Spray Pyrolysis Equipment.

Characterizations

The information about the thickness of the prepared thin films was derived by means of the Stylus Profiler Bruker’s (Dektak XT, model: DXT-18-1715). The Rigaku Miniflex 600 X-Ray diffractometer which uses 1.5406-Å Cu-Kα radiation was used to assess the structural characteristics of the films. The features of surface morphology of the samples were extracted from the images produced by Scanning electron microscope (ZEISS, EVO-18-15-57). The presence of the dopant Eu was confirmed in the doped films by means of the spectra obtained from energy-dispersive analysis by X-rays (EDS). The analysis of the constituent composition in the films was done via XPS (HAXPES beamline, PES-BL14). A Shimadzu 1800 spectrophotometer working in UV, visible, and NIR wavelength was used to measure the transmittance and absorbance of the samples. Photoluminescence of the samples at room temperature was obtained as spectra with the help of a Jasco FP8300 fluorescence spectrometer. The estimation of the samples’ third-order nonlinear optical parameters was understood using the data obtained through analysis using the Z-scan technique.