Introduction

Due to their beneficial attributes, such as high specific capacitance, higher power density than batteries, higher energy density than conventional capacitors, long cycle life, high efficiency, and quick charge–discharge behavior [1,2,3,4], supercapacitors have been regarded as high-performance energy storage devices. In the recent past, with the rapid development of portable, foldable, and wearable devices, there is an increased demand for energy storage devices that could meet the three most important requirements of improved flexibility, weight, and performance [5]. While conventional energy storage devices, such as batteries and capacitors, offer high performance, generally they are too rigid and bulky for their application in flexible electronics [6]. Therefore, flexible energy storage devices, for example, flexible supercapacitors with superior mechanical strength and high performance, are suitable alternatives to conventional energy storage devices.

The most widely studied materials for flexible supercapacitors are carbonaceous materials and transition metal oxides. Among transition metals oxides, iron oxides (FeOx) are promising electrodes because of their low cost, variable oxidation states, high theoretical capacitance, and environmental benignity [7,8,9]. Notwithstanding their high energy and power densities, they have inadequacies, such as low conductivity and short cycle lives due to poor structural stability resulting from continuous volume changes during charge–discharge cycles, which need to be addressed [10, 11]. On the other hand, carbon-based electrodes offer high power density, better conductivity, long cycle life, and high chemical stability [1] while having low specific capacitance. Therefore, an effective approach to improve the overall performance of iron oxides is to combine with carbon materials to prepare composite electrodes as carbon materials offer low cost, high surface, and high chemical and structural stability [12, 13].

For flexible supercapacitors, finding the appropriate substrate that is low cost, and the preparation technique that ensures quick, economical, and scalable fabrication are the key challenges. Although various fabrication methods have been reported in the past for the preparation of iron oxides supercapacitor electrodes [7, 9, 10, 14,15,16,17], most of these techniques have long processing times, are high cost, and especially, are not suitable for low-temperature and flexible substrates. In general, elastic properties and flexibility of the substrate are concomitant with low-temperature processing. This makes high-temperature thermal processing of the flexible electrodes impossible using conventional methods because they involve exposure of the substrate to elevated temperatures for an extended period of time, resulting in structural damage. Herein, we report an extremely quick and low-cost fabrication of binder-free FeOx–rGO electrodes using a novel photothermal processing technique that not only allows for high-temperature processing on flexible substrates but also offers roll-to-roll (R2R) processing, a requirement for industrial settings to maintain high speed of production and cost-effectiveness. By preparing binder-free electrodes, we eliminated both the contact resistance and the extra weight associated with a binder. Owing to the unique processing mechanism of this high-intensity photonic processing, which, to the best of our knowledge, has not been reported for fabrication of the flexible electrodes, the electrodes were prepared in several seconds in contrast to conventional methods with longer processing times.

The electrochemical performance of an electrode depends on its specific surface area, which is determined by its structure and morphology. In this work, we have prepared nanostructured and highly porous FeOx–rGO electrodes. The high porosity of nanostructures (i) offers high specific surface area, (ii) ensures shortened ion diffusion lengths and enhanced mass transport [17], (iii) increases the utilization of the electrode materials, resulting in high specific capacitance, and (iv) accommodates the volume changes during charge–discharge processes.

The potential applicability of the as-prepared flexible FeOx–rGO electrodes were evaluated by typical electrochemical measurements (e.g., cyclic voltammetry (CV), charge discharge tests, and electrochemical impedance spectroscopy (EIS)) and showed an initial specific capacitance of 179 F/g at a constant current density of 2 A/g. Finally, even after 5000 continuous charge–discharge cycles, the electrode shows high specific capacitance retention of 70%, indicating its excellent electrochemical performance which is especially noteworthy on a polyethylene terephthalate (PET) substrate.

Results and discussion

Conventional rapid thermal processing (e.g., ovens) offers cost-effectiveness and high exposure area. However, its long processing times (⁓ several hours) involve exposure of the substrate along with the active materials to high temperatures, making it unsuitable for temperature-sensitive substrates (e.g., plastic). On the other hand, laser-based processing techniques offer spatial selectivity but are high-cost and have a small exposure area (⁓ 1 cm2). Herein, we present photothermal processing as a novel technique that offers the economics of the ovens and uniformity of the laser-based techniques. Photonic processing involves the irradiation of the precursor materials with high-intensity pulsed light from a xenon lamp to instantaneously process them. Thanks to its extremely short pulse duration (0.01 s), the precursor materials can be heated to high temperatures (⁓ 1000 ºC) in a short time (ms), and the processing can be safely accomplished almost instantaneously (several seconds) on inexpensive and low temperature and substrates, which is a departure from long processing times of conventional techniques. While the first few pulses of the irradiation evaporate the residual solvent, further pulses provide sufficient thermal energy to start organic decomposition and local crystallization, trapping metastable phases. With further irradiation, a high local temperature is achieved, which is followed by the formation of the iron oxide nanostructure. Finally, we get a sintered and conductive thin-film electrode. Our past reports [18,19,20] describe the photonic processing mechanism in detail.

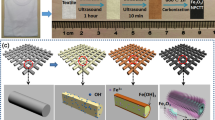
As schematically shown in Fig. 1a and b, the thin-film deposition was performed using an air spray and the as-sprayed film was processed using a novel photonic processing mechanism. It is well known that the morphology and structure of a pseudocapacitor electrode, along with its material properties, play a vital role in its electrochemical performance as electrochemical reactions, mainly Faradaic redox reactions, take place on electrode’s surface. Therefore, increasing the surface area of an electrode enhances its specific capacitance. The morphology of the as-prepared electrode was studied by using scanning electron microscopy images, as shown in Fig. 2. From the surface SEM images [Fig. 2a and b and Figure S1 (a, Supporting Information)], the electrode shows dense morphology before processing. After processing, such dense morphology transforms into desirable nonporous morphology, as shown in Fig. 2c and d and Figure S1 (b,c, Supporting Information). As seen from the images, the electrode contains uniformly distributed nanometric porosity across its surface. This morphology plays a crucial roles as evidenced during electrochemical measurements, i.e., it presents a large specific surface area and concomitantly decreases the ion diffusion length, and accommodate the volume change caused by multiple redox reactions [21], leading to improved structural stability over long cycling. Furthermore, the increased amount of electrolyte ions can penetrate through the nano-porous network, utilization of the active material is significantly enhanced, resulting in high capacitance. Figure S1 (d, Supporting Information) shows the morphology of the electrode after the cycling test. The elemental composition of the as-prepared electrode was investigated by using an EDX spectrum, as shown in Fig. 2 (e). Expectedly, the spectrum verifies the presence of C, Fe, and O with various weights and atomic percentages.

Figure 1
figure 1

Schematic representation of spray-coating technique (a) and photothermal processing technique (b).

Full size image
Figure 2
figure 2

SEM images of precursor film before curing (a, b) and after curing (c, d). EDX spectrum of the cured sample (e).

Full size image

The crystal phase and structure of the electrode were investigated by using XRD and Raman spectra. Figure S2 (SI) shows the XRD spectrum of the electrode after curing. While the strong peak centered at 26° is due to the substrate, the peaks at 30°, 47°, and 53° can be assigned to (206), (024), and (116) planes of α-phase of Fe2O3 [15, 22]. Figure 3 shows the Raman spectra of the electrode before and after curing. The spectrum (after curing) shows the peaks associated with various vibrational modes of Fe2O3, confirming the existence of Fe2O3 in the sample. While the peaks centered at 218, 272, and 389 cm−1 are due to Eg mode vibration of Fe2O3, the peaks centered 486 at 601 cm−1 correspond to A1g mode vibration of Fe2O3 [14, 23, 24]. Moreover, the spectrum also exhibits two characteristics peaks centered at 1342 and 1587 cm−1, also known as D and G peaks, respectively. The D represents the defects and disordered carbon and is associated with the breathing mode vibration of six-atom rings and requires a defect for its activation [25, 26]. On the other hand, the G peaks are due to the stretching of in-plane vibration of doubly degenerate E2g mode vibration of sp2-hybridized C–C bonds in a two-dimensional hexagonal lattice and indicate the presence of graphitic carbon. Additionally, the intensity ratio of the D and G peak, ID/IG, could be used to quantify the disorder and defect degree of carbonaceous materials and the extent of reduction of graphene oxide in the film as higher ratios are associated with increased defect and low graphitized degree of carbon atom [27]. The presence of conductive graphitic carbon, as shown by the Raman spectra, not only reinforces the structural stability of the electrode but also enhances its conductivity.

Figure 3
figure 3

Raman spectra of the electrode before and after curing.

Full size image

Finally, using the values of intensity ratio ID/IG, we can calculate the approximate in-plane graphitic crystallite size (La) (nm) of the disordered carbon materials, as ID/IG is inversely proportional to the microcrystalline planar size, and the following equations [28]:

$${L}_{\text{a}}=\frac{4\cdot 4}{\left(\frac{{I}_{\text{D}}}{{I}_{\text{G}}}\right)}$$
(1)

Using the above equation, the crystallite size was calculated to be 3.32 nm.

To evaluate the electrochemical performance of the as-prepared flexible Fe2O3–rGO as supercapacitor electrodes, electrochemical measurements, such as CV, EIS, and galvanostatic charge–discharge test were performed in a three-electrode measurement configuration at room temperature in 1 M KOH aqueous solution as the electrolyte. Figure 4 shows the photographs of the electrode in freestanding and bending modes, revealing its flexibility. The CV curves at various scan rates ranging from 5 to 100 mV/s and charge–discharge curves at various current densities were recorded in the potential window of − 1.2 to 0.0 V (vs. Hg/HgO). Figure 5a and b respectively show the CV curves at various scan rates for the bare substrate at various scan rates and the CV curves at 30 mV/s scan rate for the as-prepared Fe2O3–rGO and the bare substrate. At all scan rates, the CV curves for PET show the flat lines, confirming its negligible electrochemical contribution. Figure 5c shows the CV curves for the Fe2O3–rGO electrode at various scan rates. The CV curves exhibited non-rectangular shapes with the presence of characteristic redox peaks, indicating the pseudocapacitive charge storage characteristics of the electrode. The as-obtained CV curves are consistent with the previously reported work for iron oxide electrodes [10, 14, 29]. The absence of obvious shape changes in the CV curves even at high scan rates indicates the electrode’s excellent reversibility and rate capability [30]. The presence of oxidation peak around − 0.65 V (anodic scan) and reduction peak (cathodic scan) around − 1.18 V verifies the faradaic behavior of Fe2O3–rGO electrode involving reversible Fe2+/Fe3+ couple as represented by the following equations [14]:

$${\text{Activation: Fe}}_{2} {\text{O}}_{3} + {\text{ H}}_{2} {\text{O}} \to 2{\text{FeOOH}},$$
(2)
$${\text{Charging: FeOOH }} + {\text{ H}}_{2} {\text{O }} + {\text{ e}}^{ - } \to {\text{Fe }}\left( {{\text{OH}}} \right)_{2} + {\text{ OH}}^{ - },$$
(3)
$${\text{Discharging: Fe }}\left( {{\text{OH}}} \right)_{2} + {\text{ OH}}^{ - } \to {\text{FeOOH }} + {\text{ H}}_{2} {\text{O }} + {\text{ e}}^{ - }.$$
(4)
Figure 4
figure 4

Photographs of: (a) spray-coated electrode before curing, (b) cured electrode in standing mode, and (c, d) cured electrodes in bending mode.

Full size image
Figure 5
figure 5

Electrochemical performance of the electrode. (a) CV curves at various scan rates for the bare PET substrate, (b) CV curves at 30 mV/s scan rates for the sample and the substrate, (c) CV curves at various scan rates for the sample, and (d) calculation of ‘b’ parameter from Log (i) vs. Log (v) plot.

Full size image

To further understand the electrochemical behavior of the electrode, the charge storage mechanism can be semi-quantitatively analyzed from the current response using the CV curves at various scan rates. In general, the relationship between the generated current (i) and the scan rate (v) can be expressed by following equations [31, 32]:

$$i=a{\nu }^{b},$$
(5)
$${\text{log}}i={\text{log}}a+b{\text{log}}v,$$
(6)

where a and b are adjustable parameters, and with the value of b, which could be calculated from the slope of log (i) vs. log (v) plot, we can distinguish the dominating electrochemical mechanism in the electrode. If the value of b = 1, then the electrochemical processes are capacitive in nature and if the value of b = 0.5, then the electrochemical processes are diffusion controlled in nature [33]. This is because the current in semi-infinite diffusion-controlled processes is inversely proportional to the square root of scan rate, according to the following Randles–Sevcik equation [34]:

$$i=\left(2\cdot 69\times {10}^{5}\right){n}^\frac{3}{2}AC{D}^\frac{1}{2}{v}^\frac{1}{2}$$
(7)

where, ip, n, A, D, C, and v, respectively, are the peak current, the number of electrons involved in the reaction, the surface area of the electrode, the diffusion coefficient of the electrode material, the concentration of the electrolyte, and the scan rate. On the other hand, in capacitive processes, the current is directly proportional to the scan rate, which can be described by the following equation [32, 35]:

$$i=vCA$$
(8)

where C is the double layer capacitance, A is the surface area of the electrode, and v is the scan rate. Using Eq. (4), we calculated the ‘b’ values for Fe2O3–rGO at − 0.63 and − 1.11 V peak potentials to be 0.75 and 0.70, respectively, as shown in Fig. 5d. This means at these peak potentials; the electrochemical processes are mostly the combination of both the surface capacitive and diffusion-controlled processes. On the other hand, at other potentials (e.g., − 1 V, − 0.8 V, − 0.63 V, − 0.5 V etc.), for both anodic and cathodic scans, the ‘b’ values ranged from 0.59 to 0.95, as shown in Figure S3 (Supplementary Information), indicating that the electrochemical processes are coupled mechanism of capacitive and diffusion-controlled processes. Figure 6 shows the b-values at different potentials.

Figure 6
figure 6

The b-values at different potentials.

Full size image

We can also calculate the individual contribution of the capacitive and the diffusion-controlled processes from the following relationship [36, 37]:

$$i\left(V\right)={k}_{1}v+{k}_{2}{v}^\frac{1}{2}$$
(9)

where k1v and k2v1/2 were individual current contributions from capacitive and diffusion-controlled processes, respectively. We can rearrange express Eq. (9) as follows:

$$\frac{i\left(V\right)}{{\nu }^\frac{1}{2}}={k}_{1}{\nu }^\frac{1}{2}+{k}_{2}.$$
(10)

The values of k1 and k2 can be determined from the slope and intercept of the linear fitting of voltametric currents from the plot of \({v}^\frac{1}{2}\) and \(i(V)/{v}^\frac{1}{2}\). We calculated these values at various potentials (during both the anodic and the cathodic scans) as shown in Figure S4 (Supplementary Information). From these values, the total charge can be divided into the charges contributed from the capacitive current and diffusion-controlled current. With the value of k1, we calculated the current–voltage profile due to surface-based capacitive processes at 5 mV/s scan rate, as shown in Fig. 7a. Figure S5 (Supplementary Information) shows the current–voltage profile due to capacitive processes at 10 and 20 mV/s scan rates compared to the total measured current. Although we have calculated the specific capacitance from the charge–discharge curves, for comparison, we calculated the approximate specific capacitance contribution from capacitive and diffusion-controlled processes. For the as-prepared electrode, at 5 mV/s scan rate, we calculated that the capacitive-controlled capacitance makes up about 39% of total capacitance, whereas at 10 and 20 mV/s scan rates, this value increased to 45 and 51%, respectively, as shown in Fig. 7b. From this calculation, we observed that the current from diffusion-controlled processes decreased with increasing scan rates.

Figure 7
figure 7

Calculation of capacitance contribution from surface controlled and diffusion-controlled processes: (a) at 5 mV/s scan rate and (b) at 5, 10, and 20 mV/s scan rates shown as bar diagram.

Full size image

To further analyze the electrochemical properties, charge–discharge tests were performed at various current densities. As shown in Fig. 8a and Figure S6 (Supporting Information), the non-linear nature of the charge–discharge curves along with the characteristic voltage drops at the start of the discharge processes further confirm the pseudocapacitive charge storage mechanism. The presence of such voltage drops could be attributed to the internal resistance (IR) of the electrode. Another important parameter for the supercapacitor electrode is the rate capacity measurement, which was analyzed by performing GCD measurements at various current densities and specific capacitance was calculated as shown in Fig. 8b. Generally, the pseudocapacitive electrode materials have capacitances dependent on certain potential windows [38]. Therefore, we calculated the areal capacitance (CA) and gravimetric capacitance (CS) for the as-prepared electrode from the discharge curves, instead of calculating from CV curves, by using the following equation [39]:

Figure 8
figure 8

Electrochemical characterization of the electrode. (a) GCD curves at various applied current densities, (b and c) areal and gravimetric capacitance of the electrode at different applied current densities, and (d) specific capacitance and capacitance retention after various number of charge-discharge cycles with inset showing charge/discharge cycle curves.

Full size image
$$\mathrm{C_A }= {\frac{I *\Delta t}{A*\Delta V}} \;{\text{and}}\; {\mathrm{C_S}} = {\frac{I *\Delta t}{m*\Delta V}},$$
(11)

where I (mA), Δt (s), A (cm2), ΔV (V), and m (g) are the discharge current, discharge time, area of the electrode, the discharge potential window excluding the IR drop, and the mass of the active material, respectively. Using the above equation, we calculated both the areal and gravimetric capacitance of the electrode. The electrode showed an initial areal capacitance of 53 mF/cm2 at 0.6 mA/cm2 constant areal current density, and gravimetric capacitance of 179 F/g at 2 A/g constant current density.

The rate capability of an electrode is a crucial parameter for its practical application as a supercapacitor. As shown in Fig. 8c, the rate capability was analyzed by performing charge discharge curves at various applied current densities and by calculating specific capacitance at respective current densities. The as-prepared Fe2O3–rGO showed excellent rate capability as it maintains 58% capacitance retention even after increasing the discharge current from 2 to 10 A/g. As can be seen from the figure, as the current goes higher, the electrode shows a gradual decrease in specific capacitance. This is because, at higher current densities, only the outer surface of the electrode can take part in redox reactions as electrolyte ions cannot penetrate deep into the electrode due to slow diffusion. On the other hand, at lower current densities, the electrolyte ions have sufficient time to interact with the bulk of the electrode material, resulting in enhanced utilization of active material due to increased rate of intercalation/deintercalation. Therefore, the specific capacitance is high at lower currents.

The electrode showed an initial specific capacitance of 179 F/g, which is comparable to or higher than previous reports for iron oxide electrodes [7, 8, 16, 17, 40,41,42,43,44,45,46,47,48]. Areal and gravimetric capacitance after various number of charge–discharge cycles at 0.6 mA/cm2 and 2 A/g constant current densities are shown in Figures S7 (Supporting Information) and Fig. 8d, respectively.

For the long-term application of the electrode, cyclic stability is a crucial requirement along with high specific capacitance. To test the life cycle of the Fe2O3–rGO, we performed the charge–discharge measurements for 5,000 cycles at a constant current density of 2 A/g. Figure 8d shows the specific capacitance and specific capacitance retention after various number charge–discharge cycles. Even after this many cycles, the electrode exhibits 70% of its initial capacitance, exhibiting its excellent capacitance retention. Table S2 (Supporting Information) shows a comparison of the electrode preparation times and the electrochemical performance of the as-prepared Fe2O3–rGO with already reported iron oxides supercapacitor electrodes in aqueous electrolytes. Such superior electrochemical performance of the electrode could be attributed to the synergistic effect between Fe2O3 and rGO and its desirable porous nanostructures which offers (i) enhanced redox-active sites due to high specific surface area, (ii) facilitates the rapid transport of electrolyte ions into the electrode, and (iii) improved structural integrity by accommodating the volume changes during redox processes.

To further study the electrochemical behavior of the electrode, electrochemical impedance spectroscopy (EIS) measurement was performed over the frequency range of 100 kHz to 10 mHZ, as shown in Fig. 9 in the form of a Nyquist plot. Normally, a typical Nyquist plot contains a semicircle in the high-frequency region and a vertically rising line in the low-frequency region. From the high-frequency region of the plot, the intercept on the real axis gives the series resistance (Rs) of the electrode while the diameter of the semicircle gives the charge transfer resistance (Rct) [18,19,20, 49]. The presence of a vertically rising line in the low-frequency region is associated with electrolyte ion diffusion to the active material. This could be represented by Warburg behavior, and the higher slope of this line is indicative of faster ion diffusion.

Figure 9
figure 9

Nyquist plot of the EIS measurement for the Fe2O3–rGO electrode.

Full size image

Conclusions

We have presented a novel and highly scalable method to prepare iron oxides and carbon nanocomposite supercapacitor electrodes. Using this novel photonic processing method, we prepared flexible electrodes quickly (near instantaneously), eliminating the long processing times (several hours) of conventional methods. Thanks to the unique processing mechanism and extremely short processing times of this photothermal method, we prepared electrodes on flexible, low-cost, and temperature-sensitive PET substrate, in ambient conditions, which is not possible with conventional ovens. While this technique is also applicable to different types of substrates, including metal, paper, plastic etc., it is especially the flexible substrates with which it offers roll-to-roll (R2R) processing ability, making it a highly scalable method able to meet the industrial-scale production demands. Additionally, its small footprint, quick and room-temperature processing on inexpensive substrates keep the overall production cost low, helping its commercialization. Although conventional thermal and laser-based techniques have been used for years thanks to their beneficial attributes, this photothermal processing offers the economics of  conventional thermal processing and selectivity of laser processing. The as-prepared Fe2O3–rGO electrode not only exhibits high specific capacitance but also shows long cycle life and excellent capacitance retention of 70% even after 5000 continuous charge–discharge cycles, which is crucial for its long-term applications.

Materials and methods

Thin-film deposition

0.5 g organometallic precursor Fe (III)-acetylacetonate powder (Sigma Aldrich, St. Louis, USA) was dissolved in 20 mL acetone (Sigma Aldrich, St. Louis, USA) to prepare the precursor solution and the solution was put in ultrasonication system for 20 minutes. Then the solution was deposited on indium tin oxide (ITO)-coated polyethylene terephthalate (PET) (kjdElectronics, NH, USA) using an air-spray gun (Paasche Airbrush, Chicago, USA). The spray coating was performed in ambient conditions and was accomplished in several seconds.

Preparation of Fe2O3 -rGO electrode

The as-sprayed precursor thin-film electrodes were processed in ambient conditions through a novel pulsed photothermal processing technique using a PulseForge 1300 (NovaCentrix, Austin, USA) curing system. The curing is achieved through the irradiation of precursor films with pulsed light from a xenon flash lamp with an output spectrum of 220–1000 nm, and the electrodes could be prepared instantaneously as opposed to longer processing times of conventional techniques. The energy density of the light pulse was measured before irradiation using an in situ integrated bolometer. Once the irradiation was complete, the powdered and non-conductive precursor films transformed into solid and conductive thin-film electrodes. After the photonic processing, the mass loading of the electrodes was calculated to be 0.3 mg. The photothermal processing parameters are shown in Table S1 (Supporting Information).

Characterization

Scanning electron microscopy (SEM) (Hitachi S-4800, Hitachi Corp., Tokyo, Japan) was used to characterize the nanostructure of the electrodes. To analyze the crystal structure, a DXR Raman Microscope (Thermo Scientific, Waltham, USA) with a 532 nm laser as the excitation source was performed. The crystallite structure was further analyzed by X-ray diffractometer (XRD) (Rigaku Smart Lab, Rigaku Corp., USA) with a Cu Kα radiation at 40 kV voltage and 40 mA current. The elemental composition of the electrode was verified by Energy dispersive X-ray spectroscopy (EDS) (Hitachi Corp. 3400, Tokyo, Japan).

Electrochemical characterization

All the electrochemical measurements, including cyclic voltammetry (CV), galvanostatic charge-discharge tests, and electrochemical impedance spectroscopy (EIS) were performed in a three-electrode configuration with the as-prepared Fe2O3–rGO, Hg/HgO and platinum wire as working, reference, and counter electrodes, respectively. The measurements were carried out at room temperature (23 °C) using an electrochemical workstation (Autolab, Metroohm, The Netherlands) in 1 M KOH aqueous electrolyte. The CV curves were recorded at various scan rates, ranging from 5 to 100 mV/s in the working potential window of 0.0 to − 1.2 V (vs. Hg/HgO). The EIS measurements were performed over the frequency range of 100 kHz to 10 mHz by applying an AC perturbation amplitude of 10 mV. Electrochemical measurements of the bare substrate were also performed.