Introduction

The development of bioinks plays an essential role in the evolving field of biofabrication. They need to ensure cell survival during printing and simultaneously enable the fabrication of high-resolution 3D constructs. These two requirements are hard to reconcile and therefore create a bottleneck for biofabrication. The so-called biofabrication window implies the loss of cytocompatibility if the polymer concentration in bioinks is increased to improve the printing result towards higher resolution and shape fidelity. Initially, such high concentrations result in increased shear stress during extrusion, which can be cell-damaging. Furthermore, after gelation, the cells are immobilized in the dense polymer network inhibiting their spreading, proliferation, migration, and colonization [1]. Besides approaches conducting chemical functionalization to improve cross-linking properties, making use of composite materials was recently identified to be applicable in the field of biofabrication [2].

The introduction of filler materials such as nano- or microfibers offers new possibilities to tune the matrix viscosity by stabilizing the internal structure on the secondary, microscopic level. The concept of applying composite approaches to widen the materials’ parameter range is widely used, e.g., to increase tensile strength in weaker matrix materials such as modern carbon fiber reinforced polymers. Early approaches applying this concept in the field of tissue engineering conducted gel casting on fiber systems to create reinforcement, but this batch to batch process is not applicable for clinical scale oriented bioprinting [3]. Consequently, to apply fiber reinforcement in biofabrication, printable fiber fragments need to be homogeneously dispersed in a bioink. Recently published results displayed improved printability of bioinks, that were blended with e.g. short silk fibers or nanocellulose fibers [4,5,6]. Furthermore, the mechanical stability of the printed constructs was shown to significantly improve, when incorporating e.g. PLA, PLLA fibers [7, 8], cellulose nanocrystals [9, 10], nanoclay [11] or bioactive glass particles [12, 13]. Strikingly such fiber-reinforced hydrogels also resulted in superior biocompatibility as compared to pure hydrogel matrices. In two other approaches, external magnetic and electric fields were applied to align magnetic PLGA fibers and gold nanofibers resulting in anisotropic structures that served as cell-guiding morphology for aligned neuronal and myoblast cell growth [14, 15]. Such oriented cell growth is known to be a crucial aspect for the biofunctionality of various tissues such as muscle or nerve tissue [16, 17]. Furthermore, fiber dimensions were identified to play a crucial role regarding mechanical support and biological functionality. Previous work has demonstrated that fiber diameters in the range of several hundred nanometers to a few micrometers are suitable for cell adhesion, alignment and proliferation [18, 19]. As an example, the comparison between nanofibers and nanocrystals made from cellulose revealed that only the fiber form enhanced the overall toughness and promoted fibroblast attachment, viability and proliferation, strongly emphasizing the importance of morphology [20].

The combination of improved bioink printing, increased construct stability and higher tissue biofunctionality renders fiber-reinforced hydrogels an all-rounder candidate towards biofabrication. Based on the outstanding potential of such composite hydrogels, the development of analytical tools to systematically investigate the impact of fibers on bioink rheology is a fundamental step towards the formulation of general design criteria for optimizing fiber-reinforced bioinks. Ideally, this includes rheological characterization and viscoelastic modelling, which should be correlated to printing results to identify the most relevant parameters to prospectively predict printability. Recent approaches applying rheological models to describe material printability have demonstrated the complexity and need for further research. To describe material behavior during 3D printing, Sutornnond et al. developed a mathematical model based on fundamental flow equations, but their model would predict thinner strut diameter at higher applied pressure for the investigated 25% w/v Pluronic [21]. This contradicts the expected behavior in a real printing setup. Kiyotake et al. demonstrated that viscosity alone is not sufficient to correlate rheological properties with printing results for their investigated pentanoate-functionalized hyaluronic acid hydrogel (PHA). They concluded that a yield-stress behavior or high viscosities with immediate post-print crosslinking are favorable for the shape fidelity of printed constructs [22]. Göhl et al. used the software package IPS IBUFlow to simulate the strut behavior of two different alginate–nanocellulose fiber composites [23]. They achieved good description of the experimental strut data with their computer assisted simulation. However, the applied rheological Maxwell-model displays major differences compared to the measured data, especially in the low frequency regime. This regime is of major importance for the time dependent structural integrity of the as-printed strut. Beyond that, no time influence on the strut diameter or height and applicability for other hydrogel composites is presented in the publication.

Considering that concentrated polymer solutions and hydrogels are viscoelastic materials, we hypothesize, that it is explicitly the time-dependent strut-spreading behavior that needs to be accessible to quantify the shape fidelity of bioinks. Furthermore, this time-dependency is a crucial parameter to determine the time frame in which crosslinking of the hydrogel must be completed. In this study, we investigated the application of strut spreading measurements to correlate rheological parameters of fiber-reinforced hydrogel systems with real printing behavior. Therefore, alginate and Pluronic were chosen as matrices, representing two fundamentally different hydrogels: sodium alginate is generally printed from solution state and is subsequently cross-linked via addition of calcium ions to form a stable hydrogel. Pluronic on the other hand is printed as a hydrogel, undergoing shear thinning upon printing and immediate hydrogel-reformation via sol-gel transition after printing. These matrices were supplemented with three different concentrations of cellulose nanofibers and a recently developed type of PCL-fiber fragments, produced in a one-step electrospinning approach [24]. PCL is an FDA-approved biopolymer, which is frequently applied in the biomedical sector such as e.g. drug delivery devices, adhesion barriers and suture materials. The dumbbell-like morphology of the generated fragments perfectly fits the design criteria of a bioink filler material as it displays a length shorter than the inner diameter of the print nozzle to avoid clogging, while the diameter is big enough to be detectable for cells that might use the fibers as substrates or for orientation (Fig. S1). To verify the predictability of printing behavior based on shear-rheology, a multi-step procedure (Fig. 1) was established starting with amplitude sweeps and frequency sweeps to determine the critical amplitude and complex viscosity at low shear rates representing the state of as-printed struts. In the next step, the measured data were modelled using the integrated Burgers model, which was shown to sufficiently fit the measured data. Based on the model parameters of the springs E1, E2 and the dashpot viscosities η1, η2, a characteristic time τ was determined resembling the relaxation time of the Maxwell part in the Burgers model, which turned out to be dominated by the presence of fibers. Subsequently, rheological parameters were correlated to the real time-dependent strut spreading behavior as recorded by a video-camera equipped bioprinter. Since the first layer is crucial for the printing result of a 3D construct, we focused our investigation on the flow behavior of single struts with varying material and printing parameters.

Figure 1
figure 1

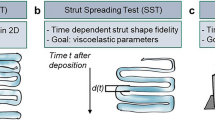
Schematic overview of the strategy: initially, alginate and Pluronic were combined with different concentrations of PCL-microfibers and cellulose nanofibers as filler materials (a). Shear-rheology was applied to characterize the respective ink compositions for subsequent modelling with an integrated Burgers model (b). Simultaneous analysis of the time-dependent strut-spreading was performed to determine shape fidelity (c) and correlate the respective data with predictions based on the viscoelastic modelling.

Full size image

Results

Morphology of fiber fragments and fiber matrix interaction

To examine the impact of PCL fiber fillers on the structural features, reinforced alginate and Pluronic strands were freeze-dried and analyzed via SEM. Interestingly, SEM images clearly indicate, that PCL fibers are not only incorporated in the matrix, but significantly trigger the overall structure in the freeze-dried state, while the addition of CeNF did not show a notable impact. Pure 25% w/v Pluronic hydrogels display an interconnected porous structure with pore diameters of 50–150 µm and dense walls with a thickness of 5–10 µm (Fig. 2a). Similar dense structures are detectable when 2% w/v CeNF are added to the hydrogel (Fig. 2b), with the single CeNF being too small to be detected in the SEM (Fig. S2). In contrast, incorporating 10% w/v of PCL fibers resulted in network formation with smaller pore diameters of 20–50 µm and a significantly reduced wall thickness of around 2 µm (Fig. 2c). Thereby, embedded fiber fragments protrude the matrix at the breaking edge, point into the open space and provide interconnection of structures. Comparable effects were examined for alginate. Pure 3% w/v alginate samples show a structure of compactly stacked sheets with rough surfaces and a thickness < 1 µm (Fig. 2d). Again, the addition of CeNF in maximum concentration does not lead to any significant structural change (Fig. 2e). For PCL, the structure changes drastically with the addition of 10% w/v PCL microfiber fragments resulting in an open porous and interconnected network (Fig. 2f) (all filler concentrations can be seen in the Supplement Fig. S3). Thereby, the rough surface structure is still detectable while fibers protrude the breaking interface and create connections within the network structure. It can be concluded that hydrophobic PCL fragments can be distributed within the hydrogels, thereby disturbing the formation of macroscopic structures, and inducing open porous network formation, while CeNF are smoothly incorporated in the established network structure and do not show a detectable influence on the morphology of the freeze-dried samples. Considering, that Pluronic can be printed as a hydrogel by shear-induced disassembly of micellular structures, it is expected, that PCL fragments will have a significant impact on the rheological characteristics of Pluronic. For alginate, which is usually printed as a solution and crosslinked after extrusion, the rheological impact of PCL fibers will rather be based on the presence of the filler than on structural changes of the matrix.

Figure 2
figure 2

SEM analysis of 25% w/v Pluronic hydrogel and 3% w/v alginate solution in freeze dried state with and without 2% w/v CeNF and 10% w/v PCL fiber filling. The micrographs (a–c) display two different magnifications of Pluronic in blank state (a), with CeNF (b) and with PCL (c) fiber reinforcement. The images on the right (d–f) represent alginate blank (d) and filled with CeNF (e) and PCL (f) fibers. The white boxes indicate the area of higher magnification in the image below.

Full size image

Shear-rheological analysis

To determine the data required for subsequent modelling, shear-rheological experiments were performed with both, filled and unfilled alginate solutions as well as filled and unfilled Pluronic hydrogels as shown in Fig. 3.

Figure 3
figure 3

Oscillatory rheological measurements performed with Pluronic (a–d) and alginate (e–h) with different concentrations of fiber reinforcement. The impact of the addition of fiber fragments on the storage modulus with increasing oscillation strain is displayed for Pluronic (a) and alginate (e). The change in critical amplitude for both composite systems is reported in Pluronic (c) and alginate (g). The graphs of Pluronic (b) and alginate (f) show the influence of fiber filling on the complex viscosity with increasing angular frequency. The dotted line marks the value of the complex viscosity at 1 rad/s which is separately evaluated for Pluronic (d) and alginate (h).

Full size image

The amplitude sweeps of both systems show shear thinning behavior, but the plateau value of the storage modulus varies at an order of several magnitudes (Fig. 3a, e). For small amplitudes, Pluronic ranges around 10 kPa, while pure alginate has a storage modulus around 50 Pa, which could be increased to > 1 kPa when supplemented with 10% w/v PCL microfibers or 2% w/v CeNF. The plot of the strain dependent storage modulus of Pluronic (Fig. 3a) shows the typical shear thinning behavior with a steady linear viscoelastic (LVE) region at low oscillation strain rates and a pronounced decrease when exceeding the critical amplitude (full measurement data including G′, G″ for all PCL-concentrations can be seen in the Supplement Fig. S4). With increasing filler concentrations, the storage modulus in the LVE region increases from 1.1 ± 0.7 kPa for unfilled up to 2.0 ± 1.0 kPa with 10% w/v PCL fiber fragments and 2.0 ± 0.7 kPa with 2% w/v CeNF. In both composite systems, this is an increase of ~ 80%. Comparing these results with the same filler concentrations in a 3% w/v alginate solution (Fig. 3e), the LVE storage modulus increases from 40 ± 13 Pa for unfilled up to 1.2 ± 0.3 kPa with 10% w/v PCL fiber fragments and 1.3 ± 0.04 kPa with 2% w/v CeNF. Consequently, there is an increase of the LVE storage modulus of ~ 3000% in both systems. The result is remarkable as it was shown, that in both, alginate solutions and Pluronic hydrogels, similar values for the LVE storage modulus were achieved with 10% w/v PCL and 2% w/v CeNF.

Comparing the critical amplitude (Fig. 3c, g) and complex viscosities (Fig. 3d, h) of unfilled and filled systems, characteristic differences could be determined between alginate and Pluronic. In both cases, the critical amplitude was decreased, but in Pluronic the decrease was significantly less pronounced than in alginate. With PCL fibers, there was a slight increase of critical amplitude from 1 to 1.2% when adding a low fiber concentration (2% w/v) and then progressively decrease down to 0.5% when adding high fiber concentrations (10% w/v). For the addition of CeNF, the critical amplitude decreases to 0.6% even at low concentrations of 0.5% w/v CeNF and then remains on this level also at higher filler concentrations. Interestingly, the picture completely changes when looking at alginate solutions. The initial critical amplitude of 3% w/v alginate is at 90% and it decreases significantly by the addition of PCL fragments and CeNF to 4% and 10% respectively for the lowest fiber concentration. The value for the highest fiber concentration decreases to 1% for PCL and 2% for CeNF.

The shear thinning behavior is also eminent for both materials in the frequency sweep where Pluronic (Fig. 3b) shows a linear (power-law behavior) decrease of several orders of magnitude in the double logarithmic display from 100 kPa s at 0.1 rad/s to 100 Pa s at 100 rad/s. The linear (power-law) behavior does not change over the range of frequencies and is similar for all matrix–filler compositions (full measurement data including G′, G″, η* for all PCL-concentrations can be seen in the Supplement Fig. S5). By contrast, pure alginate, and alginate with low filler concentrations (0.5% w/v CeNF, 2% w/v and 5% w/v PCL) displays a plateau-like region (Fig. 3f) with subsequent shear thinning at > 1 rad/s. Above a critical filler concentration, the flow characteristics are dominated by power-law-behavior. Similar trends could also be demonstrated via flow experiments (Fig. S6).

These observations can be further elucidated by comparison of the complex viscosity at 1 rad/s for both systems. In case of the Pluronic hydrogel, the addition of both types of fiber fragments results in a linear increase from 7.3 kPa to a maximum complex viscosity of 12.2 kPa for PCL and 18.9 kPa when CeNF are added (Fig. 3d). It must be noted that the lowest concentration of CeNF already leads to a stronger increase (13.0 kPa) in complex viscosity than the addition of the maximum concentration of PCL fragments. This strikingly displays that the effect of the CeNF on the complex viscosity of Pluronic is much more promoted than the effect of PCL fragments. A different behavior is observed for the alginate solution, where low concentrations of fillers (0.5% w/v CeNF, 2% w/v and 5% w/v PCL) did not show any significant viscosity increase (Fig. 3h). High filler concentrations in contrast increased the complex viscosity drastically to values that are 10–20-fold higher than the initial one of 21 Pa s, and again a stronger impact of the CeNF could be noted.

Applying rheological modelling

To determine characteristic parameters that should be applicable as an indicator for printability, viscoelastic modelling was performed based on the Burgers model. In theory, the Burgers model can be translated into a variety of other models by defining zero or infinite values for distinct model components. The elimination of the linear spring of the Burgers model for example would result in the Lethersich model, while an infinitely high viscosity of the linear dashpot should perform as the ZenerK-system. In this study, one single model should be applied for both, alginate solutions and Pluronic hydrogels with and w/o. fillers. Crucially, although the non-modified Burgers model (Eq. 1) reflected filled alginate solutions, it was not applicable to describe the viscoelastic solid behavior of Pluronic, resulting in an adjusted R2 value of 0.5 and lower. Significantly better results were achieved with the integrated Burgers model (Eq. 2).

$${\text{Burgers DEQ}}:\sigma+A\cdot {\dot{\sigma}}+B\cdot {\ddot{\sigma}}=C\cdot{\dot{\varepsilon}}+D\cdot{\ddot{\varepsilon}},$$
(1)
$${\text{Burgers Int DEQ}}:{\sigma }_{\mathrm{I}}+A\cdot\sigma+B\cdot{\dot{\sigma}}=C\cdot\varepsilon+D\cdot{\dot{\varepsilon}}.$$
(2)

The antiderivative \({\sigma }_{\mathrm{I}}\) can be derived from the basic material function of σ (Eq. 2).

$${\sigma}_{\text{I}}=\frac{-{E}^{\prime}\cdot\widehat{\varepsilon}\cdot\cos\left(\omega t\right)}{\omega}+\frac{{E}^{\prime\prime}\cdot{\widehat{\varepsilon}}\cdot\sin\left(\omega t\right)}{\omega}=-\frac{1}{{\omega}^{2}}\cdot{\dot{\sigma}}.$$
(3)

Table 1 gives an overview of the resulting most suitable model systems and the corresponding R2 values. All composites were tested for the whole filler degree range. The lowest adjusted R2 value is given as representative for each hydrogel–fiber-composite.

TABLE 1 Overview of most suitable model systems.
Full size table

The calculated E-moduli and dashpot viscosities for all tested composite systems are shown in Fig. 4. As expected, there is a consistent increase of all elastic moduli and dashpot viscosities when loading Pluronic hydrogels and alginate solutions with PCL fibers or CeNF. Interestingly, when disregarding the numerical filler concentration and simply comparing low (PCL: 2% w/v, CeNF: 0.5% w/v), medium (PCL: 5% w/v, CeNF: 1% w/v) and high (PCL: 10% w/v, CeNF: 2% w/v) fiber concentrations, the model parameters of CeNF and PCL infiltrated alginate display a highly consistent trend. This also accounts for Pluronic resulting in the hypothesis, that from the shear rheological data and viscoelastic fitting, similar rheological effects should be achieved with both filler systems which might be transferable to the printing process.

Figure 4
figure 4

Elastic moduli and dashpot viscosities of the integrated Burgers model for Pluronic (a, c) and alginate (b, d) with PCL and CeNF filler materials. Every measurement point is plotted with its correlating calculated error. For a better interpretation of the resulting data, a half-transparent line connects the related data points.

Full size image

When comparing alginate and Pluronic, the trend of all model parameters seems to be constantly increasing with increasing filler concentration for alginate, whereas in Pluronic the impact of filler material on model parameters appears to be asymptotic, indicating saturation of the composite system. Unlike in alginate, where the Maxwell spring (E1) dominates, Pluronic displays a dominating Kelvin–Voigt spring constant (E2) (Fig. 4a, b). This can be attributed to the liquid characteristics of alginate solutions and the solid characteristics of Pluronic hydrogels. To quantify the impact of filler materials on the Maxwell as well as Kelvin–Voigt elements, characteristic times were calculated for all compositions (Fig. 5). Those characteristic times result from dividing the dashpot viscosity by its correlated elastic modulus (Maxwell or Kelvin–Voigt) according to Eq. 4:

Figure 5
figure 5

Calculated characteristic times for Pluronic (a) and alginate (b) with both filler systems, dependent on the filler content.

Full size image
$${\text{Characteristic time }}\tau=\frac{\eta}{E}.$$
(4)

As shown in Fig. 5, the characteristic Maxwell time of alginate composites can be drastically increased by the addition of CeNF. This increase is also observable for high infills of PCL fiber fragments. The characteristic time of the Kelvin–Voigt model is not remarkably influenced by the addition of PCL or CeNF. Pluronic samples did not show a significant relation between fiber concentration and characteristic times from model parameters.

Strut spreading measurements

To correlate the modelled parameter based on shear rheology with the real printing performance of the respective composite inks, printing experiments were performed with all fiber–matrix compositions. Herein, the time-dependent strut spreading was applied as an indicator for shape fidelity. On the one hand, the impact of the chosen throughput–printspeed-ratio (also named kappa κ) on the shape fidelity of printed struts was examined, thereby keeping the fiber infill constant. Furthermore, by keeping the κ value constant, the sole influence of fiber infill on shape fidelity could be determined. In accordance to our previous findings [25], the time-dependent strut spreading can be described by exponential fit following Eq. 5.

$$d\left(t\right)={d}_{\infty }-\Delta d\cdot {\mathrm{e}}^{-\frac{t}{\tau }}.$$
(5)

Here, d(t) resembles the time dependent strut diameter. \({d}_{\infty }\) is defined as strut diameter for infinite long times, also designated as equilibrium strut diameter. The characteristic time is denoted as τ. \(\Delta d\) is introduced as parameter due to the delay of data capturing compared to the real strut placement, which is not accessible experimentally.

A common trend for all tested hydrogel composites is evident for the relation between κ and the time dependent strut diameter. Consequently, lower κ values always result in lower equilibrium strut diameters. The value of κ also represents the cross-sectional area of the strut (Fig. 1). Nevertheless, this parameter is highly important and must be considered when systematically analyzing printing performance of hydrogels.

For alginate PCL composites, all tested systems show a clear relation of time and strut diameter as can be seen in Fig. 6. The strut diameter increases over time, until a plateau is reached, representing an equilibrium state between gravimetrically driven spreading and the material’s surface tension. The positive effect of filler materials on the printing performance becomes obvious, when comparing pure alginate solution (Fig. 6a) with PCL (Fig. 6c) and CeNF (Fig. 6b) filled alginate solutions. Thereby, not only the initial strut diameter is reduced, indicating less spreading, but also the equilibrium strut diameter. This effect is more pronounced for CeNF-filled alginate than in the case of PCL-fragments.

Figure 6
figure 6

Strut spreading behavior of alginate solutions (a–c) and Pluronic hydrogels (d–f) in blank state (a, d) and with the highest degree of filling of 2% w/v CeNF (b, e) and 10% w/v PCL (c, f). For a better visual distinction of the single graphs, only every second point is plotted here.

Full size image

On the other hand, the well-known good printing properties of Pluronic can be examined as the strut diameter of pure Pluronic remains constant for all κ values (Fig. 6d). This ideal behavior is also not affected by the addition of CeNF (Fig. 6e). However, although the shear-rheological examinations demonstrated comparable characteristics of CeNF and PCL fillers in Pluronic, the printing performance significantly differs. At concentrations of 5 and 10% w/v (Fig. 6f) and κ values higher than ~ 0.8, significant strut spreading takes place after a short delay of ~ 5 s. This so far undescribed effect was not observed at PCL fiber concentrations below 5% w/v revealing the limited predictability of printing behavior based on solely shear-rheological measurements and emphasizing the need of advanced rheological analysis as proposed in this approach. Excerpts from the evaluated footage for the strut spreading measurements can be seen in Fig. S7.

Nevertheless, the shear-rheologically determined model parameters could be correlated with the strut spreading behavior applying a machine learning approach to solve the linear regression model. We thereby assumed a power-law correlation between the equilibrium strut diameter and the strut cross-section area κ as well as the model parameter values. Several iterations of modelling revealed that two factors are mainly influencing the value of the equilibrium strut diameter, namely κ and the dashpot viscosity \({\eta }_{1}\) as obtained from the Maxwell-element in the Burgers model:

$${d}_{\infty,{\text{c}}}=3.39\,{\text{mm}}\cdot{\left(\frac{\kappa}{{\text{mm}}^{2}}\right)}^{0.46}\cdot{\left(\frac{{\eta}_{1}}{{\text{Pa s}}}\right)}^{-0.7}.$$
(6)

Figure 7 displays the relations of predicted and measured equilibrium strut diameters including all PCL-fibers and CeNF compositions in alginate. The solid red line (linear function, zero intercept, slope of one) depicts a perfect model and demonstrates the applicability of the proposed model.

Figure 7
figure 7

Measured vs predicted equilibrium strut diameters for all alginate samples (CeNF- and PCL-filled).

Full size image

Discussion

The main purpose of this work was to develop an analytical tool to systematically correlate fiber-reinforced bioink rheology with the result of a real printing process. We identified time-dependent strut spreading as an excellent indicator to assess shape fidelity and printing resolution on the one hand and further concluded that these data can be applied to determine the time frame in which crosslinking of a bioink must be completed to maintain structural integrity. Shear rheological analysis was conducted to quantify the impact of PCL and CeNF fillers within alginate and Pluronic matrices. As expected, all combinations resulted in increased complex viscosity with increasing filler concentration. While cellulose nanofibers resulted in a significant rheological impact already at relatively low concentrations (0.5–2% w/v), much higher amounts of PCL microfibers were needed to achieve similar effects (5–10% w/v) as depicted in Fig. 3. Due to the smaller dimensions of cellulose nanofibers, the surface to volume ratio is greatly increased and enhances the possible interactions between the fiber surface and the matrix. These effects could also be seen in the rheological modelling, where the integrated Burgers Model was chosen as best suited to describe all measured composite systems. For alginate solutions, the addition of both filler types did not significantly influence the viscosity of the Kelvin–Voigt dashpot, but drastically increased the viscosity of the Maxwell model dashpot (Fig. 4). Additionally, the characteristic Maxwell time increased sharply with the addition of CeNF already at low concentrations while PCL fibers only showed significant influence at the maximum concentration (Fig. 5). These effects could be directly verified in the printing experiments as the pronounced strut spreading of unfilled alginate solutions was significantly reduced, requiring only low CeNF concentrations or high PCL fiber concentrations (Fig. 6a–c). Correlation between the equilibrium strut diameter and the strut cross-section κ with the viscoelastic model-based parameters displays the excellent applicability of our approach to predict reinforced alginate bioink printability (Fig. 7). These findings extend our previous assumption that the Maxwell-dashpot mainly contributes to the spreading behavior of hydrogels in 3D bioprinting. As recently determined Schubert et al., the theoretical exponent for correlating \({d}_{\infty }\) and κ can be derived as 0.5 (unpublished work). However, in theory the viscosity of the material itself, and therefore the dashpot viscosities of the rheological model system, does not influence the equilibrium strut diameter. This contribution may result from the surface drying of the hydrogel strut, which reduces the spreading behavior above a critical time. Therefore, high dashpot viscosities lead to slow spreading speeds and a lower strut diameter when the critical drying time is reached, resulting in a reduced experimental equilibrium strut diameter.

For Pluronic composite hydrogels, structural integrity was dominated by the matrix and thus no significant trend was observed in the rheological modelling, either on the dashpot viscosities or the characteristic time, irrespective of the fiber types and infill. Strikingly, these results were not reflected in the real printing performance. Unlike for cellulose, where shape fidelity was demonstrated to constantly increase with increasing CeNF content as expected, overcoming a critical concentration of PCL-fibers in Pluronic resulted in dramatically promoted strut spreading. Correlating this effect with SEM-results, the phenomenon could be attributed to structural changes of the hydrogel matrix as induced by the presence of hydrophobic PCL-fibers. It is hypothesized that incorporating hydrophobic PCL surface groups interferes with the hydrophilic interactions, which build up the micellar network that allows for gelation of Pluronic [26, 27]. Transitions from dense structures to more delicate and open porous networks have also been demonstrated for decellularized extracellular cartilage hydrogels, supplemented with gelatin/PLGA fibers, and showed to be beneficial for cell infiltration and proliferation in cell-seeded scaffolds [28, 29].

To sum it up, we demonstrated the feasibility of correlating shear-rheological analysis and viscoelastic modelling to the printing performance of filled bioink systems and proposed an analytical setup to verify the model-based parameters via time-resolved optical analysis of the strut spreading behavior. Interfering effects of PCL-microfibers with a Pluronic matrix were not obvious in the shear rheological data but could be quantified in the strut spreading experiments emphasizing the need of such process-related rheological analysis. Considering that this behavior was only evident for high κ-values, it is essential that printing parameters need to be well determined to allow for systematic conclusions. Other research groups that compared printing results with constant printing speeds, already included such considerations by varying the applied printing pressures, which resulted in different throughputs and printing performances [6, 30,31,32]. These findings however were rarely analyzed or elaborated, since no correlation of applied printing pressure and material throughput was presented. Thus, our findings are an important step towards systematically measuring, modelling and documenting bioink rheology to allow for data comparability and furthermore generate a holistic understanding of bioinks undergoing a printing process. Future research will also evaluate the influence of different fillers on contact angle and surface tension of hydrogel composites, in order to reveal general and artifact free scaling laws for relevant process characteristics. Furthermore, it is evident, that the common reporting of applied printing pressure is not sufficient for scientific research. Both, the material throughput as well as the printing speed need to be reported and compared, to enable the interpretation of real material properties and their influence on printing results.

Materials and methods

PCL and cellulose fiber fragment production

PCL (polycaprolactone average Mn 45,000, Merck KGaA, Germany) was dissolved in 99% hexafluoroisopropanol (HFIP, abcr GmbH, Germany) at a concentration of 20% w/v and electrospun in a custom-built electrospinning device at precisely balanced spinning parameters to allow for in situ fiber fragmentation (data not shown). The electrospun fiber fragments were disassembled from the spun sheet by application of high intensity ultrasound for 2 h in EtOH. The suspension was filtered with 50 µm pore size meshes and dried at 37 °C for 72 h. The resulting fiber fragments are 3.14 ± 0.8 µm in diameter and provide an aspect ratio of 15.3 ± 10.

For the isolation of cellulose nanofibers (CeNF; Herrera et al. 2015), bleached banana residue pulp, prepared at Pontifical Bolivarian University (Medellin, Colombia), was used. The cellulose pulp was mechanically fibrillated following a procedure previously reported (Berglund et al. 2016) using a supermasscolloider MKCA6-3 ultrafine friction grinder (Masuko Sangyo Co., Ltd., Japan). The suspension, at a consistency of 2% w/v was dispersed prior to the grinding with a shear mixer Silverson L4RT (Silverson Machines Ltd., UK). The fibrillation was carried out in contact mode directly after initial feeding and was gradually adjusted to 90 µm (negative), while maintaining the rotor speed at 1500 rpm throughout the process. The energy demand of the mechanical fibrillation process was 9.2 kWh/kg based on the direct measurement of power and processing time. AFM measurements revealed an average diameter of 14 nm with a narrow distribution, ranging between 5 and 30 nm [33, 34].

Composite bioink preparation

Alginate PH176 was provided by Vivapharm(R) (Batch#: 4503283839; JRS PHARMA GmbH & Co. KG, Germany). The solution was prepared by slowly adding the weighed polymer to the appropriate amount of water during continuous stirring to create a 3% w/v solution. After complete dissolution of the polymer, the solution was stored at 4 °C subsequently.

Poloxamer 407 (Pluronic™ F127-P2443) was provided by Sigma Aldrich (Merck KGaA, Germany). The hydrogel was prepared by adding the weighed amount of polymer to 4 °C cold water to create a 25% w/v solution. The solution was stirred overnight in cooled state to dissolve the polymer and stored at 4 °C subsequently.

The composite bioinks were created by splitting up the previously created stock solutions into several vials and supplemented with the fiber fragments to create composite systems with 0.5/1/2% w/v CeNF and 2/5/10% w/v PCL fragments. The suspensions were thoroughly mixed using a modified mechanical stirring tool with 700 rpm to provide homogenous distribution of the fragments in the gels. Vacuum was applied to remove the introduced air bubbles. The suspensions were loaded via a syringe (5 ml, B. Braun SE, Germany) into the printing cartridge (5 ml, Cellink AB, Sweden). The prepared gels were stored in an overhead shaker until use to prevent the fragments from descending due to gravitational forces.

SEM analysis

100–200 mg of the prepared materials were extruded into 1.5 ml Eppendorf tubes with ventilation openings in the lid and frozen at − 80 °C for 1 h. The samples were subsequently lyophilized in a Free Zone 2.5 Liter Benchtop freeze drier (Labconco Corporation, MO, USA) for 72 h. The dried samples were cut with a scalpel to enable analysis of the internal structure and sections were fixed on SEM stubs with carbon adhesive discs. The prepared samples were stored in a desiccator to prevent rehydration until being sputtered with 1.3 nm of platinum and analyzed with SEM (Apreo VolumeScope, FEIThermo Fischer Scientific Inc., MA, USA) in the “Standard” use case at magnifications of 1000 and × 5000.

Three-dimensional bioprinting of fiber reinforced hydrogels

An extrusion based bioprinter (Inkredible™, Cellink, AB, Sweden) was used to extrude the prepared composites for strut spreading experiments. The cartridges were heated to 25 °C for 20 min prior to each printing procedure and printed with high-precision 21G-12.7 mm blunt needles (Cellink, AB, Sweden). The printing parameters were adjusted to generate comparable throughputs for the strut spreading experiments. All samples were printed at controlled room temperature of 25 °C.

Strut spreading measurement

To enable filming and post evaluation of the strut spreading behavior over time with video analysis software, the printer setup was modified. The side covers were removed to enable the installation of a neon tube in front of the printed sample. The HEPA filter on the top of the printer was removed to enable installation of a transparent PMMA plate where the camera was placed to film the printing from the top. The printing bed was equipped with a upside down glass Petri dish to be printed on top. Underneath the area of the printed strut, a tilted glass slide was placed to reflect the light from the neon tube and create a high contrast when the strut is printed and enable automated tracking of the strut edges by using the free and open-source video analysis tool Kinovea. The choice of software, however, is up to personal preference.

Before the strut printing measurements, the throughput was determined for each sample at two different pressures by continuous extrusion of 10 s on a weighing pan and weighing the extruded material. This was repeated three times for each pressure and a mean value was calculated for the throughput as value of extruded mass per second. The applied pressures were chosen by visual evaluation when a continuous strut is formed as starting pressure and 15 kPa above the previous value as second pressure. Three different speeds were set up as printing speeds. For the blank hydrogels without fibers the speeds were set to 1000/2000/3000 mm/min. Together with the measured throughput, a κ value was determined. This value is defined by the ratio of throughput (in mm3/s) divided by the printing speed (in mm/s) and resembles the area of the strut cross-section. To keep the κ values constant throughout the measurements, the speed was adjusted to the measured throughputs accordingly.

Single lines were printed with the generated settings and the behavior of printed struts were filmed for at least 40 s after the printing procedure. For statistical relevance, every measurement was triplicated. Each sample set, defined by matrix and filler material, was printed using six different κ values to gain detailed insights and for revealing correlations between rheological properties and printing results. The change of strut diameter is plotted against measurement time and fitted with an exponential function.

Rheological characterization

All rheological measurements are performed using a DHR-3 rotational rheometer (TA Instruments, DE, USA). To ensure artifact free measurements a 40 mm plate-plate geometry is used. The gap distance is set to 500 µm for all rheological measurements and the temperature is set to 25 °C. Temperature control is ensured by the used Peltier-element. To prevent edge-drying of the samples a solvent trap filled with PBS is equipped.

The used measurement procedure is rather simple and deterministic but yields sufficient information for the subsequently performed rheological modelling. Preliminary experiments led to the following six-step approach. The protocol begins after the sample is loaded into the geometry. Therefore, approximately 1 ml of hydrogel or composite material is placed in the middle of the lower measurement geometry. The upper plate is lowered to 520 µm and excessive material is removed from the edge before it is then lowered to the measurement gap of 500 µm.

Step 1: sample conditioning at 25 °C for 180 s

This first step ensures identical start conditions for all subsequent measurements.

Step 2: oscillatory amplitude sweep

Amplitude sweeps are commonly used for the determination of the linear viscoelastic regime of polymeric samples. The frequency is set to constant 10 rad/s and the amplitude is varied from 0.01 to 200%. Preliminary tests showed no influence of the amplitude sweep on subsequent measurement steps. The end of the linear viscoelastic regime is reached when the storage modulus G′ drops 10% of the plateau value for small deformations.

Step 3: oscillatory time sweep

The time sweep measurement, performed at 10 rad/s and an amplitude of 0.1%, characterizes the recovery behaviour of the hydrogel samples. This step results in two parameters for further discussion on recovery kinetic. The characteristic time is reached if the complex viscosity reaches a plateau value. Furthermore, the percentage of recovery capability is as characteristic value for the quality of hydrogel bioinks.

Step 4: oscillatory frequency sweep

Oscillatory frequency sweeps resemble the core for discussions of viscoelastic properties. The used amplitude is chosen inside the viscoelastic regime. The value of 1% proved to be suitable for nearly all materials. Only alginate filled with 10% w/v showed a drop in G’ close to this value. However, no non-linearities are observed in the raw data, even if 1% deformation is used. For detailed information on material behaviour, three magnitudes of order regarding measurement frequency are covered, ranging from 0.1 to 100 rad/s. The resulting data is also used for the rheological modelling.

Step 5: flow sweep

For a direct correlation of rheological properties and printing results, flow sweeps are performed after frequency measurements. However, only alginate samples can be characterized using this rotational type of measurement, since sample detachment occurred for all Pluronic measurements. Here, the adhesion between sample and upper measurement geometry is not ensured, even for low rotational speeds. alginate composites are characterized in the range of 0.01 to 1000 1/s.

Rheological modelling

The rheological modelling can be divided into two main goals. First, one can determine a suitable rheological model for the material system. Therefore, a variety of commonly used model systems, consisting of various springs and dashpots in linear or parallel arrangement, is investigated. Such model systems can resemble viscoelastic material properties, due to the combination of pure elastic (springs) and pure viscous (dashpot) components. A detailed explanation of the modelling approach is already published by Schrüfer et al. [25]. Statistika (StatSoft, 2018) is used for all linear regressions. The suitability of each model is evaluated by its resulting adjusted R2 value. Those systems can be further divided into three subgroups, namely rheological solids, liquids, and hybrids. The type of the most suitable model system already yields important information for the correlation to printing results and modelling outcomes. Furthermore, the elastic moduli of springs, the viscosities of dashpots and their dependence on material properties such as polymer or filler concentration are evaluated. This highly condensed data, which reduces a whole frequency sweep to just four parameters in the case of the Burgers model, enables more concise experimental evaluation and correlations between rheological and process parameters.