Solid solution hardening in CrMnFeCoNi-based high entropy alloy systems studied by a combinatorial approach

Abstract

Solid solution hardening in high entropy alloys was studied for the Cantor alloy using diffusion couples and nanoindentation. We study a continuous variation of the alloying content and directly correlate the nanoindentation hardness to the local composition up to the phase boundary. The composition dependent hardness is analysed using the Labusch model and the more recent Varvenne model. The Labusch model has been fitted to experimental data and confirms Cr as the most potent strengthening element. For comparison of the experimental hardness and the predicted yield strength of the Varvenne model, a concentration-dependent strain-hardening factor is introduced to account for strain hardening during indentation, which leads to a very good agreement between experiment and model. A study of the input parameters of the Varvenne model, performed by atomistic computer simulations, shows no significant effect of fluctuations in the atomic size misfit volumes or in the local shear modulus to the computed yield strength.

Graphic Abstract

Introduction

The role of solid solution hardening (SSH) in chemically complex alloys e.g. high entropy alloys (HEAs) [1] has been subject of substantial attention in the past few years [2,3,4,5,6]. However, a generalised and validated model for the prediction of solid solution hardening in HEAs is still needed [2, 7]. The conventional Labusch SSH model [8, 9] describes the interaction of obstacles and dislocations in dilute solid solution alloys based on a combination of two elastic effects (namely size and modulus misfits). In the Labusch model solid solution hardening is described as the change in critical shear stress $\Delta \tau_{\text{Labusch}} \propto \Delta c^{2/3}$ required for dislocation motion, where $\Delta c$ is the change in concentration of the solute. This conventional SSH model requires a clearly defined differentiation of solute and solvent species [8, 9]. The issue applying the Labusch model to HEAs is that no atomic species can be taken as solute or solvent as all elements are present in similar fractions in the alloy.

An early approach for modelling SSH in HEAs was proposed by Senkov [4] using the Labusch model. In this case, the TiZrNbHfTa body-centered cubic (BCC) alloy was modelled as pseudo-binary in terms of atomic size misfit and modulus misfit, which resulted in a yield strength difference of 18% between model and experiment. This approach, however has not been generalized for all HEAs, especially for alloys which cannot be split into pseudo-binaries.

A more recent approach for modelling SSH in highly concentrated face-centered cubic (FCC) HEAs was proposed by Varvenne [10, 11]. The Varvenne model describes a HEA as a homogeneous monoatomic matrix with average mechanical properties, in which the different constituents of the HEA are embedded. These randomly distributed solutes are responsible for the observed strengthening. Therefore, a dislocation moving through a HEA sees this homogeneous background matrix and the influence of the different solutes. The strain fields of the solutes interact with the dislocation line, exhibiting an interaction force [10,11,12]. Whereas in the classical SSH models local fluctuations in the shear modulus ($\Delta \mu$) are assumed to influence the magnitude of this interaction force [8, 9], the Varvenne model only considers an atomic size misfit ($\Delta V$), neglects these fluctuations, and depends on an average shear modulus. Nevertheless, satisfactory agreement between experimental and predicted strength was obtained in previous studies of Cantor alloy subsystems [5, 6, 13].

In this paper, we study diffusion couples of the Cantor (CrMnFeCoNi) alloy [14] with its pure constituent elements to determine nanoindentation hardness as a function of local composition in a continuous manner. This approach allows us to study SSH in HEAs having access to a wide range of chemical compositions up to the solubility limit of each constituent element. Concentrations up to the phase boundary can thereby be accessed, which would be impossible using samples prepared with discrete concentrations (compare Refs. [5, 6]). We use this unique data set to correlate hardness and local composition to test the two SSH models and isolate the individual strength contributions of the different solutes in the Cantor alloy system.

Results

Nanoindentation hardness measurements

Figure 1a shows the hardness as a function of indentation depth h of pure Ni and Cantor (H–h curves of the other diffusion couples are shown in the Appendix). The indentation size effect (ISE) causes a decreasing hardness with increasing indentation depth until a depth independent macroscopic H is reached [15]. To minimize the contributions from the indentation size effect and also to ensure a high lateral resolution, the hardness is averaged over an indentation depth interval from 900 to 1000 nm. Indentations to higher depth (2500 nm) on discrete Ni-diluted Cantor subsystems (Ni20, Ni60, Ni92) have shown a concentration independent internal length scale (h* ≈ 0.4) and thus a comparable ISE in the FCC solid solution of the Cantor alloy [16]. Since the ISE is expected to be comparable for all compositions investigated, the averaged hardness from 900 to 1000 nm indentation depth can be used to evaluate the SSH. Furthermore, indentation strain rate jump tests on the aforementioned discrete Ni-diluted Cantor subsystems revealed a negligible strain rate sensitivity in the range of 0.004 (pure Ni) to 0.009 (Cantor). Furthermore, all indentation experiments are performed at a constant strain rate, no effects on the evaluation of SSH are expected due to strain rate sensitivity. The pile-up behavior was measured and no significant pile-up could be detected for all investigations up the phase boundary. From these results, a composition independent pile-up behavior and strain rate sensitivity is assumed for these samples, thus, the used Tabor´s equation holds true and no effects on the evaluation of solid solution hardening is expected.

Figure 1

(a) Typical measurement of nanoindentation hardness H and indentation modulus E as function of indentation depth h for Cantor and Ni. (b) Light microscopy image of the indentation field across the interdiffusion zone of the diffusion couple CrMnFeCoNi + Fe.

The effect of SSH in the CrMnFeCoNi alloy can be clearly seen in the indentation data in Fig. 1a as the hardness increases upon addition of Cr, Mn, Fe, and Co to Ni. The indentation modulus E is constant for each indentation but shows a concentration dependency, as can be seen for Ni and Cantor. A mean indentation modulus of 198.3 ± 7.9 GPa is obtained for the Cantor alloy and 221.4 ± 2.4 GPa for Ni, both being in good agreement with literature data of single phase materials [17, 18].

Concentration and hardness profiles

The local concentration, crystal structure and hardness were measured over the whole interdiffusion zone using a diffusion couple approach; here only the FCC single-phase region is shown. For more details on the microstructure and a detailed discussion of the different diffusion profiles and the stability ranges of other phases see Ref. [19]. A light microscopy image of a representative indentation field across the complete interdiffusion zone between Cantor and Fe is shown in Fig. 1b. We can assume that the composition within the plastic zone beneath the indenter is nearly uniform, as we limited the penetration depth to 1000 nm. Due to the large grain size of ≈ 100 µm, grain boundary strengthening effects can be neglected, as each indent probes only a single grain. Furthermore, we do not observe a gradient in grain size along the interdiffusion zone. For the evaluation of SSH, only indents with a minimum distance of the plastic zone’s diameter from the phase boundary were considered.

Figure 2 shows the hardness as a function of varying concentrations (solid lines) of the FCC structure in the interdiffusion zone (IDZ) starting from the equiatomic composition of the Cantor alloy with a hardness level of ≈ 2.2 GPa on the right. The coefficient of variation (ratio of the standard deviation to the mean value), caused by the nanoindentation testing setup, is shaded in gray. The maximum coefficient of variation was determined by reference measurements in the equiatomic Cantor alloy as well as in the pure elements and is assumed as being constant within the concentration gradients (max. ± 3%). On the x-axis, the relative position in the IDZ is shown, while the concentrations of the constituents are given by colored lines. Figure 2a shows the diffusion couple CrMnFeCoNi + Ni, with a single FCC phase over the entire compositional gradient, thus, the complete hardness profile can be used to analyse the effect of SSH starting from a constant and equiatomic composition. Up to a Ni concentration of 70 at.%, the hardness remains almost constant at a hardness level of about 2.2 GPa and decreases with further increase in Ni. The hardness decreases to the hardness of pure Ni as the Ni concentration approaches 1.

Figure 2

Concentration profiles for the different Cantor + i diffusion couples measured using EDX. d is the relative position within the IDZ starting from the Cantor alloy on the right. The respective diffusion partner is Ni, Cr, Co, Fe, and Mn going from (a) to (e). Only the single-phase FCC region for each sample is shown. Due to oxidation effects of Mn (e), the evaluation of the hardness is limited to the Mn concentration interval from 20 to 55 at. %. The full concentration profiles can be found in Ref. [19]. The nanoindentation hardness is scaled on the secondary y-axis. For further details regarding the error bars (grey), please see the full text.

If a phase transition takes place within the interdiffusion zone (Fig. 2b–d), only the FCC phase region will be considered in the further analysis. The concentrations of the respective diffusion partner elements Co or Fe can be increased substantially up to ≈ 65 at.% until a phase transition takes place [19], it is possible to evaluate SSH up to ≈ 55 at.%. As Co and Fe increase in concentration, all other constituent elements show a decreasing concentration. The diffusion couple CrMnFeCoNi + Co (Fig. 2c) shows nearly no influence of changing concentrations on the hardness level. An increase in Fe (Fig. 2d) results in a continuously decreasing hardness. The diffusion couple CrMnFeCoNi + Cr shows the formation of an intermetallic phase above ≈ 35 at.%. The relatively small increase in Cr prior to the formation of an intermetallic phase leads to a hardness increase of 0.3 GPa up to 29 at.% Cr.

Due to oxidation and other surface defects in the CrMnFeCoNi + Mn diffusion couple (evident from the scattering of the nanoindentation data), the evaluation of the hardness is limited to Mn concentrations below 55 at.%. The hardness increases in this concentration interval with increasing Mn content from 2.2 to 2.5 GPa.

Discussion

The direct correlation between hardness and chemical gradients allows to draw conclusions about solid solution hardening. The measured concentration profiles are used as an input for the Labusch model [8, 9] and alternatively the Varvenne model [10, 11]. Both applied models will then be validated against the experimentally measured hardness. By adding each constituent species to the equiatomic composition, the respective influence can be investigated over the complete compositional ranges for all five diffusion couples, where the FCC structure of the Cantor alloy is (meta-)stable.

Application of the Labusch model

To apply the Labusch model to highly concentrated multi component alloys—including HEAs, we generalize the model introducing a different strengthening parameter $k_{n}$ for each element n leading to the following formulation of the Labusch strengthening model (Eq. 1). Here it is assumed that $\Delta \tau_{\text{Labusch}}$ contributions are additive per constituent of the alloy:

$$\Delta \tau_{\text{Labusch}} = \mathop \sum \limits_{n} k_{n} \Delta c_{n}^{2/3} \propto \Delta H$$

(1)

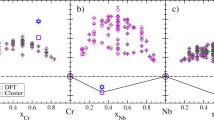
Equation 1 is used to fit the modified Labusch model to the experimental hardness data. The individual $k_{n}$ parameters are found using the change in hardness ($\Delta H$) and the change in concentration ($\Delta c$) for the two boundary phases (equiatomic Cantor alloy and composition at phase boundary) for all five diffusion couples simultaneously and solving the resulting system of linear equations. The following strengthening parameters in units of GPa/at.%^2/3) were obtained: $k_{\text{Cr}} = 0.0514, \,k_{\text{Mn}} = 0.0058, \,k_{\text{Fe}} = - 0.0470,\, k_{\text{Co}} = - 0.0109, \,k_{\text{Ni}} = - 0.0342$. The absolute value and sign of the strengthening parameter determine the effect of a changing concentration of the specific element on the strength of the equiatomic Cantor alloy. Based on these k-values and the measured concentration profiles, the concentration dependent hardness is modelled and compared to experimental results. The measured and calculated hardness values normalised by the hardness of the Cantor alloy are shown in Fig. 3. Discrete points denote our measurements, while solid lines give the Labusch solution. Please note, that the different data series are shifted by a constant offset to improve readability. The modified Labusch model is able to accurately describe the measured hardness for Cr, Mn, Co, and Fe. For Ni on the other hand, the hardness plateau up to ≈ 70 at.% Ni is not captured by this model. It predicts a continuously decreasing hardness in the Cantor + Ni sample.

Figure 3

Measured hardness as function of the concentration of the Cantor alloy partner in each diffusion couple (symbols). The fit results from the modified Labusch model (Eq. (1)) are given by solid lines. For clarity, each sample has been shifted along the ordinate. The coloured bars represent the error of the indentation experiments.

As outlined in “Relating yield stress to hardness” section, the conversion between changes in the hardness of a material and its yield strength is not straight forward. Fitting Eq. (1) however, allows us to circumvent these uncertainties as they are incorporated in the different $k_{n}$ values. Therefore, the apparent deviation of the Ni hardness series from the prediction cannot be explained by concentration dependent strain hardening or the ISE.

Even though, the modified Labusch model is not predictive (the strengthening parameters $k_{n}$ cannot be known a priori) it provides important insights into the strengthening characteristics of the Cantor system. Note that we have not only used the narrow concentration gradient towards the phase boundary of the diffusion couple Cantor + Cr but we also solved the linear system of equations using all five diffusion couples simultaneously. Based on the obtained strengthening parameters, Cr (positive $k_{n}$) seems to be the most potent strengthening element. This observation is consistent with results from Wu et al. [3], where Cr was identified as the element with the strongest impact on strength, which they attributed to modulus mismatch effects. They suggest that the effect is caused by the different shear modulus of Cr compared to the other constituents, based on the assumption of the elastic constants of the elements in their ground state. But it should still be considered, that the Cantor alloy shows a well-defined shear modulus distribution (Fig. 6), which raise the question how the shear modulus misfit needs to be taken into account.

Fe on the other hand shows a contrary effect as it leads to a decrease in hardness, which has already been observed by Bracq et al. [5] for discrete compositions. This behavior is expressed by a negative strengthening parameter.

Application of the Varvenne model

The Labusch model can be used to describe the measured hardness data, but given its large number of tunable parameters it can hardly be used to predict the concentration dependent strength of a HEA. The Varvenne model in its simplified elastic form given by Eqs. (2)–(4) (see methodology “Varvenne solid solution-hardening model” section), on the other hand, remains parameter-free and can therefore be used as a predictive tool. However, the Varvenne model cannot provide the absolute hardness measured by nanoindentation, as it describes only a concentration dependent critical shear stress at zero strain. Therefore, we rescaled the experimental and predicted hardness by the Cantor hardness level: $\Delta \sigma_{\text{SSS}} \propto H\left( {c_{n} } \right)/H_{\text{Cantor}} \propto fCM\Delta \tau_{\text{Varvenne}}$ and the ratio between the composition of the equiatomic Cantor alloy on the one side and the local composition at the phase boundary on the other side. This ratio ($H\left( {c_{n} } \right)/H_{\text{Cantor}}$) is considered in Fig. 4. This approach is similar to the normalisation chosen in Refs. [5, 6]. Additionally, a strain hardening factor f (c) is introduced, which includes concentration dependent strain hardening and other effects during indentation. The normalization $H/H_{\text{Cantor}}$ cancels out errors in the conversion from H to $\sigma_{y}$ for the Cantor alloy. Concentrations far away from equimolarity have different strain hardening contributions and this effect can be compensated by the strain hardening factor. Initially, a concentration independent strain hardening was assumed using a constant f parameter of 2 (≈ 1.84 found in tensile tests [20]), which leads to the results shown in Fig. 4a, where the predicted and measured hardness ratios over the concentration of the main element in the diffusion couple are shown. Here the solid lines corresponds to the yield strength obtained from the Varvenne model at 300 K. The required pure metal material constants were taken from Refs. [21, 22], model specific parameters e.g. $\alpha$ and $\Delta V_{n}$ were taken from Ref. [11] and are summarized in Table 2.

Figure 4

Predicted (solid lines) and measured hardness (symbols) normalized by $H_{\text{Cantor}}$ as function of the concentration of the Cantor alloy partner in each diffusion couple. (a) shows the calculated results from the Varvenne model (Eqs. (2)–(4). (b) shows the Varvenne fit results with a concentration dependent f factor for Cr, Fe, Mn and Ni. The respective f factors are shown in the inset. For Co and Fe a constant f of 2 is assumed as it describes the measured hardness data well. For Cantor + Ni a constant hardness value was introduced to describe the indentation base hardness of pure Ni (dashed lines). The coloured bars represent the error of the indentation experiments.

The Varvenne model is able to describe the hardness gradients for the increase in Co and Fe, but it fails to predict the hardening behavior for Cr or Mn, or the softening for Ni accurately. In case of the CrMnFeCoNi + Ni couple, the model predicts a decreasing hardness down to 0 GPa for pure Ni. This behavior is caused by the fact that for pure elements, the atomic size misfit in Eq. (2) becomes zero and consequently the predicted critical shear stress is zero. In order to take the indentation base hardness of Ni (1.5 GPa) into account, we shifted the predicted hardness by this constant hardness level: $H\left( c \right) = H_{\text{Ni}} + fCM\tau_{\text{Varvenne}}$. The superposition of the Ni base hardness and the Varvenne model is now represented by a dashed line in Fig. 4a and good agreement is found. Moreover, the Varvenne model is able to capture the plateau in hardness upon addition of Ni. Since we are not able to describe all diffusion couples sufficiently well with the model, the question arises whether this is due to the basic assumptions of the Varvenne model (grey matrix, fixed misfit volumes) or due to the comparison between computed yield strength at zero strain and nanoindentation hardness. To address the first issue, we have determined the standard deviation of the atomic misfit volumes using atomistic computer simulations (Appendix C.2.: Misfit volumes) and integrated these into Eqs. (2) and (3) according to Ref. [11]. Here $\Delta V_{n}^{2}$ is replaced by ($\Delta \bar{V}_{n}^{2} + \sigma_{{\Delta V_{n} }}^{2}$), where $\Delta \bar{V}_{n}$ is the mean misfit volume and $\sigma$ denotes its standard deviation. The respective standard deviations of the solutes are determined to: $\sigma_{{\Delta V_{\text{Cr}} }}^{2} = 0.0887 {\text{\AA}}^{3} , \,\sigma_{{\Delta V_{\text{Mn}} }}^{2} = 0.0900 {\text{\AA}}^{3} , \,\sigma_{{\Delta V_{\text{Fe}} }}^{2} = 0.0754 {\text{\AA}}^{3} , \,\sigma_{{\Delta V_{\text{Co}} }}^{2} = 0.0773 {\text{\AA}}^{3} ,\, \sigma_{{\Delta V_{\text{Ni}} }}^{2} = 0.0673 {\text{\AA}}^{3}$. Furthermore, we determined the distribution of the local shear modulus (Appendix C.1: Local shear modulus) and implemented the standard deviation of the local shear modulus (6.246 GPa) as additive strengthening contribution into the aforementioned equations ($\bar{\mu }$ is changed to $\bar{\mu } + \sigma_{\mu }$). Inserting both standard deviations ($\sigma_{{\Delta V_{n} }}^{2}$ and $\sigma_{\mu }$) is only physically meaningful, if there is a correlation between the atomic size misfit and the local shear modulus in the HEA-matrix. Even though simulations could not show a correlation, it serves as an upper limit for yield strength predictions of the Varvenne model. Including the standard deviations, a maximum increase in yield strength of roughly 13% can be observed for the equiatomic Cantor alloy, which is mostly attributed to the variation in shear modulus. Nevertheless, the absolute nanoindentation hardness is not provided.

Despite the consideration of the standard deviations, some hardness trends (Cr and Mn) cannot be described by the model. Therefore, a concentration-dependent strain-hardening behavior has now been introduced. Figure 4b shows the fit using a concentration dependent f factor for describing the nanoindentation hardness evolution for all diffusion couples. Substantial concentration changes are found within the IDZ and as a consequence, parameters such as the stacking fault energy (SFE) will change, which in turn affects the local strain hardening behavior and thus the parameter f. The concentration dependent parameter f was fitted based on the measured hardness to account for the strain hardening of changing compositions within the interdiffusion zone. Since we do not have access to all required experimental data for the direct derivation of the concentration-dependent f factor for all diffusion couples, in the following we will assume a linear dependency. As it can be seen in Fig. 4b, a linearly increasing hardening behavior from 2.0 for Cantor to 2.3 for Cr rich compositions and to 2.75 for Mn rich compositions describes the increasing hardness with increasing Cr or Mn concentration well. The introduction of a concentration dependent f factor leads to good agreement using the Varvenne SSS model and nanoindentation hardness mapping, whereas fluctuations in the local shear modulus and atomic size misfit volumes show negligible effects on the predicted hardness.

Bracq et al. [5] tested 24 discrete compositions based on the Cantor alloy with four elements staying in equiatomic ratio, while the respective fifth element is varied in concentration within the FCC phase space. Using discrete compositions gives better statistics for the mechanical characterisation on each sample, but the investigation of the vast compositional range of HEAs is strongly limited due to a high experimental effort. The diffusion couple approach on the other hand can be considered as a high-throughput screening method investigating broad concentration ranges up to the phase boundary. A quantitative comparison of the nanoindentation hardness values seems to be not appropriate, as the evaluation of hardness took place at different indentation depth. Furthermore, the equiatomic ratio of the other elements can not be kept while adding the respective fifth element during interdiffusion heat treatment. However, a qualitative comparison shows similarities for the addition of Co, Fe, Ni and differences for Cr, Mn. While Bracq et al. [5] could not notice any effect of Mn or Cr increase on hardness, we observe an increase in hardness especially by adding Cr up to the FCC phase boundary. This observation is consistent with the results from Wu et al. [3], where Cr was also identified as the most potent strengthener element.

Summary and conclusion

The diffusion couple approach enables the investigation of multicomponent alloys over wide compositional intervals regarding phase stability or solid solution strengthening. In this work, the superposition of EDX and nanoindentation hardness measurements was used to investigate SSH as a function of the chemical composition up to the phase boundary of the FCC phase of the Cantor alloy system. It has been shown that nanoindentation hardness mapping can be used for fast exploration of SSH of various chemical compositions. Moreover, the experimentally measured hardness was compared to the hardness predicted by a modified Labusch model and the more recent Varvenne model.

• 1. The Labusch model can be modified and fit to experimental nanoindentation data. Trends and effects for different constituent elements and solute additions (Co, Cr, Fe) are described well, but the model fails to describe trends for the large compositional range to pure Ni. According to this model, Cr seems to be the most potent strengthening element due to its highest strengthening parameter.

• 2. The Varvenne model qualitatively describes the trends in most diffusion couples over the whole compositional range in the FCC structure. A concentration dependent correlation factor was introduced to consider changing strain hardening behavior and to fit the Varvenne model to experimental nanoindentation results, leading to good quantitative agreement.

• 3. Considerable fluctuations in the local shear modulus as well as in the atomic size misfit volumes were calculated by atomistic computer simulations, which in turn have no significant effect on the yield strength predictions of the Varvenne model and could be neglected.

Methodology

Varvenne solid solution-hardening model

The Varvenne solid solution model specifically designed to describe highly concentrated FCC alloys based on the assumption of a homogeneous average background matrix. There are various notations for the Varvenne model, which contain different prefactors. The notation we will be using follows Ref. [23] and is valid for FCC samples:

$$\Delta \tau_{y0} = 0.01785\alpha^{ - 1/3} \bar{\mu }\left( {\frac{{1 + \bar{\nu }}}{{1 - \bar{\nu }}}} \right)^{4/3} \left[ {\frac{{\mathop \sum \nolimits_{n} c_{n} \Delta V_{n}^{2} }}{{b^{6} }}} \right]^{2/3}$$

(2)

$$\Delta E_{b} = 1.5618\alpha^{1/3} \bar{\mu }b^{3} \left( {\frac{{1 + \bar{\nu }}}{{1 - \bar{\nu }}}} \right)^{2/3} \left[ {\frac{{\mathop \sum \nolimits_{n} c_{n} \Delta V_{n}^{2} }}{{b^{6} }}} \right]^{1/3}$$

(3)

$$\tau_{y} = \tau_{y0} \left[ {1 - \left( {\frac{{k_{B} T}}{{\Delta E_{b} }}ln\frac{{\dot{\varepsilon }_{0} }}{{\dot{\varepsilon }}} } \right)^{{\frac{2}{3}}} } \right]$$

(4)

Parameters of the model are the mean shear modulus $\bar{\mu }$ and Poisson’s ratio $\bar{\upsilon }$ of the alloy, the length of the Burgers vector b, the concentration of each constituent $c_{n}$ and the corresponding misfit volume $\Delta V_{n}$. The temperature T can then be used to calculate the critical shear stress $\tau_{y}$ at finite temperatures. Further parameters and their derivation are explained in Ref. [11]. The mean properties of the HEA are commonly obtained from a rule-of-mixture, $\bar{\xi } = \mathop \sum \limits_{n} c_{n} \xi_{n}$, where $\xi$ is the physical property of interest [23]. The misfit volumes of the Cantor system are taken from Ref. [11]. The flow stress is linked to the predicted shear stress (cf. Eq. (4)) by the Taylor factor M (equal to 3.06 for polycrystalline FCC samples) [11]. The Varvenne model only considers a mean shear modulus and the respective atomic size misfit volumes $\Delta V_{n}$, whereas Labusch describes the strengthening based on the addition of two elastic contributions: atomic size and shear modulus mismatch [8, 9].

Experimental procedure

Diffusion couples were prepared from a homogenized Cr_20.7Mn_18.5Fe_20.2Co_20.5Ni_20.1 Cantor alloy and its constituent pure elements. The purity levels of the diffusion partner elements (> 99.0%), sample preparation, heat treatment and quenching conditions can be found in Ref. [19]. The used heat treatment procedure avoids decomposition and retains the FCC phase stable of the Cantor alloy at ambient temperatures despite being potentially metastable. Cross sections of the diffusion couples were prepared by a mechano-chemical polishing down to colloidal silica to prepare deformation free and smooth surfaces, required for chemical, structural and mechanical investigations within the interdiffusion zone. The mechanical properties were investigated by nanoindentation testing, using a G200 nanoindentation system (KLA) equipped with a diamond Berkovich tip (Synton-MDP). The local mechanical properties were measured with a continuous stiffness measurement (CSM) [24, 25], with an oscillation frequency of 45 Hz and a harmonic displacement of 2 nm. An input strain rate ($\dot{\varepsilon } = \frac{{\dot{p}}}{p}$) of 0.05 was chosen. The maximum indentation depth was set to 1000 nm and the hardness is averaged over an indentation range of 900–1000 nm. The pile-up behavior around the indent was measured via a Laser Scanning Microscope (Olympus Lext OLS 4100). A scanning electron microscope (TESCAN Mira3) was used to investigate the chemical and phase distribution within the interdiffusion zone by energy dispersive X-ray spectroscopy (EDX) and electron backscatter diffraction (EBSD).

Relating yield stress to hardness

With SSS models, the contribution of individual alloying elements onto the yield stress are determined, whereas these models do not quantify possible changes in the defect storage, annihilation and thus work hardening behaviour of the alloys. The experimentally determined hardness H however comprises different factors besides solid solution strengthening, for example work hardening in presence of the indentation strain gradient needs to be considered. Hence, the difference in hardness between an alloy and the pure matrix element (referred to as unalloyed) is used to quantify solid solution strengthening using nanoindentation: $\Delta \sigma_{\text{SSH}} \propto \Delta H_{\text{SSH}} = H_{\text{alloy}} - H_{\text{unalloyed}}$ [26]. Figure 5 schematically depicts an approach to relate the depth h and concentration dependent indentation hardness H (h) to the concentration dependent yield strength $\sigma_{y} \left( {x_{i} } \right)$. The hardness can be related to the flow stress $\sigma$ at representative strain using Tabor’s equation [27]: $H \approx C\sigma \left({\varepsilon_{\text{rep}} } \right)$, where C represents the constraint factor C = 3 [28] and $\varepsilon_{\text{rep}}$ is the representative strain. The dependency of the constraint factor on the elastic/plastic work ratio according to Leitner et al. [29] was used and a fully plastic behavior was observed for all compositions up to the phase boundary and we do not expect any influence for the further model analysis. For the used Berkovich tip, a representative strain of $\varepsilon_{\text{rep}} \approx 8 \%$ [28] is found. Tabor’s eq. only holds true if other contributions to the experimental hardness, like strain hardening, indentation size effect (ISE), pile-up behavior and strain rate sensitivity, are independent of concentration [26, 30]. For the tested material systems pile-up and rate sensitivity can be neglected, and the ISE is considered to be comparable for all compositions (as shown for Cantor and pure Ni in Fig. 1). However, knowledge of the strain hardening behavior $\sigma = \sigma_{0} \varepsilon^{n}$ where the work hardening exponent n depends on the composition is essential for a correlation between flow stress at representative strain and the yield strength $\sigma_{y}$ at zero strain. In particular, the stacking fault energy (SFE) will change with composition and thus affect the local strain-hardening behavior ($+ \Delta \sigma$, see Fig. 5) [31, 32]. Finally, the yield strength can be related to a hardness value and thus nanoindentation hardness mapping as function of the concentration c allows us to investigate solid solution strengthening in a continuous manner. Bracq et al. [5] also compared the indentation hardness of various FCC HEAs based on the Cantor alloy with a calculated yield strength using Tabor´s eq. and assumed a 20% uncertainty.

Figure 5

Relation between depth and concentration-dependent hardness H (h, c) and the yield strength $\sigma_{y}$ as function of the concentration change $\Delta c$ using Tabors eq. Knowledge of the strain hardening $\sigma_{\text{strain}}$ is required to extrapolate from the experimentally measured hardness to the yield strength.

Appendices

Appendix A: List of symbols

See Table 1.

TABLE 1 List of symbols.

Appendix B: Material parameter

See Table 2.

TABLE 2 Material parameters used as input for the yield strength calculations based on the Varvenne model [11, 21, 22].

Appendix C: Atomistic computer simulations

C.1: Local shear modulus

The Varvenne model is based on the assumption of an average background matrix, into which solutes are embedded [10, 11]. This average matrix has an average shear modulus $\bar{\mu }$, which is taken as homogeneous over the whole sample. The interaction of the dislocation with the local chemical fluctuations of the HEA are included by means of the volume misfit term $\Delta V$, which accounts for the size difference of the elements. Atomistic computer simulations are used to investigate whether the HEA matrix can be seen as an average matrix with a homogeneous shear modulus or if there are strong local fluctuations which need to be treated individually (Fig. 6).

Figure 6

Distribution of the local VRH shear modulus ($\mu_{\text{VRH,local}}$) in the equimolar Cantor alloy. For comparison the VRH shear modulus for the same alloy determined from Hooke’s law is given ($\mu_{\text{VRH,global}}$). The inset shows a snapshot of the sample with atoms color-coded based on their local shear modulus.

To answer this question, we calculate the local stiffness tensor for each atom in a Cantor alloy sample using the computational approach presented in Ref. [33]. Calculations were performed using LAMMPS [34] and the equimolar CrMnFeCoNi HEA was described by the 2-nearest neighbor modified embedded atom method (MEAM) interatomic potential [35] parametrized by Choi et al. [36]. The single crystalline FCC sample was prepared using ATOMSK [37] and contained 5 × 10⁵ lattice sites occupied by randomly distributed Cr, Mn, Fe, Co, and Ni atoms. We determined the macroscopic elastic constants from finite deformations of the simulation cell using Hooke’s law. Post processing and visualization were performed in OVITO [38].

From this data the Voigt–Reuss–Hill (VRH) [39] averaged local shear modulus can be obtained for each atom. Fig. 6 shows a histogram of the local shear modulus ($\mu_{\text{VRH, local}}$) compared to the VRH shear moduli obtained from Hooke’s law for the whole simulation cell ($\mu_{\text{VRH,global}}$). The inset shows a snapshot of the simulated sample with the atoms color-coded based on their local shear modulus.

The mean of the local shear modulus distribution is located at 52 GPa which is lower than the one reported by Wu et al. [3] 80 GPa. Nevertheless, the atomic shear modulus shows a broad distribution with a full width a standard deviation of 6.25 GPa and a full width at half maximum of 14 GPa. The inset shows no significant clustering of low (high) shear modulus atoms forming subvolumes of locally decreased (increased) stiffness. Given that the strain field of the dislocation is farther reaching than multiple interatomic distances [40] and with the activation volume for dislocation glide in the Cantor alloy being about 70–360 b³ [41], it remains unclear whether these short ranged fluctuations of the shear modulus need to be included in a SSH model.

C.2.: Misfit volumes

The misfit volume is a key quantity strongly influencing the yield strength predicted by the Varvenne model. It can be obtained from experiments on binary subsystems of the HEA [11], the rule-of-mixtures [23], or from atomistic computer simulations of the full HEA [12]. In the following, we determine the misfit volume of the different constituents in the Cantor alloy using atomistic computer simulations based on the approach developed by Yin and Curtin [12].

Similar to the local shear modulus, the local atomic volume in a HEA is not a single number, but varies locally depending on the chemical environment. We use poly-disperse Voronoi tessellation as implemented in OVITO [38] to determine the volume associated to each atomic species in the HEA. We used the sample prepared in sec. Appendix C.1 as it contained a sufficiently large number of atoms to achieve representative results. The elemental Goldschmidt radii are used as input for the tessellation and the resulting atomic volume distribution $V_{i}$ is shown in Fig. 7. Additionally, the average atomic volume $\bar{V}_{\text{CrMnFeCoNi}}$ is indicated. The five constituent elements show differences between their element specific Voronoi volume and the average atomic volume of the matrix $\bar{V}$ in the range of 0.14–0.56 Å³. The Voronoi volumes confirm that the atomic volume in the HEA is not a single number, but follows a normal distribution with standard deviations in the range of 0.0674 Å³ for Ni to 0.0909 Å³ for Mn. If the atomic volumes in a HEA show a finite width distribution, the corresponding misfit volumes need to have a similar distribution. While the finite width of the misfit volume distribution is included as $\sigma_{{\Delta V_{n} }}$ in the original equations of the Varvenne SSH model (see Ref. [11] Eqs. 15 and 16) this value is usually set to 0 ({e.g. Refs. [11, 12, 23]).

Figure 7

Distribution of the static atomic volume V_i for each atomic species in the CrMnFeCoNi HEA determined by polydisperse Voronoi tessellation at 0 K. The average atomic volume $\bar{V}$ is indicated as well.

Appendix D: Nanoindentation hardness data

See Fig. 8.

Figure 8

Nanoindentation hardness as a function of indentation depth for the equiatomic composition (named as Cantor) and the composition at phase boundary for the respective diffusion partner element (named as phase boundary). Please note here, only indents with a minimum distance of the plastic zone’s diameter from the phase boundary were considered. For clarity, not all data points are displayed and each sample has been shifted along the ordinate.