Background

Since their inception in the early 2000s,1,2 compositionally complex alloys (CCAs), also referred to as “high-entropy” alloys (HEAs), have attracted a great deal of attention due to a unique combination of properties seldom found in other material types.3,4,5,6,7,8,9,10,11 This makes them potentially attractive as candidate materials for a number of technological applications in harsh environments such as elevated temperatures, irradiation, or corrosion.12,13,14,15 As an example, Figure 1a shows an Ashby diagram of the fracture toughness versus the yield strength, showing generic HEAs as superior to almost all other material classes.11 The basic idea behind creating alloys of this type is to combine a number of elements (typically four or more) in similar proportions to achieve solid-solution phase stability through the large configurational entropy of the system. Due to the large chemical and configurational space available to create these materials, several hundred different HEA combinations now exist, each with their own distinct compositions, structure, and properties.16,17 The large volume of research on the topic over the last decade has resulted in a fast-evolving field full of new findings, unexplained results, and unresolved controversies. The reader is referred to the numerous reviews and monographs published over the last several years for more details.3,4,5,6,7,8,9,10,18,19 Note that, although the term “multicomponent” or “multielement” alloys is sometimes preferred in the literature over “high-entropy” alloys (particularly when the number of elemental constituents is less than five), here, we use all interchangeably.

Figure 1
figure 1

(a) Ashby chart of the fracture toughness versus yield strength showing the region occupied by high-entropy alloys. Adapted with permission from Reference 11. © 2014 AAAS. (b) Engineering strain versus engineering stress curves for the Nb25Mo25Ta25W25 alloy obtained during compression testing at elevated temperature. Adapted with permission from Reference 20. © 2011 Elsevier.

Full size image

Among the different materials proposed, refractory multi-element alloys (RMEAs) are a special class of alloys composed of typically four or more refractory metal elements (Nb, Mo, Ta, V, W, Cr, Hf, Zr). Although compositionally complex, these systems generally crystallize into a simple body-centered-cubic (bcc) phase, found to be stable up to very high temperatures.9,20,21,22,23,24,25 Similar to their pure bcc metal counterparts, RMEAs could suffer from a lack of ductility at low temperatures,20,26 which is thought to be associated with segregation of interstitial impurities at grain boundaries27 and a high plastic flow localization propensity due to highly orientation-dependent slip.28 However, they retain a high strength and ductility at high temperatures, making them attractive candidates for high-temperature structural applications, such as in the power, aerospace, or nuclear sector.12,13,14,18,29 Figure 1b shows compression test results for the Nb25Mo25Ta25W25 system, clearly illustrating both features just discussed.

However, although the deformation mechanisms of bcc metals and their alloys are relatively well understood, theories that explain the behavior observed in bcc RMEAs have only recently begun to be developed.30,31,32 These theories are built around the idea that each atom in the alloy can be regarded as a solute atom in an effective matrix defined by the average properties of the constituent elements. As such, every single atom in the lattice contributes to (solution) hardening, potentially resulting in a large strengthening effect. At the same time, compositional fluctuations are seen to lead to “rough” dislocation lines.33,34,35,36 This effect is directly connected to the existence of a disordered energy landscape that sacrifices extra dislocation line length for lower overall “chemical” energy. For screw dislocations, the manifestation of this roughness is an enhanced concentration of equilibrium kinks on screw dislocation lines,37 thus potentially reducing the importance of kink-pair nucleation and shifting it instead to kink lateral motion. For edge dislocations, it could lead to a thermal concentration of defects38 that reduce their mobility and add extra strength at intermediate and high temperatures. Both of these instances signify a departure from “classical” bcc metal plasticity, which is known to be controlled by the thermally activated glide of screw dislocations and little or no participation of edge dislocations at low to intermediate temperatures.39,40,41,42

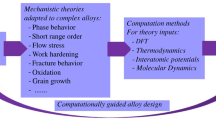
Thus, CCAs introduce a new physical framework where compositional fluctuations constantly alter the energy landscape over which dislocations move, leading to line roughness and the emergence of “chemical” defects that can fundamentally change how CCAs deform plastically at all scales. In this article, we discuss methodologies for modeling dislocation glide processes in CCAs, including atomistic simulations of dislocation glide using molecular dynamics, kinetic Monte Carlo simulations of screw dislocation motion, and phase-field models of dislocation evolution over complex energy landscapes. From a methodological point of view, the focus is on developing comprehensive simulation approaches that connect an atomic-level description of the compositional complexity of CCAs with their mesoscopic dislocation-mediated plastic response. Without loss of generality, we focus our discussion on refractory bcc alloys as paradigmatic of the next generation of high-temperature resistant, high-strength alloys called to be deployed in the extreme environments of the new energy and transportation future.

Atomistic modeling of CCAs

Dislocation glide is regulated by the underlying energy barriers that conform the potential energy landscape (PEL), through which dislocation motion proceeds by elemental mechanisms along the lowest (free) energy pathways. In the standard picture of plasticity for pure bcc metals, screw dislocation movement is governed by three elementary processes, each characterized by its own energy barrier: (1) the so-called Peierls mechanism, (2) kink-pair nucleation, and (3) kink gliding. These processes are associated with a “smooth” PEL that is spatially uniform (or, in the case of dilute alloys, subjected to minor local alterations). In CCA, the locally high chemical variability inevitably influences these mechanisms and their corresponding energy barriers, and hence the structure of the PEL and dislocation motion behavior. In the following, we study dislocation glide both by direct atomistic simulations and by sampling the intrinsic glide energy landscape to understand cooperative versus competitive atomistic processes that mediate dislocation motion. We note that one of the most salient features pertaining to CCAs is the existence of chemical short-range order (SRO),43 and thus we also study its role in dislocation glide mechanisms.

Atomistic simulations of dislocation gliding

Molecular dynamics (MD) has been widely used for investigating dislocation glide in CCAs.44,45 By constructing supercells with a single dislocation, one can resolve the individual glide mechanisms and derive the dislocation mobility within a typical stress and temperature range. For example, atomistic simulations of dislocation in bcc CCAs reveal an intermittent motion and sluggish mobility compared to those in pure bcc systems. These effects originate from chemical fluctuation-imposed trapping of local dislocation segments.46,47 When SRO is introduced, dislocation motion is further hindered due to diffuse antiphase boundary (APB) generation induced by dislocation glide.47,48 By resolving the atomic structure of moving dislocations, the underlying mechanisms, such as kink-pair nucleation and kink glide, can be extracted to understand the effects of compositional fluctuations on net dislocation motion. The role of SRO in dislocation movement mechanisms can also be revealed by tuning the local chemical order. For instance, MD simulations show that the presence of chemical SRO shifts the rate-limiting mechanism from kink-pair formation to kink glide. Note that, because of the simulation time-scale limitation in MD—typically less than 100 ns—MD simulations of dislocation motion must be performed at high stresses and/or high temperatures. Long time-scale atomistic simulation approaches, such as energy landscape sampling,49,50,51 can enable modeling at lower stresses over time scales of seconds and beyond.

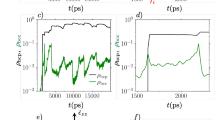
By systematically varying the temperature and the stress, MD simulations are able to model stress-driven and thermally activated events. For example, it is found that, depending on stress and temperature, cross-kink breaking has two distinct mechanisms: (1) stress-driven cross-kink unpinning at high stress and low temperature, and (2) thermally activated and diffusion-mediated cross-kink annihilation at low stress and high temperature.37,47 Figure 2a shows cross-kink formation and breaking at 300 K. This stress-driven unpinning generates “debris” (self-interstitials or vacancies) behind the moving dislocation.37,52 In contrast, cross-kink unpinning at 900 K takes place by a diffusion process53 involving cross-kink motion (Figure 2b). When an interstitial type cross-kink meets a vacancy-type one, the cross-kinks annihilate (akin to interstitial and vacancy recombination).

Figure 2
figure 2

Cross-kink breaking mechanism at low and intermediate temperatures. (a) Stress-driven cross-kink unpinning and production of vacancies and self-interstitials at 300 K. (b) Thermally activated and diffusion-mediated cross-kink annihilation at 900 K. Adapted with permission from Reference 47. © 2022 Elsevier.

Full size image

Energy landscape of dislocation glide

Calculations of energy barriers and PEL in bcc CCAs were performed by minimum energy pathway determination.47 Figure 3a shows the constructed Peierls energy landscape for equiatomic Mo–Nb–Ta–W. When compared with the landscape of pure bcc metals (Figure 3b), the CCA exhibits a hierarchical structure with a series of local basins (akin to Peierls valleys) embedded in large metabasins. This notable feature results from strong local compositional inhomogeneities in the random solution, consistent with experimental observations.54,55 Unlike the pure bcc metals, whose PEL can be characterized by a single energy barrier, the CCA contains a broad distribution of Peierls barriers. A similar characteristic also emerges for single kink glide, seen in Figure 4a. The landscape of lateral kink glide along a dislocation is highly rugged and displays a structural hierarchy of energy barriers, featuring small basins and large metabasins.

Figure 3
figure 3

(a) Minimum energy pathway and potential energy landscape spanning 25 Peierls valleys in pure Nb and MoNbTaW random solid solution (RSS) system. (b) The statistical distributions of Peierls barriers in RSS. Adapted with permission from Reference 47. © 2022 Elsevier.

Full size image
Figure 4
figure 4

(a) The potential energy landscape of kink gliding over 615b distance in random solid solution (RSS) (upper panel). The unfilled symbols indicate kink-pair events. (b) The statistical distributions of single kink glide energy barriers. Adapted with permission from Reference 47. © 2022 Elsevier.

Full size image

The hierarchical and multilevel structure of the energy landscape can trap dislocations in deep metabasins and considerably hinder their motion. For example, when a dislocation attempts to escape from one metabasin to an adjacent one, it must go through a sequence of local hopping barriers, making backward jumps during metabasin climbing energetically favorable compared to forward jumps. This emergent PEL feature, stemming from local compositional fluctuations, exerts a trapping force and back stress on local barrier activations, hence delaying dislocation movement. The hierarchy of the energy landscape, obtained from minimum energy pathway calculation, is regarded as the salient character of CCAs that makes them different from pure metals and dilute alloys.

The rugged PEL with a wide range of energy barriers results in a wavy dislocation line and jerky dislocation motion in different CCAs. For example, experiments and simulations in fcc CCAs have also revealed a wavy dislocation line shape as the minimum energy configuration of the system.35,56 The motion of dislocations thus proceed in a jerky manner due to strong local pinning/depinning events associated with a large variation of local energy barriers. Broadly, the degree of PEL roughness and its variability within the alloy due to compositional and chemical disorder is a crucial aspect affecting dislocation motion and potentially explains the unusual strengthening behavior observed in CCAs.

Another important feature of CCAs is the spatial concentration undulation, including chemical SRO that is driven by the enthalpic interactions between constituent elements. When chemical SRO is introduced into the system, the PEL along the glide direction (e.g., the Peierls coordinate) is tilted, as shown in Figure 5a. This is because when a dislocation glides through the chemically ordered region, it breaks the local order and generates a diffuse antiphase boundary (DAPB). The breaking of order and generation of DAPB result in an enhanced resistance to dislocation glide. As shown in Figure 5b, the SRO shows an overall higher energy barrier than the RSS (Figure 3b), indicating an enhanced lattice resistance to dislocation glide in a chemically ordered environment. Because dislocation strength is the sum of the strengthening processes from segments/kinks gliding and cross-kinking, evaluating the solute strengthening and SRO effect in CCA requires mesoscale models capturing the individual mechanisms, which will be discussed in the next section. The effect of SRO on dislocation motion, patterning, and microstructure evolution in an fcc CCA has been computationally studied,48 which reveals SRO appreciably lowers the propensity for faulting and martensitic transformation, accompanied by an intensification of planar slip and strain localization.

Figure 5
figure 5

(a) Potential energy landscape spanning 25 Peierls valleys in MoNbTaW chemical short-range order (SRO) system. (b) The statistical distributions of Peierls barriers in SRO. DAPB, diffuse antiphase boundary. Adapted with permission from Reference 47. © 2022 Elsevier.

Full size image

Mesoscale models

Beyond atomistic methods, mesoscale techniques attempt to model the motion of discrete dislocations gliding in a continuum. The benefits of these types of methods over those with atomic-scale fidelity lie with the larger time and length scales that can be accessed. Next, we describe two such approaches: (1) the kinetic Monte Carlo (kMC) model, and (2) the phase-field (PF) model. The first represents dislocation lines as piece-wise segments that interact elastically with one another, with inelastic corrections added to the Hamiltonian describing the system that account for compositional fluctuations. The second tracks dislocation motion through the evolution of a phase-field variable that represents the slipped area of the material. In terms of spatiotemporal coverage, kMC simulations act as a bridge between a purely atomistic description of CCAs and an effective-medium representation in PF models. As we will demonstrate in the following, both methods can complement one another and explore different aspects of the extensive parametric space representative of CCAs.

kMC model of screw dislocation glide in CCAs

As previously discussed, plasticity in bcc metals is governed by the motion of screw dislocations over a periodic energy landscape known as the Peierls potential UP. Due to the high critical stresses associated with UP, slip generally proceeds via thermally activated nucleation of steps on the dislocation line known as kink-pairs and their subsequent sideward relaxation. Kink-pair nucleation is a rare event (i.e., one that occurs with a low probability over the scale of atomic vibrations). Thus, methods with high temporal resolution such as molecular dynamics are not suitable for simulating the long-term kinetics of the system. Instead, kMC models of thermally activated screw dislocation motion have been developed and applied to pure and dilute bcc alloys.41,57,58 In kMC, one simply specifies the transition rates of different events, which represent the probability per unit time that they will occur, and then time evolves in discrete increments. With this approach, the atomistic features of the dislocation core, such as atomic arrangements and local atomic distortions, are not directly resolved, but their effective kinetic behavior is condensed into physical transition rates that can be characterized atomistically. This is what allows us to explore mesoscopic length and time scales. The underlying topology supporting dislocation and kink segments is a discrete bcc lattice oriented along the ⟨111⟩ direction, as shown in Figure 6. The figure shows a schematic depiction of a dislocation of total length L containing several kink-pairs and a cross-kink (the dashed segments). The crystal model thus includes all possible lattice point locations, which will be useful when extending the kMC model to multielement systems. Simulations can be done with periodic boundary conditions or with finite-sized lines.

Figure 6
figure 6

Schematic depiction of an arbitrarily kinked screw dislocation line in a generic body-centered-cubic metal showing kink-pairs on two different {110} planes. The arrows indicate the direction of motion of kinks under an applied stress that creates a force on the dislocation in the \(\overline 1 \overline 1 2\) direction. The dashed segments depict a cross-kink. Shaded quadrilaterals represent the area swept by the dislocation on different glide planes when a kink-pair is produced. Adapted with permission from Reference 41. © 2015 Elsevier.

Full size image

The pure metal formulation has been presented in several papers,41,57,58 and here, we briefly describe the modifications undertaken to extend the model to CCAs. Following prevalent theories,29,59 the model employed to describe multicomponent alloys involves the superposition of an effective substrate (often referred to as the “gray” material) whose properties are taken as the compositional average of each of the individual element properties, and a set of lattice atoms representing the chemical composition of the alloy.

As in standard models, the kink-pair nucleation rate is expressed as a function of stress and temperature as:41

$$\upomega_{{{\text{kp}}}} (\uptau ,T) = \nu_{0} \frac{L - w}{b}\exp \left( { - \frac{{\Delta H_{{{\text{kp}}}} (\uptau )}}{kT}} \right),$$
(1)

where τ and T are the local resolved shear stress and the temperature, respectively, ν0 is an attempt frequency, L is the total dislocation length, w is the distance needed to enclose a full kink-pair at nucleation (w is composed of the kink-pair-width, λ, and the kink spread, a), b is the Burgers vector’s modulus, and ΔHkp is the kink-pair activation enthalpy. In CCAs, ΔHkp(τ) is written as a sum that includes all the pertinent “solute” interaction energies:

$$\Delta H_{{{\text{kp}}}} (\uptau ) = \left( {\Delta H_{{0}} + \Delta E_{{{\varvec{x}} \to {\varvec{x}} + {\varvec{h}}}}^{{\text{int}}} } \right)\left( {1 - \left( {\frac{\uptau }{{\uptau_{{\text{P}}} }}} \right)_{{}}^{p} } \right)^{q} ,$$
(2)

where ΔH0 is the formation energy of a pair of isolated complementary kinks in the substrate material (average across all constituent elements), ΔEintx→x +h is the change of “chemical” energy across one Peierls valley (i.e., between a position x and x + h, h is a vector representing the wavelength of the Peierls potential) on a given dislocation segment (of length L), τP is the Peierls stress of the average material, and p and q are fitting parameters. Contrary to pure metals, kink motion is itself thermally activated and thus treated also as an Arrhenius process with activation energy equal to ΔEinty→y+b (i.e., the excess energy in moving from one atomic position to the next along the ⟨111⟩ y-direction):

$$\upomega_{{\text{k}}} (\uptau ;T) = \nu_{1} \exp \left( { - \frac{{\Delta H_{{{\varvec{y}} \to {\varvec{y}} + {\varvec{b}}}}^{{\text{int}}} - \uptau \upomega_{k} }}{kT}} \right),$$
(3)

where ν1 is another attempt frequency and Ωk is the kink formation volume (simply taken here as the atomic volume). Defined in this fashion, ωk(T) represents the hopping rate of a kink segment going from a position y to another y + b (the position of the next atomic site along the kink propagation direction). Note that if ΔEinty→y+b ≪ kT, one can revert to the mechanical-diffusive treatment previously explained using the properties of the substrate material. Equations 1 and 3 are then sampled according to the kMC algorithm for any available dislocation segment with length greater than w. In these two equations, the dependence on stress is through the resolved shear stress (RSS), τ, which is a scalar quantity that represents the local projection of the total stress tensor σ on the glide plane of the dislocation, including non-Schmid effects if appropriate. σ contains contributions from the externally applied stress and from the different dislocation segment stress fields, as described in References 41 and 60. Simulations can be carried out both under stress41 and/or strain-rate controlled conditions.37 In the former case, the input function is the applied stress tensor σ0 and the response function is the dislocation velocity, whereas in the latter the input function is the applied shear rate \({\dot{\gamma }}_{0}\) and the response function is the stress. Both are interchangeable through the use of an appropriately chosen dislocation density ρd.

Calculation of excess energies for kink-pair nucleation and kink-pair propagation events

ΔEintx→x+h and ΔEinty→y+b represent excess energies in translating segments of the dislocation from one location to another. As such, they are calculated for a specific spatial arrangement of lattice atoms, which needs to be constructed prior to being able to compute these energies. To that end, a local environment containing all the lattice sites around a given dislocation segment is generated on the fly, as shown in Figure 7. Given that the alloy under study can be considered perfectly random for all practical purposes, each lattice site is assigned a chemical element with a probability equal to the relative alloy composition and the total interaction energy is computed as:

$$\Delta E_{{{\varvec{x}} \to {\varvec{x}} + {\varvec{h}}}}^{{\text{int}}} = \sum\limits_{j} {n_{j} e_{j}^{{\text{int}}} |_{{{\varvec{x}} + {\varvec{h}}}} - } \sum\limits_{i} {n_{i} e_{i}^{{\text{int}}} |_{{\varvec{x}}} } ,$$
(4)

where eintj are the solute (of type j) interaction energies and nj is the number of solutes of type j surrounding the dislocation core along that segment. For this calculation, two surrounding “prisms” must be constructed, one centered on x + h and one on x. Also, this process is repeated for each potential glide plane common to the dislocation segment (in our case, all six planes of the [111] zone, as seen in Figure 6). Note that ΔEintx→x+h could be positive or negative, indicating a favorable or unfavorable effect on kink-pair nucleation, respectively. Once these spatial configurations have been used, they are deleted from memory and a “fresh” environment is constructed for the next set of event rates. Those environments not selected during the normal Monte Carlo sampling in each step are kept intact going forward in time until the dislocation line has moved past them. At that point they too are deleted from memory and new updated environments are generated.

Figure 7
figure 7

Exemplars of atomic environments around a dislocation line in Nb–V–Ta generated on the fly to calculate kink event rates as described in this section. (a) View along the [111] direction of the transition paths that the dislocation core can follow. (b) \([1\overline{1 }0]\) view of the extended structure of a kink. A kink spread of a = 12b has been assumed. The color code is red for Nb, white for V, and blue for Ta atoms. Adapted with permission from Reference 37. © 2021 Elsevier.

Full size image

Likewise, ΔEinty→y+b is obtained as the excess energy resulting from an atomic-sized translation of each kink along the [111] direction, from position y to y + b, for example:

$$E_{{{\varvec{c}} \to {\varvec{y}} \pm {\varvec{b}}}}^{{\text{int}}} = e_{{{\varvec{y}} + {\varvec{b}}}}^{{\text{int}}} \mp e_{{\varvec{y}}}^{{\text{int}}} .$$
(5)

This excess energy is calculated in the forward and backward directions of the kink (left and right), hence the ± signs. Stress biases this directionality by way of a suitable activation volume Ωk, as shown in Equation 3. Contrary to Equation 4, ΔEinty→y+b is calculated only for the glide plane on which the kink in question lies. Similarly, however, it can be positive or negative, indicating attraction toward the next atomic position or repulsion from it. Figure 7 shows views along the [111] and \([1\overline{1 }0]\) directions of the local environments constructed to calculate ΔEintx→x+h and ΔEinty→y+b in an equiatomic Nb–Ta–V medium-entropy alloy. Values for the specific energies eintj (j = ‘Nb’, ‘Ta’, or ‘V’) calculated by Maresca et al.30 have been used here. Screw dislocation-specific properties, such as the single kink spread a, and the coefficients p and q have been obtained using a line tension model with the elastic constants for the gray material, as demonstrated by He et al.61 Those constants, together with the rest of the relevant parameters are given in Reference 37.

Atomistic parameterization of the kMC model

Atomistic calculations are needed to parameterize Equations 1–5 and use the kMC model. A partial list of variables for this purpose is given by Zhou et al. for equiatomic Nb–Ta–V alloys.37 In brief, ΔH0 and τP are obtained from the MD simulations, as discussed earlier. The kink-pair width and kink spread, λ and a, are obtained from zero-stress molecular statics relaxations of screw dislocation dipoles. This is possible because kink-pairs will appear on screw dislocation lines even in the absence of any applied stress, which is directly related to the rugged PEL in CCA, resulting in a wavy dislocation line and jerky dislocation motion. Finally, for p and q we simply use the asymptotic values furnished by isotropic elasticity theory.61

Demonstrative results

The rugged chemical energy landscape along screw dislocation lines in these complex alloys results in nonnegligible thermal concentration of kink-pairs and cross-kinks even at zero stress. Figure 8a shows their concentration per unit length in the Nb–V–Ta alloy as a function of temperature, together with exponential fits to the simulation data points. As the graph shows, the results point to the existence of two regimes: an almost athermal one at low temperatures characterized by an effective activation energy of \(\widetilde{E}\) = 0.02 eV, and a higher temperature one characterized by an energy of 0.20 eV. In other words, Boltzmann sampling of the complex PEL defined by Equations 2, 4, and 5 leads to effective kink-pair (and cross-kink) nucleation energies that are an order of magnitude lower than the Peierls potential in a uniform crystal would suggest. Figure 8c shows the ground-state configuration (zero applied stress) of a 400b-dislocation line at 900 K, clearly illustrating the equivalence between line roughness and high densities of kinks and cross-kinks.

Figure 8
figure 8

Thermal concentration (per unit Burgers vector length) of (a) kink-pairs and cross-kinks on screw dislocation lines in N–V–Ta. (b) Strength–strain rate curves for pure Nb, V, Ta, for the average mixture of materials, and for the actual Nb–V–Ta alloy. (c) Ground-state configuration (at zero stress) of a 400b-dislocation line at 900 K showing a rough structure containing a kinks and cross-kinks. The structure of a cross-kink is highlighted. Adapted with permission from Reference 37. © 2021 Elsevier.

Full size image

Line roughness characterized by atomic-sized defects is of course a manifestation of the intrinsic tortuosity of minimum energy states in CCAs. Most importantly, the presence of these defects along dislocation lines in unstressed conditions predisposes the system to hardening, as directional glide—driven by the resolved stress—is hampered due to their existence. Dislocation line roughness is therefore not just the static manifestation of complex PEL in equilibrium in CCAs, but rather a seed for potential extra dynamic strengthening. Figure 8b shows the strength dependence on strain rate (calculated from Orowan’s equation) at 300 K for the pure elements,62,63,64,65 an artificial system defined by the weighted average of the properties of the three elements, and for the actual Nb–V–Ta alloy.66 The simulations clearly reveal a “cocktail” effect, as the CCA displays a higher strength than the individual elements and the mixed average. This is again justified by the existence of complex PEL in conjunction with the presence of a high density of kinks and cross-kinks even at zero stress.

Phase-field modeling

Mesoscale models have proven valuable in simulating the motion of discrete dislocations at longer time and length scales than atomistic approaches, while still retaining the effects of dislocation stress fields and line character. Phase-field-based dislocation dynamics67,68,69 is a 3D, real-space technique that predicts the pathways taken by dislocations with little to no rules or adjustable parameters. All material parameter inputs, such as full anisotropic stiffness tensor and stacking-fault energies, can be obtained either via experimental measurement or density functional theory, limiting the use of empirical interatomic potentials. At a fine scale, the model predicts basic core structures, such as planar dissociated cores characterized by a stacking-fault width in fcc metals, or nonplanar screw cores with threefold symmetry in bcc metals.70,71

Phase-field dislocation dynamics was first applied to a CCA in 2019 by Zheng et al., who studied the glide of long edge dislocations in an fcc Ni–Co–Fe–Cr–Mn alloy.71 The atomic-scale variation in chemical composition of CCAs was incorporated into the model by randomly assigning intrinsic stacking-fault energies (SFEs) to different Voronoi-tessellated regions on the dislocation glide plane, creating the appearance of different “patches” with distinct intrinsic SFEs. As the dislocations glide under shear stress, they adopt wavy morphologies, lingering in regions with relatively low intrinsic SFE, consistent with MD and kMC simulation results presented earlier. Larger stresses are required to glide the entire dislocation compared to the same dislocation gliding through a homogeneous metal with the mean intrinsic SFE. The critical stress is controlled by the portion of the dislocation that must overcome an energy barrier to move into a relatively higher SFE patch. It maximizes when the size of the SFE patch is near the equilibrium stacking-fault width and increases with greater variance in SFE among the patches.

Variations in chemical composition in a dislocation glide plane would lead to smooth changes in the local SFE with some amount of local spatial correlation. Later mesoscale dislocation models attempted to capture this effect through a correlation length l in the SFE, which is intended to scale with the degree of chemical short-range ordering (CSRO).72,73,74 Zhang et al.75 introduced a one-dimensional correlated SFE in a Peierls–Nabarro (PN) model, to study the Peierls stress, the resistance to glide of a dislocation element, a short segment that remains straight during glide.72 The local SFE at a material point were scaled by a normally distributed random variable ω with correlation length l. The mean and variance in the Peierls stress increased with increasing variance in ω, consistent with trends in Zheng et al.71 Unlike in a pure metal, in the CCA, the dislocation eventually becomes pinned, and increased variance in ω decreases the glide distance before pinning. The model was extended to consider “line hardening,” resistance to glide of an infinitely long dislocation. In the CCA, the energetic barrier varies along the line, and under driving stress, parts of the dislocation line are allowed to glide forward in relatively easier regions where others are held back at harder ones. The calculations demonstrated that the inherent chemical variability in a CCA increases glide stresses through the creation of local pinning points. The critical stress to move the dislocation increased linearly with larger l and variance in ω(x).

Dislocation glide in a plane with correlated energy barriers characterized by l were later treated in References 73,74,75 using a phase-field dislocation model. Simulations considered a model refractory MoNbTi ternary CCA, for which in situ and ex situ experimental analysis showed evidence of wavy, mixed-character dislocations, gliding on the {112}, {123}, and {134} planes, with notably fewer dislocations on the {110} planes and little to no cross-slip.76 To study glide plane hardening, calculations involved long dislocation ≤100 nm gliding over distances of 100b in several tens of locations in the CCA, initially of either screw or edge character. Screw dislocations under stress adopted a wavy morphology, appearing to lose their screw-orientation during glide excursion. The composition variations in the plane allow for “chemical kink pairs” to form randomly along the line without the randomness from thermal noise. The waviness seen is the result of variable rates of kink-pair formation and migration along the length of the dislocation, where nanoscale segments with higher rates extend further. Edge dislocations also exhibit wavy glide, losing their initial edge character, as they glide. The wavelengths, however, are on average smaller and amplitudes much larger than those of moving screw dislocations. Chemical kink-pair formation occurs at a higher rate than kink-pair migration in edge dislocations.

Importantly, both screw and edge dislocations exhibit jerky glide, a frequent transition between nonstop, free glide with nonzero kink-pair activation rates and complete arrest with zero kink-pair activation rates. Jerky glide indicates glide plane hardening, in which the critical stress to mobilize the dislocation increases as it propagates. The screw dislocation takes on a wavy morphology as it glides continuously and then becomes nearly straight, close to its original screw orientation, when it stops (Figure 9a).74,75 The additional applied stress needed to restart wavy glide from the fully arrested state is determined by the weakest region for forming and migrating a kink-pair anywhere along the screw dislocation line in its new location. Edge dislocations also exhibit start-stop behavior but remain wavy when arrested under stress.75 The long edge dislocation propagates by populating the line by chemical kink-pairs and by kink-pairs forming on kink-pairs. Some parts move noticeably forward more than other parts, leading to its pronounced wavy appearance. The arrested state corresponds to a line decorated by pinning points, at those relatively high energy barriers and the required stress increment corresponds to depinning.

Figure 9
figure 9

(a) A schematic of screw dislocation glide in MoNbTi. (b) A sample of stress–strain curves associated with screw dislocation glide for different correlation lengths l. USFE, unstable stacking-fault energy. Adapted with permission from Reference 69. © 2020 Elsevier.

Full size image

Substantial strain hardening behavior is associated with this CCA-induced jerky glide behavior, where the critical stress increases, on average, 20–30% from the stress to first activate motion. The characteristics of hardening vary substantially, such that no two pathways and stress–strain curves are alike among different starting locations (Figure 9b). The glide plane hardening becomes more pronounced with greater statistical variation in the energy barriers and longer l. Both features enhance the chances the dislocation encounters relatively higher barriers in material in which kink-pair activation for screw or depinning for edge is not possible along the entire dislocation length, causing it to fully arrest. Controlled by the need for frequent depinning, edges exhibit far more glide plane hardening than screw dislocations, which would suggest edges play a much greater role in CCAs than in a traditional alloy. Screw dislocations on the (110) plane experience the greatest increase in critical stress and strongest enhancements in this stress with l. The lack of active {110} slip seen experimentally could indicate that glide plane hardening, rather than the initial critical stress, selects the preferred glide plane.

The strength of metals is also related to the nucleation of dislocations. Smith et al. studied formation of loops from screw and edge-oriented Frank-Read sources on correlated glide planes in the bcc ternary CCA Mo–Nb–Ti.69 These sources are dislocation line segments pinned at two ends in the plane by distance L. Conventionally, the threshold stress to activate the source corresponds to the minimum stress needed to bow out the dislocation line against line tension to a half elliptical configuration between the points, where it becomes unstable. In the CCA, loops typically form with anisotropic shapes and wavy morphologies (Figure 10). The varying energy barriers in the CCA altered the critical step for source activation from that of a conventional source. Screw-oriented sources require formation of a kink-pair along its segment followed by bow out (Figure 10a). Edge-oriented ones were activated by a two-step mechanism: first, the edge segment glides forward, producing two long straight screw segments and second, a kink-pair forms in one of the low energy barrier regions along the screw portions (Figure 10b). Consequently, activating both types of sources depends on the local chemical environment and nucleation stresses become statistically distributed with the dispersion increasing with increased variance in energy barriers in the plane and l, particularly when l exceeded L. The chemical fluctuations also introduced a new size dependence on L. The weakest-link kink-pair mechanism for the screw sources caused a stronger dependence of nucleation stress on L compared to that predicted for a pure metal. In contrast, the mechanism for edge-source activation has a much weaker dependence. Therefore, the screw-to-edge ratio for nucleation increases with L.

Figure 10
figure 10

Frank–Read source operation in MoNbTi for a screw-oriented (a) and an edge-oriented (b) source. The red-pink lines show the dislocation, with lighter colors indicating later timesteps. The underlying surface is colored by the local unstable stacking-fault energy (USFE). The correlation length l is 4w0 and 5w0 in the screw and edge cases, respectively, where w0 is 2.15b. Adapted with permission from Reference 69. © 2020 Elsevier.

Full size image

Conclusions and outlook

There are several key observations that emerge from a combined atomistic/mesoscopic approach to study dislocation glide in refractory CCAs. First, atomistic models have established a hierarchy of PEL sublevels that go beyond atomic-scale chemical fluctuations. This is likely to imply the existence of order on multiple length scales, including medium-range order. Second, it is clear that traditional coarse-graining approaches based on statistical averaging from distributions obtained from atomistic calculations are not adequate for CCAs. Dislocation glide is highly influenced by (1) relatively high thermal concentrations of atomic-sized defects that are part of the ground state of the dislocation line at zero stress, and (2) compositional fluctuations that can lead to breakaway behavior in ways that are not captured in mean-field models. These two effects combined negate the strong thermally activated nature of glide processes typically observed in bcc metals, as chemical energy can supplant thermal energy and lead to kink-pair nucleation with a need for thermal fluctuations. Third, the extra strengthening generally observed in CCAs relative to their pure metal or dilute alloy counterparts is a direct consequence of this rough three-dimensional potential energy landscape associated with their complex chemistry. This is true at low temperatures, when controlled by screw dislocations, and intermediate-to-high temperatures, when cross-kinks are seen to dissolve by mutual annihilation.

Although works like the one presented here are helping us gain a deeper understanding of plastic processes in CCAs, these are just starting to unveil the rich and complex physics underlying these alloy systems. Among the outstanding issues that call for further research are:

  • Studies have shown that in medium and high-entropy alloys the observed glide plane for screw dislocations often deviates from the canonical {110} and {112} planes.77 Although “anomalous” slip is not uncommon in bcc metals,72 the observation of such nonclose-packed planes is lacking sufficient explanation at the moment.

  • Unlike in pure bcc metals or dilute bcc alloys, edge dislocations have been shown to play a fundamental role in refractory CCAs.38,44,46,73,74 In some alloys, particularly those containing Mo, Nb, and W, an intermediate-temperature high-strength plateau is observed.9,75,76 There are some proposed explanations for such observation,38,78 but more research is needed to ascertain the reasons behind such peculiar behavior.

  • Another interesting aspect affecting dislocation glide in single-phase CCAs is the existence of long wavelength solute fluctuations. This effect has been seen in a number of alloys,54,55,79 with strong implications on the overall plastic slip behavior of the material. These spatial correlations could be akin to what we denote as “metabasins” above (i.e., local chemical energy traps that pin dislocation segments and contribute to strengthening).

  • Studying the interaction between dislocations and interstitial atoms, such as O, N, and H, can further improve our understanding of embrittlement behaviors that are common in these alloys.27,58,80 Likewise, modest additions of B interstitials have been seen to provide promising levels of ductility in these systems,81,82 believed to be caused by an enhanced grain-boundary cohesion. It would thus be of interest to study the differences among these impurities in the overall mechanical behavior of these materials.

In summary, much research remains to be done to fully understand the whole picture of dislocation slip in refractory CCAs. As we have shown, atomistic modeling coupled to mesoscale simulations can be a helpful tool to address the chemical complexity and rich physics of plastic slip in these materials.