Predictive materials modeling

Materials science as a discipline has benefited tremendously from the possibility of solving numerically the electronic-structure problem for a condensed phase of matter. Supported by the steady decrease of the cost of computation, the availability of high-quality open-source software1 and by a better understanding of the approximations that are needed to make the many-body quantum problem tractable,2,3 computational discovery of materials has become a reality, pursued by high-throughput calculations4,5 whose results can be made available through public databases.6,7,8 The vast majority of these high-throughput calculations, however, describe materials in a highly idealized fashion, as ideal crystalline structures with a static configuration of their atoms. This is a severe limitation: the properties of real materials can be strongly influenced by the presence of defects, or just the disorder that is induced by thermal fluctuations, as well as by the quantum mechanical nature of the nuclei.9 Including these effects, however, is computationally demanding: rather than evaluating the properties of a single structure, hundreds of thousands of calculations must be performed to collect representative configurations of the distorted configurations that are seen at finite temperature. Following classical works that pioneered “ab initio” molecular dynamics simulations,10,11 several groups have been working to streamline, and minimize the cost, of evaluating the finite-temperature thermodynamics of materials, for metals (where the work of Neugebauer and collaborators is particularly noteworthy12,13) as well as for hydrogen-bonded systems14 and molecular materials.15,16,17,18

Figure 1
figure 1

Predictive modeling of atomic-scale properties. Quantum calculations provide accurate, but computationally demanding, predictions of the ground-state properties of any structure A, which is defined by the nature \(a_i\) and coordinates \( {\mathbf{r}} \) of each atom. Data-driven surrogate models allow interpolating between a small number of reference calculations (e.g., to estimate the interatomic potential V). Invariant \(|A\rangle\) (or equivariant \(|A;\uplambda \upmu\rangle\), that transform like spherical harmonics \(Y^\upmu _\uplambda\) under rotation) structural descriptors can be used to evaluate scalar (or tensorial) properties with a much reduced effort. This includes dipole moments \( {{\upmu }} \), scalar fields such as the electron density \(\uprho (\mathbf {x})\), or the Hamiltonian matrix H. ML, machine learning.

Full size image

The past decade has seen the rise of a different approach to the problem. Rather than solving directly a quantum mechanical problem to predict a property y of a structure A, the idea is to use a small number of reference calculations to fit a more or less sophisticated functional form \(\tilde{y}(A)\), which can then be used to achieve predictions that are (almost) as accurate as the underlying quantum calculations, but computationally much less demanding, and with a more benign scaling with system size (Figure 1). The idea was not new: quantum chemists have been constructing potential energy functions for small molecules by interpolating between few high-end quantum calculations,19,20 and materials scientists have for decades fitted cluster expansion expressions to compute the thermodynamics of alloys.21 Behler and Parrinello22 and later Bartók, Csányi, and collaborators23-demonstrated how these ideas could be extended to condensed phases and off-lattice configurations, laying the foundations for the flourishing of machine-learned interatomic potentials (MLIPs). The interested reader may find an historical overview that covers also some of the latest developments in a recent review by Behler.24 The essential ingredients that underlie the success of MLIPs, and that in particular are incorporated in both the structural descriptors25,26 and the models, will be familiar to many computational materials scientists: A locality ansatz that decomposes the energy of a material in a hierarchy of atom-centered, body-ordered terms—pair, three body, many-body potentials27 that add up to give the energetic contribution from an atom and its environment; the incorporation of physical principles such as the invariance of the energy under symmetry operations;28,29 the construction of reference data sets that cover the range of configurations and compositions that are relevant for the problem at hand. Similar considerations have been incorporated in ML models of molecules:30,31 even though (much as for electronic-structure calculations) chemical and materials modeling often use a different language, and the technical details may differ, there is substantial unity in the way machine learning has been incorporated into atomistic modeling.32,33

Figure 2
figure 2

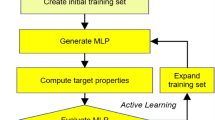
Schematic representation of a possible machine learning (ML)-based workflow to compute quantum anharmonic free energies of different phases of molecular crystals. Original figure published in Reference 34 under the CC-BY 4.0 license (https://creativecommons.org/licenses/by/4.0/). MLP, machine learning potential; DFT, density functonal theory; MD, molecular dynamics; DFTB density function tight binding.

Full size image

First-principles thermodynamics made easy

Sampling of disorder, and thermal fluctuations, is the perfect application for data-driven potentials. Computing finite-temperature properties involves generating a large number M of configurations A, consistent with the thermodynamic ensemble, and averaging over their properties, \(\langle y \rangle =\sum _{A=1}^M y(A)/M\). Even for liquid configurations, the fluctuations involve comparatively small structural differences, which make it relatively easy for interpolative techniques such as MLIPs to achieve accurate predictions from a small number of reference configurations. It is not by chance that many of the early applications focused on the calculation of phase diagrams or phase transitions35,36 as well as finite-temperature thermodynamics of solid phases37 and more traditional studies of extended lattice defects.38 From water39,40 to oxides,41,42,43 from metals44,45 and to amorphous materials,46,47,48 from molecular materials34 to hybrid perovskites,49 there is virtually no class of materials for which MLIP have not been successfully used to facilitate the study of materials in disordered, or finite-temperature, conditions. Again, it is worth noting that also in molecular applications the focus has shifted from the prediction of the properties of minimum-energy geometries30,50,51 to flexible potentials,52,53 the transition states of chemical reactions,54 and the modeling of the quantum mechanical fluctuations of the nuclei.55

MLIPs have reached a considerable level of maturity, and so there is a good understanding of their mathematical foundations,25 their efficient implementation,56 and of the best practices connected with the construction of the training set to obtain a robust, transferable model.57 What is more, several pragmatic solutions have emerged to solve their limitations, to enable applications to highly nontrivial problems. An obvious strategy to tackle limitations in stability and accuracy of MLIPs is not to use them alone, but in tandem with traditional materials modeling techniques. Rather than training a model directly to high-end quantum calculations, one could use an affordable semi-empirical method such as density functional tight binding (DFTB)58 as a baseline, that is corrected by a MLIP that evaluates only the difference to a higher level of theory.59,60 This can be combined with all sorts of well-established tricks, such as multiple-time stepping,61,62 to reduce the cost of the baseline calculations. Reference 63, which discusses calculations of solvation and acid-base equilibra that are relevant for regioselective homogeneous catalysis, demonstrates several of the techniques that simplify the description of a challenging, reactive system using a MLIP, including subtle effects such as the quantum mechanical fluctuations of the nuclei. Another way to combine data-driven and traditional calculations involves correcting the free energies computed using a MLIP to promote them to explicit first-principles accuracy (Figure 2). This technique, that has also been used in the past to reduce the cost of direct first-principles thermodynamics,12 involves selecting a few hundred uncorrelated configurations \(\{A\}\) from an ML-driven calculation, computing the reference and ML potentials (\(V_\text {REF}\) and \(V_\text {ML}\)) for them, and evaluating the free-energy perturbation correction

$$\begin{aligned} \Delta _{\text {ML}\rightarrow \text {REF}} = k_BT \ln M^{-1}\sum _{A=1}^M e^{-(V_\text {REF}(A)-V_\text {ML}(A))/k_B T}. \end{aligned}$$
(1)

This expression accounts for the possible discrepancy between \(V_\text {REF}\) and \(V_\text {ML}\). Applying the correction to each phase allows to recover relative free-energy differences that are not affected by the residual error of the ML approximation, which can be important in cases where free-energy differences are small, or dependent on energy contributions that are hard to capture by local MLIPs (e.g., proton disorder in ice).39 The computational cost is a tiny fraction of what would be required for a direct first-principles evaluation of finite-temperature thermodynamics.

Another idea that has facilitated greatly the use of ML for materials modeling is that of active learning.64 A preliminary version of a MLIP is used to perform molecular dynamics, or any kind of atomistic simulations that requires repeated evaluation of interatomic forces. Every time a configuration is encountered that departs too much from those included in the training set, it is recomputed with the reference first-principles method, and the MLIP updated (inline, or in batches) to generate a more reliable and transferable data-driven model.49,65,66,67 Efficient active learning requires a way to assess the accuracy of ML predictions: some models, such as those based on Gaussian process regression,68 provide built-in uncertainty quantification. A strategy to estimate prediction errors that is simple, inexpensive, and can be applied to any regression scheme involves constructing an ensemble of models,69 whose mean provides the best estimate of the target property, while the (calibrated) standard deviation gives a measure of uncertainty.70 The ensemble of predictions can easily be used to perform uncertainty propagation and estimate the error on derived quantities, and even the error associated with the sampling of configurations performed using the mean ensemble potential.71

More than energy and forces

Even though MLIPs are widely used, and have transformed the landscape of atomic-scale materials modeling, they only replace one of the tasks that have made first-principles simulations successful. Having access to the ground-state (and excited state) electronic structure of a material allows evaluating all sorts of response properties,72 which has made it possible to compute Raman and infrared spectra,73 nuclear magnetic shieldings,74 ferroelectricity,75 and much more. To realize the full potential of ML, all of these functional properties should be as easily accessible as the interatomic potential and forces. This, however, poses additional challenges. To begin with, there is much less empirical experience about what works and what does not work to build an effective ML model. We roughly know what range of interactions, and what parameters of the most widespread frameworks, can be used as a reliable initial guess to build a MLIP for a metal, or a molecular solid, but literature is much sparser when it comes to predicting, for example, polarizability. Furthermore, the algebraic structure of the target property could differ from that of the potential energy, that is a scalar and is only defined as a global, extensive property. Scalar NMR chemical shieldings,76,77 for instance, are atom-centered properties: even though this may appear as a small issue, given that most MLIPs construct the total potential as a sum of atom-centered terms, the need to predict individual atomic contributions may exacerbate some of the shortcomings of the most common descriptors of local atomic structure.78 The electron density of states g(E) is another global property that can be decomposed in atom-centered contributions, but each atomic environment contributes an energy-dependent term \(g_i(E)\), which begs the additional question of what is the most efficient way to encode the energy dependency in the ML targets.79

Figure 3
figure 3

(a) Schematic overview of the transformations of a molecular vector property under the action of a rigid rotation. The property and any symmetry-adapted model must transform in a prescribed way. Similar equivariance rules must be obeyed by symmetry-adapted descriptors. (b) A symmetric Cartesian tensor (e.g., the polarizability \({\upalpha}\)) can be more conveniently written in an irreducible spherical form, with a scalar component \(\upalpha^0\), and five components that transform like \(l=2\) spherical harmonics. The \(l=1\) component is associated with the asymmetric part of the tensor, and is therefore zero.

Full size image

A more substantial problem is associated with the prediction of properties that are not scalars, but have a vectorial/tensorial geometric nature. To see why this is an issue, one should consider that one of the fundamental physical priors that are incorporated in the vast majority of MLIPs is the notion that energy is invariant to rigid rotations \(\hat{R}\) of a structure A, as well as to permutation of the atom label \(\hat{\Pi }\). Thus, a model \(\tilde{y}\) predicting scalar properties should fulfill the invariance condition \(\tilde{y}(\hat{R}\hat{\Pi } A) =\tilde{y}(A)\). This is achieved easily by ensuring that the descriptors that are used to represent the atomic structures are themselves invariant to rotations,28 so that any model that uses them as inputs inherits this property.Footnote 1 Consider instead a property that is covariant to rotations (e.g., the dipole moment of a molecule [Figure 3a]). A ML model that is consistent with basic physical principles should ensure that \(\tilde{y}_\upalpha (\hat{R} A) = \sum _\upbeta R_{\upalpha \upbeta }\tilde{y}_\upbeta (A)\), where \(\upalpha ,\upbeta\) refer to the Cartesian components, and \(R_{\upalpha \upbeta }\) is the rotation matrix associated with \(\hat{R}\).80,81,82 The need to build symmetry-adapted models has driven the development of equivariant machine learning schemes that incorporate the appropriate (covariant or invariant) behavior depending on the nature of the target.83 Appreciating the subtleties involved requires a certain degree of mathematical sophistication. Reference 84 provides an excellent and comparatively accessible overview from the more general perspective of geometric ML. In a nutshell, symmetry operations on tensors are most efficiently described in terms of irreducible representations—combinations of the Cartesian components that transform linearly into each other when the object they refer to is transformed. As a concrete example, the trace of the polarizability tensor, \(\upalpha _{xx}+\upalpha _{yy}+\upalpha _{zz}\) is invariant to rotations, and so it is easier to manipulate than the individual diagonal components (Figure 3b). For the case of proper rotations (corresponding to the SO(3) group), the irreducible representations correspond to spherical harmonics, and rotating a structure mixes the components \(\upmu\) of each angular momentum value \(\uplambda\) according to

$$\begin{aligned} \tilde{y}^\upmu _\uplambda (\hat{R} A) = \sum _{\upmu ^\prime} D^\uplambda _{\upmu \upmu ^\prime}(\hat{R}) \tilde{y}^{\upmu ^\prime}_\uplambda (A), \end{aligned}$$
(2)

where \(\mathbf {D}^\uplambda\) is known as a Wigner D-matrix.85

One way to obtain symmetry-adapted models is to construct them based on equivariant descriptors, which themselves transform as spherical harmonics. To understand the basic idea, consider a linear model to predict\({y}^\upmu _\uplambda (A):\)

$$\tilde{y}_{\uplambda }^{\upmu } \left( A \right) = \sum\limits_{q} {\left\langle {\left. y \right|q} \right\rangle } \left\langle {q\left| {A;\uplambda \upmu } \right.} \right\rangle .$$
(3)

In this notation (Reference 25, Section 3.1) \(\left\langle {y\left| q \right.} \right\rangle\) indicates the regression weights for the q-th feature, and \(\left\langle {\left. q \right|A;\uplambda \upmu } \right\rangle\) the q-th component of the feature vector that describes the structure A. Crucially, for each feature there are \(2\uplambda +1\) components, indexed by \(\upmu\) that describe their behavior under rotation. It is easy to see that this linear model will be consistent with the requirements of Equation 2 as long as:

$$\langle { q |\hat{R}A;\uplambda \upmu } \rangle = \sum\limits_{{\upmu ^{\prime}}} {D_{{\upmu \upmu ^{\prime}}}^{\uplambda } } \!\left( {\hat{R}} \right)\langle { q |A;\uplambda \upmu ^{\prime}}\rangle$$
(4)

holds true for each feature.

Figure 4
figure 4

Symmetry-adapted modeling of the single-particle Hamiltonian of benzene in a minimal basis. The model enforces the correct molecular symmetries, which means that (a) even training on a randomized Hamiltonian yields a prediction that is consistent with \(D_{6h}\) point-group symmetries; (b) the symmetry and degeneracies of the eigenstates are consistent with the character tables of the group; (c) the way degeneracies are split by a deformation is also consistent with molecular orbital theory. Reprinted with permission from Reference 86. © 2022 American Institute of Physics.

Full size image

These equivariant representations have been used to machine-learn force vectors,82 molecular dipoles87 and polarizabilities,88 an atom-based expansion of the electron density89,90 and of the single-particle electronic Hamiltonian.86 The advantages of using a symmetry-adapted model are demonstrated in Figure 4 for the learning of a molecular Hamiltonian: incorporating rotation and permutation equivariance ensures that point-group symmetries, when present, are automatically accounted for.

Symmetry considerations underlie also the latest developments in geometric machine learning, with equivariant models91,92,93,94 showing greatly improved performance compared to their invariant counterparts.95 In fact, it is possible to treat within the same formalism shallow models based on atom-centered features and the most recent families of equivariant neural networks;96 a unification that may expedite the systematic optimization of the model architecture. Furthermore, the use of equivariant representations or networks is not the only way to obtain a symmetry-adapted model. For relatively rigid molecules, one can simply learn the components of the tensors in the local reference frame.80,81 Another strategy involves predicting atomic partial charges, combining them with atomic positions to obtain a vectorial prediction for properties such as dipole moments.87,97,98 Computing dipoles by predicting the position of localized centers of charge,99 or constructing covariant descriptors by formally assigning fixed charges to the atoms and computing “operator derivatives” of atom-centered descriptors100 with respect to a fictitious electric field, are equivalent to atomic-dipole schemes, despite the superficial similarity with models based on the prediction of atomic charges. Alternative approaches are also available to predict electronic properties: the charge density can be predicted as a scalar field by using descriptors centered on grid points, rather than on atoms.101,102 The single-particle energy levels can be predicted by modeling an invariant effective Hamiltonian.103

It is also worth noting that equivariant representations are not only useful to build symmetry-adapted models of tensorial properties. The vast majority of atom-centered descriptors used to build MLIPs can be understood in terms of symmetrized correlations of the atomic neighbor density,104 which can be constructed iteratively105 by projecting tensor products of the one-neighbor density onto the irreducible representations of the rotation group. The invariant part of these high-order descriptors provides a complete linear basis to expand scalar atomic properties, which is used in the construction of the moment tensor potentials (MTP)106 and the atomic cluster expansion (ACE)107–two classes of MLIPs with an excellent accuracy/cost ratio. Equivariant NNs are often used to predict invariant targets, even though they obviously are ideally suited to predict tensorial properties, and recent results on single-particle Hamiltonians have demonstrated remarkable performance for these tasks.108

Integrated ML models

Having simultaneous access to ML predictions of energy, forces and functional properties opens the way to simulations that describe all the aspects of the electronic structure of materials, and that use state-of-the-art sampling techniques to access static and dynamic behavior at finite temperature, without compromising on the cell size or trajectory length. Advanced data analytics can then be used to interpret the outcome of increasingly complex data sets and simulations.109,110,111,112 For example, it is now possible to compute vibrational spectroscopies of water as the Fourier transform of the correlations between dielectric response functions, using a ML potential to drive the dynamics and an equivariant model to predict dipole moments and polarizability.97,99,113,114 Similarly, one can model with first-principles accuracy thermodynamic and dielectric properties of the archetypal ferroelectric perovskite \(\hbox {BaTiO}_3\), without limitations on simulation size or duration.115 The fact that the models are computationally affordable means that it is possible to go beyond a purely classical description of the nuclei, including an approximate description of nuclear quantum dynamics.113,116 The quantum mechanical nature of the atomic nuclei, that is an important contributor to the fluctuations of light atoms such as hydrogen, has a substantial effect on many observables (Figure 5). The availability of integrated ML models is making it easy to investigate them, as in a recent study that showed how much they contribute to the nuclear chemical shifts in molecular crystals.117

Figure 5
figure 5

Sum-frequency generation spectrum for a liquid water–vacuum interface, built using an integrated model describing interatomic potentials, dipole, and polarizability with machine learning. The curves compare experimental results118 (dashed line) with two types of quantum dynamics (green, blue) and with classical MD (red), which is significantly blue-shifted. Reprinted with permission from Reference 116. © 2021 American Chemical Society. MD, molecular dynamics; TI-PACMD, Takahashi-Imada partially adiabatic centroid molecular dynamics.

Full size image

Another area in which ML needs to go beyond potentials to describe materials involves all properties associated with the electronic degrees of freedom. This involves both predictions of the conductivity (at least through the proxy of the density of electronic states at the Fermi level119) as well as the estimation of the contribution to thermophysical properties arising from electronic excitations,120,121,122 that is relevant for matter at extreme conditions, but also for refractory metals at high temperature.12,123,124 Magnetic states and magnetic excitations can also be treated with machine learning potentials that take into account the spin degrees of freedom.125 Potentials that describe electronic excited state rather than the ground state are making it possible to perform nonadiabatic molecular dynamics,126,127 extending further the range of applicability of ML beyond ground-state properties.

An important practical issue that may slow down the adoption of this new class of integrated models has to do with the need to combine different frameworks, and different types of advanced simulation strategies. Even though general-purpose models that treat on the same footings potential energy and functional properties will become prevalent, there may still be cases in which one wants to combine models from different sources, and/or to implement complicated simulation setups that require their own dedicated software stack. The design of modular software that can be easily interfaced with different packages, such as the atomic simulation environment (ASE),128 i-PI,129 as well as free-energy sampling plugins PLUMED130 or SSAGES131 provide the necessary “glue” to combine MLIPs, equivariant property models, and accelerated sampling with thermal and quantum fluctuations.

Conclusions

ML techniques have been incorporated, and largely normalized, as essential tools for the atomic-scale modeling of matter. The progress in the field has been incredibly fast, and shows no sign of slowing down, with new ideas being proposed to tackle the limitations of the best-established approaches, from the incompleteness of some descriptors78,132 to the lack of long-range interactions, that are now being included with point-charge and static multipole models,133,134 self-consistent charge equilibration schemes,135,136,137 as well as with bespoke descriptors that reproduce the asymptotics of long-range physics.138,139 Still, some of the core concepts have begun to crystallize. The mathematical foundations of the kind of descriptors that are needed to encode atomic composition and geometry are now better understood, and clear similarities have been revealed between different approaches.96,104,107

Interatomic potentials, the first quantity that was directly targeted by data-driven surrogate models, have reached a certain maturity, and have made the calculation of thermodynamic properties of materials from first principles—once requiring careful planning and large investments of computer time—relatively routine. Thanks to the extension of symmetry-adapted models to vectorial and tensorial quantities, other microscopic properties that can be computed by solving the electronic-structure problem can also be predicted by ML. The same kind of uncompromising accuracy that has become possible for the prediction of the stability of materials may soon be available for functional properties and all sorts of experimental observables, through integrated ML schemes that combine models of energy and electronic properties with advanced statistical sampling. Still, these developments are unlikely to mark the end of an era for first-principles simulations. On the contrary, more accurate electronic-structure methods will become necessary to bring simulations even closer to reality, and data-driven techniques will serve as an accelerator, to translate results on benchmark systems into applications to large-scale simulations. What is more, one can see the first signs of the emergence of hybrid modeling techniques, that combine electronic-structure calculations with data-driven approaches—from the superficial use of semi-empirical models as a baseline,59,63 to the use of electronic-structure quantities as descriptors,140,141 to the prediction of electronic density142 as the first step in the calculation of standard, and soon data-driven,143,144 density functionals. Bridging the divide between physics and data-driven modeling, deductive and inductive paradigms of scientific inquiry, hybrid frameworks indicate the direction to follow to complete the integration of artificial intelligence into the theory and practice of computational materials science.