Introduction

Topology can be realized in real and momentum space. In mathematics, topology is a concept that concerns the surfaces of objects. The topology of a mathematical structure is identical if it is preserved under continuous deformation. A pancake has the same topology as a cube, a donut as a coffee cup, and a pretzel as a board with three holes. The classification of all nonmagnetic inorganic materials via their topology in momentum space (electronic structure) has recently become available and surprisingly nearly 80% of all inorganic compounds and alloys show signatures of a nontrivial topology not too far from the Fermi energy, the energy that separates the valence band or bonding states from the conduction band or antibonding states.1,2,3 Based on a single-particle picture, the space group, the Wyckoff positions, and the elementary band representation of a material are classified by the topology of its electronic structure. By shedding light on the band structure of topological materials, via the identification of certain signatures such as crossing points, nodal lines, flat bands, and Van Hove singularities, it is possible to identify potentially promising quantum properties of known and new materials, through high-throughput calculations. Beyond the single-particle picture, the classification of all magnetic space groups has been developed,4,5,6 but the experimental realization of magnetic topological materials and a deep understanding of their physical properties are still in its infancy.

Adding spin offers additional structure—a new degree of freedom—for the realization of new states of matter that are not known in nonmagnetic materials. Magnetic topological materials can support chiral channels of electrons and spins, and can be used for an array of applications from information storage, control of dissipationless spin and charge transport, to giant responses under external stimuli such as temperature and light.6 Besides topologically protected surface states, the phase of the wave function is important, especially for Weyl and chiral fermions. In Weyl semimetals, nodes in the electronic structure come in pairs with opposite chiralities, or handednesses, corresponding to two forms of the Weyl Hamiltonian, and can be defined alternatively as Berry curvature monopoles and antimonopoles, or sources and sinks of Berry curvature in momentum space. The projections of these nodes onto the Fermi surface are connected by topologically protected Fermi arc surface states.7

Here, we focus on one materials class, namely the extended family of Heusler compounds, which show a wide range of properties, and when heavy elements that can give rise to strong spin–orbit coupling (SOC) are incorporated into them, nontrivial topological phases of matter, such as topological insulators (TIs) and Weyl semimetals can be realized (see Figure 1a–b).8,9,10 The interplay of symmetry, SOC, and magnetic structure in Heusler compounds allows for the realization of a wide variety of topological phases through Berry curvature design.11,12,13,14 Weyl points and nodal lines can be manipulated by various external perturbations such as magnetic fields, which result in exotic properties, such as large anomalous Hall and Nernst effects.11,12,13,14,15,16,17,18,19,20 Manganese-rich Heusler compounds Mn2YZ (Y and Z are, respectively, a transition metal and a main group metal) can be distorted along the [111] or [100] directions, resulting in a hexagonal and a tetragonal structure, respectively. For magnetic compounds, these anisotropic crystal structures can lead to large magnetocrystalline anisotropies and, depending on the magnetocrystalline energy, the preferred magnetization orientation can, thus, be tuned from in-plane to out-of-plane directions and sometimes in stabilizing complex noncollinear magnetic orders. Noncollinear magnetism and evidence for the presence of skyrmionic objects via the observation of a topological Hall effect were first found in Mn2RhSn (see Figure 1c).21,22 The combination of a noncollinear magnetic structure and Berry curvature gives rise to a nonzero anomalous Hall effect, even in antiferromagnets, which was first observed in the hexagonal antiferromagnets, Mn3Sn and Mn3Ge (see Figure 1d).15,16,20 These two hexagonal Heusler compounds appear in the structural phase diagram of manganese-rich Heusler compounds at higher temperatures and are competing phases to the cubic and tetragonal Heusler structures. The manganese layers show a Kagome spin arrangement, which is the result of magnetic frustration. The possibility of directly manipulating the Berry curvature shows the importance of understanding both the electronic and magnetic structures of Heusler compounds, and how they are connected.

Figure 1
figure 1

Various topological states realized in Heusler compounds. (a) Topological insulator in a half Heusler compound, (b) Weyl semimetal in a full Heusler compound, (c) Mn3Z and the chiral spin structure, and (d) antiskyrmion state in an inverse tetragonal Heusler compound.10 We thank Christina Pouss for the design of this figure.

Full size image

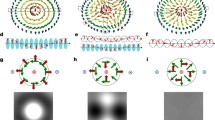
In addition to collinear ferromagnetic, ferrimagnetic, and antiferromagnetic spin arrangements, some Heusler compounds, depending on their crystal symmetry, can host a variety of topological spin arrangements, including Bloch and Néel skyrmions and antiskyrmions (see Figure 2).23,24,25,26 Skyrmions and antiskyrmions are mesoscale whirling objects with distinct chiral magnetic boundaries and opposite topological charges of  +1 and −1, respectively. Skyrmions are isotropic and are only formed with either Bloch or Néel-type walls (Figure 2a–b), whereas antiskyrmions have a swirling pattern that consists of successive Bloch and Néel wall segments along alternating [100] and [110] crystallographic directions of the D2d structure (Figure 2c).23 The anisotropic arrangement of Bloch and Néel walls of alternating chirality could provide directional controllability of the current-induced motion of antiskyrmions (i.e., a crystal direction-dependent skyrmion Hall angle). It was predicted that the antiskyrmion Hall angle could be tuned to zero by applying currents along specific crystallographic directions.27

Figure 2
figure 2

Examples of various skyrmions. Spin textures of (a) Bloch skyrmion, (b) Néel skyrmion, and (c) antiskyrmion.23

Full size image

Magnetic skyrmions are topologically protected vortices of magnetization that are stabilized in chiral noncentrosymmetric magnets, but recently skyrmions were claimed to be realized in a centrosymmetric compound.28 So far skyrmion lattices have been experimentally realized at low temperatures and typically in the presence of a magnetic field in various bulk cubic B20 transition metal compounds, including, MnSi,29 Mn1−xFexSi,30 Mn1−xCoxSi,31 Fe1−xCoxSi,32 FeGe,33 Mn1−xFexGe,34 and the multiferroic insulator Cu2OSeO3.35,36 Co8Zn8Mn437 with a β-Mn-type structure hosts Bloch skyrmions at ambient temperature. For many of these systems, skyrmion lattices are found to be stable only in a narrow region in the temperature–magnetic field phase diagram, which limits their application. Therefore, it has been a prime goal to design and investigate novel materials that could host skyrmion lattices at ambient temperature and low magnetic fields. Tetragonal inverse Heusler compounds host antiskyrmion lattices that have been directly imaged using Lorentz transmission electron microscopy (LTEM), well beyond room temperature. LTEM is one of the best methods for real-space imaging of skyrmions and can also be used to acquire videos of moving skyrmions as well as to visualize magnetic phase transitions.

Skyrmions have the potential to be used as magnetic bits in high-density storage devices such as racetrack memories,38,39,40 as well as for neuromorphic computing systems that go beyond Moore’s Law. This article summarizes the studies of topological properties of skyrmion states in high-quality single crystals and thin films of magnetic Heusler compounds.

Why Heusler compounds?

For the design of new materials hosting skyrmions, the following Hamiltonian must be translated into a material’s properties:

$$H=-\frac{1}{2}{{\sum }_{{\varvec{i}},{\varvec{j}}}{J}_{i,j}{{\varvec{m}}}_{{\varvec{i}}}}\cdot {{\varvec{m}}}_{{\varvec{j}}}+{{\sum }_{{\varvec{i}},{\varvec{j}}}{D}_{i,j}\cdot {{\varvec{m}}}_{{\varvec{i}}}}\times {{\varvec{m}}}_{{\varvec{j}}}+{\sum }_{{\varvec{i}}}{K}_{i}({{\varvec{m}}}_{{\varvec{i}}}{{\cdot {\varvec{e}}}_{{\varvec{i}}})}^{2}+{\sum }_{{\varvec{i}},{\varvec{j}}}\frac{1}{{r}_{i,j}^{3}}[{{\varvec{m}}}_{{\varvec{i}}}{\cdot {\varvec{m}}}_{{\varvec{j}}}-({{\varvec{m}}}_{{\varvec{i}}}{\cdot {\varvec{e}}}_{{\varvec{i}}})({{\varvec{m}}}_{{\varvec{j}}}{\cdot {\varvec{e}}}_{{\varvec{j}}})].$$

These chiral objects are typically observed in magnetic materials with broken inversion symmetry giving rise to the Dzyaloshinskii–Moriya exchange Interaction (DMI) and arise as a result of a competition between the direct Heisenberg exchange mechanism (first term of the Hamiltonian) and an antisymmetric DMI term (second term of the Hamiltonian).41,42 The ratio of the Heisenberg exchange constant to the magnitude of the DMI determines, to a first approximation, the size of the skyrmions or the associated pitch of the spin helix that is typically found in the magnetic field–temperature phase diagram directly adjacent to the skyrmion existence window. The chirality of magnetic skyrmions essentially depends on the lattice symmetry and the sign of the DMI. Depending on the nature of the spin rotation, different types of skyrmion textures have been observed, such as Bloch and Néel skyrmions and very recently, antiskyrmions.23,24,25,26 A skyrmion and an antiskyrmion have opposite topological charges of +1 and −1, respectively. For the application of skyrmions in spintronics, a key requirement is that the material should have a magnetic ordering beyond room temperature and that the skyrmion states should be stable over an extended temperature range. In addition, it is extremely important to control the magnetic anisotropy (third term of the Hamiltonian), which can influence the competition between a spiral magnetic state, skyrmion textures, and collinear spin states. In this context, tetragonal magnetic Heusler compounds, X2YZ (where X, Y are transition metals and Z is a main group element) with two magnetic sublattices (X) are potential candidates for the design of anisotropic and noncentrosymmetric room-temperature magnets,43,44,45 which provide a unique route to the formation and stabilization of antiskyrmion and skyrmion lattices.

The antiskyrmion was discovered in the inverse tetragonal Heusler compound Mn1.4Pt0.9Pd0.1Sn, which has a D2d crystal symmetry, in which Pt gives significant spin–orbit coupling and, thereby, a DMI. It was found that the bulk phase of Mn2PtSn can only be stabilized with the introduction of significant Mn vacancies. A single-phase material Mn1.4PtSn that crystallizes in a noncentrosymmetric tetragonal structure with space group I \(\overline{4 }\) 2 m could be obtained with uniformly distributed Mn vacancies exclusively in the Mn-Pt NaCl type substructure. In order to carry out small-angle neutron scattering to explore antiskyrmions in the bulk, large single crystals are needed. However, untwinned single crystals are difficult to synthesize due to the martensitic phase transition. Recently, a successful method to grow micron-sized, twin-free, single crystals of Mn1.4PtSn based on a self-flux method was established. The direction-dependent magnetic properties show a ferromagnetic transition at TC = 392 K as well as a spin-reorientation transition at 170 K with a saturation moment of 4.7 μB/f.u. at 2 K. These transitions are also reflected in the temperature-dependent resistivity, which is metallic to the lowest temperatures explored.46 Additionally, a small amount of Pd that was substituted in place of Pt was found to enhance the tetragonality, which is responsible for the strong uniaxial magnetic anisotropy, a prerequisite for the establishment of the antiskyrmion phase.45

Antiskyrmions

Experimental evidence for the topological noncollinear spin texture, an antiskyrmion (aSk), was first found in the Heusler material Mn1.4Pt0.9Pd0.1Sn, at room temperature and above by direct imaging with LTEM23 using an FEI TITAN G2 80–300 and double-tilt stages with variable temperature capabilities (100–400 K and 10–300 K). Wedge-shaped lamellae of Mn1.4Pt0.9Pd0.1Sn were prepared by Ga+-focused ion beam (FIB) milling from a bulk single crystal. In Figure 3a, an SEM (scanning electron microscopy) image of an exemplary lamella that was used for these experiments is shown. The Lorentz mode in TEM has the capability of nearly magnetic field-free imaging and is a powerful method for real-space imaging of skyrmions due to its high spatial resolution, and due to the fact that it measures the integrated B-field throughout the thickness of the sample. In LTEM imaging, an aSk appears as two bright and two dark lobes, as shown in Figure 3b. Due to the presence of alternating chiral spin textured walls around the boundary of the nano-object, namely helicoid and cycloid spin propagations, the transmitted electron beam converges toward the boundary of the aSk in the vertical direction in Figure 3b, whereas it diverges in the horizontal direction in Figure 3b. This assignment has been verified by micromagnetic simulations of the LTEM pattern.

Figure 3
figure 3

Lorentz transmission electron microscope (LTEM) images of chiral spin textures in Mn1.4PtSn. (a) Scanning electron microscope image and schematic drawing of a wedge-shaped lamella where α and β correspond to the double-stage tilt angles. LTEM images of (b) an antiskyrmion imaged from a uniform thickness lamella in the presence of a magnetic field of 368 mT, and (c) evolution of helical phase and antiskyrmions as a function of thickness of a lamella that is increasing in thickness from right to left (116 to 206 nm) along the horizontal direction at magnetic fields of 0, 192, and 320 mT. All LTEM images are recorded at an underfocus value of 1.5 mm except for (b), which was recorded at an underfocus value of 2 mm. The magnetic field is applied along z ([001]) in all cases (i.e., perpendicular to the lamella).47

Full size image

LTEM can identify transformations from the helical magnetic phase that is stable at low fields, to the aSk phase and eventually to the fully aligned magnetic state, as the magnetic field is increased over a wide range of temperature. The temperature–field phase stability of antiskyrmions in Mn1.4Pt0.9Pd0.1Sn was found to depend strongly on the thickness of the lamella. LTEM measurements of a wedge-shaped lamella formed from a single crystal of Mn1.4Pt0.9Pd0.1Sn are shown in Figure 3c. One drawback of LTEM is that the sample must be thin enough to allow for the transmission of the electron beam. This limits the thickness to ~300 nm; for thicker studies, one must use other techniques such as variable temperature magnetic force microscopy (MFM) or, for larger-sized spin textures, magneto-optic Kerr microscopy is possible. Exemplary MFM images are shown in Figure 4a–d.

Figure 4
figure 4

Magnetic force microscope images of the antiskyrmion phase. (a) Helical phase in zero magnetic field and evolution to aSk phase as the field is increased to (b) 300 mT (c), 420 mT, and (d) 480 mT. The scanned area is 8 × 16 μm2 where the thickness increases from left to right from 630 nm to 4260 nm. (e) aSk size versus thickness for various magnetic fields. Inset shows aSk size versus thickness for a second wedge determined from Lorentz transmission electron microscope (LTEM) images. The field is applied perpendicular to the lamella.47

Full size image

The most interesting findings in this study are that stable and metastable aSk lattice states are realized over a large region in the B–T phase diagram over the whole temperature range that was explored. The field stabilized aSk lattice at 300 K is very promising for applications. By varying the thickness of the host material, it is possible to manipulate the diameter of the antiskyrmions from ~100 nm to more than 1.1 μm (see Figure 4e). LTEM (and MFM) images of the wedge-shaped lamella show a helical phase at zero-field (0 mT), and the evolution of the helical phase and the antiskyrmion phase as the thickness of the lamella is increased from right to left along the horizontal direction in Figure 3c and left to right in Figure 4a–d. A helimagnetic ground state, propagating in the tetragonal basal plane, transforms into an aSk lattice state under magnetic fields applied along the tetragonal axis [001] over a wide range of temperatures (100–400 K). Similarly, the periodicity of the long-range helical spin textures from which the antiskyrmions arise, can be tuned by altering the material thickness.47 This is due to the interplay between the DMI and long-range dipole–dipole interactions (fourth term of the Hamiltonian previously shown). This tunability arises from the long-range magneto-dipolar interactions that depend on the symmetry of the DMI that is determined by the crystal structure of the host material. The dipole–dipole interactions are much more important for antiskyrmions than, for example, skyrmions in the B20 systems, which have been extensively studied. The size tunability and robust stability of antiskyrmions is beneficial for the generation and detection of antiskyrmions in magnetic devices with engineered geometries, which are promising for spintronic applications.

The magnetic phase diagram of antiskyrmions is distinct from those reported for the skyrmion phase in B20-type cubic chiral magnets, where the skyrmion phase is, rather, rapidly destabilized as the thickness of the sample is increased. This is due to the difference in DMI in the noncentrosymmetric crystal structures of D2d and B20-type crystals, where the former symmetry supports anisotropic and the latter isotropic DMI vectors.25

Scalar magnetic x-ray tomography has been used to investigate the three-dimensional shape of the skyrmions in the Heusler compound Mn1.4Pt0.9Pd0.1Sn.48 Skyrmion strings were identified along the [001] magnetization direction via tomographic reconstruction. The antiskyrmion strings extend throughout the thickness of the lamella. The strings in Heusler compounds might also host magnetic monopoles, so-called Bloch points, as originally proposed by Feldtkeller49 and Döring.50 Recently, it has been demonstrated using electron holography that magnetostatic charges are generated by Néel type magnetization rotations. Due to the fact that the opposite chirality of the Néel walls results in an opposite sign of the magnetostatic charge, a closed-loop magnetic flux forms in the region between two magnetic antiskyrmions.51

As mentioned earlier, skyrmions are potential candidates as magnetic bits for a “racetrack memory”38,39 in which these digital data bits are moved along magnetic nanowires, the racetracks, via torques supplied by spin currents. However, the motion of skyrmions under longitudinal currents takes a transverse trajectory to that of the applied current direction that is the so-called “skyrmion Hall effect.”52,53 This sideways movement can cause the collision of these nano-objects with the device boundary, which eventually leads to their destruction. However, magnetic antiskyrmions that have distinct topological characteristics can avoid such a current-induced transverse motion, depending on the current direction compared to the underlying crystal structure to which the antiskyrmion is intimately connected.

Néel and Bloch skyrmions

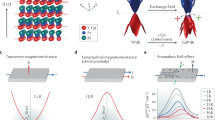
The dipole–dipole interaction (DDI) has a significant impact on the spin textures of antiskyrmions in D2d materials. Usually, skyrmions and antiskyrmions are stabilized in different magnetic materials by either isotropic or anisotropic DMI, respectively, which are directly tied to the crystal structure of the host material. It is noteworthy that DDI prefers Bloch-type skyrmions. At lower temperatures, as shown in Figure 5, DDIs become more relevant and elliptical Bloch skyrmions are stabilized in Heusler compounds whose symmetry otherwise supports antiskyrmions. The DDI also modifies the shape of circularly shaped antiskyrmions to square-shaped objects at room temperature. The Bloch parts of the antiskyrmion along the [100] and [010] directions are favored by DDI leading to an enlargement of these parts. On the contrary, the Néel parts are unfavorable, leading to shrinking of these parts and, thereby, giving rise to square-shaped antiskyrmions. Due to the sensitivity of Lorentz imaging to the in-plane magnetic induction of magnetic objects, the distinction between the in-plane magnetization distributions of elliptical Bloch skyrmions from that of antiskyrmions was unambiguously possible using LTEM. By tuning the thickness of the sample, the coexistence of elliptical skyrmions with antiskyrmions was directly observed.24 The formation of two such distinct chiral spin textures with opposite topological charges of ±1 in one material system is exceptional. The coexistence of two different magnetic nano-objects at room temperature has the potential to be utilized in an advanced racetrack memory device where information could be encoded as 0 and 1 bits in a sequence of antiskyrmions and elliptical Bloch skyrmions (see Figure 5).

Figure 5
figure 5

Two topological spin textures coexisting in Mn1.4Pt0.9Pd0.1Sn. Simulated magnetic contrast of (a, b) elliptical Bloch skyrmion, (c) round antiskyrmion, (d) square antiskyrmion. Experimental Lorentz transmission electron microscope images of (e–f) elliptical Bloch skyrmions at 200 K, (g) round antiskyrmions at 300 K and (h) square antiskyrmions at 300 K; and (i) schematic representation of an advanced racetrack memory device in which skyrmions represent 1 bits (blue) and antiskyrmions 0 bits (red). (j) Coexistence of skyrmions and antiskyrmions via topological Hall effect measurements on a thin film of Mn2RhSn. The scale bar in e–h corresponds to 300 nm.54,55

Full size image

Following the observation of two different magnetic textures in a single D2d Heusler compound, their coexistence in nano-stripes with varying widths was explored using LTEM54—a sketch is shown in Figure 5i. In this study, it was shown that both spin textures could be stabilized in such confined geometries at room temperature, which is of great relevance to racetrack memory.

Magnetic skyrmions are coupled to applied electrical currents very efficiently. The current is deflected by the Lorentz force induced by the emergent magnetic field of the spin textures. The emergent magnetic field from each skyrmion is quantized and is directly proportional to the skyrmion winding number. For topologically trivial magnetic phases, such as a helical phase or a field-polarized state, the winding number vanishes, resulting in zero emergent magnetic field and, hence, no additional contribution to the deflecting traverse currents. Therefore, an additional transverse Hall voltage gives evidence of the presence of a nontrivial spin texture whose magnitude arises from the emergent magnetic field. In this way, it is possible to detect and differentiate the presence of skyrmions or antiskyrmions from the direction of the deflection of traversing electrons that is opposite for these two objects as a result of the opposite sign of their winding numbers. This additional contribution to the Hall effect caused by the nonzero winding number is referred to as a topological Hall effect (THE). THE measurements have been used to identify the coexistence of skyrmions and antiskyrmions in thin films of the tetragonal inverse Heusler material Mn2RhSn55 that has the same D2d symmetry as Mn1.4Pt0.9Pd0.1Sn. Two peaks in the THE, as shown in Figure 5j, are observed, whose magnitudes vary with both temperature and applied magnetic field. The variation in magnitude and sign of the two THE peaks can be used to identify the presence of skyrmions and antiskyrmions. From THE measurements, it was shown that skyrmions are dominant at low temperatures, while antiskyrmions are dominant at higher temperatures and both objects are seen in an intermediate temperature range. This observation is similar to LTEM studies on single-crystalline lamellae of Mn1.4Pt0.9Pd0.1Sn, as discussed before, where real-space imaging shows the presence of elliptical Bloch skyrmions at lower temperatures and antiskyrmions at higher temperatures. This electrical detection of chiral magnetic nano-objects is highly beneficial for identifying such textures in ultrathin films, where magnetic imaging via LTEM is difficult.

The wide temperature-field stability, the size tunability of the magnetic antiskyrmions, and the stabilization of two distinct topological objects make tetragonal inverse Heusler materials unique for spintronic applications at room temperature. However, in real spintronic devices, the presence of long-range dipole fields derived from the moments of small magnetic nano-objects might limit their use, for example, in dense packing of magnetic memory elements. Antiskyrmions in low or even zero-moment hosting materials are insensitive to the fringing magnetic field, thus, paving a way to highly dense magnetic storage devices. However, due to the absence of a net magnetic moment, it is difficult to image such materials with LTEM, because the LTEM signal is directly proportional to the average magnetic induction of the specimen. However, antiskyrmions have been observed in a low magnetization ferrimagnetic tetragonal inverse Heusler compound over a wide range of temperature and magnetic field in both single-crystalline bulk and thin-film material.56,57 These results open the path to the exploitation of the considerable tunability of Heusler compounds for antiferromagnetic antiskyrmions.

There have been several reports of the stabilization of Néel skyrmions in magnetic multilayers where a chiral DMI arises from the broken symmetry at the interface of the multilayer. In the case of bulk materials, Néel skyrmions have only been observed in two insulating polar compounds, in GaV4S8 at very low temperatures (below 13 K)58 and VOSe2O5.59 For the first time, by employing LTEM and MFM, robust Néel skyrmions have been observed in a metallic compound PtMnGa at relatively high temperatures, as shown in Figure 6. The structure of this material, in contrast to the literature, was shown to be noncentrosymmetric C3v, thereby supporting the observation of Néel skyrmions. LTEM measurements confirm the Néel-type chirality of the magnetic structure that appears as half-bright and half-dark magnetic spots.26 These Néel skyrmions are stable over a wide temperature range up to ~220 K and can be stabilized at zero field after a suitable field-cooling procedure. Interestingly, the size of these Néel skyrmions increases significantly from ~90 to ~720 nm as the thickness of a [001] oriented lamella is varied from 90 nm to 4 μm, as demonstrated by MFM (Figure 6i). This is attributed to the presence of magneto-dipolar interactions, together with DMI, which preserves the Néel character of the magnetic nano-objects. The observation of Néel skyrmions in a metallic compound over a wide range of magnetic field and temperature, together with the possibility of manipulation of the skyrmion size, makes PtMnGa interesting for current-driven motion studies.

Figure 6
figure 6

Néel skyrmions in PtMnGa. (a) Perspective view of the structure of PtMnGa. Distances are given in nanometers. (b) Spin texture of a Néel skyrmion, (f) Selected-area electron diffraction pattern obtained at room temperature from a [0001] oriented lamella. Under-focused (1.5 mm) Lorentz transmission electron microscope images recorded at 100 K with tilt angle as follows: (c) α = −9°, (d) β = −19°, (g) α = +9°, and (h) β = +16°. These images were recorded under a perpendicular applied field of 0.28 T. The dashed white lines in (c), (d), (g), and (h) represent the tilt axis, curved arrows represent the tilting direction, and yellow circles identify a single skyrmion. (e) Schematic representation of sample tilting along the x- and y-axes defining positive and negative α and β tilt angles. (i) MFM image of Néel skyrmions in a wedged lamella taken at 100 K and in a perpendicular applied field of 0.096 T. The lamella is uniform in thickness along the vertical direction and varies in thickness from left to right as shown by the lower x coordinate. The left and top axes show the size of the wedge.26

Full size image

High-quality epitaxial thin films of MnxPtSn were grown by sputtering. The Mn content (x) and thickness were tuned, which enables microscopic control of the magnetic exchange parameters that can be detected electrically with the THE.60,61 Specifically, the role of x to tune the ratio of antiferromagnetic and ferromagnetic exchange interactions, which is crucial for the stabilization of antiskyrmions was found. Fine-tuning of x enables discrete adjustment of the antiskyrmions below the spin-reorientation temperature (TSR). This effect is observable from low temperatures up to ∼200 K, depending on x. As expected, the magnetic dipole–dipole interactions play the largest role in determining the thin-film limit. The THE changes substantially with x and the topological Berry curvature can be fine-tuned by modifying the film composition. The topological origin of the observed effects is confirmed by a combination of magnetotransport and magnetization measurements.

An alternative method for determining the topological signatures is possible, whereby the anomalous Hall and Nernst effects are measured for micropatterned thin films. For Mn1.8PtSn films, below TSR ≈ 190 K, a large THE and a topological Nernst effect (TNE), SxyT = 115 nV K−1 was measured in the same microstructured device,62 which has a similar magnitude to that of bulk MnGe (SxyT ≈ 150 nV K−1), the only material to date for which a TNE has been reported. These data serve as a model system to introduce a topological quantity, which enables the detection of the presence of topological transport effects without independent magnetometry data.

Outlook

Heusler compounds are a rich playground for exploring and designing topological electronic and spin textures. The structure and properties of the Heusler compounds can be significantly modified via chemical tuning. Similarly, in Heuslers with magnetic atoms, there is considerable interplay between the magnetic structure and the crystal structure. In the hexagonal Heuslers, frustration can lead to the formation of Kagome antiferromagnetic lattices that display a range of highly interesting properties directly coupled to Berry phase curvature derived from the electronic structure. In Heusler compounds with heavy atoms, the magnetic structures can be noncollinear and, in noncentrosymmetric materials, a significant vector exchange in the form of a DMI can arise that leads to a host of chiral spin textures ranging from skyrmions to antiskyrmions. Indeed, just recently new objects, namely fractional skyrmions and antiskyrmions have been observed for the first time in a ferrimagnetic Heusler compound.63 Further complexity to these structures derives from the significant role of dipole–dipole interactions that lead to distortions of the antiskyrmion and its eventual transfiguration into an elliptical skyrmion, a distinct topological spin texture. The Heusler compounds are one of the few systems in which two distinct topological spin textures can coexist. Additionally, non-centrosymmetric Heusler compounds may be an excellent platform for investigating multistate memory devices based on the ensemble of skyrmionic structures such as antiskyrmions, elliptical Bloch skyrmions, fractional (anti)skyrmions, and trivial bubbles that are found in these compounds. Furthermore, the 2D and 3D magnetization dynamics of various types of glassy states formed in response to system defects, temperature, and field protocols are interesting to investigate. The outlook for designer topological spin textures intertwined with electronic effects in Heusler compounds is very bright. The future is likely to bring progress in the manipulation of these complex topological textures via electrical and optical means as well as via the application of uniform and nonuniform pressure and even electrochemical and electromechanical effects. Beyond the individual materials themselves, the development of thin-film techniques to allow for highly chemically ordered Heuslers, for example, by chemical templating techniques,64 will allow for the exploitation of the properties of two or more Heusler compounds via proximity and interface effects. Just one highly interesting possibility is the use of skyrmion textures to host Majorana fermions.65,66,67