Abstract
Since the high entropy concept was proposed at the beginning of the millennium, the research focus of this alloy family has been wide ranging. The initial search for single-phase alloys has expanded with the aim of improving mechanical properties. This can be achieved by several strengthening mechanisms such as solid-solution hardening, hot and cold working and precipitation hardening. Both single- and multiphase high- and medium-entropy alloys can be optimized for mechanical strength via several processing routes, as is the case for conventional alloys with only one base element, such as steels or Ni-based superalloys.
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The most striking feature of the mechanical properties of high-entropy alloys (HEAs), especially those with the face-centered-cubic (fcc) structure, is excellent combination of high strength and high ductility.1,2,3 It is important, however, to note that not all HEAs exhibit such excellent mechanical properties. In fact, HEAs and medium-entropy alloys (MEAs) exhibit a wide range of mechanical properties (in terms of strength and ductility) which are comparable to conventional alloys (e.g., Figures 1–3 in Reference 4). This indicates that deformation mechanisms of single-phase HEAs are essentially similar to those of conventional solid-solution alloys. Mechanical properties of HEAs can therefore be described by already proposed models for the deformation behavior of conventional solid-solution alloys,5 although some modification may be needed in the presence of high local complexity of HEAs and MEAs.
Most alloys in structural application exhibit multiphase microstructures, as a good balance of mechanical properties (especially high strength) is rarely achieved in single-phase alloys.6,7 This is also the case for HEAs where multiphase microstructures are needed for optimal properties. A high entropy matrix phase with a simple crystal structure is needed in most cases to increase ductility. While it is important to characterize the mechanical properties of the HEA matrix phase, it is also vital to understand how the incorporation of additional phases affects the mechanical properties. Within this article, we restrict discussion to mechanical properties such as strength and ductility obtained by uniaxial tension/compression tests.6
Both single- and multiphase HEAs and MEAs can be tuned toward high strength using different process routes, the most common being hot or cold deformation followed by recrystallization for grain refinement (Hall–Petch strengthening). Spectacular mechanical properties in HEAs can be obtained by combining several strengthening mechanisms.8,9,10 The influence of the individual mechanisms has been calculated in several studies and varies from one study to the other.11,12,13 In this article, uniaxial mechanical properties will be discussed with respect to deformation mechanisms and models proposed for conventional alloys. Thereby, we can clarify if the behavior of HEAs and MEAs is similar to or different from that of conventional alloys.
Single-phase HEAs
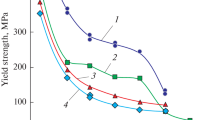
Following the discovery of the CrMnFeCoNi quinary equiatomic HEA,14 George et al. made a systematic study on the formation of quaternary and ternary equiatomic MEAs of its subsystems2,15 and on tensile properties of their polycrystals in a wide temperature range of 77–673 K.2,16 The investigated HEA and all its MEAs exhibit a strong temperature dependence of yield stress σY below room temperature (Figure 3a of Reference 16) and tensile ductility is larger at 77 K than at room temperature for many of these alloys (Figure 3c of Reference 16). The increased tensile ductility at lower temperatures is not common to conventional alloys and is ascribed to a dynamic Hall–Petch effect due to the occurrence of deformation twinning at low temperatures.15,17 However, the temperature dependence of σY of these alloys seems to be well interpreted in terms of thermally activated dislocation glide, as in conventional solid-solution hardened alloys.5,18 Figure 1a shows this by fitting the σY-temperature curves16 with the classical formulation5 long established for solid-solution hardening,
where \(T\) and \({T}_{a}\) correspond to the deformation temperature and the athermal temperature, τath and τth are athermal and thermal components of σY, p and q values are fitting parameters for the σY-temperature curve. The deduced values of p and q (Table I) for all alloys are within the range (0 < p < 1 and 1 < q < 2) reported for conventional fcc solid-solution alloys,5 indicating that solid-solution strengthening mechanisms proposed for conventional alloys operate also for HEAs and MEAs.
The high strength appears to be related to their severely distorted crystal lattice, which is also one of the most remarkable features in atomic structures of HEAs. Many different theoretical approaches have been attempted to obtain correlations between the strength of HEAs and MEAs and appropriate parameters that describe the distorted crystal lattices.19,20,21,22 Details of the theoretical approaches are provided in the Curtin et al. article in this issue. Figure 1b shows one example of such an approach, showing a nice correlation between the 0 K σY of polycrystals of HEA and MEAs deduced from Eq. (1) and mean-square atomic displacement MSAD (\(Average\;MSAD=\sum {c}_{i}{MSAD}_{i}\); ci denotes atomic fraction of element i).22,23 The square root of MSAD22 gives the degree to which alloy atoms are displaced from the ideal lattice (in this case, the fcc lattice positions). The good correlation seen in Figure 1b suggests that a dislocation will interact with such atomic-scale distortions and induce strengthening proportional to average displacements, but it lacks a connection to a specific mechanism. Nevertheless, it is worth noting that the MSAD model correctly predicts the magnitudes of solid-solution strengthening of not only HEAs and MEAs but also conventional binary and ternary alloys.22 Historically, the interaction energy of a solute with a dislocation, resulting mainly from solute misfit volume, is known to be a key for solid-solution hardening.5,18,24,25 Some excellent theoretical models that incorporate the solute-dislocation interaction energy are available for describing strengths of HEAs and MEAs.19,20
In the discussion of σY, we ignored the contribution of the Hall–Petch effect (grain-boundary strengthening) to σY of polycrystals. Although the Hall–Petch effect is believed to be significant in HEAs when compared to conventional alloys,15,26 the analysis shown in Figure 1 may not be significantly affected, as polycrystals of similar grain sizes were used in experiments by George et al.16
Characteristic features of tensile stress–strain curves observed in single crystals of the equiatomic CrMnFeCoNi HEA (Figure 9 of Reference 27) are mostly similar to those for conventional fcc alloys with a low stacking fault energy.18,28 Stage I of low work-hardening rate extends to more than 10% strain, followed by stage II of high work-hardening rate. Regardless of temperature, the linear work-hardening rate of stage II is around G/250, where G is the shear modulus, which is in the range for most conventional fcc alloys.18,28 Primary slip occurs during stage I so that the slip steps gradually fill the entire gage length, while during stage II, in addition to primary slip, conjugate slip starts to contribute to deformation with its extent increasing with increasing strain level. Failure occurs at the end of stage II (at about 100% strain) at room temperature whereas at 77 K, stage II is followed by deformation twinning on the conjugate system (Figure 10 of Reference 27), leading to much higher tensile ductility (failure at more than 200% strain). The higher tensile ductility at 77 K than at room temperature was similarly observed for polycrystals of the equiatomic CrMnFeCoNi HEA by George et al.,15,17 although the tensile ductility is generally much smaller for polycrystals (70% and 100% strain at room temperature and 77 K).15,17 The higher tensile ductility at lower temperatures for polycrystals is ascribed to a dynamic Hall–Petch effect due to the occurrence of deformation twinning at low temperatures.15,17 This is consistent with what is observed for the single crystals27 and with the general belief that deformation twinning occurs more readily at lower temperatures in fcc metals and alloys.29,30 However, the twining behavior is quite different for single crystals and polycrystals of the equiatomic CrMnFeCoNi HEA. Twinning occurs in general at much smaller strain and stress levels in polycrystals.15,17 The higher propensity of secondary slip in polycrystals due to grain constraint may promote twinning at smaller strain levels, as twinning is known in general to occur after activation of secondary slip.29,30 The Hall–Petch hardening as well as higher work-hardening due to the secondary slip activation from the beginning of deformation may also contribute to quickly reaching the critical twinning stress (if twinning is indeed stress-controlled in this HEA).
The high ductility of HEAs and MEAs at low temperatures is usually observed to be accompanied by the occurrence of deformation twinning15,17,27,31,32,33,34,35 whose propensity is believed to increase with decreasing stacking fault (SF) energy. This clearly indicates the importance of tuning the SF energy in controlling the ductility of HEAs. Comparison of the twinning behavior of polycrystals of CrMnFeCoNi and CrCoNi indicates that the twinning stress increases with decreasing SF energy,17,33 which is opposite to what is long believed for conventional fcc alloys.29,30 More work is definitely needed to explore the temperature- and SF energy-dependence of twinning stress in HEAs and MEAs. The decreased SF energy at lower temperatures as suggested by DFT (density functional theory) calculations36,37 indicates a possibility that not only twinning but also HCP (hexagonal close-packed) phase transformation occurs at low temperatures through the motion of the identical Shockley partial dislocation. This is indeed experimentally observed in CrCoNi31,32,35 and some other MEAs.38 Many efforts have been made to increase the tensile ductility of HEAs and MEAs utilizing TWIP (twinning-induced plasticity) and TRIP (transformation-induced plasticity) effects through controlling the SF energy1,4 with some excellent examples.39,40
Short-range ordering (SRO) is known to occur even in dilute binary alloys due to mixing enthalpy contribution with the extent depending on heat treatment and its occurrence and evolution have been proved by x-ray and electron diffraction41,42 as well as by electrical resistivity and specific heat measurements.43,44 SRO has been a recent focus45,46,47,48,49 of special atomic structures of HEAs and many attempts have been made to elucidate atomic-scale structural features and correlate these features with strength.48,49 Detailed studies to correlate the degree of SRO with the strength have not yet been done for HEAs and MEAs. A substantial increase in σY (by 25%) is reported for tensile-tested CrCoNi polycrystals49 by promoting the SRO formation with furnace cooling from 1273 K after homogenization at 1473 K for 48 h. On the other hand, no significant effect of SRO on σY is observed for tensile-tested CrCoNi polycrystals subjected to low-temperature annealing (at either 873 or 973 K for 384 h followed by water quenching) to induce SRO after homogenization at 1373 K for 24 h.50 No significant change in σY in compression is noted also for single crystals of CrMnFeCoNi homogenized at 1473 K for 168 h and then annealed at 1073, 1173, or 1273 K for 168 h followed by water quenching to induce SRO.51 It is important to note that all the above studies assumed the development of SRO by annealing at low temperature but the existence of SRO was not proved experimentally. The existence of SRO seems difficult to prove by simple x-ray and electron diffraction methods in particular for HEAs and MEAs in the Cr–Mn–Fe–Co–Ni system and its sub-systems due to the very small difference in atomic scattering factor of the constituent elements. More work is needed to explore the effect of SRO on the strength of HEAs and MEAs.
Multiphase HEAs and MEAs with fcc matrix
Unlike the initial assumption in the early years of HEA research, most HEAs are not single-phase but multiphase. Because of the high number of possible alloys, we divide them in different groups:
-
solidification segregation-induced multiphase alloys that can be homogenized and adapted with an adequate thermomechanical treatment52,53
-
eutectic HEAs, which crystallize into usually two phases with a similar phase fraction54,55
-
matrix-dominated HEAs consisting of a matrix and one or more precipitate phase(s)56,57,58
-
HEAs relying on deformation-induced phase transformation that can lead to grains consisting of different phases (see TRIP HEAs40,59)
The yield strength σY of an alloy can be estimated by considering the different strength contributions. In some cases a linear addition can be assumed, as is in Reference 60 and this is often used for theoretical estimations.
In most cases, the different stresses can convert into each other and are not independent. The stresses contributing to the yield strength are:
\({\sigma }_{0}\) the lattice friction stress or the Peierls stress,
σss solid-solution hardening,
σgb grain-boundary refinement (Hall–Petch, \(\sim {d}^{-1/2}\)),
σwh work hardening (\(\sim G\times {\varvec{b}}\times \sqrt{{\uprho }_{d}}\)),
σph precipitation hardening,
σtw twinning, with d = the grain size, G the shear modulus, b the Burgers vector, and ρd the dislocation density. All contributions can be used in both single- and multiphase HEAs and MEAs, except for the σph term, which is unique to multiphase alloys. The processing of HEAs follows the same general behavior as is known from conventional alloys and is thus not unique to this group of alloys.61 For a better comparison of single- and multiphase HEAs, it would thus be convenient to consider alloys that are close to an equilibrium condition. As there are few studies that aim for an alloy state close to the equilibrium condition, the comparison in this paper focuses on processed and optimized states of various single- and multiphase HEAs and MEAs.
Figure 2 plots the product of ultimate tensile strength (UTS) × elongation to fracture (EL) (i.e., an energy necessary to obtain fracture) versus the yield strength σY for various single- and multiphase HEAs/MEAs in comparison to commercially available austenitic steels and Ni-based alloys.10,15,62,63,64,65,66,67,68,69,70,71,72,73 A wide range of mechanical properties can be obtained: some alloys performing better for long-term application (high yield strength), some being more appropriate for emergency situations (high product of ultimate tensile strength and elongation to failure) (e.g., a car crash). Some show a great balance between the two aspects. A few outstanding alloys and their properties are presented in more detail.
The best performing alloy Al7(CoFeNi)86Ti7 is a two-phase HEA,65 which shows its best properties following thermomechanical treatment. The UTS, σY and EL of this alloy are 1450 MPa, 1050 MPa, and 50%, respectively. These exceptional values can be attributed not only to precipitation strengthening, but to a combination with a particular form of grain refinement, very small misorientation angles, and microband-induced plasticity.
An extremely high yield strength can be obtained in a single-phase alloy called MP35N (35 wt% Co-35 wt% Ni-20 wt% Cr-10 wt% Mo),68 which, at the time of its investigation in 2002, did not bear the name of HEA or MEA, because these terms were not yet invented. After a complex thermomechanical heat treatment, MP35N reaches UTS, σY and EL values of 2079 MPa, 2027 MPa and 11.3%, respectively.
Most information on uniaxial properties in multiphase HEAs has been obtained at room temperature (see References 9,61 references therein and many others). Little information is available at cryogenic temperature, one example being AlCrCoFeNi2.1 eutectic HEA.74 At high temperature, this alloy is scarcely investigated. Unfortunately, the process-induced strengthening methods, which are efficient at room temperature are often detrimental at higher temperature. For example, a small grain size, used at room temperature for strengthening, leads to softening at high temperature and reduces thus the alloys’ strength. At high temperatures, generally above 50% homologous temperature, precipitate strengthening takes over and is the most effective mechanism of all.
Several microstructures have been tested in different groups and the most effective for high-temperature application is the same as for Ni-based superalloys—a disordered fcc structured matrix containing coherent ordered L12 structured precipitates. This combination leads to a ductile behavior with high yield strength.56,57,75,76,77,78 Another good option is the use of carbides as a second phase. This approach leads to particularly interesting behavior in an emergency case, the product UTS × EL is high in carbide strengthened HEAs. Figure 3 presents a few examples of mechanical data for multiphase HEAs and MEAs at elevated temperatures (~ 973 K) in comparison to a commercially available austenitic steel and Ni-based alloys. At higher temperatures Ni-based alloys set a benchmark that is not reached by alloys of the HEA and MEA family.
Conclusions and future outlook
Despite the unique definition of HEAs and the fact that no element can be considered as base element in which all other elements have to dissolve, the mechanical behavior of single- and multiphase HEAs and MEAs is spread over a wide range and does not differ from that of conventional alloys. All known strengthening mechanisms, for example, solid solution and work hardening as well as precipitate strengthening can be applied. Depending on the existence and morphology of secondary phases, different strengthening mechanisms can be used for different application demands. So far, no new strengthening mechanism, unique to HEAs or MEAs, has been discovered.
The wide field of alloying possibilities still allows for an extended research of new materials that can be used in different operating conditions. The search for new, high-performing multicomponent materials has only just begun.
References
E.P. George, D. Raabe, R.O. Ritchie, Nat. Rev. Mater. 4, 515 (2019)
A. Gali, E.P. George, Intermetallics 39, 74 (2013)
B. Gludovatz, A. Hohenwarter, D. Catoor, E.H. Chang, E.P. George, R.O. Ritchie, Science 345, 1153 (2014)
E.P. George, W.A. Curtin, C.C. Tasan, Acta Mater. 188, 435 (2020)
A.S. Argon, Strengthening Mechanisms in Crystal Plasticity (Oxford University Press, Oxford, 2008)
W.F. Hosford, Mechanical Behavior of Materials, 2nd edn. (Cambridge University Press, Cambridge, 2009)
U. Glatzel, F. Schleifer, C. Gadelmeier, F. Krieg, M. Müller, M. Mosbacher, R. Völkl, Metals 11, 1130 (2021)
S.S. Sohn, A.K. da Silva, Y. Ikeda, F. Körmann, W.J. Lu, W.S. Choi, B. Gault, D. Ponge, J. Neugebauer, D. Raabe, Adv. Mater. 31, 1807142 (2019)
Y.-J. Liang, L. Wang, Y. Wen, B. Cheng, Q. Wu, T. Cao, Q. Xiao, Y. Xue, G. Sha, Y. Wang, Y. Ren, X. Li, L. Wang, F. Wang, H. Cai, Nat. Commun. 9, 4063 (2018)
P. Asghari-Rad, P. Sathiyamoorthi, J.W. Bae, H. Shahmir, A. Zargaran, H.S. Kim, Adv. Eng. Mater. 22, 9 (2020)
J.Y. He, H. Wang, H.L. Huang, X.D. Xu, M.W. Chen, Y. Wu, X.J. Liu, T.G. Nieh, K. An, Z.P. Lu, Acta Mater. 102, 187 (2016)
L. Guo, X. Ou, S. Ni, Y. Liu, M. Song, Mater. Sci. Eng. A 746, 356 (2019)
H. Cheng, H.Y. Wang, Y.C. Xie, Q.H. Tang, P.Q. Dai, Mater. Sci. Technol. 33(17), 2032 (2017)
B. Cantor, I.T.H. Chang, P. Knight, A.J.B. Vincent, Mater. Sci. Eng. A 375–377, 213 (2004)
F. Otto, A. Dlouhy, C. Somsen, H. Bei, G. Eggeler, E.P. George, Acta Mater. 61, 5743 (2013)
Z. Wu, H. Bei, G.M. Pharr, E.P. George, Acta Mater. 81, 428 (2014)
G. Laplanche, A. Kostka, O.M. Horst, G. Eggeler, E.P. George, Acta Mater. 118, 152 (2016)
P. Haasen, Mechanical Properties of Solid Solutions (Elsevier Science, Amsterdam, 1996)
I. Toda-Caraballo, P.E.J. Rivera-Díaz-del-Castillo, Acta Mater. 85, 14 (2015)
C. Varvenne, G.P.M. Leyson, M. Ghazisaeidi, W.A. Curtin, Acta Mater. 124, 660 (2017)
Y.Y. Zhao, T.G. Nieh, Intermetallics 86, 45 (2017)
N.L. Okamoto, K. Yuge, K. Tanaka, H. Inui, E.P. George, AIP Adv. 6, 125008 (2016)
K. Niitsu, M. Asakura, K. Yuge, H. Inui, Mater. Trans. 61, 1874 (2020)
R. Labusch, Phys. Status Solidi B 41, 659 (1970)
G.P.M. Leyson, W.A. Curtin, L.G. Hector, C.F. Woodward, Nat. Mater. 9, 750 (2010)
N.L. Okamoto, S. Fujimoto, Y. Kambara, M. Kawamura, Z.M.T. Chen, H. Matsunoshita, K. Tanaka, H. Inui, E.P. George, Sci. Rep. 6, 35863 (2016)
M. Kawamura, M. Asakura, N.L. Okamoto, K. Kishida, H. Inui, E.P. George, Acta Mater. 203, 116454 (2021)
T.E. Mitchell, Prog. Appl. Mater. Res. 6, 117 (1964)
J.A. Venables, Deformation Twinning in fcc Metals (Gordon and Breach Science Publishers, New York, 1964)
J.W. Christian, S. Mahajan, Prog. Mater. Sci. 39, 1 (1995)
J. Miao, C.E. Slone, T.M. Smith, C. Niu, H. Bei, M. Ghazisaeidi, G.M. Pharr, M.J. Mills, Acta Mater. 132, 35 (2017)
C. Niu, C.R. LaRosa, J. Miao, M.J. Mills, M. Ghazisaeidi, Nature 9, 1363 (2018)
G. Laplanche, A. Kostka, C. Reinhart, J. Hunfeld, G. Eggeler, E.P. George, Acta Mater. 128, 292 (2017)
Z. Zhang, H. Sheng, Z. Wang, B. Gludovatz, Z. Zhang, E.P. George, Q. Yu, S.X. Mao, R.O. Ritchie, Nat. Commun. 8, 14390 (2017)
L. Li, Z.H. Chen, S. Kuroiwa, M. Ito, K. Kishida, H. Inui, E.P. George, Int. J. Plast. 148, 103144 (2022)
S. Zhao, G.M. Stocks, Y. Zhang, Acta Mater. 134, 334 (2017)
Y.H. Zhang, Y. Zhuang, A. Hu, J.J. Kai, C.T. Liu, Scr. Mater. 130, 96 (2017)
Q. Lin, J. Liu, X. An, H. Wang, Y. Zhang, X. Liao, Mater. Res. Lett. 6, 236 (2018)
Z. Li, D. Raabe, JOM 69, 2099 (2017)
Z.M. Li, K.G. Pradeep, Y. Deng, D. Raabe, C.C. Tasan, Nature 534, 227 (2016)
A. Marucco, J. Mater. Sci. 30, 4188 (1995)
A. Marucco, B. Nath, J. Mater. Sci. 23, 2107 (1988)
A. Taylor, K.G. Hinton, J. Inst. Met. 81, 169 (1952–1953)
N.R. Dudova, R.O. Kaibyshev, V.A. Valitov, Phys. Met. Metallogr. 108, 625 (2009)
A. Tamm, A. Aabloo, M. Klintenberg, M. Stocks, A. Caro, Acta Mater. 99, 307 (2015)
F.X. Zhang, S. Zhao, K. Jin, H. Xue, G. Velisa, H. Bei, R. Huang, J.Y.P. Ko, D.C. Pagan, J.C. Neuefeind, W.J. Weber, Y. Zhang, Phys. Rev. Lett. 118, 205501 (2017)
J. Ding, Q. Yu, M. Asta, R.O. Ritchie, Proc. Natl. Acad. Sci. U.S.A. 115, 8919 (2018)
Q.-J. Li, H. Sheng, E. Ma, Nature 10, 3563 (2019)
R. Zhang, S. Zhao, J. Ding, Y. Chong, T. Jia, C. Ophus, M. Asta, R.O. Ritchie, A.M. Minor, Nature 581, 283 (2020)
B. Yin, S. Yoshida, N. Tsuji, W.A. Curtin, Nat. Commun. 11, 2507 (2020)
D. Zhou, Z. Chen, K. Ehara, K. Nitsu, K. Tanaka, H. Inui, Scr. Mater. 191, 173 (2021)
W.Y. Tang, M.H. Chuang, H.Y. Chen, J.W. Yeh, Adv. Eng. Mater. 11, 788 (2009)
Y.J. Zhou, Y. Zhang, Y.L. Wang, G.L. Chen, Appl. Phys. Lett. 90, 181904 (2007)
I. Baker, M. Wu, Z. Wang, Mater. Charact. 147, 545 (2019)
F. He, Z.J. Wang, P. Cheng, Q. Wang, J.J. Li, Y.Y. Dang, J.C. Wang, C.T. Liu, J. Alloys Compd. 656, 284 (2016)
Y.-T. Chen, Y.-J. Chang, H. Murakami, S. Gorsse, A.-C. Yeh, Scr. Mater. 187, 177 (2020)
T.K. Tsao, A.C. Yeh, C.M. Kuo, K. Kakehi, H. Murakami, J.W. Yeh, S.R. Jian, Sci. Rep. 7, 9 (2017)
H.M. Daoud, A.M. Manzoni, N. Wanderka, U. Glatzel, JOM 67, 2271 (2015)
Z.M. Li, C.C. Tasan, K.G. Pradeep, D. Raabe, Acta Mater. 131, 323 (2017)
N. Kamikawa, K. Sato, G. Miyamoto, M. Murayama, N. Sekido, K. Tsuzaki, T. Furuhara, Acta Mater. 83, 383 (2015)
A.M. Manzoni, U. Glatzel, in Encyclopedia of Materials: Metals and Alloys, vol. 2,F.G. Caballero, M.C. Gao, Eds. (Elsevier, Amsterdam, The Netherlands, 2022), pp. 441–453
S.Y. Chen, K.K. Tseng, Y. Tong, W.D. Li, C.W. Tsai, J.W. Yeh, P.K. Liaw, J. Alloys Compd. 795, 19 (2019)
B. Gludovatz, A. Hohenwarter, K.V.S. Thurston, H.B. Bei, Z.G. Wu, E.P. George, R.O. Ritchie, Nat. Commun. 7, 10602 (2016)
K.S. Ming, X.F. Bi, J. Wang, Scr. Mater. 137, 88 (2017)
T. Yang, Y.L. Zhao, Y. Tong, Z.B. Jiao, J. Wei, J.X. Cai, X.D. Han, D. Chen, A. Hu, J.J. Kai, K. Lu, Y. Liu, C.T. Liu, Science 362, 933 (2018)
P. Shi, W. Ren, T. Zheng, Z. Ren, X. Hou, J. Peng, P. Hu, Y. Gao, Y. Zhong, P.K. Liaw, Nat. Commun. 10, 489 (2019)
J. He, S.K. Makineni, W. Lu, Y. Shang, Z. Lu, Z. Li, B. Gault, Scr. Mater. 175, 1 (2020)
K. Han, A. Ishmaku, Y. Xin, H. Garmestani, V.J. Toplosky, R. Walsh, C. Swenson, B. Lesch, H. Ledbetter, S. Kim, M. Hundley, J.R. Sims, IEEE Trans. Appl. Supercond. 12, 1244 (2002)
J.B. Seol, J.W. Bae, Z. Li, J. ChanHan, J.G. Kim, D. Raabe, H.S. Kim, Acta Mater. 151, 366 (2018)
J. Tian, K. Tang, Y.K. Wu, T.H. Cao, J.B. Pang, F. Jiang, Mater. Sci. Eng. A 811, 141054 (2021)
W. Lu, X. Luo, Y. Yang, B. Huang, P. Li, Intermetallics 129, 107036 (2021)
https://www.thyssenkrupp-materials.co.uk/stainless-steel-304-14301.html (2021)
https://www.sandmeyersteel.com/A800-A800H-A800AT.html (2021)
T. Bhattacharjee, R. Zheng, Y. Chong, S. Sheikh, S. Guo, I.T. Clark, T. Okawa, I.S. Wani, P.P. Bhattacharjee, A. Shibata, N. Tsuji, Mater. Chem. Phys. 210, 207 (2018)
S. Haas, A.M. Manzoni, F. Krieg, U. Glatzel, Entropy 21, 169 (2019)
A. Manzoni, S. Haas, H. Daoud, U. Glatzel, C. Förster, N. Wanderka, Entropy 20, 646 (2018)
B.X. Cao, H.J. Kong, Z.Y. Ding, S.W. Wu, J.H. Luan, Z.B. Jiao, J. Lu, C.T. Liu, T. Yang, Scr. Mater. 199, 113826 (2021)
X.W. Liu, N. Gao, J. Zheng, Y. Wu, Y.Y. Zhao, Q. Chen, W. Zhou, S.Z. Pu, W.M. Jiang, Z.T. Fan, J. Mater. Sci. Technol. 72, 29 (2021)
Acknowledgments
This work was supported by Grant-in-Aids for Scientific Research on Innovative Areas on High Entropy Alloys through Grant Nos. JP18H05450 and JP18H05451, and in part by JSPS KAKENHI Grant Nos. JP20K21084, JP21H01651, JP19H00824, JP19K22053, and by the Elements Strategy Initiative for Structural Materials (ESISM) from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan. Financial support by the Deutsche Forschungsgemeinschaft (DFG) through the Priority Program SPP 2006 “Compositionally Complex Alloys – High Entropy Alloys (CCA-HEA),” as well as GL181/50 and 56 and MA7004/1 is highly acknowledged.
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Inui, H., Kishida, K., Li, L. et al. Uniaxial mechanical properties of face-centered cubic single- and multiphase high-entropy alloys. MRS Bulletin 47, 168–174 (2022). https://doi.org/10.1557/s43577-022-00280-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1557/s43577-022-00280-y