Introduction

There has been considerable effort to develop transparent oxide semiconductors for use in large area electronics such as displays or solar cell electrodes.1,2,3,4,5 This field has recently been extended to include back-end-of-line (BEOL) semiconductor devices.6,7,8,9 A typical application of these electronic rather than optical devices is that they act as switches with a particularly low off-state leakage current for charge storage devices (down to 10−20 A).7 So far, the successful oxides were mainly n-type, such as ZnO, Ga2O3, or amorphous In-Ga-ZnO4, whereas p-type materials have been much less successful.10,11

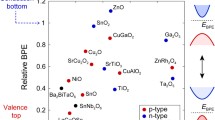
The ability to dope any semiconductor, not just an oxide, can be understood using the concept of doping limits.12,13,14,15,16 This involves plotting the range of Fermi energies that can be accessed by doping in a given semiconductor on an energy scale referred to the vacuum level Evac as in Figure 1. It is found that the Fermi energy EF of a semiconductor can be moved above the conduction band edge Ec if Ec lies deep enough below Evac. On the other hand, the semiconductor can be doped p-type and Ef can enter its valence band if its valence band edge Ev lies high enough compared to Evac. These conditions for n- or p-type doping will occur for each band edge energy separately; note that there is no overall condition on the band gap size itself. Thus, overall, the band edges should lie within an energy range of ~ 3.7 eV to  ~ 6.5 eV below Evac in Figure 1 for doping to occur.

Figure 1
figure 1

Band alignments of possible p-type and n-type oxides. The vacuum level is set to zero. Black lines are the charge neutrality levels (CNLs) of each compound. Band alignment of HfO2 is shown as a possible dielectric and MoO3 is shown as an electrode of large work function.

Full size image

P-type doping

The main problem for oxides generally is on the p-type side. Oxygen is very electronegative so that oxide energy levels tend to be very deep below Ev. One problem is that the oxide valence band states often have a high effective mass, so that most substitutional acceptors in oxides such as ZnO or Ga2O3 are deep defects and difficult to ionize.

An early solution to this problem was to use defossalite structure oxides such as CuAlO2, or similar oxides,17,18,19,20 rather than the simpler Cu2O structure.21 In Cu2O, hybridization of Cu 3d orbitals with the O 2p orbitals can form a relatively low effective mass (m*) state at the valence band maximum Ec.17,18 Introducing Al into the Cu2O lattice allows the O–Cu–O links not to share a common vertex. This widens the band gap and makes CuAlO2 transparent. Nevertheless, the mobility of CuAlO2 is rather low and the layered defossalite structure is inconvenient for making an amorphous phase. On the other hand, an important but less recognized function of Al3+ here is to widen the stability range of CuAlO2 by ~ 2 eV compared to the limited stability range of the Cu1+ ion in Cu2O itself, as seen in stability diagram given by Scanlon et al.22

A second solution is to use metal oxides such as SnO, which have metal lone pair s states. Here SnO acts as a p-type semiconductor, and its Sn 5s states hybridize with the oxygen 2p states to give a mixed Sn s/O 2p valence band maximum with a low m* value.23,24 The Sn 5s states play a similar role to the Cu 3d states in Cu2O. However, SnO is poor semiconductor with a low field-effect mobility of ~ 2.4 cm2/V s; it has a small, indirect gap of 0.7 eV despite a near 3 eV direct gap,25 and its Sn2+ state has only a modest stability range between Sn metal and tetravalent Sn4+ states.

Semiconductors differ from insulators in that they can be doped. For doping to occur, the dopant must be (a) soluble in the host, (b) have an ionizable defect level, and (c) it should not spontaneously create native defects that can compensate the resulting free carriers.12,13,14,15,16

The critical criterion here is (c) that any free carriers should not immediately be compensated by native defects of the opposite sign. Thus, if donors create electrons that raise EF toward the conduction band edge, then no deep donors should be created exothermically that can compensate these carriers. Thus, the formation energy Eform of any such defects must exceed 0 eV, so that they do not inhibit doping. (What the idea of doping limits does is to separate a problem of considering each dopant in each host to being a problem just of the host.)

Recently, high-throughput computational searches26,27,28,29,30,31 have been employed to test a wider range of p-type transparent conductors, given the importance of this problem. The searches have identified some low m* systems, and their total energies were compared to a “convex hull” (a hull-shaped curve of relative stabilities of binary oxides30) of overall stabilities. We focus on the ability of the host compound not to create compensating defects if doping shifts EF toward either band edge, rather than the oxide’s effective hole mass or optical band gap. We stress instead its stability range over which it does not easily form compensating native defects.

A unifying feature of these newly identified oxides is that they possess one cation which has retained an s-like lone pair state, such as the Sn2+ site in SnTa2O6, the Bi3+ site in di-perovskites such as Ba2BiTaO6,32,33 and the Bi3+ site in the photocatalyst BiVO4.34,35,36,37,38 The low-hole m* state is caused by cation s lone pairs. The low m* hole state is created by the hybridization of the cation lone pair state with the O 2p states, and one of these states forms the highest valence band. However, being essentially a perovskite, the valence band as a whole is rich in O 2p states, which causes it to have low-energy n-type defects which act against the p-type character of the low mh* band edge state.

The band structures of some of these representative oxides were calculated by the VASP pseudopotential code using the Heyd–Scuseria–Ernzerhof (HSE) hybrid functional. The electron affinity (EA) of the conduction band minimum (Ec) and the ionization potential (IP) of the valence band maximum (Ev) were also calculated for nonpolar oxide surfaces using supercells of solid slabs separated by 20 Å of vacuum.

SnTa2O6

The crystal structure of SnTa2O6 is shown in Figure 2a. The SnTa2O6 structure is related to the perovskite unit in that the Ta sites have six oxygen neighbors, while the Sn atoms have eight oxygen neighbors. These Sn bonds are arranged as four short bonds and four longer bonds that include the Sn s-like lone pair, in a Sn2+ site geometry reminiscent of SnO itself. Figure 2b shows the phase stability diagram for SnTa2O6, which is found using free energies calculated by the HSE functional. This diagram shows an unusually wide stability range, much wider than that for the related Sn2Ta2O7 phase.30 It is also much wider than that for the related SnNb2O6 phase seen in Figure 2c, for which there are experimental data.39,40

Figure 2
figure 2

(a) The crystal structure of SnTa2O6. (b) stability phase diagram of SnTa2O6 based on calculated Heyd–Scuseria–Ernzerhof (HSE) total energies. (c) Stability diagram of SnNb2O6 for comparison. Note the much narrower width than for SnTa2O6. The green area shows the thermodynamically stable region. (d) The calculated band structures, showing the notably dispersive upper valence band and (e) partial density of states (PDOS). (f) Calculated defect formation energy. The chemical potential window of oxygen ranges from − 3.66 eV to − 1 eV, determined from the phase diagram. The dopable region where the defect formation energy is positive is shaded red. CNL, charge neutrality level.

Full size image

The band structure of SnTa2O6 in Figure 2d shows a notably dispersive Sn s-like feature in its upper valence band. The main O 2p-like valence band lies  ~ 2 eV below the Ev in the partial density of states (PDOS) as seen in Figure 2e, so that the highest VB retains this low m* value. The upper dispersive band is formed by the hybridization of Sn s-like states and O 2p states, as in SnO itself. A significant advantage of crystalline SnTa2O6 compared to pure SnO monoxide is that the small 0.7 eV indirect band gap of SnO is now opened up to 3.3 eV.

The doping response of the various oxides can be determined by the defect formation energy of the host. This energy ∆Hq is given as a function of EF by

$$ \Delta H_{q} (\mu _{\alpha } ,E_{F} ){\text{ }} = {\text{ }}E_{q} {-}E_{H} + q(E_{v} + \Delta E_{F} ){\text{ }} + \sum _{\alpha } n_{\alpha } \mu _{\alpha } + \Delta V $$
(1)

where μα is the chemical potential of element α, nα is the number of atoms of element α, with charge q, ΔEF is the Fermi energy with respect to valence band maximum (VBM) and ∆V is an electrostatic correction term for the supercell size. The chemical potentials for SnTa2O6 obey μSn + 2μTa + 6μO = H(SnTa2O6) with μα < 0, as given in the stability phase diagram.30

The formation energy of the most stable native donor and acceptor defects of SnTa2O6 is shown in Figure 2d for both O-rich and metal-rich (O-poor) conditions, μO ~ − 1 eV and − 3.66 eV values do not correspond to the simple μO = 0 and the metal/metal oxide equilibrium due to extra limits from the ternary phase diagram. The slope of the lines in defect diagram Figure 2d gives the stable defect charge state at that EF value. We see that the lowest cost native defects are the VSn, VO vacancies and the SnTa antisites, which all have a positive formation energy near Ev, as required for p-type behavior and no compensating defect. However, while the defects themselves have suitable ionization energies near EV, the relatively low Eform of these sites means that compensating defects can form relatively easily and need experimental testing.

We note the EF values for which Eform is positive lie toward Ev. This means that for hole doping the compensating defects have a positive formation energy and the defects are uncompensated. This is the critical observation, it is not sufficient to have a low-hole m*, the hole must also be uncompensated.

A simpler way to compare individual cases of doping is to calculate the charge neutrality level (CNL) or the branch point energy (BPE) of each semiconductor.41,42 The CNL is the energy where the Greens function of the bulk band structure averaged over the Brillioun zone equals zero:

$$ G(E) = \mathop \int \limits_{BZ} \frac{{N(E^{\prime})d^{\prime}E}}{{E - {E^{\prime}}}}. $$
(2)

This expresses that the CNL is the energy where the deep gap states at interfaces change character from being valence band-like to conduction band-like, as the electron energy moves across the gap.41,42,43,44,45,46 The doping limits can be visualized by plotting the band energies against the vacuum level as in Figure 1. The summation in Equation (2) means that if there are a large number of valence band states, such as oxygen 2p states in ABO3, then this repels the CNL upwards and favors n-type conduction. In contrast, many conduction band states (due to empty cation states) will repel the CNL downward and favor p-type conduction.45,46

These effects on the energy ranges in Equation 2 are important. The CNL first arose in the treatment of Schottky barrier heights, where all valence bands and many of the conduction bands were included in integral in Equation (2).41,42,43 Recently, a narrower range of bands was used for tetrahedral semiconductors, such as in Schleife.47 However, for solids with more varied bonding types than just tetrahedral, the integral should cover all valence and conduction states relevant to the gap states, but excluding the higher lying conduction bands such as the Sr states of SrTiO3. The original definition of CNL in Equation 2 was previously used to predict the band offset HfO2 with Si.43

The CNL of SnTa2O6 is found by counting all the valence bands down to − 8 eV, not just those close to the VBM. This gives a CNL close to midgap, rather than near the VBM itself, which would correspond to a true p-type semiconductor with a wide, low m* valence band. Thus, a compound such as SnTa2O6 could be called pseudo p-type; it has the low m* VBM character and p-type behavior, which originates from the cation lone pair, but it also has some n-type character of a ABO3 perovskite, which arises from the general O-rich character of the valence band.

This also favors a low CNL lying near Ev. However, the relatively low value of Eform may lead to complications with multiple defects. The key point is that the stability range of SnTa2O6 is large, so that EF can vary over a wide energy range before compensating native defects constrain the doping. This is why when compensating defects rather than m* values are the dominant criteria in doping, it is the stability range of the oxide that matters, not the local band extrema.

Other perovskites

The second example is the di-perovskite Ba2BiTaO6 whose crystal structure is shown in Figure 3a.32 This compound has a low m* band edge for its highest valence band, (Figure 3b). This originates from the R3c distortion of the originally cubic di-perovskite lattice causing the hybridization of the Bi 6s lone pair/O 2p states. Its partial density of states is shown in Figure 3c. It also has a relatively large band gap. But the key issue here is the high oxygen stoichiometry of the compound. Its oxygen-rich quality as a perovskite suggests that its CNL should lie in the upper gap and this oxide should be n-type, not p-type.29 However, its Bi s-like lone pair tries to move the CNL downward. Overall its CNL remains well above midgap, as shown in Figure 3b, suggesting that a n-type behavior wins. Figure 3d shows the defect formation energy diagram. Although the allowed red-shaded region reaches down to toward EV, it is very narrow, and the formation energies themselves are low. This suggests that any p-type doping will be heavily compensated.

Figure 3
figure 3

(a) The atomic model of R3 phase Ba2BiTaO6. (b) The calculated band structures and (c) partial density of states (PDOS). (d) The calculated defect formation energy in the O-rich limit. The dopable region of positive defect formation energy is shown as red shading. HSE, Heyd–Scuseria–Ernzerhof; CNL, charge neutrality level.

Full size image

Finally, there is BiVO4 in Figure 4. The crystal structure of BiVO4 is given by Sivula.34 Its band structure is shown in Figure 4a, with a reasonably low effective mass valence band top. This compound has a smaller oxygen content than the true perovskites and it also has a Bi s lone pair, two factors, which could lead to the CNL lying below midgap. However, the CNL lies above midgap, as can be seen in Figure 4b. Its defect formation energies have previously been calculated38 and can be summarized as shown in Figure 4b. This shows a narrow red-shaded area that reaches toward EV. However, this crystal shows a complex arrangement of low defect formation energies, and it is classed as n-type and as a photocatalyst.34

Figure 4
figure 4

(a) The calculated band structures and (b) partial density of states (PDOS) of monoclinic BiVO4. HSE, Heyd–Scuseria–Ernzerhof; CNL, charge neutrality level.

Full size image

A key property of the n-type oxides such as IGZO is that their s-like conduction band minimum states are unaffected by disorder. A major strength of SnTa2O6 is that the s-like valence band maximum could play the same role for SnTa2O6 in the p-type oxides. The amorphous phases were simulated by ab initio molecular dynamics by subjecting a 108 atom cell of SnTa2O6 to a density functional theory annealing at 2200°K for 6 ps and quenching it for 12 ps. The electronic structure of the resulting structure of Figure 5 was then calculated by the HSE functional. A similar structure for Sn2Ta2O7 was also found (not shown here). This has a slightly lower mobility for polycrystalline samples experimentally. Here, the amorphous phase shows a smaller gap than the crystalline phase, but otherwise it has a very similar density of valence states. Thus, its valence states are unaffected by disorder. SnTa2O6 would, therefore, be the first amorphous p-type semiconductor that is unaffected by disorder or having less desirable features such as being layered similar to the oxy-chalcogenides or containing a refractory metal (ZnIr2O4).20

Figure 5
figure 5

(a) SnTa2O6 amorphous network after high-temperature annealing, quenching, and final relaxation. (b) The corresponding partial density of states (PDOS). HSE, Heyd–Scuseria–Ernzerhof.

Full size image

Device integration

Figure 1 compares the band alignments with those of other p- and n-type oxides.48 We see that SnTa2O6 has an ionization potential compatible with limited p-type dopability.12,13,14,15,16,46 Figure 1 also shows that HfO2 has large enough band offsets with SnTa2O6 to be suitable dielectric to integrate with this oxide. Finally, Figure 6 shows that the heat of formation per O atom of SnTa2O6 is similar to that of SnO2 or IGZO for device integration. Figure 1 also shows that Ev of these oxides lies around 6.5 eV. Contacts to such oxides would require a conducting metal oxide such as MoO3 to inject holes, as used in organic light-emitting diodes (OLEDs). MoO3 is one of the few truly high work function materials with ϕ = 6.5 eV49 (compared to ϕ = 5.65 eV for Pt).

Figure 6
figure 6

Heat of formation per O atom of some oxides versus their metal work function, including Sn and Bi. Those with Eform lower than − 4.85 eV are stable in contact with Si.

Full size image

It should be noted that the band edge energies can also be shown referring to a charge neutrality level zero, instead of the vacuum level.16,30,46 Again, n-type oxides should have conduction band edges lying not too far above the CNL, and p-type oxides should have valence band edges lying not too far below the CNL. Generally, the problem is that oxide valence bands lie too far below the CNL.26,30

Doping limits also constrain some applications of Ga2O3. In this case, the valence band edge of Ga2O3 is just too deep to allow p-type doping (Figure 1), but p-type doping can form blocking undoped layers which are of use in device design.50

Summary

In conclusion, a general search for alternative p-type oxide conductors, including high-throughput calculations has suggested various oxides, including some that possess cation s-like lone pair states. This was of interest for the back-end-of-line devices for the semiconductor industry. The defect energies of these alternative oxides were calculated in detail. The example SnTa2O6 was found to be of interest, but other oxides based more closely on the perovskite structure were found to be closer to n-type than p-type. When choosing transparent conducting oxides, band gap and band edge effective masses are key factors. However, for use in electronic devices, the most important factors are the possible compensation of doping by compensating native defects. In this case, the stability range matters because this sets the amount of Fermi energy shift that is allowed before the formation energy of compensating native defects constrains the doping limits.