Abstract
Some of the stable isotopes of silicon and carbon have zero nuclear spin, whereas many of the other elements that constitute semiconductors consist entirely of stable isotopes that have nuclear spins. Silicon and diamond crystals composed of nuclear-spin-free stable isotopes (28Si, 30Si, or 12C) are considered to be ideal host matrixes to place spin quantum bits (qubits) for quantum-computing and -sensing applications, because their coherent properties are not disrupted thanks to the absence of host nuclear spins. The present paper describes the state-of-the-art and future perspective of silicon and diamond isotope engineering for development of quantum information-processing devices.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Quantum computing and sensing are emerging concepts that can surpass the theoretical achievable limit of current classical computing and sensing technologies. The realization of quantum computers and sensors in industrially compatible solid-state platforms such as silicon and diamond will allow their integration with state-of-the-art classical devices such as silicon-integrated circuits, compound semiconductor lasers and photodiodes, metallic magnetic mediums, and microelec-tromechanical systems. This paper describes the present status and future of silicon quantum-computing and diamond quantum-sensing research, from the point of view of materials scientists who have been developing the isotope engineering of silicon and diamond. Although isotope engineering has been employed over the past two decades to understand the basic properties of semiconductors,[1,2] it was B. E. Kane who foresaw its importance in quantum computation applications in 1998.[3] Here, the use of the single 31P nuclear spin in each phosphorus donor placed in silicon as a quantum bit (qubit) was introduced. The importance of eliminating background 29Si nuclear spins (4.7% isotopic abundance in naturally available silicon) was suggested because 29Si nuclear spins could act as a source of magnetic noise, disturbing the 31P nuclear spin quantum information.[3] Such elimination of background host nuclear spins is not possible with widely studied III-Vsemiconduc-tor quantum structures. Other researchers, including one of the present authors, have suggested that 29Si nuclear spins could be employed as qubits if their positions can be controlled at the atomic level in a 28Si host.[4–6] At around the same time, the nitrogen-vacancy (NV) center in diamond was identified as a single qubit that could be operational at room temperature.[7–9] This discovery was followed immediately by studies to use NV qubits for quantum computing[10] and sensing (metrology).[11–14] Similar to the case of silicon, the enrichment of diamond by the nuclear-spin-free 12C stable isotope preserves the quantum information in the NV centers.[15] This review provides a perspective on the use of isotope engineering for quantum computation and sensing using silicon and diamond. For general aspects of the challenges associated with materials science, readers are encouraged refer to October’s 2013 issue of the MRS Bulletin featuring Materials Issues for Quantum Computation.
Silicon quantum computation
Silicon-based quantum computer proposals
A review on the developments of silicon-based quantum computers was published recently.[16] This subsection provides a brief summary on the studies on Si-based quantum computers that require isotope engineering. Figure 1 shows two examples of silicon quantum computer proposals that use isotope engineering. The report by Kane Fig. 1(a)- proposed to use the nuclear spins of phosphorus donors embedded in isotopically enriched 28Si as qubits.[3] The phosphorus donors form a one-dimensional array with a separation of ~20 nm. The quantum information stored and processed by each 31P nuclear spin (I = 1/2) is read out by the tunneling current induced by the electron bound to 31P as it transports to the adjacent phosphorus donor. At the beginning of the calculation, each nuclear spin is initialized, so that they have identical nuclear spin states, ms = 1/2 or —1/2. This can be achieved by reading out each nuclear spin state using the tunneling current and performing nuclear magnetic resonance (NMR) on the 31P qubits to align them into the correct state when their initial state is incorrect. No action is taken if the 31P qubit is already in the correct state. NMR is also used for the quantum logic operation of the 31P qubits. Qubit selectivity is achieved by applying an electronic bias to a gate that is placed immediately above each qubit (A-gate). This causes the 31P to be either in or out of resonance with the frequency employed during the NMR. The two-qubit interactions are switched on and off by electric gates placed between the neighboring qubits (J-gates). The electrons bound to the phosphorus donors mediate the 31P–31P nuclear spin interactions between the adjacent qubits. The nuclear spin state for each 31P qubit is read out at the end of the calculation by detecting the single-electron tunneling current using a single-electron transistor (SET). Kane’s vision has triggered many proposals that use the electron spins in donors imbedded in silicon as qubits.[17–19]
The second class of silicon-based quantum computation studies uses 29Si nuclear spins as qubits.[4-6] Fig. 1(b) shows the one-dimensional array of the 29Si nuclear spins formed on an isoto-pically enriched nuclear-spin-free 28Si substrate.[6] Here, the dipolar coupling between adjacent 29Si nuclear spins is used for two-qubit operations and the qubit selectivity is ensured by the large magnetic field gradient induced by a small magnet placed near the array. Readout of each qubit is achieved by shuttling the state to the end of the chain by a sequence of swap operations between the adjacent qubits. The 29Si nuclear spin state at the end of the chain was read out from the electron in the phosphorus atom that is placed next to the 29Si atom.
The third class of silicon-based quantum computing studies uses the electrons in quantum dots as qubits.[20–22] A single-electron spin is confined in each quantum dot and is employed as a qubit. The qubit state is described by either the spin state of electrons in a dot or a single electron within a pair of two quantum dots.[16]
Isotopically engineered silicon for quantum computation
Naturally available silicon (natSi) is composed of 92.2% 28Si, 4.7% 29Si, and 3.1% 30Si. These stable isotopes can be separated by centrifuging SiF4 gas.[23,24] The first isotopically engineered silicon was produced in 1958 to characterize the electron spin resonance (ESR) of donors in silicon.[25] Since then, no results on this topic were reported until a strong interest emerged in the mid-1990s, when isotopically enriched 28Si single crystals were employed as the standard to define the Avogadro constant.[26–28] The goal was to produce silicon crystals with a well-defined number of Si atoms per unit volume and to establish the definition of the kilogram by the mass of a given number of silicon atoms. Silicon was chosen because there had been extensive industrial efforts in Si electronics. Silicon has unsurpassed crystalline quality and chemical purity in comparison with other crystalline materials. Isotope enrichment with the stable isotopes is needed because the Si-Si bond length depends on the combination of isotopes.[29,30] Fluctuations in the bond lengths for different isotopes must be removed to obtain a well-defined number of Si atoms per unit volume. The floating-zone growth performed at the Leibniz Institute for Crystal Growth (IKZ) in Berlin resulted in a 5-kg 28Si single crystal of 99.99% isotopically enriched silicon with <1015 cm—3 background carbon content, <1013 cm—3 electrically active impurities such as boron and phosphorus, and was free of dislocations.[31,32] The silicon crystals fabricated for the Avogadro measurement were shaped into precise spheres and the sawn-off pieces generated during the shaping process were used to perform basic characterization on the crystal. Some pieces were also used in some of the silicon quantum information research described below. Herein, these samples will be referred to as the “Avogadro samples”. They had the highest isotopic and chemical purity and the best crystalline quality among all of the isotopically enriched silicon crystals ever produced.
The second group of isotopically enriched, bulk Si crystals was also grown at the IKZ and will be referred to as the “IKZ crystals”. IKZ established various Czochralski[23,33] and floating-zone[34] growth techniques to maintain the isotopic composition of the starting charge. Here various isotopes (28Si, 29Si, and 30Si) of different enrichments were employed as starting charges as described in Ref. 23. They also developed a method to dope the crystal with the desired group V donors during its growth. A variety of dislocation-free, isotopically enriched 28Si, 29Si, and 30Si crystals were grown at IKZ to fulfill orders placed by the Simon Fraser University, Canada,[35,36] the Keio University, Japan,[23,37] and the University of California (UC), Berkeley, CA, USA.[34,38]
The third group of isotopically enriched, bulk Si crystals was grown at Keio University, Japan and will be referred to as the “Keio crystals”. The floating-zone growth machine at Keio was designed to grow small crystals (<7 mm diameter) of high crystalline quality and chemical purity.[39] The machine is suited to grow isotopically mixed crystals with arbitrary compositions of 28Si, 29Si, and 30Si. Isotopically mixed bulk Si crystals have been produced exclusively at Keio University.[40]
The isotopically enriched 28Si chemical vapor deposition (CVD) films were grown from isotopically enriched silane (28SiH4) gas by the Isonics Corporation, USA, from 1998 to 2005. Because centrifuge isotope separation was performed using SiF4 as described elsewhere 23, the resulting isotopically enriched 28SiF4 was transformed to 28SiH4 (silane) by an electronic materials company named Voltaix. The quality of the Isonics epilayers, especially the residual impurity concentration, fluctuated significantly between the different epilayers because the company outsourced the CVD growth to other companies. Therefore, obtaining quantum-information-research-grade 28Si CVD wafers, including 28Si on insulator (SOI) wafers,[41] required in-depth discussions with Isonics to establish appropriate fabrication procedures. High quality, Isonics 28Si ep-wafers employed in single-qubit experiments (the section “Single-spin qubits in silicon”) have been grown at Lawrence Semiconductor Research Laboratory, Inc. The Isonics 28Si CVD epi-layers have the isotopic compositions 28Si (~99.924%), 29Si (~0.073%), and 30Si (~0.003%).
Isotopically enriched, strained 28Si thin layers were grown by solid-source molecular beam epitaxy (MBE) at the Technical University of Munich (TUM), Germany[42] and by CVD at Princeton University, USA.[43] Some electron double-quantum dots were fabricated using the strained silicon.[44] Other isotopically controlled silicon low-dimensional structures, typically grown by MBE,[45–48] have been employed, predominantly for diffusion[49–52] and amorphization[53] studies.
Proof-of-concept experiments with spin ensembles in isotopically engineered silicon
A qubit must be made of a single quantum. However, one can prepare an ensemble of identical qubits, initialize them in the same quantum states, manipulate them together quantum mechanically (perform quantum calculations), and read them out all at once to obtain the results expected for single quantum bit operation. To demonstrate this, phosphorus donors in silicon were used. Figure 2(a) shows two phosphorus donors placed in natSi. Each phosphorus atom has an electron spin for the bound electron and the 31P nuclear spin in the nucleus; it has two qubits. This was used to determine whether the two phosphorus donors in Fig. 2(a) are quantum mechanically identical. They are not because of the coexistence of 28Si, 29Si, and 30Si stable isotopes and their random distribution in natSi, and the silicon isotope configuration around each phosphorus donor differed from those of others. Additionally, the mass difference between the stable isotopes changes the bond lengths (the local lattice strain), leading to perturbation of the hyperfine interactions between the electron spin and the 31P nuclear spin in each phosphorus atom. This could lead to a shift in the NMR frequencies of the 31P between different donors, making each phosphorus atom distinguishable and the ensemble of phosphorus donors would not be able to be manipulated all together. Moreover, there was a random distribution of 29Si that changes the local magnetic field near each phosphorus donor. This leads to even larger changes in the 31P NMR and electron paramagnetic resonance (EPR) frequencies than those caused by the mass fluctuations. Therefore, the silicon matrix must be composed of a single type of stable isotopes with no nuclear spins, either 28Si or 30 Si. Fi gure 2(b) shows two phosphorus donors placed in an isotopically enriched, 28Si single crystal. The two phosphorus donors could be considered identical if the separation between them was long enough to have small interactions. This changes their EPR frequencies, where their quantum states could be initialized to be the same such that the electron and nuclear spins were set in the up (or down) state in every donor. By using an ensemble of identical phosphorus donors, one can start from the same quantum states, perform the same quantum calculation using every donor in parallel and read them all out together to obtain the result from the quantum calculation that is expected for a single phosphorus donor qubit. Therefore, isotope enrichment is a powerful and necessary tool to allow for proof-of-concept quantum computer experiments with an ensemble of identical qubits in silicon to be carried out.
One important issue yet to be mentioned thus far is the coherence time (T2) of the qubits. If the coherence time (the quantum information storage time) is too short, particularly shorter than the total time required for completing the desired quantum computation routine, the quantum computer will lose information in the middle of the calculation. Because a high crystalline quality and low concentration of residual impurities can be achieved with silicon, the major decoherence source of the electron and nuclear spins in silicon has been assumed to be caused by magnetic field fluctuations arising from the flip-flops of the 29Si nuclear spins in the matrix.[54] The mass variations in the isotopes also change the local lattice strain to vary the spin manipulation frequencies. However, they are static and have little effect on the coherence time. Therefore, the first step was to understand the decoherence mechanisms of the electron and nuclear spins in silicon as a function of the host 29Si contents. An example of this is a series of pulsed EPR measurements performed on an ensemble of phosphorus donors using the Keio bulk crystals in which the 29Si fraction was deliberately changed.[40,55–57] The spin coherence time of the phosphorus-bound electron and its interaction with the precessing 29Si nuclear spins in the neighboring atoms [electron spin echo envelope modulation (ESEEM)] was determined experimentally and compared with the theory[58–60] to achieve a solid understanding of the decoherence mechanisms. The most important issue associated with quantum computation is how far the phosphorus coherence time can be extended by eliminating 29Si from the matrix. The first experiment of this type was performed by Gordon and Bowers in 1958 using an isotopically enriched, Si bulk single crystal. However, no significant improvement in the coherence was obtained because it was limited by the interactions between the donor electrons, caused by the relatively high concentration of phosphorus.[25] More recently, in 2003, an extended coherence time of the electron spins bound to the phosphorus donors in isotopically enriched, Isonics 28Si epilayers was reported by the Princeton University group.[61] The coherence was improved even further in 2011 by the international collaboration headed by the same group using the IKZ 28Si bulk crystals.[62] The study achieved electron coherence times exceeding seconds. This time is long enough to perform a quantum error correction protocol that, in principle, can store information forever. The dominant decoherence mechanisms were recorded as a function of temperature.[62] Because the 31P nuclear spins couple to the electron spins bound to phosphorus, the nuclear spin coherence can be affected by the presence of 29Si through hyperfine interactions with the electron spins. Therefore, the research team headed by the Simon Fraser University used the isotopically enriched, 28Si Avogadro crystal to probe the coherence time of the 31P nuclear spins in neutral[63] and ionized[64] donors. Thanks to the removal of the background 29Si nuclear spins, coherence time of the 31P nuclear spin in its neutral state at the cryogenic temperature exceeded 180 s, [63] while that of ionized donors at room and cryogenic temperatures exceeded 39 min and 3 h, respective-ly.[64] The important finding here was that the coherence times of not only the electron but also the nuclear spins of the phosphorus donors in silicon were extended by eliminating the 29Si nuclear spins through isotope engineering. These coherence times are more than sufficient for practical application in quantum computing.
Following the success of phosphorus in isotopically enriched 28Si, the group headed by the Simon Fraser University and University College London investigated other shallow donors, focusing on bismuth in isotopically enriched 28Si.[65,66] The coherence times of the bismuth electron spins were as long as those of the phosphorus atoms.[65] The existence of the optimal magnetic field (atomic clock transition), at which the electron decoherence was suppressed by its insensitivity to the external magnetic field perturbation was demonstrated.[66] The Keio University group investigated the hyperfine clock transition of bismuth using the magnetic field at which the resonant frequency was insensitive to fluctuations in the hyperfine constant in isotopically enriched 28Si[67] using the spin-dependent-recombination EPR technique developed especially for this purpose.[68]
The decoherence and decoupling mechanisms for the 29Si nuclear spins as qubits were investigated with bulk natSi and isotopically enriched IKZ 29Si at Stanford University, USA and Keio University, Japan.[69] The decoupling pulse sequences were used to extend the 29Si coherence time up to 20 s and beyond at room temperature.[69]
Confirmation of long-enough coherence times in various electron and nuclear spins in silicon encouraged researchers to develop qubit initialization schemes. Although initialization of the electron spins can be achieved by reducing the sample temperature and increasing the externally applied magnetic field to make the thermal energy much smaller than the Zeeman split electronic levels,[38,70] initialization ofthe nuclear spins is not straightforward. This is because of the extremely small gyromagnetic ratios of the nuclear spins that do not allow a large-enough Zeeman energy separation with respect to the thermal energy, even with an externally applied magnetic field~10 Tat a temperature of ~1 K. Therefore, it was necessary to develop a method to polarize the nuclear spins in silicon using reasonable experimental conditions. Again, isotope engineering was proven useful for such purposes. The international collaboration led by Simon Fraser University developed an all-optical NMR of 31P using the Avogadro bulk 28Si samples.[71] When the inhomogeneous broadening inherent in natural Si was eliminated using enriched 28Si, the photoluminescence excitation (PLE) spectrum of the ensemble of phosphorus-bound excitons revealed a well-resolved hyperfine splitting resulting from the 31P nuclear spin (Fig. 3).[71–73] Furthermore, introducing one more laser irradiation at one of the phosphorus PLE peak frequencies, corresponding to the 31P nuclear spin up or down, led to extremely fast (~0.1 s) electron and nuclear polarizations of 90 and 76%, respectively.[74] This fast initialization and nuclear spin readout technique was employed to demonstrate the long P nuclear coherence times reported in Refs. 63, 64. Using isotopically enriched 28Si device structures, it was demonstrated that all-electrical 3 P nuclear polarization was possible."75" Inhomogeneous broadening of the bismuth-bound exciton photoluminescence peaks were also dominated by variations in the masses of the silicon isotopes.[76]28Si enrichment allowed for the 209Bi nuclear spin peaks to be clearly observed.[77]
Comparison of the PLE spectra for an ensemble of phosphorus-bound excitons in natSi and isotopically enriched 28Si. The spectrum of natSi is significantly broader because of the random distribution of the three stable isotopes, while that of 28Si has sharp doublet features, corresponding to the hyperfine splittings due to the 31P nuclear spins.[71]
Achieving a large polarization for the 29Si nuclear spins in silicon was challenging because, unlike donor nuclear spins, there is no electron spin that couples strongly to the 29Si at the substitutional lattice sites. One approach taken by the international collaboration led by Keio University was to enrich the phosphorus doped single silicon crystal with 29Si to reduce the average distance between the phosphorus electrons and the 29Si nuclear spins.[78–81] In this phenomenon, referred to as dynamical nuclear polarization, selective excitation of the symmetry prohibited ESR transitions in the phosphorus donor coupling to the nearby 29Si, led to preferential relaxation to a certain 29Si nuclear spin state (solid effect). This nuclear spin polarization around the phosphorus atom diffused through the crystal via nuclear spin diffusion (29Si–29Si flip-flops). However, this process is slow (>1 h) and the highest 29Si polarization achieved was only ~4%.[81] An efficient method would be to prepare electron spins that couple more directly to the 29Si nuclear spins, similar to the way that an electron bound to a phosphorus atom couples strongly to the 31P nuclear spin. To achieve this condition, the group led by Keio University employed vacancy-oxygen complexes in silicon that had 29Si nearest neighbors.[82–84] This defect is unique as it can be excited into the spin triplet state to achieve large electron spin polarization that can be transferred to the nearby 29Si nuclear spins. This allowed a very large, most likely >90%, polarization of the 29Si nuclear spins.[83]
Taking the advantages of the long coherence time and the absence of inhomogeneous broadening in the phosphorus ESR and electron nuclear double resonance (ENDOR) lines for the phosphorus donors in isotopically enriched IKZ bulk 28Si, the international collaboration led by John Morton (formally at University of Oxford and presently at University College London) succeeded in a series of proof-of-concept two-qubit experiments. Here, one qubit was the electron spin of the phosphorus atom and the other was the 31P nuclear spin. By sharpening the electron ESR and 31P ENDOR transitions in Si, the quantum manipulation fidelity of the ensemble of phosphorus donor states was improved significantly. Additionally, eliminating the 29Si nuclear spins from the matrix provided enough coherence time to complete the operation and readout procedures, such as the coherent transfer of the quantum states,[38] and create and detect the two-qubit entanglement[70] between the phosphorus electron and 31P nuclear spins. The same team also succeeded in employing an ensemble of phosphorus electron spins to store and retrieve multiple microwave pulses, demonstrating the basic operation of the so-called quantum holographic memory[85] and the geometric phase gate operation of the phosphorus electron spins for fault-tolerant quantum computation.[86] They also performed fundamental experiments testing the nature of the quantum superposition states.[87] In parallel, the Keio-UCL collaboration demonstrated coherent transfer between the electron spin states and 29Si nuclear spin states for two-qubit operations.[83] These accomplishments, obtained with ensembles of donor electron spins, donor nuclear spins, and 29Si nuclear spins in silicon formed the foundation of single-bit quantum information processing (QIP) in silicon, which will be discussed in the next section.
The properties of ensembles containing boron accepters were studied using IKZ bulk 28Si single crystals. It is well known that the ESR spectra of acceptors are broadened by the existence of the random strains that lift the degeneracy of the light- and heavy-hole bands from one acceptor to another by different amounts. However, the main source of random strain has not been identified. The group led by Keio University and TUM identified that the source of strain was the random distribution of the three stable isotopes in natSi. They observed significant narrowing of the boron ESR lines in 28Si.[88,89] However, the coherence time of the holes bound to the boron acceptors were limited by the short-hole relaxation time (T1), even at 3 K. Further cooling is needed to extend the T1 and T2 for the application of boron acceptors in quantum information processing. Additionally, the properties of the donors have been studied in isotopically enriched, 28Si device structures. The group led by Berkeley investigated the spin-dependent scattering in 28Si field-effect transistors.[90] The formation of 29Si nuclear spin wires was also attempted by tem-plating a silicon substrate,[91] followed by forcing the alignment of MBE-deposited Si atoms.[92] However, a 29Si device is yet to be realized.
Single-spin qubits in silicon
The most important steps toward realizing a silicon-based quantum computer are to prepare, operate, and readout a single charge (or double-quantum dot) qubit or single electron and/or nuclear spin qubit placed in a silicon matrix. While, truly single qubit operations in silicon have been reported in the past few years,[93–96] it was only this year that the isotope engineering of silicon was proven essential, even for single qubits in sili-con.[97,98] For a single qubit, such as a single donor, a single quantum dot or a single double-quantum dot, a variety of foreign materials and structures, including gate insulators, metal contacts, and SETs for readouts should be placed nearby. Therefore, unlike the ensemble of isolated donors described in the previous section whose coherence was limited by the presence of 29Si nuclear spins in natSi, the common assumption was that purifying the isotope to eliminate 29Si would not be effective in extending the coherence time because the major decoherence sources would come from foreign objects rather than the 29Si nuclear spin fluctuations. Despite such skepticism, the “let us try and see” approach employed by experimentalists has shown that isotope enrichment is essential to successfully fabricate single-donor spin qubits[97] and single quantum-dot qubits[98] in silicon.
Figure 4 shows a scanning electron microscope (SEM) image of the single phosphorus device developed by the group led by Andera Morello and Andrew Dzurak at the University of New South Wales (UNSW). This device allowed, not only initialization, operation, and readout of the quantum information stored in a single-electron qubit and the single 31Pnu-clear qubit associated with the single phosphorus atom, but also coherent transfer between the electron and nuclear spin qubits. The device structure was essentially the same as the one developed by the same group using a natSi substrate, demonstrating single-electron spin[94] and nuclear spin[95] qubits. Figures 5(a) and 5(b) compare the Rabi oscillations of the single phosphorus qubits in natSi[94] and 28Si, respectively.[97] The single-electron spin qubit placed near the surface had a much longer coherence (T*2) when isotopically enriched Si was employed. In fact, every aspect of the qubit properties were significantly improved in the 28Si wafer (summarized in Table I).
SEM image of the single phosphorus spin qubit device developed at UNSW. The red spin indicates where the single phosphorus qubit is placed.[97]
Isotope engineering was also proven to be highly beneficial for the single-electron spin quantum-dot qubits in the 28Si samples fabricated and measured by the same group at UNSW.[98] Fi gure 6 shows the device structure and the Rabi oscillations of the electrons. Table I summarizes the coherence times that are orders of the magnitude longer than other quantum-dot qubits. Moreover, the ESR linewidth of the quantum-dot qubit was only 2.4 kHz and its resonant frequency could easily be shifted by more than 3000 times the linewidth by tuning the gate voltage. This ensured the selectivity to specific qubits integrated in large-scale systems, which could be fabricated using the standard silicon complementary metal-oxide-semiconductor (CMOS) technologies.
Developments in the design of quantum mechanically coupled, multiple phosphorus qubits and quantum dots are required for future large-scale integration. The two experiments described in this section showed that using isotope engineering to eliminate the background nuclear spins is crucial to extend the coherence time to a useful level. It was also shown in Fig. 2 of Ref. 99 that the isotope enrichment is needed to improve the gate fidelity. Overall, single qubits in 28Si have greatly surpassed the properties of the other single qubits tested in semiconductor systems.
Diamond quantum sensing
Diamond quantum sensing
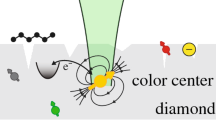
Diamond has been identified as one of the ideal matrixes for use in solid-state QIP[100] when ESR of a single NV center was re-alized.[101] The group from the University of Stuttgart, Germany performed a series of pioneering works on the qubit operations of single NV centers at room tempera-ture.[7,9,102,103] Their ground-breaking works were extended to a variety of applications of single NV centers in QIP.[104–109] In parallel, studies on how to use quantum phenomena in metrology and sensing emerged, aiming to reach sensitivities beyond the limit imposed by classical phys-ics.[110,111] While discussions continue on the ultimate limit of quantum sensing,[112–116] the use of single-electron spins bound to single NV centers in diamond has been pro-posed.[11,12,14] An example of quantum sensing by the NV centers is shown in Fig. 7, demonstrating the basic configuration used to probe the magnetic field that arose from the single nuclear spin of an atom, which is one of the constituents of a molecule. A single NV (blue arrow) embedded in a diamond substrate was used as a quantum sensor to probe the field coming from a molecule placed on the surface [Fig. 7(a)], while a single NV placed at the tip of a cantilever was used as a quantum sensor [Fig. 7(b)]. To realize such measurements, two criteria must be fulfilled: (i) the electron spin of each NV is tilted by 90° with respect to the direction of the externally applied magnetic field (B), so that it precesses around the B-field axis. The change in the precession rate is measured to probe the magnetic field arising from the nuclear spins of the molecule, thus, longer precession times have better sensitivities. The precession hold time decays exponentially and the coherence time (T2*) forthe DC measurements and the T2 forthe AC measurements are the relevant figures-of-merit because the minimum magnetic field required is proportional to 1/ \(1{\rm{/}}\sqrt {{T_2}} \). (ii) Because the magnetic field strength decreases by 1/d3, where d is the distance, the distance between the target nuclear spins and the NV electron sensor must be reduced, preferably to the order of a few nanometers, to detect single nuclear spins. The NV center has advantages over other quantum system because its single-electron spin, T2, is long and can be measured at room temperature. Because an NV electron is spatially confined within 1 nm, it can be placed within a few nanometers from the target. Therefore, research leading to the application of NV centers for magnetic sensing has become very active recently[117–128] and the use of such sensors in solid-state physics research is emerging.[129–131] Because the electronic levels of NVs are affected by temperature[132] and other external perturbations, NVs can be used to sense temperature,[133–135] electric fields,[136] pressure,[137] and mechanical motions.[138] Moreover, diamond is biocompatible and harmless, allowing for in-vivo quantum sensing in biology and medicine.[139–141]
(a) SEM image of a gate-defined single-electron quantum-dot qubit in silicon. (b) Rabi oscillations for a single-electron spin confined in a quantum dot.[98]
Diamond isotope engineering for quantum sensing
Pioneering works on the isotope engineering of bulk diamonds have been performed at the National Institute for Research in Inorganic Materials (currently the National Institute of Materials Science) in Japan[142] and at the General Electric Company, USA.[143] The isotope effect on the band gap was investigated at Waseda University using 13C isotopically enriched CVD diamond.[144] The National Institute of Advanced Industrial Science and Technology (AIST) in Japan pioneered an isotope superlattice consisting of alternating thin layers of 12C and 13c.[145–147]12C and 13C enriched methane gases used in CVD at AIST were obtained from Cambridge Isotope Laboratories, Inc. Similar to silicon, the coherence time of the NV centers was studied in isotopically controlled diamond as a function of the background 13C nuclear spin concentration.[148] It was extended to ~2 ms at room temperature by isotopic enrichment with nuclear-spin-free 12C.[15] Here, the isotopically enriched diamond grown by Element Six was employed. The long coherence time was maintained in 100 nm thick, isotopically enriched 12C CVD single-crystalline films where NV centers were introduced by nitrogen doping during growth.[149] In the isotopically enriched, 12C CVD poly-crystalline films, NV centers were introduced by nitrogen doping during growth.[150–152] In the isotopically enriched 12C CVD films, NV centers were introduced by nitrogen ion implantation and post-implantation annealing.[153,154] Thus, the remaining challenge for the application of quantum sensors is placing negatively charged NV— centers as close as possible to the diamond surface. If the NV— center loses its paramagnetic electron spin, it becomes a neutral NV0 center and cannot function as a quantum sensor. This happens near the surface of the film (within 5 nm) because of the existence of surface states that can change significantly with the crystalline quality of the surface and variations in surface-terminating spe-cies.[155–157] To improve the crystalline quality, CVD isotopically enriched 12C diamond films were used. Shallow NV— centers can be introduced into isotopically enriched CVD 12C diamond films either by nitrogen doping during CVD,[149,158] which is sometimes followed by electron beam irradiation to create vacancies,[159] or by ion implantation and annealing.[160] Figure 8 compares the typical NV— electron T2 values, measured by the Hahn echo sequence at room temperature. Figure 8(a) shows an isotopically enriched 12C bulk crystal.[15] Figure 8(b) shows a 100-nm-thick isotopically enriched 12C film[149] and Fig. 8(c) displays a 5-nm-thick isotopically enriched 12C film.[158] For the 100-nm-thick film, T2~ 1.7 ms [Fig. 8(b)]. This was the same as the bulk value of T2~ 1.7 ms [Fig 8(a)]. T2~45 μs in the 5-nm-thick film, which was shortened significantly by decoherence, most likely caused by the surface states. Making use of the long NV— electron T2,ex-tended by 12C enrichment, a single NV— situated in the deep region (away from the surface) has been used to detect a single 13C nuclear spin situated either next to the NV—[161] or far away from it, but still in the same diamond crystal.[162] In a similar manner, a shallow NV— placed near the surface should be able to detect nuclear fields that originate from the nuclear spins on the surface of the diamond. In this regard, the T2 ~ 45 μs in the 5-nm-thick film was long enough (at least theoretically) to detect a magnetic field from a single-proton nuclear spin.[158] There have been two types of isotopically enriched, C diamond CVD films containing shallow NV— centers that have succeeded in detecting the magnetic field from a small ensemble of proton nuclear spins; one was produced by UC Santa Barbara (UCSB)[159] and the other was fabricated by the Keio University-AIST collaboration in Japan.[158] While the UCSB sample was employed successfully by the IBM Almaden Research Center to detect the NMR of the proton spins confined in 4 nm3 of polymethyl methacrylate (PMMA), placed directly on the diamond surface,[163] the Keio-AIST sample succeeded in (along with the Keio-AIST-ETH collaboration) detecting ~6000 nuclear spins in an emulsion oil placed on the surface of diamond.[158] The nanoscale NMRs of the protons placed on the diamond surface were also demonstrated using shallow NV- centers created in natural diamond.[164,165] Because the coherence time of the shallow NV- is currently limited by some sorts of defects near the surface rather than by the presence of 13C nuclear spins, advantage of isotopically enriched C is limited to the absence of oscillations in the echo decay (ESEEM) of the NV electron precession arising from the precession of the nearby 13C nuclear spins. ESEEM is an additional noise that occurs when the nuclear spins on the surface are the targets for detection. However, the coherence times (T ) of the shallow NVs in both natural and 1 C diamonds are limited by the fluctuations that arise from the surface electronic states. At present, efforts are focused on identifying and understanding the nature of the surface electron spins using single shallow NV- centers as a sensor.[166–168] However, for the noise spectra, such as the intensity of the detected AC magnetic fields versus AC frequency, there is a disagreement between publications, indicating that the near-surface spin states are different for samples that have been prepared differently. Advancements in the materials science of diamond thin-film growth and surface preparation are needed to understand why these differences occur. One interesting direction explored recently was investigating the surface orientation rather than the (100) direction, which is usually studied; recently the (111) surface has been extensively studied.[169–171] Other defects in diamond, such as silicon vacancy complexes, may be of interest for sensing in the future. Such defects have been studied recently using isotopically enriched 12C diamond.[172]
Summary and outlook
State-of-the-art materials science and quantum information experiments involving isotope engineering have been reviewed for silicon and diamond. The role of isotope engineering in silicon quantum computing has been shown to be crucial. The implementation of isotope engineering in todays advanced silicon material technologies is fully developed. However, the availability of isotopically enriched 8Si in industrially adopted forms, such as silane and trichlorosilane, are limited. The advantages of the isotope engineering of diamond for quantum-sensing applications have been shown. However, while the availabilityof1 C in various forms is not a problem, furtherim-provements in increasing the crystallinity and understanding of the surface states in diamond are needed in orderto take full advantage of the possibilities of isotopic engineering as already demonstrated in Si.[172]
References
E.E. Haller: Isotopically engineered semiconductors. J. Appl. Phys. 77, 2857 (1995).
M. Cardona and M.L.W. Thewalt: Isotope effects on the optical spectra of semiconductors. Rev. Mod. Phys. 77, 1173 (2005).
B.E. Kane: A silicon-based nuclear spin quantum computer. Nature 393, 133 (1998).
T.D. Ladd, J.R. Goldman, F. Yamaguchi, Y. Yamamoto, E. Abe, and K.M. Itoh: All-silicon quantum computer. Phys. Rev. Lett. 89, 017901 (2002).
I. Shlimak, V.I. Safarov, and I.D. Vagner: Isotopically engineered silicon/silicon-germanium nanostructures as basic elements for a nuclear spin quantum computer. J. Phys. -Condens. Matter 13, 6059 (2001).
K.M. Itoh: An all-silicon linear chain NMR quantum computer. Solid State Commun. 133, 747 (2005).
F. Jelezko, I. Popa, A. Gruber, C. Tietz, J. Wrachtrup, A. Nizovtsev, and S. Kilin: Single spin states in a defect center resolved by optical spectroscopy. Appl. Phys. Lett. 81, 2160 (2002).
F. Jelezko, T. Gaebel, I. Popa, A. Gruber, and J. Wrachtrup: Observation of coherent oscillations in a single electron spin. Phys. Rev. Lett. 92, 076401 (2004).
F. Jelezko, T. Gaebel, I. Popa, M. Domhan, A. Gruber, and J. Wrachtrup: Observation of coherent oscillation of a single nuclear spin and realization of a two-qubit conditional quantum gate. Phys. Rev. Lett. 93, 130501 (2004).
J. Wrachtrup and F. Jelezko: Processing quantum information in diamond. J. Phys. -Condens. Maffer 18, S807 (2006).
C.L. Degen: Scanning magnetic field microscope with a diamond singlespin sensor. Appl. Phys. Lett. 92, 243111 (2008).
J.M. Taylor, P. Cappellaro, L. Childress, L. Jiang, D. Budker, P. R. Hemmer, A. Yacoby, R. Walsworth, and M.D. Lukin: High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 4, 810 (2008).
J.R. Maze, P.L. Stanwix, J.S. Hodges, S. Hong, J.M. Taylor, P. Cappellaro, L. Jiang, M.V.G. Dutt, E. Togan, A.S. Zibrov, A. Yacoby, R.L. Walsworth, and M.D. Lukin: Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 455, 644 (2008).
G. Balasubramanian, I.Y. Chan, R. Kolesov, M. Al-Hmoud, J. Tisler, C. Shin, C. Kim, A. Wojcik, P.R. Hemmer, A. Krueger, T. Hanke, A. Leitenstorfer, R. Bratschitsch, F. Jelezko, and J. Wrachtrup: Nanoscale imaging magnetometry with diamond spins under ambient conditions. Nature 455, 648 (2008).
G. Balasubramanian, P. Neumann, D. Twitchen, M. Markham, R. Kolesov, N. Mizuochi, J. Isoya, J. Achard, J. Beck, J. Tissler, V. Jacques, P.R. Hemmer, F. Jelezko, and J. Wrachtrup: Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater. 8, 383 (2009).
F.A. Zwanenburg, A.S. Dzurak, A. Morello, M.Y. Simmons, L.C.L. Hollenberg, G. Klimeck, S. Rogge, S.N. Coppersmith, and M. A. Eriksson: Silicon quantum electronics. Rev. Mod. Phys. 85, 961 (2013).
R. Vrijen, E. Yablonovitch, K. Wang, H.W. Jiang, A. Balandin, V. Roychowdhury, T. Mor, and D. DiVincenzo: Electron-spin-resonance transistors for quantum computing in silicon-germanium heterostruc-tures. Phys. Rev. A 62, 012306 (2000).
R. de Sausa, J.D. Delgado, and S. Das Sarma: Silicon quantum computation based on magnetic dipolar coupling. Phys. Rev. A 70, 052304 (2004).
L.C.L. Hollenberg, A.D. Greentree, A.G. Fowler, and C.J. Wellard: Two-dimensional architectures for donor-based quantum computing. Phys. Rev. B 74, 045311 (2006).
M. Friesen, P. Rugheimer, D.E. Savage, M.G. Lagally, D.W. van der Weide, R. Joynt, and M.A. Eriksson: Practical design and simulation of silicon-based quantum-dot qubits. Phys. Rev. B 67, 121301 (R) (2003).
M.A. Eriksson, S.N. Coppersmith, and M.G. Lagally: Semiconductor quantum dot qubits. MRS Bull. 38, 794 (2013).
Z. Shi, C.B. Simmons, J.R. Prance, J.K. Gamble, T.S. Koh, Y.P. Shim, X.D. Hu, D.E. Savage, M.G. Lagally, M.A. Eriksson, M. Friesen, and S.N. Coppersmith: Fast hybrid silicon double-quantum-dot qubit. Phys. Rev. Lett. 108, 140503 (2012).
K.M. Itoh, J. Kato, M. Uemura, A.K. Kaliteevski, O.N. Godisov, G. G. Devyatych, A.D. Bulanov, A.V. Gusev, I.D. Kovalev, P.G. Sennikov, H.J. Pohl, N.V. Abrosimov, and H. Riemann: High purity isotopically enriched Si-29 and Si-30 single crystals: isotope separation, purification, and growth. Jpn. J. Appl. Phys. 1 - Regul. Pap. Short Notes Rev. Paper. 42, 6248 (2003).
P.G. Sennikov, A.V. Vodopyanov, S.V. Golubev, D.A. Mansfeld, M. N. Drozdov, Y.N. Drozdov, B.A. Andreev, L.V. Gavrilenko, D. A. Pryakhin, V.I. Shashkin, O.N. Godisov, A.I. Glasunov, A.J. Safonov, H.J. Pohl, M.L.W. Thewalt, P. Becker, H. Riemann, N.V. Abrosimov, and S. Valkiers: Towards 0.99999 Si-28. Solid State Commun. 152, 455 (2012).
J.P. Gordon and K.D. Bowers: Microwave spin echoes from donor electrons in silicon. Phys. Rev. Lett. 1, 368 (1958).
P. Becker, H. Bettin, P. Debievre, C. Holm, U. Kutgens, F. Spieweck, J. Stumpel, S. Valkiers, and W. Zulehner: The Si-28 path to the Avogadro constant - first experiments and outlook. IEEE Trans. Instrum. Meas. 44, 522 (1995).
K. Fujii, A. Waseda, and N. Kuramoto: Development of a silicon density standard and precision density measurements of solid materials by hydrostatic weighing. Meas. Sci. Technol. 12, 2031 (2001).
P. Becker, H.J. Pohl, H. Riemann, and N. Abrosimov: Enrichment of silicon for a better kilogram. Phys. Status SolldIA -Appl. Mater. 207, 49 (2010).
E. Sozontov, L.X. Cao, A. Kazimirov, V. Kohn, M. Konuma, M. Cardona, and J. Zegenhagen: X-ray standing wave analysis of the effect of isotopic composition on the lattice constants of Si and Ge. Phys. Rev. Lett. 86, 5329 (2001).
A. Yang, M. Steger, H.J. Lian, M.L.W. Thewalt, M. Uemura, A. Sagara, K. M. Itoh, E.E. Haller, J.W. Ager, S.A. Lyon, M. Konuma, and M. Cardona: High-resolution photoluminescence measurement of the isotopic-mass dependence of the lattice parameter of silicon. Phys. Rev. 677, 113203 (2008).
P. Becker, D. Schiel, H.J. Pohl, A.K. Kaliteevski, O.N. Godisov, M. F. Churbanov, G.G. Devyatykh, A.V. Gusev, A.D. Bulanov, S. A. Adamchik, V.A. Gawa, I.D. Kovalev, N.V. Abrosimov, B. Hallmann-Seiffert, H. Riemann, S. Valkiers, P. Taylor, P. De Bievre, and E.M. Dianov: Large-scale production of highly enriched Si-28 for the precise determination of the Avogadro constant. Meas. Sci. Technol. 17, 1854 (2006).
P. Becker: Determination of the Avogadro constant - a contribution to the new definition of the mass unit kilogram. Eur. Phys. J. - Spec. Top. 172, 343 (2009).
A.D. Bulanov, G.G. Devyatych, A.V. Gusev, P.G. Sennikov, H.J. Pohl, H. Riemann, H. Schilling, and P. Becker: The highly isotopic enriched (99.9%), high-pure Si-28 single crystal. Cryst. Res. Technol. 35, 1023 (2000).
J.W. Ager, J.W. Beeman, W.L. Hansen, E.E. Haller, I.D. Sharp, C. Liao, A. Yang, M.L.W. Thewalt, and H. Riemann: High-purity, isotopically enriched bulk silicon. J. Electrochem. Soc. 152, G448 (2005).
M.L.W. Thewalt, M. Steger, A. Yang, N. Stavrias, M. Cardona, H. Riemann, N.V. Abrosimov, M.F. Churbanov, A.V. Gusev, A. D. Bulanov, I.D. Kovalev, A.K. Kaliteevskii, O.N. Godisov, P. Becker, H. J. Pohl, J.W. Ager, and E.E. Haller: Can highly enriched Si-28 reveal new things about old defects? Physlca B 401, 587 (2007).
M. Steger, A. Yang, N. Stavrias, M.L.W. Thewalt, H. Riemann, N. V. Abrosimov, M.F. Churbanov, A.V. Gusev, A.D. Bulanov, I. D. Kovalev, A.K. Kaliteevskii, O.N. Godisov, P. Becker, and H.J. Pohl: Reduction of the linewidths of deep luminescence centers in (28)Si reveals fingerprints of the isotope constituents. Phys. Rev. Lett. 100, 177402 (2008).
J. Kato, K.M. Itoh, H. Yamada-Kaneta, and H.J. Pohl: Host isotope effect on the localized vibrational modes of oxygen in isotopically enriched Si-28, Si-29, and Si-30 single crystals. Phys. Rev. B 68, 035205 (2003).
J.J.L. Morton, A.M. Tyryshkin, R.M. Brown, S. Shankar, B.W. Lovett, A. Ardavan, T. Schenkel, E.E. Haller, J.W. Ager, and S.A. Lyon: Solid-state quantum memory using the (31)P nuclear spin. Nature 455, 1085 (2008).
K. Takyu, K.M. Itoh, K. Oka, N. Saito, and V.I. Ozhogin: Growth and characterization of the isotopically enriched Si-28 bulk single crystal. Jpn. J. Appl. Phys. 2-Lett. 38, L1493 (1999).
E. Abe, K.M. Itoh, J. Isoya, and S. Yamasaki: Electron-spin phase relaxation of phosphorus donors in nuclear-spin-enriched silicon. Phys. Rev. B 70, 033204 (2004).
C.C. Lo, A. Persaud, S. Dhuey, D. Olynick, F. Borondics, M.C. Martin, H. A. Bechtel, J. Bokor, and T. Schenkel: Device fabrication and transport measurements of FinFETs built with Si-28 SOI wafers toward donor qubits in silicon. Semicond. Sci. Technol. 24, 105022 (2009).
J. Sailer, V. Lang, G. Abstreiter, G. Tsuchiya, K.M. Itoh, J.W. Ager, E. E. Haller, D. Kupidura, D. Harbusch, S. Ludwig, and D. Bougeard: A Schottky top-gated two-dimensional electron system in a nuclear spin free Si/SiGe heterostructure. Phys. Status Solidi - Rapid Res. Lett. 3, 61 (2009).
J.Y. Li, C.T. Huang, L.P. Rokhinson, and J.C. Sturm: Extremely high electron mobility in isotopically-enriched Si-28 two-dimensional electron gases grown by chemical vapor deposition. Appl. Phys. Lett. 103, 162105 (2013).
A. Wild, J. Kierig, J. Sailer, J.W. Ager, E.E. Haller, G. Abstreiter, S. Ludwig, and D. Bougeard: Fewelectron double quantum dot in an isotopically purified Si-28 quantum well. Appl. Phys. Lett. 100, 143110 (2012).
T. Kojima, R. Nebashi, K.M. Itoh, and Y. Shiraki: Growth and characterization of Si-28(n)/Si-30(n) isotope superlattices. Appl. Phys. Lett. 83, 2318 (2003).
Y. Shimizu, Y. Kawamura, M. Uematsu, K.M. Itoh, M. Tomita, M. Sasaki, H. Uchida, and M. Takahashi: Atom probe microscopy of three-dimensional distribution of silicon isotopes in Si-28/Si-30 isotope superlattices with sub-nanometer spatial resolution. J. Appl. Phys. 106, 076102 (2009).
Y. Shimizu, Y. Kawamura, M. Uematsu, M. Tomita, T. Kinno, N. Okada, M. Kato, H. Uchida, M. Takahashi, H. Ito, H. Ishikawa, Y. Ohji, H. Takamizawa, Y. Nagai, and K.M. Itoh: Depth and lateral resolution of laser-assisted atom probe microscopy of silicon revealed by isotopic heterostructures. J. Appl. Phys. 109, 036102 (2011).
H. Bracht, N. Wehmeier, S. Eon, A. Plech, D. Issenmann, J.L. Hansen, A. N. Larsen, J.W. Ager, and E.E. Haller: Reduced thermal conductivity of isotopically modulated silicon multilayer structures. Appl. Phys. Lett. 101, 064103 (2012).
H. Bracht, E.E. Haller, and R. Clark-Phelps: Silicon self-diffusion in isotope heterostructures. Phys. Rev. Lett. 81, 393 (1998).
H. Bracht, J.F. Pedersen, N. Zangenberg, A.N. Larsen, E.E. Haller, G. Lulli, and M. Posselt: Radiation enhanced silicon self-diffusion and the silicon vacancy at high temperatures. Phys. Rev. Lett. 91, 245502 (2003).
Y. Shimizu, M. Uematsu, and K.M. Itoh: Experimental evidence of the vacancy-mediated silicon self-diffusion in single-crystalline silicon. Phys. Rev. Lett. 98, 095901 (2007).
Y. Shimizu, M. Uematsu, K.M. Itoh, A. Takano, K. Sawano, and Y. Shiraki: Behaviors of neutral and charged silicon self-interstitials during transient enhanced diffusion in silicon investigated by isotope super-lattices. J. Appl. Phys. 105, 013504 (2009).
Y. Shimizu, M. Uematsu, K.M. Itoh, A. Takano, K. Sawano, and Y. Shiraki: Quantitative evaluation of silicon displacement induced by arsenic implantation using silicon isotope superlattices. Appl. Phys. Express 1, 021401 (2008).
M. Chiba and A. Hirai: Electron-spin echo decay behaviors of phosphorus doped silicon. J. Phys. Soc. Jpn. 33, 730 (1972).
E. Abe, J. Isoya, and K.M. Itoh: Electron spin coherence of phosphorus donors in isotopically purified Si-29. J. Supercond. 18, 157 (2005).
E. Abe, J. Isoya, and K.M. Itoh: Pulsed EPR study of spin coherence time of P donors in isotopically controlled Si. Physica B 376, 28 (2006).
E. Abe, A.M. Tyryshkin, S. Tojo, J.J.L. Morton, W.M. Witzel, A. Fujimoto, J.W. Ager, E.E. Haller, J. Isoya, S.A. Lyon, M.L.W. Thewalt, and K. M. Itoh: Electron spin coherence of phosphorus donors in silicon: effect of environmental nuclei. Phys. Rev. 6 82, 121201 (2010).
W.M. Witzel, X.D. Hu, and S.D. Sarma: Decoherence induced by anisotropic hyperfine interaction in Si spin qubits. Phys. Rev. 6 76, 035212 (2007).
W.M. Witzel and S. Das Sarma: Quantum theory for electron spin decoherence induced by nuclear spin dynamics in semiconductor quantum computer architectures: spectral diffusion of localized electron spins in the nuclear solid-state environment. Phys. Rev. 674, 035322 (2006).
R. de Sousa and S. Das Sarma: Theory of nuclear-induced spectral diffusion: spin decoherence of phosphorus donors in Si and GaAs quantum dots. Phys. Rev. 6 68, 115322 (2003).
A.M. Tyryshkin, S.A. Lyon, A.V. Astashkin, and A.M. Raitsimring: Electron spin relaxation times of phosphorus donors in silicon. Phys. Rev. B 68, 193207 (2003).
A.M. Tyryshkin, S. Tojo, J.J.L. Morton, H. Riemann, N.V. Abrosimov, P. Becker, H.J. Pohl, T. Schenkel, M.L.W. Thewalt, K.M. Itoh, and S. A. Lyon: Electron spin coherence exceeding seconds in high-purity silicon, Nat Mater. 11, 143 (2012).
M. Steger, K. Saeedi, M.L.W. Thewalt, J.J.L. Morton, H. Riemann, N. V. Abrosimov, P. Becker, and H.J. Pohl: Quantum information storage for over 180 s using donor spins in a Si-28 “Semiconductor Vacuum”. Science 336, 1280 (2012).
K. Saeedi, S. Simmons, J.Z. Salvail, P. Dluhy, H. Riemann, N. V. Abrosimov, P. Becker, H.J. Pohl, J.J.L. Morton, and M. W. Thewalt: Room-temperature quantum bit storage exceeding 39 minutes using ionized donors in silicon-28. Science 342, 830 (2013).
G. Wolfowicz, S. Simmons, A.M. Tyryshkin, R.E. George, H. Riemann, N. V. Abrosimov, P. Becker, H.J. Pohl, S.A. Lyon, M.L.W. Thewalt, and J.J. L. Morton: Decoherence mechanisms of Bi-209 donor electron spins in isotopically pure Si-28. Phys. Rev. 6 86, 245301 (2012).
G. Wolfowicz, A.M. Tyryshkin, R.E. George, H. Riemann, N. V. Abrosimov, P. Becker, H.J. Pohl, M.L.W. Thewalt, S.A. Lyon, and J.J.L. Morton: Atomic clock transitions in silicon-based spin qubits. Nat Nanotechnol. 8, 561 (2013).
P.A. Mortemousque, S. Berger, T. Sekiguchi, C. Culan, R.G. Elliman, and K.M. Itoh: Hyperfine clock transitions of bismuth donors in silicon detected by spin-dependent recombination. Phys. Rev. 6 89, 155202 (2014).
P.A. Mortemousque, T. Sekiguchi, C. Culan, M.P. Vlasenko, R. G. Elliman, L.S. Vlasenko, and K.M. Itoh: Spin dependent recombination based magnetic resonance spectroscopy of bismuth donor spins in silicon at low magnetic fields. Appl. Phys. Lett. 101, 082409 (2012).
T.D. Ladd, D. Maryenko, Y. Yamamoto, E. Abe, and K.M. Itoh: Coherence time of decoupled nuclear spins in silicon. Phys. Rev. 6 71, 014401 (2005).
S. Simmons, R.M. Brown, H. Riemann, N.V. Abrosimov, P. Becker, H. J. Pohl, M.L.W. Thewalt, K.M. Itoh, and J.J.L. Morton: Entanglement in a solid-state spin ensemble. Nature 470, 69 (2011).
A. Yang, M. Steger, D. Karaiskaj, M.L.W. Thewalt, M. Cardona, K.M. Itoh, H. Riemann, N.V. Abrosimov, M.F. Churbanov, A.V. Gusev, A. D. Bulanov, A.K. Kaliteevskii, O.N. Godisov, P. Becker, H.J. Pohl, J. W. Ager, and E.E. Haller: Optical detection and ionization of donors in specific electronic and nuclear spin states. Phys. Rev. Lett. 97, 227401 (2006).
M. Steger, T. Sekiguchi, A. Yang, K. Saeedi, M.E. Hayden, M. W. Thewalt, K.M. Itoh, H. Riemann, N.V. Abrosimov, P. Becker, and H. J. Pohl: Optically-detected NMR of optically-hyperpolarized P-31 neutral donors in Si-28. J. Appl. Phys. 109, 102411 (2011).
M.L.W. Thewalt, A. Yang, M. Steger, D. Karaiskaj, M. Cardona, H. Riemann, N.V. Abrosimov, A.V. Gusev, A.D. Bulanov, I.D. Kovalev, A.K. Kaliteevskii, O.N. Godisov, P. Becker, H.J. Pohl, E.E. Haller, J. W. Ager, and K.M. Itoh: Direct observation of the donor nuclear spin in a near-gap bound exciton transition: P-31 in highly enriched Si-28. J. Appl. Phys. 101, 081724 (2007).
A. Yang, M. Steger, T. Sekiguchi, M.L.W. Thewalt, T.D. Ladd, K.M. Itoh, H. Riemann, N.V. Abrosimov, P. Becker, and H.J. Pohl: Simultaneous subsecond hyperpolarization of the nuclear and electron spins of phosphorus in silicon by optical pumping of exciton transitions. Phys. Rev. Lett 102, 257401 (2009).
C.C. Lo, C.D. Weis, J. van Tol, J. Bokor, and T. Schenkel: All-electrical nuclear spin polarization of donors in silicon. Phys. Rev. Lett. 110, 057601 (2013).
T. Sekiguchi, M. Steger, K. Saeedi, M.L.W. Thewalt, H. Riemann, N. V. Abrosimov, and N. Notzel: Hyperfine structure and nuclear hyperpolarization observed in the bound exciton luminescence of Bi donors in natural Si. Phys. Rev. Lett. 104, 137402 (2010).
K. Saeedi llkhchy, M. Steger, M.L.W. Thewalt, N. Abrosimov, H. Riemann, P. Becker, and H.-J. Pohl: Bi donor hyperfine state populations studied by optical transitions of donor bound excitons in enriched Si-28. AIP Conf. Proc. 1566, 552 (2013).
A.S. Verhulst, D. Maryenko, Y. Yamamoto, and K.M. Itoh: Double and single peaks in nuclear magnetic resonance spectra of natural and Si-29-enriched single-crystal silicon. Phys. Rev. B 68, 054105 (2003).
A.S. Verhuist, I.G. Rau, Y. Yamamoto, and K.M. Itoh: Optical pumping of Si-29 nuclear spins in bulk silicon at high magnetic field and liquid helium temperature. Phys. Rev. B 71, 235206 (2005).
H. Hayashi, K.M. Itoh, and L.S. Vlasenko: Nuclear magnetic resonance linewidth and spin diffusion in (29)Si isotopically controlled silicon. Phys. Rev. B 78, 153201 (2008).
H. Hayashi, T. Itahashi, K.M. Itoh, L.S. Vlasenko, and M.P. Vlasenko: Dynamic nuclear polarization of Si-29 nuclei in isotopically controlled phosphorus doped silicon. Phys. Rev. 6 80, 045201 (2009).
W. Akhtar, H. Morishita, K. Sawano, Y. Shiraki, L.S. Vlasenko, and K. M. Itoh: Electrical detection of cross relaxation between electron spins of phosphorus and oxygen-vacancy centers in silicon. Phys. Rev. B 84, 045204 (2011).
W. Akhtar, V. Filidou, T. Sekiguchi, E. Kawakami, T. Itahashi, L. Vlasenko, J.J.L. Morton, and K.M. Itoh: Coherent storage of photoex-cited triplet states using Si-29 nuclear spins in silicon. Phys. Rev. Lett. 108, 097601 (2012).
W. Akhtar, T. Sekiguchi, T. Itahashi, V. Filidou, J.J.L. Morton, L. Vlasenko, and K.M. Itoh: Rabi oscillation and electron-spin-echo envelope modulation of the photoexcited triplet spin system in silicon. Phys. Rev. 686, 115206 (2012).
H. Wu, R.E. George, J.H. Wesenberg, K. Molmer, D.I. Schuster, R. J. Schoelkopf, K.M. Itoh, A. Ardavan, J.J.L. Morton, and G.A.D. Briggs: Storage of multiple coherent microwave excitations in an electron spin ensemble. Phys. Rev. Lett. 105, 140503 (2010).
H. Wu, E.M. Gauger, R.E. George, M. Mottonen, H. Riemann, N. V. Abrosimov, P. Becker, H.J. Pohl, K.M. Itoh, M.L.W. Thewalt, and J.J.L. Morton: Geometric phase gates with adiabatic control in electron spin resonance. Phys. Rev. A 87, 032326 (2013).
G.C. Knee, S. Simmons, E.M. Gauger, J.J.L. Morton, H. Riemann, N. V. Abrosimov, P. Becker, H.J. Pohl, K.M. Itoh, M.L.W. Thewalt, G.A.D. Briggs, and S.C. Benjamin: Violation of a Leggett-Garg inequality with ideal non-invasive measurements. Nat. Commun. 3, 606 (2012).
H. Tezuka, A.R. Stegner, A.M. Tyryshkin, S. Shankar, M.L.W. Thewalt, S. A. Lyon, K.M. Itoh, and M.S. Brandt: Electron paramagnetic resonance of boron acceptors in isotopically purified silicon. Phys. Rev. 681, 161203 (2010).
A.R. Stegner, H. Tezuka, T. Andlauer, M. Stutzmann, M.L.W. Thewalt, M. S. Brandt, and K.M. Itoh: Isotope effect on electron paramagnetic resonance of boron acceptors in silicon. Phys. Rev. B 82, 115213 (2010).
C.C. Lo, J. Bokor, T. Schenkel, A.M. Tyryshkin, and S.A. Lyon: Spin-dependent scattering off neutral antimony donors in (28)Si field-effect transistors. Appl. Phys. Lett. 91, 242106 (2007).
S. Yoshida, T. Sekiguchi, and K.M. Itoh: Atomically straight steps on vicinal Si(111) surfaces prepared by step-parallel current in the kink-up direction. Appl. Phys. Lett. 87, 106101 (2005).
T. Sekiguchi, S. Yoshida, and K.M. Itoh: Self-assembly of parallel atomic wires and periodic clusters of silicon on a vicinal Si(111) surface. Phys. Rev. Lett. 95, 106101 (2005).
B.M. Maune, M.G. Borselli, B. Huang, T.D. Ladd, P.W. Deelman, K. S. Holabird, A.A. Kiselev, I. Alvarado-Rodriguez, R.S. Ross, A. E. Schmitz, M. Sokolich, C.A. Watson, M.F. Gyure, and A.T. Hunter: Coherent singlet-triplet oscillations in a silicon-based double quantum dot. Nature 481, 344 (2012).
J.J. Pla, K.Y. Tan, J.P. Dehollain, W.H. Lim, J.J.L. Morton, D. N. Jamieson, A.S. Dzurak, and A. Morello: A single-atom electron spin qubit in silicon. Nature 489, 541 (2012).
J.J. Pla, K.Y. Tan, J.P. Dehollain, W.H. Lim, J.J.L. Morton, F. A. Zwanenburg, D.N. Jamieson, A.S. Dzurak, and A. Morello: High-fidelity readout and control of a nuclear spin qubit in silicon. Nature 496, 334 (2013).
Z. Shi, C.B. Simmons, D.R. Ward, J.R. Prance, R.T. Mohr, T.S. Koh, J. K. Gamble, X. Wu, D.E. Savage, M.G. Lagally, M. Friesen, S. N. Coppersmith, and M.A. Eriksson: Coherent quantum oscillations and echo measurements of a Si charge qubit. Phys. Rev. B 88, 075416 (2013).
J.T. Muhonen, J.P. Dehollain, A. Laucht, F.E. Hudson, R. Karla, T. Sekiguchi, K.M. Itoh, D.N. Jamieson, J.C. McCallum, A.S. Dzurak, and A. Morello: Storing quantum information for 30 seconds in a nano-delectronic device. Nat. Nanotechnol., DOI: 10.1038/nnano.2014.211 (2014).
M. Veldhorst, J.C.C. Hwang, C.H. Yang, A.W. Leenstra, B. de Ronde, J.P. Dehollain, J.T. Muhonen, F.E. Hudson, K.M. Itoh, A. Morello, and A.S. Dzurak: An addressable quantum dot qubit with fault-tolerant control fidelity. Nat Nanotechnol., DOI: 10.1038/nnano.2014.216 (2014).
A. Laucht, C.D. Hill, and A. Morello: Robusttwo-qubit gates for donors in silicon controlled by hyperfine interactions. Phys. Rev. X 4, 021044 (2014).
M.S. Shahriar, P.R. Hemmer, S. Lloyd, P.S. Bhatia, and A.E. Craig: Solid-state quantum computing using spectral holes. Phys. Rev. A 66, 032301 (2002).
A. Gruber, A. Drabenstedt, C. Tietz, L. Fleury, J. Wrachtrup, and C. von Borczyskowski: Scanning confocal optical microscopy and magnetic resonance on single defect centers. Science 276, 2012 (1997).
F. Jelezko, C. Tietz, A. Gruber, I. Popa, A. Nizovtsev, S. Kilin, and J. Wrachtrup: Spectroscopy of single N-V centers in diamond. Single Mol. 2, 255 (2001).
F. Jelezko and J. Wrachtrup: Single defect centres in diamond: a review. Phys. Status Solidi A-Appl. Mater. 203, 3207 (2006).
L. Childress, M.V.G. Dutt, J.M. Taylor, A.S. Zibrov, F. Jelezko, J. Wrachtrup, P.R. Hemmer, and M.D. Lukin: Coherent dynamics of coupled electron and nuclear spin qubits in diamond. Science 314, 281 (2006).
M.V.G. Dutt, L. Childress, L. Jiang, E. Togan, J. Maze, F. Jelezko, A. S. Zibrov, P.R. Hemmer, and M.D. Lukin: Quantum register based on individual electronic and nuclear spin qubits in diamond. Science 316, 1312 (2007).
P.C. Maurer, J.R. Maze, P.L. Stanwix, L. Jiang, A.V. Gorshkov, A. A. Zibrov, B. Harke, J.S. Hodges, A.S. Zibrov, A. Yacoby, D. Twitchen, S.W. Hell, R.L. Walsworth, and M.D. Lukin: Far-field optical imaging and manipulation of individual spins with nanoscale resolution. Nat. Phys. 6, 912 (2010).
P. Neumann, R. Kolesov, B. Naydenov, J. Beck, F. Rempp, M. Steiner, V. Jacques, G. Balasubramanian, Ml. Markham, D.J. Twitchen, S. Pezzagna, J. Meijer, J. Twamley, F. Jelezko, and J. Wrachtrup: Quantum register based on coupled electron spins in a room-temperature solid. Nat Phys. 6, 249 (2010).
P. Neumann, J. Beck, M. Steiner, F. Rempp, H. Fedder, P.R. Hemmer, J. Wrachtrup, and F. Jelezko: Single-shot readout of a single nuclear spin. Science 329, 542 (2010).
F. Dolde, I. Jakobi, B. Naydenov, N. Zhao, S. Pezzagna, C. Trautmann, J. Meijer, P. Neumann, F. Jelezko, and J. Wrachtrup: Room-temperature entanglement between single defect spins in diamond. Nat. Phys. 9, 139 (2013).
V. Giovannetti, S. Lloyd, and L. Maccone: Quantum metrology. Phys. Rev. Lett. 96, 010401 (2006).
V. Giovannetti, S. Lloyd, and L. Maccone: Advances in quantum metrology. Nat Photonics 5, 222 (2011).
J. Joo, W.J. Munro, and T.P. Spiller: Quantum metrology with entangled coherent states. Phys. Rev. Lett. 107, 083601 (2011).
D. Braun and J. Martin: Heisenberg-limited sensitivity with decoherence-enhanced measurements. Nat. Commun. 2, 223 (2011).
N. Thomas-Peter, B.J. Smith, A. Datta, L.J. Zhang, U. Dorner, and I. A. Walmsley: Real-world quantum sensors: evaluating resources for precision measurement. Phys. Rev. Lett. 107, 113603 (2011).
M. Zwierz, C.A. Perez-Delgado, and P. Kok: Ultimate limits to quantum metrology and the meaning of the Heisenberg limit. Phys. Rev. A 85, 042112 (2012).
P. Cappellaro, G. Goldstein, J.S. Hodges, L. Jiang, J.R. Maze, A. S. Sorensen, and M.D. Lukin: Environment-assisted metrology with spin qubits. Phys. Rev. A 85, 032336 (2012).
A. Laraoui, J.S. Hodges, and C.A. Meriles: Magnetometry of random ac magnetic fields using a single nitrogen-vacancy center. Appl. Phys. Lett. 97, 143104 (2010).
V.M. Acosta, E. Bauch, A. Jarmola, L.J. Zipp, M.P. Ledbetter, and D. Budker: Broadband magnetometry by infrared-absorption detection of nitrogen-vacancy ensembles in diamond. Appl. Phys. Lett. 97, 174104 (2010).
L.M. Pham, D. Le Sage, P.L. Stanwix, T.K. Yeung, D. Glenn, A. Trifonov, P. Cappellaro, P.R. Hemmer, M.D. Lukin, H. Park, A. Yacoby, and R. L. Walsworth: Magnetic field imaging with nitrogen-vacancy ensembles. New J. Phys. 13, 045021 (2011).
G. Waldherr, J. Beck, P. Neumann, R.S. Said, M. Nitsche, M. L. Markham, D.J. Twitchen, J. Twamley, F. Jelezko, and J. Wrachtrup: High-dynamic-range magnetometry with a single nuclear spin in diamond. Nat Nanotechnol. 7, 105 (2012).
G. de Lange, D. Riste, V.V. Dobrovitski, and R. Hanson: Single-spin magnetometry with multipulse sensing sequences. Phys. Rev. Lett. 106, 080802 (2011).
M. Schaffry, E.M. Gauger, J.J.L. Morton, and S.C. Benjamin: Proposed spin amplification for magnetic sensors employing crystal defects. Phys. Rev. Lett. 107, 207210 (2011).
M. Hirose, C.D. Aiello, and P. Cappellaro: Continuous dynamical decoupling magnetometry. Phys. Rev. A 86, 062320 (2012).
L. Rondin, J.P. Tetienne, P. Spinicelli, C. Dal Savio, K. Karrai, G. Dantelle, A. Thiaville, S. Rohart, J.F. Roch, and V. Jacques: Nanoscale magnetic field mapping with a single spin scanning probe magnetometer. Appl. Phy. Leff. 100, 153118 (2012).
C.S. Shin, C.E. Avalos, M.C. Butler, D.R. Trease, S.J. Seltzer, J. P. Mustonen, D.J. Kennedy, V.M. Acosta, D. Budker, A. Pines, and V. S. Bajaj: Room-temperature operation of a radiofrequency diamond magnetometer near the shot-noise limit. J. Appl. Phys. 112, 124519 (2012).
K.J. Fang, V.M. Acosta, C. Santori, Z.H. Huang, K.M. Itoh, H. Watanabe, S. Shikata, and R.G. Beausoleil: High-sensitivity magnetometry based on quantum beats in diamond nitrogen-vacancy centers. Phys. Rev. Lett. 110, 130802 (2013).
P. Maletinsky, S. Hong, M.S. Grinolds, B. Hausmann, M.D. Lukin, R. L. Walsworth, M. Loncar, and A. Yacoby: A robust scanning diamond sensor for nanoscale imaging with single nitrogen-vacancy centres. Nat. Nanotechnol. 7, 320 (2012).
A. Cooper, E. Magesan, H.N. Yum, and P. Cappellaro: Time-resolved magnetic sensing with electronic spins in diamond. Nat. Commun. 5, 3141 (2014).
L.S. Bouchard, V.M. Acosta, E. Bauch, and D. Budker: Detection of the Meissner effect with a diamond magnetometer. New J. Phys. 13, 025017 (2011).
A. Waxman, Y. Schlussel, D. Groswasser, V.M. Acosta, L.S. Bouchard, D. Budker, and R. Folman: Diamond magnetometry of superconducting thin films. Phys. Rev. B 89, 054509 (2014).
J.-P. Tetienne, T. Hingant, J.-V. Kim, L. Herrera Diez, J.-P. Adam, K. Garcia, J.-F. Roch, S. Rohart, A. Thiaville, D. Ravelosona, and V. Jacques: Nanoscale imaging and control of domain-wall hopping with a nitrogen-vacancy center microscope. Science 344, 1366 (2014).
V.M. Acosta, E. Bauch, M.P. Ledbetter, A. Waxman, L.S. Bouchard, and D. Budker: Temperature dependence of the nitrogen-vacancy magnetic resonance in diamond. Phys. Rev. Lett. 104, 070801 (2010).
G. Kucsko, P.C. Maurer, N.Y. Yao, M. Kubo, H.J. Noh, P.K. Lo, H. Park, and M.D. Lukin: Nanometre-scale thermometry in a living cell. Nature 500, 54 (2013).
D.M. Toyli, C.F. de las Casas, D.J. Christie, V.V. Dobrovitski, and D. D. Awschalom: Fluorescence thermometry enhanced by the quantum coherence of single spins in diamond. Proc. Natl. Acad. Sci. U. S. A. 110, 8417 (2013).
P. Neumann, I. Jakobi, F. Dolde, C. Burk, R. Reuter, G. Waldherr, J. Honert, T. Wolf, A. Brunner, J.H. Shim, D. Suter, H. Sumiya, J. Isoya, and J. Wrachtrup: High-precision nanoscale temperature sensing using single defects in diamond. Nano Lett. 13, 2738 (2013).
F. Dolde, H. Fedder, M.W. Doherty, T. Nobauer, F. Rempp, G. Balasubramanian, T. Wolf, F. Reinhard, L.C.L. Hollenberg, F. Jelezko, and J. Wrachtrup: Electric-field sensing using single diamond spins. Nat. Phys. 7, 459 (2011).
M.W. Doherty, V.V. Struzhkin, D.A. Simpson, L.P. McGuinness, Y. F. Meng, A. Stacey, T.J. Karle, R.J. Hemley, N.B. Manson, L.C.L. Hollenberg, and S. Prawer: Electronic properties and metrology applications of the diamond NV-center under pressure. Phys. Rev. Lett 112, 047601 (2014).
S. Kolkowitz, A.C.B. Jayich, Q.P. Unterreithmeier, S.D. Bennett, P. Rabl, J.G.E. Harris, and M.D. Lukin: Coherent sensing of a mechanical resonator with a single-spin qubit. Science 335, 1603 (2012).
L.P. McGuinness, Y. Yan, A. Stacey, D.A. Simpson, L.T. Hall, D. Maclaurin, S. Prawer, P. Mulvaney, J. Wrachtrup, F. Caruso, R. E. Scholten, and L.C.L. Hollenberg: Quantum measurement and orienta tion tracking of fluorescent nanodiamonds inside living cells. Nat. Nanotechnol. 6, 358 (2011).
R. Igarashi, Y. Yoshinari, H. Yokota, T. Sugi, F. Sugihara, K. Ikeda, H. Sumiya, S. Tsuji, I. Mori, H. Tochio, Y. Harada, and M. Shirakawa: Real-time background-free selective imaging of fluorescent nanodiamonds in vivo. Nano Lett. 12, 5726 (2012).
L.T. Hall, G.C.G. Beart, E.A. Thomas, D.A. Simpson, L.P. McGuinness, J. H. Cole, J.H. Manton, R.E. Scholten, F. Jelezko, J. Wrachtrup, S. Petrou, and L.C.L. Hollenberg: High spatial and temporal resolution wide-field imaging of neuron activity using quantum NV-diamond. Sci Rep. 2, 401 (2012).
A.T. Collins, G. Davies, H. Kanda, and G.S. Woods: Spectroscopic studies of C-13 synthetic diamond. J. Phys. C - Solid State Phys. 21, 1363 (1988).
T.R. Anthony, W.F. Banholzer, J.F. Fleischer, L.H. Wei, P.K. Kuo, R. L. Thomas, and R.W. Pryor: Thermal-diffusivity of isotopically enriched C-12 diamond. Phys. Rev. B 42, 1104 (1990).
A. Yamaguchi, S. Yamashita, T. Tsutsumi, and H. Kawarada: Temperature and incident beam-current dependence of dominant free-exciton recombination radiation from high-purity Chemical-Vapor-Deposition (Cvd) diamonds. Jpn. J. Appl. Phys. 2 - Lett. 33, L1063 (1994).
H. Watanabe, C.E. Nebel, and S. Shikata: Isotopic homojunction band engineering from diamond. Science 324, 1425 (2009).
H. Watanabe and S. Shikata: Superlattice structures from diamond. Diam. Relat. Mater. 20, 980 (2011).
H. Watanabe, T. Koretsune, S. Nakashima, S. Saito, and S. Shikata: Isotope composition dependence of the band-gap energy in diamond. Phys. Rev. B 88, 205420 (2013).
N. Mizuochi, P. Neumann, F. Rempp, J. Beck, V. Jacques, P. Siyushev, K. Nakamura, D.J. Twitchen, H. Watanabe, S. Yamasaki, F. Jelezko, and J. Wrachtrup: Coherence of single spins coupled to a nuclear spin bath of varying density. Phys. Rev. B 80, 041201 (2009).
T. Ishikawa, K.M.C. Fu, C. Santori, V.M. Acosta, R.G. Beausoleil, H. Watanabe, S. Shikata, and K.M. Itoh: Optical and spin coherence properties of nitrogen-vacancy centers placed in a 100 nm thick isotopically purified diamond layer. Nano Lett. 12, 2083 (2012).
T. Teraji, T. Taniguchi, S. Koizumi, K. Watanabe, M.Y. Liao, Y. Koide, and J. Isoya: Chemical vapor deposition of C-12 isotopically enriched poly-crystalline diamond. Jpn. J. Appl. Phys. 51, 090104 (2012).
T. Teraji, T. Taniguchi, S. Koizumi, Y. Koide, and J. Isoya: Effective use of source gas for diamond growth with isotopic enrichment. Appl. Phys. Express 6, 055601 (2013).
K.D. Jahnke, B. Naydenov, T. Teraji, S. Koizumi, T. Umeda, J. Isoya, and F. Jelezko: Long coherence time of spin qubits in C-12 enriched poly-crystalline chemical vapor deposition diamond. Appl. Phys. Lett. 101, 012405 (2012).
T. Yamamoto, T. Umeda, K. Watanabe, S. Onoda, Ml. Markham, D. J. Twitchen, B. Naydenov, L.P. McGuinness, T. Teraji, S. Koizumi, F. Dolde, H. Fedder, J. Honert, J. Wrachtrup, T. Ohshima, F. Jelezko, and J. Isoya: Extending spin coherence times of diamond qubits by high-temperature annealing. Phys. Rev. B 88, 075206 (2013).
T. Yamamoto, C. Muller, L.P. McGuinness, T. Teraji, B. Naydenov, S. Onoda, T. Ohshima, J. Wrachtrup, F. Jelezko, and J. Isoya: Strongly coupled diamond spin qubits by molecular nitrogen implantation. Phys. Rev. B 88, 201201 (R) (2013).
L. Rondin, G. Dantelle, A. Slablab, F. Grosshans, F. Treussart, P. Bergonzo, S. Perruchas, T. Gacoin, M. Chaigneau, H.C. Chang, V. Jacques, and J.F. Roch: Surface-induced charge state conversion of nitrogen-vacancy defects in nanodiamonds. Phys. Rev. B 82, 115449 (2010).
M.V. Hauf, B. Grotz, B. Naydenov, M. Dankerl, S. Pezzagna, J. Meijer, F. Jelezko, J. Wrachtrup, M. Stutzmann, F. Reinhard, and J.A. Garrido: Chemical control of the charge state of nitrogen-vacancy centers in diamond. Phys. Rev. B 83, 081304 (2011).
B. Grotz, M.V. Hauf, M. Dankerl, B. Naydenov, S. Pezzagna, J. Meijer, F. Jelezko, J. Wrachtrup, M. Stutzmann, F. Reinhard, and J.A. Garrido: Charge state manipulation of qubits in diamond. Nat. Commun. 3, 729 (2012).
K. Ohashi, T. Rosskopf, H. Watanabe, M. Loretz, Y. Tao, R. Hauert, S. Tomizawa, T. Ishikawa, J. Ishi-Hayase, S. Shikata, C.L. Degen, and K.M. Itoh: Negatively charged nitrogen-vacancy centers in a 5 nm thin C-12 diamond film. Nano Lett. 13, 4733 (2013).
K. Ohno, F.J. Heremans, L.C. Bassett, B.A. Myers, D.M. Toyli, A.C.B. Jayich, C.J. Palmstrom, and D.D. Awschalom: Engineering shallow spins in diamond with nitrogen delta-doping. Appl. Phys. Lett. 101, 082413 (2012).
J.O. Orwa, C. Santori, K. M.C. Fu, B. Gibson, D. Simpson, I. Aharonovich, A. Stacey, A. Cimmino, P. Balog, M. Markham, D. Twitchen, A. D. Greentree, R.G. Beausoleil, and S. Prawer: Engineering of nitrogen-vacancy color centers in high purity diamond by ion implantation and annealing. J. Appl. Phys. 109, 083530 (2011).
P.C. Maurer, G. Kucsko, C. Latta, L. Jiang, N.Y. Yao, S.D. Bennett, F. Pastawski, D. Hunger, N. Chisholm, M. Markham, D.J. Twitchen, J. I. Cirac, and M.D. Lukin: Room-temperature quantum bit memory exceeding one second. Science 336, 1283 (2012).
N. Zhao, J. Honert, B. Schmid, M. Klas, J. Isoya, M. Markham, D. Twitchen, F. Jelezko, R.B. Liu, H. Fedder, and J. Wrachtrup: Sensing single remote nuclear spins. Nat. Nanotechnol. 7, 657 (2012).
H.J. Mamin, M. Kim, M.H. Sherwood, C.T. Rettner, K. Ohno, D. D. Awschalom, and D. Rugar: Nanoscale nuclear magnetic resonance with a nitrogen-vacancy spin sensor. Science 339, 557 (2013).
T. Staudacher, F. Shi, S. Pezzagna, J. Meijer, J. Du, C.A. Meriles, F. Reinhard, and J. Wrachtrup: Nuclear magnetic resonance spectroscopy on a (5-nanometer)(3) sample volume. Science 339, 561 (2013).
M. Loretz, S. Pezzagna, J. Meijer, and C.L. Degen: Nanoscale nuclear magnetic resonance with a 1.9-nm-deep nitrogen-vacancy sensor. Appl. Phys. Lett. 104, 033102 (2014).
M.S. Grinolds, P. Maletinsky, S. Hong, M.D. Lukin, R.L. Walsworth, and A. Yacoby: Quantum control of proximal spins using nanoscale magnetic resonance imaging. Nat. Phys. 7, 687 (2011).
T. Rosskopf, A. Dussaux, K. Ohashi, M. Loretz, R. Schirhagl, H. Watanabe, S. Shikata, K.M. Itoh, and C.L. Degen: Investigation of surface magnetic noise by shallow spins in diamond. Phys. Rev. Lett. 112, 147602 (2014).
B.A. Myers, A. Das, M.C. Dartiailh, K. Ohno, D.D. Awschalom, and A. C. Bleszynski Jayich: Probing surface noise with depth-calibrated spins in diamond. Phys. Rev. Lett. 113, 027602 (2014).
J. Michl, T. Teraji, S. Zaiser, I. Jakobi, G. Waldherr, F. Dolde, P. Neumann, M.W. Doherty, N.B. Manson, J. Isoya, and J. Wrachtrup: Perfect alignment and preferential orientation of nitrogen-vacancy centers during chemical vapor deposition diamond growth on (111) surfaces. Appl. Phys. Lett. 104, 102407 (2014).
T. Fukui, Y. Doi, T. Miyazaki, Y. Miyamoto, H. Kato, T. Matsumoto, T. Makino, S. Yamasaki, R. Morimoto, N. Tokuda, M. Hatano, Y. Sakagawa, H. Morishita, T. Tashima, S. Miwa, Y. Suzuki, and N. Mizuochi: Perfect selective alignment of nitrogen-vacancy centers in diamond. Appl. Phys. Expressl, 055201 (2014).
M. Lesik, J.P. Tetienne, A. Tallaire, J. Achard, V. Mille, A. Gicquel, J. F. Roch, and V. Jacques: Perfect preferential orientation of nitrogen-vacancy defects in a synthetic diamond sample. Appl. Phys. Lett. 104, 113107 (2014).
L.J. Rogers, K.D. Jahnke, M.W. Doherty, A. Dietrich, L.P. McGuinness, C. Muller, T. Teraji, H. Sumiya, J. Isoya, N.B. Manson, and F. Jelezko: Electronic structure of the negatively charged silicon-vacancy center in diamond. Phys. Rev. B 89, 235101 (2014).
Acknowledgments
We thank Mike Thewalt, John Morton, Steve Lyon, Andrea Morello, Andrew Dzurak, Martin Brandt, Thomas Schenkel, Christian Degen, Fedor Jelezko, Tokuyuki Teraji, Junichi Isoya, and Junko Hayase for their helpful discussions. The research was supported in part by a Grant-in-Aid for scientific research by MEXT, in part by Cannon Foundation, and in part by the JSPS Core-to-Core Program.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Itoh, K.M., Watanabe, H. Isotope engineering of silicon and diamond for quantum computing and sensing applications. MRS Communications 4, 143–157 (2014). https://doi.org/10.1557/mrc.2014.32
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1557/mrc.2014.32