On anomalous depth-dependency of the hardness of NiTi shape memory alloys in spherical nanoindentation

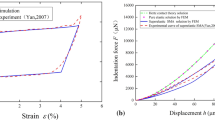
Abstract

An experimental study on the indentation hardness of NiTi shape memory alloys (SMAs) by using a spherical indenter tip and a finite element investigation to understand the experimental results are presented in this paper. It is shown that the spherical indentation hardness of NiTi SMAs increases with the indentation depth. The finding is contrary to the recent study on the hardness of NiTi SMAs using a sharp Berkovich indenter tip, where the interfacial energy plays a dominant role at small indentation depths. Our numerical investigation indicates that the influence of the interfacial energy is not significant on the spherical indentation hardness of SMAs. Furthermore, the depth dependency of SMA hardness under a spherical indenter is explained by the elastic spherical contact theory incorporating the deformation effect of phase transformation of SMAs. Hertz theory for purely elastic contact shows that the spherical hardness increases with the square root of the indentation depth. The phase transformation beneath the spherical tip weakens the depth effect of a purely elastic spherical hardness. This study enriches our knowledge on the basic concept of hardness for SMAs under spherical indentation at micro- and nanoscales.

Appendix: Numerical Method to Estimate the Interfacial Area and the Transformation Zone Volume

The method to estimate the interfacial area and the transformation zone volume from the FE simulations is detailed in this appendix. Applying the FE model presented in the paper, the spherical indentation test of SMAs can be simulated. Figure A1 shows a typical distribution of the phase transformation strain under indentation, which is used to define the phase transformation zone. The phase transformation zone boundary has the equivalent phase transformation strain value of 0.2%, which is the same as the plastic strain value used to define proof stress in classical elasto-plastic problems.

FIG. A1

Phase transformation zone from the FE simulation of a typical spherical indentation test.

To estimate the interfacial area and the phase transformation zone volume, the irregular phase transition zone from the FE simulations is approximated by a cylinder with the radius of a_tr and the depth of b_tr. Both the parameters are defined in Fig. A1. The interfacial area A_i can be estimated as

$${A_{\text{i}}} = 2{{\pi }}a_{{\text{tr}}}^2 + 2{{\pi }}{a_{{\text{tr}}}}{b_{{\text{tr}}}}.$$

((A1))

The volume V_m of the phase transformation zone can be estimated as

$${V_{\text{m}}} = {{\pi }}a_{{\text{tr}}}^2 \times {b_{{\text{tr}}}}.$$

((A2))

It is worth commenting that the presented method to estimate the interfacial area and the transformation zone volume serves the purpose to qualitatively analyze the indentation problem to get a simple scaling of the problem. It is not an accurate study.