An Invitation to Formal Power Series

Abstract

This is an account on the theory of formal power series developed entirely without any analytic machinery. Combining ideas from various authors we are able to prove Newton’s binomial theorem, Jacobi’s triple product, the Rogers–Ramanujan identities and many other prominent results. We apply these methods to derive several combinatorial theorems including Ramanujan’s partition congruences, generating functions of Stirling numbers and Jacobi’s four-square theorem. We further discuss formal Laurent series and multivariate power series and end with a proof of MacMahon’s master theorem.

1 Introduction

In a first course on abstract algebra students learn the difference between polynomial (real-valued) functions familiar from high school and formal polynomials defined over arbitrary fields. In courses on analysis they learn further that certain “well-behaved” functions possess a Taylor series expansion, i.e. a power series which converges in a neighborhood of a point. On the other hand, the formal world of power series (where no convergence questions are asked) is not so often addressed in undergraduate courses.

The purpose of these expository notes is to give a far-reaching introduction to formal power series without appealing to any analytic machinery (we only use an elementary discrete metric). In doing so, we go well beyond a dated account undertaken by Niven [31] in 1969 (for instance, Niven cites Euler’s pentagonal theorem without proof). An alternative approach with different emphases can be found in Tutte [40, 41]. To illustrate the usefulness of formal power series we offer several combinatorial applications including some deep partition identities due to Ramanujan and others. This challenges the statement “While the formal analogies with ordinary calculus are undeniably beautiful, strictly speaking one can’t go much beyond Euler that way…” from the introduction of the recent book by Johnson [20]. While most proofs presented here are not new, they are scattered in the literature spanning five decades and, up to my knowledge, cannot be found in a unified treatment. Our main source of inspiration is the accessible book by Hirschhorn [17] (albeit based on analytic reasoning) in combination with numerous articles cited when appropriate. I hope that the present notes may serve as the basis of seminars for undergraduate and graduate students alike. The prerequisites do not go beyond a basic abstract algebra course (from Sect. 7 on, some knowledge of algebraic and transcendental field extensions is assumed).

The material is organized as follows: In the upcoming section we define the ring of formal power series over an arbitrary field and discuss its basis properties. Thereafter, we introduce our toolkit consisting of compositions, derivations and exponentiations of power series. In Sect. 4 we first establish the binomial theorems of Newton and Gauss and later obtain Jacobi’s famous triple product identity, Euler’s pentagonal number theorem and the Rogers–Ramanujan identities. In the subsequent section we apply the methods to combinatorial problems to obtain a number of generating functions. Most notably, we prove Ramanujan’s partitions congruences (modulo 5 and 7) as well as his so-called “most beautiful” formula. Another section deals with Stirling numbers, permutations, Faulhaber’s formula and the Lagrange–Jacobi four-square theorem. In Sect. 7 we consider formal Laurent series in order to prove the Lagrange–Bürmann inversion formula and Puiseux’ theorem on the algebraic closure. In the following section, multivariate power series enter the picture. We give proofs of identities of Vieta, Girad–Newton and Waring on symmetric polynomials. We continue by developing multivariate versions of Leibniz’ differentiation rule, Faá di Bruno’s rule and the inverse function theorem. In the final section we go somewhat deeper by taking matrices into account. After establishing the Lagrange–Good inversion formula, we culminate by proving MacMahon’s master theorem. Along the way we indicate analytic counterparts, connections to other areas and insert a few exercises.

2 Definitions and Basic Properties

The sets of positive and non-negative integers are denoted by $\mathbb{N}=\{1,2,\ldots \}$ and $\mathbb{N}_{0}=\{0,1,\ldots \}$ respectively.

Definition 2.1

• 1. The letter $K$ will always denote a (commutative) field. In this section there are no requirements on $K$, but at later stages we need that $K$ has characteristic 0 or contains some roots of unity.

• 2. A (formal) power series over $K$ is just an infinite sequence $\alpha =(a_{0},a_{1},\ldots )$ with coefficients $a_{0},a_{1},\ldots \in K$. The set of power series forms a $K$-vector space denoted by $K[[X]]$ with respect to the familiar componentwise operations:

  $$ \alpha +\beta :=(a_{0}+b_{0},a_{1}+b_{1},\ldots ),\qquad \lambda \alpha :=(\lambda a_{0},\lambda a_{1},\ldots ),$$

  where $\beta =(b_{0},b_{1},\ldots )\in K[[X]]$ and $\lambda \in K$. We identify the elements of $a\in K$ with the constant power series $(a,0,\ldots )$. In general we call $a_{0}$ the constant term of $\alpha$ and set $\inf (\alpha ):=\inf \{n\in \mathbb{N}_{0}:a_{n}\ne 0\}$ with $\inf (0)=\inf \varnothing =\infty$ (as a group theorist I avoid calling $\inf (\alpha )$ the order of $\alpha$ as in many sources).

• 3. To motivate a multiplication on $K[[X]]$ we introduce an indeterminant $X$ and its powers

  $$ X^{0}:=1=(1,0,\ldots ),\qquad X=X^{1}=(0,1,0,\ldots ), $$
  $$ X^{2}=(0,0,1,0, \ldots ),\qquad \ldots .$$

  We can now formally write

  $$ \alpha =\sum _{n=0}^{\infty }a_{n}X^{n}.$$

  If there exists some $d\in \mathbb{N}_{0}$ with $a_{n}=0$ for all $n>d$, then $\alpha$ is called a (formal) polynomial. The smallest $d$ with this property is the degree $\deg (\alpha )$ of $\alpha$ (by convention $\deg (0)=-\infty$). In this case, $a_{\deg (\alpha )}$ is the leading coefficient and $\alpha$ is called monic if $a_{\deg (\alpha )}=1$. The set of polynomials (inside $K[[X]]$) is denoted by $K[X]$.

• 4. We borrow from the usual multiplication of polynomials (sometimes called Cauchy product or discrete convolution) to define

  $$ \boxed{\alpha \cdot \beta :=\sum _{n=0}^{\infty}\Bigl(\sum _{k=0}^{n}a_{k}b_{n-k}\Bigr)X^{n}}$$

  for arbitrary $\alpha ,\beta \in K[[X]]$ as above.

Note that $1,X,X^{2},\ldots$ is a $K$-basis of $K[X]$, but not of $K[[X]]$. Indeed, $K[[X]]$ has no countable basis. Opposed to a popular trend to rename $X$ to $q$ (as in [17]), we always keep $X$ as “formal” as possible.

Lemma 2.2

With the above defined addition and multiplication $(K[[X]],+,\cdot )$ is an integral domain with identity 1, i.e. $K[[X]]$ is a commutative ring such that $\alpha \cdot \beta \ne 0$ for all $\alpha ,\beta \in K[[X]]\setminus \{0\}$. Moreover, $K$ and $K[X]$ are subrings of $K[[X]]$.

Proof

Most axioms follows from the definition in a straight-forward manner. To prove the associativity of ⋅, let $\alpha =(a_{0},\ldots )$, $\beta =(b_{0},\ldots )$ and $\gamma =(c_{0},\ldots )$ be power series. The $n$-th coefficient of $\alpha \cdot (\beta \cdot \gamma )$ is

$$ \sum _{i=0}^{n}a_{i}\sum _{j=0}^{n-i}b_{j}c_{n-i-j}=\sum _{i+j+k=n}a_{i}b_{j}c_{k}= \sum _{i=0}^{n}\Bigl(\sum _{j=0}^{i}a_{j}b_{i-j}\Bigr)c_{n-i},$$

which happens to be the $n$-th coefficient of $(\alpha \cdot \beta )\cdot \gamma$.

Now let $\alpha \ne 0\ne \beta$ with $k:=\inf (\alpha )$ and $l:=\inf (\beta )$. Then the $(k+l)$-th coefficient of $\alpha \cdot \beta$ is $\sum _{i=0}^{k+l}a_{i}b_{k+l-i}=a_{k}b_{l}\ne 0$. In particular, $\inf (\alpha \cdot \beta )=\inf (\alpha )+\inf (\beta )$ and $\alpha \cdot \beta \ne 0$.

Since $K\subseteq K[X]\subseteq K[[X]]$ and the operations agree in these rings, it is clear that $K$ and $K[X]$ are subrings of $K[[X]]$ (with the same neutral elements). □

The above proof does not require $K$ to be a field. It works more generally for integral domains and this is needed later in Definition 8.1. From now on we will usually omit the multiplication symbol ⋅ and apply multiplications always before additions. For example, $\alpha \beta -\gamma$ is shorthand for $(\alpha \cdot \beta )+(-\gamma )$. The scalar multiplication is compatible with the ring multiplication, i.e. $\lambda (\alpha \beta )=(\lambda \alpha )\beta =\alpha (\lambda \beta )$ for $\alpha ,\beta \in K[[X]]$ and $\lambda \in K$. This turns $K[[X]]$ into a $K$-algebra.

Example 2.3

• 1. The following power series can be defined for any $K$:

  $$ 1-X,\qquad \sum _{n=0}^{\infty }X^{n},\qquad \sum _{n=0}^{\infty }nX^{n}, \qquad \sum _{n=0}^{\infty }(-1)^{n}X^{n}.$$

  We compute

  $$ (1-X)\sum _{n=0}^{\infty }X^{n}=\sum _{n=0}^{\infty }X^{n}-\sum _{n=1}^{ \infty }X^{n}=1.$$

• 2. For a field $K$ of characteristic 0 (like $K=\mathbb{Q}$, ℝ or ℂ) we can define the formal exponential series

  $$ \boxed{\exp (X):=\sum _{n=0}^{\infty}\frac{X^{n}}{n!}=1+X+\frac{X^{2}}{2}+\frac{X^{3}}{6}+\cdots \in K[[X]].}$$

  We will never write $e^{X}$ for the exponential series, since Euler’s number $e$ simply does not live in the formal world.

Definition 2.4

• 1. We call $\alpha \in K[[X]]$ invertible if there exists some $\beta \in K[[X]]$ such that $\alpha \beta =1$. As usual, $\beta$ is uniquely determined and we write $\alpha ^{-1}:=1/\alpha :=\beta$. As in any ring, the invertible elements form the group of units denoted by $K[[X]]^{\times}$.

• 2. For $\alpha ,\beta ,\gamma \in K[[X]]$ we write more generally $\alpha =\frac{\beta}{\gamma}$ if $\alpha \gamma =\beta$ (regardless whether $\gamma$ is invertible or not). For $k\in \mathbb{N}_{0}$ let $\alpha ^{k}:=\alpha \cdots \alpha$ with $k$ factors and $\alpha ^{-k}:=(\alpha ^{-1})^{k}$ if $\alpha \in K[[X]]^{\times}$.

• 3. For $\alpha \in K[[X]]$ let $(\alpha ):=\bigl\{\alpha \beta :\beta \in K[[X]]\bigr\}$ the principal ideal generated by $\alpha$.

The reader may know that every ideal of $K[X]$ is principal. The next lemma implies that every proper ideal of $K[[X]]$ is a power of $(X)$ (hence, $K[[X]]$ is a discrete valuation ring with unique maximal ideal $(X)$).

Lemma 2.5

Let $\alpha =\sum a_{n}X^{n}\in K[[X]]$. Then the following holds

• 1. $\alpha$ is invertible if and only if $a_{0}\ne 0$. Hence, $K[[X]]^{\times}=K[[X]]\setminus (X)$.

• 2. If there exists some $m\in \mathbb{N}$ with $\alpha ^{m}=1$, then $\alpha \in K$. Hence, the elements of finite order in $K[[X]]^{\times}$ lie in $K^{\times}$.

Proof

• 1. Let $\beta =\sum b_{n}X^{n}\in K[[X]]$ such that $\alpha \beta =1$. Then $a_{0}b_{0}=1$ and $a_{0}\ne 0$. Assume conversely that $a_{0}\ne 0$. We define $b_{0},b_{1},\ldots \in K$ recursively by $b_{0}:=1/a_{0}$ and

  $$ b_{k}:=-\frac{1}{a_{0}}\sum _{i=1}^{k}a_{i}b_{k-i}\in K$$

  for $k\ge 1$. Then

  $$ \sum _{i=0}^{k}a_{i}b_{k-i}= \textstyle\begin{cases} 1&\text{if }k=0, \\ 0&\text{if }k>0. \end{cases} $$

  Hence, $\alpha \beta =1$ where $\beta :=\sum b_{n}X^{n}$.

• 2. We may assume that $m>1$. For any prime divisor $p$ of $m$ it holds that $(\alpha ^{m/p})^{p}=1$. Thus, by induction on $m$, we may assume that $m=p$. By way of contradiction, suppose $\alpha \notin K$ and let $n:=\min \{k\ge 1:a_{k}\ne 0\}$. The $n$-th coefficient of $\alpha ^{p}=1$ is $pa_{0}^{p-1}a_{n}=0$. Since $\alpha$ is invertible (indeed $\alpha ^{-1}=\alpha ^{m-1}$), we know $a_{0}\ne 0$ and conclude that $p=0$ in $K$ (i.e. $K$ has characteristic $p$). Now we investigate the coefficient of $X^{np}$ in $\alpha ^{p}$. Obviously, it only depends on $a_{0},\ldots ,a_{np}$. Since $p$ divides $\binom{p}{k}=\frac{p(p-1)\ldots (p-k+1)}{k!}$ for $0< k< p$, the binomial theorem yields $(a_{0}+a_{1}X)^{p}=a_{0}^{p}+a_{1}^{p}X^{p}$. This familiar rule extends inductively to any finite number of summands. Hence,

  $$ (a_{0}+\cdots +a_{np}X^{np})^{p}=a_{0}^{p}+a_{n}^{p}X^{np}+a_{n+1}^{p}X^{(n+1)p}+ \cdots +a_{np}^{p}X^{np^{2}}.$$

  In particular, the $np$-th coefficient of $\alpha ^{p}$ is $a_{n}^{p}\ne 0$; a contradiction to $\alpha ^{p}=1$.

 □

Example 2.6

• 1. By Example 2.3 we obtain the familiar formula for the formal geometric series

  $$ \frac{1}{1-X}=\sum _{n=0}^{\infty }X^{n}$$

• 2. For any $\alpha \in K[[X]]\setminus \{1\}$ and $n\in \mathbb{N}$ an easy induction yields

  $$ \sum _{k=0}^{n-1}\alpha ^{k}=\frac{1-\alpha ^{n}}{1-\alpha}.$$

• 3. For distinct $a,b\in K\setminus \{0\}$ one has the partial fraction decomposition

  $$ \frac{1}{(a+X)(b+X)}=\frac{1}{b-a}\Bigl(\frac{1}{a+X}-\frac{1}{b+X} \Bigr), $$

  (2.1)

  which can be generalized depending on the algebraic properties of $K$.

We now start forming infinite sums of power series. To justify this process we introduce a discrete norm, which behaves much simpler than the euclidean norm on ℂ, for instance.

Definition 2.7

For $\alpha =\sum a_{n}X^{n}\in K[[X]]$ let

$$ |\alpha |:=2^{-\inf (\alpha )}\in \mathbb{R}$$

be the norm of $\alpha$ with the convention $|0|=2^{-\infty}=0$.

The number 2 in Definition 2.7 can of course be replaced by any real number greater than 1. Note that $\alpha$ is invertible if and only if $|\alpha |=1$. The following lemma turns $K[[X]]$ into an ultrametric space.

Lemma 2.8

For $\alpha ,\beta \in K[[X]]$ we have

• 1. $|\alpha |\ge 0$ with equality if and only if $\alpha =0$,

• 2. $|\alpha \beta |=|\alpha ||\beta |$,

• 3. $|\alpha +\beta |\le \max \{|\alpha |,|\beta |\}$ with equality if $|\alpha |\ne |\beta |$.

Proof

• 1. This follows from the definition.

• 2. Without loss of generality, let $\alpha \ne 0\ne \beta$. We have already seen in the proof of Lemma 2.2 that $\inf (\alpha \beta )=\inf (\alpha )+\inf (\beta )$.

• 3. From $a_{n}+b_{n}\ne 0$ we obtain $a_{n}\ne 0$ or $b_{n}\ne 0$. It follows that $\inf (\alpha +\beta )\ge \min \{\inf (\alpha ),\inf (\beta )\}$. This turns into the ultrametric inequality $|\alpha +\beta |\le \max \{|\alpha |,|\beta |\}$. If $\inf (\alpha )>\inf (\beta )$, then clearly $\inf (\alpha +\beta )=\inf (\beta )$.

 □

Theorem 2.9

The distance function $d(\alpha ,\beta ):=|\alpha -\beta |$ for $\alpha ,\beta \in K[[X]]$ turns $K[[X]]$ into a complete metric space.

Proof

Clearly, $d(\alpha ,\beta )=d(\beta ,\alpha )\ge 0$ with equality if and only if $\alpha =\beta$. Hence, $d$ is symmetric and positive definite. The triangle inequality follows from Lemma 2.8:

$$\begin{aligned} d(\alpha ,\gamma )&=|\alpha -\gamma |=|\alpha -\beta +\beta -\gamma | \le \max \bigl\{ |\alpha -\beta |,|\beta -\gamma |\bigr\} \\ &\le |\alpha -\beta |+|\beta -\gamma |=d(\alpha ,\beta )+d(\beta , \gamma ). \end{aligned}$$

Now let $\alpha _{1},\alpha _{2},\ldots \in K[[X]]$ by a Cauchy sequence with $\alpha _{m}=\sum a_{m,n}X^{n}$ for $m\ge 1$. For every $k\ge 1$ there exists some $M=M(k)\ge 1$ such that $|\alpha _{m}-\alpha _{M}|<2^{-k}$ for all $m\ge M$. This shows $a_{m,n}=a_{M,n}$ for all $m\ge M$ and $n\le k$. We define

$$ a_{k}:=a_{M(k),k}$$

and $\alpha =\sum a_{k}X^{k}$. Then $|\alpha -\alpha _{m}|<2^{-k}$ for all $m\ge M(k)$, i.e. $\lim _{m\to \infty}\alpha _{m}=\alpha$. Therefore, $K[[X]]$ is complete with respect to $d$. □

Note that $K[[X]]$ is the completion of $K[X]$ with respect to $d$. In order words: power series can be regarded as Cauchy series of polynomials. For convergent sequences $(\alpha _{k})_{k}$ and $(\beta _{k})_{k}$ we have (as in any metric space with multiplication)

$$ \lim _{k\to \infty}(\alpha _{k}+\beta _{k})=\lim _{k\to \infty} \alpha _{k}+\lim _{k\to \infty}\beta _{k},\qquad \lim _{k\to \infty}( \alpha _{k}\beta _{k})=\lim _{k\to \infty}\alpha _{k}\cdot \lim _{k \to \infty}\beta _{k}.$$

The infinite sum

$$ \sum _{k=1}^{\infty}\alpha _{k}:=\lim _{n\to \infty}\sum _{k=1}^{n} \alpha _{k}$$

can only converge if $(\alpha _{k})_{k}$ is a null sequence, that is, $\lim _{k\to \infty}|\alpha _{k}|=0$. Surprisingly and in stark contrast to euclidean spaces, the converse is also true as we are about to see. This crucial fact makes the arithmetic of formal power series much simpler than the analytic counterpart.

Lemma 2.10

For every null sequence $\alpha _{1},\alpha _{2},\ldots \in K[[X]]$ the series $\sum _{k=1}^{\infty}\alpha _{k}$ and $\prod _{k=1}^{\infty}(1+\alpha _{k})$ converge, i.e. they are well-defined in $K[[X]]$.

Proof

By Theorem 2.9 it suffices to show that the partial sums form Cauchy sequences. For $\epsilon >0$ let $N\ge 0$ such that $|\alpha _{k}|<\epsilon$ for all $k\ge N$. Then, for $k>l\ge N$, we have

$$\begin{aligned} \Bigl|\sum _{i=1}^{k}\alpha _{i}-\sum _{i=1}^{l}\alpha _{i}\Bigr|&= \Bigl|\sum _{i=l+1}^{k}\alpha _{i}\Bigr|\overset{2.8}{\le} \max \bigl\{ |\alpha _{i}|:i=l+1,\ldots ,k\bigr\} < \epsilon , \\ \Bigl|\prod _{i=1}^{k}(1+\alpha _{i})-\prod _{i=1}^{l}(1+\alpha _{i}) \Bigr|&=\prod _{i=1}^{l}\underbrace{|1+\alpha _{i}|}_{\le 1}\Bigl| \prod _{i=l+1}^{k}(1+\alpha _{i})-1\Bigr| \\ &\le \Bigl|\sum _{ \varnothing \ne I\subseteq \{l+1,\ldots ,k\}}\prod _{i\in I}\alpha _{i} \Bigr| \\ &\le \max \bigl\{ |\alpha _{i}|:i=l+1,\ldots ,k\bigr\} < \epsilon . \end{aligned}$$

 □

We often regard finite sequences as null sequences by extending them silently by 0. Let $\alpha _{1},\alpha _{2},\ldots \in K[[X]]$ be a null sequence and $\alpha _{k}=\sum _{n=0}^{\infty }a_{k,n}X^{n}$ for $k\ge 1$. For every $n\ge 0$ only finitely many of the coefficients $a_{1,n},a_{2,n},\ldots$ are non-zero. This shows that the coefficient of $X^{n}$ in

$$ \sum _{k=1}^{\infty}\alpha _{k}=\sum _{n=0}^{\infty}\Bigl(\sum _{k=1}^{ \infty }a_{k,n}\Bigr)X^{n} $$

(2.2)

depends on only finitely many terms. The same reasoning applies to the $\prod _{k=1}^{\infty}(1+\alpha _{k})$.

For $\gamma \in K[[X]]$ and null sequences $(\alpha _{k})$, $(\beta _{k})$ it holds that $\sum \alpha _{k}+\sum \beta _{k}=\sum (\alpha _{k}+\beta _{k})$ and $\gamma \sum \alpha _{k}=\sum \gamma \alpha _{k}$ as expected. Moreover, a convergent sum does not depend on the order of summation. In fact, for every bijection $\pi \colon \mathbb{N}\to \mathbb{N}$ and $n\in \mathbb{N}$ there exists some $N\in \mathbb{N}$ such that $\pi (k)>n$ for all $k>N$. Hence, $\alpha _{\pi (1)},\alpha _{\pi (2)},\ldots$ is a null sequence. We often exploit this fact by interchanging summation signs (discrete Fubini’s theorem).

Example 2.11

• 1. For $\alpha \in (X)$ we have $|\alpha ^{n}|=|\alpha |^{n}\le 2^{-n}\to 0$ and therefore $\sum _{n=0}^{\infty }\alpha ^{n}=\frac{1}{1-\alpha}$. So we have substituted $X$ by $\alpha$ in the geometric series. This will be generalized in Definition 3.1.

• 2. Since every non-negative integer has a unique 2-adic expansion, we obtain

  $$ \prod _{k=0}^{\infty}(1+X^{2^{k}})=1+X+X^{2}+\cdots =\frac{1}{1-X}.$$

  Equivalently,

  $$ \prod _{k=0}^{\infty}(1+X^{2^{k}})=\prod _{k=0}^{\infty} \frac{(1+X^{2^{k}})(1-X^{2^{k}})}{1-X^{2^{k}}}=\prod _{k=0}^{\infty} \frac{1-X^{2^{k+1}}}{1-X^{2^{k}}}=\frac{1}{1-X}.$$

  More interesting series will be discussed in Sect. 5.

3 The Toolkit

Definition 3.1

Let $\alpha =\sum _{n=0}^{\infty }a_{n}X^{n}\in K[[X]]$ and $\beta \in K[[X]]$ such that $\alpha \in K[X]$ or $\beta \in (X)$. We define

$$ \boxed{\alpha \circ \beta :=\alpha (\beta ):=\sum _{n=0}^{\infty }a_{n}\beta ^{n}.}$$

If $\alpha$ is a polynomial, it is clear that $\alpha (\beta )$ is a valid power series, while for $\beta \in (X)$ the convergence of $\alpha (\beta )$ is guaranteed by Lemma 2.10. In the following we will always assume that one of these conditions is fulfilled. Observe that $|\alpha (\beta )|\le |\alpha |$ if $\beta \in (X)$.

Example 3.2

For $\alpha =\sum _{n=0}^{\infty }a_{n}X^{n}\in K[[X]]$ we have $\alpha (0)=a_{0}$ and $\alpha (X^{2})=\sum _{n=0}^{\infty }a_{n}X^{2n}$. On the other hand for $\alpha =\sum _{n=0}^{\infty }X^{n}$ we are not allowed to form $\alpha (1)$.

Lemma 3.3

For $\alpha ,\beta ,\gamma \in (X)$ and every null sequence $\alpha _{1},\alpha _{2},\ldots \in K[[X]]$ we have

$$\begin{aligned} \Bigl(\sum _{k=1}^{\infty}\alpha _{k}\Bigr)\circ \beta &=\sum _{k=1}^{ \infty }\alpha _{k}(\beta ), \end{aligned}$$

(3.1)

$$\begin{aligned} \Bigl(\prod _{k=1}^{\infty}(1+\alpha _{k})\Bigr)\circ \beta &=\prod _{k=1}^{ \infty}(1+\alpha _{k}(\beta )), \end{aligned}$$

(3.2)

$$\begin{aligned} \alpha \circ (\beta \circ \gamma )&=(\alpha \circ \beta )\circ \gamma . \end{aligned}$$

(3.3)

Proof

Since $|\alpha _{k}(\beta )|\le |\alpha _{k}|\to 0$ for $k\to \infty$, all series are well-defined. Using the notation from (2.2) we deduce:

$$ \Bigl(\sum _{k=1}^{\infty}\alpha _{k}\Bigr)\circ \beta =\sum _{n=0}^{ \infty}\Bigl(\sum _{k=1}^{\infty }a_{k,n}\Bigr)\beta ^{n}=\sum _{k=1}^{ \infty}\Bigl(\sum _{n=0}^{\infty }a_{k,n}\beta ^{n}\Bigr)=\sum _{k=1}^{ \infty}\alpha _{k}(\beta ). $$

We begin proving (3.2) with only two factors, say $\alpha _{1}=\sum _{n=0}^{\infty }a_{n}X^{n}$ and $\alpha _{2}=\sum _{n=0}^{\infty }b_{n}X^{n}$:

$$ (\alpha _{1}\alpha _{2})\circ \beta =\sum _{n=0}^{\infty}\Bigl(\sum _{k=0}^{n}a_{k}b_{n-k} \Bigr)\beta ^{n}=\sum _{n=0}^{\infty}\sum _{k=0}^{n}(a_{k}\beta ^{k})(b_{n-k} \beta ^{n-k})=(\alpha _{1}\circ \beta )(\alpha _{2}\circ \beta ).$$

Inductively, (3.2) holds for finitely many factors. Now taking the limit using Lemma 2.8 gives

$$ \Bigl|\prod _{k=1}^{\infty}(1+\alpha _{k}(\beta ))-\Bigl(\prod _{k=1}^{n}(1+ \alpha _{k})\Bigr)\circ \beta \Bigr|=\prod _{k=1}^{n}|1+\alpha _{k}( \beta )|\Bigl|\prod _{k=n+1}^{\infty}(1+\alpha _{k}(\beta ))-1\Bigr| \to 0$$

as $n\to \infty$. Using (3.1) and (3.2), the validity of (3.3) reduces to the trivial case where $\alpha =X$. □

We warn the reader that in general

$$ \alpha \circ \beta \ne \beta \circ \alpha ,\qquad \alpha \circ ( \beta \gamma )\ne (\alpha \circ \beta )(\alpha \circ \gamma ),\qquad \alpha \circ (\beta +\gamma )\ne \alpha \circ \beta +\alpha \circ \gamma .$$

Nevertheless, the last statement can be corrected for the exponential series (Lemma 3.6).

Theorem 3.4

The set $K[[X]]^{\circ}:=(X)\setminus (X^{2})\subseteq K[[X]]$ forms a group with respect to ∘.

Proof

Let $\alpha ,\beta ,\gamma \in K[[X]]^{\circ}$. Then $\alpha (\beta )\in K[[X]]^{\circ}$, i.e. $K[[X]]^{\circ}$ is closed under ∘. The associativity holds by (3.3). By definition, $X\in K[[X]]^{\circ}$ and $X\circ \alpha =\alpha =\alpha \circ X$.

To construct inverses we argue as in Lemma 2.5. Let $\alpha ^{k}=\sum _{n=0}^{\infty }a_{k,n}X^{n}$ for $k\in \mathbb{N}_{0}$. Since $a_{0}=0$, also $a_{k,n}=0$ for $n< k$ and $a_{n,n}=a_{1}^{n}\ne 0$. We define recursively $b_{0}:=0$, $b_{1}:=\frac{1}{a_{1}}\ne 0$ and

$$ b_{n}:=-\frac{1}{a_{n,n}}\sum _{k=0}^{n-1}a_{k,n}b_{k}$$

for $n\ge 2$. Setting $\beta :=\sum b_{n}X^{n}\in K[[X]]^{\circ}$, we obtain

$$ \beta (\alpha )=\sum _{k=0}^{\infty }b_{k}\alpha ^{k}=\sum _{k=0}^{ \infty}\sum _{n=0}^{\infty }b_{k}a_{k,n}X^{n}=\sum _{n=0}^{\infty} \Bigl(\sum _{k=0}^{n}b_{k}a_{k,n}\Bigr)X^{n}=X.$$

As in any monoid, this automatically implies $\alpha (\beta )=X$. □

For $\alpha \in K[[X]]^{\circ}$, we call the unique $\beta \in K[[X]]^{\circ}$ with $\alpha (\beta )=X=\beta (\alpha )$ the reverse of $\alpha$. To avoid confusion with the inverse $\alpha ^{-1}$ (which is not defined here), we refrain from introducing a symbol for the reverse.

Example 3.5

• 1. Let $\alpha$ be the reverse of $X+X^{2}+\cdots =\frac{X}{1-X}$. Then

  $$ X=\frac{\alpha}{1-\alpha}$$

  and it follows that $\alpha =\frac{X}{1+X}=X-X^{2}+X^{3}-\cdots$. In general, it is much harder to find a closed-form expression for the reverse. We do so for the exponential series with the help of formal derivatives (Example 3.11). Later we provide the explicit Lagrange–Bürmann inversion formula (Theorem 7.5) using the machinery of Laurent series.

• 2. For the field $\mathbb{F}_{p}$ with $p$ elements (where $p$ is a prime), the subgroup $N_{p}:=X+(X^{2})$ of $\mathbb{F}_{p}[[X]]^{\circ}$ is called Nottingham group. One can show that every finite $p$-group is a subgroup of $N_{p}$ (see [9, Theorem 3]), so it must have a very rich structure.

Lemma 3.6

Functional equation

Let $\operatorname{char}K=0$. For every null sequence $\alpha _{1},\alpha _{2},\ldots \in (X)\subseteq K[[X]]$,

$$ \boxed{\exp \Bigl(\sum _{k=1}^{\infty}\alpha _{k}\Bigr)=\prod_{k=1}^{\infty}\exp (\alpha _{k}).} $$

(3.4)

In particular, $\exp (nX)=\exp (X)^{n}$ for $n\in \mathbb{Z}$.

Proof

Since $\sum _{k=1}^{\infty}\alpha _{k}\in (X)$ and $\exp (\alpha _{k})\in 1+\alpha _{k}+\frac{\alpha _{k}^{2}}{2}+ \cdots$, both sides of (3.4) are well-defined. For two summands $\alpha ,\beta \in (X)$ we compute

$$\begin{aligned} \exp (\alpha +\beta )&=\sum _{n=0}^{\infty} \frac{(\alpha +\beta )^{n}}{n!}=\sum _{n=0}^{\infty}\sum _{k=0}^{n} \binom{n}{k}\frac{\alpha ^{k}\beta ^{n-k}}{n!} \\ &=\sum _{n=0}^{\infty}\sum _{k=0}^{n} \frac{\alpha ^{k}\beta ^{n-k}}{k!(n-k)!}=\sum _{n=0}^{\infty} \frac{\alpha ^{n}}{n!}\cdot \sum _{n=0}^{\infty}\frac{\beta ^{n}}{n!}= \exp (\alpha )\exp (\beta ). \end{aligned}$$

By induction we obtain (3.4) for finitely many $\alpha _{k}$. Finally,

$$ \Bigl|\prod _{k=1}^{\infty}\exp (\alpha _{k})-\exp \Bigl(\sum _{k=1}^{n} \alpha _{k}\Bigr)\Bigr|=\prod _{k=1}^{n}|\exp (\alpha _{k})|\Bigl| \prod _{k=n+1}^{\infty}\exp (\alpha _{k})-1\Bigr|\to 0$$

as $n\to \infty$.

For the second claim let $n\in \mathbb{N}_{0}$. Then $\exp (nX)=\exp (X+\cdots +X)=\exp (X)^{n}$. Since

$$ \exp (nX)\exp (-nX)=\exp (nX-nX)=\exp (0)=1,$$

we also have $\exp (-nX)=\exp (nX)^{-1}=\exp (X)^{-n}$. □

Definition 3.7

For $\alpha =\sum a_{n}X^{n}\in K[[X]]$ we call

$$ \boxed{\alpha ':=\sum _{n=1}^{\infty }na_{n}X^{n-1}\in K[[X]]}$$

the (formal) derivative of $\alpha$. Moreover, let $\alpha ^{(0)}:=\alpha$ and $\alpha ^{(n)}:=(\alpha ^{(n-1)})'$ the $n$-th derivative for $n\in \mathbb{N}$.

It seems natural to define formal integrals as counterparts, but this is less useful, since in characteristic 0 we have $\alpha =\beta$ if and only if $\alpha '=\beta '$ and $\alpha (0)=\beta (0)$.

Example 3.8

As expected we have $1'=0$, $X'=1$ as well as

$$ \exp (X)'=\sum _{n=1}^{\infty }n\frac{X^{n-1}}{n!}=\sum _{n=0}^{ \infty}\frac{X^{n}}{n!}=\exp (X).$$

Note however, that $(X^{p})'=0$ if $K$ has characteristic $p$.

In characteristic 0, derivatives provide a convenient way to extract coefficients of power series. For $\alpha =\sum a_{n}X^{n}\in K[[X]]$ we see that $\alpha ^{(0)}(0)=\alpha (0)=a_{0}$, $\alpha '(0)=a_{1}$, $\alpha ''(0)=2a_{2},\ldots ,\alpha ^{(n)}(0)=n!a_{n}$. Hence, Taylor’s theorem (more precisely, the Maclaurin series) holds

$$ \boxed{\alpha =\sum _{n=0}^{\infty}\frac{\alpha ^{(n)}(0)}{n!}X^{n}.} $$

(3.5)

Over arbitrary fields we are not allowed to divide by $n!$. Alternatively, one may use the $k$-th Hasse derivative defined by

$$ H^{k}(\alpha ):=\sum _{n=k}^{\infty}\binom{n}{k}a_{n}X^{n-k}$$

(the integer $\binom{n}{k}$ can be embedded in any field). Note that $H^{k}(\alpha )=k!\alpha ^{(k)}$ and $\alpha =\sum _{n=0}^{\infty }H^{n}(\alpha )(0)X^{n}$. In the following we restrict ourselves to complex power series.

Lemma 3.9

For $\alpha ,\beta \in K[[X]]$ and every null sequence $\alpha _{1},\alpha _{2},\ldots \in K[[X]]$ the following rules hold:

Proof

• 1. Using the notation from (2.2), we have

  $$\begin{aligned} \Bigl(\sum _{k=1}^{\infty}\alpha _{k}\Bigr)' & =\Bigl(\sum _{n=0}^{ \infty}\sum _{k=1}^{\infty }a_{k,n}X^{n}\Bigr)'=\sum _{n=0}^{\infty} \sum _{k=1}^{\infty }n a_{k,n}X^{n-1}=\sum _{k=1}^{\infty}\Bigl(\sum _{n=0}^{ \infty }na_{k,n}X^{n-1}\Bigr)\\& =\sum _{k=1}^{\infty}\alpha _{k}'. \end{aligned}$$

• 2. By (i) we may assume $\alpha =X^{k}$ and $\beta =X^{l}$. In this case,

  $$ (\alpha \beta )'=(X^{k+l})'=(k+l)X^{k+l-1}=kX^{k-1}X^{l}+lX^{l-1}X^{k}= \alpha '\beta +\beta '\alpha .$$

• 3. Without loss of generality, suppose $\alpha _{k}\ne -1$ for all $k\in \mathbb{N}$ (otherwise both sides vanish). Let $|\alpha _{k}|<2^{-N-1}$ for all $k>n$. The coefficient of $X^{N}$ on both sides of the equation depends only on $\alpha _{1},\ldots ,\alpha _{n}$. From (ii) we verify inductively:

  $$ \Bigl(\prod _{k=1}^{n}(1+\alpha _{k})\Bigr)'=\prod _{k=1}^{n}(1+ \alpha _{k})\sum _{k=1}^{n}\frac{\alpha _{k}'}{1+\alpha _{k}}$$

  for all $n\in \mathbb{N}$. Now the claim follows with $N\to \infty$.

• 4. By (ii),

  $$ \alpha '=\Bigl(\frac{\alpha}{\beta}\beta \Bigr)'=\Bigl( \frac{\alpha}{\beta}\Bigr)'\beta +\frac{\alpha \beta '}{\beta}.$$

• 5. By (iii), the power rule $(\alpha ^{n})'=n\alpha ^{n-1}\alpha '$ holds for $n\in \mathbb{N}_{0}$. The sum rule implies

  $$ (\alpha \circ \beta )'=\Bigl(\sum _{n=0}^{\infty }a_{n}\beta ^{n} \Bigr)'=\sum _{n=0}^{\infty }a_{n}(\beta ^{n})'=\sum _{n=1}^{\infty }na_{n} \beta ^{n-1}\beta '=\alpha '(\beta )\beta '. $$

 □

The product rule implies the rather trivial factor rule $(\lambda \alpha )'=\lambda \alpha '$ for $\lambda \in K$ as well as Leibniz’ rule

$$ (\alpha \beta )^{(n)}=\sum _{k=0}^{n}\binom{n}{k}\alpha ^{(k)}\beta ^{(n-k)}$$

for $\alpha ,\beta \in K[[X]]$. A generalized version of the latter and a chain rule for higher derivatives are proven in Sect. 8.

Exercise 3.10

Let $\alpha ,\beta \in (X)$ such that $\beta \notin (X^{2})$. Prove L’Hôpital’s rule $\frac{\alpha}{\beta}(0)=\frac{\alpha '(0)}{\beta '(0)}$.

Example 3.11

For $\operatorname{char}K=0$ we define the (formal) logarithm by

$$ \boxed{\log (1+X):=\sum _{n=1}^{\infty}\frac{(-1)^{n-1}}{n}X^{n}=X-\frac{X^{2}}{2}+\frac{X^{3}}{3}\mp \ldots \in K[[X]].}$$

By Theorem 3.4, $\alpha :=\exp (X)-1$ possesses a reverse and $\log (\exp (X))=\log (1+\alpha )\in K[[X]]^{\circ}$. Since

$$ \log (1+X)'=1-X+X^{2}\mp \ldots =\sum (-X)^{n}=\frac{1}{1+X},$$

the chain rules yields

$$ \log (1+\alpha )'=\frac{\alpha '}{1+\alpha}=\frac{\exp (X)}{\exp (X)}=1.$$

This shows that $\log (\exp (X))=X$. Therefore, $\log (1+X)$ is the reverse of $\alpha =\exp (X)-1$ as expected from analysis. Moreover, $\log (1-X)=-\sum _{n=1}^{\infty }\frac{X^{n}}{n}$.

The only reason why we called the power series $\log (1+X)$ instead of $\log (X)$ or just log is to keep the analogy to the natural logarithm (as an analytic function).

Lemma 3.12

Functional equation

Let $\operatorname{char}K=0$. For every null sequence $\alpha _{1},\alpha _{2}, \ldots \in (X)\subseteq K[[X]]$,

$$ \boxed{\log \Bigl(\prod _{k=1}^{\infty}(1+\alpha _{k})\Bigr)=\sum _{k=1}^{\infty}\log (1+\alpha _{k}).} $$

(3.6)

Proof

$$\begin{aligned} \log \Bigl(\prod _{k=1}^{\infty}(1+\alpha _{k})\Bigr)&=\log \Bigl( \prod _{k=1}^{\infty}\exp (\log (1+\alpha _{k}))\Bigr) \overset{\text{(3.4)}}{=}\log \Bigl(\exp \Bigl(\sum _{k=1}^{\infty} \log (1+\alpha _{k})\Bigr)\Bigr) \\ &=\sum _{k=1}^{\infty}\log (1+\alpha _{k}). \end{aligned}$$

 □

Example 3.13

By (3.6),

$$ \log \Bigl(\frac{1}{1-X}\Bigr)=-\log (1-X)=\sum _{n=1}^{\infty} \frac{X^{n}}{n}. $$

Definition 3.14

Let $\operatorname{char}K=0$. For $c\in K$ and $\alpha \in (X)$ let

$$ \boxed{(1+\alpha )^{c}:=\exp \bigl(c\log (1+\alpha )\bigr).}$$

If $c=1/k$ for some $k\in \mathbb{N}$, we write more customary $\sqrt[k]{1+\alpha}:=(1+\alpha )^{1/k}$ and in particular $\sqrt{1+\alpha}:=\sqrt[2]{1+\alpha}$.

By Lemma 3.6,

$$ (1+\alpha )^{c}(1+\alpha )^{d}=\exp \bigl(c\log (1+\alpha )+d\log (1+ \alpha )\bigr)=(1+\alpha )^{c+d}$$

for every $c,d\in K$ as expected. Consequently, $\bigl(\sqrt[k]{1+\alpha}\bigr)^{k}=1+\alpha$ for $k\in \mathbb{N}$, i.e. $\sqrt[k]{1+\alpha}$ is a $k$-th root of $1+\alpha$ with constant term 1. Suppose that $\beta \in K[[X]]$ also satisfies $\beta ^{k}=1+\alpha$. Then $\beta ^{-1}\sqrt[k]{1+\alpha}$ has order $\le k$ in $K[[X]]^{\times}$. From Lemma 2.5 we conclude that $\beta ^{-1}\sqrt[k]{1+\alpha}$ is constant, i.e. $\beta =\beta (0)\sqrt[k]{1+\alpha}$. Consequently, $\sqrt[k]{1+\alpha}$ is the unique $k$-th of $1+\alpha$ with constant term 1.

The inexperienced reader may find the following exercise helpful.

Exercise 3.15

Check that the following power series in $\mathbb{C}[[X]]$ are well-defined:

$$\begin{array}{rlrl}sin(X)& :=\sum _{n=0}^{\mathrm{\infty }}\frac{{(-1)}^n}{(2n+1)!}{X}^{2n+1},& cos(X)& :=\sum _{n=0}^{\mathrm{\infty }}\frac{{(-1)}^n}{(2n)!}{X}^{2n},\\ tan(X)& :=\frac{sin(X)}{cos(X)},& sinh(X)& :=\sum _{k=0}^{\mathrm{\infty }}\frac{X^{2k+1}}{(2k+1)!},\\ arcsin(X)& :=\sum _{n=0}^{\mathrm{\infty }}\frac{(2n)!}{{(2^{n}n!)}^2}\frac{X^{2n+1}}{2n+1},& arctan(X)& :=\sum _{k=0}^{\mathrm{\infty }}\frac{{(-1)}^k}{2k+1}{X}^{2k+1}.\end{array}$$

Show that

• 1. (Euler’s formula) $\exp (\mathrm{i}X)=\cos (X)+\mathrm{i}\sin (X)$ where $\mathrm{i}=\sqrt{-1}\in \mathbb{C}$.

• 2. $\sin (2X)=2\sin (X)\cos (X)$ and $\cos (2X)=\cos (X)^{2}-\sin (X)^{2}$.

  Hint: Use (a) and separate real from non-real coefficients.

• 3. (Pythagorean identity) $\cos (X)^{2}+\sin (X)^{2}=1$.

• 4. $\sinh (X)=\frac{1}{2}(\exp (X)-\exp (-X))$.

• 5. $\sin (X)'=\cos (X)$ and $\cos (X)'=-\sin (X)$.

• 6. $\arctan \circ \tan =X$.

  Hint: Mimic the argument for $\log (1+X)$.

• 7. $\arctan (X)=\frac{\mathrm{i}}{2}\log \Bigl( \frac{\mathrm{i}+X}{\mathrm{i}-X}\Bigr)$.

• 8. $\arcsin (X)'=\frac{1}{\sqrt{1-X^{2}}}$.

• 9. $\arcsin \circ \sin =X$.

4 The Main Theorems

The field ℚ can be embedded into any field $K$ of characteristic 0. For $c\in K$ and $k\in \mathbb{N}$ we extend the definition of usual binomial coefficient by

$$ \binom{c}{k}:=\frac{c(c-1)\ldots (c-k+1)}{k!}\in K$$

(it is useful to know that numerator and denominator both have exactly $k$ factors). The next theorem is a vast generalization of the binomial theorem (take $c\in \mathbb{N}$) and the geometric series (take $c=-1$).

Theorem 4.1

Newton’s binomial theorem

Let $\operatorname{char}K=0$. For $\alpha \in (X)$ and $c\in K$ the following holds

$$ \boxed{(1+\alpha )^{c}=\sum _{k=0}^{\infty}\binom{c}{k}\alpha ^{k}.} $$

(4.1)

Proof

It suffices to prove the equation for $\alpha =X$ (we may substitute $X$ by $\alpha$ afterwards). By the chain rule,

$$ \bigl((1+X)^{c}\bigr)'=\exp (c\log (1+X))'=c\frac{(1+X)^{c}}{1+X}=c(1+X)^{c-1}$$

and inductively, $\bigl((1+X)^{c}\bigr)^{(k)}=c(c-1)\ldots (c-k+1)(1+X)^{c-k}$. Now the claim follows from Taylor’s theorem (3.5). □

A striking application of Theorem 4.1 will be given in Theorem 6.12.

Example 4.2

Let $\zeta \in \mathbb{C}$ be an $n$-th root of unity and let $\alpha :=(1+X)^{\zeta}-1\in (X)$. Then

$$ \alpha \circ \alpha =\bigl(1+(1+X)^{\zeta}-1\bigr)^{\zeta}-1=(1+X)^{ \zeta ^{2}}-1$$

and inductively $\alpha \circ \cdots \circ \alpha =(1+X)^{\zeta ^{n}}-1=X$. In particular, the order of $\alpha$ in the group $\mathbb{C}[[X]]^{\circ}$ divides $n$. Thus in contrast to the group $K[[X]]^{\times}$ studied in Lemma 2.5, the group $\mathbb{C}[[X]]^{\circ}$ possesses “interesting” elements of finite order.

Since we do not call our indeterminant $q$ (as in many sources), it makes no sense to introduce the $q$-Pochhammer symbol $(q;q)_{n}$. Instead we devise a non-standard notation in reminiscence of the binomial coefficient.

Definition 4.3

For $n\in \mathbb{N}_{0}$ let $X^{n}!:=(1-X)(1-X^{2})\ldots (1-X^{n})$. For $0\le k\le n$ we call

a Gaussian coefficient. If $k<0$ or $k>n$ let .

As for the binomial coefficients, we have and for all $n\in \mathbb{N}_{0}$ and $k\in \mathbb{Z}$. Moreover, . The familiar recurrence formula for binomial coefficients needs to be altered as follows.

Lemma 4.4

For $n\in \mathbb{N}_{0}$ and $k\in \mathbb{Z}$,

(4.2)

Proof

For $k>n+1$ or $k<0$ all parts are 0. Similarly, for $k=n+1$ or $k=0$ both sides equal 1. Finally, for $1\le k\le n$ it holds that

 □

Since and are polynomials, (4.2) shows inductively that all Gaussian coefficients are polynomials. We may therefore evaluate at $X=1$. Indeed, (4.2) becomes the recurrence for the binomial coefficients if $X=1$. Hence . This can be seen more directly by writing

We will interpret the coefficients of in Theorem 5.4.

Example 4.5

The next formulas resemble $(1+X)^{n}=\sum _{k=0}^{n}\binom{n}{k}X^{k}$ and $(1-X)^{-n}= \sum _{k=0}^{\infty}\binom{n+k-1}{k}X^{k}$ from Newton’s binomial theorem. The first is a finite sum, the second an infinite formal series arising from some sort of inverses. We will encounter many more such “dual pairs” in Theorem 6.9, Theorem 8.4 and (9.3), (9.4).

Theorem 4.6

Gauß’ binomial theorem

For $n\in \mathbb{N}$ and $\alpha \in K[[X]]$ the following holds

Proof

We argue by induction on $n$.

• 1. For $n=1$ both sides become $1+\alpha$. For the induction step we let all sums run from $-\infty$ to $\infty$ (this will not change the equation, but makes index shifts much more transparent):

  

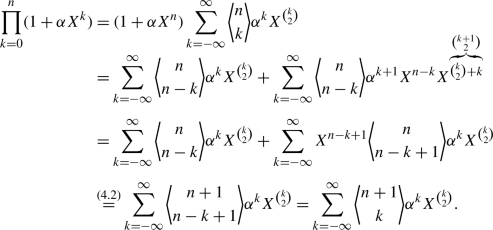
• 2. Here, $n=1$ is the geometric series $\frac{1}{1-\alpha X}=\sum _{k=0}^{\infty}\alpha ^{k}X^{k}$. In general:

  

 □

Remark 4.7

We emphasize that in the proof of Theorem 4.6, $\alpha$ is treated as a variable independent of $X$. The proof and the statement are therefore still valid if we substitute $X$ by some $\beta \in (X)$ without changing $\alpha$ to $\alpha (\beta )$.

Using

(4.3)

we obtain an infinite variant of Gauss’ theorem:

Corollary 4.8

Euler

For all $\alpha \in K[[X]]$,

$$\begin{aligned} \prod _{k=0}^{\infty}(1+\alpha X^{k})&=\sum _{k=0}^{\infty} \frac{\alpha ^{k}X^{\binom{k}{2}}}{X^{k}!}, \end{aligned}$$

(4.4)

$$\begin{aligned} \prod _{k=1}^{\infty}\frac{1}{1-\alpha X^{k}}&=\sum _{k=0}^{\infty} \frac{\alpha ^{k}X^{k}}{X^{k}!}. \end{aligned}$$

(4.5)

If $\alpha \in (X)$, we can apply (4.5) with $\alpha X^{-1}$ to obtain

$$ \prod _{k=0}^{\infty}\frac{1}{1-\alpha X^{k}}=\sum _{k=0}^{\infty} \frac{\alpha ^{k}}{X^{k}!}. $$

(4.6)

We are now in a position to derive one of the most powerful theorems on power series.

Theorem 4.9

Jacobi’s triple product identity

For every $\alpha \in K[[X]]\setminus (X^{2})$ the following holds

$$ \boxed{\prod _{k=1}^{\infty}(1-X^{2k})(1+\alpha X^{2k-1})(1+\alpha ^{-1}X^{2k-1})=\sum _{k=-\infty}^{\infty }\alpha ^{k}X^{k^{2}}.}$$

Proof

We follow Andrews [2]. Observe that $\alpha ^{-1}X^{2k-1}$ is a power series for all $k\ge 1$, since $\alpha \notin (X^{2})$. Also, both sides of the equation are well-defined. According to Remark 4.7 we are allowed to substitute $X$ by $X^{2}$ and simultaneously $\alpha$ by $\alpha ^{-1} X$ in (4.4):

$$\begin{aligned} \prod _{k=1}^{\infty }(1+\alpha ^{-1} X^{2k-1})&=\prod _{k=0}^{ \infty }(1+\alpha ^{-1} X^{2k+1})=\sum _{k=0}^{\infty} \frac{\alpha ^{-k}X^{k^{2}}}{(1-X^{2})\ldots (1-X^{2k})} \\ &=\prod _{k=1}^{\infty}\frac{1}{1-X^{2k}}\sum _{k=0}^{\infty}\alpha ^{-k}X^{k^{2}} \prod _{l=0}^{\infty}(1-X^{2l+2k+2}). \end{aligned}$$

Again, $\alpha ^{-k}X^{k^{2}}$ is still a power series. Since for negative $k$ the product over $1-X^{2l+2k+2}$ vanishes, we may sum over $k\in \mathbb{Z}$. A second application of (4.4) with $X^{2}$ instead of $X$ and $-X^{2k+2}$ in the role of $\alpha$ shows

$$\begin{aligned} \prod _{k=1}^{\infty }(1+\alpha ^{-1} X^{2k-1})(1-X^{2k})&=\sum _{k=- \infty}^{\infty}\alpha ^{-k}X^{k^{2}}\sum _{l=0}^{\infty} \frac{(-1)^{l}X^{l^{2}+l+2kl}}{(1-X^{2})\ldots (1-X^{2l})} \\ &=\sum _{l=0}^{\infty } \frac{(-\alpha X)^{l}}{(1-X^{2})\ldots (1-X^{2l})}\sum _{k=-\infty}^{ \infty }X^{(k+l)^{2}}\alpha ^{-k-l}. \end{aligned}$$

After the index shift $k\mapsto -k-l$, the inner sum does not depend on $l$ anymore. We then apply (4.6) on the first sum with $X$ replaced by $X^{2}$ and $-\alpha X\in (X)$ instead of $\alpha$:

$$\begin{aligned} \prod _{k=1}^{\infty }(1+\alpha ^{-1} X^{2k-1})(1-X^{2k})&=\prod _{k=0}^{ \infty}\frac{1}{1+\alpha X^{2k+1}}\sum _{k=-\infty}^{\infty }X^{k^{2}} \alpha ^{k}\\&=\prod _{k=1}^{\infty}\frac{1}{1+\alpha X^{2k-1}}\sum _{k=- \infty}^{\infty }X^{k^{2}}\alpha ^{k}. \end{aligned}$$

We are done by rearranging terms. □

Remark 4.10

Since the above proof is just a combination of Euler’s identities, we are still allowed to replace $X$ and $\alpha$ individually. Furthermore, we have required the condition $\alpha \notin (X^{2})$ only to guarantee that $\alpha ^{-1}X$ is well-defined. If we replace $X$ by $X^{m}$, say, the proof is still sound for $\alpha \in K[[X]]\setminus (X^{m+1})$.

A (somewhat analytical) proof only making use of (4.4) can be found in [45]. There are numerous purely combinatorial proofs like [23, 27, 38, 39, 44, 46], which are meaningful for formal power series.

Example 4.11

• 1. Choosing $\alpha \in \{\pm 1,X\}$ in Theorem 4.9 reveals the following elegant identities:

  $$\begin{aligned} \prod _{k=1}^{\infty}(1-X^{2k})(1+X^{2k-1})^{2}&=\sum _{k=-\infty}^{ \infty }X^{k^{2}}, \end{aligned}$$

  (4.7)
  $$\begin{aligned} \prod _{k=1}^{\infty}\frac{(1-X^{k})^{2}}{1-X^{2k}}=\prod _{k=1}^{ \infty}(1-X^{2k})(1-X^{2k-1})^{2}&=\sum _{k=-\infty}^{\infty}(-1)^{k} X^{k^{2}}, \end{aligned}$$

  (4.8)
  $$\begin{aligned} \prod _{k=1}^{\infty}(1-X^{2k})(1+X^{2k})^{2}&=\frac{1}{2}\sum _{k=- \infty}^{\infty }X^{k^{2}+k}=\sum _{k=0}^{\infty }X^{k^{2}+k}, \end{aligned}$$

  (4.9)

  where in (4.9) we made use of the bijection $k\mapsto -k-1$ on ℤ. These formulas are needed in the proof of Theorem 6.17. In (4.9) we find $X$ only to even powers. By equating the corresponding coefficients, we may replace $X^{2}$ by $X$ to obtain

  $$ \prod _{k=1}^{\infty}(1-X^{2k})(1+X^{k})=\prod _{k=1}^{\infty}(1-X^{k})(1+X^{k})^{2}= \sum _{k=0}^{\infty }X^{\frac{k^{2}+k}{2}}.$$

  A very similar identity will be proved in Theorem 4.13.

• 2. Relying on Remark 4.10, we can replace $X$ by $X^{3}$ and $\alpha$ by $-X$ at the same time in Theorem 4.9. This leads to

  $$ \prod _{k=1}^{\infty }(1-X^{6k})(1-X^{6k-2})(1-X^{6k-4})=\sum _{k=- \infty}^{\infty }(-1)^{k}X^{3k^{2}+k}.$$

  Substituting $X^{2}$ by $X$ provides Euler’s celebrated pentagonal number theorem:

  $$ \boxed{\prod _{k=1}^{\infty}(1-X^{k})=\prod _{k=1}^{\infty}(1-X^{3k})(1-X^{3k-1})(1-X^{3k-2})=\sum _{k=-\infty}^{\infty}(-1)^{k}X^{\frac{3k^{2}+k}{2}}.} $$

  (4.10)

  There is a well-known combinatorial proof of (4.10) by Franklin, which is reproduced in the influential book by Hardy–Wright [14, Sect. 19.11].

• 3. The following formulas arise in a similar manner by substituting $X$ by $X^{5}$ and selecting $\alpha \in \{-X,-X^{3}\}$ afterwards (this is allowed by Remark 4.10):

  $$\begin{aligned} \prod _{k=1}^{\infty }(1-X^{5k})(1-X^{5k-2})(1-X^{5k-3})=\sum _{k=- \infty}^{\infty }(-1)^{k}X^{\frac{5k^{2}+k}{2}}, \end{aligned}$$

  (4.11)
  $$\begin{aligned} \prod _{k=1}^{\infty }(1-X^{5k})(1-X^{5k-1})(1-X^{5k-4})=\sum _{k=- \infty}^{\infty }(-1)^{k}X^{\frac{5k^{2}+3k}{2}}. \end{aligned}$$

  (4.12)

  This will be used in the proof of Theorem 4.15.

To obtain yet another triple product identity, we first consider a finite version due to Hirschhorn [15].

Lemma 4.12

For all $n\in \mathbb{N}_{0}$,

(4.13)

Proof

The proof is by induction on $n$: Both sides are 1 if $n=0$. So assume $n\ge 1$ and let $Q_{n}$ be the right hand side of (4.13). The summands of $Q_{n}$ are invariant under the index shift $k\mapsto -k-1$ and vanish for $|k|>n$. Hence, we may sum over $k\in \mathbb{Z}$ and divide by 2. A threefold application of formula (4.2) gives:

The second and third sum amount to $(1+X^{2n})Q_{n-1}$. We apply the transformations $k\mapsto k+1$ and $k\mapsto k-1$ in the first sum and fourth sum respectively:

 □

Theorem 4.13

Jacobi

We have

$$ \boxed{\prod _{k=1}^{\infty}(1-X^{k})^{3}=\sum _{k=0}^{\infty}(-1)^{k}(2k+1)X^{\frac{k^{2}+k}{2}}.}$$

Proof

By Lemma 4.12, we have

 □

In an analytic framework, Theorem 4.13 can be derived from Theorem 4.9 (see [14, Theorem 357]). A combinatorial proof was given in [21].

As a preparation for the infamous Rogers–Ramanujan identities [35], we start again with a finite version due to Bressoud [7]. The impatient reader may skip these technical results and start right away with the applications in Sect. 5 (Theorem 4.15 is only needed in Theorem 5.5(v), (vi)).

Lemma 4.14

For $n\in \mathbb{N}_{0}$,

(4.14)

(4.15)

Proof

Note that all sums are actually finite. We follow a simplified proof by Chapman [10]. Let $\alpha _{n}$ and $\tilde{\alpha}_{n}$ be the left and the right hand side respectively of (4.14). Similarly, let $\beta _{n}$ and $\tilde{\beta}_{n}$ be the left and right hand side respectively of (4.15). Note that all four sums are actually finite. We show both equations at the same time by establishing a common recurrence relation between $\alpha _{n}$, $\beta _{n}$ and $\tilde{\alpha}_{n}$, $\tilde{\beta}_{n}$.

We compute $\alpha _{0}=\beta _{0}=\tilde{\alpha}_{0}=\tilde{\beta}_{0}=1$. For $n\ge 1$,

These recurrences characterize $\alpha _{n}$ and $\beta _{n}$ uniquely. The familiar index transformation $k\mapsto -k-1$ implies . This is used in the following computation:

By induction on $n$, it follows that $\alpha _{n}=\tilde{\alpha}_{n}$ and $\beta _{n}=\tilde{\beta}_{n}$ as desired. □

Theorem 4.15

Rogers–Ramanujan identities

We have

Proof

 □

The Rogers–Ramanujan identities were long believed to lie deeper within the theory of elliptic functions (Hardy [14, p. 385] wrote “No proof is really easy (and it would perhaps be unreasonable to expect an easy proof.”; Andrews [4, p. 105] wrote “…no doubt it would be unreasonable to expect a really easy proof.”). Meanwhile a great number of proofs were found, some of which are combinatorial (see [3] or the recent book [36]). An interpretation of these identities is given in Theorem 5.5 below. We point out that there are many “finite identities”, like Lemma 4.14, approaching the Rogers–Ramanujan identities (as there are many rational sequences approaching $\sqrt{2}$).

One can find many more interesting identities, like the quintuple product, along with comprehensive references (and analytic proofs) in Johnson [20].

5 Applications to Combinatorics

In this section we bring to life all of the abstract theorems and identities of the previous section. If $a_{0},a_{1},\ldots$ is a sequence of numbers usually arising from combinatorial context, the power series $\alpha =\sum a_{n}X^{n}$ is called the generating function of $(a_{n})_{n}$. Although this seems pointless at first, power series manipulations often reveal explicit formulas for $a_{n}$, which can hardly be seen by inductive arguments. We give a first impression with the most familiar generating functions.

Example 5.1

• 1. The number of $k$-element subsets of an $n$-element set is $\binom{n}{k}$ with generating function $(1+X)^{n}$. A $k$-element multi-subset $\{a_{1},\ldots ,a_{k}\}$ of $\{1,\ldots ,n\}$ with $a_{1}\le \cdots \le a_{k}$ (where elements are allowed to appear more than once) can be turned into a $k$-element subset $\{a_{1},a_{2}+1,\ldots ,a_{k}+k-1\}$ of $\{1,\ldots ,n+k-1\}$ and vice versa. The number of $k$-element multi-subsets of an $n$-element set is therefore $\binom{n+k-1}{k}$ with generating function $(1-X)^{-n}$ by Newton’s binomial theorem.

• 2. The number of $k$-dimensional subspaces of an $n$-dimensional vector space over a finite field with $q<\infty$ elements is 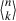evaluated at $X=q$ (indeed there are $(q^{n}-1)(q^{n}-q)\ldots (q^{n}-q^{n-k+1})$ linearly independent $k$-tuples and $(q^{k}-1)(q^{k}-q)\ldots (q^{k}-q^{k-1})$ of them span the same subspace). The generating function is closely related to Gauss’ binomial theorem.

• 3. The Fibonacci numbers $f_{n}$ are defined by $f_{n}:=n$ for $n=0,1$ and $f_{n+1}:=f_{n}+f_{n-1}$ for $n\ge 1$. The generating function $\alpha$ satisfies $\alpha =X+X^{2}\alpha +X\alpha$ and is therefore given by $\alpha =\frac{X}{1-X-X^{2}}$. An application of the partial fraction decomposition (2.1) leads to the well-known Binet formula

  $$ f_{n}=\frac{1}{\sqrt{5}}\Bigl(\frac{1+\sqrt{5}}{2}\Bigr)^{n}- \frac{1}{\sqrt{5}}\Bigl(\frac{1-\sqrt{5}}{2}\Bigr)^{n}.$$

• 4. The Catalan numbers $c_{n}$ are defined by $c_{n}:=n$ for $n=0,1$ and $c_{n}:=\sum _{k=1}^{n-1}c_{k}c_{n-k}$ for $n\ge 2$ (most authors shift the index by 1). Its generating function $\alpha$ fulfills $\alpha -\alpha ^{2}=X$, i.e. it is the reverse of $X-X^{2}$. This quadratic equation has only one solution $\alpha =\frac{1}{2}(1-\sqrt{1-4X})$ in $\mathbb{C}[[X]]^{\circ}$. Newton’s binomial theorem can be used to derive $c_{n+1}=\frac{1}{n+1}\binom{2n}{n}$. A slightly shorter proof based on Lagrange–Bürmann’s inversion formula is given in Example 7.6 below.

We now focus on combinatorial objects which defy explicit formulas.

Definition 5.2

A partition of $n\in \mathbb{N}$ is a sequence of positive integers $\lambda =(\lambda _{1},\ldots ,\lambda _{l})$ such that $\lambda _{1}+\cdots +\lambda _{l}=n$ and $\lambda _{1}\ge \cdots \ge \lambda _{l}$. We call $\lambda _{1},\ldots ,\lambda _{l}$ the parts of $\lambda$. The set of partitions of $n$ is denoted by $P(n)$ and its cardinality is $p(n):=|P(n)|$. For $k\in \mathbb{N}_{0}$ let $p_{k}(n)$ be the number of partitions of $n$ with each part $\lambda _{i}\le k$. Finally, let $p_{k,l}(n)$ be the number of partitions of $n$ with each part $\le k$ and at most $l$ parts in total. Clearly, $p_{1}(n)=p_{n,1}(n)=1$ and $p_{n}(n)=p_{n,n}(n)=p(n)$. Moreover, $p_{k,l}(n)=0$ whenever $n>kl$. For convenience let $p(0)=p_{0}(0)=p_{0,0}(0)=1$ (0 can be interpreted as the empty sum).

Example 5.3

The partitions of $n=7$ are

$$\begin{gathered} (7),(6,1),(5,2),(5,1^{2}),(4,3),(4,2,1),(4,1^{3}),(3^{2},1), \\ (3,2^{2}),(3,2,1^{2}),(3,1^{4}),(2^{3},1),(2^{2},1^{3}),(2,1^{5}),(1^{7}). \end{gathered}$$

Hence, $p(7)=15$, $p_{3}(7)=8$ and $p_{3,3}(7)=2$.

Theorem 5.4

The generating functions of $p(n)$, $p_{k}(n)$ and $p_{k,l}(n)$ are given by

Proof

It is easy to see that $p_{k}(n)$ is the coefficient of $X^{n}$ in

$$ \begin{gathered} (1+X^{1}+X^{1+1}+\cdots )(1+X^{2}+X^{2+2}+\cdots )\ldots (1+X^{k}+X^{k+k}+ \cdots ) \\ =\frac{1}{1-X}\frac{1}{1-X^{2}}\ldots \frac{1}{1-X^{k}}= \frac{1}{X^{k}!}. \end{gathered} $$

(5.1)

This shows the second equation. The first follows from $p(n)=\lim _{k\to \infty}p_{k}(n)$. For the last claim we argue by induction on $k+l$ using (4.2). If $k=0$ or $l=0$, then both sides equal 1. Thus, let $k,l\ge 1$. Pick a partition $\lambda =(\lambda _{1},\lambda _{2},\ldots )$ of $n$ with each part $\le k$ and at most $l$ parts. If $\lambda _{1}< k$, then all parts are $\le k-1$ and $\lambda$ is counted by $p_{k-1,l}(n)$. If on the other hand $\lambda _{1}=k$, then $(\lambda _{2},\lambda _{3},\ldots )$ is counted by $p_{k,l-1}(n-k)$. Conversely, each partition counted by $p_{k,l-1}(n-k)$ can be extended to a partition counted by $p_{k,l}(n)$. We have proven the recurrence

$$ p_{k,l}(n)=p_{k-1,l}(n)+p_{k,l-1}(n-k).$$

Induction yields

 □

Theorem 5.5

The following assertions hold for $n,k,l\in \mathbb{N}_{0}$:

• 1. $p_{k,l}(n)=p_{l,k}(n)=p_{k,l}(kl-n)$ for $n\le kl$.

• 2. The number of partitions of $n$ into exactly $k$ parts is the number of partitions with largest part $k$.

• 3. (Glaisher) The number of partitions of $n$ into parts not divisible by $k$ equals the number of partitions with no part repeated $k$ times (or more).

• 4. (Euler) The number of partitions of $n$ into unequal parts is the number of partitions into odd parts.

• 5. (Schur) The number of partitions of $n$ in parts which differ by more than 1 equals the number of partitions in parts of the form $\pm 1+5k$.

• 6. (Schur) The number of partitions of $n$ in parts which differ by more than 1 and are larger than 1 equals the number of partitions into parts of the form $\pm 2+5k$.

Proof

• 1. Since , we obtain $p_{k,l}(n)=p_{l,k}(n)$ by Theorem 5.4. Let $\lambda =(\lambda _{1},\ldots ,\lambda _{s})$ be a partition counted by $p_{k,l}(n)$. After adding zero parts if necessary, we may assume that $s=l$. Then $\bar{\lambda}:=(k-\lambda _{l},k-\lambda _{l-1},\ldots ,k-\lambda _{1})$ is a partition counted by $p_{k,l}(kl-n)$. Since $\bar{\bar{\lambda}}=\lambda$, we obtain a bijection between the partitions counted by $p_{k,l}(n)$ and $p_{k,l}(kl-n)$.

• 2. The number of partitions of $n$ with largest part $k$ is $p_{k}(n)-p_{k-1}(n)$. The number of partitions with exactly $k$ parts is

  $$ p_{n,k}(n)-p_{n,k-1}(n)\overset{(i)}{=}p_{k,n}(n)-p_{k-1,n}(n)=p_{k}(n)-p_{k-1}(n).$$

• 3. Looking at (5.1) again, it turns out that the desired generating function is

  $$\begin{aligned} \prod _{k\,\nmid \, m}\frac{1}{1-X^{m}}&=\prod _{m=1}^{\infty} \frac{1-X^{km}}{1-X^{m}}\\&=(1+X+\cdots +X^{k-1})(1+X^{2}+\cdots +X^{2(k-1)}) \ldots . \end{aligned}$$

• 4. Take $k=2$ in (iii).

• 5. According to [36, Sect. 2.4], it was Schur, who first gave this interpretation of the Rogers–Ramanujan identities. The coefficient of $X^{n}$ on the left hand side of (4.16) is the number of partitions into parts of the form $\pm 1+5k$. The right hand side can be rewritten (thanks to Theorem 5.4) as

  $$ \sum _{k=0}^{\infty}\sum _{n=0}^{\infty }p_{k}(n)X^{n+k^{2}}=\sum _{n=0}^{ \infty}\sum _{k=0}^{n}p_{k}(n-k^{2})X^{n}.$$

  By (ii), $p_{k}(n-k^{2})$ counts the partitions of $n-k^{2}$ with at most $k$ parts. If $(\lambda _{1},\ldots ,\lambda _{k})$ is such a partition (allowing $\lambda _{i}=0$ here), then $(\lambda _{1}+2k-1,\lambda _{2}+2k-3,\ldots ,\lambda _{k}+1)$ is a partition of $n-k^{2}+1+3+\cdots +2k-1=n$ with exactly $k$ parts, which all differ by more than 1.

• 6. This follows similarly using $k^{2}+k=2+4+\cdots +2k$.

 □

There is a remarkable connection between (iii), (iv) and (v) of Theorem 5.5: Numbers not divisible by 3 are of the form $\pm 1+3k$, while odd numbers are of the form $\pm 1+4k$.

Example 5.6

For $n=7$ the following partitions are counted by Theorem 5.5:

exactly three parts:	(5,12),	(4,2,1),	(32,1),	(3,22)
largest part 3:	(32,1),	(3,22),	(3,2,12),	(3,14)
unequal parts:	(7),	(6,1),	(5,2),	(4,3),	(4,2,1)
odd parts:	(7),	(5,12),	(32,1),	(3,14),	(17)
parts differ by more than 1:	(7),	(6,1),	(5,2)
parts of the form ±1 + 5k	(6,1),	(4,13),	(17)
parts ≥2 differ by more than 1:	(7),	(5,2)
parts of the form ±2 + 5k	(7),	(3,22)

Some of the statements in Theorem 5.5 permit nice combinatorial proofs utilizing Young diagrams (or Ferres diagrams). We refer the reader to the introductory book [5]. The following exercise (inspired by [5]) can be solved with formal power series.

Exercise 5.7

Prove the following statements for $n,k\in \mathbb{N}$:

• 1. The number of partition of $n$ into even parts is the number of partitions whose parts have even multiplicity.

• 2. (Legendre) If $n$ is not of the form $\frac{1}{2}(3k^{2}+k)$ with $k\in \mathbb{Z}$, then the number of partitions of $n$ into an even number of unequal parts is the number of partitions into an odd number of unequal parts.

  Hint: Where have we encountered $\frac{1}{2}(3k^{2}+k)$ before?

• 3. (Subbarao) The number of partitions of $n$ where each part appears 2, 3 or 5 times equals the number of partitions into parts of the form $\pm 2+12k$, $\pm 3+12k$ or $6+12k$.

• 4. (MacMahon) The number of partitions of $n$ where each part appears at least twice equals the number of partitions in parts not of the form $\pm 1+6k$.

The reader may have noticed that Euler’s pentagonal number theorem (4.10) is just the inverse of the generating function of $p(n)$ from Theorem 5.4, i.e.

$$ \sum _{n=0}^{\infty }p(n)X^{n}\cdot \sum _{k=-\infty}^{\infty}(-1)^{k}X^{ \frac{3k^{2}+k}{2}}=1$$

and therefore

$$ \sum _{k=-n}^{n}(-1)^{k}p\Bigl(n-\frac{3k^{2}+k}{2}\Bigr)=0$$

for $n\in \mathbb{N}$, where $p(k):=0$ whenever $k<0$. This leads to a recurrence formula

$$\begin{aligned} p(0)&=1, \\ p(n)&=p(n-1)+p(n-2)-p(n-5)-p(n-7)+\cdots \qquad (n\in \mathbb{N}). \end{aligned}$$

Example 5.8

We compute

$$\begin{array}{rlrl}p(1)& =p(0)=1,& p(4)& =p(3)+p(2)=3+2=5,\\ p(2)& =p(1)+p(0)=2,& p(5)& =p(4)+p(3)-p(0)=5+3-1=7,\\ p(3)& =p(2)+p(1)=3,& p(6)& =p(5)+p(4)-p(1)=7+5-1=11\end{array}$$

(see https://oeis.org/A000041 for more terms).

The generating functions we have seen so far all have integer coefficients. If $\alpha ,\beta \in \mathbb{Z}[[X]]$ and $d\in \mathbb{N}$, we write $\alpha \equiv \beta \pmod{d}$, if all coefficients of $\alpha -\beta$ are divisible by $d$. This is compatible with the ring structure of $\mathbb{Z}[[X]]$, namely if $\alpha \equiv \beta \pmod{d}$ and $\gamma \equiv \delta \pmod{d}$, then $\alpha +\gamma \equiv \beta +\delta \pmod{d}$ and $\alpha \gamma \equiv \beta \delta \pmod{d}$. Now suppose $\alpha \in 1+(X)$. Then the proof of Lemma 2.5 shows $\alpha ^{-1}\in \mathbb{Z}[[X]]$. In this case $\alpha \equiv \beta \pmod{d}$ is equivalent to $\alpha ^{-1}\equiv \beta ^{-1}\pmod{d}$. If $d=p$ happens to be a prime, we have

$$ (\alpha +\beta )^{p}=\sum _{k=0}^{p}\frac{p(p-1)\ldots (p-k+1)}{k!} \alpha ^{k}\beta ^{p-k}\equiv \alpha ^{p}+\beta ^{p}\pmod{p},$$

as in any commutative ring of characteristic $p$.

With this preparation, we come to a remarkable discovery by Ramanujan [34].

Theorem 5.9

Ramanujan

The following congruences hold for all $n\in \mathbb{N}_{0}$:

$$ \boxed{p(5n+4)\equiv 0\pmod{5},\qquad p(7n+5)\equiv 0\pmod{7}.}$$

Proof

Let $\alpha :=\prod _{k=1}^{\infty}(1-X^{k})$. By the remarks above, $\alpha ^{5}=\prod _{k=1}^{\infty}(1-X^{k})^{5}\equiv \prod _{k=1}^{ \infty}(1-X^{5k})\equiv \alpha (X^{5})\pmod{5}$ and $\alpha ^{-5}\equiv \alpha (X^{5})^{-1}\pmod{5}$. For $k\in \mathbb{Z}$ we compute

$$ \frac{1}{2}(k^{2}+k)\equiv \textstyle\begin{cases} 0&\text{if }k\equiv 0,-1\pmod{5}, \\ 1&\text{if }k\equiv 1,-2\pmod{5}, \\ 3&\text{if }k\equiv 2\pmod{5}. \end{cases} $$

This allows to write Jacobi’s identity (4.13) in the form

where $\alpha _{i}$ is formed by the monomials $a_{k}X^{k}$ with $k\equiv i\pmod{5}$. Now Theorem 5.4 implies

$$ \sum _{n=0}^{\infty }p(n)X^{n}=\alpha ^{-1}= \frac{(\alpha ^{3})^{3}}{(\alpha ^{5})^{2}}\equiv \frac{(\alpha _{0}+\alpha _{1})^{3}}{\alpha (X^{5})^{2}}\pmod{5}. $$

(5.2)

If we expand $(\alpha _{0}+\alpha _{1})^{3}$, then only terms $X^{k}$ with $k\equiv 0,1,2,3\pmod{5}$ occur, while in $\alpha (X^{5})^{-2}$ only terms $X^{5k}$ occur. Therefore the right hand side of (5.2) contains no terms of the form $X^{5k+4}$. So we must have $p(5k+4)\equiv 0\pmod{5}$.

For the congruence modulo 7 we compute similarly $\frac{1}{2}(k^{2}+k)\equiv 0,1,3,6\pmod{7}$, where the last case only occurs if $k\equiv 3\pmod{7}$ and in this case $2k+1\equiv 0\pmod{7}$. As before we may write $\alpha ^{3}\equiv \alpha _{0}+\alpha _{1}+\alpha _{3}\pmod{7}$. Then

$$ \sum _{n=0}^{\infty }p(n)X^{n}=\alpha ^{-1}= \frac{(\alpha ^{3})^{2}}{\alpha ^{7}}\equiv \frac{(\alpha _{0}+\alpha _{1}+\alpha _{3})^{2}}{\alpha (X^{7})} \pmod{7}. $$

Again $X^{7k+5}$ does not appear on the right hand side. □

Ramanujan has also discovered the congruence $p(11n+6)\equiv 0\pmod{11}$ for all $n\in \mathbb{N}_{0}$ (the reader finds the history of this and other results in [5, 17], for instance). This was believed to be more difficult to prove, until elementary proofs were found by Marivani [29], Hirschhorn [16] and others (see also [17, Sect. 3.5]). The details are however extremely tedious to verify by hand.

By the Chinese remainder theorem, two congruence of coprime moduli can be combined as in

$$ p(35n+19)\equiv 0\pmod{35}.$$

Ahlgren [1] (building on Ono [33]) has shown that in fact for every integer $k$ coprime to 6 there is such a congruence modulo $k$. Unfortunately, they do not look as nice as Theorem 5.9. For instance,

$$ p(11^{3}\cdot 13n+237)\equiv 0\pmod{13}.$$

The next result explains the congruence modulo 5 and is known as Ramanujan’s “most beautiful” formula (since Theorem 4.15 was first discovered by Rogers).

Theorem 5.10

Ramanujan

We have

$$ \boxed{\sum _{n=0}^{\infty }p(5n+4)X^{n}=5\prod _{k=1}^{\infty}\frac{(1-X^{5k})^{5}}{(1-X^{k})^{6}}.}$$

Proof

The arguments are taken from [17, Chap. 5], leaving out some unessential details. This time we start with Euler’s pentagonal number theorem. Since

$$ \frac{3k^{2}+k}{2}\equiv \textstyle\begin{cases} 0&\text{if }k\equiv 0,-2\pmod{5}, \\ 1&\text{if }k\equiv -1\pmod{5}, \\ 2&\text{if }k\equiv 1,2\pmod{5}, \end{cases} $$

we can write (4.10) in the form

$$ \alpha :=\prod _{k=1}^{\infty}(1-X^{k})=\sum _{k=-\infty}^{\infty }(-1)^{k}X^{ \frac{3k^{2}+k}{2}}=\alpha _{0}+\alpha _{1}+\alpha _{2},$$

where $\alpha _{i}$ is formed by the terms $a_{k}X^{k}$ with $k\equiv i\pmod{5}$. In fact,

$$ \alpha _{1}=\sum _{k=-\infty}^{\infty }(-1)^{5k-1}X^{ \frac{3(5k-1)^{2}+5k-1}{2}}=-X\sum _{k=-\infty}^{\infty}(-1)^{k}X^{ \frac{75k^{2}-25k}{2}}=-X\alpha (X^{25}). $$

(5.3)

On the other hand we have

$$ \sum _{k=0}^{\infty}(-1)^{k}(2k+1)X^{\frac{k^{2}+k}{2}} \overset{\text{(4.13)}}{=}\alpha ^{3}=(\alpha _{0}+\alpha _{1}+ \alpha _{2})^{3}.$$

When we expand the right hand side, the monomials of the form $X^{5k+2}$ all occur in $3\alpha _{0}(\alpha _{0}\alpha _{2}+\alpha _{1}^{2})$. Since we have already realized in the proof of Theorem 5.9 that $(k^{2}+k)/2\not \equiv 2\pmod{5}$, we conclude that

$$ \alpha _{1}^{2}=-\alpha _{0}\alpha _{2}. $$

(5.4)

Let $\zeta \in \mathbb{C}$ be a primitive 5-th root of unity. Using that

$$ X^{5}-1=\prod _{i=0}^{4}(X-\zeta ^{i})=\zeta ^{1+2+3+4}\prod _{i=0}^{4}( \zeta ^{-i}X-1)=\prod _{i=0}^{4}(\zeta ^{i}X-1),$$

we compute

$$ \prod _{i=0}^{4}\alpha (\zeta ^{i}X)=\prod _{k=0}^{\infty}\prod _{i=0}^{4}(1- \zeta ^{ik}X^{k})=\alpha (X^{5})^{5}\prod _{5\,\nmid \,k}(1-X^{5k})= \frac{\alpha (X^{5})^{6}}{\alpha (X^{25})}.$$

This leads to

$$\begin{aligned} \sum _{n=0}^{\infty}& p(n)X^{n}=\frac{1}{\alpha}= \frac{\alpha (X^{25})}{\alpha (X^{5})^{6}}\alpha (\zeta X)\alpha ( \zeta ^{2}X)\alpha (\zeta ^{3}X)\alpha (\zeta ^{4}X) \\ &=\frac{\alpha (X^{25})}{\alpha (X^{5})^{6}}(\alpha _{0}+\zeta \alpha _{1}+\zeta ^{2}\alpha _{2})(\alpha _{0}+\zeta ^{2}\alpha _{1}+ \zeta ^{4}\alpha _{2})(\alpha _{0}+\zeta ^{3}\alpha _{1}+\zeta \alpha _{2}) \\ &\quad{}\times(\alpha _{0}+\zeta ^{4}\alpha _{1}+\zeta ^{3}\alpha _{2}). \end{aligned}$$

(5.5)

We are only interested in the monomials $X^{5n+4}$. Those arise from the products $\alpha _{0}^{2}\alpha _{2}^{2}$, $\alpha _{0}\alpha _{1}^{2}\alpha _{2}$ and $\alpha _{1}^{4}$. To facilitate the expansion of the right hand side of (5.5), we notice that the Galois automorphism $\gamma$ of the cyclotomic field $\mathbb{Q}_{5}$ sending $\zeta$ to $\zeta ^{2}$ permutes the four factors cyclically. Whenever we obtain a product involving some $\zeta ^{i}$, say $\alpha _{0}^{2}\alpha _{2}^{2}\zeta ^{3}$, the full orbit under $\langle \gamma \rangle$ must occur, which is $\alpha _{0}^{2}\alpha _{2}^{2}(\zeta +\zeta ^{2}+\zeta ^{3}+\zeta ^{4})=- \alpha _{0}^{2}\alpha _{2}^{2}$. Now there are six choices to form $\alpha _{0}^{2}\alpha _{2}^{2}$. Four of them form a Galois orbit, while the two remaining appear without $\zeta$. The whole contribution is therefore $(1+1-1)\alpha _{0}^{2}\alpha _{2}^{2}=\alpha _{0}^{2}\alpha _{2}^{2}$. In a similar manner we compute,

$$\begin{aligned} \sum p(5n+4)X^{5n+4}&=\frac{\alpha (X^{25})}{\alpha (X^{5})^{6}}( \alpha _{0}^{2}\alpha _{2}^{2}-3\alpha _{0}\alpha _{1}^{2}\alpha _{2}+ \alpha _{1}^{4})\\&\overset{\text{(5.4)}}{=}5 \frac{\alpha (X^{25})}{\alpha (X^{5})^{6}}\alpha _{1}^{4} \overset{\text{(5.3)}}{=}5X^{4} \frac{\alpha (X^{25})^{5}}{\alpha (X^{5})^{6}}. \end{aligned}$$

The claim follows after dividing by $X^{4}$ and replacing $X^{5}$ by $X$. □

Partitions can be generalized to higher dimensions. A plane partition of $n\in \mathbb{N}$ is an $n\times n$-matrix $\lambda =(\lambda _{ij})$ consisting of non-negative integers such that

• $\lambda _{i,1}\ge \lambda _{i,2}\ge \ldots$ and $\lambda _{1,j}\ge \lambda _{2,j}\ge \ldots$ for all $i,j$,

• $\sum _{i,j=1}^{n}\lambda _{ij}=n$.

Ordinary partitions can be regarded as plane partitions with only one non-zero row. The number $pp(n)$ of plane partitions of $n$ has the fascinating generating function

$$ \sum _{n=0}^{\infty }pp(n)X^{n}=\prod _{k=1}^{\infty} \frac{1}{(1-X^{k})^{k}}=1+X+3X^{2}+6X^{3}+13X^{4}+24X^{5}+\cdots $$

discovered by MacMahon (see [37, Corollary 7.20.3]).

6 Stirling Numbers

We cannot resist to present a few more exciting combinatorial objects related to power series. Since literally hundreds of such combinatorial identities are known, our selection is inevitably biased by personal taste.

Definition 6.1

A set partition of $n\in \mathbb{N}$ is a disjoint union $A_{1}\mathbin{\dot{\cup}}\ldots \mathbin{\dot{\cup}} A_{k}=\{1,\ldots ,n \}$ of non-empty sets $A_{i}$ in no particular order (we may require $\min A_{1}<\cdots <\min A_{k}$ to fix an order). The number of set partitions of $n$ is called the $n$-th Bell number $b(n)$. The number of set partitions of $n$ with exactly $k$ parts is the Stirling number of the second kind . In particular, . We set describing the empty partition of the empty set.

Example 6.2

The set partitions of $n=3$ are

$$ \{1,2,3\}=\{1\}\cup \{2,3\}=\{1,3\}\cup \{2\}=\{1,2\}\cup \{3\}=\{1\} \cup \{2\}\cup \{3\}.$$

Hence, $b(3)=5$ and .

Unlike the binomial or Gaussian coefficients the Stirling numbers do not obey a symmetry as in Pascal’s triangle. While the generating functions of $b(n)$ and have no particularly nice shape, there are close approximations which we are about to see.

Lemma 6.3

For $n,k\in \mathbb{N}_{0}$,

(6.1)

Proof

Without loss of generality, let $1\le k\le n$. Let $A_{1}\cup \cdots \cup A_{k-1}$ a set partition of $n$ with $k-1$ parts. Then $A_{1}\cup \cdots \cup A_{k-1}\cup \{n+1\}$ is a set partition of $n+1$ with $k$ parts. Now let $A_{1}\cup \cdots \cup A_{k}$ be a set partition of $n$. We can add the number $n+1$ to each of the $k$ sets $A_{1},\ldots ,A_{k}$ to obtain a set partition of $n+1$ with $k$ parts. Conversely, every set partition of $n+1$ arises in precisely one of the two described ways. □

Lemma 6.4

For $n\in \mathbb{N}_{0}$,

$$ b(n+1)=\sum _{k=0}^{n}\binom{n}{k}b(k).$$

Proof

Every set partition $\mathcal{A}$ of $n+1$ has a unique part $A$ containing $n+1$. If $k:=|A|-1$, there are $\binom{n}{k}$ choices for $A$. Moreover, $\mathcal{A}\setminus A$ is a uniquely determined partition of the set $\{1,\ldots ,n\}\setminus A$ with $n-k$ elements. Hence, there are $b(n-k)$ possibilities for this partition. Consequently,

$$ b(n+1)=\sum _{k=0}^{n}\binom{n}{k}b(n-k)=\sum _{k=0}^{n}\binom{n}{k}b(k). $$

 □

Theorem 6.5

For $n\in \mathbb{N}$ we have

Proof

We prove both assertions by induction on $n$.

• 1. For $n=1$, we have

  

  as claimed. Assuming the claim for $n$, we have

  

• 2. Since $\exp (X)-1\in (X)$, we can substitute $X$ by $\exp (X)-1$ in $\exp (X)$. Let

  $$ \alpha :=\exp \bigl(\exp (X)-1\bigr)=\sum _{n=0}^{\infty} \frac{a_{n}}{n!}X^{n}.$$

  Then $a_{0}=\exp (\exp (0)-1)=\exp (0)=1=b(0)$. The chain rule gives

  $$\begin{aligned} \sum _{n=0}^{\infty}\frac{a_{n+1}}{n!}X^{n}&=\alpha '=\exp (X)\exp ( \exp (X)-1) \\ &=\Bigl(\sum _{k=0}^{\infty}\frac{1}{k!}X^{k}\Bigr)\Bigl(\sum _{k=0}^{ \infty}\frac{a_{k}}{k!}X^{k}\Bigr)=\sum _{n=0}^{\infty}\sum _{k=0}^{n} \frac{a_{k}}{k!(n-k)!}X^{n}. \end{aligned}$$

  Therefore, $a_{n+1}=\sum _{k=0}^{n}\binom{n}{k}a_{k}$ for $n\ge 0$ and the claim follows from Lemma 6.4.

 □

Now we discuss permutations.

Definition 6.6

Let $S_{n}$ be the symmetric group consisting of all permutations on the set $\{1,\ldots ,n\}$. The number of permutations in $S_{n}$ with exactly $k$ (disjoint) cycles including fixed points is denoted by the Stirling number of the first kind . By agreement, (the identity on the empty set has zero cycles).

Example 6.7

There are permutations in $S_{4}$ with exactly two cycles:

$$\begin{gathered} (1,2,3)(4),\ (1,3,2)(4),\ (1,2,4)(3),\ (1,4,2)(3),\ (1,3,4)(2),\ (1,4,3)(2), \\ (1)(2,3,4),\ (1)(2,4,3),\ (1,2)(3,4),\ (1,3)(2,4),\ (1,4)(2,3). \end{gathered}$$

Since $|S_{n}|=n!$, there is no need for a generating function of the number of permutations.

Lemma 6.8

For $k,n\in \mathbb{N}_{0}$,

(6.2)

Proof

Without loss of generality, let $1\le k\le n$. Let $\sigma \in S_{n}$ with exactly $k-1$ cycles. By appending the 1-cycle $(n+1)$ to $\sigma$ we obtain a permutation counted by . Now assume that $\sigma$ has $k$ cycles. When we write $\sigma$ as a sequence of $n$ numbers and $2k$ parentheses, there are $n$ meaningful positions where we can add the digit $n+1$. For example, there are three ways to add 4 in $\sigma =(1,2)(3)$, namely

$$ (4,1,2)(3),\quad (1,4,2)(3),\quad (1,2)(4,3).$$

This yields $n$ distinct permutations counted by . Conversely, every permutation counted by arises in precisely one of the described ways. □

While the recurrences relations we have seen so far appear arbitrary, they can be explained in a unified way (see [24]).

It is time to present the next dual pair of formulas resembling Theorem 4.6.

Theorem 6.9

The following generating functions of the Stirling numbers hold for $n\in \mathbb{N}$:

Proof

This is another induction on $n$.

• 1. The case $n=1$ yields 1 on both sides of the equation. Assuming the claim for $n$, we compute

  

• 2. For $n=1$, we get the geometric series $\frac{1}{1-X}=\sum X^{k}$ on both sides. Assume the claim for $n-1$. Then

  

 □

For readers who still do not have enough, the next exercise might be of interest.

Exercise 6.10

• 1. Prove Vandermonde’s identity $\sum _{k=0}^{n}\binom{a}{k}\binom{b}{n-k}=\binom{a+b}{n}$ for all $a,b\in \mathbb{C}$ by using Newton’s binomial theorem.

• 2. For every prime $p$ and $1< k< p$, show that is divisible by $p$ (a property shared with $\binom{p}{k}$).

• 3. Prove that

  

  for $n\in \mathbb{N}_{0}$.

• 4. Determine all $n\in \mathbb{N}$ such that the Catalan number $c_{n}$ is odd.

  Hint: Consider the generating function modulo 2.

• 5. The Bernoulli numbers $b_{n}\in \mathbb{Q}$ are defined directly by their (exponential) generating function

  $$ \frac{X}{\exp (X)-1}=\sum _{n=0}^{\infty }\frac{b_{n}}{n!}X^{n}.$$

  Compute $b_{0},\ldots ,b_{3}$ and show that $b_{2n+1}=0$ for every $n\in \mathbb{N}$.

  Hint: Replace $X$ by $-X$.

The cycle type of a permutation $\sigma \in S_{n}$ is denoted by $(1^{a_{1}},\ldots ,n^{a_{n}})$, meaning that $\sigma$ has precisely $a_{k}$ cycles of length $k$.

Lemma 6.11

The number of permutations $\sigma \in S_{n}$ with cycle type $(1^{a_{1}},\ldots ,n^{a_{n}})$ is

$$ \frac{n!}{1^{a_{1}}\ldots n^{a_{n}}a_{1}!\ldots a_{n}!}.$$

Proof

Each cycle of $\sigma$ determines a subset of $\{1,\ldots ,n\}$. The number of possibilities to choose such subsets is given by the multinomial coefficient

$$ \frac{n!}{(1!)^{a_{1}}\ldots (n!)^{a_{n}}}.$$

Since the $a_{i}$ subsets of size $i$ can be permuted in $a_{i}!$ ways, each corresponding to the same permutation (as disjoint cycles commute), the number of relevant choices is only

$$ \frac{n!}{(1!)^{a_{1}}\ldots (n!)^{a_{n}}a_{1}!\ldots a_{n}!}.$$

A given subset $\{\lambda _{1},\ldots ,\lambda _{k}\}\subseteq \{1,\ldots ,n\}$ can be arranged in $k!$ permutations, but only $(k-1)!$ different cycles, since $(\lambda _{1},\ldots ,\lambda _{k})=(\lambda _{2},\ldots ,\lambda _{k}, \lambda _{1})=\cdots$. Hence, the number of permutations in question is

$$ \frac{n!}{(1!)^{a_{1}}\ldots (n!)^{a_{n}}a_{1}!\ldots a_{n}!}\bigl((1-1)! \bigr)^{a_{1}}\ldots \bigl((n-1)!\bigr)^{a_{n}}= \frac{n!}{1^{a_{1}}\ldots n^{a_{n}}a_{1}!\ldots a_{n}!}. $$

 □

The following is a sibling to Glaisher’s theorem. For a non-negative real number $r$ we denote the largest integer $n\le r$ by $n=\lfloor r\rfloor$.

Theorem 6.12

Erdős–Turán

Let $n,d\in \mathbb{N}$. The number of permutations in $S_{n}$, whose cycle lengths are not divisible by $d$ is

$$ n!\prod _{k=1}^{\lfloor n/d\rfloor}\frac{kd-1}{kd}.$$

Proof

According to [30], the idea of the proof is credited to Pólya. We need to count permutations with cycle type $(1^{a_{1}},\ldots ,n^{a_{n}})$ where $a_{k}=0$ whenever $d\mid k$. By Lemma 6.11, the total number divided by $n!$ is the coefficient of $X^{n}$ in

$$\begin{aligned} \prod _{\substack{k=1\\d\,\nmid \, k}}^{\infty}\sum _{a=0}^{\infty } \frac{1}{a!}\Bigl(\frac{X^{k}}{k}\Bigr)^{a}&=\prod _{d\,\nmid \, k} \exp \Bigl(\frac{X^{k}}{k}\Bigr)\overset{\text{(3.4)}}{=}\exp \Bigl( \sum _{d\,\nmid \, k}\frac{X^{k}}{k}\Bigr)=\exp \Bigl(\sum _{k=1}^{ \infty}\frac{X^{k}}{k}-\sum _{k=1}^{\infty}\frac{X^{dk}}{dk}\Bigr) \\ &=\exp \Bigl(-\log (1-X)+\frac{1}{d}\log (1-X^{d})\Bigr) \overset{\text{(3.6)}}{=}\sqrt[d]{1-X^{d}}\,\frac{1}{1-X} \\ &=\frac{1-X^{d}}{1-X}(1-X^{d})^{\frac{1-d}{d}} \\ &\overset{\text{(4.1)}}{=}\Bigl(\sum _{r=0}^{d-1} X^{r}\Bigr) \biggl(\sum _{q=0}^{\infty}\binom{(1-d)/d}{q}(-X^{d})^{q}\biggr). \end{aligned}$$

Therein, $X^{n}$ appears if and only if $n=qd+r$ with $0\le r< d$ and $q=\lfloor n/d\rfloor$ (Euclidean division). In this case the coefficient is

$$ (-1)^{q}\binom{(1-d)/d}{q}=(-1)^{q}\prod _{k=1}^{q} \frac{\frac{1}{d}-k}{k}=\prod _{k=1}^{q}\frac{kd-1}{kd}. $$

 □

Example 6.13

A permutation has odd order as an element of $S_{n}$ if and only all its cycles have odd length. The number of such partitions is therefore

$$ n!\prod _{k=1}^{\lfloor n/2\rfloor}\frac{2k-1}{2k}= \textstyle\begin{cases} 1^{2}\cdot 3^{2}\cdot \ldots \cdot (n-1)^{2}&\text{if $n$ is even}, \\ 1^{2}\cdot 3^{2}\cdot \ldots \cdot (n-2)^{2}\cdot n& \text{if $n$ is odd}. \end{cases} $$

Exercise 6.14

Find and prove a similar formula for the number of permutations $\sigma \in S_{n}$ whose cycle lengths are all divisible by $d$.

We insert a well-known application of Bernoulli numbers.

Theorem 6.15

Faulhaber

For every $d\in \mathbb{N}$ there exists a polynomial $\alpha \in \mathbb{Q}[X]$ of degree $d+1$ such that $1^{d}+2^{d}+\cdots +n^{d}=\alpha (n)$ for every $n\in \mathbb{N}$.

Proof

We compute the generating function

$$\begin{aligned} \sum _{d=0}^{\infty}\Bigl(\sum _{k=1}^{n-1}k^{d}\Bigr) \frac{X^{d}}{d!}&=\sum _{k=1}^{n-1}\sum _{d=0}^{\infty} \frac{(kX)^{d}}{d!}=\sum _{k=1}^{n-1}\exp (kX)=\sum _{k=1}^{n-1}\exp (X)^{k}= \frac{\exp (X)^{n}-1}{\exp (X)-1} \\ &=\frac{\exp (nX)-1}{X}\frac{X}{\exp (X)-1}\overset{6.10(e)}{=} \sum _{k=0}^{\infty}\frac{n^{k+1}}{(k+1)!}X^{k}\sum _{l=0}^{\infty} \frac{b_{l}}{l!}X^{l} \\ &=\sum _{d=0}^{\infty}\sum _{k=0}^{d}\Bigl( \frac{n^{k+1}b_{d-k}d!}{(k+1)!(d-k)!}\Bigr)\frac{X^{d}}{d!} \\ &=\sum _{d=0}^{\infty}\sum _{k=0}^{d}\Bigl(\frac{1}{k+1}\binom{d}{k}b_{d-k}n^{k+1} \Bigr)\frac{X^{d}}{d!} \end{aligned}$$

and define $\alpha :=\sum _{k=0}^{d}\frac{1}{k+1}\binom{d}{k}b_{d-k}(X+1)^{k+1} \in \mathbb{Q}[X]$. Since $b_{0}=1$, $\alpha$ is a polynomial of degree $d+1$ with leading coefficient $\frac{1}{d+1}$. □

Example 6.16

For $d=3$ the formula in the proof evaluates with some effort (using Exercise 6.10) to:

$$\begin{aligned} \alpha &=b_{3}(X+1)+\frac{3}{2}b_{2}(X+1)^{2}+b_{1}(X+1)^{3}+ \frac{1}{4}b_{0}(X+1)^{4}=\frac{1}{4}(X+1)^{2}X^{2}\\&=\binom{X+1}{2}^{2}. \end{aligned}$$

This is known as Nicomachus’s identity:

$$ 1^{3}+2^{3}+\cdots +n^{3}=(1+2+\cdots +n)^{2}.$$

Even though Faulhaber’s formula $1^{d}+2^{d}+\cdots +n^{d}=\alpha (n)$ has not much to do with power series, there still is a dual formula, again featuring Bernoulli numbers:

$$ \sum _{k=1}^{\infty}\frac{1}{k^{2d}}=(-1)^{d+1} \frac{(2\pi )^{2d}b_{2d}}{2(2d)!}\qquad (d\in \mathbb{N}).$$

Strangely, no such formula is known to hold for odd negative exponents (perhaps because $b_{2d+1}=0$?). In fact, it is unknown if Apéry’s constant $\sum _{k=1}^{\infty}\frac{1}{k^{3}}=1{,}202\ldots$ is transcendent.

We end this section with a power series proof of the famous four-square theorem.

Theorem 6.17

Lagrange–Jacobi

Every positive integer is the sum of four squares. More precisely,

$$ q(n):=\bigl|\{(a,b,c,d)\in \mathbb{Z}^{4}:a^{2}+b^{2}+c^{2}+d^{2}=n\} \bigr|=8\sum _{4\,\nmid \, d\,\mid \,n}d$$

for $n\in \mathbb{N}$.

Proof

We follow [17, Sect. 2.4]. Obviously, it suffices to prove the second assertion (by Jacobi). Since the summands $(-1)^{k}(2k+1)X^{\frac{k^{2}+k}{2}}$ in Theorem 4.13 are invariant under the transformation $k\mapsto -k-1$, we can write

$$ \prod _{k=1}^{\infty}(1-X^{k})^{3}=\frac{1}{2}\sum _{k=-\infty}^{ \infty}(-1)^{k}(2k+1) X^{\frac{k^{2}+k}{2}}.$$

Taking the square on both sides yields

$$ \alpha :=\prod _{k=1}^{\infty}(1-X^{k})^{6}=\frac{1}{4}\sum _{k,l=- \infty}^{\infty }(-1)^{k+l}(2k+1)(2l+1)X^{\frac{k^{2}+k+l^{2}+l}{2}}.$$

The pairs $(k,l)$ with $k\equiv l\pmod{2}$ are transformed by $(k,l)\mapsto (s,t):=\frac{1}{2}(k+l,k-l)$, while the pairs $k\not \equiv l\pmod{2}$ are transformed by $(s,t):=\frac{1}{2}(k-l-1,k+l+1)$. Notice that $k=s+t$ and $l=s-t$ or $l=t-s-1$ respectively. Hence,

$$\begin{aligned} \alpha &=\frac{1}{4}\sum _{s,t=-\infty}^{\infty }(2s+2t+1)(2s-2t+1)X^{ \frac{(s+t)^{2}+s+t+(s-t)^{2}+s-t}{2}} \\ &\quad -\frac{1}{4}\sum _{s,t=-\infty}^{\infty}(2s+2t+1)(2t-2s-1)X^{ \frac{(s+t)^{2}+s+t+(t-s-1)^{2}+t-s-1}{2}} \\ &=\frac{1}{4}\sum _{s,t=-\infty}^{\infty}\bigl((2s+1)^{2}-(2t)^{2} \bigr)X^{s^{2}+s+t^{2}}-\frac{1}{4}\sum _{s,t=-\infty}^{\infty}\bigl((2t)^{2}-(2s+1)^{2} \bigr)X^{s^{2}+s+t^{2}} \\ &=\frac{1}{2}\sum _{s,t=-\infty}^{\infty}\bigl((2s+1)^{2}-(2t)^{2} \bigr)X^{s^{2}+s+t^{2}} \\ &=\frac{1}{2}\sum _{t=-\infty}^{\infty }X^{t^{2}}\sum _{s=-\infty}^{ \infty}(2s+1)^{2}X^{s^{2}+s}-\frac{1}{2}\sum _{s=-\infty}^{\infty }X^{s^{2}+s} \sum _{t=-\infty}^{\infty }(2t)^{2}X^{t^{2}}. \end{aligned}$$

For $\beta :=\sum X^{t^{2}}$ and $\gamma :=\frac{1}{2}\sum X^{s^{2}+s}$ we have $\gamma +4X\gamma '=\frac{1}{2}\sum (2s+1)^{2}X^{s^{2}+s}$ and therefore

$$ \alpha =\beta (\gamma +4X\gamma ')-4X\beta '\gamma =\beta \gamma +4X( \beta \gamma '-\beta '\gamma ).$$

Now we apply the infinite product rule to (4.7) and (4.9):

$$\begin{aligned} \beta '&=\Bigl(\prod _{k=1}^{\infty}(1-X^{2k})(1+X^{2k-1})^{2}\Bigr)'= \beta \sum _{k=1}^{\infty}\Bigl(2\frac{(2k-1)X^{2k-2}}{1+X^{2k-1}}- \frac{2kX^{2k-1}}{1-X^{2k}}\Bigr) \\ \gamma '&=\Bigl(\prod _{k=1}^{\infty}(1-X^{2k})(1+X^{2k})^{2}\Bigr)'= \gamma \sum _{k=1}^{\infty}\Bigl(2\frac{2kX^{2k-1}}{1+X^{2k}}- \frac{2kX^{2k-1}}{1-X^{2k}}\Bigr) \end{aligned}$$

We substitute:

$$\begin{aligned} \alpha &=\beta \gamma \Bigl(1+8\sum _{k=1}^{\infty}\Bigl( \frac{2kX^{2k}}{1+X^{2k}}-\frac{(2k-1)X^{2k-1}}{1+X^{2k-1}}\Bigr) \Bigr). \end{aligned}$$

Here,

$$\begin{aligned} \beta \gamma &=\prod _{k=1}^{\infty}(1-X^{2k})^{2}(1+X^{2k-1})^{2}(1+X^{2k})^{2}= \prod _{k=1}^{\infty}(1-X^{2k})^{2}(1+X^{k})^{2}\\&=\prod _{k=1}^{\infty}(1-X^{2k})^{4}(1-X^{k})^{-2}. \end{aligned}$$

After we set this off against $\alpha$, it remains

$$\begin{aligned} \Bigl(\sum _{k=-\infty}^{\infty }(-1)^{k}X^{k^{2}}\Bigr)^{4} &\overset{\text{(4.8)}}{=}\prod _{k=1}^{\infty} \frac{(1-X^{k})^{8}}{(1-X^{2k})^{4}}=\frac{\alpha}{\beta \gamma}\\&=1+8 \sum _{k=1}^{\infty}\Bigl(\frac{2kX^{2k}}{1+X^{2k}}- \frac{(2k-1)X^{2k-1}}{1+X^{2k-1}}\Bigr) \end{aligned}$$

Finally we replace $X$ by $-X$:

$$\begin{aligned} \sum q(n)X^{n}&=\Bigl(\sum _{k=-\infty}^{\infty }X^{k^{2}}\Bigr)^{4}=1+8 \sum _{k=1}^{\infty}\Bigl(\frac{2kX^{2k}}{1+X^{2k}}+ \frac{(2k-1)X^{2k-1}}{1-X^{2k-1}}\Bigr) \\ &=1+8\sum _{k=1}^{\infty}\Bigl(\frac{(2k-1)X^{2k-1}}{1-X^{2k-1}}+ \frac{2kX^{2k}}{1-X^{2k}}-\frac{2kX^{2k}}{1-X^{2k}}+ \frac{2kX^{2k}}{1+X^{2k}}\Bigr) \\ &=1+8\sum _{k=1}^{\infty}\Bigl(\frac{kX^{k}}{1-X^{k}}- \frac{4kX^{4k}}{1-X^{4k}}\Bigr)=1+8\sum _{4\,\nmid \, k} \frac{kX^{k}}{1-X^{k}} \\ &=1+8\sum _{4\,\nmid \, k}k\sum _{l=1}^{\infty }X^{kl}=1+8\sum _{n=1}^{ \infty}\sum _{4\,\nmid \, d\,\mid \, n}dX^{n}. \end{aligned}$$

 □

Example 6.18

For $n=28$ we obtain

$$ \sum _{4\,\nmid \, d\,\mid \, 28}d=1+2+7+14=24.$$

Hence, there are $8\cdot 24=192$ possibilities to express 28 as a sum of four squares. However, they all arise as permutations and sign-choices of

$$ 28=5^{2}+1^{2}+1^{2}+1^{2}=4^{2}+2^{2}+2^{2}+2^{2}=3^{2}+3^{2}+3^{2}+1^{2}.$$

Theorem 6.17 is best possible in the sense that every integers $n\equiv 7\pmod{8}$ is not the sum of three squares since $a^{2}+b^{2}+c^{2}\not \equiv 7\mod{8}$.

If $n,m\in \mathbb{N}$ are sums of four squares, so is $nm$ by the following identity of Euler (encoding the multiplicativity of the norm in Hamilton’s quaternion skew field):

$$\begin{gathered} (a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2})(b_{1}^{2}+b_{2}^{2}+b_{3}^{2}+b_{4}^{2})=(a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}+a_{4}b_{4})^{2} \\ +(a_{1}b_{2}-a_{2}b_{1}+a_{3}b_{4}+a_{4}b_{3})^{2}+(a_{1}b_{3}-a_{3}b_{1}+a_{4}b_{2}-a_{2}b_{4})^{2} \\ +(a_{1}b_{4}-a_{4}b_{1}+a_{2}b_{3}-a_{3}b_{2})^{2} \end{gathered}$$

This reduces the proof of the first assertion (Lagrange’s) of Theorem 6.17 to the case where $n$ is a prime.

Waring’s problem ask for the smallest number $g(k)$ such that every positive integer is the sum of $g(k)$ non-negative $k$-th powers. Hilbert proved that $g(k)<\infty$ for all $k\in \mathbb{N}$. We have $g(1)=1$, $g(2)=4$ (Theorem 6.17), $g(3)=9$, $g(4)=19$ and in general it is conjectured that

$$ g(k)=\Bigl\lfloor \Bigl(\frac{3}{2}\Bigr)^{k}\Bigr\rfloor +2^{k}-2$$

(see [25]). Curiously, only the numbers $23=2\cdot 2^{3}+7\cdot 1^{3}$ and $239=2\cdot 4^{3}+4\cdot 3^{3}+3\cdot 1^{3}$ require nine cubes. It is even conjectured that every sufficiently large integer is a sum of only four non-negative cubes (see [11]).

7 Laurent Series

Every integral domain $R$ can be embedded into its field of fractions consisting of the formal fractions $\frac{r}{s}$ where $r,s\in R$ and $s\ne 0$ (this is the smallest field containing $R$ as a subring). For our ring $K[[X]]$ these fractions have a more convenient shape.

Definition 7.1

A (formal) Laurent series in the indeterminant $X$ over the field $K$ is a sum of the form

$$ \alpha =\sum _{k=m}^{\infty }a_{k}X^{k}$$

where $m\in \mathbb{Z}$ and $a_{k}\in K$ for $k\ge m$ (i.e. we allow $X$ to negative powers). We often write $\alpha =\sum _{k=-\infty}^{\infty }a_{k}X^{k}$ assuming that $\inf (\alpha )=\inf \{k\in \mathbb{Z}:a_{k}\ne 0\}$ exists. The set of all Laurent series over $K$ is denoted by $K((X))$. Laurent series can be added and multiplied like power series:

$$ \alpha +\beta =\sum _{k=-\infty}^{\infty}(a_{k}+b_{k})X^{k},\qquad \alpha \beta =\sum _{k=-\infty}^{\infty}\Bigl(\sum _{l=-\infty}^{ \infty }a_{l}b_{k-l}\Bigr)X^{k}$$

(one should check that the inner sum is finite). Moreover, the norm $|\alpha |$ and the derivative $\alpha '$ are defined as for power series.

If a Laurent series is a finite sum, it is naturally called a Laurent polynomial. The ring of Laurent polynomials is denoted by $K[X,X^{-1}]$, but plays no role in the following. In analysis one allows double infinite sums, but then the product is no longer well defined as in $\Bigl(\sum _{n=-\infty}^{\infty }X^{n}\Bigr)^{2}$.

Theorem 7.2

The field of fractions of $K[[X]]$ is naturally isomorphic to $K((X))$. In particular, $K((X))$ is a field.

Proof

Repeating the proof of Lemma 2.2 shows that $K((X))$ is a commutative ring. Let $\alpha \in K((X))\setminus \{0\}$ and $k:=\inf (\alpha )$. By Lemma 2.5, $X^{-k}\alpha \in K[[X]]^{\times}$. Hence, $X^{-k}(X^{-k}\alpha )^{-1}\in K((X))$ is the inverse of $\alpha$. This shows that $K((X))$ is a field. By the universal property of the field of fractions $Q(K[[X]])$, the embedding $K[[X]]\subseteq K((X))$ extends to a (unique) field monomorphism $f\colon Q(K[[X]])\to K((X))$. If $k=\inf (\alpha )<0$, then $f\bigl(\frac{X^{-k}\alpha}{X^{-k}}\bigr)=\alpha$ and $f$ is surjective. □

Of course, we will view $K[[X]]$ as a subring of $K((X))$. In fact, $K[[X]]$ is the valuation ring of $K((X))$, i.e. $K[[X]]=\{\alpha \in K((X)):|\alpha |\le 1\}$. The field $K((X))$ should not be confused with the field of rational functions $K(X)$, which is the field of fractions of $K[X]$.

If $\alpha \in K((X))$ and $\beta \in K[[X]]^{\circ}$, the substitute $\alpha (\beta )$ is still well-defined and Lemma 3.3 remains correct ($\alpha$ deviates from a power series by only finitely many terms).

Definition 7.3

The (formal) residue of $\alpha =\sum a_{k}X^{k}\in K((X))$ is defined by $\operatorname{res}(\alpha ):=a_{-1}$.

The residue is a $K$-linear map such that $\operatorname{res}(\alpha ')=0$ for all $\alpha \in K((X))$.

Lemma 7.4

For $\alpha ,\beta \in K((X))$ we have

$$\begin{array}{rl}res({\alpha }^{\prime }\beta )& =-res(\alpha {\beta }^{\prime })\\ res({\alpha }^{\prime }/\alpha )& =inf(\alpha )& & (\alpha \ne 0)\\ res(\alpha )inf(\beta )& =res(\alpha (\beta ){\beta }^{\prime })& & (\beta \in (X))\end{array}$$

Proof

• 1. This follows from the product rule

  $$ 0=\operatorname{res}((\alpha \beta )')=\operatorname{res}(\alpha ' \beta )+\operatorname{res}(\alpha \beta ').$$

• 2. Let $\alpha =X^{k}\gamma$ with $k=\inf (\alpha )$ and $\gamma \in K[[X]]^{\times}$. Then

  $$ \frac{\alpha '}{\alpha}= \frac{kX^{k-1}\gamma +X^{k}\gamma '}{X^{k}\gamma}=kX^{-1}+\gamma ' \gamma ^{-1}.$$

  Since $\gamma ^{-1}\in K[[X]]$, it follows that $\operatorname{res}(\alpha '/\alpha )=k=\inf (\alpha )$.

• 3. Since $\operatorname{res}$ is a linear map, we may assume that $\alpha =X^{k}$. If $k\ne -1$, then

  $$ \operatorname{res}(\alpha (\beta )\beta ')=\operatorname{res}(\beta ^{k} \beta ')=\operatorname{res}\Bigl(\Bigl(\frac{\beta ^{k+1}}{k+1}\Bigr)' \Bigr)=0=\operatorname{res}(\alpha )=\operatorname{res}(\alpha )\inf ( \beta ).$$

  If $k=-1$, then

  $$ \operatorname{res}(\alpha (\beta )\beta ')=\operatorname{res}(\beta '/ \beta )\overset{(ii)}{=}\inf (\beta )=\operatorname{res}(\alpha ) \inf (\beta ). $$

 □

Theorem 7.5

Lagrange–Bürmann’s inversion formula

Let $\operatorname{char}K=0$. The reverse of $\alpha \in K[[X]]^{\circ}$ is

$$ \boxed{\sum _{k=1}^{\infty }\frac{\operatorname{res}(\alpha ^{-k})}{k}X^{k}.}$$

Proof

The proof is influenced by [12]. Let $\beta \in K[[X]]^{\circ}$ be the reverse of $\alpha$, i.e. $\alpha (\beta )=X$. From $\alpha \in K[[X]]^{\circ}$ we know that $\alpha \ne 0$. In particular, $\alpha$ is invertible in $K((X))$. By Lemma 3.3, we have $\alpha ^{-k}(\beta )=X^{-k}$. Now the coefficient of $X^{k}$ in $\beta$ turns out to be

$$\begin{aligned} \frac{1}{k}\operatorname{res}(kX^{-k-1}\beta )&=-\frac{1}{k} \operatorname{res}\bigl((X^{-k})'\beta \bigr)=\frac{1}{k} \operatorname{res}(X^{-k}\beta ')=\frac{1}{k}\operatorname{res}\bigl( \alpha ^{-k}(\beta )\beta '\bigr)\\& =\frac{1}{k}\operatorname{res}( \alpha ^{-k}) \end{aligned}$$

by Lemma 7.4. □

Since Theorem 7.5 is actually a statement about power series, it should be mentioned that $\operatorname{res}(\alpha ^{-k})$ is just the coefficient of $X^{k-1}$ in the power series $(X/\alpha )^{k}$. This interpretation will be used in our generalization to higher dimensions in Theorem 9.8.

Example 7.6

Recall from Example 5.1 that the generating function $\alpha$ of the Catalan numbers $c_{n}$ is the reverse of $X-X^{2}$. Since

$$ \Bigl(\frac{X}{X-X^{2}}\Bigr)^{n+1}=(1-X)^{-n-1} \overset{\text{(4.1)}}{=}\sum _{k=0}^{\infty}\binom{-n-1}{k}(-1)^{k}X^{k},$$

we compute

$$ c_{n+1}=\frac{\operatorname{res}(\alpha ^{-n-1})}{n+1}=\frac{1}{n+1}(-1)^{n} \binom{-n-1}{n}=\frac{1}{n+1}\frac{(n+1)\ldots 2n}{n!}=\frac{1}{n+1} \binom{2n}{n}\!.$$

Our next objective is the construction of the algebraic closure of $\mathbb{C}((X))$. We need a well-known tool.

Lemma 7.7

Hensel

Let $R:=K[[X]]$. For a polynomial $\alpha =\sum _{k=0}^{n}a_{k}Y^{k}\in R[Y]$ let

$$ \bar{\alpha}:=\sum _{k=0}^{n} a_{k}(0)Y^{k}\in K[Y].$$

Let $\alpha \in R[Y]$ be monic such that $\bar{\alpha}=\alpha _{1}\alpha _{2}$ for some coprime monic polynomials $\alpha _{1},\alpha _{2}\in K[Y]\setminus K$. Then there exist monic $\beta ,\gamma \in R[Y]$ such that $\bar{\beta}=\alpha _{1}$, $\bar{\gamma}=\alpha _{2}$ and $\alpha =\beta \gamma$.

Proof

By hypothesis, $n:=\deg (\alpha )=\deg (\alpha _{1})+\deg (\alpha _{2})\ge 2$. Observe that $\bar{\alpha}$ is essentially the reduction of $\alpha$ modulo the ideal $(X)$. In particular, the map $R[Y]\to K[Y]$, $\alpha \mapsto \bar{\alpha}$ is a ring homomorphism. For $\sigma ,\tau \in R[Y]$ and $k\in \mathbb{N}$ we write more generally $\sigma \equiv \tau \pmod{(X^{k})}$ if all coefficients of $\sigma -\tau$ lie in $(X^{k})$. First choose any monic polynomials $\beta _{1},\gamma _{1}\in R[Y]$ with $\bar{\beta _{1}}=\alpha _{1}$ and $\bar{\gamma _{1}}=\alpha _{2}$. Then $\deg (\beta _{1})=\deg (\alpha _{1})$, $\deg (\gamma _{1})=\deg (\alpha _{2})$ and $\alpha \equiv \beta _{1}\gamma _{1}\pmod{(X)}$. We construct inductively monic $\beta _{k},\gamma _{k}\in R[Y]$ for $k\ge 2$ such that

• 1. $\beta _{k}\equiv \beta _{k+1}$ and $\gamma _{k}\equiv \gamma _{k+1}\pmod{(X^{k})}$,

• 2. $\alpha \equiv \beta _{k}\gamma _{k}\pmod{(X^{k})}$.

Suppose that $\beta _{k},\gamma _{k}$ are given. Choose $\delta \in R[Y]$ such that $\alpha =\beta _{k}\gamma _{k}+X^{k}\delta$ and $\deg (\delta )< n$. Since $\alpha _{1},\alpha _{2}$ are coprime in the Euclidean domain $K[Y]$, there exist $\sigma ,\tau \in R[Y]$ such that $\bar{\beta}_{k}\bar{\sigma}+\bar{\gamma}_{k}\bar{\tau}=\alpha _{1} \bar{\sigma}+\alpha _{2}\bar{\tau}=1$ by Bézout’s lemma. Since $\beta _{k}$ is monic, we can perform Euclidean division by $\beta _{k}$ without leaving $R[Y]$. This yields $\rho ,\nu \in R[Y]$ such that $\tau \delta =\beta _{k}\rho +\nu$ and $\deg (\nu )<\deg (\beta _{k})$. Let $d:=\deg (\gamma _{1})$ and write $\sigma \delta +\gamma _{k}\rho =\mu +\eta Y^{d}$ with $\deg (\mu )< d$. Then

$${\beta }_{k+1}:={\beta }_k+X^k\nu ,{\gamma }_{k+1}:={\gamma }_k+X^k\mu$$

are monic and satisfy (a). Moreover,

$$ \delta \equiv (\beta _{k}\sigma +\gamma _{k}\tau )\delta \equiv \beta _{k}(\sigma \delta +\gamma _{k}\rho )+\gamma _{k}\nu \equiv \beta _{k}\mu +\beta _{k}\eta Y^{d}+\gamma _{k}\nu \pmod{(X)}.$$

Since the degrees of $\delta$, $\beta _{k}\mu$ and $\gamma _{k}\nu$ are all smaller than $n$ and $\deg (\beta _{k}\eta Y^{d})\ge n$, it follows that $\bar{\eta}=0$. Therefore,

$$ \beta _{k+1}\gamma _{k+1}\equiv \alpha -X^{k}\delta +(\beta _{k}\mu + \gamma _{k}\nu )X^{k}\equiv \alpha \pmod{(X^{k+1})}, $$

i.e. (b) holds for $k+1$. This completes the induction.

Let $\beta _{k}=\sum _{j=0}^{e}b_{kj}Y^{j}$ and $\gamma _{k}=\sum _{j=0}^{d}c_{kj}Y^{j}$ with $b_{ij},c_{ij}\in R$. By construction, $|b_{kj}-b_{k+1,j}|\le 2^{-k}$ and similarly for $c_{kj}$. Consequently, $b_{j}:=\lim _{k}b_{kj}$ and $c_{j}:=\lim _{k}c_{kj}$ converge in $R$. We can now define $\beta :=\sum _{j=0}^{e} b_{j}Y^{j}$ and $\gamma :=\sum _{j=0}^{d} c_{j}Y^{j}$. Then $\bar{\beta}=\bar{\beta}_{1}=\alpha _{1}$ and $\bar{\gamma}=\bar{\gamma}_{1}=\alpha _{2}$. Since $\beta \gamma \equiv \beta _{k}\gamma _{k}\equiv \alpha \pmod{(X^{k})}$ for every $k\ge 1$, it follows that $\alpha =\beta \gamma$. □

One can proceed to show that $\beta$ and $\gamma$ are uniquely determined in the situation of Lemma 7.7, but we do not need this in the following. Indeed, since $R$ is a principal ideal domain, $R[Y]$ is a factorial ring (also called unique factorization domain) by Gauss’ lemma. This means that every monic polynomial in $R[Y]$ has a unique factorization into monic irreducible polynomials. For every irreducible factor $\omega$ of $\alpha$, $\bar{\omega}$ either divides $\alpha _{1}$ or $\alpha _{2}$ (but not both). This determines the prime factorization of $\beta$ and $\gamma$ uniquely.

Example 7.8

Let $n\in \mathbb{N}$, $a\in (X)\subseteq \mathbb{C}[[X]]=:R$ and $\alpha =Y^{n}-1-a\in R[Y]$. Then $\bar{\alpha}=Y^{n}-1=\alpha _{1}\alpha _{2}$ with coprime monic $\alpha _{1}=Y-1$ and $\alpha _{2}=Y^{n-1}+\cdots +Y+1$. By Hensel’s lemma there exist monic $\beta ,\gamma \in R[Y]$ such that $\bar{\beta}=Y-1$, $\bar{\gamma}=\alpha _{2}$ and $\alpha =\beta \gamma$. We may write $\beta =Y-1-b$ for some $b\in (X)$. Then $(1+b)^{n}=1+a$ and the remark after Definition 3.14 implies $1+b=\sqrt[n]{1+a}$. The constructive procedure in the proof above must inevitably lead to Newton’s binomial theorem $1+b=\sum _{k=0}^{\infty}\binom{1/n}{k}a^{k}$.

We have seen that invertible power series in $\mathbb{C}[[X]]$ have arbitrary roots. On the other hand, $X$ does not even have a square root in $\mathbb{C}((X))$. This suggests to allow $X$ not only to negative powers, but also to fractional powers.

Definition 7.9

A Puiseux series over $K$ is defined by

$$ \sum _{k=m}^{\infty }a_{\frac{k}{n}}X^{\frac{k}{n}},$$

where $m\in \mathbb{Z}$, $n\in \mathbb{N}$ and $a_{\frac{k}{n}}\in K$ for $k\ge m$. The set of Puiseux series is denoted by $K\{\{X\}\}$. For $\alpha ,\beta \in K\{\{X\}\}$ there exists $n\in \mathbb{N}$ such that $\tilde{\alpha}:=\alpha (X^{n})$ and $\tilde{\beta}:=\beta (X^{n})$ lie in $K((X))$. We carry over the field operations from $K((X))$ via

$$ \alpha +\beta :=(\tilde{\alpha}+\tilde{\beta})(X^{\frac{1}{n}}),\qquad \alpha \cdot \beta :=(\tilde{\alpha}\tilde{\beta})(X^{\frac{1}{n}}).$$

It is straight-forward to check that $(K\{\{X\}\},+,\cdot )$ is a field. At this point we have established the following inclusions:

$$ K\subseteq K[X]\subseteq K[[X]]\subseteq K((X))\subseteq K\{\{X\}\}.$$

Theorem 7.10

Puiseux

The algebraic closure of $\mathbb{C}((X))$ is $\mathbb{C}\{\{X\}\}$.

Proof

We follow Nowak [32]. Set $R:=\mathbb{C}[[X]]$, $F:=\mathbb{C}((X))$ and $\hat{F}:=\mathbb{C}\{\{X\}\}$. We show first that $\hat{F}$ is an algebraic field extension of $F$. Let $\alpha \in \hat{F}$ be arbitrary and $n\in \mathbb{N}$ such that $\beta :=\alpha (X^{n})\in F$. Let $\zeta \in \mathbb{C}$ be a primitive $n$-th root of unity. Define

$$ \Gamma :=\prod _{i=1}^{n}\bigl(Y-\beta (\zeta ^{i}X)\bigr)=Y^{n}+ \gamma _{1}Y^{n-1}+\cdots +\gamma _{n}\in F[Y].$$

Replacing $X$ by $\zeta X$ permutes the factors $Y-\beta (\zeta ^{i}X)$ and thus leaves $\Gamma$ invariant. Consequently, $\gamma _{i}(\zeta X)=\gamma _{i}$ for $i=1,\ldots ,n$. This means that there exist $\tilde{\gamma}_{i}\in F$ such that $\gamma _{i}=\tilde{\gamma}_{i}(X^{n})$. Now let

$$ \tilde{\Gamma}:=Y^{n}+\tilde{\gamma}_{1}Y^{n-1}+\cdots +\tilde{\gamma}_{n} \in F[Y].$$

Substituting $X$ by $X^{n}$ in $\tilde{\Gamma}(\alpha )$ gives $\Gamma (\beta )=0$. Thus, also $\tilde{\Gamma}(\alpha )=0$. This shows that $\alpha$ is algebraic over $F$ and $\hat{F}$ is an algebraic extension of $F$.

Now we prove that $\hat{F}$ is algebraically closed. Let $\Gamma =Y^{n}+\gamma _{1}Y^{n-1}+\cdots +\gamma _{n}\in \hat{F}[Y]$ be arbitrary with $n\ge 2$. We need to show that $\Gamma$ has a root in $\hat{F}$. Without loss of generality, $\Gamma \ne Y^{n}$. After applying the Tschirnhaus transformation $Y\mapsto Y-\frac{1}{n}\gamma _{1}$, we may assume that $\gamma _{1}=0$. Let

$$ r:=\min \Bigl\{ \frac{1}{k}\inf (\gamma _{k}):k=1,\ldots ,n\Bigr\} \in \mathbb{Q}$$

and $m\in \mathbb{N}$ such that $\gamma _{k}(X^{m})\in F$ for $k=1,\ldots ,n$ and $r=\frac{s}{m}$ for some $s\in \mathbb{Z}$. Define $\delta _{0}:=1$ and $\delta _{k}:=\gamma _{k}(X^{m})X^{-ks}\in F$ for $k=1,\ldots ,n$. Since

$$ \inf (\delta _{k})=m\inf (\gamma _{k})-ks=m(\inf (\gamma _{k})-kr) \ge 0,$$

$\Delta :=Y^{n}+\delta _{2}Y^{n-2}+\cdots +\delta _{n}\in R[Y]$. Consider $\bar{\Delta}:=Y^{n}+\delta _{2}(0)Y^{n-2}+\cdots +\delta _{n}(0)\in \mathbb{C}[Y]$. Since $\inf (\delta _{k})=0$ for at least one $k\ge 1$, we have $\bar{\Delta}\ne Y^{n}$ Since $\delta _{1}=0$, also $\bar{\Delta}\ne (Y-c)^{n}$ for all $c\in \mathbb{C}$. Using that $\mathbb{C}[Y]$ is algebraically closed, we can decompose $\bar{\Delta}=\bar{\Delta}_{1}\bar{\Delta}_{2}$ with coprime monic polynomials $\bar{\Delta}_{1},\bar{\Delta}_{2}\in \mathbb{C}[Y]$ of degree $< n$. By Hensel’s Lemma 7.7, there exists a corresponding factorization $\Delta =\Delta _{1}\Delta _{2}$ with $\Delta _{1},\Delta _{2}\in R[Y]$. Finally, replace $X$ by $X^{\frac{1}{m}}$ in $\Delta _{i}$ to obtain $\Gamma _{i}\in \hat{F}[Y]$. Then

$$\begin{aligned} \Gamma &=X^{nr}\sum _{k=0}^{n}\gamma _{k}X^{-kr}(YX^{-r})^{n-k}=X^{nr} \sum _{k=0}^{n}\delta _{k}(X^{\frac{1}{m}})(YX^{-r})^{n-k}\\&=X^{nr} \Gamma _{1}(YX^{-r})\Gamma _{2}(YX^{-r}). \end{aligned}$$

Induction on $n$ shows that $\Gamma$ has a root and $\hat{F}$ is algebraically closed. □

8 Multivariate Power Series

In Remark 4.7 and even more in the last two results it became clear that power series in more than one indeterminant make sense. We give proper definitions now.

Definition 8.1

• 1. The ring of formal power series in $n$ indeterminants $X_{1},\ldots ,X_{n}$ over a field $K$ is defined inductively via

  $$ K[[X_{1},\ldots ,X_{n}]]:=K[[X_{1},\ldots ,X_{n-1}]][[X_{n}]].$$

  Its elements have the form

  $$ \alpha =\sum _{k_{1},\ldots ,k_{n}\ge 0}a_{k_{1},\ldots ,k_{n}}X_{1}^{k_{1}} \ldots X_{n}^{k_{n}}$$

  where $a_{k_{1},\ldots ,k_{n}}\in K$. We (still) call $a_{0,\ldots ,0}$ the constant term of $\alpha$. Let $\inf (\alpha ):=\inf \{k_{1}+\cdots +k_{n}:a_{k_{1},\ldots ,k_{n}} \ne 0\}$ and

  $$ |\alpha |:=2^{-\inf (\alpha )}.$$

• 2. If all but finitely many coefficients of $\alpha$ are zero, we call $\alpha$ a (formal) polynomial in $X_{1},\ldots ,X_{n}$. In this case,

  $$ \deg (\alpha ):=\sup \{k_{1}+\cdots +k_{n}:a_{k_{1},\ldots ,k_{n}} \ne 0\}$$

  is the degree of $\alpha$, where $\deg (0)=\sup \varnothing =-\infty$. Moreover, a polynomial $\alpha$ is called homogeneous if all monomials occurring in $\alpha$ (with non-zero coefficient) have the same degree. The set of polynomials is denoted by $K[X_{1},\ldots ,X_{n}]$.

Once we have convinced ourselves that Lemma 2.2 remains true when $K$ is replaced by an integral domain, it becomes evident that also $K[[X_{1},\ldots ,X_{n}]]$ is an integral domain. Likewise the norm $|\alpha |$ still gives rise to a complete ultrametric (to prove $|\alpha \beta |=|\alpha ||\beta |$ one may assume that $\alpha$ and $\beta$ are homogeneous polynomials) and the crucial Lemma 2.10 holds in $K[[X_{1},\ldots ,X_{n}]]$ too. We stress that this metric is finer than the one induced from $K[[X_{1},\ldots ,X_{n-1}]]$ as, for example, the sequence $(X_{1}^{k}X_{2})_{k}$ converges in the former, but not in the latter (with $n=2$). Moreover, a power series $\alpha$ is invertible in $K[[X_{1},\ldots ,X_{n}]]$ if and only if its constant term is non-zero. Indeed, after scaling, the constant term is 1 and

$$ \alpha ^{-1}=\frac{1}{1-(1-\alpha )}=\sum _{k=0}^{\infty}(1-\alpha )^{k}$$

converges.

Unlike $K[X]$ or $K[[X]]$, the multivariate rings are not principal ideal domains, but one can show that they are still factorial (see [26, Theorem IV.9.3]). We do not require this fact in the sequel.

The degree function equips $K[X_{1},\ldots ,X_{n}]$ with a grading, i.e. we have

$$ K[X_{1},\ldots ,X_{n}]=\bigoplus _{d=0}^{\infty }P_{d}$$

and $P_{d}P_{e}\subseteq P_{d+e}$ where $P_{d}$ denotes the set of homogeneous polynomials of degree $d$. In the following we will restrict ourselves mostly to polynomials of a special type. Note that if $\alpha ,\beta _{1},\ldots ,\beta _{n}\in K[X_{1},\ldots ,X_{n}]$, we can substitute $X_{i}$ by $\beta _{i}$ in $\alpha$ to obtain $\alpha (\beta _{1},\ldots ,\beta _{n})\in K[X_{1},\ldots ,X_{n}]$. It is important that these substitutions happen simultaneously and not one after the other (more about this at the end of the section).

Definition 8.2

A polynomial $\alpha \in K[X_{1},\ldots ,X_{n}]$ is called symmetric if

$$ \alpha (X_{\pi (1)},\ldots ,X_{\pi (n)})=\alpha (X_{1},\ldots ,X_{n})$$

for all permutations $\pi \in S_{n}$.

It is easy to see that the symmetric polynomials form a subring of $K[X_{1},\ldots ,X_{n}]$.

Example 8.3

• 1. The elementary symmetric polynomials are $\sigma _{0}:=1$ and

  $$ \sigma _{k}:=\sum _{1\le i_{1}< \cdots < i_{k}\le n}X_{i_{1}}\ldots X_{i_{k}} \qquad (k\ge 1).$$

  Note that $\sigma _{k}=0$ for $k>n$ (empty sum).

• 2. The complete symmetric polynomials are $\tau _{0}:=1$ and

  $$ \tau _{k}:=\sum _{1\le i_{1}\le \cdots \le i_{k}\le n}X_{i_{1}} \ldots X_{i_{k}}\qquad (k\ge 1).$$

• 3. The power sum polynomials are $\rho _{k}:=X_{1}^{k}+\cdots +X_{n}^{k}$ for $k\ge 0$.

Keep in mind that $\sigma _{k}$, $\tau _{k}$ and $\rho _{k}$ depend on $n$. All three sets of polynomials are homogeneous. The elementary and complete symmetric polynomials are special instances of Schur polynomials, which we do not attempt to define here.

Theorem 8.4

Vieta

The following identities hold in $K[[X_{1},\ldots ,X_{n},Y]]$:

Proof

The first equation is only a matter of expanding the product. The second equation follows from

$$ \prod _{k=1}^{n}\frac{1}{1-X_{k}Y}=\prod _{k=1}^{n}\sum _{l=0}^{ \infty }(X_{k}Y)^{l}=\sum _{k=0}^{\infty}\Bigl(\sum _{l_{1}+\cdots +l_{n}=k}X_{1}^{l_{1}} \ldots X_{n}^{l_{n}}\Bigr)Y^{k}=\sum _{k=0}^{\infty }\tau _{k}Y^{k}. $$

 □

When we specialize $X_{1}=\cdots =X_{n}=1$ in Vieta’s theorem (as we may), we recover the generating functions of the binomial coefficients and the multiset counting coefficients in Example 5.1. When we substitute $X_{k}=k$ for $k=1,\ldots ,n$, we obtain a new formula for the Stirling numbers by virtue of Theorem 6.9.

It is easy to see that the grading by degree carries over to symmetric polynomials. The following theorem shows that the elementary symmetric polynomials are the building blocks of all symmetric polynomials.

Theorem 8.5

Fundamental theorem on symmetric polynomials

For every symmetric polynomial $\alpha \in K[X_{1},\ldots ,X_{n}]$ there exists a unique $\gamma \in K[X_{1},\ldots ,X_{n}]$ such that $\alpha =\gamma (\sigma _{1},\ldots ,\sigma _{n})$.

Proof

We first prove the existence of $\gamma$: Without loss of generality, let

$$ \alpha =\sum _{i_{1},\ldots ,i_{n}}a_{i_{1},\ldots ,i_{n}}X_{1}^{i_{1}} \ldots X_{n}^{i_{n}}\ne 0.$$

We order the tuples $(i_{1},\ldots ,i_{n})$ lexicographically and argue by induction on

$$ f(\alpha ):=\max \bigl\{ (i_{1},\ldots ,i_{n}):a_{i_{1},\ldots ,i_{n}} \ne 0\bigr\} $$

(see Example 8.6 below for an illustration). If $f(\alpha )=(0,\ldots ,0)$, then $\gamma :=\alpha =a_{0,\ldots ,0}\in K$. Now let $f(\alpha )=(d_{1},\ldots ,d_{n})>(0,\ldots ,0)$. Since $\alpha =\alpha (X_{\pi (1)},\ldots , X_{\pi (n)})$ for all $\pi \in S_{n}$, $d_{1}\ge \cdots \ge d_{n}$. Let

$$ \beta :=a_{d_{1},\ldots ,d_{n}}\sigma _{1}^{d_{1}-d_{2}}\sigma _{2}^{d_{2}-d_{3}} \ldots \sigma _{n-1}^{d_{n-1}-d_{n}}\sigma _{n}^{d_{n}}.$$

Then we have $f(\sigma _{k}^{d_{k}-d_{k+1}})=(d_{k}-d_{k+1})f(\sigma _{k})=(d_{k}-d_{k+1}, \ldots ,d_{k}-d_{k+1},0,\ldots , 0)$ and

$$ f(\beta )=f(\sigma _{1}^{d_{1}-d_{2}})+\cdots +f(\sigma _{n}^{d_{n}})=(d_{1}, \ldots ,d_{n}).$$

Hence, the symmetric polynomial $\alpha -\beta$ satisfies $f(\alpha -\beta )<(d_{1},\ldots ,d_{n})$ and the existence of $\gamma$ follows by induction.

Now we show the uniqueness of $\gamma$: Let $\gamma ,\delta \in K[X_{1},\ldots ,X_{n}]$ such that $\gamma (\sigma _{1},\ldots , \sigma _{n})=\delta (\sigma _{1},\ldots , \sigma _{n})$. For $\rho :=\gamma -\delta$ it follows that $\rho (\sigma _{1},\ldots ,\sigma _{n})=0$. We have to show that $\rho =0$. By way of contradiction, suppose $\rho \ne 0$. Let $d_{1}\ge \cdots \ge d_{n}$ be the lexicographically largest $n$-tuple such that the coefficient of $X_{1}^{d_{1}-d_{2}}X_{2}^{d_{2}-d_{3}}\ldots X_{n}^{d_{n}}$ in $\rho$ is non-zero. As above, $f(\sigma _{1}^{d_{1}-d_{2}}\ldots \sigma _{n}^{d_{n}})=(d_{1}, \ldots ,d_{n})$. For every other summand $X_{1}^{e_{1}-e_{2}}\ldots X_{n}^{e_{n}}$ of $\rho$ we obtain $f(\sigma _{1}^{e_{1}-e_{2}}\ldots \sigma _{n}^{e_{n}})<(d_{1}, \ldots ,d_{n})$. This yields $f\bigl(\rho (\sigma _{1},\ldots ,\sigma _{n})\bigr)=(d_{1},\ldots ,d_{n})$ in contradiction to $\rho (\sigma _{1},\ldots ,\sigma _{n})=0$. □

Example 8.6

Consider $\alpha =XY^{3}+X^{3}Y-X-Y\in K[X,Y]$. With the notation from the proof above, $f(\alpha )=(3,1)$ and

$$ \beta :=\sigma _{1}^{2}\sigma _{2}=(X+Y)^{2}XY=X^{3}Y+2X^{2}Y^{2}+XY^{3}.$$

Thus, $\alpha -\beta =-2X^{2}Y^{2}-X-Y$. In the next step we have $f(\alpha -\beta )=(2,2)$ and

$$ \beta _{2}:=-2\sigma _{2}^{2}=-2X^{2}Y^{2}.$$

It remains: $\alpha -\beta -\beta _{2}=-X-Y=-\sigma _{1}$. Finally,

$$ \alpha =\beta +\beta _{2}-\sigma _{1}=\sigma _{1}^{2}\sigma _{2}-2 \sigma _{2}^{2}-\sigma _{1}=\gamma (\sigma _{1},\sigma _{2})$$

where $\gamma =X^{2}Y-2Y^{2}-X$.

From an algebraic point of view, Theorem 8.5 (applied to $\alpha =0$) states that the elementary symmetric polynomials $\sigma _{1},\ldots ,\sigma _{n}$ are algebraically independent over $K$, so they form a transcendence basis of $K(X_{1},\ldots ,X_{n})$ (recall that $K(X_{1},\ldots ,X_{n})$ has transcendence degree $n$). The identities in the next theorem express the $\sigma _{i}$ recursively in terms of the $\tau _{j}$ and in terms of the $\rho _{j}$. So the latter sets of symmetric polynomials form transcendence bases too. It is no coincidence that $\deg (\sigma _{k})=\deg (\tau _{k})=\deg (\rho _{k})=k$ for $k\le n$. A theorem from invariant theory (in characteristic 0) implies that any algebraically independent, symmetric, homogeneous polynomials $\lambda _{1},\ldots ,\lambda _{n}$ have degrees $1,\ldots ,n$ in some order (see [19, Proposition 3.7]).

Theorem 8.7

Girard–Newton identities

The following identities hold in $K[X_{1}, \ldots ,X_{n}]$ for all $n,k\in \mathbb{N}$:

$$\begin{aligned} \boxed{ \textstyle\begin{array}{rcl} \displaystyle \sum _{i=0}^{k}(-1)^{i}\sigma _{i} \tau _{k-i}&=&0, \\ \displaystyle\sum _{i=1}^{k}\rho _{i}\tau _{k-i}&=&k\tau _{k}, \\ \displaystyle \sum _{i=1}^{k}(-1)^{i}\sigma _{k-i}\rho _{i}&=&-k\sigma _{k}. \end{array}\displaystyle } \end{aligned}$$

Proof

Let $\sigma =\sum _{k=0}^{n}(-1)^{k}\sigma _{k}Y^{k}=\prod _{k=1}^{n}(1-X_{k}Y)$ and $\tau :=\sum _{k=0}^{n}\tau _{k}Y^{k}= \prod _{k=1}^{n} \frac{1}{1-X_{k}Y}$ as in Vieta’s theorem.

• 1. The claim follows by comparing coefficients of $Y^{k}$ in

  $$ 1=\sigma \tau =\sum _{k=0}^{\infty}\Bigl(\sum _{i=0}^{k}(-1)^{i} \sigma _{i}\tau _{k-i}\Bigr)Y^{k}.$$

• 2. We differentiate with respect to $Y$ using the product rule while noticing that $\bigl(\frac{1}{1-X_{k}Y}\bigr)'=\frac{X_{k}}{(1-X_{k}Y)^{2}}$:

  $$\begin{aligned} \sum _{k=1}^{\infty }k\tau _{k}Y^{k}&=Y\tau '=\tau \sum _{k=1}^{n} \frac{X_{k}Y}{1-X_{k}Y}=\tau \sum _{k=1}^{n}\sum _{i=1}^{\infty}(X_{k}Y)^{i} \\ &=\tau \sum _{i=1}^{\infty}\rho _{i}Y^{i}=\sum _{k=1}^{\infty}\Bigl( \sum _{i=1}^{k}\rho _{i}\tau _{k-i}\Bigr)Y^{k}. \end{aligned}$$

• 3. We differentiate again with respect to $Y$ (this idea is often attributed to [6, p. 212]):

  $$\begin{aligned} -\sum _{k=0}^{\infty}(-1)^{k}k\sigma _{k}Y^{k}&=-Y\sigma '=\sigma \sum _{k=1}^{n}\frac{X_{k}Y}{1-X_{k}Y}=\sigma \sum _{k=1}^{\infty} \rho _{k}Y^{k}\\&=\sum _{k=1}^{\infty}\Bigl(\sum _{i=1}^{k}(-1)^{k-i} \sigma _{k-i}\rho _{i}\Bigr) Y^{k}. \end{aligned}$$

 □

Now that we know that each of the $\sigma _{i}$, $\tau _{i}$ and $\rho _{i}$ can be expressed by the other two sets of polynomials, it is natural to ask for explicit formulas. This is achieved by Waring’s formula. Here $P(n)$ stands for the set of partitions of $n$ as introduced in Definition 5.2.

Theorem 8.8

Waring’s formula

Let $\operatorname{char}K=0$. The following holds in $K[X_{1},\ldots , X_{n}]$ for all $n,k\in \mathbb{N}$:

$$\begin{aligned} \boxed{ \textstyle\begin{array}{rcl} \rho _{k}&=& \displaystyle (-1)^{k}k\sum _{(1^{a_{1}}, \ldots ,k^{a_{k}})\in P(k)}(-1)^{a_{1}+\cdots +a_{k}} \frac{(a_{1}+\cdots +a_{k}-1)!}{a_{1}!\ldots a_{k}!}\sigma _{1}^{a_{1}} \ldots \sigma _{k}^{a_{k}}, \\ &=& \displaystyle -k\sum _{(1^{a_{1}},\ldots ,k^{a_{k}})\in P(k)}(-1)^{a_{1}+\cdots +a_{k}} \frac{(a_{1}+\cdots +a_{k}-1)!}{a_{1}!\ldots a_{k}!}\tau _{1}^{a_{1}} \ldots \tau _{k}^{a_{k}}. \end{array}\displaystyle } \end{aligned}$$

Proof

We introduce a new variable $Y$ and compute in $K[[X_{1},\ldots ,X_{n},Y]]$. The generating function of $(-1)^{k}\frac{\rho _{k}}{k}$ is

$$\begin{aligned} \sum _{k=1}^{\infty }(-1)^{k}\frac{\rho _{k}}{k}Y^{k}&=-\sum _{i=1}^{n} \sum _{k=1}^{\infty }(-1)^{k-1}\frac{(X_{i}Y)^{k}}{k}=-\sum _{i=1}^{n} \log (1+X_{i}Y)\\ &\overset{\text{(3.6)}}{=}-\log \Bigl(\prod _{i=1}^{n}(1+X_{i}Y) \Bigr) \\ &\overset{\text{(8.1)}}{=}-\log \Bigl(1+\sum _{i=1}^{n}\sigma _{i}Y^{i} \Bigr)=\sum _{l=1}^{\infty}\frac{(-1)^{l}}{l}\Bigl(\sum _{i=1}^{n} \sigma _{i}Y^{i}\Bigr)^{l}. \end{aligned}$$

Now we use the multinomial theorem to expand the inner sum:

$$\begin{aligned} \sum _{k=1}^{\infty }(-1)^{k}\frac{\rho _{k}}{k}Y^{k}&=\sum _{l=1}^{ \infty}\frac{(-1)^{l}}{l}\sum _{a_{1}+\cdots +a_{n}=l} \frac{l!}{a_{1}!\ldots a_{n}!}\sigma _{1}^{a_{1}}\ldots \sigma _{n}^{a_{n}}Y^{a_{1}+2a_{2}+ \cdots +na_{n}} \\ &=\sum _{k=1}^{\infty}\sum _{(1^{a_{1}},\ldots ,k^{a_{k}})\in P(k)}\!(-1)^{a_{1}+ \cdots +a_{k}}\frac{(a_{1}+\cdots +a_{k}-1)!}{a_{1}!\ldots a_{k}!} \sigma _{1}^{a_{1}}\ldots \sigma _{k}^{a_{k}} Y^{k}. \end{aligned}$$

Note that $\sigma _{k}=0$ for $k>n$. This implies the first equation. For the second we start similarly:

$$\begin{aligned} \sum _{k=1}^{\infty }\frac{\rho _{k}}{k}Y^{k}& =\sum _{i=1}^{n}\sum _{k=1}^{ \infty }\frac{(X_{i}Y)^{k}}{k}=\sum _{i=1}^{n}\log \bigl((1-X_{i}Y)^{-1} \bigr)=\log \Bigl(\prod _{i=1}^{n}\frac{1}{1-X_{i}Y}\Bigr) \\& \overset{\text{(8.2)}}{=}\log \Bigl(1+\sum _{i=1}^{\infty}\tau _{i}Y^{i} \Bigr). \end{aligned}$$

Since we are only interested in the coefficient of $X^{k}$, we can truncate the sum to

$$ \log \Bigl(1+\sum _{i=1}^{k}\tau _{i}Y^{i}\Bigr)=-\sum _{l=1}^{\infty} \frac{(-1)^{l}}{l}\sum _{a_{1}+\cdots +a_{k}=l} \frac{l!}{a_{1}!\ldots a_{k}!}\tau _{1}^{a_{1}}\ldots \tau _{k}^{a_{k}}Y^{a_{1}+2a_{2}+ \cdots +ka_{k}}$$

and argue as before. □

Example 8.9

Since we are dealing with polynomials, it is legitimate to evaluate the indeterminants at actual numbers. Let $x_{1},x_{2},x_{3}\in \mathbb{C}$ be the roots of

$$ \alpha =X^{3}+2X^{2}-3X+1\in \mathbb{C}[X]$$

(guaranteed to exist by the fundamental theorem of algebra). By Vieta’s theorem,

$$ \sigma _{1}(x_{1},x_{2},x_{3})=-2,\qquad \sigma _{2}(x_{1},x_{2},x_{3})=-3, \qquad \sigma _{3}(x_{1},x_{2},x_{3})=-1.$$

The partitions of 3 are $(1^{3},2^{0},3^{0})$, $(1^{1},2^{1},3^{0})$ and $(1^{0},2^{0},3^{1})$. We compute with the first Waring formula

$$ x_{1}^{3}+x_{2}^{3}+x_{3}^{3}=\rho _{3}(x_{1},x_{2},x_{3})=-3\Bigl(- \frac{2!}{3!}(-2)^{3}+(-2)(-3)-(-1)^{3}\Bigr)=-29$$

without knowing what $x_{1},x_{2},x_{3}$ are! Here is an alternative approach for the readers who like matrices. The companion matrix

$$ A= \begin{pmatrix} 0&0&-1 \\ 1&0&3 \\ 0&1&-2 \end{pmatrix} $$

of $\alpha$ has characteristic polynomial $\alpha$. Hence, the eigenvalues of $A^{k}$ are $x_{1}^{k}$, $x_{2}^{k}$ and $x_{3}^{k}$. This shows $\rho _{k}(x_{1},x_{2},x_{3})=\operatorname{tr}(A^{k})$.

We invite the reader to prove the other four transition formulas.

Exercise 8.10

Let $\operatorname{char}K=0$. Show that the following holds in $K[X_{1},\ldots ,X_{n}]$ for all $n,k\in \mathbb{N}$:

$$\begin{aligned} \sigma _{k}&=(-1)^{k}\sum _{(1^{a_{1}},\ldots ,k^{a_{k}})\in P(k)}(-1)^{a_{1}+ \cdots +a_{k}}\frac{(a_{1}+\cdots +a_{k})!}{a_{1}!\ldots a_{k}!}\tau _{1}^{a_{1}} \ldots \tau _{k}^{a_{k}}, \\ &=(-1)^{k}\sum _{(1^{a_{1}},\ldots ,k^{a_{k}})\in P(k)} \frac{(-1)^{a_{1}+\cdots +a_{k}}}{1^{a_{1}}a_{1}!\ldots k^{a_{k}}a_{k}!} \rho _{1}^{a_{1}}\ldots \rho _{k}^{a_{k}}, \end{aligned}$$

(8.3)

$$\begin{aligned} \tau _{k}&=(-1)^{k}\sum _{(1^{a_{1}},\ldots ,k^{a_{k}})\in P(k)}(-1)^{a_{1}+ \cdots +a_{k}}\frac{(a_{1}+\cdots +a_{k})!}{a_{1}!\ldots a_{k}!} \sigma _{1}^{a_{1}}\ldots \sigma _{k}^{a_{k}}, \\ &=\sum _{(1^{a_{1}},\ldots ,k^{a_{k}})\in P(k)} \frac{1}{1^{a_{1}}a_{1}!\ldots k^{a_{k}}a_{k}!}\rho _{1}^{a_{1}} \ldots \rho _{k}^{a_{k}}. \end{aligned}$$

(8.4)

Hint: For (8.3) and (8.4), mimic the proof of Theorem 6.12 (these are specializations of Frobenius’ formula on Schur polynomials).

We leave polynomials to fully develop multivariate power series.

Definition 8.11

For $\alpha \in K[[X_{1},\ldots ,X_{n}]]$ and $1\le i\le n$ let $\partial _{i}\alpha$ be the $i$-th partial derivative with respect to $X_{i}$, i.e. we regard $\alpha$ as a power series in $X_{i}$ with coefficients in $K[[X_{1},\ldots ,X_{i-1},X_{i+1},\ldots ,X_{n}]]$ and form the usual (formal) derivative. For $k\in \mathbb{N}_{0}$ let $\partial _{i}^{k}\alpha$ be the $k$-th derivative with respect to $X_{i}$.

Note that $\partial _{i}$ is a linear operator, which commutes with $\partial _{j}$ for $j=1,\ldots ,n$ (Schwarz’ theorem). Indeed, by linearity it suffices to check

$$ \partial _{i}\partial _{j}(X_{i}^{k}X_{j}^{l})=\partial _{i}(lX_{i}^{k}X_{j}^{l-1})=klX_{i}^{k-1}X_{j}^{l-1}= \partial _{j}(kX_{i}^{k-1}X_{j}^{l})=\partial _{j}\partial _{i}(X_{i}^{k}X_{j}^{l}).$$

We need a fairly general form of the product rule.

Lemma 8.12

Leibniz’ rule

Let $\operatorname{char}K=0$. Let $\alpha _{1},\ldots ,\alpha _{s}\in K[[X_{1},\ldots ,X_{n}]]$ and $k_{1},\ldots ,k_{n}\in \mathbb{N}_{0}$. Then

$$ \boxed{\partial _{1}^{k_{1}}\ldots \partial _{n}^{k_{n}}(\alpha _{1}\ldots \alpha _{s})=\sum _{l_{11}+\cdots +l_{1s}=k_{1}}\ldots \sum _{l_{n1}+\cdots +l_{ns}=k_{n}}\frac{k_{1}!\ldots k_{n}!}{\prod _{i,j}l_{ij}!}\prod _{t=1}^{s}\partial _{1}^{l_{1t}}\ldots \partial _{n}^{l_{nt}}\alpha _{t}.}$$

Proof

For $n=1$ the claim is more or less equivalent to the familiar multinomial theorem

$$ (a_{1}+\cdots +a_{s})^{k}=\sum _{l_{1}+\cdots +l_{s}=k} \frac{k!}{l_{1}!\ldots l_{s}!}a_{1}^{l_{1}}\ldots a_{s}^{l_{s}},$$

where $a_{1},\ldots ,a_{s}$ lie in any commutative ring. With every new indeterminant we simply apply the case $n=1$ to the formula for $n-1$. In this way the multinomial coefficients are getting multiplied. □

Our next goal is the multivariate chain rule for (higher) derivatives. We equip $K[[X_{1},\ldots ,X_{n}]]^{n}$ with the direct product ring structure and use the shorthand notation $\alpha :=(\alpha _{1},\ldots ,\alpha _{n})$ and $0:=(0,\ldots ,0)$. Write

$$ \alpha \circ \beta :=\bigl(\alpha _{1}(\beta _{1},\ldots ,\beta _{n}), \ldots ,\alpha _{n}(\beta _{1},\ldots ,\beta _{n})\bigr)$$

provided this is well-defined. It is not difficult to show that

$$ \begin{aligned} (\alpha +\beta )\circ \gamma =(\alpha \circ \gamma )+( \beta \circ \gamma ), \\ (\alpha \cdot \beta )\circ \gamma =(\alpha \circ \gamma )\cdot ( \beta \circ \gamma ) \end{aligned} $$

(8.5)

as in Lemma 3.3. It was remarked by M. Hardy [13] that Leibniz’ rule as well as the chain rule become slightly more transparent when we give up on counting multiplicities of derivatives as follows.

Theorem 8.13

Faá di Bruno’s rule

Let $\alpha ,\beta _{1},\ldots ,\beta _{n}\in K[[X_{1},\ldots ,X_{n}]]$ such that $\alpha (\beta _{1},\ldots ,\beta _{n})$ is defined. Then for $1\le k_{1},\ldots ,k_{s}\le n$ we have

$$ \boxed{\textstyle\begin{array}{l} \displaystyle \partial _{k_{1}}\ldots \partial _{k_{s}}\bigl(\alpha (\beta _{1},\ldots ,\beta _{n})\bigr) \\ \quad \displaystyle =\sum _{t=1}^{s}\sum _{1\le i_{1},\ldots ,i_{t}\le n}\sum _{\substack{A_{1}\dot{\cup}\ldots \dot{\cup} A_{t}\\=\{1,\ldots ,s\}}}(\partial _{A_{1}}\beta _{i_{1}})\ldots (\partial _{A_{t}}\beta _{i_{t}})(\partial _{i_{1}}\ldots \partial _{i_{t}}\alpha )(\beta _{1},\ldots ,\beta _{n}), \end{array}\displaystyle } $$

where $A_{1}\dot{\cup}\ldots \dot{\cup} A_{t}$ runs through the set partitions of $s$ and $\partial _{A_{t}}:=\prod _{a\in A_{t}}\partial _{k_{a}}$.

Proof

By (8.5), we may assume that $\alpha =X_{1}^{a_{1}}\ldots X_{n}^{a_{n}}$. Then by the product rule,

$$ \partial _{k}\bigl(\alpha (\beta _{1},\ldots ,\beta _{n})\bigr)=\sum _{i=1}^{n}( \partial _{k}\beta _{i})a_{i}\beta _{1}^{a_{1}}\ldots \beta _{i}^{a_{i}-1} \ldots \beta _{n}^{a_{n}}=\sum _{i=1}^{n}(\partial _{k}\beta _{i})( \partial _{i}\alpha )(\beta _{1},\ldots ,\beta _{n}). $$

(8.6)

This settles the case $s=1$. Now assume that the claim for some $s$ is established. When we apply some $\partial _{k_{s+1}}$ on the right hand side of the induction hypothesis, we need the product rule again. There are two cases: either $s+1$ is added to some of the existing sets $A_{t}$ or $\partial _{k_{s+1}}$ is applied to $(\partial _{i_{1}}\ldots \partial _{i_{t}}\alpha )(\beta _{1}, \ldots ,\beta _{n})$. In the latter case $s$ increases to $s+1$, $A_{s+1}=\{s+1\}$ and $i_{s+1}$ is introduced as in (8.6). □

Example 8.14

For $n=1$ and $\operatorname{char}K=0$, Theorem 8.13 “simplifies” to

$$\begin{aligned} &(\alpha (\beta ))^{(s)}=\sum _{t=1}^{s}\sum _{A_{1}\dot{\cup}\ldots \dot{\cup}A_{t}}\beta ^{(|A_{1}|)}\ldots \beta ^{(|A_{t}|)}\alpha ^{(t)}( \beta ) \\ &\hspace{1cm}=\sum _{(1^{a_{1}},\ldots ,s^{a_{s}})\in P(s)} \frac{s!}{(1!)^{a_{1}}\ldots (s!)^{a_{s}}a_{1}!\ldots a_{s}!}(\beta ')^{a_{1}} \ldots (\beta ^{(s)})^{a_{s}}(\alpha (\beta ))^{(a_{1}+\cdots +a_{s})}, \end{aligned}$$

where $(1^{a_{1}},\ldots ,s^{a_{s}})$ runs over the partitions of $s$ and the coefficient is explained just as in Lemma 6.11.

9 MacMahon’s Master Theorem

In this final section we enter a non-commutative world by making use of matrices. The ultimate goal is the master theorem found and named by MacMahon [28, Chapter II]. Since $K[[X_{1},\ldots ,X_{n}]]$ can be embedded in its field of fractions, the familiar rules of linear algebra (over fields) remain valid in the ring $K[[X_{1},\ldots ,X_{n}]]^{n\times n}$ of $n\times n$-matrices with coefficients in $K[[X_{1},\ldots ,X_{n}]]$. In particular, the determinant of $A=(\alpha _{ij})_{i,j}$ can be defined by Leibniz’ formula (not rule)

$$ \det (A):=\sum _{\sigma \in S_{n}}\operatorname{sgn}(\sigma )\alpha _{1 \sigma (1)}\ldots \alpha _{n\sigma (n)}.$$

It follows that $\det (A(0))=\det (A)(0)$ by (8.5). Recall that the adjoint of $A$ is defined by $\operatorname{adj}(A):=\bigl((-1)^{i+j}\det (A_{ji})\bigr)_{i,j}$ where $A_{ji}$ is obtained from $A$ by deleting the $j$-th row and $i$-th column. Then

$$ A\operatorname{adj}(A)=\operatorname{adj}(A)A=\det (A)1_{n},$$

where $1_{n}$ denotes the identity $n\times n$-matrix. This shows that $A$ is invertible if and only if $\det (A)$ is invertible in $K[[X_{1},\ldots ,X_{n}]]$, i.e. $\det (A)$ has a non-zero constant term. Expanding the entries of $A$ as $\alpha _{ij}=\sum a^{(i,j)}_{k_{1},\ldots ,k_{n}}X_{1}^{k_{1}} \ldots X_{n}^{k_{n}}$ gives rise to a natural bijection

$$\begin{aligned} \Omega \colon K[[X_{1},\ldots ,X_{n}]]^{n\times n}&\to K^{n\times n}[[X_{1}, \ldots ,X_{n}]], \\ A&\mapsto \sum _{k_{1},\ldots ,k_{n}}\bigl(a^{(i,j)}_{k_{1},\ldots ,k_{n}} \bigr)_{i,j}X_{1}^{k_{1}}\ldots X_{n}^{k_{n}}. \end{aligned}$$

Clearly, $\Omega$ is a vector space isomorphism. To verify that it is even a ring isomorphism, it is enough to consider matrices $A$, $B$ with only one non-zero entry each. But then $AB=0$ or $AB$ is just the multiplication in $K[[X_{1},\ldots ,X_{n}]]$. So we can now freely pass from one ring to the other, keeping in mind that we are dealing with power series with non-commuting coefficients! Allowing some flexibility, we can also expand $A=\sum _{i} A_{i}X_{k}^{i}$ where $k$ is fixed and $A_{i}\in K[[X_{1},\ldots ,X_{k-1},X_{k+1},\ldots ,X_{n}]]^{n\times n}$. This suggests to define

$$ \partial _{k}A:=\sum _{i=1}^{\infty }iA_{i}X_{k}^{i-1}=(\partial _{k} \alpha _{ij})_{i,j}.$$

The sum and product differentiation rules remain correct, but the power rule $\partial _{k}(A^{s})=s\partial _{k}(A)A^{s-1}$ (and in turn Leibniz’ rule) does not hold in general, since $A$ might not commute with $\partial _{k}A$.

The next two results are just warm-ups and are not needed later on.

Lemma 9.1

Let $A\in K[[X_{1},\ldots ,X_{n}]]^{n\times n}$ and $1\le k\le n$. Then $\partial _{k}\det (A)= \operatorname{tr}\bigl(\operatorname{adj}(A) \partial _{k}A\bigr)$.

Proof

Write $A=(\alpha _{ij})$. By Leibniz’ formula and the product rule, it follows that

$$\begin{aligned} \partial _{k}\det (A)&=\partial _{k}\Bigl(\sum _{\sigma \in S_{n}} \operatorname{sgn}(\sigma )\alpha _{1\sigma (1)}\ldots \alpha _{n \sigma (n)}\Bigr) \\ &=\sum _{i=1}^{n}\sum _{\sigma \in S_{n}}\operatorname{sgn}(\sigma ) \alpha _{1\sigma (1)}\ldots \partial _{k}(\alpha _{i\sigma (i)}) \ldots \alpha _{n\sigma (n)} \\ &=\sum _{i=1}^{n}\sum _{j=1}^{n}\sum _{ \substack{\sigma \in S_{n}\\\sigma (j)=i}}\operatorname{sgn}(\sigma ) \alpha _{1\sigma (1)}\ldots \partial _{k}(\alpha _{ji})\ldots \alpha _{n \sigma (n)}. \end{aligned}$$

The permutations $\sigma \in S_{n}$ with $\sigma (j)=i$ correspond naturally to

$$ \tau :=(i,i+1,\ldots ,n)^{-1}\sigma (j,j+1,\ldots ,n)\in S_{n-1}$$

with $\operatorname{sgn}(\tau )=(-1)^{i+j}\operatorname{sgn}(\sigma )$. Hence, Leibniz’ formula applied to $\det (A_{ji})$ gives

$$ \sum _{j=1}^{n}\sum _{\substack{\sigma \in S_{n}\\\sigma (j)=i}} \operatorname{sgn}(\sigma )\alpha _{1\sigma (1)}\ldots \partial _{k}( \alpha _{ji})\ldots \alpha _{n\sigma (n)}=\sum _{j=1}^{n}(-1)^{i+j} \det (A_{ji})\partial _{k}(\alpha _{ji}).$$

Since this is the entry of $\operatorname{adj}(A)\partial _{k}A$ at position $(i,i)$, the claim follows. □

If $\operatorname{char}K=0$ and $A\in K^{n\times n}[[X_{1},\ldots ,X_{n}]]$ has zero constant term, then $\exp (A)=\sum _{k=0}^{\infty}\frac{A^{k}}{k!}$ converges in the topology induced by the norm. Since the constant term is $1_{n}$, $\exp (A)$ is invertible.

Theorem 9.2

Jacobi’s determinant formula

Let $\operatorname{char}K=0$ and $A\in K^{n\times n}[[X_{1}, \ldots ,X_{n}]]$ with zero constant term. Then

$$ \boxed{\det (\exp (A))=\exp (\operatorname{tr}(A)).}$$

Proof

We introduce a new variable $Y$ and consider $B:=\exp (AY)$. Denoting the derivative with respect to $Y$ by ′, we have

$$ B'=\Bigl(\sum _{k=0}^{\infty}\frac{A^{k}}{k!}Y^{k}\Bigr)'=\sum _{k=1}^{ \infty}\frac{A^{k}}{(k-1)!}Y^{k-1}=AB.$$

Invoking Lemma 9.1 and using that $B$ is invertible, we compute:

$$\begin{aligned} \det (B)'&=\operatorname{tr}(\operatorname{adj}(B)B')=\det (B) \operatorname{tr}(B^{-1}AB)=\det (B)\operatorname{tr}(A). \end{aligned}$$

This is a differential equation, which can be solved as follows. Write $\det (B)=\sum _{k=0}^{\infty }B_{k}Y^{k}$ with $B_{k}\in K[[X_{1},\ldots ,X_{n}]]$. Then $B_{0}=\det (B(0))=\det (\exp (0)1_{n})=\det (1_{n})=1$ and $B_{k+1}=\frac{1}{k+1}\operatorname{tr}(A)B_{k}$ for $k\ge 0$. This yields

$$ \det (B)=1+\operatorname{tr}(A)Y+\frac{\operatorname{tr}(A)^{2}}{2}Y^{2}+ \cdots =\exp (\operatorname{tr}(A)Y).$$

Since we already know that $\exp (A)$ converges, we are allowed to evaluate $Y$ at 1 in $B$, from which the claim follows. □

Definition 9.3

For $\alpha =(\alpha _{1},\ldots ,\alpha _{n})\in K[[X_{1},\ldots ,X_{n}]]^{n}$ we call

$$ J(\alpha ):=(\partial _{j}\alpha _{i})_{i,j}\in K[[X_{1},\ldots ,X_{n}]]^{n \times n}$$

the Jacobi matrix of $\alpha$.

Example 9.4

The Jacobi matrix of the power sum polynomials $\rho =(\rho _{1},\ldots ,\rho _{n})$ is a deformed Vandermonde matrix $J(\rho )=(iX_{j}^{i-1})_{i,j}$ with determinant $n!\prod _{i< j}(X_{j}-X_{i})$. The next theorem furnishes a new proof for the algebraic independence of $\rho _{1},\ldots ,\rho _{n}$.

Theorem 9.5

Let $\operatorname{char}K=0$. Polynomials $\alpha _{1},\ldots ,\alpha _{n}\in K[X_{1},\ldots ,X_{n}]$ form a transcendence basis of $K(X_{1},\ldots ,X_{n})$ if and only if $\det (J(\alpha ))\ne 0$.

Proof

The proof follows [19, Proposition 3.10]. Suppose first that $\alpha _{1},\ldots ,\alpha _{n}$ are algebraically dependent. Then there exists $\beta \in K[X_{1},\ldots ,X_{n}]\setminus K$ such that $\beta (\alpha _{1},\ldots ,\beta _{n})=0$ and we may assume that $\deg (\beta )$ is as small as possible. By (8.6),

$$ \sum _{i=1}^{n}(\partial _{k}\alpha _{i})(\partial _{i}\beta )( \alpha _{1},\ldots \alpha _{n})=\partial _{k}(\beta (\alpha _{1}, \ldots ,\beta _{n}))=0$$

for $k=1,\ldots ,n$. This is a homogeneous linear system over $K(X_{1},\ldots ,X_{n})$ with coefficient matrix $J(\alpha )^{\mathrm{t}}$ (the transpose of $F(\alpha )$). Since $\beta \notin K$ and $\operatorname{char}K=0$, there exists $1\le k\le n$ such that $\partial _{k}\beta \ne 0$. Now $(\partial _{k}\beta )(\alpha _{1},\ldots ,\alpha _{n})\ne 0$, because $\deg (\beta )$ was chosen to be minimal. Hence, the linear system has a non-trivial solution and $\det (J(\alpha ))$ must be 0.

Assume conversely, that $\alpha _{1},\ldots ,\alpha _{n}$ are algebraically independent over $K$. Since $K(X_{1},\ldots ,X_{n})$ has transcendence degree $n$, the polynomials $X_{i},\alpha _{1},\ldots ,\alpha _{n}$ are algebraically dependent for each $i=1,\ldots ,n$. Let $\beta _{i}\in K[X_{0},X_{1},\ldots ,X_{n}]\setminus K$ such that $\beta _{i}(X_{i},\alpha _{1},\ldots ,\alpha _{n})=0$ and $\deg (\beta _{i})$ as small as possible. Again by (8.6),

$$\begin{aligned} & \delta _{ik}(\partial _{0}\beta _{i})(X_{i},\alpha _{1},\ldots , \alpha _{n})+\sum _{j=1}^{n}(\partial _{k}\alpha _{j})(\partial _{j} \beta _{i})(X_{i},\alpha _{1},\ldots \alpha _{n})\\&\quad =\partial _{k}( \beta _{i}(X_{i},\alpha _{1},\ldots ,\beta _{n}))=0 \end{aligned}$$

for $i=1,\ldots ,n$. Since $\alpha _{1},\ldots ,\alpha _{n}$ are algebraically independent, $X_{0}$ must occur in every $\beta _{i}$. In particular, $\partial _{0}\beta _{i}\ne 0$ has smaller degree than $\beta _{i}$. The choice of $\beta _{i}$ implies $(\partial _{0}\beta _{i})(X_{i},\alpha _{1},\ldots \alpha _{n})\ne 0$ for $i=1,\ldots ,n$. This leads to the following matrix equation in $K[X_{1},\ldots ,X_{n}]$:

$$ \bigl((\partial _{j}\beta _{i})(X_{i},\alpha _{1},\ldots ,\alpha _{n}) \bigr)_{i,j}J(\alpha )=-\bigl(\delta _{ij}(\partial _{0}\beta _{i})(X_{i}, \alpha _{1},\ldots ,\alpha _{n})\bigr)_{i,j}.$$

Since the determinant of the diagonal matrix on the right hand side does not vanish, also $\det (J(\alpha ))$ cannot vanish. □

Definition 9.6

Let $C_{a}\subseteq K[[X_{1},\ldots ,X_{n}]]$ be the set of power series with constant term $a\in K$, i.e. $\alpha \in C_{a}\iff \alpha (0)=a$. Let

$$ K[[X_{1},\ldots ,X_{n}]]^{\circ}:=\bigl\{ \alpha \in C_{0}^{n}:\det (J( \alpha ))\notin C_{0}\bigr\} \subseteq K[[X_{1},\ldots ,X_{n}]]^{n}.$$

For $n=1$ we have $\alpha \in K[[X_{1},\ldots ,X_{n}]]^{\circ}\iff \alpha (0)=0\ne \alpha '(0)\iff \alpha \in (X)\setminus (X^{2})$, so our notation is consistent with Theorem 3.4. The following is a multivariate analog.

Theorem 9.7

Inverse function theorem

The set $K[[X_{1},\ldots ,X_{n}]]^{\circ}$ is a group with respect to ∘ and

$$ K[[X_{1},\ldots ,X_{n}]]^{\circ}\to \operatorname{GL}(n,K),\qquad \alpha \mapsto J(\alpha )(0)$$

is a group epimorphism.

Proof

Let $\alpha ,\beta \in K[[X_{1},\ldots ,X_{n}]]^{\circ}$. Clearly, $\alpha \circ \beta \in C_{0}^{n}$. By (8.6),

$$ \partial _{j}(\alpha _{i}(\beta ))=\sum _{k=1}^{n}(\partial _{j} \beta _{k})(\partial _{k}\alpha _{i})(\beta )$$

and $J(\alpha \circ \beta )=J(\alpha )(\beta )\cdot J(\beta )$. It follows that

$$ J(\alpha \circ \beta )(0)=J(\alpha )(0)J(\beta )(0)\ne 0 $$

(9.1)

and $\alpha \circ \beta \in K[[X_{1},\ldots ,X_{n}]]^{\circ}$. By fully exploiting (8.5), the associativity $(\alpha \circ \beta )\circ \gamma =\alpha \circ (\beta \circ \gamma )$ can be reduced to the case where $\alpha =(0,\ldots ,0,X_{i},0,\ldots ,0)$. In this case the statement is clear. The identity element of $K[[X_{1},\ldots ,X_{n}]]^{\circ}$ is clearly $(X_{1},\ldots ,X_{n})$. For the construction of inverse elements, we first assume that $J(\alpha )(0)=1_{n}$. Here we can adapt the proof of Theorem 8.5. We sort the $n$-tuples of indices lexicographically and define $\beta _{i,1}:=X_{i}\in C_{0}$. For a given $\beta _{i,j}$ let $f(i,j):=(k_{1},\ldots ,k_{n})$ be the minimal tuple such that the coefficient $c$ of $X_{1}^{k_{1}}\ldots X_{n}^{k_{n}}$ in $\beta _{i,j}(\alpha _{1},\ldots ,\alpha _{n})-X_{i}$ is non-zero (if there is no such tuple we are done). Now let

$$ \beta _{i,j+1}:=\beta _{i,j}-cX_{1}^{k_{1}}\ldots X_{n}^{k_{n}}\in C_{0}.$$

Since $(\partial _{j}\alpha _{k})(0)=\delta _{kj}$, $X_{k}$ is the unique monomial of degree 1 in $\alpha _{k}$. Consequently, $X_{1}^{k_{1}}\ldots X_{n}^{k_{n}}$ is the unique lowest degree monomial in $\alpha _{1}^{k_{1}}\ldots \alpha _{n}^{k_{n}}$. Hence, going from $\beta _{i,j}(\alpha _{1},\ldots ,\alpha _{n})$ to $\beta _{i,j+1}(\alpha _{1},\ldots ,\alpha _{n})$ replaces $X_{1}^{k_{1}}\ldots X_{n}^{k_{n}}$ with terms of higher degree. Consequently, $f(i,j+1)>f(i,j)$ and $\beta _{i}:=\lim _{j\to \infty}\beta _{i,j}\in C_{0}$ exists with $\beta _{i}(\alpha _{1},\ldots ,\alpha _{n})=X_{i}$.

Now we consider the general case. As explained before, $\det (J(\alpha ))\notin C_{0}$ implies that $J(\alpha )$ is invertible. Let $S:=(s_{ij})=J(\alpha )^{-1}(0)\in K^{n\times n}$ and

$$ \tilde{\alpha}_{i}:=\sum _{j=1}^{n}s_{ij}\alpha _{j}\in C_{0}$$

for $i=1,\ldots ,n$. Then

$$ J(\tilde{\alpha})(0)=(\partial _{j}\tilde{\alpha}_{i})_{i,j}(0)= \Bigl(\sum _{k=1}^{n}s_{ik}(\partial _{j}\alpha _{k})(0)\Bigr)_{i,j}=SJ( \alpha )(0)=1_{n}.$$

By the construction above, there exists $\tilde{\beta}\in C_{0}^{n}$ with $\tilde{\alpha}\circ \tilde{\beta}=(X_{1},\ldots ,X_{n})$. Define $\tilde{X}_{i}:=\sum _{j=1}^{n}s_{ij}X_{j}\in C_{0}$ and $\beta _{i}:=\tilde{\beta}_{i}(\tilde{X}_{1},\ldots ,\tilde{X}_{n}) \in C_{0}$ for $i=1,\ldots ,n$. Then

$$ \sum _{j=1}^{n}s_{ij}\alpha _{i}(\beta _{1},\ldots ,\beta _{n})= \tilde{\alpha}_{i}\circ \beta =\tilde{\alpha}_{i}\circ \tilde{\beta} \circ (\tilde{X}_{1},\ldots ,\tilde{X}_{n})=\tilde{X}_{i}=\sum _{j=1}^{n}s_{ij}X_{j}.$$

Since $S$ is invertible, it follows that $\alpha _{i}(\beta _{1},\ldots ,\beta _{n})=X_{i}$ for $i=1,\ldots ,n$. By (9.1), $J(\beta )(0)=S$ and $\beta \in K[[X_{1},\ldots ,X_{n}]]^{\circ}$ is the inverse of $\alpha$ with respect to ∘. This shows that $K[[X_{1},\ldots ,X_{n}]]^{\circ}$ is a group. The map $\alpha \mapsto J(\alpha )(0)$ is a homomorphism by (9.1). For $A=(a_{ij})\in \operatorname{GL}(n,K)$ let $\alpha _{i}:=a_{i1}X_{1}+\cdots +a_{in}X_{n}$. Then $\alpha \in C_{0}$ and $J(\alpha )(0)=A$. So our map is surjective. □

If $\operatorname{char}K=0$ and $\alpha _{1},\ldots ,\alpha _{n}\in K[X_{1},\ldots ,X_{n}]$ are polynomials such that $\det (J(\alpha ))\in K^{\times}$, the Jacobi conjecture (put forward by Keller [22] in 1939) claims that there exist polynomials $\beta _{1},\dots ,\beta _{n}$ such that $\alpha \circ \beta =(X_{1},\ldots ,X_{n})$. This is still open even for $n=2$ (see [42]).

An explicit formula for the reverse (i.e. the inverse with respect to ∘) is given by the following multivariate version of Theorem 7.5. To simplify the proof (which is still difficult) we restrict ourselves to those $\beta \in K[[X_{1},\ldots ,X_{n}]]$ such that $\beta _{i}\in X_{i}C_{1}\subseteq C_{0}$. Note that $J(\beta )(0)=1_{n}$ here.

Theorem 9.8

Lagrange–Good’s inversion formula

Let $\operatorname{char}K=0$, $\alpha \in K[[X_{1}, \ldots ,X_{n}]]$ and $\beta _{i}\in X_{i}C_{1}$ for $i=1,\ldots ,n$. Then

$$ \alpha =\sum _{k_{1},\ldots ,k_{n}\ge 0}c_{k_{1},\ldots ,k_{n}}\beta _{1}^{k_{1}} \ldots \beta _{n}^{k_{n}} $$

(9.2)

where $c_{k_{1},\ldots ,k_{n}}\in K$ is the coefficient of $X_{1}^{k_{1}}\ldots X_{n}^{k_{n}}$ in

$$ \alpha \Bigl(\frac{X_{1}}{\beta _{1}}\Bigr)^{k_{1}+1}\ldots \Bigl( \frac{X_{n}}{\beta _{n}}\Bigr)^{k_{n}+1}\det (J(\beta )).$$

Proof

The proof is taken from Hofbauer [18]. By the inverse function theorem, there exists $\gamma \in K[[X_{1},\ldots ,X_{n}]]^{\circ}$ such that $\gamma \circ \beta =(X_{1},\ldots ,X_{n})$. Replacing $X_{i}$ by $\gamma _{i}(\beta )$ in $\alpha$ yields an expansion in the form (9.2) where we denote the coefficients by $\bar{c}_{k_{1},\ldots ,k_{n}}$ for the moment. Observe that $\tau _{i}:=X_{i}/\beta _{i}\in C_{1}$ and $\det (J(\beta ))\in C_{1}$. For $l_{1},\ldots ,l_{n}\ge 0$ we define

$$ \rho _{l_{1},\ldots ,l_{n}}:=\tau _{1}^{l_{1}+1}\ldots \tau _{n}^{l_{n}+1} \det (J(\beta ))\in C_{1}.$$

Then $c_{l_{1},\ldots ,l_{n}}$ is, by definition, the coefficient of $X_{1}^{l_{1}}\ldots X_{n}^{l_{n}}$ in $\alpha \rho _{l_{1},\ldots ,l_{n}}$. So it also must be the coefficient of $X_{1}^{l_{1}}\ldots X_{n}^{l_{n}}$ in

$$ \sum _{ \substack{k_{1},\ldots ,k_{n}\ge 0\\\forall i\,:\,k_{i}\le l_{i}}} \bar{c}_{k_{1},\ldots ,k_{n}}X_{1}^{k_{1}}\ldots X_{n}^{k_{n}}\rho _{l_{1}-k_{1}, \ldots ,l_{n}-k_{n}}.$$

It is easy to see that $c_{0,\ldots ,0}=\alpha (0)=\bar{c}_{0,\ldots ,0}$ as claimed. Hence, it suffices to show that $X_{1}^{k_{1}}\ldots X_{n}^{k_{n}}$ does not occur in $\rho _{k_{1},\ldots ,k_{n}}$ for $(k_{1},\ldots ,k_{n})\ne (0,\ldots ,0)$. By the product rule,

$$ \tau _{i}\partial _{j}\beta _{i}=\partial _{j}(\beta _{i}\tau _{i})- \beta _{i}\partial _{j}\tau _{i}=\delta _{ij}-X_{i} \frac{\partial _{j}\tau _{i}}{\tau _{i}}.$$

Since the (Jacobi) determinant is linear in every row, it follows that

$$ \rho _{k_{1},\ldots ,k_{n}}=\det \bigl(\delta _{ij}\tau _{i}^{k_{i}}-X_{i} \tau _{i}^{k_{i}-1}\partial _{j}\tau _{i}\bigr)=\sum _{\sigma \in S_{n}} \operatorname{sgn}(\sigma )\prod _{i=1}^{n}\bigl(\delta _{i\sigma (i)} \tau _{i}^{k_{i}}-X_{i}\tau _{i}^{k_{i}-1}\partial _{\sigma (i)}\tau _{i} \bigr).$$

By the (multivariate) Taylor series, we want to show that $(\partial _{1}^{k_{1}}\ldots \partial _{n}^{k_{n}}\rho _{k_{1}, \ldots ,k_{n}})(0)=0$.

Leibniz’ rule applied to the inner product yields

$$ P_{\sigma}:=\!\sum _{l_{11}+\cdots +l_{1s}=k_{1}}\!\ldots\! \sum _{l_{n1}+ \cdots +l_{ns}=k_{n}}\!\!\frac{k_{1}!\ldots k_{n}!}{\prod _{i,j}l_{ij}!} \prod _{t=1}^{n}\partial _{1}^{l_{1t}}\ldots \partial _{n}^{l_{nt}} \bigl(\delta _{t\sigma (t)}\tau _{t}^{k_{t}}-X_{t}\tau _{t}^{k_{t}-1} \partial _{\sigma (t)}\tau _{t}\bigr)$$

Therein, we find

$$ \bigl(\partial _{1}^{l_{1t}}\ldots \partial _{n}^{l_{nt}}(X_{t}\tau _{t}^{k_{t}-1} \partial _{\sigma (t)}\tau _{t})\bigr)(0)=l_{tt}\bigl(\partial _{1}^{l_{1t}} \ldots \partial _{t}^{l_{tt}-1}\ldots \partial _{n}^{l_{nt}}(\tau _{t}^{k_{t}-1} \partial _{\sigma (t)}\tau _{t})\bigr)(0).$$

In particular, the product is zero if $\sigma (t)\ne t$ and $l_{tt}=0$. We will disregard this case in the following. This also means that $t_{\sigma (t)\sigma (t)}< k_{t}$ whenever $\sigma (t)\ne t$. We set $\mu _{i}:=\tau _{i}^{k_{i}}$ and observe that $\frac{1}{k_{t}}\partial _{\sigma (t)}(\mu _{t})=\tau _{t}^{k_{t}-1} \partial _{\sigma (t)}\tau _{t}$. Hence, the inner product of $P_{\sigma}(0)$ takes the form

$$ \prod _{t=1}^{n}\bigl(\delta _{t\sigma (t)}\partial _{1}^{l_{1t}} \ldots \partial _{n}^{l_{nt}}\mu _{t}-\frac{l_{tt}}{k_{t}}\partial _{1}^{l_{1t}} \ldots \partial _{t}^{l_{tt}-1}\ldots \partial _{\sigma (t)}^{l_{ \sigma (t)t}+1}\ldots \partial _{n}^{l_{nt}}\mu _{t}\bigr).$$

Finally, we transform the indices via $l_{jt}\mapsto m_{jt}:=l_{jt}-\delta _{jt}+\delta _{j\sigma (t)}$ (the problematic cases $l_{tt}=0$ and $l_{\sigma (t)\sigma (t)}=k_{\sigma (t)}$ were excluded above). Note that $m_{1t}+\cdots +m_{nt}=k_{t}$ and

$$ \frac{l_{tt}}{l_{1t}!\ldots l_{nt}!}= \frac{l_{\sigma (t)t}+1}{l_{1t}!\ldots (l_{tt}-1)!\ldots (l_{\sigma (t)t}+1)!\ldots l_{nt}!}= \frac{m_{\sigma (t)t}}{m_{1t}!\ldots m_{nt}!}.$$

This turns $P_{\sigma}(0)$ into

$$ P_{\sigma}(0)=\sum _{m_{ij}} \frac{k_{1}!\ldots k_{n}!}{\prod _{i,j}m_{ij}!}\prod _{t=1}^{n} \partial _{1}^{m_{1t}}\ldots \partial _{n}^{m_{nt}}(\mu _{t})(0) \Bigl(\delta _{t\sigma (t)}-\frac{m_{\sigma (t)t}}{k_{t}}\Bigr).$$

Since only the last term actually depends on $\sigma$, we conclude

$$\begin{aligned} & (\partial _{1}^{k_{1}}\ldots \partial _{n}^{k_{n}}\rho _{k_{1}, \ldots ,k_{n}})(0)\\&\quad =\sum _{m_{ij}} \frac{k_{1}!\ldots k_{n}!}{\prod _{i,j}m_{ij}!}\prod _{t=1}^{n} \partial _{1}^{m_{1t}}\ldots \partial _{n}^{m_{nt}}(\mu _{t})(0)\sum _{ \sigma \in S_{n}}\operatorname{sgn}(\sigma )\prod _{t=1}^{n}\Bigl( \delta _{t\sigma (t)}-\frac{m_{\sigma (t)t}}{k_{t}}\Bigr). \end{aligned}$$

The final sum is the determinant of $(\delta _{ij}-m_{ji}/k_{i})_{ij}$. This matrix is singular, since each column sum is $1-\frac{1}{k_{i}}\sum _{j=1}^{n}m_{ji}=0$. This completes the proof of $(\partial _{1}^{k_{1}}\ldots \partial _{n}^{k_{n}}\rho _{k_{1}, \ldots ,k_{n}})(0)=0$. □

In an attempt to unify and generalize some dual pairs we have already found, we study the following setting. Let $A=(a_{ij})\in K^{n\times n}$ and $D=\operatorname{diag}(X_{1},\ldots ,X_{n})$. For $I\subseteq N:=\{1,\ldots ,n\}$ let $A_{I}:=(a_{ij})_{i,j\in I}$ and $X_{I}=\prod _{i\in I}X_{i}$. Since the determinant is linear in every row, we obtain

$$\begin{aligned} &\det (1_{n}+DA)\\&\quad= \begin{vmatrix} 1&0&\cdots &0 \\ a_{21}X_{2}&1+a_{22}X_{2}& &a_{2n}X_{2} \\ \vdots &&\ddots &\vdots \\ a_{n1}X_{n}&\cdots &\cdots &1+a_{nn}X_{n} \end{vmatrix}+ \begin{vmatrix} a_{11}&\cdots &a_{1n} \\ a_{21}X_{2}&&a_{2n}X_{2} \\ \vdots &&\vdots \\ a_{n1}X_{n}&\cdots &1+a_{nn}X_{n} \end{vmatrix}X_{1} \\ &\quad= \begin{vmatrix} 1+a_{22}X_{2}&\cdots &a_{2n}X_{2} \\ \vdots &\ddots &\vdots \\ a_{n2}X_{n}&\cdots &1+a_{nn}X_{n} \end{vmatrix}+ \begin{vmatrix} a_{11}&\cdots &\cdots &a_{1n} \\ 0&1&0&0 \\ a_{31}X_{3}&&&a_{3n}X_{3} \\ \vdots &&&\vdots \\ a_{n1}X_{n}&\cdots &\cdots &1+a_{nn}X_{n} \end{vmatrix}X_{1} \\ &\qquad + \begin{vmatrix} a_{11}&\cdots &a_{1n} \\ a_{21}&\cdots &a_{2n} \\ a_{31}X_{3}&\cdots &a_{3n}X_{3} \\ \vdots &&\vdots \\ a_{n1}X_{n}&\cdots &1+a_{nn}X_{n} \end{vmatrix}X_{1}X_{2}=\cdots \\ &\quad=1+\sum _{i=1}^{n}a_{ii}X_{i}+\sum _{i< j}\det (A_{\{i,j\}})X_{i}X_{j}+ \cdots +\det (A)X_{N}. \end{aligned}$$

Altogether,

$$ \det (1_{n}+DA)=\sum _{I\subseteq N}\det (A_{I})X_{I}, $$

(9.3)

where $\det (A_{\varnothing})=1$ for convenience. The dual equation, discovered by Vere-Jones [43], uses the permanent $\operatorname{per}(A)=\sum _{\sigma \in S_{n}}a_{1\sigma (1)}\ldots a_{n \sigma (n)}$ of $A$:

$$ \frac{1}{\det (1_{n}-DA)}=\sum _{k=0}^{\infty}\sum _{I\in N^{k}} \operatorname{per}(A_{I})\frac{X_{I}}{k!}, $$

(9.4)

where $I$ now runs through all tuples of elements in $N$ (in contrast to the determinant, $\operatorname{per}(A_{I})$ does not necessarily vanish if $A_{I}$ has identical rows). We will derive (9.4) in Corollary 9.10 from the following result, which seems more amenable to applications.

Theorem 9.9

MacMahon’s Master Theorem

Let $\operatorname{char}K=0$, $A=(a_{ij})\in K^{n\times n}$ and $D=\operatorname{diag}(X_{1},\ldots ,X_{n})$. Then

$$ \boxed{\frac{1}{\det (1_{n}-DA)}=\sum _{k_{1},\ldots ,k_{n}\ge 0}c_{k_{1},\ldots ,k_{n}}X_{1}^{k_{1}}\ldots X_{n}^{k_{n}},} $$

(9.5)

where $c_{k_{1},\ldots ,k_{n}}\in K$ is the coefficient of $X_{1}^{k_{1}}\ldots X_{n}^{k_{n}}$ in

$$ \prod _{i=1}^{n}(a_{i1}X_{1}+\cdots +a_{in}X_{n})^{k_{i}}.$$

Proof

Let $A_{i}:=a_{i1}X_{1}+\cdots +a_{in}X_{n}$ and $\beta _{i}:=X_{i}(1+A_{i})^{-1}\in X_{i}C_{1}$ for $i=1,\ldots ,n$. Let $D(\beta ):=\operatorname{diag}(\beta _{1},\ldots ,\beta _{n})$ and $\alpha :=\det (1_{n}-D(\beta )A)^{-1}$. Since $\partial _{j} A_{i}=a_{ij}$, we obtain

$$ \partial _{j}\beta _{i}= \frac{\delta _{ij}(1+A_{i})-X_{i}a_{ij}}{(1+A_{i})^{2}}= \frac{\delta _{ij}-\beta _{i}a_{ij}}{1+A_{i}}$$

and

$$ \alpha \det (J(\beta ))=\prod _{i=1}^{n}\frac{1}{1+A_{i}}.$$

Hence, by Theorem 9.8, the coefficient of $\beta _{1}^{k_{1}}\ldots \beta _{n}^{k_{n}}$ in $\alpha$ is the coefficient of $X_{1}^{k_{1}}\ldots X_{n}^{k_{n}}$ in

$$ \Bigl(\frac{X_{1}}{\beta _{1}}\Bigr)^{k_{1}+1}\ldots \Bigl( \frac{X_{n}}{\beta _{n}}\Bigr)^{k_{n}+1}\prod _{i=1}^{n} \frac{1}{1+A_{i}}=\prod _{i=1}^{n}(1+a_{i1}X_{1}+\cdots +a_{in}X_{n})^{k_{i}}.$$

Since the product on the right hand side has degree $k_{1}+\cdots +k_{n}$, the additional summand 1 plays no role and the desired coefficient really is $c_{k_{1},\ldots ,k_{n}}$. By Theorem 9.7, the $X_{i}$ can be substituted by some $\gamma _{i}$ such that $\beta _{1}^{k_{1}}\ldots \beta _{n}^{k_{n}}$ becomes $X_{1}^{k_{1}}\ldots X_{n}^{k_{n}}$ and $\alpha$ becomes $\det (1_{n}-DA)^{-1}$. □

A graph-theoretical proof of Theorem 9.9 was given by Foata and is presented in [8, Sect. 9.4]. There is also a short analytic argument which reduces the claim to the easy case where $A$ is a triangular matrix.

Corollary 9.10

Equation (9.4) holds.

Proof

By the multinomial theorem we have

$$\begin{aligned} &\prod _{i=1}^{n}(a_{i1}X_{1}+\cdots +a_{in}X_{n})^{k_{i}} \\ &=\sum _{k_{11}+\cdots +k_{1n}=k_{1}}\!\ldots\! \sum _{k_{n1}+\cdots +k_{nn}=k_{n}}\! \frac{k_{1}!\ldots k_{n}!}{\prod _{i,j}k_{ij}!}a_{11}^{k_{11}}a_{12}^{k_{12}} \ldots a_{nn}^{k_{nn}}X_{1}^{k_{11}+\cdots +k_{n1}}\ldots X_{n}^{k_{1n}+ \cdots +k_{nn}}. \end{aligned}$$

To obtain $c_{k_{1},\ldots ,k_{n}}$ one needs to run only over those indices $k_{ij}$ with $\sum _{i} k_{ij}=k_{j}$ for $j=1,\ldots ,n$.

On the other hand, we need to sum over those tuples $I\in N^{k_{1}+\cdots +k_{n}}$ in (9.4) which contain $i$ with multiplicity $k_{i}$ for each $i=1,\ldots ,n$. The number of those tuples is $\frac{(k_{1}+\cdots +k_{n})!}{k_{1}!\ldots k_{n}!}$. The factor $(k_{1}+\cdots +k_{n})!$ cancels with $\frac{1}{k!}$ in (9.4). Since the permanent is invariant under permutations of rows and columns, we may assume that $I=(1^{k_{1}},\ldots ,n^{k_{n}})$. Then $A_{I}$ has the block form $A_{I}=(A_{ij})_{i,j}$ where

$$ A_{ij}=a_{ij} \begin{pmatrix} 1&\cdots &1 \\ \vdots &&\vdots \\ 1&\cdots &1 \end{pmatrix} \in K^{k_{i}\times k_{j}}.$$

In the definition of $\operatorname{per}(A_{I})$, every permutation $\sigma$ corresponds to a selection of $n$ entries in $A_{I}$ such that one entry in each row and each column is selected. Suppose that $k_{ij}$ entries in block $A_{ij}$ are selected. Then $\sum _{i} k_{ij}=k_{j}$ and $\sum _{j} k_{ij}=k_{i}$. To choose the rows in each $A_{ij}$ there are $\frac{k_{1}!\ldots k_{n}!}{\prod k_{ij}!}$ possibilities. We get the same number for the selections of columns. Finally, once rows and columns are fixed, there are $\prod k_{ij}!$ choices to permute the entries in each block $A_{ij}$. Now the coefficient of $X_{1}^{k_{1}}\ldots X_{n}^{k_{n}}$ in (9.4) turns out to be

$$ \sum _{ \substack{k_{ij}\\\sum _{i}k_{ij}=k_{j}\\\sum _{j}k_{ij}=k_{i}}} \frac{k_{1}!\ldots k_{n}!}{\prod _{i,j} k_{ij}!}a_{11}^{k_{11}}a_{12}^{k_{12}} \ldots a_{nn}^{k_{nn}}=c_{k_{1},\ldots ,k_{n}}. $$

 □

We illustrate with some examples why MacMahon called Theorem 9.9 the master theorem (as he was a former major, I am tempted to called it the $M^{4}$-theorem).

Example 9.11

• 1. The expression $\det (1_{n}-DA)$ is reminiscent to the definition of the characteristic polynomial $\chi _{A}=X^{n}+s_{n-1}X^{n-1}+\cdots +s_{0}\in K[X]$ of $A$. In fact, setting $X:=X_{1}=\cdots =X_{n}$ allows us to regard $\det (1_{n}-XA)$ as a Laurent polynomial in $X$. We can then introduce $X^{-1}$ to obtain

  $$ \det (1_{n}-XA)=X^{n}\det (X^{-1}1_{n}-A)=X^{n}\chi _{A}(X^{-1})=1+s_{n-1}X+ \cdots +s_{0}X^{n}.$$

  Now (9.3) in combination with Vieta’s theorem yields

  $$ \sum _{\substack{I\subseteq N\\|I|=k}}\det (A_{I})=(-1)^{k}s_{n-k}= \sigma _{k}(\lambda _{1},\ldots ,\lambda _{n}),$$

  where $\lambda _{1},\ldots ,\lambda _{n}$ are the eigenvalues of $A$ (in some splitting field). This extends the familiar identities $\det (A)=\lambda _{1}\ldots \lambda _{n}$ and $\operatorname{tr}(A)=\lambda _{1}+\cdots +\lambda _{n}$. With the help of Exercise 8.10, one can also express $s_{k}$ in terms of $\rho _{l}(\lambda _{1},\ldots ,\lambda _{n})=\operatorname{tr}(A^{l})$.

• 2. If $A=1_{n}$ and $X_{1}=\cdots =X_{n}=X$, then (9.3) and (9.5) become

  $$\begin{aligned} (1+X)^{n}&=\sum _{I\subseteq N}X^{|I|}=\sum _{k=0}^{n}\binom{n}{k}X^{k}, \\ (1-X)^{-n}&=\sum _{k_{1},\ldots ,k_{n}\ge 0}X^{k_{1}+\cdots +k_{n}}= \sum _{k=0}^{\infty}\binom{n+k-1}{k}X^{k}, \end{aligned}$$

  since the $k$-element multisets correspond to the tuples $(k_{1},\ldots ,k_{n})$ with $k_{1}+\cdots +k_{n}=k$ where $k_{i}$ encodes the multiplicity of $i$.

• 3. Taking $A=1_{n}$ and $X_{k}=X^{k}$ in (9.5) recovers an equation from Theorem 5.4:

  $$ \prod _{k=1}^{n}\frac{1}{1-X^{k}}=\sum _{k_{1},\ldots ,k_{n}\ge 0}X^{k_{1}+2k_{2}+ \cdots +nk_{n}}=\sum _{k=0}^{\infty }p_{n}(k)X^{k}.$$

  Similarly, choosing $X_{k}=kX$ or $X_{k}=X_{k}Y$ leads more of less directly to Theorem 6.9 and Theorem 8.4 respectively.

• 4. Take $(X_{1},X_{2},X_{3})=(X,Y,Z)$ and

  $$ A= \begin{pmatrix} 0&1&-1 \\ -1&0&1 \\ 1&-1&0 \end{pmatrix} $$

  in (9.5). Then by Sarrus’ rule,

  $$\begin{aligned} \frac{1}{\det (1_{3}-DA)}&=\frac{1}{1+XZ+YZ+XY}=\sum _{k=0}^{\infty}(-1)^{k}(XY+YZ+ZX)^{k} \\ &=\sum _{k=0}^{\infty}(-1)^{k}\sum _{a+b+c=k}\frac{k!}{a!b!c!}X^{a+c}Y^{a+b}Z^{b+c}. \end{aligned}$$

  The coefficient of $(XYZ)^{2n}$ is easily seen to be $(-1)^{n}\frac{(3n)!}{(n!)^{3}}$. On the other hand, the same coefficient in

  $$\begin{aligned} &(Y-Z)^{2n}(Z-X)^{2n}(X-Y)^{2n}\\&\quad =\sum _{a,b,c\ge 0}\binom{2n}{a} \binom{2n}{b}\binom{2n}{c}(-1)^{a+b+c}X^{c-b+2n}Y^{a-c+2n}Z^{b-a+2n} \end{aligned}$$

  occurs for $a=b=c$. This yields Dixon’s identity:

  $$ (-1)^{n}\frac{(3n)!}{(n!)^{3}}=\sum _{k=0}^{2n}(-1)^{k}\binom{2n}{k}^{3}.$$

We end with a short outlook. Power series with an infinite set of indeterminants $\{X_{i}:i\in I\}$ can be defined by

$$ K[[X_{i}:i\in I]]:=\bigcup _{\substack{J\subseteq I\\|J|< \infty}}K[[X_{j}:j \in J]].$$

Moreover, power series in non-commuting indeterminants exists and form what is sometimes called the Magnus ring $K\langle \langle X_{1},\ldots ,X_{n}\rangle \rangle$ (the polynomial version is the free algebra $K\langle X_{1},\ldots ,X_{n}\rangle$). The Lie bracket $[a,b]:=ab-ba$ turns $K\langle \langle X_{1},\ldots ,X_{n}\rangle \rangle$ into a Lie algebra and fulfills Jacobi’s identity

$$ [a,[b,c]]+[b,[c,a]]+[c,[a,b]]=0.$$

The functional equation for $\exp (X)$ is replaced by the Baker–Campbell–Hausdorff formula in this context.

The reader might ask about formal Laurent series in multiple indeterminants. Although the field of fractions $K((X_{1},\ldots ,X_{n}))$ certainly exists, its elements do not look like one might expect. For example, the inverse of $X-Y$ could be $\sum _{k=1}^{\infty }X^{-k}Y^{k-1}$ or $-\sum _{k=1}^{\infty }X^{k-1}Y^{-k}$. The first series lies in $K((X))((Y))$, but not in $K((Y))((X))$. For the second series it is the other way around.