Abstract
This is an overview of the solar modulation of cosmic rays in the heliosphere. It is a broad topic with numerous intriguing aspects so that a research framework has to be chosen to concentrate on. The review focuses on the basic paradigms and departure points without presenting advanced theoretical or observational details for which there exists a large number of comprehensive reviews. Instead, emphasis is placed on numerical modeling which has played an increasingly significant role as computational resources have become more abundant. A main theme is the progress that has been made over the years. The emphasis is on the global features of CR modulation and on the causes of the observed 11-year and 22-year cycles and charge-sign dependent modulation. Illustrative examples of some of the theoretical and observational milestones are presented, without attempting to review all details or every contribution made in this field of research. Controversial aspects are discussed where appropriate, with accompanying challenges and future prospects. The year 2012 was the centennial celebration of the discovery of cosmic rays so that several general reviews were dedicated to historical aspects so that such developments are briefly presented only in a few cases.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Galactic cosmic rays encounter a turbulent solar wind with an embedded heliospheric magnetic field (HMF) when entering the heliosphere. This leads to significant global and temporal variations in their intensity and in their energy as a function of position inside the heliosphere. This process is identified as the solar modulation of cosmic rays (CRs). For this review, CRs are considered to have energies above 1 MeV/nuc and come mainly from outside the heliosphere, with the exception of the anomalous component of cosmic rays (ACRs) which originates inside the heliosphere.
The purpose of this overview is to explain and discuss progress of this process with its intriguing facets. The modulation of CRs is considered to happen from below ∼ 30 GeV/nuc. The review also includes some aspects of ACRs but solar energetic particles, compositional abundances and isotopes are not included. The fascinating origin of CRs and acceleration in galactic space and beyond are not discussed. The emphasis is on the global features of CR modulation and on the causes of the observed 11-year and 22-year cycles and phenomena such as charge-sign dependent modulation. Shorter-term CR variations, on scales shorter than one solar rotation, are not part of this review. Space weather and related issues are reviewed by Shea and Smart (2012), amongst others.
The spotlight is first on the global features of the heliosphere and how it responds to solar activity. It is after all this extensive volume in which solar modulation takes place, mainly determined by what happens on and with the Sun. Transport and modulation theory is explained and the recurrent behaviour that CRs exhibit in the heliosphere is discussed within this context. Major predictions and accomplishments based on numerical modeling and some observational highlights are given. This overview is meant to be informative and didactic in nature.
2 The Global Heliosphere and its Main Features
2.1 Physical boundaries
The heliosphere moves through the interstellar medium so that an interface is formed. In the process the solar wind undergoes transitions with the main constituents its termination shock (TS), the heliopause (HP), and a bow wave (BW), with the regions between the TS, the HP, and the BW defined as the inner and outer heliosheath, respectively. An important goal of the heliospheric exploration by the two Voyager spacecraft has always been to observe this TS and HP. The TS is predicted to be highly dynamic in its location and structure, both globally and locally, and is as such confirmed observationally by Voyager 1 to be at 94 AU in December 2004 and at 84 AU by Voyager 2 in August 2007 (Stone et al., 2005, 2008). Observing the TS in situ was a true milestone. According to Voyager 2 plasma observations, the low solar wind dynamic pressure beyond the TS lead to an inward movement of the TS of about 10 AU to an assumed minimum position of 73 AU in 2010 (Richardson and Wang, 2011). By the end of 2013, Voyager 1 will be at 126.4 AU while Voyager 2 will be at 103.6 AU, both moving into the nose region of the heliosphere but at a totally different heliolatitude, about 60° apart in terms of heliocentric polar angles, and with a significant azimuthal difference (see http://voyager.gsfc.nasa.gov).
Webber and McDonald (2013) reported that Voyager 1 might have crossed the HP (or something that behaves like it) at the end of August 2012, a conclusion based on various CR observations. This is another major milestone for the Voyager mission. Since their launch in 1977, the two spacecraft have explored heliospace from Earth to the HP over almost four decades and will next explore a region probably very close to the pristine local interstellar medium. The passage of the Voyager 1 and 2 spacecraft through the inner heliosheath has revealed a region somewhat unlike than what was observed up-stream of the TS (towards the Sun). The question arises if the modulation of CRs in this region is actually different from the rest of the heliosphere?
Based on magnetohydrodynamic (MHD) modeling, it is generally accepted that the heliospheric structure is asymmetric in terms of a nose-tail (azimuthal) direction, yielding a ratio of ∼ 1:2 for the upwind-to-downwind TS distance from the Sun. This asymmetry is pronounced during solar minimum conditions because the TS propagates toward or away from the Sun with changing solar activity. The exact dependence is still unknown. Encounters with big transients in the HMF may also cause the TS position to change and even oscillate locally with interesting effects on CRs. The HP has always been considered as the heliospheric boundary from a CR modulation point of view because it supposedly separates the solar and interstellar media. Ideally, the solar wind should not propagate beyond this boundary. According to MHD models the HP is properly demarcated in the direction that the heliosphere is moving but not so in the tail direction. Some instabilities can be anticipated at the HP that may modify this picture (e.g., Zank et al., 2009). It is expected that these aspects will be studied with models in greater detail in future. The general features of the heliospheric geometry are shown in Figure 1. For illustrations of these features obtained with magnetohydrodynamic (MHD) models, see, e.g., Opher et al. (2009a) and Pogorelov et al. (2009b).
The basic features of the global heliospheric geometry according to the hydrodynamic (HD) models of Ferreira and Scherer (2004) in terms of the solar wind density (upper panel) and solar wind speed (lower panel). The heliosphere is moving through the interstellar medium to the right. Typical solar minimum conditions are assumed so that the solar wind speed has a strong latitudinal dependence.
The last decade witnessed the development of CR transport models based on improved HD and MHD models of the heliosphere that provide realistic geometries and detailed backgrounds (solar wind flow and corresponding magnetic field lines) to global transport models, called hybrid models. It is known that CRs exert pressure and, therefore, also modify the heliosphere (e.g., Fahr, 2004). These MHD models also predict an asymmetry in a north-south (meridional or polar) direction, making it most likely that the heliosheath is wider in the direction that Voyager 1 is moving than in the Voyager 2 direction. The local interstellar magnetic field causes the heliosphere to become tilted as featured already in earlier global simulations of the heliosphere (e.g., Ratkiewicz et al., 1998; Linde et al., 1998). Although this asymmetry seems somewhat controversial from a MHD point of view, energetic neutral particle (ENAs) observations from the IBEX mission sustain this view of the heliosphere (McComas et al., 2012b). This mission also established that the boundary where the heliosphere begins to disturb the interstellar medium, because it is moving with respect to this medium, should not be seen as a bow shock but rather as a bow wave (McComas et al., 2012a). The relative motion of the Sun with respect to the interstellar medium seems slower and also in a slightly different direction than previously thought. See also Zank et al. (2013). A schematic presentation of this new view of the geometrical shape of the heliosphere is shown in Figure 2. Models of the heliosphere based on HD and MHD approaches have become very sophisticated over the past decade and many of the predicted features still have to be incorporated in the hybrid modeling approach. Whether these detailed features are contributing more than higher order effects to the global solar modulation of CRs is to be determined. For reviews on MHD modeling, see, e.g., Opher et al. (2009b) and Pogorelov et al. (2009a).
A schematic view of an asymmetric heliosphere together with the directions of the interstellar magnetic field lines. The measured ENA flux at ∼ 1.1 keV is superposed on the heliopause with the bright ENA ribbon appears to correlate with where the field is most strongly curved around it. (From the Interstellar Boundary Explorer, IBEX spacecraft’s first all-sky maps of the interstellar interaction at the edge of the heliosphere.) See McComas et al. (2009) for details. Image credit: Adler Planetarium/Southwest Research Institute.
It is to be determined if the outer heliosheath, the region beyond the HP, has any effect on CRs when they enter this region from the interstellar medium. Scherer et al. (2011) presented arguments that this may be the case followed by Strauss et al. (2013b) who presented numerical modeling that produces at 100 MeV a small radial intensity gradient between 0.2% to 0.4% per AU, depending on solar activity, and if the BW is assumed at 250 AU. It may also be that CRs do not enter the heliosphere completely isotropic as always been assumed (e.g., Ngobeni and Potgieter, 2011, 2012).
For informative reviews on several advanced aspects of the outer heliosphere see Jokipii (2012) and Florinski et al. (2011) and for a review on the solar cycle from a solar physics point of view, see Hathaway (2010).
The point to be made here is that the global features of the heliosphere, and in particular the variability and dynamics of the heliospheric boundary lagers, do influence the modulation and the longer-term variations of CRs, even at Earth. How important this all is, will unfold in the coming years.
2.2 Solar wind and heliospheric magnetic field
2.2.1 Global magnetic field geometry
Parker (2001) reviewed how the expansion of the solar corona provides the solar wind with an embedded solar magnetic field that develops into the HMF. He had predicted a well-defined spiral structure for the HMF (Parker, 1958). Over the years modifications to this field have been proposed but the realization of Fisk (1996) that the differential rotation of the Sun and the rigid rotation of polar coronal holes has a significant effect on the structure of the HMF, led to second generation global HMF models that are much more complex and controversial and as such not yet fully appreciated of what it may imply for CR modulation (e.g., Sternal et al., 2011, and references therein). These specific features will have to be studied with MHD modeling to resolve the dispute. The Parker-type field and moderate modification thereof (e.g., Smith and Bieber, 1991) are still widely used in CR modeling. See also the review by Heber and Potgieter (2006).
A straightforward equation for the spiral HMF is
with unit vector components er and eφ in the radial and azimuthal direction respectively; r0 = 1 AU for dimensional purposes and ψ is the (spiral) angle between the radial and the average HMF direction at a certain position. It is given by
and indicates how tightly wound the HMF is, with Ω the angular speed of the Sun, and with r⊙ = 0.005 AU the radius of the solar surface. A typical value at Earth is ψ ≈ 45°, increasing to ∼ 90° with increasing radial distance r beyond 10 AU in the equatorial plane. The solar wind speed is V and θ is the polar angle so that the magnitude of the HMF is
with an average value of 5 nT at Earth or as determined by B0.
The main attribute of the HMF is that it follows a 22-year cycle with a reversal about every ∼ 11 years at the time of extreme solar activity (e.g., Petrovay and Christensen, 2010). It exhibits many distinct shorter scale features (e.g., Balogh and Jokipii, 2009), also associated with the TS and the heliosheath region (Burlaga et al., 2005; Burlaga and Ness, 2011). One of the largest of these magnetic structures was encountered by Voyager 1 in 2009.7 when it already was ∼ 17 AU beyond the TS when the shock had been observed at 94 AU. At this time the field direction suddenly changed indicating a sector crossing. This means that these features, which are well-known in the inner heliosphere, are also occurring in some evolved form in the inner heliosheath. For a review, see Richardson and Burlaga (2011). In this context, it is expected that more interesting and surprising observations and subsequent modeling will follow from the Voyager mission.
A major corotating structure of the HMF of important to CR modulation is the heliospheric current sheet (HCS), which divides the solar magnetic field into hemispheres of opposite polarity. The ∼ 11-year period when it is directed outwards in the northern hemisphere has become known as A > 0 epochs, such as during the 1970s and 1990s, while the 1980s and the period 2002–2014 are known as A < 0 cycles. The HCS has a wavy structure, parameterized by using its tilt angle α (Hoeksema, 1992) and is well correlated to solar activity. During high levels of activity α = 75°, but then becomes undetermined during times of extreme solar activity, while during minimum activity α = 3°–10°. The waviness of the HCS plays an important role in CR modulation (Smith, 2001). It is still the best proxy for solar activity from this point of view. It is widely used in numerical modeling and some aspects are discussed below. A disadvantage is that it is not known how the waviness is preserved as it moves into the outer heliosphere, and especially what happens to it in the heliosheath. The waviness becomes compressed in the inner heliosheath as the outward flow decreases across the TS. It should also spread in latitudinal and azimuthal directions in the nose of the heliosphere. A schematic presentation of how the waviness of the HCS could differ from the nose to the tail regions of the heliosphere is shown in Figure 3. The dynamics of the HCS in the inner heliosheath was investigated by Borovikov et al. (2011) amongst others.
A schematic presentation of how the waviness of the HCS could differ ideally from the nose to the tail regions of the heliosphere. The waviness depicted here corresponds to moderate solar activity. For an elaborate illustration of the dynamics of the HCS obtained with MHD models, see, e.g., Borovikov et al. (2011). Image reproduced by permission from Kóta (2012), copyright by Springer.
Drake et al. (2010) suggested the compacted HCS could lead to magnetic reconnection, otherwise, it could become so densely wrapped that the distance between the wavy layers becomes less than the gyro-radius of the CRs, which may lead to different transport-effects. The behaviour of the HCS in the nose and tail directions of the heliosheath, and its role in transporting CRs, is a study in progress (e.g., Florinski, 2011). It appears that the heliosheath may even require additional transport physics to be included in the next generation of transport models. What happens to the HMF closer to the HP, in the sense of is it still embedded in the solar wind as the HP is approached, is another study in progress.
2.2.2 Global solar wind features
A well reported feature of the global solar wind velocity is that it can be considered basically as radially directed from close to the Sun, across the TS and deep into the inner heliosheath. However, during periods of minimum solar activity this radial flow becomes distinctively latitude dependent, changing easily from an average of 450 km s−1 in the equatorial plane to 800 km s−1 in the polar regions as observed by the Ulysses mission (see the reviews by Heber and Potgieter, 2006, 2008, and reference therein). This aspect is also illustrated in the bottom panel of Figure 1. This significant effect disappears with increasing solar activity. These features are incorporated in most CR modulation models.
The solar wind gradually evolves as it moves outward from the Sun. Its speed is, on average, constant out to ∼ 30 AU, then starts a slow decrease caused by the pickup of interstellar neutrals, which reduces its by ∼ 20% before the TS is reached. These pickup ions heat the thermal plasma so that the solar wind temperature increases outside ∼ 25 AU. The solar wind pressure changes by a factor of 2 over a solar cycle and the structure of the solar wind is modified by interplanetary coronal mass ejections (ICMEs) near solar maximum. The first direct evidence of the TS was the observation of streaming energetic particles by both Voyager 1 and 2 beginning ∼ 2 years before their respective TS crossings. The second evidence was a decrease in the solar wind speed commencing 80 days before Voyager 2 crossed the TS. The TS seems to be a weak, quasi-perpendicular shock, which transferred the solar wind flow energy mainly to the pickup ions (Richardson and Stone, 2009).
Across the TS, the radial solar wind speed slowed down from an average of 400 km s−1 to ∼ 130 km s−1. It then had decreased essentially to zero as Voyager 1 approached the HP but based on non-plasma observations (Krimigis et al., 2011). This appears to happen differently at Voyager 2 and will certainly be different in the tail direction of the heliosphere. Voyager 2, with a working plasma detector, has observed heliosheath plasma since August 2007, which indicates how it has evolved across the inner heliosheath. The radial speed slowly decreased as the plasma flow slowly turned tailward but remained above 100 km s−1, which implies that Voyager 2 was still a substantial distance from the HP in 2012 and that its approach towards the HP is also developing differently from a solar wind point of view (Richardson et al., 2008; Richardson and Wang, 2011). The inner heliosheath is clearly a highly variable region.
The magnitude of the radial component of the solar wind velocity in terms of polar angle and radial distance in AU, as is typically used in numerical models, up to just beyond the TS, is given by
where V0 = 400 km s−1, s = 2.5 and L = 1.2 AU. The TS is positioned at rTS, L is the TS scale length, and s is the compression ratio of the TS, which changes position over a solar cycle. The top and bottom signs respectively correspond to the northern (0 ≤ θ ≤ π/2) and southern hemisphere (π/2 ≤ θ ≤ π) of the heliosphere, with θT = α + 15π/180. This determines at which polar angle the solar wind speed changes from a slow to a fast region during solar minimum activity conditions. This equation is only for such conditions and must also be modified if the solar wind velocity obtains a strong latitudinal and azimuthal component when approaching the HP.
For reviews on observations and interpretations of the solar wind in the outer heliosphere, see Richardson and Stone (2009) and Richardson and Burlaga (2011).
3 Cosmic Rays in the Heliosphere
3.1 Anomalous cosmic rays
The anomalous component of cosmic rays (ACRs) was discovered in the early 1970s (Hovestadt et al., 1973; Garcia-Munoz et al., 1973). This component, with kinetic energy E between ∼ 10 to 100 MeV/nuc, does not display the same spectral behaviour as galactic CRs but increases significantly with decreasing energy. Galactic CRs have harder spectra than ACRs. Their composition consists of hydrogen, helium, nitrogen, oxygen, neon, and argon and is primarily singly ionized (Cummings and Stone, 2007). They originate as interstellar neutrals that become ionized when flowing towards the Sun and then, as so-called pick-up ions, become accelerated in the solar wind (Fisk et al., 1974; Fisk, 1999). Pesses et al. (1981) suggested that ACRs were to be accelerated at the TS. Strictly speaking they are not CRs because they have a heliospheric origin, with the spectrum of ACRs determined by heliospheric processes. To become ACRs, these pick-up ions must be accelerated by four orders of magnitude. They are subjected to solar modulation and depict mostly, but not always, the same modulation features than CRs upstream of the TS (e.g., McDonald et al., 2000, 2003, 2010). Only the ACRs with the highest rigidity (oxygen) can reach Earth (e.g., Leske et al., 2011; Strauss and Potgieter, 2010). See the introductory review on this topic by Fichtner (2001) and reviews of recent developments by Giacalone et al. (2012) and Mewaldt (2012).
The principal acceleration mechanism was considered to be diffusive shock acceleration, a topic of considerable debate since Voyager 1 crossed the TS (Fisk, 2005). At the location of the TS there was no direct evidence of the effective local acceleration of ACR protons but particles with lower energies were effectively accelerated and have since become known as termination shock particles (TSP). The higher energy ACRs thus seem disappointingly unaffected by the TS but have increased gradually in intensity away from the TS (Stone et al., 2005, 2008; Decker et al., 2005). They clearly gain energy as they move inside the inner heliosheath and seem to be trapped largely in this region. It is expected that their intensity will drop sharply over the HP but some should escape out of the inner heliosheath (e.g., Scherer et al., 2008a). Several very sophisticated mechanisms have been proposed how these particles may gain their energy beyond the TS and has become one of the most severely debated issues in this field of research (e.g., Gloeckler et al., 2009; Zhang and Lee, 2011; Zhang and Schlickeiser, 2012).
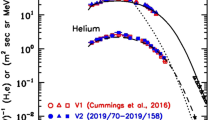
Typical observed proton, helium and oxygen spectra for TSP, ACRs and galactic CRs are shown in Figure 4 for early in 2005 when Voyager 1 already had crossed the TS (2004.96) when at 94.01 AU. Computed ACR spectra at the TS are shown for comparison. Figure 5 displays how the observed TSPs, ACRs, and galactic CRs for helium evolved and unfolded at Voyager 1 and Voyager 2 from late in 2004 to early in 2008.
Observed proton, helium, and oxygen spectra for TSP, ACRs and galactic CRs are shown for days in 2005 as indicated when Voyager 1 already had crossed the TS on 16 December 2004. Computed ACR spectra at the TS, assuming diffusion shock acceleration for two values of the TS compression ratio, are shown for comparison. Image reproduced by permission from Stone et al. (2005), copyright by AAAS.
A display of how the observed TSPs (exhibiting a power-law trent at low energies), ACRs (typically between 10 MeV and 100 MeV) and galactic spectrum (typically above 100 MeV) for helium had evolved and unfolded at Voyager 1 (in red) and Voyager 2 (in blue) from late in 2004 to early in 2008. Voyager 1 and Voyager 2 crossed the TS on 2004.96 and 2007.66 respectively. Image reproduced by permission from Cummings et al. (2008), copyright by AIP.
Adding to the controversy, comparing computational results with spacecraft observations, it was found by Strauss et al. (2010a) that the inclusion of multiply charged ACRs (Mewaldt et al., 1996a, b; Jokipii, 1996) in a modulation model could explain the observed strange spectrum of anomalous oxygen in the energy range from 10–70 MeV per nucleon (Webber et al., 2007). The more effective acceleration of these multiply charged anomalous particles at the TS causes a significant deviation from the usual exponential cut-off spectrum to display instead of a power law decrease up to 70 MeV per nucleon where galactic oxygen starts to dominate. This can only happen if some acceleration takes place at the TS. In addition, the model reproduces the features of multiply charged oxygen at Earth so that a good comparison is obtained between computations and observations. An extensive study on the intensity gradients of anomalous oxygen was done by Cummings et al. (2009) and Strauss and Potgieter (2010). For a comprehensive review on ACR measurements at Earth and interesting conclusions, see Leske et al. (2011).
Undoubtedly, the controversy indicates that we do not yet understand what is really happening to the ACRs in the inner heliosheath and only future observations with inquisitive modeling may enlighten us. On the other hand, the TSPs are accelerated at the TS. Surely, TSPs and ACRs are fascinating topics, from how they originate to their acceleration and modulation inside the heliosheath, and for the highest rigidity ACRs also up to Earth. For additional reviews of how these aspects have developed over time, see Heber and Potgieter (2008), Potgieter (2008), and Florinski (2009).
3.2 Galactic cosmic rays
Cosmic rays are defined for the purpose of this overview as fully ionized nuclei as well as antiprotons, electrons, and positrons that are not produced on the Sun or somewhere in the heliosphere. As a rule they have kinetic energy E ≳ 1 MeV.
3.2.1 Local interstellar spectra
A crucially important aspect of the modulation modeling of galactic CRs in the heliosphere is that the local interstellar spectra (LIS) need to be specified as input spectra at an assumed modulation boundary and then be modulated throughout the heliosphere as a function of position, energy, and time. A primary objective of the Voyager mission is to measure these LIS once the spacecraft enter the interstellar medium. Because of solar modulation and the fact that the nature of the heliospheric diffusion coefficients is not yet fully established, all cosmic ray LIS at kinetic energies E ≲ 1 GeV remain contentious. This is true from an astrophysical and heliospheric point of view.
Galactic spectra (GS), from a solar modulation point of view, are referred to as spectra that are produced from astrophysical sources, usually assumed to be evenly distributed through the Galaxy, typically very far from the heliosphere. Computed GS usually do not contain the contributions of any specific (local) sources within parsecs from the heliosphere so that an interstellar spectrum may be different from an average GS, which may again be different from a LIS (thousands of AU away) from the Sun, which might be different from a very LIS or what may be called a heliopause spectrum, right at the edge of the heliosphere, say 200 AU away from the Sun. Proper understanding of the extent of modulation cycles of galactic CRs in the heliosphere up to energies of ∼ 30 GeV requires knowledge of these GS and LIS for the various species. More elaborate approaches to the distribution of sources have also been followed (e.g., Büsching and Potgieter, 2008), even considering contributions of sources or regions relatively closer to the heliosphere (e.g., Büsching et al., 2008) with newer developments (e.g., Blasi et al., 2012). These spectra are calculated using various approaches based on different assumptions but mostly using numerical models, e.g., the well-known GALPROP propagation model (Moskalenko et al., 2002; Strong et al., 2007). For energies below ∼ 10 GeV, which is of great interest to solar modulation studies, the galactic propagation processes are acknowledged as less precise as illustrated comprehensively by Ptuskin et al. (2006) and Webber and Higbie (2008, 2009).
The situation for galactic electrons at low energies has always been considered somewhat better because electrons radiate synchrotron radiation so that radio data assist in estimating the electron GS at these low energies. For a discussion of this approach and some examples of consequent electron spectra, see Langner et al. (2001), Webber and Higbie (2008), Strong et al. (2011), Potgieter and Nndanganeni (2013b), and references therein.
Potgieter and Ferreira (2002) and Potgieter and Langner (2004a) showed that the heliospheric TS could in principle re-accelerate low-energy galactic electrons to energies as high as ∼ 1 GeV so that a heliopause spectrum could be different from a TS spectrum. Such a spectrum may even be higher than a LIS, depending on the energies considered. However, because the TS was observed as rather weak (Richardson et al., 2008), obtaining such high energies now seems improbable. In fact, only a factor of 2 increase was observed close to the TS for 6–14 MeV electrons but since then Voyager 1 has observed an increase of a factor of ∼ 60 on its way to the HP (Webber et al., 2012; Nkosi et al., 2011). It seems that the influence of the heliospheric TS on all LIS, in terms of the re-acceleration of these CRs, may generally thus be neglected.
The formation of a magnetic wall (barrier) at the HP, if significant, may cause a drop in low energy CRs, surely in the flux of TSPs and the ACRs while high energy CRs are not expected to change much. If low energy particles are partially trapped inside the inner heliosheath, the LIS of low energy CRs will not be known until well beyond the HP.
For a compilation of computed galactic spectra based on the GALPROP code for CR protons, anti-protons, electrons, positrons, helium, boron and carbon and many more, see Moskalenko et al. (2002). Peculiarly, the solar modulation of many of these species and their isotopes has not been properly modeled, probably because of uncertainties in their LIS.
3.2.2 Main cosmic ray modulation cycles
The dominant and the most important time scale in CRs related to solar activity is the 11-year cycle. This quasi-periodicity is convincingly reflected in the records of sunspots since the early 1600s and also in the galactic CR intensity observed at ground and sea level since the 1950s. This was the period when neutron monitors (NMs) were widely deployed as Earth bound CR detectors, especially during the International Geophysical Year (IGY). The year 2007 was celebrated as the 50th anniversary if the IGY and was called the International Heliophysical Year (IHY). These NMs have been remarkably reliable with good statistics over five full 11-year cycles.
The discovery of another important cycle, the 22-year cycle, was a milestone in the exploration and modeling of CRs in the heliosphere. It is directly related to the reversal of the HMF during each period of extreme solar activity. The causes of these cycles will be discussed in more detail in later sections. Figure 6 displays the 11-year and 22-year cycles in galactic CRs as observed by the Hermanus NM in South Africa at a cut-off rigidity of 4.6 GV and a mean response energy of ∼ 18 GeV.
Additional short periodicities are evident in NM and other CR data, e.g., the 25–27-day variation owing to the rotational Sun, and the daily variation owing to the Earth’s rotation (e.g., Alania et al., 2011, and references therein). These variations seldom have magnitudes of more than 1% with respect to the previous quite time fluxes. Corotating interaction regions (CIRs), caused when a fast solar wind region catches up with a lower region, usually merge as they propagate outwards to form various types of larger interaction regions. The largest ones are known as global merged interaction regions (GMIRs), discussed in some detail later. They are related to coronal mass ejections (CMEs) that are prominent with increased solar activity but dissipating during solar minimum. Although CIRs may be spread over a large region in azimuthal angle, they do not cause long-term CR periodicities on the scale (amplitude) of the 11-year cycle. An isolated GMIR may cause a decrease similar in magnitude than the 11-year cycle but it usually lasts only several months (as happened in 1991). A series of GMIRs, on the other hand, may contribute significantly to long-term CR modulation during periods of increased solar activity, in the form of large discrete steps, increasing the overall amplitude of the 11-year cycle (e.g., Potgieter and le Roux, 1992; Le Roux and Potgieter, 1995).
The galactic CR flux is not expected to be constant along the trajectory of the solar system in the galaxy. Interstellar conditions should differ significantly over very long time-scales, for example, when the Sun moves in and out of the galactic spiral arms (Büsching and Potgieter, 2008). It is accepted that the concentration of Be10 nuclei in polar ice exhibits temporal variations on a very long time scale in response to changes in the flux of the primary CRs. Exploring CR modulation over time scales of hundreds of years and longer and during times when the heliosphere was significantly different from the present epoch is a very interesting topic and a work in progress. See the reviews by, e.g., Scherer et al. (2006), McCracken and Beer (2007), and Usoskin (2013).
There are indications of CR periods of 50–65 years and 90–130 years, also for a periodicity of about 220 and 600 years. Quasibiennial oscillations have also been detected as a prominent scale of variability in CR data (Laurenza et al., 2012). It is not yet clear whether these variabilities should be considered ‘perturbations’, stochastic in nature or truly time-structured to be figured as superposition of several periodic processes. Cases of strong ‘perturbations’ of the consecutive 11-year cycles are the ‘grand minima’ in solar activity, with the prime example the Maunder minimum (1640–1710) when sunspots almost completely disappeared. Assuming the HMF to have vanished as well or without any reversals during the Maunder minimum would be an oversimplification. The heliospheric modulation of CRs could have continued during this period but much less pronounced (with a small amplitude). It is reasonable to infer that less CMEs occurred so that the total flux of CRs at Earth then should have been higher than afterwards. In this context, see the reviews by, e.g., Beer et al. (2011) and McCracken et al. (2011).
An interesting reoccurring phenomenon, called the Gnevyshev Gap has been observed in all solar-terrestrial parameters and consists of a relatively short period of decreased solar activity during the extreme maximum phase of each 11-year cycle, yielding structured maxima with a first peak at the end of the increasing activity phase and a second one at the start of the declining phase. For a review, see Storini et al. (2003).
4 Solar Modulation Theory
The paradigm of CR transport in the heliosphere has developed soundly over the last ∼ 50 years. The basic processes are considered to be known. However, it is still quite demanding to relate the modulation of galactic CRs and of the ACRs to their true causes and to connect these causes over a period of a solar cycle or more, from both a global and microphysics level. The latter tends to be of a fundamental nature, attempting to understand the physics from first principles (ab initio) whereas global descriptions generally tend to be phenomenological, mostly driven by observations and/or the application of new numerical methods and models. In this context, global numerical models with relevant transport parameters are essential to make progress. Obviously, major attempts are made to have these models based on good assumptions, which then have to agree with all major heliospheric observations.
Understanding the basics of solar modulation of CRs followed only in the 1950s when Parker (1965) formulated a constructive transport theory. At that stage NMs already played a major role in observing solar activity related phenomena in CRs. Although Parker’s equation contained an anti-symmetric term in the embedded tensor accounting for regular gyrating particle motion, it was only until the development of numerical models in the mid-1970s (Fisk, 1971, 1976, 1979) that progress in appreciation the full meaning of transport theory advanced significantly.
4.1 Basic transport equation and theory
A basic transport equation (TPE) was derived by Parker (1965). Gleeson and Axford (1967) came to the same equation more rigorously. They also derived an approximate solution to this TPE, the so called force-field solution, which had been widely used and was surpassed only when numerical models became available (Gleeson and Axford, 1968). For a formal overview of these theoretical aspects and developments, see Schlickeiser (2002). See also Quenby (1984), Fisk (1999), and Moraal (2011) for overviews of the TPEs relevant to CR modulation. The basic TPE follows from the equations of motion of charged particles in fluctuating magnetic fields (on both large and small scales) and averages over the pitch and phase angles of propagation particles. It is based on the reasonable assumption that CRs are approximately isotropic. This equation is remarkably general and is widely used to model CR transport in the heliosphere. The heliospheric TPE according to Parker (1965), but in a rewritten form, is
where f(r, P, t) is the CR distribution function, P is rigidity, t is time, r is the position in 3D, with the usual three coordinates r, θ, and φ specified in a heliocentric spherical coordinate system where the equatorial plane is at a polar angle of θ = 90°. A steady-state solution has ∂f/∂t = 0 (part a), which means that all short-term modulation effects (such as periods shorter than one solar rotation) are neglected, which is a reasonable assumption for solar minimum conditions. Terms on the right hand side respectively represent convection (part b), with V the solar wind velocity; averaged particle drift velocity 〈vd〉 caused by gradients and curvatures in the global HMF (part c); diffusion (part d), with Ks the symmetrical diffusion tensor and then the term describing adiabatic energy changes (part e). It is one of the four major modulation processes and is crucially important for galactic CR modulation in the inner heliosphere. If (∇ · V) > 0, adiabatic energy losses are described, which become quite large in the inner heliosphere (see the comprehensive review by Fisk, 1979). If (∇ · V) < 0, energy gains are described, which may be the case for ACRs in the heliosheath (illustrated, e.g., by Langner et al., 2006b; Strauss et al., 2010b). If (∇ · V) = 0, no adiabatic energy changes occur for CRs, perhaps the case beyond the TS. This is probably an over simplification but it was shown that the effect is insignificant for galactic CRs but crucially important for ACRs (e.g., Langner et al., 2006a). For recent elaborate illustrations of these effects, see Strauss et al. (2010a,b).
In cases when anisotropies are large, other types of transport equations must be used (see, e.g., Schlickeiser, 2002). Close to the Sun and Jupiter, and even close to the TS, where large observed anisotropies in particle flux sometimes occur (e.g., Kóta, 2012), Equation (5) thus needs to be modified or even replaced to describe particle propagation based on the Fokker-Planck equation. The ‘standard’ TPE as given by Equation (5) also needs modification by inserting additional terms relevant to the conditions beyond the TS (e.g., Strauss et al., 2010a,b).
For clarity on the role of diffusion, particle drifts, convection, and adiabatic energy loss, the TPE can be written in terms of a heliocentric spherical coordinate system as follows:
where it is assumed that the solar wind is axis-symmetrical and directed radially outward, i.e., V = Ver. This version of the TPE is rearranged in order to emphasize the various terms that contribute to diffusion, drift, convection, and adiabatic energy losses, so that Equation (6) becomes
Here Krr, Krθ, Krφ, Kθr, Kθθ, Kθφ, Kφr, Kφθ, and Kφφ, are the nine elements of the 3D diffusion tensor, based on a Parkerian type HMF. Note that Krr, Krφ, Kθθ, Kφr, Kφφ describe the diffusion processes and that Krθ, Kθr, Kθφ, Kφθ, describe particle drifts, in most cases consider to be gradient, curvature, and current sheet drifts. For this equation it is assumed that the solar wind velocity has only a radial component, which is not the case in the outer parts of the heliosheath, close to the HP.
A source function may also be added to this equation, e.g., if one wants to study the modulation of Jovian electrons (e.g., Ferreira et al., 2001).
The components of the drift velocity are given in the next Section 4.2. It is important to note that the drift velocity in Equation (5) is multiplied with the gradient in f so when the CR intensity gradients are reduced by changing the contribution from diffusion, drift effects on CR modulation become implicitly reduced. This reduction will unfold differently from changing the drift coefficient explicitly.
It is more useful to calculate the differential intensity of CRs, e.g., as a function of kinetic energy to obtain spectra, which can be compared to observations. In this context, a few useful definitions and relations are as follows:
Particle rigidity is defined as
where p is the magnitude of the particle’s relativistic momentum, q = Ze its charge, its speed, its relativistic mass, and the speed of light in outer space.
For a relativistic particle, the total energy in terms of momentum is given by
with the kinetic energy and E0 the rest-mass energy of the particle (e.g., E0 = 938 MeV for protons and E0 = 5.11 × 10−1 MeV for electrons) and m0 the particle’s rest mass.
The kinetic energy per nucleon in terms of particle rigidity is then
so that rigidity can be written in terms of kinetic energy per nucleon as
with the atomic number and the mass number of the CR particle. The ratio of a particle’s speed to the speed of light, β, in terms of rigidity is given by
and in terms of kinetic energy it is
The relation between rigidity, kinetic energy, and β is therefore
Particle density within a region d3r, for particles with momenta between p and p + dp, is related to the full CR distribution function (which includes a pitch angle distribution) by
where d3p = p2 dp dΩ. The differential particle density, Up, is related to n by
which gives
The omni-directional (i.e., pitch angle) average of F(r, p, t) is calculated as
which leads to
The differential intensity, in units of particles/unit area/unit time/unit solid angle/unit momentum, is
so that
where j(r, p, t) is the differential intensity in units of particles/area/time/solid angle/energy. The relation between and is simply (P)2.
4.2 Basic diffusion coefficients
The diffusion coefficients of special interest in a 3D heliocentric spherical coordinate system are
where Krr is the effective radial diffusion coefficient, a combination of the parallel diffusion coefficient and the radial perpendicular diffusion coefficient K⊥r, with ψ the spiral angle of the average HMF; Kθθ = K⊥θ is the effective perpendicular diffusion coefficient in the polar direction. Here, describes the effective diffusion in the azimuthal direction and Kφr is the diffusion coefficient in the φr-plane, etc. Both are determined by the choices for and K⊥. Beyond ∼ 20 AU in the equatorial plane ψ → 90°, so that Krr is dominated by K⊥r whereas Kφφ is dominated by K∥, but only if the HMF is Parkerian in its geometry. These differences are important for the modulation of galactic CRs in the inner heliosphere (e.g., Ferreira et al., 2001). The important role of perpendicular diffusion (radial and polar) in the inner heliosphere has become increasingly better understood over the past decade since it was realized that it should be anisotropic (Jokipii, 1973), with reasonable consensus that K⊥θ > K⊥r away from the equatorial regions. The expressions for these diffusion coefficients become significantly more complicated when advanced geometries are used for the HMF (e.g., Burger et al., 2008; Effenberger et al., 2012).
A typical empirical expression as used in numerical models for the diffusion coefficient parallel to the average background HMF is given by
where (K∥)0 is a constant in units of 1022 cm2 s−1, with the rest of the equation written to be dimensionless with P0 = 1 GV and Bm the modified HMF magnitude with Bn = 1 nT (so that the units remain cm2 s−1). Here, a is a power index that can change with time (e.g., from 2006 to 2009); b = 1. 95 and together with a determine the slope of the rigidity dependence respectively above and below a rigidity with the value Pk, whereas c = 3.0 determines the smoothness of the transition. This means that the rigidity dependence of K∥ is basically a combination of two power laws. The value Pk determines the rigidity where the break in the power law occurs and the value of a specifically determines the slope of the power law at rigidities below Pk (e.g., Potgieter et al., 2013).
Perpendicular diffusion in the radial direction is usually assumed to be given by
This is quite straightforward but still a very reasonable and widely used assumption in numerical models. It is to be expected that this ratio could not just be a constant but should at least be energy-dependent. Advanced and complicated fundamental approaches had been followed, e.g., by Burger et al. (2000) with subsequent CR modulation results that are not qualitatively different from a global point of view. Advances in diffusion theory and subsequent predictions for the heliospheric diffusion coefficients (e.g., Teufel and Schlickeiser, 2002) make it possible to narrow down the parameter space used in typical modulation models, e.g., the rigidity dependence at Earth. This is a work in progress.
The role of polar perpendicular diffusion, K⊥θ, in the inner heliosphere has become increasingly better understood over the past decade since it was realized that perpendicular diffusion should be anisotropic, with reasonable consensus that K⊥θ > K⊥r away from the equatorial regions (Potgieter, 2000). Numerical modeling shows explicitly that in order to explain the small latitudinal gradients observed for protons by Ulysses during solar minimum modulation in 1994, an enhancement of latitudinal transport with respect to radial transport is required (e.g., Heber and Potgieter, 2006, 2008, and reference therein). The perpendicular diffusion coefficient in the polar direction is thus assumed to be given by
with
Here A± = (d ± 1)/2, θF = 35°, θA = θ for θ ≤ 90° but θA = 180° − θ with θ ≥ 90°, and d = 3.0. This means that Kθθ = K⊥θ is enhanced towards the poles by a factor d with respect to the value of K∥ in the equatorial regions of the heliosphere. This enhancement is an implicit way of reducing drift effects by changing the CR intensity gradients significantly. For motivations, applications and discussions, see Potgieter (2000), Ferreira et al. (2003a,b), Moeketsi et al. (2005), and Ngobeni and Potgieter (2008, 2011). The procedure usually followed to solve Equation (6) is described by, e.g., Ferreira et al. (2001) and Nkosi et al. (2008).
4.3 The drift coefficient
The pitch angle averaged guiding center drift velocity for a near isotropic CR distribution is given by 〈vd〉 = ∇ × (KdeB), with eB = B/B where B is the magnitude of the background HMF usually assumed to have a basic Parkerian geometry in the equatorial plane. This geometry gives very large drifts over the polar regions of the heliosphere so that it is standard practice to modify it in the polar regions, e.g., Smith and Bieber (1991) and Potgieter (1996, 2000).
Under the assumption of weak scattering, the drift coefficient is straightforwardly given as
where (Kd)0 is dimensionless; if (Kd)0 = 1.0, it describes what Potgieter et al. (1989) called 100% drifts (i.e., full ‘weak scattering’ gradient and curvature drifts). Drift velocity components in terms of Krθ, Kθr, Kφθ, Kθφ are
with A = ±1; when this value is positive (negative) an A > 0 (A < 0) polarity cycle is described. The polarity cycle around 2009 is indicated by A < 0, as was also the case for the years around 1965 and 1987. During such a cycle, positively charged CRs are drifting into the inner heliosphere mostly through the equatorial regions, thus having a high probability of encountering the wavy HCS.
Idealistic global drift patterns of galactic CRs in the heliosphere are illustrated in Figure 7 for positively charged particles in an A > 0 and A < 0 magnetic polarity cycle respectively, together with a wavy HCS as expected during solar minimum conditions. Different elements of the diffusion tensor are also shown in the left panel with respect to the HMF spiral for illustrative purposes.
The parallel and two perpendicular diffusion orientations, indicated by the corresponding elements of the diffusion tensor, are shown with respect to the HMF spiral direction (left) for illustrative purposes. The arrows with V indicate the radially expanding solar wind (convection). Idealistic global drift patterns of positively charged particles in an A > 0 and A < 0 magnetic polarity cycle are schematically shown in the right panel, together with a wavy HCS as expected during solar minimum conditions. Image reproduced by permission from Heber and Potgieter (2006), copyright by Springer.
A formal and fundamental description of global curvature, gradient and current sheet drifts in the heliosphere is still unsettled. The spatial and rigidity dependence of Kd is entirely based on the assumption of weak-scattering. A deviation from this weak scattering form is given by
This means that below Pd0 (in GV) particle drifts are progressively reduced with respect to the weak scattering case. This is required to explain the small latitudinal gradients at low rigidities observed by Ulysses (Heber and Potgieter, 2006, 2008; De Simone et al., 2011). This reduction is in line with what Potgieter et al. (1989), Webber et al. (1990), Ferreira and Potgieter (2004), and Ndiitwani et al. (2005) found when describing modulation in terms of drifts with a HCS tilt angle dependence in numerical models. Theoretical arguments and numerical simulations have been presented requiring the reduction of particle drifts, in particular with increasing solar activity. For a summary of the essence of the problem, see Tautz and Shalchi (2012). This aspect must fit into the picture where Ulysses observations of CR latitudinal gradients especially at lower energies, require particle drifts to be reduced. It thus remains a theoretical challenge to explain why reduced drifts in the heliosphere is needed to explain some of these major CR observations, and what type of particle drifts apart from gradient and curvature drifts may occur in the heliosphere.
4.4 Gradient, curvature, and current sheet drifts
The realization that particle drifts could not be neglected in the solar modulation of CRs was elevated by the development of numerical models, which reached sophisticated levels already in the late 1980s and early 1990s including a full tensor. The importance of particle drifts in the heliosphere was at first discussed only theoretically but it was soon discovered compellingly in various existing CR observations. It should be noted that it was rather fortuitous that the sharp peak in the 1965 intensity-time profiles of CRs was followed by a really flat intensity-time profile in the 1970s, not to repeat again so evidently. The mini-modulation-cycle around 1974 had little to do with drifts (e.g., Wibberenz et al., 2001). The recent A < 0 polarity cycle also did not produce such a sharp peak as during previous A < 0 cycles as shown in Figure 6. See also the review by Potgieter (2013).
Convincing theoretical arguments for the importance of particle drifts were presented by Jokipii et al. (1977) and later followed by persuasive numerical modeling (e.g., Jokipii and Kopriva, 1979; Jokipii and Thomas, 1981; Kóta and Jokipii, 1983; Potgieter and Moraal, 1985), which illustrated that gradient and curvature drifts could cause charge-sign dependent modulation and a 22-year cycle. The main reason for this to occur is that the solar magnetic field reverses polarity every ∼ 11 years so that galactic CRs of opposite charge will reach Earth from different heliospheric directions. This also makes the wavy HCS of the HMF a very important modulation feature with its tilt angle (Hoeksema, 1992) being a very useful modulation parameter. When protons drift inwards mainly through the equatorial regions of the heliosphere (A < 0 polarity cycles) they encounter the dynamic HCS and get progressively reduced by its increasing waviness as solar activity surges. This produces the sharp peaks in the galactic CR intensity-time profiles whereas during the A > 0 cycles the profiles are generally flatter (for recent updates see, e.g., Potgieter, 2011; Krymsky et al., 2012; Potgieter, 2013). The effect reverses for negatively charged galactic CRs causing charge-sign dependent effects as reviewed by, e.g., Heber and Potgieter (2006, 2008) and Kóta (2012).
Figure 8 is an illustration of the computed intensity distribution caused by drifts for the two HMF polarity cycles, in this case for 1 MeV/nuc anomalous oxygen in the meridional plane of the heliosphere. The position of the rTS = 90 AU is indicated by the white dashed line. The contours are significantly different in the inner heliosphere, with the intensity reducing rapidly towards Earth. The distribution is quite different beyond the TS, where the region of preferred acceleration of these ACRs is assumed to be away from the TS, closer to the HP near the equatorial plane, positioned at 140 AU, for illustrative purposes (Strauss et al., 2010a,b).
An illustration of the computed intensity distribution caused by drifts for the two HMF polarity cycles, in this case for 1 MeV/nuc ACR oxygen in the meridional plane of the heliosphere. The position of the TS at 90 AU is indicated by the white dashed line. Note how the coloured contours differ in the inner heliosphere for the two cycles and how the intensity decreases towards Earth, and how the distribution is quite different beyond the TS. In this case, the region of preferred acceleration for these ACRs is assumed near the equatorial plane and close to the HP at 140 AU. Image reproduced by permission from Strauss et al. (2011b), copyright by COSPAR.
Another indication of the role of gradient and curvature drifts came in the form of a 22-year variation in the direction of the daily anisotropy vector in the galactic CR intensity as measured by NMs from one polarity cycle to another (Levy, 1976; Potgieter and Moraal, 1985). Potgieter et al. (1980) also discovered a 22-year cycle in the differential response function of NMs used for geomagnetic latitude surveys at sea-level in 1965and 1976 (see also Moraal et al., 1989).
Some of the key outcomes of gradient, curvature and current sheet drifts as applied to the solar modulation of CRs, are:
-
1.
Particles of opposite charge will experience solar modulation differently because they sample different regions of the heliosphere during the same polarity epoch before arriving at Earth or at another observation point. Particle drift effects inside the heliosheath, on the other hand, may be different from upstream (towards the Sun) of the TS.
-
2.
A well-established 22-year cycle occurs in the solar modulation of galactic CRs, which is not evident in other standard proxies for solar activity (see Figure 6). This is also evident in the directional changes of the diurnal anisotropy vector with every HMF polarity reversal (e.g., Potgieter and Moraal, 1985; Nkosi et al., 2008; Ngobeni and Potgieter, 2010) and from the changes in differential response functions of NMs obtained during geomagnetic latitude surveys.
-
3.
The wavy HCS plays a significant role in establishing the features of this 22-year cycle in the solar modulation of CRs.
-
4.
Cosmic ray latitudinal and radial intensity gradients in the heliosphere are significantly different during the two HMF polarity cycles and repeated ideal modulation conditions will display a 22-year cycle (e.g., Heber and Potgieter, 2006, 2008; Potgieter et al., 2001; De Simone et al., 2011). An illustration is shown in Figure 9 of how the computed radial gradients change with kinetic energy for the two polarity cycles at different positions in the heliosphere. In Figure 10 the difference caused by drifts in the computed latitudinal proton gradients between the two polarity cycles is shown as a function of rigidity in comparison with the observed gradient from PAMELA and Ulysses for the period 2007 (De Simone et al., 2011).
-
5.
Cosmic ray proton spectra are softer during A > 0 cycles so that below 500 MeV the A > 0 solar minima spectra are always higher than the corresponding A < 0 spectra (Beatty et al., 1985; Potgieter and Moraal, 1985). This means that the adiabatic energy losses that CRs experience in A < 0 cycles are somewhat different than during the A > 0 cycles (Strauss et al., 2011a,c). This also causes the proton spectra for two consecutive solar minima to cross at a few GeV (Reinecke and Potgieter, 1994).
-
6.
Drift effects are not necessarily the same during every 11-year cycle, not even at solar minimum because the recent solar minimum was different than other A < 0 cycles. The intriguing interplay among the major modulation mechanisms changes with the solar cycles (Potgieter et al., 2013).
-
7.
Drifts also influence the effectiveness by which galactic CRs are re-accelerated at the solar wind TS (e.g., Jokipii, 1986; Potgieter and Langner, 2004a). However, it is unclear whether particle drifts play a significant role in the heliosheath and to what extent drift patterns are different than in the inner heliosphere.
Left panels: Computed radial gradients for galactic protons, in % AU−1, as a function of kinetic energy for both polarity cycles and for solar minimum conditions in the equatorial plane at 1, 50, and 91 AU, respectively (top to bottom panels). Right panels: Similar but at a polar angle θ = 55°. Two sets of solutions are shown in all panels, first without a latitude dependence (black lines) and second with a latitude-dependent compression ratio for the TS (red lines). In this case, the TS is at 90 AU and the HP is at 120 AU. Image reproduced by permission from Ngobeni and Potgieter (2010), copyright by COSPAR.
The difference caused by drifts in the computed latitudinal gradients (% degree−1) for protons in the inner heliosphere for the two HMF polarity cycles as a function of rigidity Potgieter et al. (2001). Marked by the black line-point is the latitudinal gradient calculated from a comparison between Ulysses and PAMELA observations for 2007. Image reproduced by permission from De Simone et al. (2011).
Particle drifts, as a modulation process, has made a major impact on solar modulation theory and was eclipsed only in the early 2000s when major efforts were made to understand diffusion theory better together with the underlying heliospheric turbulence theory (as reviewed by Bieber, 2003 and McKibben, 2005). It was also then finally realized that particle drifts do not dominate solar modulation over a complete solar cycle but that it is part of an intriguing interplay among basically four mechanisms and that this play-off changes over the solar cycle and from one cycle to another. The latest prolonged solar minimum brought additional insight in how this interplay can change as the Sun keeps on surprising us (Potgieter et al., 2013).
4.5 Aspects of diffusion and turbulence theory relevant to solar modulation
Progress has been made over the last decade to improve the understanding of heliospheric turbulence, in particular to overcome some of the deficiencies of standard scattering theories such as quasi-linear theory (QLT). New approaches have taken into account the dynamical character and the three-dimensional geometry of magnetic field fluctuations. Historically, it is important to note that in order to reconcile observations with the theoretical mean free paths, Bieber et al. (1994) advocated a composite model for the turbulence, which consists of ∼ 20% slab and ∼ 80% 2D fluctuations. At high rigidities the simpler theory can be used to describe particle transport parallel to the mean field, but at low rigidities the dynamical theory predicts a much more efficient scattering, which reduces the parallel mean path compared to standard QLT for ions, but gives large values for electrons. Dröge (2005) showed that standard QLT underestimated mean free paths of low energy electrons by almost two orders of magnitude even with a corrected slab fraction for magnetic turbulence. A general conclusion seems to be that the parallel mean free path of CRs is a key input parameter for CR transport but not nearly the only one. Teufel and Schlickeiser (2002), amongst others, produced analytical formulae for the parallel mean free path as a function of rigidity at Earth for CR protons and electrons, which differ significantly at lower energies for these two species.
The diffusion of particles across the mean HMF is an important area of study. It is very nearly radially directed towards the Sun for distances beyond 10 AU. For CRs to reach Earth, they must cross the mean HMF, otherwise it would require large parallel mean-free paths and subsequently very large anisotropies, which are not observed. Cross-field diffusion remains puzzling, with the dimensionality of the underlying turbulence of critical importance. Conceptually, it is understood that the local transport across individual magnetic lines and the motion of particles along spatially meandering magnetic field lines can both occur. Simulations of particle transport in irregular magnetic fields were performed by, e.g., Giacalone and Jokipii (1994, 1999) and Qin and Shalchi (2012) with insightful results. Later, a new theory with different assumption, was developed by Matthaeus et al. (2003) and Bieber et al. (2004). This nonlinear guiding-center (NLGC) theory is promising for understanding perpendicular transport. This topic is evidently a very specialized field of theoretical research and for these details the reader is referred to the reviews by Bieber (2003) and Giacalone (2011). Developing a full ab initio theory of CR transport and modulation, especially for perpendicular diffusion, by integrating turbulence quantities with diffusion coefficients throughout the heliosphere is a work in progress (e.g., Burger et al., 2000; Pei et al., 2010). Unfortunately, the ab initio approach cannot as yet produce elements of the diffusion tensor than can explain all observations consistently when used in global modulation models so that phenomenological approaches remain very useful. For comprehensive monographs on transport theory, see Schlickeiser (2002) and Shalchi (2009).
For elaborate reviews on turbulence effects in the heliosphere and on the fundamental process of reconnection and acceleration of particles, see Fisk and Gloeckler (2009, 2012), Lazarian et al. (2012), Lee et al. (2012), Matthaeus and Velli (2011), and several other contributions in the same issue of Space Science Reviews.
4.6 Development of numerical modulation models
The wide-ranging availability of fast computers has brought significant advances in numerical modeling of solar modulation. In-situ observations have always been limited so that numerical modeling plays an important role to broaden our understanding of solar modulation. For comprehensive global modeling it is essential to have a sound transport theory, reliable numerical schemes with appropriate boundary conditions, local interstellar spectra as initial input spectra and properly considered transport parameters. Furthermore, a basic knowledge of the solar wind and HMF and how they change throughout the whole heliosphere is required. This is quite a task and takes major efforts to accomplish.
Fisk (1971) developed the first numerical solution of the TPE by assuming a steady-state and spherical symmetry, i.e., a one-dimensional (1D) model with radial distance as the only spatial variable, and of course an energy dependence. Later, a polar angle dependence was included to form an axisymmetric (2D) steady-state model without drifts (Fisk, 1976). In 1979, Jokipii and Kopriva (1979) and Moraal et al. (1979) presented their separately developed 2D steady-state models including gradient and curvature drifts for a flat HCS. The first 2D models to emulate the waviness of the HCS were developed by Potgieter and Moraal (1985) and Burger and Potgieter (1989). Three-dimensional (3D) steady-state models including drifts with a 3D wavy HCS were developed by Jokipii and Thomas (1981) and Kóta and Jokipii (1983) with similar models developed later by Hattingh et al. (1997) and Gil et al. (2005). Haasbroek and Potgieter (1998), Fichtner et al. (2000) and Ferreira et al. (2001) independently developed steady-state models including the Jovian magnetosphere as a source of low-energy electrons.
The first 1D time-dependent model (numerically thus three dimensions: radial distance, energy, and time) was developed by Perko and Fisk (1983). Extension to two spatial dimensions was done by Le Roux and Potgieter (1990) including drifts and the effect of outwards propagating GMIRs at large radial distance thus enabling the study of long-term CR modulation effects (Potgieter et al., 1993). Fichtner et al. (2000) developed a 3D time-dependent model for electrons, but approximated adiabatic cooling of electrons at lower energies by doing a momentum averaging of the Parker TPE.
The inclusion of the effects of a heliospheric TS was done by Jokipii (1986) who developed the first 2D time-dependent, diffusion shock acceleration model. Potgieter and Moraal (1988) demonstrated that it was possible to include shock acceleration in a steady-state spherically symmetric model by specifying the appropriate boundary conditions with regard to the CR streaming and spectra at the TS. This model was expanded to 2D by Potgieter (1989). Later on 2D shock acceleration models with discontinuous and continuous transitions of the solar wind velocity across the TS were developed to study ACRs (e.g., Steenberg and Moraal, 1996; Le Roux et al., 1996; Langner and Potgieter, 2004a,b). Haasbroek and Potgieter (1998) developed a model that could handle all possible geometrical elongation of the heliosphere by assuming a non-spherical heliospheric boundary geometry. All the above mentioned numerical models were developed using the Crank-Nicholson and Alternating Direction Implicit (ADI) schemes, with some deviations depending on the complexity of the studied physics (Fichtner, 2005).
The intricacy of the TPEs applicable to CR modulation may cause numerical models to have notorious problems with instability when solving in higher (five numerical) dimensions. Solving the relevant TPEs by means of stochastic differential equations (SDEs) has become therefore quite popular after earlier noteworthy attempts were not truly appreciated (e.g., Fichtner et al., 1996; Gervasi et al., 1999; Yamada et al., 1999; Zhang, 1999). This method has several advantages, most notably unconditional numerical stability and an independence of a spatial grid size. The method is highly suitable for parallel processing. Recently, models developed around SDEs have become rather sophisticated (e.g., Kopp et al., 2012) but not always focussed on additional insight into CR modulation. It has been illustrated that additional physical insights can be extracted from this approach, e.g., Florinski and Pogorelov (2009), Strauss et al. (2011a,c, 2012c, 2013a), and Bobik et al. (2012). Some aspects are discussed next.
4.6.1 Illustrations of SDE based modeling
The following figures are illustrations of CR modulation based on the SDE approach to solar modulation as examples of what can be done additionally to the ‘standard’ numerical approaches. Figure 11 shows pseudo-particle traces for 100 MeV protons in the A < 0 cycle and varying values of the tilt angle α, projected onto the meridional plane in comparison with a projection of the wavy HCS onto the same plane. These particles propagate mainly in latitudes covered by the HCS, and their transport is greatly affected by the waviness of the HCS but mainly for small values of α, as diffusion disrupts the drift pattern. Diffusion can in principle almost wipe out these drift patterns as illustrated by Strauss et al. (2012c). This realistic picture of the combination of global and HCS drifts is in sharp contrast to the idealist picture shown in Figure 7. Studies that are focusing on drifts as the sole modulation process give scenarios that are unrealistic (e.g., Roberts, 2011). Perfect drift dominated CR transport does not exist because CR modulation essentially is a convection-diffusion process. As mentioned, inspection of Equation (5) shows that when changing diffusion the CR intensity gradients are changed directly, which subsequently changes the effects of drifts implicitly (Potgieter et al., 2013) while explicit changes in drifts and consequently of drift effects are done by changing the drift coefficient directly (Equation (27)).
Pseudo-particle traces (trajectories) for galactic protons in the A < 0 HMF cycle projected onto the meridional plane for four values of the HCS tilt angle, shown as red lines. The HP position is indicated by the dashed lines, while the dotted lines show a projection of the waviness of HCS onto the same plane. The simulation is done for 100 MeV protons. Image reproduced by permission from Strauss et al. (2012c), copyright by Springer.
In Figure 12 binned propagation times for 100 MeV galactic electrons between Earth and the HP (at 140 AU) for three scenarios: the A < 0 polarity cycle (left panel), the A > 0 cycle (middle panel), and the non-drift case (right panel). For the latter, the propagation time follows a normal distribution, peaking at ∼ 400 days, while for the different drift cycles, the distribution tends to be more Poisson like (CR cannot reach Earth infinitely fast) with lower propagation times. The reason for the shorter propagation times, ∼ 240 days for the A > 0 cycle and ∼ 110 days for the A < 0 cycle, is that drifts cause a preferred direction of transport for these CR electrons, thereby allowing them to propagate faster to Earth. The propagation times for the A < 0 cycle is shorter than for the A > 0 cycle because these electrons can easily escape through the heliospheric poles than drifting along the HCS in the A > 0 cycle (Strauss et al., 2011a,c).
Binned propagation times for galactic electrons released at Earth at 100 MeV for the A < 0 (left panel), A > 0 (middle panel), and for the no-drift scenarios (right panel). For each computation 10000 particle trajectories were integrated using the SDE approach to modulation modeling. Image reproduced by permission from Strauss et al. (2011a), copyright AAS.
The propagation times and energy loss of 100 MeV protons propagating from the HP (at 100 AU) to Earth as a function of the HCS tilt angle (α) for A < 0 polarity cycles of the HMF are shown in Figure 13. Note that the increase in propagation time significantly slows down above α = 40°. The energy loss levels off above α = 40°. See Strauss et al. (2011a,c) for additional illustrations.
The propagation times and energy loss of 100 MeV protons propagation from the HP to Earth as a function of the HCS tilt angle (α) for A < 0 polarity cycles of the HMF. Note the change in propagation time at α = 40° and how the energy loss levels off above α = 50°. Image reproduced by permission from Strauss et al. (2012c), copyright by Springer.
4.7 Charge-sign dependent modulation
It was not until around 1976–1978 that particle drifts were considered seriously as a competitive modulation process, in addition to the conventional convective, diffusive, and adiabatic energy loss processes. It was experienced as controversial when introduced and it took 10 years to become widely accepted. Even today the full extent of its relevance and importance over a complete solar activity cycle is debated. See, as an example, the critical review by Cliver et al. (2011). The early stages of this theoretical development, and the status of the research round that time, were reviewed by Quenby (1984). The realization also came that the only way to understand the full scope of particle drifts on galactic CR modulation was with numerical modeling. Therefore, since the early 1980s increasingly more sophisticated numerical models had been introduced that kept on improving as discussed above. See Potgieter (2013) for a full review on this topic, parts of which is also repeated here.
Simultaneous measurements of CR electrons and positrons (protons and anti-protons) serve as a crucial test of our present understanding of how large charge-sign dependent modulation in the heliosphere is, as a function of energy and position over a complete solar activity cycle. It is expected that the effects of drifts on CRs should become more evident closer to minimum solar activity. Observations of CR particles and their anti-particles have been done over the years and are presently been made simultaneously by PAMELA (e.g., Boezio et al., 2009; Sparvoli, 2012; Boezio and Mocchiutti, 2012) and the AMS-02 mission (e.g., Battiston, 2010). PAMELA is a satellite-borne experiment designed for cosmic-ray antimatter studies. The instrument is flying on board the Russian Resurs-DK1 satellite since June 2006, following a semi-polar near-Earth orbit. For an overview of balloon-based observations, see Seo (2012).
Before these simultaneous measurements, charge-sign dependent solar modulation was mostly studied using ‘electrons’, which was actually the sum of electrons and positrons, together with CR protons and helium of the same rigidity. The first sturdy observational evidence of charge-sign dependent solar modulation was reported by Webber et al. (1983) and modelled by Potgieter and Moraal (1985) using a first generation drift model. This is shown in Figure 14 as electron spectra during two consecutive solar minimum modulation periods in 1965 and 1977. The corresponding charge-sign dependent effect is illustrated in Figure 15, comparing proton and electron measurements made during two consecutive solar minimum periods (1965 as A < 0 and 1977 as A > 0). The ratio of differential intensities, DI(1977)/DI(1965–66), is shown for both electrons and protons as a function of E. Evidently, electrons behaved different from protons during these consecutive solar minimum epochs, again convincingly revealing a 22-year modulation cycle and charge-sign dependence.
Galactic CR electron observations for two consecutive solar minimum modulation periods in 1965 (open circles) and 1977 (filled circles) compared to the predictions of a first generation drift-modulation model (band between solid lines) containing gradient, curvature, and current sheet drifts. Clearly, a 22-year modulation cycle is portrayed (Potgieter and Moraal, 1985, and references therein).
Ratios of proton and electron measurements for 1977 (A > 0 polarity cycle) to 1965–66 (A < 0 polarity cycle) as a function of kinetic energy compared to the predictions made with a drift-modulation model illustrating how differently protons behave to electrons during two solar minimum periods with opposite solar magnetic field polarity (Webber et al., 1983; Potgieter and Moraal, 1985, and references therein).
A newer generation drift-modulation model was used by Ferreira (2005) to illustrate how the modulation of galactic electrons differ form one polarity cycle to another as shown in Figure 16 (right panel). For electrons the influence of particle drifts is evident over an energy range from 50 MeV to 5 GeV with a maximum effect around 200 MeV to 500 MeV as shown in the left panel. It also illustrates how the drift effect changes with increasing distance from the Sun.
Panel (a): Computed differential intensities of galactic electron at 1, 5, 60 and 90 AU (from bottom to top) in the heliospheric equatorial plane for the A > 0 and A < 0 polarity cycles. Panel (b): Ratio of the computed intensities for the A > 0 and A < 0 cycles as a function of kinetic energy and for the radial distance as in (a). Image reproduced by permission from Ferreira (2005), copyright by COSPAR.
Drift-modulation models predicted that during A > 0 polarity cycles the ratio of electron to proton (e−/p) intensities as a function of time (with solar activity as described by the wavy HCS) should exhibit an inverted V shape while during A < 0 cycles it should exhibit an upright V around minimum modulation periods (see the reviews by Potgieter et al., 2001; Heber and Potgieter, 2006, 2008; Strauss et al., 2012b). This means that as a function of time electrons would exhibit a sharper intensity time profile than protons or helium during A > 0 solar epochs. This was displayed eloquently by Ulysses observations of electrons, helium and protons at 1.3 GV and 2.5 GV for the period 1990 to 2004 as reproduced in Figure 17. The e−/p ratio indeed formed an inverted V around the 1997 solar minimum shown in the bottom panel. This effect was also shown by Ferreira et al. (2003a) and Ferreira et al. (2003b) for the 1987 solar minimum (A < 0 cycle) when a V-shape was displayed in the e−/He ratio.
Observed % changes respectively of helium (1.2 GV), electrons (1.2 GV and 2.5 GV), and protons (2.5 GV), as a function of time (solar activity) for the Ulysses mission from 1990 to 2005. The period from 1990 to 2000 was an A > 0 polarity epoch but changed to an A < 0 epoch around 2000–2001. Clearly the electrons exhibited a sharper profile over this A > 0 cycle than protons and helium in accord with predictions of drift-modulation models. Adapted by Heber from Heber et al. (2002, 2003, 2009).
A first illustration of the charge-sign dependent effect for the modulation of protons and anti-protons was made by Webber and Potgieter (1989). This is shown in Figure 18. These first generation drift models predicted a change of a factor of 10 in the \({\bar {\rm p}}/{\rm p}\) ratio at 200 MeV from A > 0 to A < 0 solar minima but less for increased solar activity periods. This was done in an attempt to reproduce the data displayed in this figure with the GS as assumed in those days. Comprehensive modeling has later been done for electron-positron (e−/e+) and proton-antiproton modulation (Langner and Potgieter, 2004a,b; Potgieter and Langner, 2004a) and heavier CR species such as boron and carbon (Potgieter and Langner, 2004b). They relied heavily on the computations of galactic spectra with the GALPROP code (e.g., Moskalenko et al., 2002; Strong et al., 2007). Apart from drifts, their model also included the effects of the solar wind TS. These results are shown in Figure 19 respectively for e−/e+ and \({\bar {\rm p}}/{\rm p}\) as a function of E for the two solar polarity cycles during typical solar minimum modulation conditions. This is compared to the corresponding ratio of the local interstellar spectra (LIS). See also Della Torre et al. (2012).
A comparison of the observed anti-proton to proton ratio (below 10 GeV with first generation drift-model computations for solar minimum conditions with the HCS tilt angle α = 10° and for solar maximum conditions with α = 70°. The − and + signs indicate A < 0 and A > 0 polarity cycles, respectively. The corresponding ratio for the galactic spectra is indicated as IS. Image reproduced by permission from Webber and Potgieter (1989), copyright by AAS.
Left: Computed electron to positron ratios at Earth for two polarity cycles (A > 0, e.g., 1997, 2020 and A < 0, e.g., 1985, 2009) of the HMF compared to the ratio of the LIS at the heliopause (120 AU). Differences above about 80 MeV are caused by gradient, curvature, and current sheet drifts in the heliosphere during solar minimum activity. Right: Similar to left panel, but for computed ratios of galactic protons to anti-protons (Langner and Potgieter, 2004a).
Evidently, the charge-sign effect is significant but seems less than what was predicted by the first generation models. Strauss et al. (2012a) applied a newly developed 3D modulation model based on the SDE approach to study the modulation of galactic protons and anti-protons inside the heliosphere. They also found a maximum drift effect of a factor of 10 below ∼ 100 MeV for the \({\bar {\rm p}}/{\rm p}\), which gradually subsides with increasing to become negligible above 10 GeV. They predict that for the next solar minimum period (A > 0 cycle) this ratio will be lower than in the preceding A < 0 cycle and noted that if modulation conditions during the next solar minimum would be the same as in the previous A < 0 minimum of 2009, CR intensities will be even higher at Earth because of drifts. They illustrated convincingly with pseudo-particle traces how protons drift differently than anti-protons through the heliosphere to Earth during the same modulation cycle. See also Bobik et al. (2011, 2012). For an illustration of charge-sign-dependent effects in the outer heliosphere and heliosheath see, e.g., Langner and Potgieter (2004a).
In order to establish how large the effect is over an energy range considered relevant to solar modulation, precise and simultaneous measurements of CRs and their antiparticles by the same instrumentation are necessary. The PAMELA mission has introduced an era of such precise measurements of protons (anti-protons) and electrons (positron) done simultaneously to energies down to ∼ 100 MeV so that solar modulation can also be studied and particle drifts thoroughly tested. The preliminary proton and electron data as monthly averages, from mid-2006 to the end of December 2009, were reported in the PhD theses of Di Felice (2010) and De Simone (2011), and the Master’s theses of Vos (2011) and Munini (2011). The finalized proton spectra for this period were reported by Adriani et al. (2013) with the electron and positron data for this period to be finalized in 2013. Yearly averages were reported by Sparvoli (2012) and Boezio and Mocchiutti (2012). The PAMELA data shown here as Figure 20 illustrate how protons between 0.5–1.0 GV responded differently over the mentioned period than electrons at the same rigidity. Protons had increased by an average of a factor of ∼ 2.5 over 4.5 years whereas electrons of the same rigidity had increased by only a factor of ∼ 1.4 over the same period. This trend once again reveals the inverted V shape as discussed above.
Normalized proton (light-red lines) and electron (light-blue lines) differential intensities at (0.75 ± 0.2) GV as a function of time, from July 2006 to December 2009. The red and blue symbols represent the average intensities of protons and electrons, respectively. These intensity-time profiles are normalized to the intensity measured in July 2006. Image reproduced by permission from Vos (2011). See also Di Felice (2010) and De Simone (2011).
De Simone (2011) reported for the year 2009 that e−/e+ = 6 at 200 MeV changed to e−/e+ = 15 at 8 GeV, which demonstrates a similar trend as the prediction in Figure 6 but seemly larger. This provides ample motivation to apply a comprehensive drift model to the PAMELA data for CRs with opposite charge to establish the exact extent of drifts during the recent prolonged solar minimum.
What happens to the e−/p or e−/He ratios at times of solar maximum activity was demonstratively discussed by, e.g., Ferreira (2005), Heber and Potgieter (2006, 2008), and Potgieter (2011). PAMELA observations after 2009 could be most helpful in this regard.
It follows from Figure 19 that the optimum energy range for observations to test the extent of drift effects for electrons and positrons is between 50 MeV and 5 GeV. Below 50 MeV, electrons observed at Earth get ‘contaminated’ by Jovian electrons (Potgieter and Nndanganeni, 2013a).
4.8 Main causes of the complete 11-year and 22-year solar modulation cycles
Apart from the 11-year and 22-year cycles, regular steps are superposed on the intensity-time profiles of CR modulation. A departure point for these time-dependent steps (both increases and decreases) from a global point of view is that ‘propagating barriers’ are formed and later dissipate in the outer heliosphere during the 11-year activity cycle. These ‘barriers’ are basically formed by solar wind and magnetic field co-rotating structures which are inhibiting the easy access of CRs to a relative degree. This is especially applicable to the phase of the solar activity cycle before and after solar maximum conditions when large steps in the particle intensities had been observed. A wide range of interaction regions occur in the heliosphere, with GMIRs the largest, as introduced by Burlaga et al. (1993). They observed that a clear relation exists between CR decreases (recoveries) and the time-dependent decrease (recovery) of the HMF magnitude and extent local to the observation point. The paradigm on which these modulation barriers is based is that interaction and rarefaction regions form with increasing radial distance from the Sun (see also Potgieter and le Roux, 1989, and references therein). These relatively narrow interaction regions can grow latitudinally and especially azimuthally and as they propagate outwards they spread, merge and interact to form eventually GMIRs that can become large in extent and capable of causing the large step-like changes in CRs. Potgieter et al. (1993) illustrated that their affects on long-term modulation depend on their rate of occurrence, the radius of the heliosphere (i.e., how long they stay inside the modulation volume), the speed with which they propagate, their spatial extent and amplitude, especially their latitudinal extent (to disturb drifts), and the background modulation conditions they encounter. Drifts on the other hand, normally dominate periods of solar minimum modulation up to four years so that during an 11-year cycle a transition must occur (depending how solar activity develops) from a period dominated by drifts to a period dominated by these propagating structures. The largest of the step decreases and recoveries shown in Figure 6 are caused by these GMIRs.
The 11-year and 22-year cycles together with the step-like modulation are good examples of the interplay among the main modulation mechanisms as illustrated by Le Roux and Potgieter (1995). They showed that it was possible to simulate, to the first order, a complete 22-year modulation cycle by including a combination of drifts with time-dependent tilt angles and GMIRs in a time-dependent modulation model. See also Potgieter (1995, 1997) and references therein. Le Roux and Fichtner (1999) confirmed that a series of GMIRs cannot on their own reproduce the fully observed 11-year modulation cycle. This is achieved by adding a well-defined time variation in the propagation process such as for the diffusion coefficients, or using the time-dependent wavy HCS. A major issue with time-dependent modeling, apart from the global dynamic features such as the wavy HCS, is what to assume for the time dependence of the diffusion coefficients mentioned above.
A subsequent step in understanding long-term modulation came when Cane et al. (1999) pointed out that the step decreases observed at Earth could not be primarily caused by GMIRs because they occurred well before any GMIRs could form beyond 10–20 AU. Instead, they suggested that time-dependent global changes in the HMF over an 11-year cycle are responsible for long-term modulation. Potgieter and Ferreira (2001) and Ferreira and Potgieter (2004) combined these changes with time-dependent drifts, naming it the compound modeling approach. It was assumed that all the diffusion coefficients change with time proportional to B(t)−n(P, t), with B(t) the observed, time-dependent HMF magnitude close to Earth, and n(P, t) a function of rigidity and the HCS tilt angle, which introduces an additional time dependence related to solar activity. These changes are then propagated outwards at the solar wind speed to form propagating modulation barriers throughout the heliosphere, changing with the solar cycle. With simply n = 1, and with B(t) changing by an observed factor of 2 over a solar cycle, this approach resulted in a variation of the diffusion coefficients by a factor of 2 only, which is perfect for simulating the 11-year modulation at NM energies at Earth, as seen in Figure 6, but not at all for lower rigidities. In order to reproduce spacecraft observations at energies below a few GeV, n(P, t) must depend on time (solar activity) and on rigidity. For a more advanced treatment and recent application of this approach, see Manuel et al. (2011a,b).
Ferreira and Potgieter (2004) confirmed that using the HCS tilt angles as the only time-dependent modulation parameter resulted in compatibility only with solar minimum observations. Using the compound approach resolved this problem. Applied at Earth and along the Ulysses and Voyager 1 and 2 trajectories, this approach is remarkably successful over a period of 22 years, e.g., when compared with 1.2 GV electron and helium observations at Earth, it produces the correct modulation amplitude and most of the modulation steps. Some of the simulated steps did not have the correct magnitude and phase, indicating that refinement of this approach is needed by allowing for merging of the propagating structures. However, solar maximum modulation could be largely reproduced for different CR species using this relatively simple concept, while maintaining all the other major modulation features during solar minimum, such as charge-sign dependence discussed above.
An important accomplishment of this compound approach is that it also produces the observed charge-sign dependent CR modulation from solar minimum to maximum activity. Figure 21 depicts the computed 1.2 GV electron (e−) to helium ratio at Earth for 1976–2000 in comparison with the observed e−/He obtained from electron measurements of ISEE3/ICE, helium measurements from IMP and electron measurements from KET (Heber et al., 2002, 2003). The shaded areas correspond to the period when there was not a well defined HMF polarity. Two periods, labelled A and B, were found with relatively large differences between the computed ratios and the observations that require further refinement.
Computed 1.2 GV e−/He ratio at Earth for 1976–2000 in comparison with the observed e−/He obtained from electron measurements of ISEE3/ICE, He measurements from IMP and electron measurements from KET (Heber et al., 2003). The shaded areas correspond to the period with no well-defined HMF polarity. Two periods indicated by labels A and B with relatively large differences between the computed ratios and the observations require further investigation. Image reproduced by permission from Ferreira et al. (2003a), copyright by COSPAR.
The compound approach also involves two other important modifications. First, a significant increased polar perpendicular diffusion is required to account for the observed latitude dependence of CR protons and the lack thereof for electrons along the Ulysses trajectory over the 22 year cycle. This is mainly to reduce the large latitudinal gradients caused by unmodified drifts and in addition to the time dependence of the diffusion coefficients. This effect is illustrated in Figure 22 using the computed 2.5 GV electron to proton ratio (e−/p) along the Ulysses trajectory and at Earth in comparison with the 2.5 GV e−/p observations from KET (Heber et al., 2002, 2003). The top panels show the position of Ulysses during this period. In order to model the observed e-/p as a function of time, the latitude dependence of both electrons and protons must be correctly modeled (Ferreira et al., 2003b). Second, during periods of large solar activity, drifts must be reduced additionally to improve explaining the observed electron to He intensity ratio at Earth and the electron to proton ratio along the Ulysses trajectory during the period when the HMF polarity reverses. For example, drifts had to be reduced from a 50% level at the beginning of 1999 to a 10% level by the end of 1999, to vanish during 2000, but to quickly recover after the polarity reversal during 2001 to levels above 10%. For the period after 2001, the model predicts a steady increase in drifts from 10% to 20% by the end of 2002. This indicates that in order to produce realistic charge-sign dependent modulation during extreme solar maximum conditions, the heliosphere must become diffusion (non-drift) dominated. Ndiitwani et al. (2005) calculated the percentage drifts required over a full modulation cycle, especially during extreme solar maximum, to find compatibility between the compound model and the observed e−/p. This is shown in Figure 23 in comparison to the observed tilt angles as proxy for solar activity. Obviously, little drifts are required during solar maximum in contrast to ∼ 90% at solar minimum activity. For charge-sign dependent effects in the outer heliosphere and heliosheath, see Langner et al. (2003) and Langner and Potgieter (2004a).
Computed 2.5 GV electron to proton ratio (e−/p) as a function of time along the Ulysses trajectory (solid line) and at Earth (dotted line) in comparison with the 2.5 GV ratio observed with KET (Heber et al., 2002). Top panels show the position of Ulysses. In order to simulate this observed ratio as a function of time, the latitude dependence of both electrons and protons must be correctly modeled (Ferreira et al., 2003a; Ferreira, 2005). Image reproduced by permission from Ferreira et al. (2003b), copyright by EGU.
Percentage of drifts (continuous line) in the compound model that gives realistic modulation for various stages of the solar cycle for both the 2.5 GV electron and protons. As a proxy for solar activity the tilt angles, as used in the model are shown for illustrative purposes. Image reproduced by permission from Ndiitwani et al. (2005), copyright by EGU.
A question that is relevant within the context of Voyager 1 and 2 observations is how much modulation occurs inside the heliosheath. The process is of course highly energy-dependent. An illustrative example of the amount of modulation that CR protons may experience in the heliosheath in the nose direction is shown in Figure 24. The percentage of modulation in the equatorial plane in the heliosheath is given with respect to the total modulation (between 120 AU and 1 AU) as a function of kinetic energy for both polarity cycles, for solar minimum and moderate maximum conditions (Langner et al., 2003). See also Strauss et al. (2013b) for a recent illustration of modulation in the outer heliosphere.
Computed percentage of galactic CR modulation in the heliosheath with respect to the total modulation (between 120 AU and 1 AU) for the two magnetic polarity cycles (A > 0 and A < 0), for solar minimum (α = 10°) and for moderate maximum (α = 75°) conditions, in the equatorial plane in the nose direction of the heliosphere. Negative percentages mean that the galactic CRs are reaccelerated at the TS under these assumed conditions (Langner et al., 2003).
Evidently, at E < ∼ 0.02 GeV modulation > 80% may occur in the heliosheath for both polarity cycles. For all four the conditions, the heliosheath modulation will eventually reach 0% (not shown) but at different energies, indicating that it differs significantly with energy as well as with drift cycles. How much gradient and curvature drifts actually occur in the heliosheath is still unanswered. The negative percentages indicate that the intensity is actually increasing in the heliosheath as one moves inward from the outer boundary toward the TS because of the re-acceleration of CRs at the TS. This depends on many aspects, in particular the TS compression ratio as discussed by Langner et al. (2003, 2006a,b).
In the study of the long-term CR modulation in the heliosphere, several issues need further investigation and research. Despite the apparent success of the compound numerical model described above the amount of merging taking place beyond 20 AU needs to be studied with MHD models, especially the relation between CMEs and GMIRs, and how these large barriers will modify the TS and the heliosheath. The full rigidity dependence of the compound model is as yet not well described. A major issue with time-dependent modeling, apart from global dynamic features such as the wavy HCS, is what to use for the time dependence of the diffusion coefficients in Equation (6), on top of the already complex issue of what their steady-state energy (rigidity) and spatial dependence are in the inner heliosphere. It has now also become pressing to understand the diffusion tensor in the outer heliosphere and beyond the TS. Equation (5) is probably more complex and has been extended to include mechanisms otherwise considered to be negligible. Fundamentally, from first principles, it is not yet well understood how gradient and curvature drifts reduce with solar activity. This aspect needs now also to be investigated for the region beyond the TS. For example, what happens to the wavy HCS in the heliosheath and how will the strong non-radial components of the solar wind and the associated HMF affect drifts and CR modulation in the heliosheath? To answer this, more study is needed to gain a better understanding of the finer details of these complex magnetic fields and the relation to long-term CR modulation, especially how this field changes with solar activity. An aspect that should be kept in mind is that the study of more realistic fields requires an ever more complex diffusion tensor and description of drifts. Other interesting aspects of CRs beyond the TS are discussed by Potgieter (2008). Another important question is how the heliospheric modulation volume varies with time over scales of hundreds to thousands of years, which are most relevant for the study of space climate. The Sun encounters different interstellar environments during its passage through the galaxy, and hence the outer heliospheric structure should change (e.g., Scherer et al., 2008b).
The paleo-cosmic ray records can be used to study the properties of the heliosphere and solar processes over 10000 and more years. McCracken et al. (2011) reported that both varied greatly over such as period, ranging from ∼ 26 Grand Minima of duration 50–100 years when the Sun was inactive, to periods similar to the recent 50 years of strong solar activity. The 11 and 22 year cycles of solar activity continued through the Spörer and Maunder Grand Minima. They speculated that the solar dynamo exhibits a 2300 year periodicity, wherein it alternates between two different states of activity and argued that paleo-cosmic ray evidence suggests that the Sun has now entered a more uniform period of activity, following the sequence of Grand Minima (Wolf, Spörer, Maunder, and Dalton) that occurred between 1000 and 1800 AD. See also the discussion by Usoskin et al. (2001) and the review by Usoskin (2013).
5 A Few Observational Highlights
5.1 The unusual solar minimum of 2007–2009
The past solar minimum activity period and the consequent minimum modulation conditions for galactic CRs was unusual. It was expected that the new activity cycle would begin early in 2008, assuming a 10.5 year periodicity. Instead, solar minimum modulation conditions had continued until the end of 2009, characterized by a much weaker HMF compared to previous cycles. The tilt angle of the wavy HCS, on the other hand, had not decreased as rapidly as the magnitude of the HMF at Earth during this period, but eventually also reached a minimum value at the end of 2009. Ahluwalia and Ygbuhay (2011), Stozhkov et al. (2009), Mewaldt et al. (2010) and Krymsky et al. (2012) all reported that CRs with high rigidity reached record setting intensities during this time (see also Heber et al., 2009; McDonald et al., 2010). It followed from observations for this period that the delay between the time for minimum sunspot numbers and maximum CR intensities was at least three times longer than during previous even numbered solar cycles (e.g., Kane, 2011). The decay phase of the sunspot cycle 23 exhibited two unusual features, it lasted quite long while the HMF at Earth reached the lowest value since in situ measurements in space began in 1963. See also Cliver et al. (2011), Zhao and Fisk (2011), Ahluwalia and Jackiewicz (2012), and the reviews by Aslam and Badruddin (2012) and Mewaldt (2012).
Since the beginning of the space age, the highest CR proton spectrum was observed by PAMELA in December 2009. This was unexpected because during previous A < 0 polarity cycles, proton spectra were always lower than for A > 0 cycles at kinetic energies less than a few-GeV, in full accord with drift models. The PAMELA experiment has provided important results on the antiproton (Adriani et al., 2009a) and positron galactic abundances (Adriani et al., 2009b; Boezio et al., 2009; Boezio and Mocchiutti, 2012).
The high-resolution PAMELA spectrometer also allows to perform hydrogen and helium spectral measurements up to 1.2 TV (Sparvoli, 2012), which is the highest limit achieved by this kind of experiments. Adriani et al. (2013) presented observations down to 400 MV of the absolute flux of protons from July 2006 until the end of 2009. Large proton statistics collected by the instrument allowed the measurement of the proton flux for each Carrington rotation. In Figure 25 these spectra are shown from July 2006 to the very beginning of 2010. The spectrum at the end of December 2009 was the highest recorded. In January 2010, solar activity picked up significantly so that the proton intensity had started to decrease. In order to emphasize how decreasing solar modulation conditions allowed galactic protons to increase at Earth, especially at low kinetic energies, the spectra in Figure 25 are used to calculate and plot the intensity ratios as a function of kinetic energy with respect to July 2006. This is shown in Figure 26.
Proton spectra, averaged over one Carrington rotation, as observed by the PAMELA space instrument from July 2006 to the beginning of 2010 (see the colour coding on the left). The spectrum at the end of December 2009 was the highest recorded. See Adriani et al. (2013) and also Potgieter et al. (2013).
Computed ratios of differential intensities for selected periods in 2007, 2008, 2009 with respect to Nov. 2006 as a function of kinetic energy in comparison with PAMELA proton observations (Potgieter et al., 2013).
5.2 Samples from the inner heliosphere
The Ulysses mission produced solar modulation observations from 1990 to 2009 as reviewed by Heber and Potgieter (2006, 2008) and Heber (2011). These and other CR observations had yielded several new and surprising insights and are summarized as follows:
-
It was observed by Ulysses that the galactic CR flux was not symmetric to the heliographic equator implying a North-South-asymmetry in CR modulation (McKibben et al., 1996). Surprisingly, neither the solar wind experiments nor the magnetic field investigations reported this asymmetry. Later magnetic field investigations were interpreted to give a deficit of the magnetic flux in the southern hemisphere suggesting a relatively large latitudinal offset of the location of the HCS by 10° (Smith et al., 2000). Recently, Erdős and Balogh (2010) disputed this number, arguing that the Ulysses magnetic field measurements did not give evidence for such a large displacement of the HCS, only a southward displacement of 2°–3° could be possible. It remains thus an open question whether this observation was an occurrence of events that pertained during this rapid pole to pole passage of Ulysses or was related to an asymmetrical magnetic flux.
-
Small latitudinal galactic CR gradients were observed at solar minimum, confirming that the LIS cannot be observed in the inner polar regions of the heliosphere. A particular motivation of the Ulysses mission was to explore this possibility. Drift dominated models of that time actually allowed for this (Jokipii and Kopriva, 1979). In contrast, the observed proton spectrum was highly modulated to large heliolatitudes.
-
The latitudinal gradients for CR protons as a function of rigidity was observed to reach a maximum around 2 GV, to decrease significantly below these values, in sharp contrast to what drift dominated models predicted at that time, a factor of 10 at 200 MeV.
-
A renowned observation was that recurrent particle events occurred at high heliolatitudes without corresponding features in the solar wind and magnetic field data. It appears that similar effects did not occur during the last polar excursion by Ulysses. Dunzlaff et al. (2008) reported that measurements in the fast solar wind show differences: In cycle 22 the recurrent cosmic ray decreases showed a clear maximum near 25° heliolatitude and were still present beyond 40°, whereas in cycle 23 neither such a pronounced maximum nor significant decreases were observed above 40°. The periodicity in the CR intensity that could be clearly seen in the slow solar wind appeared to have vanished in the fast solar wind.
-
Essentially no latitudinal gradients were observed for any galactic CRs at solar maximum, indicating that drifts, mainly responsible for setting-up these gradients during solar minimum conditions, were almost absent at solar maximum.
-
The observed electron to proton ratios (implicitly also containing the radial and latitudinal gradients) indicated that large particle drifts were occurring during solar minimum but diminished significantly toward solar maximum when rather diminished drifts were required in models to explain the observed values (see Figure 23).
-
Jovian electrons were observed at high heliolatitudes, implying effective latitudinal transport of electrons at these energies (∼ 10 MeV). This still has to be explained from basic theoretical considerations, in particular if this could be the cause of extraordinary effective transport for these low-energy electrons including large polar perpendicular diffusion (see also Ferreira, 2005).
-
Anomalous fluxes of oxygen, nitrogen, and neon were observed along the Ulysses trajectory and at Earth and with spatial gradients different from galactic CRs (e.g., Heber and Marsden, 2001; Cummings et al., 2009).
Several other space missions, at or near Earth, and several balloon experiments also made numerous and valuable observations of CR modulation (see the review by Mewaldt, 2012). Some of the recent PAMELA results are discussed above within a given context.
5.3 Samples from the outer heliosphere
A major surprise came from the outer heliosphere when Voyager 1 crossed the TS in 2004 and found that the intensity of the ACRs did not reach a peak intensity at the shock for energies more than a few MeV/nuc. As mentioned above, the ACR intensity kept increasing far into the heliosheath implying that they are accelerated somewhere else and probably by different processes other than diffusive shock acceleration. Continued observations from the Voyagers will hopefully offer an explanation. The TS was observed to be disappointingly weak so that it is unlikely that it will reaccelerate galactic CRs to the extent that it influences the spectral shape of the CR spectra in the heliosphere.
With Voyager 1 very close to the HP it is relevant to ask what signatures of the HP in CRs can be expected? A magnetic barrier or ‘wall’, if present, should cause a significant increase of the magnetic field magnitude at the HP. It is unlikely that high energy galactic CRs will change abruptly but the effect should be strongly energy-dependent so that the low energy part of the CR spectrum should rise steeply at the HP while the ACR intensities drop sharply.
Apart from the ACRs, the galactic electrons at low energies (E < 100 MeV) showed extraordinary behaviour in the heliosheath. This is shown in Figure 27. Note the jumps in intensity and accompanying changes in the radial gradients. After crossing the TS in late 2004, the 6–14 MeV galactic electron intensity measured at Voyager 1 increased rapidly and irregularly. By about 2008.5 this intensity was 5 times that measured when Voyager 1 crossed the shock. The local radial intensity gradient was as high as (18.5 ± 1.5) %/AU at times, to drop to as low (8 ± 1) %/AU as shown in the figure (see also Nkosi et al., 2011). Webber et al. (2012) argued that these sudden changes in intensity and in the gradients of electrons and protons are evidence that Voyager 1 crossed into regions of significantly different propagation conditions.
The 5-day running average of the 6–14 MeV electrons and E > 200 MeV protons intensities measured at Voyager 1 from 2008.5 to 2012. Note the first sudden intensity increase of electrons at 2009.70 (111.2 AU) and the change in radial gradients of both electrons and protons before and after this increase. Similar behaviour followed n the second sudden intensity increases of both electrons and protons at 2011.2 (116 AU). The continuing increase of electron and proton intensities after 2011.3 is a notable feature. Image reproduced by permission from Webber et al. (2012), copyright by AGU.
Even more spectacular is what happened in August 2012 to the intensity of 0.5 MeV protons (mainly ACRs) and 6–14 MeV galactic electrons, and E > 100 MeV proton count rates when Voyager 1 was at 121.7 AU, as displayed in Figure 28. Within a few days the intensity of the dominant energetic component above 1–2 MeV decreased by more than 90%. At the same time a sudden increase of a factor of ∼ 2 occurred in lower energy (6–100 MeV) electrons and ∼ 30–50% for the higher energy nuclei above 100 MeV. The magnitude of this intensity change for ACRs has not been observed in the 35 years of the Voyager mission except close to Jupiter. This simultaneous abrupt reduction of ACR (and TSPs) intensities at lower energies and increase in galactic CR intensities at somewhat higher energies was interpreted by Webber and McDonald (2013) as evidence of the crossing of the HP, or at least the crossing of a ‘heliocliff’. This is another spectacular milestone for the Voyager mission. It should be noted that this apparent crossing has not yet been confirmed by magnetic field observations. The crossing of the HP by Voyager 2 is expected to happen soon.
Extraordinary changes were found in the 5 day running average intensities of 0.5 MeV protons (mainly ACR), 6–14 MeV galactic electrons and E > 100 MeV protons from 2009.0 to the end of the data set as observed by Voyager 1. Note how the 0.5 MeV proton intensity drops while the E > 100 MeV protons count rate went up. Image reproduced from the preprint of Webber and McDonald (2013).
6 Constraints, Challenges, and Future Endeavours
The modeling of the modulation of galactic CRs in the heliosphere requires essential information, as was mentioned above, that needs to be improved in order to make progress. In this context, a few constraints and challenges are as follows:
The LIS for the different galactic CR species are needed as initial conditions at the ‘heliospheric boundary’, presumably the HP but probably even further out. Computed galactic CR spectra could be different from the LIS. Surprisingly, little is known about most of these galactic spectra at energies below a few GeV because of solar modulation so that the uncertainties, mostly attributed to speculation instead of solid evidence, can be rather large as illustrated by Webber and Higbie (2008, 2009). Adiabatic energy losses in the heliosphere cause the galactic CR spectral shapes for ions and anti-protons below ∼ 10 GeV to be properly disguised, progressively with decreasing energy and closer to the Sun. In contrast, the intensity of MeV-electrons is much less modified by adiabatic energy losses and also by gradient and curvature drifts. Unfortunately, from an electron LIS point of view, Jupiter is a dominant source of up to ∼ 30 MeV electrons in the inner heliosphere, also completely concealing the electron LIS in the inner heliosphere at these energies. This is not the case for positrons. The spectral shape at Earth for the low energy part of the positron spectrum is likely to be the same as for the positron LIS. There also are indications from the PAMELA observations that the LIS for positrons, and to some extent also electrons, may contain contributions from local galactic sources so that the LIS may not be as isotropic as assumed. With the two Voyager spacecraft at or close to the HP, another milestone in the solar modulation of CRs is foreseeable when the LIS gets observed.
The global features, structure, and geometry of the heliosphere as discussed above are important for modulation studies so that several issues arise, e.g., what is the difference in the distance to the ‘modulation boundary’ in the polar and tail regions? How asymmetrical is the heliosphere in the azimuthal and meridional planes and how does it affect CR modulation? See, e.g., Langner and Potgieter (2005) and Ngobeni and Potgieter (2011). How much does the ‘modulation volume’ vary from solar minimum to maximum activity and how much is the inner heliosheath contributing to this aspect? How much is the TS position oscillating (moving inward and outward) with changing solar activity? Furthermore, what is the role that the vastly extended heliospheric tail region plays? It could also be that the alignment of the HMF and the local interstellar magnetic field at the HP, together with the HCS, create regions of ideal entrance for galactic CRs introducing in the process an asymmetry in galactic CR modulation.
The wavy HCS is a successful and well-established physical entity in global modeling of solar modulation. The tilt angle of the HCS has become the most useful indicator of solar activity from a drift-modulation point of view and is widely used in data interpretation and especially in modeling. However, the calculation of this tilt angle is model dependent and it is not clear how the waviness is preserved when propagating outwards away from the Sun, especially with increasing solar activity (Jiang et al., 2010). The dynamic of the HCS has to be studied in more detail, with the first insightful contributions being made (e.g., Borovikov et al., 2011). It is also unclear whether particle drifts play a significant role in the heliosheath and to what extent drift patterns are different than in the inner heliosphere (Webber et al., 2008).
Improved knowledge about the global solar wind profile and HMF remains crucial for effective modeling. Before the Ulysses mission little was explicitly known about the latitudinal dependence of these entities in the inner heliosphere. Today, the solar wind profile can be specified in detail in models, while for the HMF came the realization that it may not be approximated in the heliospheric polar regions by the HMF that Parker envisaged in the 1960s. This aspect is contributed to interesting development in CR modulation. Nowadays, in numerical models significant modifications, mostly phenomenological, to the Parker field are applied in the polar regions, where a possible replacement is in the form of the Fisk (1996) solar magnetic field. Unfortunately, the Fisk-type fields are too complex to handle straight forwardly in standard numerical codes, but progress is being made (e.g., Burger et al., 2008; Sternal et al., 2011). At present, a conclusion for numerical modeling may be that Parkerian type HMFs are mostly too simple (although the interpretation of HMF observations keep pointing to such underlying simplicity) while Fisk-type fields are too complex to handle numerically (and seem absent in the way that HMF observations are interpreted). The question about the HMF geometry is how significant are the modulation effects of the Fisk-type HMF on CR modulation. To answer this, more study is needed to gain a better understand of the finer details of these complex magnetic fields and the relation to long-term CR modulation, especially how this field changes with solar activity. An aspect that should be kept in mind is that the study of more realistic magnetic fields requires an ever more complex diffusion tensor and description of drifts.
Progress has been made in understanding observations of small latitudinal gradients from Ulysses. In order to do so, Burger et al. (2000) argued that the rigidity dependence of the two components of the diffusion tensor, which are perpendicular to the mean HMF, should be decoupled. This approach was supported by the investigation of MeV electrons (Ferreira et al., 2001). Although the concept of increased polar perpendicular diffusion is well established, no conclusive theoretical work has been published to explain this dependence. Such an investigation may also be crucial in deciding to what extent the ‘standard’ Parker HMF has to be modified.
Three-dimensional models to describe the propagation and modulation of Jovian electrons in the inner heliosphere were applied by Fichtner et al. (2000), Ferreira et al. (2001), and Moeketsi et al. (2005). They studied the radial and latitudinal transport of these particles in detail and estimated upper and lower limits for the ratio of the parallel and perpendicular diffusion coefficients, which in numerical model is a crucial modulation parameter. This needs to be investigated further. They also disentangled the galactic and Jovian contributions to these electron observations, a process that improved understanding and the interpretation of Ulysses data (see also Strauss et al., 2013a). They found that Jovian electrons dominate the inner equatorial regions up to ∼ 10–20 AU but it is unlikely that they can dominate the low-energy galactic electrons to heliolatitudes higher than ∼ 30° off the equatorial plane. This is determined however by how large polar perpendicular diffusion is made and needs further study. Recently, Potgieter and Nndanganeni (2013a) offered computations of what can be considered lower and upper limits for galactic electrons at Earth at energies below a 100 MeV.
The acceleration and propagation of CRs and the ACRs at the TS and beyond are presently highly controversial and need further studies. The standing paradigm of the ACRs being accelerated at the TS was severely questioned when the Voyager spacecraft crossed the TS and observed unexpected results. The spectrum of ACRs did not unfold to an anticipated power-law, and the ACR fluxes simply continued to increase as the two Voyagers moved away from the TS. Magnetic reconnection (Drake et al., 2010; Lazarian and Opher, 2009) and different forms of stochastic acceleration (Fisk and Gloeckler, 2009; Strauss et al., 2010a) have been invoked as causing this phenomena, or it could simply be due to the so-called bluntness of the TS (e.g., McComas and Schwadron, 2006; Kóta and Jokipii, 2008). The answer to this unresolved question and the full grasp of where and how ACRs are accelerated should have important impacts on the transport and reacceleration of CRs in the heliosphere and elsewhere in the interstellar medium. Other interesting aspects of CRs beyond the TS were discussed by Potgieter (2008).
In the field of the long-term (11-years and longer) CR modulation in the heliosphere, several issues need further investigation and research: (1) Despite the apparent success of the compound numerical model described above the amount of merging taking place beyond 20 AU needs to be studied with MHD models, especially the relation between interplanetary CMEs and GMIRs, and how these large barriers may modify the TS, the inner heliosheath and perhaps also the HP. (2) The full rigidity dependence of the compound model is as yet not well described because the underlying effects of turbulence on the diffusion coefficients is poorly observed and understood. (3) A major issue with time-dependent modeling, apart from global dynamic features such as the wavy HCS, is what to use for the time dependence of all the diffusion coefficients in Equation (5), on top of the already complex issue of what their steady-state energy (rigidity) and spatial dependence are in the inner heliosphere (e.g., Manuel et al., 2011a,b). It has now also become vital to understand the diffusion tensor beyond the TS. Equation (5) is probably more complex for this region and needs to be extended to include processes (perhaps even completely new ones) that are otherwise considered to be negligible. (4) Fundamentally, from first principles, it is not yet well understood how gradient and curvature drifts reduce with solar activity. This aspect needs now also to be investigated for the region beyond the TS. For example, what happens to the wavy HCS in the heliosheath and how will the strong latitudinal and azimuthal components of the solar wind velocity and the associated HMF influence particle drifts and CR modulation in the heliosheath? The question arises if the modulation in this region is really fundamentally different from the rest of the heliosphere? (5) Another important question is how the heliospheric modulation volume varies with time on the scale of thousands to millions of years? The Sun encounters different interstellar environments during its passage through the galaxy, and hence the outer structure and size of heliosphere should change over such periods.
Other interesting aspects that will hopefully be addressed in future are: (1) The solar modulation of many CR species and their isotopes has not been properly modeled. The first obstacle, and therefore prime objective, will be to establish LIS for these isotopes. (2) The anisotropy of CRs at various energies as caused inside the heliosphere, also related to what a very extensive heliotail may contribute, is another specialized topic. In this context, see the review by Kóta (2012). (3) At what rigidity is the modulation of CRs beginning? This is important for the interpretation of observations of CRs, also for anisotropy studies. In modulation modeling it is simply assumed to begin at ∼ 30 GeV. (4) The extended solar cycle 23/24 minimum provides an opportunity to investigate conditions that were different than before, perhaps similar to those in the early 1900s. This may reveal a 100–120 year cycle in CR modulation. (5) Over the last decade, there has been noteworthy progress in obtaining, analyzing and interpreting Be10 and other isotopes produced by CRs in the atmosphere, which reveals a history of CRs going back to millions of years (e.g., Wieler et al., 2011). This certainly contributes to the growing interest in the topic of space climate (see Scherer et al., 2006, and reference therein).
Mewaldt (2012) noted from an experimental point of view that there are presently a dozen spacecraft measuring galactic CRs and ACRs over energies from below 1 MeV to ∼ 1 TeV and in situ from 1 to 122 AU (see his Figure 1 for current missions). These space missions are supplemented by ground-based detectors such as NMs and by balloon-flight instruments. He concluded that the challenge during the next decade will be to maintain enough of these missions and facilities to support the Voyagers’ approach and passage through the HP into interstellar space, and to record in detail the evolving story of how CRs in the heliosphere respond to the Sun’s new direction in solar activity.
7 Summary
The heliosphere shields the solar system and all living creatures from galactic CRs. Since the Sun is a variable star it produces significant modulation of these charged particles in a variety of cycles. Cosmic rays are excellent indicators of the various solar cycle variations and studying them enlighten us about the characteristics of the Sun’s electrodynamic influence sphere. Such studies also inform us about the structural features and geometry of the heliosphere, including the solar wind termination shock, the heliosheath and the heliopause because they all influence the flux of CRs in the heliosphere, up to Earth.
Tremendous progress has been made since the beginning of the space age with the deployment of several space missions for detecting CRs over a wide range of energies, which stimulated theoretical and modeling research. Ten years ago, the size and geometry of the heliosphere and the importance of shock acceleration were all major unknown issues. Now that the Voyager spacecraft had crossed the TS and Voyager 1 is close to the heliopause, some of these entities and mechanisms are becoming reasonably known, at least, they cannot be considered ‘free’ parameters any longer.
The present understanding of the mechanisms of the global solar modulation of galactic CRs in the heliosphere is considered essentially correct, an amazing accomplishment for Parker’s theory that was developed in the early 1960s. The main obstacles and challenges are insufficient knowledge of the spatial, rigidity and especially the temporal dependence of the diffusion coefficients, covering the underlying features of solar wind and magnetic field’s turbulence.
Evidently, this field of research is alive-and-well with many aspects remaining a work in progress.
References
Adriani, O., Barbarino, G.C., Bazilevskaya, G.A. et al. [PAMELA Collaboration], 2009a, “An anomalous positron abundance in cosmic rays with energies 1.5–100 GeV”, Nature, 458, 607–608. [DOI], [ADS], [arXiv:0810.4995 [astro-ph]] (Cited on page 42.)
Adriani, O., Barbarino, G.C., Bazilevskaya, G.A. et al. [PAMELA Collaboration], 2009b, “New measurement of the antiproton-to-proton flux ratio up to 100 GeV in the cosmic radiation”, Phys. Rev. Lett., 102, 051101. [DOI], [ADS], [arXiv:0810.4994 [astro-ph]] (Cited on page 42.)
Adriani, O., Barbarino, G.C., Bazilevskaya, G.A. et al. [PAMELA Collaboration], 2013, “Time Dependence of the Proton Flux Measured by PAMELA during the 2006 July–2009 December Solar Minimum”, Astrophys. J., 765, 91. [DOI], [ADS], [arXiv:1301.4108 [astro-ph.HE]] (Cited on pages 35, 42, and 43.)
Ahluwalia, H.S. and Jackiewicz, J., 2012, “Sunspot cycle 23 descent to an unusual minimum and forecasts for cycle 24 activity”, Adv. Space Res., 50, 662–668. [DOI], [ADS] (Cited on page 42.)
Ahluwalia, H.S. and Ygbuhay, R.C., 2011, “The onset of sunspot cycle 24 and galactic cosmic ray modulation”, Adv. Space Res., 48, 61–64. [DOI], [ADS] (Cited on page 42.)
Alania, M.V., Modzelewska, R. and Wawrzynczak, A., 2011, “On the Relationship of the 27-day Variations of the Solar Wind Velocity and Galactic Cosmic Ray Intensity in Minimum Epoch of Solar Activity”, Solar Phys., 270, 629–641. [DOI], [ADS] (Cited on page 14.)
Aslam, O.P.M. and Badruddin, 2012, “Solar Modulation of Cosmic Rays during the Declining and Minimum Phases of Solar Cycle 23: Comparison with Past Three Solar Cycles”, Solar Phys., 279, 269–288. [DOI], [ADS] (Cited on page 42.)
Balogh, A. and Jokipii, J.R., 2009, “The heliospheric magnetic field and its extension to the inner heliosheath”, Space Sci. Rev., 143, 85–110. [DOI], [ADS] (Cited on page 8.)
Battiston, R. [AMS Collaboration], 2010, “The Anti Matter Spectrometer (AMS-02): A particle physics detector in space”, in Astroparticle, Particle and Space Physics, Detectors and Medical Physics Applications, Proceedings of the 11th ICATPP conference, Villa Olmo, Como, Italy, 5–9 October 2009, (Eds.) Leroy, C., Rancoita, P.-G., Barone, M., Gaddi, A., Price, L., Ruchti, R., Astroparticle, Particle and Space Physics, Detectors and Medical Physics Applications, 5, pp. 741–750, World Scientific, Singapore; Hackensack, NJ. [DOI], [ADS] (Cited on page 31.)
Beatty, J.J., Garcia-Munoz, M. and Simpson, J.A., 1985, “The cosmic-ray spectra of 1H, 2H, and 4He as a test of the origin of the hydrogen superfluxes at solar minimum modulation”, Astrophys. J., 294, 455–462. [DOI], [ADS] (Cited on page 24.)
Beer, J., McCracken, K.G., Abreu, J., Heikkilä, U. and Steinhilber, F., 2011, “Cosmogenic radionuclides as an extension of the neutron monitor era into the past: Potential and imitations”, Space Sci. Rev.. [DOI] (Cited on page 15.)
Bieber, J.W., 2003, “Transport of charged particles in the heliosphere: Theory”, Adv. Space Res., 32, 549–560. [DOI], [ADS] (Cited on pages 24 and 27.)
Bieber, J.W., Matthaeus, W.H., Smith, C.W., Wanner, W., Kallenrode, M.-B. and Wibberenz, G., 1994, “Proton and electron mean free paths: The Palmer consensus revisited”, Astrophys. J., 420, 294–306. [DOI], [ADS] (Cited on page 26.)
Bieber, J.W., Matthaeus, W.H., Shalchi, A. and Qin, G., 2004, “Nonlinear guiding center theory of perpendicular diffusion: General properties and comparison with observation”, Geophys. Res. Lett., 31, L10805. [DOI], [ADS] (Cited on page 27.)
Blasi, P., Amato, E. and Serpico, P.D., 2012, “Spectral breaks as a signature of cosmic ray induced turbulence in the galaxy”, Phys. Rev. Lett., 109, 061101. [DOI], [ADS], [arXiv:1207.3706 [astro-ph.HE]] (Cited on page 13.)
Bobik, P., Boschini, M.J., Consolandi, C. et al., 2011, “Antiproton modulation in the heliosphere and AMS-02 antiproton over proton ratio prediction”, Astrophys. Space Sci. Trans., 7, 245–249. [DOI], [ADS], [arXiv:1102.0215 [astro-ph.EP]] (Cited on page 33.)
Bobik, P., Boella, G., Boschini, M.J. et al., 2012, “Systematic investigation of solar modulation of galactic protons for solar cycle 23 using a Monte Carlo approach with particle drift effects and latitudinal dependence”, Astrophys. J., 745, 132. [DOI], [ADS] (Cited on pages 28 and 33.)
Boezio, M. and Mocchiutti, E., 2012, “Chemical composition of galactic cosmic rays with space experiments”, Astropart. Phys., 39, 95–108. [DOI], [ADS] (Cited on pages 31, 35, and 42.)
Boezio, M., Pearce, M., Picozza, P. et al., 2009, “PAMELA and indirect dark matter searches”, New J. Phys., 11, 105023. [DOI], [ADS] (Cited on pages 31 and 42.)
Borovikov, S.N., Pogorelov, N.V., Burlaga, L.F. and Richardson, J.D., 2011, “Plasma near the heliosheath: Observations and modeling”, Astrophys. J., 728, L21–26. [DOI], [ADS] (Cited on pages 9 and 47.)
Burger, R.A. and Potgieter, M.S., 1989, “The calculation of neutral sheet drift in two-dimensional cosmic-ray modulation models”, Astrophys. J., 339, 501–511. [DOI], [ADS] (Cited on page 27.)
Burger, R.A., Potgieter, M.S. and Heber, B., 2000, “Rigidity dependence of cosmic ray proton latitudinal gradients measured by Ulysses spacecraft: Implications for the diffusion tensor”, J. Geophys. Res., 105, 27, 447–27, 455. [DOI], [ADS] (Cited on pages 20, 27, and 48.)
Burger, R.A., Krüger, T.P.J., Hitge, M. and Engelbrecht, N.E., 2008, “A Fisk-Parker hybrid heliospheric magnetic field with a solar-cycle dependence”, Astrophys. J., 674, 511–519. [DOI], [ADS] (Cited on pages 20 and 48.)
Burlaga, L.F. and Ness, N.F., 2011, “Current sheets in the heliosheath: Voyager 1, 2009”, J. Geophys. Res., 116, A05102. [DOI], [ADS] (Cited on page 8.)
Burlaga, L.F., McDonald, F.B. and Ness, N.F., 1993, “Cosmic ray modulation and the distant heliospheric magnetic field Voyager 1 and 2 observations from 1986 to 1989”, J. Geophys. Res., 98, 1–11. [ADS] (Cited on page 37.)
Burlaga, L.F., Ness, N.F., Akuna, M.H., Lepping, R.P., Connerney, J.E.P., Stone, E.C. and McDonald, F.B., 2005, “Crossing the termination shock into the heliosheath: Magnetic fields”, Science, 309, 2027–2029. [DOI], [ADS] (Cited on page 8.)
Büsching, I. and Potgieter, M.S., 2008, “The variability of the proton cosmic ray flux on the Sun’s way around the galactic center”, Adv. Space Res., 42, 504–509. [DOI], [ADS] (Cited on pages 13 and 14.)
Büsching, I., de Jager, O.C., Potgieter, M.S. and Venter, C., 2008, “A cosmic-ray positron anisotropy due to two middle-aged, nearby pulsars?”, Astrophys. J. Lett., 678, L39–L42. [DOI], [ADS] (Cited on page 13.)
Cane, H.V., Wibberenz, G., Richardson, I.G. and von Rosenvinge, T.T., 1999, “Cosmic ray modulation and the solar magnetic field”, Geophys. Res. Lett., 26, 565–568. [DOI], [ADS] (Cited on page 37.)
Cliver, E.W., Richardson, I.G. and Ling, A.G., 2011, “Drivers of 11-yr and long-term cosmic ray modulation”, Space Sci. Rev.. [DOI], [ADS] (Cited on pages 31 and 42.)
Cummings, A.C. and Stone, E.C., 2007, “Composition of anomalous cosmic rays”, Space Sci. Rev., 130, 389–399. [DOI], [ADS] (Cited on page 11.)
Cummings, A.C., Stone, E.C., McDonald, F.B., Heikkila, B.C., Lal, N. and Webber, W.R., 2008, “Anomalous Cosmic Rays in the Heliosheath”, in Particle Acceleration and Transport in the Heliosphere and Beyond, 7th Annual International Astrophysics Conference, Kauai, Hawaii, 7–13 March 2008, (Eds.) Li, G., Hu, Q., Verkhoglyadova, O., Zank, G.P., Lin, R.P., Luhmann, J., AIP Conference Proceedings, 1039, pp. 343–348, American Institute of Physics, Melville, NY. [DOI], [ADS] (Cited on page 13.)
Cummings, A.C., Tranquille, C., Marsden, R.G., Mewaldt, R.A. and Stone, E.C., 2009, “Radial and latitudinal gradients of anomalous cosmic ray oxygen in the inner heliosphere”, Geophys. Res. Lett., 36, L18103. [DOI], [ADS] (Cited on pages 11 and 45.)
De Simone, N., 2011, Galactic and solar proton flux measurements in the energy range 80 MeV–1.2 TeV with the PAMELA space experiment, Ph.D. thesis, University of Rome Tor Vergata, Rome. Online version (accessed 26 February 2013): http://pamela.roma2.infn.it/index.php?option=com_docman&task=doc_details&gid=538 (Cited on pages 35 and 36.)
De Simone, N., Di Felice, V., Gieseler, J., Boezio, M., Casolino, M., Picozza, P. and Heber, B. [PAMELA Collaboration], 2011, “Latitudinal and radial gradients of galactic cosmic ray protons in the inner heliosphere — PAMELA and Ulysses observations”, Astrophys. Space Sci. Trans., 7, 425–434. [DOI], [ADS] (Cited on pages 21, 24, and 26.)
Decker, R.B., Krimigis, S.M., Roelof, E.C., Hill, M.E., Armstrong, T.P., Gloeckler, G., Hamilton, D.C. and Lanzerotti, L.J., 2005, “Voyager 1 in the foreshock, termination shock, and heliosheath”, Science, 309, 2020–2024. [DOI], [ADS] (Cited on page 11.)
Della Torre, S., Bobik, P., Boschini, M.J. et al., 2012, “Effects of solar modulation on the cosmic ray positron fraction”, Adv. Space Res., 49, 1587–1592. [DOI], [ADS] (Cited on page 33.)
Di Felice, V., 2010, Low energy electron and positron measurements in space with the PAMELA Experiment, Ph.D. thesis, University of Rome Tor Vergata, Rome. Online version (accessed 6 June 2013): http://hdl.handle.net/2108/1245 (Cited on pages 35 and 36.)
Drake, J.F., Opher, M., Swisdak, M. and Chamoun, J.N., 2010, “A magnetic reconnection mechanism for the generation of anomalous cosmic rays”, Astrophys. J., 709, 963–974. [DOI], [ADS], [arXiv:0911.3098 [astro-ph.SR]] (Cited on pages 9 and 48.)
Dröge, W., 2005, “Probing heliospheric diffusion coefficients with solar energetic particles”, Adv. Space Res., 35, 532. [ADS] (Cited on page 26.)
Dunzlaff, P., Heber, B., Kopp, A., Rother, O., Müller-Mellin, R., Klassen, A., Gómez-Herrero, R. and Wimmer-Schweingruber, R., 2008, “Observations of recurrent cosmic ray decreases during solar cycles 22 and 23”, Ann. Geophys., 26, 3127–3138. [DOI], [ADS] (Cited on page 44.)
Effenberger, F., Fichtner, H., Scherer, K., Barra, S., Kleimann, J. and Strauss, R.D., 2012, “A generalized diffusion tensor for fully anisotropic diffusion of energetic particles in the heliospheric magnetic field”, Astrophys. J., 750, 108. [DOI], [ADS] (Cited on page 20.)
Erdős, G. and Balogh, A., 2010, “North-south asymmetry of the location of the heliospheric current sheet revisited”, J. Geophys. Res., 115, A01105. [DOI], [ADS] (Cited on page 44.)
Fahr, H.-J., 2004, “Global structure of the heliosphere and interaction with the local interstellar medium: three decades of growing knowledge”, Adv. Space Res., 34, 3–13. [DOI], [ADS] (Cited on page 6.)
Ferreira, S.E.S., 2005, “The transport of galactic and jovian cosmic ray electrons in the heliosphere”, Adv. Space Res., 35, 586–596. [DOI], [ADS] (Cited on pages 31, 33, 35, 39, and 44.)
Ferreira, S.E.S. and Potgieter, M.S., 2004, “Long-Term Cosmic-Ray Modulation in the Heliosphere”, Astrophys. J., 603, 744–752. [DOI], [ADS] (Cited on pages 21, 37, and 38.)
Ferreira, S.E.S. and Scherer, K., 2004, “Modulation of Cosmic-Ray Electrons in the Outer Heliosphere”, Astrophys. J., 616, 1215–1223. [DOI], [ADS] (Cited on page 6.)
Ferreira, S.E.S., Potgieter, M.S., Burger, R.A., Heber, B. and Fichtner, H., 2001, “The modulation of Jovian and galactic electrons in the heliosphere. I. Latitudinal transport of a few MeV electrons”, J. Geophys. Res., 106, 24, 979–24, 987 (Cited on pages 18, 20, 21, 27, and 48.)
Ferreira, S.E.S., Potgieter, M.S. and Heber, B., 2003a, “Particle drift effects on cosmic ray modulation during solar maximum”, Adv. Space Res., 32, 645–650. [DOI], [ADS] (Cited on pages 21, 31, 38, and 39.)
Ferreira, S.E.S., Potgieter, M.S., Heber, B. and Fichtner, H., 2003b, “Charge-sign dependent modulation over a 22-year cycle”, Ann. Geophys., 21, 1359–1366. [DOI], [ADS] (Cited on pages 21, 31, and 39.)
Fichtner, H., 2001, “Anomalous cosmic rays: Messengers from the outer heliosphere”, Space Sci. Rev., 95, 639–754. [DOI], [ADS] (Cited on page 11.)
Fichtner, H., 2005, “Cosmic rays in the heliosphere: progress in the modelling during the past 10 years”, Adv. Space Res., 35, 512–517. [DOI] (Cited on page 28.)
Fichtner, H., Sreenivasan, S.R. and Fahr, H.J., 1996, “Cosmic-ray modulation and a non-spherical heliospheric shock”, Astron. Astrophys., 308, 248–260. [ADS] (Cited on page 28.)
Fichtner, H., Potgieter, M.S., Ferreira, S.E.S. and Burger, R.A., 2000, “On the propagation of Jovian electrons in the heliosphere: Transport modelling in 4-D phase space”, Geophys. Res. Lett., 27, 1611–1614. [DOI], [ADS] (Cited on pages 27 and 48.)
Fisk, L.A., 1971, “Solar modulation of galactic cosmic rays, 2”, J. Geophys. Res., 76, 221–226. [DOI], [ADS] (Cited on pages 16 and 27.)
Fisk, L.A., 1976, “Solar modulation of galactic cosmic rays. IV. Latitude-dependent modulation”, J. Geophys. Res., 81, 4646–4650. [DOI], [ADS] (Cited on pages 16 and 27.)
Fisk, L.A., 1979, “The interactions of energetic particles with the solar wind”, in Solar System Plasma Physics, (Eds.) Parker, E.N., Kennel, C.F., Lanzerotti, L.J., pp. 177–247, North-Holland, Amsterdam; New York. [ADS] (Cited on page 16.)
Fisk, L.A., 1996, “Motion of the footpoints of heliospheric magnetic field lines at the Sun: Implications for recurrent energetic particle events at high heliographic latitudes”, J. Geophys. Res., 101, 15, 547–15, 554. [DOI], [ADS] (Cited on pages 8 and 47.)
Fisk, L.A., 1999, “An overview of the transport of galactic and anomalous cosmic rays in the heliosphere: theory”, Adv. Space Res., 23, 415–423. [DOI], [ADS] (Cited on pages 11 and 16.)
Fisk, L.A., 2005, “Journey into the unknown beyond”, Science, 09, 2016–2017. [DOI], [ADS] (Cited on page 11.)
Fisk, L.A. and Gloeckler, G., 2009, “The acceleration of anomalous cosmic rays by stochastic acceleration in the heliosheath”, Adv. Space Res., 43, 1471–1478. [DOI], [ADS] (Cited on pages 27 and 48.)
Fisk, L.A. and Gloeckler, G., 2012, “Particle acceleration in the heliosphere: Implications for astrophysics”, Space Sci. Rev., 173, 433–458. [DOI], [ADS] (Cited on page 27.)
Fisk, L.A., Kozlovsky, B. and Ramaty, R., 1974, “An Interpretation of the observed oxygen and nitrogen enhancements in low-energy cosmic rays”, Astrophys. J., 190, L35–37. [DOI], [ADS] (Cited on page 11.)
Florinski, V., 2009, “Pickup Ion Acceleration at the Termination Shock and in the Heliosheath”, Space Sci. Rev., 143, 111–124. [DOI], [ADS] (Cited on page 12.)
Florinski, V., 2011, “On the transport of cosmic rays in the distant heliosheath”, Adv. Space Res., 48, 308–313. [DOI], [ADS] (Cited on page 9.)
Florinski, V. and Pogorelov, N.V., 2009, “Four-dimensional transport of galactic cosmic rays in the outer heliosphere and heliosheath”, Astrophys. J., 701, 642–651. [DOI], [ADS] (Cited on page 28.)
Florinski, V., Ferreira, S.E.S. and Pogorelov, N.V., 2011, “Galactic cosmic rays in the outer heliosphere: Theory and models”, Space Sci. Rev.. [DOI], [ADS] (Cited on page 8.)
Garcia-Munoz, M., Mason, G.M. and Simpson, J.A., 1973, “A new test for solar modulation theory: The 1972 May–July low-energy galactic cosmic-ray proton and helium spectra”, Astrophys. J., 182, L81–84. [DOI], [ADS] (Cited on page 11.)
Gervasi, M., Rancoita, P.G., Usoskin, I.G. and Kovaltsov, G.A., 1999, “Monte-Carlo approach to galactic cosmic ray propagation in the heliosphere”, Nucl. Phys. B (Proc. Suppl.), 78, 26–31. [DOI], [ADS] (Cited on page 28.)
Giacalone, J., 2011, “Cosmic-ray transport and interaction with shocks”, Space Sci. Rev.. [DOI], [ADS] (Cited on page 27.)
Giacalone, J. and Jokipii, J.R., 1994, “Charged-particle motion in multidimensional magnetic field turbulence”, Astrophys. J., 430, L137–L140. [DOI], [ADS] (Cited on page 26.)
Giacalone, J. and Jokipii, J.R., 1999, “The transport of cosmic rays across a turbulent magnetic field”, Astrophys. J., 520, 204–214. [DOI], [ADS] (Cited on page 26.)
Giacalone, J., Drake, J.F. and Jokipii, J.R., 2012, “The acceleration mechanism of anomalous cosmic rays”, Space Sci. Rev., 173, 283–307. [DOI], [ADS] (Cited on page 11.)
Gil, A., Iskra, K., Modzelewska, R. and Alania, M.V., 2005, “On the 27-day variations of the galactic cosmic ray anisotropy and intensity for different periods of solar magnetic cycle”, Adv. Space Res., 35, 687–690. [DOI], [ADS] (Cited on page 27.)
Gleeson, L.J. and Axford, W.I., 1967, “Cosmic Rays in the Interplanetary Medium”, Astrophys. J., 149, L115–118. [DOI], [ADS] (Cited on page 16.)
Gleeson, L.J. and Axford, W.I., 1968, “Solar modulation of galactic cosmic rays”, Astrophys. J., 154, 1011–1026. [DOI], [ADS] (Cited on page 16.)
Gloeckler, G., Fisk, L.A., Geiss, J., Hill, M.E., Hamilton, D.C., Decker, R.B. and Krimigis, S.M., 2009, “Composition of interstellar neutrals and the origin of anomalous cosmic rays”, Space Sci. Rev., 143, 163–175. [DOI], [ADS] (Cited on page 11.)
Haasbroek, L.J. and Potgieter, M.S., 1998, “A new model to study galactic cosmic ray modulation in an asymmetrically bounded heliosphere”, J. Geophys. Res., 103, 2099–2104. [DOI], [ADS] (Cited on pages 27 and 28.)
Hathaway, D.H., 2010, “The Solar Cycle”, Living Rev. Solar Phys., 7, lrsp-2010-1. [DOI], [ADS]. URL (accessed 8 February 2013): http://www.livingreviews.org/lrsp-2010-1 (Cited on page 8.)
Hattingh, M., Burger, R.A., Potgieter, M.S. and Haasbroek, L.J., 1997, “Cosmic ray latitudinal effects predicted by a three-dimensional drift model”, Adv. Space Res., 19, 839–896. [DOI], [ADS] (Cited on page 27.)
Heber, B., 2011, “Cosmic rays through the solar Hale cycle”, Space Sci. Rev.. [DOI], [ADS] (Cited on page 44.)
Heber, B. and Marsden, R.G., 2001, “Cosmic ray modulation over the poles at solar maximum: Observations”, Space Sci. Rev., 97, 309–319. [DOI], [ADS] (Cited on page 45.)
Heber, B. and Potgieter, M.S., 2006, “Cosmic rays at high heliolatitudes”, Space Sci. Rev., 127, 117–194. [DOI], [ADS] (Cited on pages 8, 10, 20, 21, 22, 23, 24, 31, 35, and 44.)
Heber, B. and Potgieter, M.S., 2008, “Galactic and anomalous cosmic rays through the solar cycle: New insights from Ulysses”, in The Heliosphere through the Solar Activity Cycle, (Eds.) Balogh, A., Lanzerotti, L.J., Suess, S.T., pp. 195–249, Springer; Praxis, Berlin; New York; Chichester (Cited on pages 10, 12, 20, 21, 23, 24, 31, 35, and 44.)
Heber, B., Wibberenz, G., Potgieter, M.S. et al., 2002, “Ulysses Cosmic Ray and Solar Particle Investigation/Kiel Electron Telescope observations: Charge sign dependence and latitudinal gradients during the 1990–2000 A > 0 solar magnetic cycle”, J. Geophys. Res., 107(A10), 1274. [DOI], [ADS] (Cited on pages 34, 38, and 39.)
Heber, B., Clem, J.M., Müller-Mellin, R., Kunow, H., Ferreira, S.E.S. and Potgieter, M.S., 2003, “Evolution of the galactic cosmic ray electron to proton ratio: Ulysses COSPIN/KET observations”, Geophys. Res. Lett., 30(19), 8032. [DOI], [ADS] (Cited on pages 34, 38, and 39.)
Heber, B., Kopp, A., Gieseler, J., Müller-Mellin, R., Fichtner, H., Scherer, K., Potgieter, M.S. and Ferreira, S.E.S., 2009, “Modulation of galactic cosmic ray protons and electrons during an unusual solar minimum”, Astrophys. J., 699, 1956–1963. [DOI], [ADS] (Cited on pages 34 and 42.)
Hoeksema, J.T., 1992, “Large scale structure of the heliospheric magnetic field: 1976–1991”, in Solar Wind Seven, Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, (Eds.) Marsch, E., Schwenn, R., COSPAR Colloquia Series, 3, pp. 191–197, Pergamon Press, Oxford; New York. [ADS] (Cited on pages 9 and 23.)
Hovestadt, D., Vollmer, O., Gloeckler, G. and Fan, C.Y., 1973, “Measurement of Elemental Abundance of Very Low Energy Solar Cosmic Rays”, in 13th International Cosmic Ray Conference, Vol. 2, Proceedings of the conference held in Denver, Colorado, 17–30 August 1973, pp. 1498–1501, University of Denver, Denver. [ADS] (Cited on page 11.)
Jiang, J., Cameron, R., Schmitt, D. and Schussler, M., 2010, “Modeling the Sun’s open magnetic flux and the heliospheric current sheet”, Astrophys. J., 709, 301–307. [DOI], [ADS], [arXiv:0912.0108] (Cited on page 47.)
Jokipii, J.R., 1973, “Radial Variation of Magnetic Fluctuations and the Cosmic-Ray Diffusion Tensor in the Solar Wind”, Astrophys. J., 182, 585–600. [DOI], [ADS] (Cited on page 20.)
Jokipii, J.R., 1986, “Particle acceleration at a termination shock. I. Application to the solar wind and the anomalous component”, J. Geophys. Res., 91, 2929–2932. [DOI], [ADS] (Cited on pages 24 and 27.)
Jokipii, J.R., 1996, “Theory of multiply charged anomalous cosmic rays”, Astrophys. J., 466, L47–L50. [DOI], [ADS] (Cited on page 11.)
Jokipii, J.R., 2012, “The heliospheric termination shock”, Space Sci. Rev.. [DOI], [ADS] (Cited on page 8.)
Jokipii, J.R. and Kopriva, D.A., 1979, “Effects of particle drift on the transport of cosmic rays. III. Numerical models ofgalactic cosmic-ray modulation”, Astrophys. J., 234, 384–392. [DOI], [ADS] (Cited on pages 22, 27, and 44.)
Jokipii, J.R. and Thomas, B., 1981, “Effects of drift on the transport of cosmic rays. IV. Modulation by a wavy interplanetary current sheet”, Astrophys. J., 243, 1115–1122. [DOI], [ADS] (Cited on pages 22 and 27.)
Jokipii, J.R., Levy, E.H. and Hubbard, W.B., 1977, “Effects of particle drift on cosmic-ray transport. I — General properties, application to solar modulation”, Astrophys. J., 213, 861–868. [DOI], [ADS] (Cited on page 22.)
Kane, R.P., 2011, “Hysteresis of cosmic rays with respect to sunspot numbers during the recent sunspot minimum”, Solar Phys., 269, 451–454. [DOI], [ADS] (Cited on page 42.)
Kopp, A., Büsching, I., Strauss, R.D. and Potgieter, M.S., 2012, “A stochastic differential equation code for multidimensional Fokker-Planck type problems”, Comput. Phys. Commun., 183, 530–542. [DOI], [ADS] (Cited on page 28.)
Kóta, J., 2012, “Theory and Modeling of Galactic Cosmic Rays: Trends and Prospects”, Space Sci. Rev.. [DOI], [ADS] (Cited on pages 9, 17, 23, and 49.)
Kóta, J. and Jokipii, J.R., 1983, “Effects of drift on the transport of cosmic rays. VI. A three-dimensional model including diffusion”, Astrophys. J., 265, 573–581. [ADS] (Cited on pages 22 and 27.)
Kóta, J. and Jokipii, J.R., 2008, “Anomalous Cosmic Rays in the Heliosheath: Simulation with a Blunt Termination Shock”, in Particle Acceleration and Transport in the Heliosphere and Beyond, 7th Annual International Astrophysics Conference, Kauai, Hawaii, 7–13 March 2008, (Eds.) Li, G., Hu, Q., Verkhoglyadova, O., Zank, G.P., Lin, R.P., Luhmann, J., AIP Conference Proceedings, 1039, pp. 397–403, American Institute of Physics, Melville, NY. [DOI], [ADS] (Cited on page 48.)
Krimigis, S.M., Roelof, E.C., Decker, R.B. and Hill, M.E., 2011, “Zero outflow velocity for a plasma in a heliosheath transition layer”, Nature, 474, 359–361. [DOI] (Cited on page 10.)
Krymsky, G.F., Krivoshapkin, P.A., Gerasimova, S.K., Gololobov, P.Y., Grigor’ev, V.G. and Starodubtsev, S.A., 2012, “Heliospheric modulation of cosmic rays in solar cycles 19–23”, Astron. Lett., 38, 609–612. [DOI], [ADS] (Cited on pages 23 and 42.)
Langner, U.W. and Potgieter, M.S., 2004a, “Solar wind termination shock and heliosheath effects on the modulation of protons and antiprotons”, J. Geophys. Res., 109, A01103. [DOI], [ADS] (Cited on pages 28, 33, 36, and 39.)
Langner, U.W. and Potgieter, M.S., 2004b, “Effects of the solar wind termination shock on charge-sign dependent cosmic ray modulation”, Adv. Space Res., 34, 144–149. [DOI], [ADS] (Cited on pages 28 and 33.)
Langner, U.W. and Potgieter, M.S., 2005, “Modulation of galactic protons in an asymmetrical heliosphere”, Astrophys. J., 630, 1114–1124. [DOI], [ADS] (Cited on page 47.)
Langner, U.W., de Jager, O.C. and Potgieter, M.S., 2001, “On the local interstellar spectrum for cosmic ray electrons”, Adv. Space Res., 27, 517–522. [DOI], [ADS] (Cited on page 13.)
Langner, U.W., Potgieter, M.S. and Webber, W.R., 2003, “Modulation of cosmic ray protons in the heliosheath”, J. Geophys. Res., 108(A10), 8039. [DOI], [ADS] (Cited on pages 39, 40, and 41.)
Langner, U.W., Potgieter, M.S., Fichtner, H. and Borrmann, T., 2006a, “Effects of different solar wind speed profiles in the heliosheath on the modulation of cosmic-ray protons”, Astrophys. J., 640, 1119–1134. [DOI], [ADS] (Cited on pages 17 and 40.)
Langner, U.W., Potgieter, M.S., Fichtner, H. and Borrmann, T., 2006b, “Modulation of anomalous protons: Effects of different solar wind speed profiles in the heliosheath”, J. Geophys. Res., 111, A01106. [DOI], [ADS] (Cited on pages 16 and 40.)
Laurenza, M., Vecchio, A., Storini, M. and Carbone, V., 2012, “Quasi-biennial modulation of galactic cosmic rays”, Astrophys. J., 749, 167. [ADS] (Cited on page 15.)
Lazarian, A. and Opher, M., 2009, “A model of acceleration of anomalous cosmic rays by reconnection in the heliosheath”, Astrophys. J., 703, 8–21. [DOI], [ADS] (Cited on page 48.)
Lazarian, A., Vlahos, L., Kowal, G., Yan, H., Beresnyak, A. and de Gouveia Dal Pino, E.M., 2012, “Turbulence, magnetic reconnection in turbulent fluids and energetic particle acceleration”, Space Sci. Rev., 173, 557–622. [DOI], [ADS] (Cited on page 27.)
le Roux, J.A. and Fichtner, H., 1999, “Global merged interaction regions, the heliospheric termination shock, and time-dependent cosmic ray modulation”, J. Geophys. Res., 104, 4709–4730. [DOI], [ADS] (Cited on page 37.)
Le Roux, J.A. and Potgieter, M.S., 1990, “A time-dependent drift model for the long-term modulation of cosmic rays with special reference to asymmetries with respect to the solar minimum of1987”, Astrophys. J., 361, 275–282. [DOI], [ADS] (Cited on page 27.)
Le Roux, J.A. and Potgieter, M.S., 1995, “The simulation of complete 11 and 12 year modulation cycles for cosmic rays in the heliosphere using a drift model with global merged interaction regions”, Astrophys. J., 442, 847–851. [DOI], [ADS] (Cited on pages 14 and 37.)
Le Roux, J.A., Potgieter, M.S. and Ptuskin, V.S., 1996, “A transport model for the diffusive shock acceleration and modulation of anomalous cosmic rays in the heliosphere”, J. Geophys. Res., 101, 4791–4803. [DOI], [ADS] (Cited on page 28.)
Lee, M.A., Mewaldt, R.A. and Giacalone, J., 2012, “Shock acceleration of ions in the heliosphere”, Space Sci. Rev., 173, 247–281. [DOI], [ADS] (Cited on page 27.)
Leske, R.A., Cummings, A.C., Mewaldt, R.A. and Stone, E.C., 2011, “Anomalous and galactic cosmic rays at 1 AU during the cycle 23/24 solar minimum”, Space Sci. Rev.. [DOI], [ADS] (Cited on page 11.)
Levy, E.H., 1976, “The interplanetary magnetic field structure”, Nature, 261, 394–395. [DOI], [ADS] (Cited on page 23.)
Linde, T.J., Gombosi, T.I., Roe, P.L., Powell, K.G. and DeZeeuw, D.L., 1998, “Heliosphere in the magnetized local interstellar medium: Results of a three-dimensional MHD simulation”, J. Geophys. Res., 103, 1889–1904. [DOI], [ADS] (Cited on page 7.)
Manuel, R., Ferreira, S.E.S. and Potgieter, M.S., 2011a, “Cosmic ray modulation in the outer heliosphere: Predictions for cosmic ray intensities up to the heliopause along Voyager 1 and 2 trajectories”, Adv. Space Res., 48, 874–883. [DOI], [ADS] (Cited on pages 38 and 49.)
Manuel, R., Ferreira, S.E.S., Potgieter, M.S., Strauss, R.D. and Engelbrecht, N.E., 2011b, “Time-dependent cosmic ray modulation”, Adv. Space Res., 47, 1529–1537. [DOI], [ADS] (Cited on pages 38 and 49.)
Matthaeus, W.H. and Velli, M., 2011, “Who needs turbulence? A review of turbulence effects in the heliosphere and on the fundamental process of reconnection”, Space Sci. Rev., 160, 145–168. [DOI], [ADS] (Cited on page 27.)
Matthaeus, W.H., Qin, G., Bieber, J.W. and Zank, G.P., 2003, “Nonlinear collisionless perpendicular diffusion of charged particles”, Astrophys. J., 590, L53–L56. [DOI], [ADS] (Cited on page 27.)
McComas, D.J. and Schwadron, N.A., 2006, “An explanation of the Voyager paradox: Particle acceleration at a blunt termination shock”, Geophys. Res. Lett., 33, L04102. [DOI], [ADS] (Cited on page 48.)
McComas, D.J., Allegrini, F., Bochsler, P. et al., 2009, “Global observations of the interstellar interaction from the Interstellar Boundary Explorer (IBEX)”, Science, 326, 959–962. [DOI], [ADS] (Cited on page 7.)
McComas, D.J., Alexashov, D., Bzowski, M. et al., 2012a, “The heliosphere’s interstellar interaction: no bow shock”, Science, 336, 1291. [DOI], [ADS] (Cited on page 7.)
McComas, D.J., Dayeh, M.A., Allegrini, F. et al., 2012b, “The first three years of IBEX observations and our evolving heliosphere”, Astrophys. J. Suppl. Ser., 203, 1. [DOI], [ADS] (Cited on page 7.)
McCracken, K.G. and Beer, J., 2007, “Long-term changes in the cosmic ray intensity at Earth, 1428–2005”, J. Geophys. Res., 112, A10101. [DOI], [ADS] (Cited on page 15.)
McCracken, K.G., Beer, J., Steinhilber, F. and Abreu, J., 2011, “The heliosphere in time”, Space Sci. Rev.. [DOI], [ADS] (Cited on pages 15 and 41.)
McDonald, F.B., Heikkila, B.C., Lal, N. and Stone, E.C., 2000, “The relative recovery of galactic and anomalous cosmic rays in the distant heliosphere: Evidence for modulation in the heliosheath”, J. Geophys. Res., 105, 1. [DOI], [ADS] (Cited on page 11.)
McDonald, F.B., Stone, E.C., Cummings, A.C., Heikkila, B.C., Lal, N. and Webber, W.R., 2003, “Enhancements of energetic particles near the heliospheric termination shock”, Nature, 426, 48–51. [DOI], [ADS] (Cited on page 11.)
McDonald, F.B., Webber, W.R. and Reames, D.V., 2010, “Unusual time histories of galactic and anomalous cosmic rays at 1 AU over the deep solar minimum of cycle 23/24”, Geophys. Res. Lett., 37, L18101. [DOI], [ADS] (Cited on pages 11 and 42.)
McKibben, R.B., 2005, “Cosmic-ray diffusion in the inner heliosphere”, Adv. Space Res.,35, 518–531. [DOI], [ADS] (Cited on page 24.)
McKibben, R.B., Connell, J.J., Lopate, C., Simpson, J.A. and Zhang, M., 1996, “Observations of galactic cosmic rays and the anomalous helium during ULYSSES passage from the south to the north solar pole”, Astron. Astrophys., 316, 547–554. [ADS] (Cited on page 44.)
Mewaldt, R.A., 2012, “Cosmic rays in the heliosphere: requirements for future observations”, Space Sci. Rev.. [DOI], [ADS] (Cited on pages 11, 42, 45, and 49.)
Mewaldt, R.A., Cummings, J.R., Leske, R.A., Selesnick, R.S., Stone, E.C. and von Rosenvinge, T.T., 1996a, “A study of the composition and energy spectra of anomalous cosmic rays using the geomagnetic field”, Geophys. Res. Lett., 23, 617–620. [DOI], [ADS] (Cited on page 11.)
Mewaldt, R.A., Selesnick, R.S., Cummings, J.R., Stone, E.C. and von Rosenvinge, T.T., 1996b, “Evidence for multiply charged anomalous cosmic rays”, Astrophys. J., 466, L43–L46. [DOI], [ADS] (Cited on page 11.)
Mewaldt, R.A., Davis, A.J., Lave, K.A. et al., 2010, “Record-setting cosmic-ray intensities in 2009 and 2010”, Astrophys. J. Lett., 273, L1–L6. [DOI], [ADS] (Cited on page 42.)
Moeketsi, D.M., Potgieter, M.S., Ferreira, S.E.S., Heber, B., Fichtner, H. and Henize, V.K., 2005, “The heliospheric modulation of 3–10 MeV electrons: Modeling of changes in the solar wind speed in relation to perpendicular polar diffusion”, Adv. Space Res., 35, 597–604. [DOI], [ADS] (Cited on pages 21 and 48.)
Moraal, H., 2011, “Cosmic-Ray Modulation Equations”, Space Sci. Rev.. [DOI], [ADS] (Cited on page 16.)
Moraal, H., Gleeson, L.J. and Webb, G.M., 1979, “Effects of Charged Particle Drifts on the Modulation of the Intensity of Galactic Cosmic Rays”, in 16th International Cosmic Ray Conference, Vol. 3, Proceedings of the conference held in Kyoto, 6–18 August 1979, (Ed.) Miyake, S., pp. 1–4, University of Tokyo, Tokyo. [ADS] (Cited on page 27.)
Moraal, H., Potgieter, M.S. and Stoker, P.H. van der Walt, A.J., 1989, “Neutron monitor latitude survey of cosmic ray intensity during the 1986/1987 solar minimum”, J. Geophys. Res., 94, 1459–1464. [DOI], [ADS] (Cited on page 23.)
Moskalenko, I.V., Strong, A.W., Ormes, J.F. and Potgieter, M.S., 2002, “Secondary antiprotons and propagation of cosmic rays in the galaxy and heliosphere”, Astrophys. J., 565, 280–296. [DOI], [ADS] (Cited on pages 13, 14, and 33.)
Munini, R., 2011, Time dependence of the cosmic-ray electron and positron spectra measured by PAMELA experiment during the last solar minimum, Master’s thesis, University of Trieste, Trieste (Cited on page 35.)
Ndiitwani, D.C., Ferreira, S.E.S., Potgieter, M.S. and Heber, B., 2005, “Modeling cosmic ray intensities along the Ulysses trajectory”, Ann. Geophys., 23, 1061–1070. [DOI], [ADS] (Cited on pages 21, 39, and 40.)
Ngobeni, M.D. and Potgieter, M.S., 2008, “Cosmic ray anisotropies in the outer heliosphere”, Adv. Space Res., 41, 373–380. [DOI], [ADS] (Cited on page 21.)
Ngobeni, M.D. and Potgieter, M.S., 2010, “The heliospheric modulation of cosmic rays: Effects of a latitude dependent solar wind termination shock”, Adv. Space Res., 46, 391–401. [DOI], [ADS] (Cited on pages 24 and 25.)
Ngobeni, M.D. and Potgieter, M.S., 2011, “Modulation of galactic cosmic rays in a north-south asymmetrical heliosphere”, Adv. Space Res., 48, 300–307. [DOI], [ADS] (Cited on pages 7, 21, and 47.)
Ngobeni, M.D. and Potgieter, M.S., 2012, “Modelling of galactic Carbon in an asymmetrical heliosphere: Effects of asymmetrical modulation conditions”, Adv. Space Res., 49, 1660–1669. [DOI], [ADS] (Cited on page 7.)
Nkosi, G.S., Potgieter, M.S. and Ferreira, S.E.S., 2008, “Electron anisotropies in the inner heliosphere”, Planet. Space Sci., 56, 501–509. [DOI], [ADS] (Cited on pages 21 and 24.)
Nkosi, G.S., Potgieter, M.S. and Webber, W.R., 2011, “Modelling of low-energy galactic electrons in the heliosheath”, Adv. Space Res., 48, 1480–1489. [DOI], [ADS] (Cited on pages 14 and 45.)
Opher, M., Alouani Bibi, F., Toth, G., Richardson, J.D., Izmodenov, V.V. and Gombosi, T.I., 2009a, “A strong, highly-tilted interstellar magnetic field near the solar system”, Nature, 462, 1035–1038. [DOI], [ADS] (Cited on page 6.)
Opher, M., Richardson, J.D., Toth, G. and Gombosi, T.I., 2009b, “Confronting observations and modeling: The role of the interstellar magnetic field in Voyager 1 and 2 asymmetries”, Space Sci. Rev., 143, 43–55. [DOI], [ADS] (Cited on page 7.)
Parker, E.N., 1958, “Dynamics of the interplanetary gas and magnetic fields”, Astrophys. J., 128, 664–676. [DOI], [ADS] (Cited on page 8.)
Parker, E.N., 1965, “The passage of energetic charged particles through interplanetary space”, Planet. Space Sci., 13, 9–49. [DOI], [ADS] (Cited on page 16.)
Parker, E.N., 2001, “A history of early work on the heliospheric magnetic field”., J. Geophys. Res., 106, 15 797–15 801. [DOI], [ADS] (Cited on page 8.)
Pei, C., Bieber, J.W., Breech, B., Burger, R.A., Clem, J. and Matthaeus, W.H., 2010, “Cosmic ray diffusion tensor throughout the heliosphere”, J. Geophys. Res., 115, A03103. [DOI], [ADS] (Cited on page 27.)
Perko, J.S. and Fisk, L.A., 1983, “Solar modulation of galactic cosmic rays. 5. Time-dependent modulation”, J. Geophys. Res., 88, 9033. [DOI], [ADS] (Cited on page 27.)
Pesses, M.E., Jokipii, J.R. and Eichler, D., 1981, “Cosmic ray drift, shock wave acceleration and the anomalous component of cosmic rays”, Astrophys. J., 246, L85–L88. [DOI], [ADS] (Cited on page 11.)
Petrovay, K. and Christensen, U.R., 2010, “The magnetic sun: reversals and long-term variations”, Space Sci. Rev., 155, 371–385. [DOI], [ADS] (Cited on page 8.)
Pogorelov, N.V., Heerikhuisen, J., Zank, G.P. and Borovikov, S.N., 2009a, “Influence of the interstellar magnetic field and neutrals on the shape of the outer heliosphere”, Space Sci. Rev., 143, 31–42. [DOI], [ADS] (Cited on page 7.)
Pogorelov, N.V., Heerikhuisen, J., Zank, G.P., Mitchell, J.J. and Cairns, I.H., 2009b, “Heliospheric asymmetries due to the action of the interstellar magnetic field”, Adv. Space Res., 44, 1337–1344. [DOI], [ADS] (Cited on page 6.)
Potgieter, M.S., 1989, “Heliospheric terminal shock acceleration and modulation of the anomalous cosmic-ray component”, Adv. Space Res., 9, 21. [DOI], [ADS] (Cited on page 27.)
Potgieter, M.S., 1995, “The long-term modulation of galactic cosmic rays in the heliosphere”, Adv. Space Res., 16, 191–203. [DOI], [ADS] (Cited on page 37.)
Potgieter, M.S., 1996, “The heliospheric modulation of galactic electrons: Consequences of new calculations for the mean free path of electrons between 1 MeV and ∼ 10 GeV”, J. Geophys. Res., 101(A11), 24411–24 422. [DOI], [ADS] (Cited on page 21.)
Potgieter, M.S., 1997, “The heliospheric modulation of galactic cosmic rays at solar minimum”, Adv. Space Res., 19, 883–892. [DOI], [ADS] (Cited on page 37.)
Potgieter, M.S., 2000, “The heliospheric modulation of cosmic ray protons: role of enhanced perpendicular diffusion during periods of minimum solar modulation”, J. Geophys. Res., 105, 18,295–18,304. [DOI], [ADS] (Cited on pages 20 and 21.)
Potgieter, M.S., 2008, “Challenges to cosmic ray modeling: From beyond the solar wind termination shock”, Adv. Space Res., 41, 245–258. [DOI], [ADS] (Cited on pages 12, 41, and 48.)
Potgieter, M.S., 2011, “Cosmic Rays in the Inner Heliosphere: Insights from Observations, Theory and Models”, Space Sci. Rev.. [DOI], [ADS] (Cited on pages 23 and 35.)
Potgieter, M.S., 2013, “The charge-sign dependent effect in the solar modulation of cosmic rays”, Adv. Space Res.. [DOI] (Cited on pages 22, 23, and 31.)
Potgieter, M.S. and Ferreira, S.E.S., 2001, “Modulation of cosmic rays in the heliosphere over 11 and 22 year cycles: A modelling perspective”, Adv. Space Res., 27, 481–492. [DOI], [ADS] (Cited on page 37.)
Potgieter, M.S. and Ferreira, S.E.S., 2002, “Effects of the solar wind termination shock on the modulation of Jovian and galactic electrons in the heliosphere”, J. Geophys. Res., 107(A7), 1089. [DOI], [ADS] (Cited on page 13.)
Potgieter, M.S. and Langner, U.W., 2004a, “Heliospheric modulation of cosmic ray positrons and electrons: Effects of the heliosheath and solar wind termination shock”, Astrophys. J., 602, 993–1001. [DOI], [ADS] (Cited on pages 13, 24, and 33.)
Potgieter, M.S. and Langner, U.W., 2004b, “The heliospheric modulation of cosmic ray boron and carbon”, Ann. Geophys., 22, 3729–3740. [DOI], [ADS] (Cited on page 33.)
Potgieter, M.S. and le Roux, J.A., 1989, “More on a possible modulation barrier in the outer heliosphere”, Adv. Space Res., 9, 121–124. [DOI], [ADS] (Cited on page 37.)
Potgieter, M.S. and le Roux, J.A., 1992, “The simulated features of heliospheric cosmic-ray modulation with a time-dependent drift model. I. General effects of the changing neutral sheet over the period 1985–1990”, Astrophys. J., 386, 336–346. [DOI], [ADS] (Cited on page 14.)
Potgieter, M.S. and Moraal, H., 1985, “A drift model for the modulation of galactic cosmic rays”, Astrophys. J., 294, 425–440. [DOI], [ADS] (Cited on pages 22, 23, 24, 27, 31, and 32.)
Potgieter, M.S. and Moraal, H., 1988, “Acceleration of cosmic rays in the solar wind termination shock. A steady state technique in a spherically symmetric model”, Astrophys. J., 330, 445–455. [DOI], [ADS] (Cited on page 27.)
Potgieter, M.S. and Nndanganeni, R.R., 2013a, “The solar modulation of electrons in the heliosphere”, Astrophys. Space Sci., 345, 33–40. [DOI], [ADS] (Cited on pages 35 and 48.)
Potgieter, M.S. and Nndanganeni, R.R., 2013b, “A local interstellar spectrum for galactic electrons”, ar Xiv, e-print. [ADS], [arXiv:1302.2424 [astro-ph.HE]] (Cited on page 13.)
Potgieter, M.S., Moraal, H., Raubenheimer, B.C. and Stoker, P.H., 1980, “Modulation of cosmic rays during solar minimum. III. Comparison for the periods of solar minimum during 1954, 1965 and 1976”, S. Afr. J. Phys., 3, 90–94. [ADS] (Cited on page 23.)
Potgieter, M.S., le Roux, J.A. and Burger, R.A., 1989, “Interplanetary cosmic ray radial gradients with steady state modulation models”, J. Geophys. Res., 94, 2323–2332. [DOI], [ADS] (Cited on page 21.)
Potgieter, M.S., le Roux, J.A., Burlaga, L.F. and McDonald, F.B., 1993, “The role of merged interaction regions and drifts in the heliospheric modulation of cosmic rays beyond 20 AU: A computer simulation”, Astrophys. J., 403, 760–768. [DOI], [ADS] (Cited on pages 27 and 37.)
Potgieter, M.S., Burger, R.A. and Ferreira, S.E.S., 2001, “Modulation of cosmic rays in the heliosphere from solar minimum to maximum: a theoretical perspective”, Space Sci. Rev., 97, 295–307. [DOI], [ADS] (Cited on pages 24, 26, and 31.)
Potgieter, M.S., Vos, E.E., Boezio, M., De Simone, N., Di Felice, V. and Formato, V., 2013, “Modulation of Galactic Protons in the Heliosphere During the Unusual Solar Minimum of 2006 to 2009”, Solar Phys.. [DOI], [ADS], [arXiv:1302.1284 [astro-ph.SR]] (Cited on pages 20, 24, 28, and 43.)
Ptuskin, V.S., Moskalenko, I.V., Jones, F.C., Strong, A.W. and Zirakashvili, V.N., 2006, “Dissipation of magnetohydrodynamic waves on energetic particles: Impact on interstellar turbulence and cosmic-ray transport”, Astrophys. J., 642, 902–916. [DOI], [ADS] (Cited on page 13.)
Qin, G. and Shalchi, A., 2012, “Numerical investigation of the influence of large turbulence scales on the parallel and perpendicular transport of cosmic rays”, Adv. Space Res., 49, 1643–1652. [DOI], [ADS] (Cited on page 26.)
Quenby, J.J., 1984, “The theory of cosmic-ray modulation”, Space Sci. Rev., 37, 201–267. [DOI], [ADS] (Cited on pages 16 and 31.)
Ratkiewicz, R., Barnes, A., Molvik, G.A., Spreiter, J.R., Stahara, S.S. and Vinokur, M., 1998, “Effect of varying strength and orientation of local interstellar magnetic field on configuration of exterior heliosphere: 3D MHD simulations”, Astron. Astrophys., 335, 363–369. [ADS] (Cited on page 7.)
Reinecke, J.P.L. and Potgieter, M.S., 1994, “An explanation for the difference in cosmic ray modulation at low and neutron monitor energies during consecutive solar minimum periods”, J. Geophys. Res., 99, 14,761–14,767. [DOI], [ADS] (Cited on page 24.)
Richardson, J.D. and Burlaga, L.F., 2011, “The Solar Wind in the Outer Heliosphere and Heliosheath”, Space Sci. Rev.. [DOI], [ADS] (Cited on pages 8 and 10.)
Richardson, J.D. and Stone, E.C., 2009, “The solar wind in the outer heliosphere”, Space Sci. Rev., 143, 7–20. [DOI], [ADS] (Cited on page 10.)
Richardson, J.D. and Wang, C., 2011, “Plasma in the heliosheath: 3.5 years of observations”, Astrophys. J., 734, L21–25. [DOI], [ADS] (Cited on pages 5 and 10.)
Richardson, J.D., Kasper, J.C., Wang, C., Belcher, J.W. and Lazarus, A.J., 2008, “Cool heliosheath plasma and deceleration of the upstream solar wind at the termination shock”, Nature, 454, 63–66. [DOI], [ADS] (Cited on pages 10 and 14.)
Roberts, J.P., 2011, “PAMELA through a magnetic lens”, J. Cosmol. Astropart. Phys., 29, 1–13. [DOI], [ADS] (Cited on page 28.)
Scherer, K., Fichtner, H., Borrmann, T. et al., 2006, “Interstellar-terrestrial relations: Variable cosmic environments, the dynamic heliosphere, and their imprints on terrestrial archives and climate”, Space Sci. Rev., 127, 327–465. [DOI], [ADS] (Cited on pages 15 and 49.)
Scherer, K., Fichtner, H., Ferreira, S.E.S., Buüsching, I. and Potgieter, M.S., 2008a, “Are Anomalous Cosmic Rays the Main Contribution to the Low-Energy Galactic Cosmic Ray Spectrum?”, Astrophys. J. Lett., 680, L105–L108. [DOI], [ADS] (Cited on page 11.)
Scherer, K., Fichtner, H., Heber, B., Ferreira, S.E.S. and Potgieter, M.S., 2008b, “Cosmic ray flux at the Earth in a variable heliosphere”, Adv. Space Res., 41, 1171–1176. [DOI], [ADS] (Cited on page 41.)
Scherer, K., Fichtner, H., Strauss, R.D., Ferreira, S.E.S., Potgieter, M.S. and Fahr, H.-J., 2011, “On Cosmic Ray Modulation beyond the Heliopause: Where is the Modulation Boundary?”, Astrophys. J., 735, 128. [DOI], [ADS] (Cited on page 7.)
Schlickeiser, R., 2002, Cosmic Ray Astrophysics, Springer, Berlin; New York. [ADS], [Google Books] (Cited on pages 16, 17, and 27.)
Seo, E.S., 2012, “Direct measurements of cosmic rays using balloon borne experiments”, Astropart. Phys., 39, 76–87. [DOI], [ADS] (Cited on page 31.)
Shalchi, A., 2009, Nonlinear Cosmic Ray Diffusion Theories, Astrophysics and Space Science Library, 362, Springer, Berlin. [DOI], [ADS], [Google Books] (Cited on page 27.)
Shea, M.A. and Smart, D.F., 2012, “Space weather and the ground-level solar proton events of the 23rd solar cycle”, Space Sci. Rev., 171, 161–188. [DOI], [ADS] (Cited on page 5.)
Smith, C.W. and Bieber, J.W., 1991, “Solar cycle variation of the interplanetary magnetic field spiral”, Astrophys. J., 370, 435–441. [DOI], [ADS] (Cited on pages 8 and 21.)
Smith, E.J., 2001, “The heliospheric current sheet”, J. Geophys. Res., 106, 15819–15832. [DOI], [ADS] (Cited on page 9.)
Smith, E.J., Jokipii, J.R., Koota, J., Lepping, R.P. and Szabo, A., 2000, “Evidence of a north-south asymmetry in the heliosphere associated with a southward displacement of the heliospheric current sheet”, Astrophys. J., 533, 1084–1089. [DOI], [ADS] (Cited on page 44.)
Sparvoli, R. et al. [PAMELA Collaboration], 2012, “Main results from the PAMELA space experiment after five years in flight”, Nucl. Instrum. Methods A, 692, 29–33. [DOI], [ADS] (Cited on pages 31, 35, and 42.)
Steenberg, C.D. and Moraal, H., 1996, “An acceleration/modulation model for anomalous cosmic-ray hydrogen in the heliosphere”, Astrophys. J., 463, 776–783. [DOI], [ADS] (Cited on page 28.)
Sternal, O., Engelbrecht, N.E., Burger, R.A. et al., 2011, “Possible Evidence for a Fisk-type Heliospheric Magnetic Field: I. Analyzing Ulysses/KET Electron Observations”, Astrophys. J., 741, 23. [DOI], [ADS] (Cited on pages 8 and 48.)
Stone, E.C., Cummings, A.C., McDonald, F.B., Heikkila, B.C., Lal, N. and Webber, W.R., 2005, “Voyager 1 explores the termination shock region and the heliosheath beyond”, Science, 309, 2017–2020. [DOI], [ADS] (Cited on pages 5, 11, and 12.)
Stone, E.C., Cummings, A.C., McDonald, F.B., Heikkila, B.C., Lal, N. and Webber, W.R., 2008, “An asymmetric solar wind termination shock”, Nature, 454, 71–74. [DOI], [ADS] (Cited on pages 5 and 11.)
Storini, M., Bazilevskaya, G.A., Flückiger, E.O., Krainev, M.B., Makhmutov, V.S. and Sladkova, A.I., 2003, “The Gnevyshev gap: A review for space weather”, Adv. Space Res., 31, 895–900. [DOI], [ADS] (Cited on page 15.)
Stozhkov, Y.I., Svirzhevsky, N.S., Bazilevskaya, G.A., Kvashnin, A.N., Makhmutov, V.S. and Svirzhevskaya, A.K., 2009, “Long-term (50 years) measurements of cosmic ray fluxes in the atmosphere”, Adv. Space Res., 44, 124–1137. [DOI], [ADS] (Cited on page 42.)
Strauss, R.D. and Potgieter, M.S., 2010, “Modelling anomalous cosmic ray oxygen gradients over successive solar cycles”, J. Geophys. Res., 115, A12111. [DOI], [ADS] (Cited on page 11.)
Strauss, R.D., Potgieter, M.S. and Ferreira, S.E.S., 2010a, “The heliospheric transport and modulation of multiple charged anomalous Oxygen revisited”, Astron. Astrophys., 513, A24. [DOI], [ADS] (Cited on pages 11, 17, 23, and 48.)
Strauss, R.D., Potgieter, M.S., Ferreira, S.E.S. and Hill, M.E., 2010b, “Modelling anomalous cosmic ray oxygen in the heliosheath”, Astron. Astrophys., 522, A35. [DOI], [ADS] (Cited on pages 16, 17, and 23.)
Strauss, R.D., Potgieter, M.S., Buüsching, I. and Kopp, A., 2011a, “Modeling the modulation of galactic and Jovian electrons by stochastic processes”, Astrophys. J., 735, 83. [DOI], [ADS] (Cited on pages 24, 28, and 30.)
Strauss, R.D., Potgieter, M.S. and Ferreira, S.E.S., 2011b, “Modeling the acceleration and modulation of anomalous cosmic ray oxygen”, Adv. Space Res., 48, 65–75. [DOI], [ADS] (Cited on page 23.)
Strauss, R.D., Potgieter, M.S., Kopp, A. and Buüsching, I., 2011c, “On the propagation times and energy losses of cosmic rays in the heliosphere”, J. Geophys. Res., 116, A12105. [DOI], [ADS] (Cited on pages 24 and 28.)
Strauss, R.D., Potgieter, M.S., Boezio, M., De Simone, N., Di Felice, V., Kopp, A. and Buüsching, I., 2012a, “The heliospheric transport of protons and anti-protons: A stochastic modelling approach of PAMELA observations”, in Astroparticle, Particle, Space Physics and Detectors for Physics Applications, Proceedings of the 13th ICATPP Conference, Villa Olmo, Como, Italy, 3–7 October, 2011, (Eds.) Giani, S., Leroy, C., Price, L., Rancoita, P.-G., Ruchti, R., Astroparticle, Particle, Space Physics, Radiation Interaction, Detectors and Medical Physics Applications, 7, pp. 288–296, World Scientific, Singapore; Hackensack, NJ (Cited on page 33.)
Strauss, R.D., Potgieter, M.S. and Ferreira, S.E.S., 2012b, “Modeling ground and space based cosmic ray observations”, Adv. Space Res., 49, 392–407. [DOI], [ADS] (Cited on page 31.)
Strauss, R.D., Potgieter, M.S., Kopp, A. and Buüsching, I., 2012c, “Modelling heliospheric current sheet drift in stochastic cosmic ray transport models”, Astrophys. Space Sci., 339, 223–236. [DOI], [ADS] (Cited on pages 28, 29, and 30.)
Strauss, R.D., Potgieter, M.S. and Ferreira, S.E.S., 2013a, “Modelling and observing Jovian electron propagation times in the inner heliosphere”, Adv. Space Res., 51, 339–349. [DOI], [ADS] (Cited on pages 28 and 48.)
Strauss, R.D., Potgieter, M.S., Ferreira, S.E.S., Fichtner, H. and Scherer, K., 2013b, “Cosmic Ray Modulation Beyond the Heliopause: A Hybrid Modeling Approach”, Astrophys. J. Lett., 765, L18. [DOI], [ADS] (Cited on pages 7 and 40.)
Strong, A.W., Moskalenko, I.V. and Ptuskin, V.S., 2007, “Cosmic-ray propagation and interactions in the galaxy”, Annu. Rev. Nucl. Part. Sci., 57, 285–327. [DOI], [ADS] (Cited on pages 13 and 33.)
Strong, A.W., Orlando, E. and Jaffe, T.R., 2011, “The interstellar cosmic-ray electron spectrum from synchrotron radiation and direct measurements”, Astron. Astrophys., 534, A54. [DOI], [ADS], [arXiv:1108.4822 [astro-ph.HE]] (Cited on page 13.)
Tautz, R.C. and Shalchi, A., 2012, “Drift coefficients of charged particles in turbulent magnetic fields”, Astrophys. J., 744, 125. [DOI], [ADS] (Cited on page 22.)
Teufel, A. and Schlickeiser, R., 2002, “Analytic calculation of the parallel mean free path of heliospheric cosmic rays: I. Dynamical magnetic slab turbulence and random sweeping slab turbulence”, Astron. Astrophys., 393, 703–715. [DOI], [ADS] (Cited on pages 20 and 26.)
Usoskin, I.G., 2013, “History of Solar Activity over Millennia”, Living Rev. Solar Phys., 10, lrsp-2013-1. [DOI], [ADS]. URL (accessed 22 April 2013): http://www.livingreviews.org/lrsp-2013-1 (Cited on pages 15 and 41.)
Usoskin, I.G., Mursula, K. and Kovaltsov, G.A, 2001, “Heliospheric modulation of cosmic rays and solar activity during the Maunder minimum”, J. Geophys. Res., 106, 16,039–16,046. [DOI], [ADS] (Cited on page 41.)
Vos, E.E., 2011, Cosmic ray modulation processes in the heliosphere, Master’s thesis, North-West University, Potchefstroom, SA. URL (accessed 22 April 2013): http://hdl.handle.net/10394/7266 (Cited on pages 35 and 36.)
Webber, W.R. and Higbie, P.R., 2008, “Limits on the interstellar cosmic ray electron spectrum below ∼1–2 GeV derived from the galactic polar radio spectrum and constrained by new Voyager 1 measurements”, J. Geophys. Res., 113, A11106. [DOI], [ADS] (Cited on pages 13 and 47.)
Webber, W.R. and Higbie, P.R., 2009, “Galactic propagation of cosmic ray nuclei in a model with an increasing diffusion coefficient at low rigidities: a comparison of the new interstellar spectra with Voyager data in the outer heliosphere”, J. Geophys. Res., 114, A02103. [DOI], [ADS] (Cited on pages 13 and 47.)
Webber, W.R. and McDonald, F.B., 2013, “Recent Voyager 1 data Indicate that on August 25, 2012 at a distance of 121.7 AU from the Sun, sudden and unprecedented intensity changes were observed in anomalous and galactic cosmic rays”, Geophys. Res. Lett., 40. [DOI], [ADS], [arXiv:1212.0883 [physics.geo-ph]] (Cited on pages 5, 45, and 46.)
Webber, W.R. and Potgieter, M.S., 1989, “A new calculation of the cosmic ray anti-proton spectrum in the galaxy and heliospheric modulation effects on this spectrum using a drift plus wavy current sheet model”, Astrophys. J., 344, 779–785. [DOI], [ADS] (Cited on pages 33 and 35.)
Webber, W.R., Kish, J.C. and Schrier, D.A., 1983, “Asymmetries in the modulation of protons and helium nuclei over two solar cycles”, in 18th International Cosmic Ray Conference, Vol. 3, Proceedings of the conference held in Bangalore, India, August 22–September 3, 1983, (Eds.) Durgaprasad, N., Ramadurai, S., Ramana Murthy, P.V., Rao, M.V.S., Sivaprasad, K., pp. 35–38, Tata Institute of Fundamental Research, Bombay. [ADS] (Cited on pages 31 and 32.)
Webber, W.R., Potgieter, M.S. and Burger, R.A., 1990, “A comparison of predictions of a drift wavy neutral sheet modulation model with cosmic ray data over a whole modulation cycle, 1976–1987”, Astrophys. J., 349, 634–640. [DOI], [ADS] (Cited on page 21.)
Webber, W.R., Cummings, A.C., McDonald, F.B., Stone, E.C., Heikkila, B.C. and Lal, N., 2007, “Temporal and spectral variations of anomalous oxygen nuclei measured by Voyager 1 and Voyager 2 in the outer heliosphere”, J. Geophys. Res., 112, A06105. [DOI], [ADS] (Cited on page 11.)
Webber, W.R., Cummings, A.C., McDonald, F.B., Stone, E.C., Heikkila, B.C. and Lal, N., 2008, “Galactic cosmic ray H and He nuclei energy spectra measured by Voyagers 1 and 2 near the heliospheric termination shock in positive and negative solar magnetic polarity cycles”, J. Geophys. Res., 113, A10108. [DOI], [ADS] (Cited on page 47.)
Webber, W.R., McDonald, F.B., Cummings, A.C., Stone, E.C., Heikkila, B.C. and Lal, N., 2012, “Sudden intensity increases and radial gradient changes of cosmic ray MeV electrons and protons observed at Voyager 1 beyond 111 AU in the heliosheath”, Geophys. Res. Lett., 39, L06107. [DOI], [ADS], [arXiv:1112.3590 [physics.space-ph]] (Cited on pages 14, 45, and 46.)
Wibberenz, G., Ferreira, S.E.S., Potgieter, M.S. and Cane, H., 2001, “Time-dependent 2D model compared with observations during the 1974 mini cycle”, Space Sci. Rev., 97, 373–376. [ADS] (Cited on page 22.)
Wieler, R., Beer, J. and Leya, I., 2011, “The Galactic Cosmic Ray Intensity over the Past 106–109 Years as Recorded by Cosmogenic Nuclides in Meteorites and Terrestrial Samples”, Space Sci. Rev.. [DOI], [ADS] (Cited on page 49.)
Yamada, Y., Yanagita, S. and Yoshida, T., 1999, “A stochastic simulation method for the solar cycle modulation of cosmic rays”, Adv. Space Res., 23, 505–508. [DOI], [ADS] (Cited on page 28.)
Zank, G.P., Pogorelov, N.V., Heerikhuisen, J., Washimi, H., Florinski, V., Borovikov, S., Kryukov, I. and Muller, H.R., 2009, “Physics of the solar wind-local interstellar medium interaction: role of magnetic fields”, Space Sci. Rev., 146, 295–327. [DOI], [ADS] (Cited on page 6.)
Zank, G.P., Heerikhuisen, J., Wood, B.E., Pogorelov, N.V., Zirnstein, E. and McComas, D.J., 2013, “Heliospheric structure: the bow wave and the hydrogen wall”, Astrophys. J., 763, 20. [DOI], [ADS] (Cited on page 7.)
Zhang, M., 1999, “A Markov stochastic process theory of cosmic-ray modulation”, Astrophys. J., 513, 409–420. [DOI], [ADS] (Cited on page 28.)
Zhang, M. and Lee, M.A., 2011, “Stochastic Acceleration of Energetic Particles in the Heliosphere”, Space Sci. Rev.. [DOI], [ADS] (Cited on page 11.)
Zhang, M. and Schlickeiser, R., 2012, “A theory of bimodal acceleration of pickup ions by compressive solar wind turbulence under pressure balance”, Astrophys. J., 756, 129. [DOI], [ADS] (Cited on page 11.)
Zhao, L. and Fisk, L.A., 2011, “Understanding the behavior of the heliospheric magnetic field and the solar wind during the unusual solar minimum between cycles 23 and 24”, Solar Phys., 274, 379–397. [DOI], [ADS] (Cited on page 42.)
Acknowledgements
The author acknowledges the partial financial support of the South African National Research Foundation (NRF), the SA High Performance Computing Centre (CHPC), and the SA Space Agency’s (SANSA) Space Science Division. He also acknowledges many discussions with his MSc and PhD students, colleagues, and collaborators in the experimental, modeling, and theoretical fields of research.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Potgieter, M.S. Solar Modulation of Cosmic Rays. Living Rev. Sol. Phys. 10, 3 (2013). https://doi.org/10.12942/lrsp-2013-3
Published:
DOI: https://doi.org/10.12942/lrsp-2013-3