Abstract
We review the properties of solar magneto-convection in the top half of the convection zones scale heights (from 20 Mm below the visible surface to the surface, and then through the photosphere to the temperature minimum). Convection is a highly non-linear and nonlocal process, so it is best studied by numerical simulations. We focus on simulations that include sufficient detailed physics so that their results can be quantitatively compared with observations.
The solar surface is covered with magnetic features with spatial sizes ranging from unobservably small to hundreds of megameters. Three orders of magnitude more magnetic flux emerges in the quiet Sun than emerges in active regions. In this review we focus mainly on the properties of the quiet Sun magnetic field.
The Sun's magnetic field is produced by dynamo action throughout the convection zone, primarily by stretching and twisting in the turbulent downflows. Diverging convective upflows and magnetic buoyancy carry magnetic flux toward the surface and sweep the field into the surrounding downflow lanes where the field is dragged downward. The result is a hierarchy of undulating magnetic Ω- and U-loops of different sizes. New magnetic flux first appears at the surface in a mixed polarity random pattern and then collects into isolated unipolar regions due to underlying larger scale magnetic structures. Rising magnetic structures are not coherent, but develop a filamentary structure. Emerging magnetic flux alters the convection properties, producing larger, darker granules.
Strong field concentrations inhibit transverse plasma motions and, as a result, reduce convective heat transport toward the surface which cools. Being cooler, these magnetic field concentrations have a shorter scale height and become evacuated. The field becomes further compressed and can reach strengths in balance with the surrounding gas pressure. Because of their small internal density, photons escape from deeper in the atmosphere. Narrow evacuated field concentrations get heated from their hot sidewalls and become brighter than their surroundings. Wider magnetic concentrations are not heated so they become darker, forming pores and sunspots.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The solar convection zone is the ultimate driver of activity in the solar chromosphere and corona. It is the only available source of mechanical energy. Upper atmosphere activity and heating is empirically intimately connected with the presence of magnetic fields. Hence the need to understand the behavior of magnetic fields at the solar surface. The solar magnetic field is produced by dynamo action within the convection zone. Thus, to understand the energy source of the chromosphere and corona we need to understand the solar dynamo, magneto-convection, and the transport of magnetic flux through the convection zone. For recent reviews see Fan (2009) and Charbonneau (2010). For probing the subsurface layers of the Sun, our best tools are the various techniques of local helioseismology (Gizon and Birch, 2005). Accurate modeling of the rise through the convection zone and emergence of magnetic flux, of sunspots and active regions is needed for improving helioseismic probing of solar subsurface structure.
Convection is the transport of energy by bulk mass motions. In a convection zone, energy is transported as thermal energy, except in layers where hydrogen is only partially ionized, in which case most of the energy is transported as ionization energy. Typically, the motions are slow compared to the sound speed so that approximate horizontal pressure balance is maintained. As a result, warmer fluid is less dense and buoyant while cooler fluid is denser and gets pulled down by gravity. For a detailed review of solar surface convection see Nordlund et al. (2009).
The topology of convection is controlled by mass conservation (Stein and Nordlund, 1989). Convection has a horizontal cellular pattern, with the warm fluid ascending in separate fountainlike cells surrounded by lanes of cool descending fluid. In a stratified atmosphere, with density decreasing outward, most of the ascending fluid must turn over and be entrained in the downflows within a density scale height (ignoring gradients in velocity and filling factor). Fluid moving a distance Δr in an atmosphere with a density gradient dln ρ/dr would, if its density remained constant, be overdense compared to its surroundings by a factor Δρ/ρ = -(dlnρ/dr)Δr. This is unstable and produces a pressure excess in the upflow cell interiors that pushes the fluid to turn over into the surrounding downflow lanes. Since the fluid velocity decreases inward from the top of the convection zone, its derivative has opposite sign to that of the density, so the length scale for entrainment is increased. Warm upflows diverge and tend to be laminar, while cool downflows converge and tend to be turbulent. Temperature in stellar convection zones increases inward, so the scale height and, as a result, the size of the horizontal convective cellular pattern also increase inward. Think of the rising fluid as a cylinder. As described above, most of the fluid entering at the bottom of the cylinder must leave through its sides within a scale height. If the ratio of vertical to horizontal velocities does not change much with depth, then the radius of the cylinder can increase in proportion to the scale height and still maintain mass conservation (Stein and Nordlund, 1998).
The solar surface is covered with magnetic features with spatial sizes ranging from unobservably small to hundreds of megameters. Their distribution is featureless (Parnell et al., 2009; Thornton and Parnell, 2011). Large-scale magnetic structures, sunspots and active regions, possess some well defined global properties (Hathaway, 2010). The main observed properties of small scale magnetic structures are (de Wijn et al., 2009): Strong fields tend to be vertical and weaker fields horizontal. The strongest vertical fields are in pressure equilibrium with their surroundings and tend to occur in the magnetic network and the intergranular lanes. Horizontal fields are found predominantly inside granules and near the edges of granules. Horizontal field properties are similar in the quiet Sun, plage, and polar regions (Ishikawa and Tsuneta, 2009). Three orders of magnitude more magnetic flux emerges in the quiet Sun than emerges in active regions (Thornton and Parnell, 2011). This new flux is first seen as horizontal field inside granules followed by the appearance of vertical field at the ends of the horizontal field (Centeno et al., 2007; Martínez González and Bellot Rubio, 2009; Ishikawa et al., 2010; Guglielmino et al., 2012).
In the presence of magnetic fields, convection is altered by the Lorentz force, while convection influences the magnetic field via the curl (v × B) term in the induction equation.
Where the conductivity high, the magnetic field is frozen into the ionized plasma. Where the magnetic field is weak (magnetic energy small compared to kinetic energy), convective motions drag it around. To maintain force balance, locations of higher field strength (higher magnetic pressure) tend to have smaller plasma density and lower gas pressure. Diverging, overturning motions quickly sweep the field (on granular times of minutes) from the granules into the intergranular lanes (Tao et al., 1998a; Emonet and Cattaneo, 2001; Weiss et al., 2002; Stein and Nordlund, 2004; Vögler et al., 2005; Stein and Nordlund, 2006). In hours (mesogranular times), the field tends to collect on a mesogranule scale. In days (supergranule times), the slower, large scale supergranule motions collect the field in the magnetic network at the supergranule boundaries. Convective flows produce a hierarchy of loop structures in rising magnetic flux. Slow upflows and buoyancy raise the flux, while fast downflows pin it down, which produces Ω- and U-loops (Cheung et al., 2007). The different scales of convective motion produce loops on these different scales, with smaller loops riding piggy-back in a serpentine fashion on the larger loops (Cheung et al., 2007; Stein et al., 2010b). Dynamo action occurs in the turbulent downflows where the magnetic field lines are stretched, twisted, and reconnected, increasing the field strength (Nordlund et al., 1992; Cattaneo, 1999; Vögler and Schüssler, 2007; Schüssler and Vögler, 2008; Pietarila Graham et al., 2010).
Magnetic fields influence convection via the Lorentz force, which inhibits motion perpendicular to the field. As a result, the overturning motions that are essential for convection are suppressed and convective energy transport from the interior to the surface is reduced. Radiative energy loss to space continues, so regions of strong field cool relative to their surroundings. Being cooler, these locations have a smaller scale height. Plasma drains out of the magnetic field concentrations in a process called “convective intensification” or “convective collapse” (Parker, 1978; Spruit, 1979; Unno and Ando, 1979; Nordlund, 1986; Bercik et al., 1998; Grossmann-Doerth et al., 1998; Bushby et al., 2008). This process can continue until the magnetic pressure (plus a small gas pressure) inside the flux concentration equals the gas pressure outside, giving rise to a field strength much greater than the equipartition value with the dynamic pressure of the convective motions. These magnetic flux concentrations are cooler than their surroundings at the same geometric layer. However, because they are evacuated, their opacity is reduced so photons escape from deeper in the atmosphere (Wilson depression, Maltby, 2000). Where the magnetic concentrations are narrow, there is heating from their hotter side walls and they appear as bright points (Spruit, 1976). Where the concentrations are wide, the side wall heating is not significant and the flux concentrations appear darker than the surroundings as pores or sunspots.
Magnetic fields alter granules’ properties - producing smaller, elongated, lower intensity contrast, “abnormal” granules (Muller et al., 1989; Title et al., 1992; Bercik et al., 1998; Vögler, 2005; Cheung et al., 2007). Strong magnetic flux concentrations typically form in convective downflow lanes, especially at the vertices of several such lanes, due to the sweeping of flux by the diverging convective upflows (Vögler et al., 2005; Stein and Nordlund, 2006). They are surrounded by downflows which sometimes become supersonic.
Magneto-convection simulations have been very useful in understanding and interpreting observations. Sánchez Almeida et al. (2003), Khomenko et al. (2005), Shelyag et al. (2007), and Bello González et al. (2009) have used simulations to calibrate the procedures for analyzing and interpreting Stokes spectra in order to determine the solar vector magnetic field. Fabbian et al. (2010) has shown that magnetic fields alter line equivalent widths by altering the temperature stratification and by Zeeman broadening. These two effects act in opposite directions, but still leave a net result and hence alter abundance determinations. Zhao et al. (2007), Braun et al. (2007), Kitiashvili et al. (2009), Birch et al. (2010), and Braun et al. (2012) have used convection and magneto-convection simulation results to analyze local helioseismic inversion methods.
Magneto-convection is highly non-linear and non-local, so it needs to be modeled using numerical simulations. Two complementary approaches are being used to study magneto-convection, which we will call “idealized” and “realistic”. “Idealized” studies ignore complex physics by assuming a fully ionized, ideal plasma and energy transport by thermal conduction. Magneto-convection in the deep, slow moving, adiabatic portion of the convection zone satisfies these idealized assumptions and, in addition, can use the anelastic approximation whereby acoustic waves are eliminated from the calculation, which permits larger time steps. “Idealized” calculations are important for isolating and studying fundamental physical phenomena as well as for exploring parameter space (because they run fast). “Realistic” studies include complex physics - an equation of state for partially ionized gas, non-grey radiation transport and, in some cases, even some non-equilibrium effects. “Realistic” calculations are necessary to make quantitative comparisons with observations in order to understand the observations and to provide artificial data for evaluating data analysis procedures. In this review we focus on the “realistic” numerical modeling of solar surface magneto-convection. It updates and extends the section on magneto-convection from the review by Nordlund et al. (2009) of solar surface convection.
It is organized as follows: Section 2 states the equations that need to be solved. Section 3 describes the solar observations. Section 4 describes the simulation results for: dynamo action (4.1), flux emergence (4.2), flux concentrations (4.3), and pores and sunspots (4.4).
2 Equations
To simulate magneto-convection, the conservation equations for mass, momentum, energy and the induction equation for the magnetic field must be solved, together with Ohm’s law for the electric field and an equation of state relating pressure to the density and energy. For a detailed discussion of the equations governing convection see Nordlund et al. (2009).
Mass conservation controls the topology of stratified convection,
where ρ is the density and u the velocity.
Momentum conservation controls the plasma motions. In the presence of magnetic fields, convection is altered by the Lorentz force in the momentum equation, which becomes:
Here P is the pressure, g is the gravitational acceleration, B is the magnetic field, J = ∇ × B/μ is the current, μ is the permeability (magnetic constant), and τvisc is the viscous stress tensor,
The Lorentz force inhibits motion perpendicular to the field. As a result, the overturning motions that are essential for convection are suppressed and convective energy transport from the interior to the surface is reduced. When large depths are included where the fluid motions become slow, the coriolis force, -2ρΩ× u, needs to be included. Angular momentum conservation then produces a surface shear layer with the surface rotating slower than the bottom of the domain.
Kinetic energy is changed by energy transport and work against the forces acting on the plasma. The equation for kinetic energy is
Note that if there is no net mass flux, 〈ρu〉xyt = 0, then there is no net buoyancy work by gravity. The vertical convective velocity and density are correlated. Upflows have lower density and cover a larger area while downflows have higher density and cover a smaller area. Downflows are pulled down by gravity and upflows are buoyant. Gravity drives the convection, doing positive work on both the upflows and downflows. But the total work by gravity vanishes. Hence, the positive work on the convective motions is balanced by an equal but negative work on the mean flow. There is necessarily a horizontally averaged mean flow in the opposite direction to gravity. Such mean flows do exist in the simulations.
Internal energy is changed by transport, by PdV work, by Joule heating, by viscous dissipation, and by radiative heating and cooling. It is the fluid version of the 2nd law of thermodynamics and (together with the density) determines the plasma temperature, pressure, and entropy.
where e is the internal energy per unit volume. The radiative heating/cooling is:
Here κv is the opacity (1/ρκv = lv is the mean free path of photons of frequency v), \(I_\nu (r,\hat n,t)\) is the radiation intensity (energy at frequency v, at location r, travelling in direction \(\hat n\) , at time t, per unit area, per unit solid angle, per unit frequency, per unit time), and Sv = ∈v/κv is the source function (∈v is the rate of energy emission at frequency v per unit frequency, per unit mass, per unit time, per unit solid angle). The viscous dissipation is:
Magnetic energy changes due to transport by the Poynting flux, E × B/μ, work by the Lorentz force, u · J × B and joule dissipation, J · E,
Adding kinetic, internal and magnetic energy equations gives the equation for the total energy, ET = 1/2ρu2 + e + B2/2μ,
Convection influences the magnetic field via the curl (u × B) term in the induction equation,
where the electric field is given by Ohm’s Law. In a one-fluid MHD system, it is
where η is the resistivity, ne is the electron number density, Pe is the electron pressure, and e is the electron charge. The last two (Hall and pressure) terms are usually neglected, but the Hall term may be important in the weakly ionized photosphere. Where the magnetic field is weak and the resistivity low, the field is frozen into the ionized plasma. Convective motions drag the field around, stretching and twisting it.
To make “realistic” models of solar surface magneto-convection it is necessary to include all the significant physical processes occurring near the solar surface. In the photosphere and upper convection zone Local Thermodynamic Equilibrium (LTE) is a good approximation. For models that extend into the chromosphere non-local thermodynamic equilibrium (NLTE) effects must also be included, as is being done in the bifrost code (Gudiksen et al., 2011).
Ionization energy accounts for 2/3 of the energy transported near the solar surface and must be included to obtain the observed solar velocities and temperature fluctuations (Stein and Nordlund, 1998). An equation of state (EOS) is used to determine the pressure and temperature for the partially ionized plasma. Typically this is in tabular form and includes LTE ionization of the abundant elements as well as hydrogen molecule formation as a function of log(density) and internal energy per unit mass.
Radiation from the solar surface cools (and heats) the plasma and produces the low entropy, high density fluid whose buoyancy work drives the convective motions. Since the optical depth is of order unity in these regions, neither the diffusion approximation (Ustyugov, 2010) nor the escape probability approach (Abbett and Fisher, 2010) are sufficiently accurate. Radiative heat/cooling is calculated by explicitly solving the radiation transfer equation in both continua and lines,
where \(I_\nu (r,t;\hat n)\) is the intensity at frequency v, position r, time t, in direction \(\hat n\), ∈v is the radiation emission at that frequency, location, time, and in that direction, and χv is the absorption probability of radiation at that frequency, location, time, and direction. Since time steps in the solar case are short, the plasma state is known from the previous time step, so the emission and absorption can be calculated and the radiation transfer can be solved explicitly. The main problem is the large number of frequencies necessary to accurately represent the radiation. A multi-group approximation is used to drastically reduce the number of frequencies for which the transfer equation is solved. The opacity and emissivity are grouped into a few bins (typically 4 – 12) according the magnitude of the opacity and its frequency (Nordlund, 1982; Skartlien, 2000; Stein and Nordlund, 2003; Vögler et al., 2004; Vögler, 2004). The number of directions is also limited.
3 Observations
The solar surface is covered with magnetic features with spatial scales from smaller than can currently be resolved (∼ 70 km with the Swedish 1 m Solar Telescope) to active regions covering up to 100 Mm (Figure 1). These evolve on a correspondingly wide range of time scales, from seconds for the smallest observed features, to months for some active regions. If one counts as a single feature any contiguous collection of the same polarity with magnitude above some cutoff, then the magnetic flux distribution is a power law of slope -1.85 (Figure 2). Alternatively, if one identifies features as individual flux peaks, then the distribution is log-normal (Parnell et al., 2009; Thornton and Parnell, 2011). These power laws are featureless, they have no peaks or valleys.
Stokes V in blue wing of 630.2 nm line from Hinode. Around a sunspot (a) and in the quiet Sun (b), showing the wide range in size of magnetic structures on the Sun. The dimensions of both figures are 110 Mm and the pixel size is 108 km. Image reproduced by permission from Parnell et al. (2009), copyright by AAS.
Histogram of feature frequency vs. magnetic flux. Image reproduced by permission from Parnell et al. (2009), copyright by AAS.
The large-scale magnetic structures, sunspots, and active regions possess some well defined global properties: all active regions in a given hemisphere have the same polarities of leading/following spots, but reversed between the northern and southern hemispheres (Hale’s polarity law); the polarities reverse in a semi-periodic 22 year cycle; in each cycle spots first appear at mid latitudes and then their appearances migrate toward the equator; active regions are tilted with the leading spot closer to the equator (Joy’s law); trailing spot fields migrates toward the poles and sunspots tend to reappear at certain active longitudes (Figure 3). See review by Hathaway (2010). These properties imply the existence of a global dynamo process.
Magnetic butterfly diagram from longitudinally averaged radial magnetic field. This illustrates Hale’s polarity law, Joy’s law, transport of flux toward the poles and migration of active region emergence sites toward the equator. Image reproduced by permission from Hathaway (2010).
There is an excellent review of small-scale solar magnetic field observations (network and internetwork quiet Sun) by de Wijn et al. (2009). The main observational results are: strong fields tend to be vertical and weaker fields horizontal. Vertical kilogauss fields (in pressure equilibrium with their surroundings) are found in the magnetic network and as isolated, intermittent concentrations in intergranular lanes. Horizontal magnetic fields are found all over the Sun (Trujillo Bueno et al., 2004; Harvey et al., 2007), predominantly inside and near the edges of granules. They are transient, intermittent and have granule-scale sizes and lifetimes and strengths in the hectogauss range (generally less than equipartition with the convective dynamic pressure) (Ishikawa and Tsuneta, 2010). Weaker horizontal fields have no preferred orientation. Stronger ones tend to align with the active regions. The horizontal field properties are similar in the quiet Sun, plage, and polar regions (Ishikawa and Tsuneta, 2009). The spatially averaged horizontal magnetic field strength is 50 – 60 G, while the spatially averaged vertical field strength is only 11 G (Lites et al., 2008). This may be due to the larger area covered by horizontal fields compared to the isolated vertical field concentrations. There is no characteristic size or lifetime for the horizontal fields (they have an exponential distribution both in size and lifetime) (Danilovic et al., 2010). There is some question of the accuracy of Hinode determinations of quiet Sun transverse magnetic fields due to s/n problems (Borrero and Kobel, 2011).
Bright points in the G-band (dominated by CH molecular transitions) have been used as proxies for the magnetic field. At disk center small magnetic concentrations appear as bright points in the intergranular lanes, while larger concentrations are dark. The increased brightness in magnetic concentrations is due to their lower density compared with their surroundings. At a given geometric height, granules are hotter than the intergranular lanes, which are, in turn, hotter than G-band bright points. Although at a given geometric height the magnetic elements are cooler than the surrounding medium, one sees into deeper layers, to where the temperature is higher, due to the reduced opacity and to heating from the hot surrounding granules. Locations of large magnetic concentrations are cooler than even the G-band bright points because both convective heat transport and side wall heating are reduced.
The presence of strong magnetic fields enhances the pillow appearance of granules because their low density and resulting low opacity allow one to see deeper into the hot granules behind them (the “hot wall” effect Spruit, 1976, 1977; Keller et al., 2004; Shelyag et al., 2004; Carlsson et al., 2004). Where the fields are strong, the intergranular lanes are depressed up to 350 km below the mean height. Thus the τ = 1 surface is extremely corrugated. Toward the limb, where the surface is viewed at an angle, the low density and opacity in the strong magnetic elements allows one to see the hot granule walls behind. These are the faculae (Figure 4) (Keller et al., 2004; Carlsson et al., 2004). The excess brightness comes from a thin layer (∼ 30 km) of steep density gradient at the interface between the magnetic and nonmagnetic atmospheres. Typically there is a dark lane just centerward of the bright faculae. As the line of sight moves limbward from granule to faculae, it first intersects a granule top and is bright, then intersects cool material above the granule and inside the magnetic concentration, and finally intersects the hot granule wall on the far side of the magnetic concentration. Variations in the field strength produces variations in the density and opacity which leads to a striated appearance in the bright granule walls. Where the field is weaker, the density is higher, so the opacity larger. This effect is enhanced by a higher CH concentration also due to the higher density. Thus, where the magnetic field is weaker, the radiation emerges from higher, cooler layers, so these locations appear darker.
High resolution observations of solar faculae show that they have an asymmetric contrast profile, with some brightness extending up to one arcsecond in the limbward direction from their peak in brightness (Hirzberger and Wiehr, 2005). The wide contrast profile cannot be explained solely by the “hot wall” effect, as was noted by Lites et al. (2004). The works by Keller et al. (2004) and Steiner (2005) address this issues, with somewhat conflicting but broadly consistent explanations. One conclusion is that the limbward extension of brightness comes from seeing the granule behind the facular magnetic field through the rarefied facular magnetic flux concentration; a circumstance that observers suspected decades ago. The explanation is corroborated by the direct comparisons of observations and simulations by De Pontieu et al. (2006).
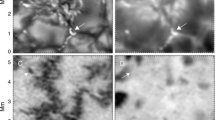
Three orders of magnitude more magnetic flux is observed to emerge as small scale loops in the quiet Sun than emerges in active regions (Thornton and Parnell, 2011). This new flux is first seen as horizontal field (linear polarization in Stokes spectra) inside granules followed by the appearance of vertical field at the ends of the horizontal field (circular polarized Stokes spectra) (Centeno et al., 2007; Martínez González and Bellot Rubio, 2009; Ishikawa et al., 2010; Guglielmino et al., 2012) (Figure 5).
Emergence of a small magnetic loop in the quiet solar photosphere. Top: continuum intensity at 630 nm. Center: total linear polarization (Stokes Q,U) in the 630.25 line. Bottom: total circular polarization (Stokes V). Signal is clipped at ± 0.1 pm. Red contours are linear polarization > 0.22 pm, while black and white contours are circular polarization > ± 0.1 pm. Distances are in acrsec. Image reproduced by permission from Martínez González and Bellot Rubio (2009), copyright by AAS.
These Ω-loop footpoints get quickly swept into the intergranular lanes and the horizontal field to the edges of the granules. They do not show a helical structure. Transient horizontal fields also appear briefly where new downflow lanes form (Danilovic et al., 2010). The flux in these emerging bipoles is small, 1016 × few × 1017 Mx, but their rate of appearance is large, around a few × 10-10 km2 s, hence their dominant contribution to the emerging flux of the Sun (Martínez González and Bellot Rubio, 2009; Ishikawa and Tsuneta, 2009; Ishikawa et al., 2010). Most of these small loops are low lying, with only about a quarter reaching up to chromospheric heights.
4 Simulations
Two types of numerical studies of magneto-convection are being undertaken: “idealized” and “realistic”. Both approaches give valuable, but different, insights into the properties of magnetoconvection. Idealized simulations were pioneered by Weiss (1966) and extensively used by Tao et al. (1998b), Cattaneo (1999), Abbett et al. (2000), Hurlburt and Rucklidge (2000), Emonet and Cattaneo (2001), Weiss et al. (2002), Cattaneo et al. (2003), and Bushby et al. (2008). See reviews by Weiss (1991) and Schüssler (2001). They are especially useful for gaining physical insights into convective properties. In these calculations an ideal gas equation of state is assumed and energy transport is assumed to be only by convection and thermal conduction. For modeling magneto-convection in the solar interior anelastic or reduced sound speed calculations with an ideal gas equation of state and diffusive radiation transport are appropriate (Miesch, 2005; Miesch et al., 2008; Fan, 2009; Miesch et al., 2011; Hotta et al., 2012). An alternative approach applicable to the deep convective layers is to reduce the sound speed (Hotta et al., 2012). This, as in the anelastice approximation, allows larger time steps. “Realistic” simulations were pioneered by Nordlund (1982) and have been extensively developed by Stein and Nordlund (1998, 2006), Steiner et al. (1998); Vögler et al. (2005), Schaffenberger et al. (2005), Hansteen et al. (2007), Abbett (2007), Jacoutot et al. (2008), Carlsson et al. (2010), and Gudiksen et al. (2011). A tabular equation of state is used, which includes the partial ionization of hydrogen, helium and other abundant elements, because below 40,000 K in the Sun ionization energy dominates over thermal energy in convective energy transport. The radiation transfer equation is solved to determine the radiative heating and cooling, because the optical depth is of order unity near the visible solar surface, so that neither the diffusion nor optically thin approximations are valid. Such detailed physics is necessary to make quantitative comparisons with observations. Here we restrict ourselves to the more “realistic” surface simulations. Magneto-convection and dynamo action in the deeper layers of the convection zone are reviewed by Miesch (2005) and Miesch and Toomre (2009).
4.1 Turbulent convection and dynamo action
Meneguzzi et al. (1981) and Cattaneo (1999) were the first to demonstrate, via magneto-convection simulations, that dynamo action will occur in turbulent convection even in the absence of rotation. These calculations were for closed, Boussinesq systems. Questions were raised whether local dynamo action is possible in the highly stratified solar convection zone (Stein et al., 2003) because in a stratified atmosphere with much stronger downflows than upflows, magnetic flux is pumped down (Tobias et al., 2001; Dorch and Nordlund, 2001). Abbett (2007), Vögler and Schüssler (2007), and Pietarila Graham et al. (2010) showed that a local surface dynamo is indeed possible. Vögler and Schüssler (2007) and Pietarila Graham et al. (2010) used a shallow, very high resolution, magneto-convection simulation with no Poynting flux in or out of the domain, but with a high magnetic diffusivity in the bottom boundary layer to mimic the loss of magnetic flux to the deeper convection zone. Pietarila Graham et al. (2010) demonstrated that during the kinematic (linear) growth phase, the primary dynamo process (95%) was stretching of magnetic field lines against the magnetic tension component of the Lorentz force by convective motions at subgranule scales (0.1 – 1 Mm) in the turbulent downdrafts, which generates still smaller scale (20 – 200 km) magnetic field. The other 5% was from work against magnetic pressure by fluid motions at granule scales (Figures 6 and 7). In addition, magnetic pressure also produces a cascade of magnetic energy from the dynamo generated scales to still smaller scales. In the saturated phase, generation by stretching is almost balanced by the compressive cascade with a little energy also going into MHD wave generation.
Dynamo energy transfers in the kinematic phase. The dominant process is turbulent stretching of magnetic field lines against the magnetic tension component of the Lorentz force. Image reproduced by permission from Pietarila Graham et al. (2010), copyright by AAS.
Dynamo net energy transfer rates as a function of horizontal spatial scale in the kinematic dynamo phase. Left: work against magnetic tension (pink dashed line) and work against magnetic pressure (green dotted line) as a function of the fluid motion spatial frequency. Right: dynamo stretching (blue dot-dash line), dynamo compression (black solid line), and magnetic energy removed by compression (red dotted line) as a function of the magnetic field spatial frequency. Image reproduced by permission from Pietarila Graham et al. (2010), copyright by AAS.
Abbett (2007) and Schüssler and Vögler (2008) showed that such small scale dynamo action produces many low-lying loops with large amounts of horizontal field overlying the granules (Figures 8 and 9). Steiner (2010) argues that the preponderance of horizontal over vertical field is an inherent consequence of the fact that granules are wider than a scale height. Consider an area of length L and height h. The horizontal (ΦH) and vertical (ΦV) fluxes for a loop are the same, so that ΦH = 〈BH〉Lh = ΦV = 〈BV〉L2, where BH is the horizontal and BV is the vertical field and L and h are the horizontal and vertical extents of the field. Hence 〈BH〉/〈BV〉 ≈ L/h and low lying loops connecting opposite sides of granules must have larger average horizontal than vertical field.
Photospheric magnetic field lines showing many low-lying, horizontally directed magnetic structure from a simulation from the upper convection zone to the corona. Image reproduced by permission from Abbett (2007), copyright by AAS.
Image of Log horizontal B in vertical slice through saturated phase of dynamo simulation of Vögler and Schüssler (2007). Mean optical depth unity is at approximately 0.9 Mm. Note many loops of different sizes closing in the photosphere. Image reproduced by permission from Schüssler and Vögler (2008), copyright by ESO.
Global dynamos have been simulated by Brun et al. (2004), Miesch (2005), Dobler et al. (2006), Browning et al. (2006), and Brown et al. (2007, 2010). See reviews by Brandenburg and Dobler (2002), Ossendrijver (2003), Miesch and Toomre (2009), and Charbonneau (2010). Note that the fact that both the rate of magnetic flux emergence and the probability distribution of magnetic flux magnitudes are featureless power laws from 1016 – 1023 Mx suggests that the solar dynamo has no preferred scale, that it acts throughout the convection zone with each scale of convective motions generating new flux on that scale (Parnell et al., 2009; Thornton and Parnell, 2011). That is, all the surface magnetic features are produced by a common process (which can not be all dominated by surface effects since the sunspots and active regions clearly are not).
4.2 Subsurface rise and emergence of magnetic flux
Magnetic fields are produced by dynamo action throughout the solar convection zone. Their emergence through the visible surface is driven by two processes: advection by convective upflows and buoyancy (to maintain approximate pressure equilibrium with their surroundings the density inside the concentration is smaller than in its surroundings). Fan (2009) has reviewed the rise of magnetic flux through the deep convection zone. Simulations of magnetic flux emerging from the surface layers of the convection zone have been initiated in three ways: either from coherent twisted flux tubes forced into the computational domain through the bottom boundary or made buoyant by lowering their density (Yelles Chaouche et al., 2005; Cheung et al., 2007, 2008; Martínez-Sykora et al., 2008, 2009; Cheung et al., 2010), or by inflows at the bottom advecting minimally structured, uniform, untwisted, horizontal field advected by inflows into the domain through the bottom boundary (Stein et al., 2010a,b), or produced locally by dynamo action (Abbett, 2007; Abbett and Fisher, 2010). These very different approaches, using several different computer codes, show several, robust, common features.
Convective flows produce a hierarchy of loop structures in rising magnetic flux (Figure 10). Magnetic flux rises through the convection zone because it is advected by broad upflows and because it is buoyant. Along the way, it encounters convective downflows piercing the upflows on smaller and smaller scales, with downflow speeds significantly larger than the upflow speeds. The portions of the magnetic concentration in the downflows will be dragged down, or at least have their upward motion slowed, while the portions still in the upflows or that have large density deficits and so large buoyancy continue to ascend rapidly (Figures 10, 11). The different scales of motions produce a hierarchy of magnetic Ω- and U-loops with small loops riding piggy-back on larger loops in a serpentine structure (Cheung et al., 2007, 2008; Kitiashvili et al., 2010; Stein et al., 2010b) (Figure 12). As a result, emergence of large, undulated Ω-loops occurs as a collection of small-scale, mixed polarity, emergence events. In general, the asymmetry of upflow and downflows (amplitudes and topology) leads to a tendency for downward transport of magnetic flux; a process known as “turbulent pumping” (Drobyshevskii et al., 1980; Nordlund et al., 1992; Petrovay and Szakály, 1993; Tobias et al., 1998; Dorch and Nordlund, 2000, 2001; Tobias et al., 2001) (Figure 10).
mpg-Movie (37927878 KB) Still from a movie showing Log B showing multiple loops and several vertical flux concentrations, one of which has become a pore (see Section 4.4). The movie shows that most of the magnetic features are being pushed down by convective downflows, but some of the loops are rising toward the surface and in places loops have opened out through the top boundary leaving vertical “flux tubes” behind. Movie produced by Sandstrom, CSC, NASA Ames Res. Ctr. (For video see appendix)
mpg-Movie (194745724 KB) Still from a movie showing Rise and emergence of initially uniform, untwisted horizontal magnetic field continuously being advected into the computational domain by inflows in the centers of supergranule cells at the bottom. Left: |B| image and velocity vectors. Right: |B| image and magnetic field vectors both in a vertical plane. The boundary field strength was gradually increased from 0.2 kG with an e-folding time of 5 hrs until it reached 5 kG and thereafter held constant. (For video see appendix)
As the magnetic flux rises it expands (Figure 13). For horizontal flux tubes, the horizontal expansion is much larger than the vertical expansion. Consider a purely horizontal field \(B = B\hat x\) in the x-direction. Suppose the rates of expansion in the horizontal and vertical directions are α = ∂vx/∂x = ∂yy/∂y and ∂vz/∂z respectively. The rate of change of the magnetic field following the fluid motion is given by the Lagrangian derivative
which becomes,
The continuity equation (1) becomes
So for emerging horizontal fields, B ∝ ρ(1+∈)/(2+∈) (Cheung et al., 2010). For isotropic expansion (∈ = 1), B ∝ ρ2/3. For vertical expansion small compared to horizontal expansion (∈ ≪ 1) B ∝ ρ1/2.
Time sequence of vertical cross-sections perpendicular to an initial coherent twisted flux tube. The grey scale is temperature and the color coding is magnetic field strength |B|. The purple line is the τ500 = 1. Image reproduced by permission from Cheung et al. (2007), copyright by ESO.
The fields first appear at the surface in localized regions as small bipoles with a small-scale, mixed pepper and salt polarity. The emergence region spreads in time (Figure 14). As the bipoles begin to emerge, horizontal and vertical fields have similar strengths, but horizontal fields are more common (cover more area) than vertical fields, except for the strongest fields. The mixed polarity fields collect into separated unipolar regions due to the underlying large scale magnetic structures (Figure 14).
mpg-Movie (169942682 KB) Still from a movie showing Time sequence of emergent continuum intensity (left), vertical magnetic field at τRoss = 0.1 (right), for an initial twisted flux half torus driven into the computational domain at 7.5 Mm depth. The initial central field strength was 21 kG and total flux 7.6 × 1021 Mx. The domain is 92 × 49 Mm wide. Image reproduced by permission from Cheung et al. (2010), copyright by AAS. (For video see appendix)
Diverging, overturning convective motions quickly sweep magnetic fields (on granular times of minutes) from the granules into the intergranular lanes (Figure 15) (Weiss, 1966; Hurlburt and Toomre, 1988; Tao et al., 1998a; Emonet and Cattaneo, 2001;Weiss et al., 2002; Steiner et al., 1998; Stein and Nordlund, 2004; Vögler et al., 2005; Stein and Nordlund, 2006). In hours (mesogranular times) the field tends to collect on a mesogranule scale. Observations averaged over several hours reveal this magnetic pattern (de Wijn et al., 2005; Ishikawa and Tsuneta, 2010), even though there is no distinct convective meso-granule scale. In days (supergranule times) the slower, large scale supergranule motions sweep the fields to the supergranule boundaries. Eventually a balance is reached where the rate of emergence of new flux balances the rate at which flux is swept to larger horizontal scales. This balance empirically occurs at supergranulation scales and produces the magnetic network at the supergranule boundaries. Here the new flux encounters existing magnetic flux, which it either cancels or augments (Simon et al., 2001; Krijger and Roudier, 2003; Isobe et al., 2008).
Sweeping of magnetic field into intergranular lanes. Initially the entire surface is covered with 30 G horizontal field. Surface magnetic field strength is shown at 0.5 min (left), 10 min (center) and 30 min (right). Black contours are zero velocity contours which outline the granules. Fields stronger than 0.5 kG appear as white and black. Field magnitudes less than 30 G are shown in grey. Diverging upflows first sweep the granules clear of strong fields and on a longer time scale sweep the interiors of mesogranules free of strong fields. Image reproduced by permission from Stein and Nordlund (2006), copyright by AAS.
The rising magnetic loops are not coherent, but rather have a filamentary structure (Figure 10). Some individual filaments rise more rapidly than others. The small-scale crenulation of the loops produces the “pepper and salt” pattern as the flux emerges through the visible surface. As the bulk of the magnetic loop reaches the surface, the different polarities concentrate in unipolar regions accompanied by flux cancellation where opposite polarities come in contact (Figures 14 and 17). This happens because the mixed polarity emergence is due to the undulating magnetic field lines produced by convective upflows and downdrafts distorting the large loops rising from below. The underlying large-scale magnetic structures organize the mixed polarity fields when they approach the surface. In order for the like polarity branches to collect, the mass trapped in the U-loops between the peaks of the small Ω-loops must be removed. This occurs by the U-loop getting pinched off and forming plasmoids which may either sink below the surface or get ejected into space (Figure 16) (Lites, 2009; Cheung et al., 2010).
Schematic scenario of how granular motions pinch off U-tubes to produce O-loops in 2D and plasmoides in 3D. Image reproduced by permission from Cheung et al. (2010), copyright by AAS.
mpg-Movie (108657227 KB) Still from a movie showing Emergent continuum intensity (left) and vertical magnetic field at τcont = 0.01 (right) from simulation with initial/boundary condition of convective inflows advecting 1 kG uniform, untwisted, horizontal field into the computational domain at 20 Mm depth. The intensity range is I/〈I〉 = [0.13, 2.5] and the magnetic field range is ± 3.5 kG. The pores may form spontaneously in vertical flux tubes from magnetic loops that have reached the surface and opened out through top boundary. Compare this with Figure 14 for the rise of a coherent twisted flux tube. (Movie shows the initial “pepper and salt” emergence, the horizontal advection of the field, its concentration into unipolar regions with cancellation where opposite polarities meet and merging of like polarities to form pores. Resolution was increased from 48 km to 24 km horizontally at time 51.7 hrs.) (For video see appendix)
Magnetic flux emergence simulations starting with horizontal, uniform, untwisted field at 20 Mm depth is shown in Figures 10, 11 and 18. Figure 18 shows magnetic field lines in the simulation box viewed from the side and slightly above. The red line in the lower left is horizontal field being advected into the domain. In the lower center is a loop like flux concentration rising toward the surface. In the upper right is a vertical flux concentration or “flux tube” through the surface (Stein and Nordlund, 2006). While the field lines form a coherent bundle near the surface, below the surface they become tangled and spread out in many different directions (Vögler et al., 2005; Schaffenberger et al., 2005). A “flux tube” at the surface forms by a loop-like flux concentration rising up through the surface and opening up through the upper boundary where the condition is that the field tends toward a potential field. This leaves behind the legs of the loop. Typically one leg is more compact and coherent than the other and persists for a longer time as a coherent entity while the other is quickly dispersed by the convective motions. Cattaneo et al. (2006) have studied the existence of flux tubes using an idealized simulation of a stably stratified atmosphere with shear in both the vertical and one horizontal direction driven by a forcing term in the momentum equation. They find that in the absence of symmetries, even in this laminar flow case, there are no flux surfaces separating the inside of a flux concentration from the outside, so that the magnetic field lines in the concentration connect chaotically to the outside and the “flux tube” is leaky (Figure 19). The fact that magnetic fields that are concentrated close to the surface tend to tangle and spread out in many directions below the surface has been demonstrated earlier by Grossmann-Doerth et al. (1998) — see also Vögler et al. (2005), Schaffenberger et al. (2005), and Stein and Nordlund (2006).
Magnetic field lines in a simulation snapshot viewed from an angle. The red line in the lower left is horizontal field being advected into the domain. In the lower center is a loop like flux concentration rising toward the surface. In the upper right is a vertical flux concentration or “flux tube” through the surface with its field lines connecting chaotically to the outside below the surface. Image reproduced by permission from Stein and Nordlund (2006), copyright by AAS.
Magnetic flux concentration at the solar surface and magnetic field lines showing the complex field line connections below the surface. The “flux tube” is a local surface phenomena. Image reproduced by permission from Schaffenberger et al. (2005).
Magnetic fields alter the granule properties - producing smaller, lower intensity contrast, “abnormal” granules (Bercik et al., 1998; Vögler, 2005). Strong magnetic flux concentrations typically form in convective downflow lanes, especially at the vertices of several such lanes, due to the sweeping of flux by the diverging convective upflows (Vögler et al., 2005; Stein and Nordlund, 2006). They are surrounded by downflows which sometimes become supersonic. The normal convective downflows are enhanced surrounding the flux concentrations by baroclinic driving due to the influx of radiation into the concentration (Deinzer et al., 1984; Knölker et al., 1991; Bercik, 2002; Vögler et al., 2005).
Granules become larger and darker as the field first emerges (due to the suppression of vertical motions by the horizontal section of the bipoles and adiabatic cooling due to their expansion) and elongate in the direction of the horizontal component of the field (Figure 20).
Emergent continuum intensity as a twisted flux tube emerges through the solar surface. Image reproduced by permission from Yelles Chaouche et al. (2005).
The main differences between these two approaches are that a coherent initial flux tube leads to a more coherent symmetrical structure when it emerges through the surface and field line connections below the surface are more localized. In the minimally structured approach organized magnetic field concentrations develop spontaneously when sufficient flux is present, instead of being imposed as initial and boundary conditions, so the emergent structures are less coherent.
4.3 Small scale flux concentrations
Magnetic concentrations arise from loops emerging into the upper solar atmosphere and leaving their legs behind and from the diverging convective upflows which sweep magnetic field into the intergranular lanes and concentrate the field into sheets and at the vertices of the lanes into “tubes” of magnetic flux (Vögler et al., 2005; Schaffenberger et al., 2005; Stein and Nordlund, 2006). To maintain force balance, locations of higher field strength (higher magnetic pressure) tend to have smaller plasma density and lower gas pressure. Strong magnetic fields, through the Lorentz force, inhibit overturning convective motions and hence the transport of energy toward the surface. Radiative energy loss to space continues, so regions of strong field cool relative to their surroundings at the same geometric layer. Being cooler, these locations have a smaller scale height. Plasma drains out of the magnetic field concentrations in a process called “convective intensification” or “convective collapse” (Parker, 1978; Spruit, 1979; Unno and Ando, 1979; Nordlund, 1986; Bercik et al., 1998; Grossmann-Doerth et al., 1998; Bushby et al., 2008). This process continues until the magnetic pressure (plus a small gas pressure) inside the flux concentration approximately equals the gas pressure outside, giving rise to a field strength much greater than the equipartition value with the dynamic pressure of the convective motions.
The opacity of magnetic flux concentrations is reduced, because they are evacuated, so photons escape from deeper in the atmosphere, that is, optical depth surfaces are depressed into the interior (Wilson depression, Maltby, 2000). Radiatively, they are holes in the surface. The temperature structure in these concentrations is nearly in radiative equilibrium with radiative heating from fluid flowing down along their sides and cooling from emission in vertical rays (Bercik, 2002, Figure 21). Where the flux concentration is narrow, heating from the side walls raises the internal temperature at optical depth unity and the concentration appears bright (Spruit, 1976). Small magnetic flux concentrations may appear especially bright in the continuum (Bercik, 2002; Keller et al., 2004; Carlsson et al., 2004; Steiner, 2010). This enhanced brightness extends for all the sight lines that pass through the low density, optically thinner, magnetic concentration where photons escape from deeper, hotter layers (Figures 22 and 23). Where the concentrations are wide, the side wall heating is not significant and the flux concentrations appear darker than the surroundings as pores or sunspots.
Radiative heating and cooling (1010 erg/g/s) in a vertical slice through a magnetic flux concentration. The top two panels show the net heating (yellow & red)/cooling (green & blue) with superimposed contours of temperature (top) and magnetic field (next to top). The bottom three panels show the net heating/cooling for vertical (cos θray,vertical = μ = 1), slanted (μ = 0.5), and nearly horizontal rays (μ = 0.05). Image reproduced by permission from Bercik (2002).
Temperature, density, and magnetic field strength along a vertical slice through magnetic and non-magnetic regions, with the average formation height for the G-band intensity for a vertical ray (black line) and at μ = 0.6 (white line). Axes are distances in Mm. The bottom panel shows temperature as function of lg τ500. Image reproduced by permission from Carlsson et al. (2004), copyright by AAS.
Schematic sketch of a magnetic flux concentration (region between the thin lines) and adjacent granules (thick lines). The dashed lines enclose the region where 80% of the continuum radiation is formed. Bright facular radiation originates from a thin layer at the hot granule wall behind the limbward side of the optically thin magnetic flux concentration. The line of sight for the dark centerward bands is shown by the dark shaded region. Image reproduced by permission from Keller et al. (2004), copyright by AAS.
In the G-band there is an additional, smaller, effect — the CH molecule becomes dissociated in the low density magnetic concentrations (Steiner et al., 2001; Carlsson et al., 2004; Shelyag et al., 2004; Steiner, 2005). The bottom panel of Figure 22 shows the temperature as function of lg τ500. The contrast in temperature between magnetic concentrations and non-magnetic areas increases with decreasing optical depth giving larger intensity contrast with increasing opacity (e.g., Ca H,K). The G-band has its mean formation height (black line in bottom panel) at lg τ500 = -0.48 corresponding to a mean formation height 54 km above where τ500 = 1, therefore giving a larger contrast than in the continuum. The contrast enhancement by the destruction of CH is seen as a dip in the curve showing the mean formation optical depth in the bottom panel. Note also that the G-band intensity has its peak contribution at similar heights as the continuum (that is why the granulation pattern looks similar). Bright points in the G-band have been used as a proxy for magnetic field concentrations. While G-band bright points are a good proxy for strong magnetic fields, there are many more regions of strong field that appear dark in the G-band, typically because they cover a larger area (Figure 24). In simulations, all the bright points correspond to locations of large field magnitude, but not all large field locations correspond to bright points (Vögler et al., 2005; Stein and Nordlund, 2006). Further, the field has a longer lifetime than the bright points. The contrast in the G-band has also been studied by Rutten et al. (2001), Sánchez Almeida et al. (2001), and Steiner et al. (2001).
4.4 Pores and sunspots
Recently, “realistic” radiative-convective MHD models of pores and sunspots have become possible. Bercik et al. (2003), Stein et al. (2003), and Vögler et al. (2005) found micropores forming spontaneously in magneto-convection simulations. Cameron et al. (2007a) modeled pores in magneto-convection simulations by imposing them as initial and boundary conditions. Stein et al. (2010b) found that large pores formed spontaneously in deep magneto-convection simulations. Schüssler and Vögler (2006) simulated a sunspot umbra where convection produced umbral dots. Heinemann et al. (2007), Scharmer et al. (2008), and Rempel et al. (2009b) started with flaring, rectangular, slab magnetic concentrations. Rempel et al. (2009a) and Rempel (2011) modeled sunspots in a magneto-convection simulation starting from a pair of axisymmetric, self-similar magnetic funnels. Cheung et al. (2010) modeled sunspots formed from an emerging, twisted half torus magnetic “flux tube”. An excellent review, especially of helioseismic applications, is Moradi et al. (2010). For more details on sunspots see the review by Rempel and Schlichenmaier (2011).
In magneto-convection simulations with initial vertical fields, micropores form spontaneously in vertices of the intergranular lanes where several lanes meet (Bercik et al., 2003; Stein et al., 2003; Vögler et al., 2005). In the typical formation scenario a small bright granule is surrounded by strong magnetic fields in the intergranular lanes. The upward velocity in the small granule reverses and it disappears with the area it occupied becoming dark. The surrounding strong fields move into the dark micropore area (Figure 28).
As the upflow velocity in a flux concentration slows and reverses, the upward heat flux decreases and the plasma inside the concentration cools by radiation through the surface (Figure 25). As a result, the density scale height decreases and the plasma settles lower. Initially the material piles up below the surface until a new hydrostatic structure is established (Figure 25). The micropores are also heated by radiation from their hotter sidewalls (Figure 21, Spruit, 1976, 1977). On the order of a granular timescale the magnetic field is dispersed and the micropore disappears.
Magnetic field (filled contours at 250 G intervals from 0 G to 3500 G) and temperature (top) (1000 K intervals from 4000 K to 16,000 K), and ln ρ (bottom) (in 0.5 intervals from -2 to 4). The τ = 1 depth is shown as the thick line around z = 0 Mm. The flux concentrations are significantly cooler than their surroundings and so have a smaller scale height. The established, strong “flux tube” in the center has been evacuated and is in equilibrium. The smaller flux concentrations on either side are in the process of being evacuated, starting above the surface and piling up plasma below the surface. Image reproduced by permission from Bercik (2002); Bercik et al. (2003).
Image of vertical velocity (red/yellow down, blue/green up in km s-1) with magnetic field contours at 0.5 kG intervals at the surface (left) and 1.5 Mm below the surface (right). Image reproduced by permission from Bercik (2002).
Pores have developed spontaneously in magneto-convection emerging flux simulations when rising Ω-loops emerge through the surface and the upper boundary, leaving behind vertical magnetic field concentrations (Stein and Nordlund, 2006). The pores grow by accumulating flux from their surroundings. The pore pictured in Figure 27 has reached a flux of 2.4 × 1020 Mx and occupies an area of 6 Mm2. The flux concentration develops first near the surface. It cools and quickly becomes partially evacuated and flux concentration extends downward, reaching all the way to the bottom of the domain (at 20 Mm depth) — Figure 29 and Figure 30, see also Kitiashvili et al. (2010). Most magnetic field lines in the pore connect to the end of a large scale loop rising from the bottom of the domain, although some connect to various other structures. Additional flux is being transported into the pore by horizontal flows along the intergranular lanes. These flows feeding the pore extend to depths of several megameters. The simulated pores have sometimes lasted for a long time — greater than 8 hrs (Kitiashvili et al., 2010) and 12 hrs in our case.
Spontaneously formed simulated pore. Clockwise from upper left: emergent intensity, vertical magnetic field at 〈τ〉 = 1, horizontal magnetic field at the same level, inclination angle to the vertical. The pore is edge brightened in part of its circumference. The field is vertical in the pore interior and becomes inclined more than 45° at the pore edge.
mpg-Movie (24956644 KB) Still from a movie showing Time sequence of temperature and density fluctuations during pore formation viewed from below (surface is at the bottom). Note the cooler temperatures extending downward from surface, followed by lower densities. Movie produced by Sandstrom, CSC, NASA Ames Res. Ctr. (For video see appendix)
mpg-Movie (34719413 KB) Still from a movie showing Time sequence of log |B| during pore formation. The flux concentration forms first at the surface and then extends downward. Near the surface the pore’s field is filamentary, but at large depths it becomes mostly coherent. Movie produced by Sandstrom, CSC, NASA Ames Res. Ctr. (For video see appendix)
Pores, like micropores, are surrounded by downflows concentrated into a few downdrafts. The ubiquitous occurrence of downflows in the close vicinity but outside magnetic flux concentrations (see, for example, also Steiner et al., 1998) has been explained in terms of baroclinic flows by Deinzer et al. (1984). The effect has been observationally verified by Langangen et al. (2007). Pores are edge brightened (Figure 27). Cameron et al. (2007b) explain this as due to the fact that the surface of unit optical depth occurs at slightly higher temperature at the edges of pores, possibly due to decreased overlying density because of the spreading magnetic field.
No one has yet produced a sunspot ab initio. Several “realistic” magneto-convection simulations of sunspots have been made starting with idealized, imposed initial magnetic field configurations. See review by Rempel and Schlichenmaier (2011). Cheung et al. (2010) has come closest, starting from an emerging, twisted, half torus magnetic “flux tube”. Others have started with monolithic, self-similar magnetic configurations. Schüssler and Vögler (2006) investigated magneto-convection in a uniform, vertical field representing a sunspot umbra. Heinemann et al. (2007), Scharmer et al. (2008), and Rempel et al. (2009b) studied flaring rectangular slab field configurations. Rempel et al. (2009a) and Rempel (2011) started with a pair of axisymmetric, self-similar funnels (Schüssler and Rempel, 2005), with the same flux but slightly different field strengths (Figure 31). All these simulations develop thin upflow plumes with surrounding downflows that are the observed umbral dots. The most challenging property of spots to model has been their penumbra, which are found to depend crucially on the existence of very inclined magnetic fields in the outer parts of the spots.
Still from a movie showing Emergent intensity and |B| (kG) in opposite polarity spot pair initiated from a pair of axial symmetric, self-similar flaring magnetic field funnels. Each spot has the same flux, but the one on the left has a slightly weaker field. The simulation domain is 98 × 49 Mm by 6 Mm depth. The vertical dimension has been stretched by a factor of 2 in the bottom panel (from Rempel et al., 2009a). (To watch the movie, please go to the online version of this review article at http://www.livingreviews.org/lrsp-2012-4.)
In the Cheung et al. (2010) simulation, spots form from an emerging Ω-loop (Figure 14). The field first emerges with mixed polarities. The opposite polarities then counterstream to collect into the opposite polarity sunspots. This counterstreaming of opposite polarities is due to the underlying large-scale structure of the coherent subsurface roots of the emerged “flux tube”, which influence the surface dynamics via the Lorentz force, especially magnetic tension (Cheung et al., 2010).
Although the strong magnetic fields in sunspots inhibit convection, they do not shut it down entirely. Umbral convection is observed as umbral dots and has been simulated by Schüssler and Vögler (2006). In such strong fields, convection manifests itself as very narrow upflow plumes of hot plasma with neighboring, narrow cool return downflows. The tendency of the magnetic field to expand as the gas pressure declines toward the surface pinches the rising plumes and accelerates the upward flow. As in normal convection, the upflows are braked rapidly near the surface where the plasma loses buoyancy due to radiative cooling. The plasma piles up, the gas pressure increases and makes the plasma expand latterly, which reduces the magnetic field strength. As a result of the enhanced density, the optical depth increases and photons can only escape from higher, cooler layers producing a dark lane through the bright umbral dot (Figure 32). Above the plume, which has been decelerated, the magnetic field again closes in, arching over the gap in a cusp shape.
Vertical slice through an umbral dot. Image is density fluctuation with respect to the surroundings. The solid line is Rossland optical depth unity. The dotted lines are isotherms. The arrows are velocity (longest is 2.7 km/s). Image reproduced by permission from Schüssler and Vögler (2006), copyright by AAS.
Heinemann et al. (2007), Scharmer et al. (2008), and Rempel (2011) have modeled sunspot penumbra (Figures 31, 33, 34). They find that penumbra are produced by overturning convective motions that occur in an inclined magnetic field and that the observed Evershed outflows (Evershed, 1909) are the horizontal flow of overturning convection channeled along the penumbral magnetic field.
Penumbral field lines color coded by velocity at several locations in a penumbra. Set 1 is in the umbra just adjacent to the penumbral head. Sets 2 – 6 are at increasing radial distance in the penumbra. Velocities are 0 – 2 km/s (red), 2 – 4 km/s (yellow), 4 – 8 km/s (green), > 8 km/s (blue). The cutting plane shows the vertical field magnitude at 〈τ〉 = 1. Image reproduced by permission from Rempel (2011), copyright by AAS.
Work as a function of radius and depth in the penumbra. The contours are where the average outflow is more than 2 and 4 km/s. The Lorentz force accelerates the fluid in the Evershed flow along the penumbral filaments, while in the inner penumbra below the surface there is an approximate balance between pressure and Lorentz forces. Image reproduced by permission from Rempel (2011), copyright by AAS.
However, unlike normal convection, it is the pressure force that that is pushing the upflow as well as the overturning horizontal flow. The downflows are in nearly hydrostatic equilibrium. Near the lower pressure photosphere the nearly vertical field lines of the penumbra spread outward (tending toward a potential field structure) and become more horizontal. The mass loading by the overturning, horizontal convective motions bends the magnetic field lines downward even more, when the initial inclination is more than 45°, which produces the nearly horizontal penumbral field (Figure 33). Cooling near τ = 1 increases the plasma density and field line bending. The Lorentz force turns the flow along the magnetic field to produce the Evershed outflow (Figure 34).
5 The Future
Rapid progress is currently occurring in solar magneto-convection simulations. What can we expect in the near future? More physics will be included: more accurate representation of the frequency dependence of the opacity, non-equilibrium ionization, partial ionization and non-LTE radiation. Such work is already begun in the bifrost (Gudiksen et al., 2011; Martínez-Sykora et al., 2012), stagger and MuRAM (Cheung and Cameron, 2012) codes. The next big step for numerical simulations of the upper photosphere and chromosphere is the inclusion of time-dependent and partial ionization effects (generalized Ohm’s Law and ambipolar diffusion) and the extension from single to multifluid equations (neutrals, ions and electrons) (Khomenko and Collados, 2012; Cheung and Cameron, 2012). The most time consuming part of “realistic” convection calculations is the radiative transfer, even with the drastic approximations currently made. Alternative numerical solutions of the transfer equation are possible (Hayek et al., 2010). Observations from larger ground (GREGOR, the Big Bear New Solar Telescope and the Advance Technology Solar Telescope) and new space based observatories (Solar Dynamics Observatory, Interface Region Imaging Spectrograph (IRIS) and Solar Orbiter) will allow more detailed comparisons between observations and simulations, which will assist in clarifying the significant physical processes that determine the solar magneto-dynamics.
The biggest unanswered questions are: exactly how does the solar dynamo work, the details of the process of mass and energy transport through and energy dissipation in the chromosphere and corona, and the origins of eruptive events. We have qualitative models of these processes. We now need a more quantitative understanding. We would like to know: how the large scale regularities of the solar cycle are produced, the relation between global and local surface dynamo action, the origin of supergranulation, the role of weak fields in energizing the chromosphere and corona, the triggers of eruptive events, and the relation between global and local coronal behavior.
References
Abbett, W.P., 2007, “The Magnetic Connection between the Convection Zone and Corona in the Quiet Sun”, Astrophys. J., 665, 1469–1488. [DOI], [ADS] (Cited on pages 14, 15, 16, and 17.)
Abbett, W.P. and Fisher, G.H., 2010, “Improving large-scale convection-zone-to-corona models”, in Chromospheric Structure and Dynamics: From Old Wisdom to New Insights, NSO Workshop #25, Sacramento Peak Observatory, Sunspot, NM, USA, August 31 - September 4, 2009, (Eds.) Tritschler, A., Reardon, K., Uitenbroek, H., vol. 81 of Mem. Soc. Astron. Ital., pp. 721–728, Italian Astronomical Society, Trieste. [ADS], [arXiv:1005.0641 [astro-ph.SR]] (Cited on pages 9 and 17.)
Abbett, W.P., Fisher, G.H. and Fan, Y., 2000, “The Three-dimensional Evolution of Rising, Twisted Magnetic Flux Tubes in a Gravitationally Stratified Model Convection Zone”, Astrophys. J., 540, 548–562. [DOI], [ADS], [arXiv:astro-ph/0004031] (Cited on page 14.)
Bello González, N., Yelles Chaouche, L., Okunev, O. and Kneer, F., 2009, “Dynamics of small-scale magnetic fields on the Sun: observations and numerical simulations”, Astron. Astrophys., 494, 1091–1106. [DOI], [ADS] (Cited on page 6.)
Bercik, D.J., 2002, A numerical investigation of the interaction between convection and magnetic field in a solar surface layer, Ph.D. thesis, Michigan State University, East Lansing. [ADS] (Cited on pages 24, 27, 28, 32, 33, and 34.)
Bercik, D.J., Basu, S., Georgobiani, D., Nordlund, Å. and Stein, R.F., 1998, “Solar Magneto-Convection”, in Cool Stars, Stellar Systems and the Sun: Tenth Cambridge Workshop, 10th Cambridge Workshop, Cambridge, MA, July 15–19, 1997, (Eds.) Donahue, R.A., Bookbinder, J.A., vol. 154 of ASP Conference Series, pp. 568–572, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on pages 6, 24, and 27.)
Bercik, D.J., Nordlund, Å. and Stein, R.F., 2003, “Magnetoconvection and micropores”, in Local and Global Helioseismology: The Present and Future, SOHO 12/GONG+ 2002 held at Big Bear Lake, California, 27 October–1 November 2002, (Ed.) Sawaya-Lacoste, H., vol. SP-517 of ESA Conference Proceedings, pp. 201–206, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 31, 32, and 34.)
Birch, A.C., Braun, D.C. and Fan, Y., 2010, “An Estimate of the Detectability of Rising Flux Tubes”, Astrophys. J. Lett., 723, L190–L194. [DOI], [ADS] (Cited on page 6.)
Borrero, J.M. and Kobel, P., 2011, “Inferring the magnetic field vector in the quiet Sun. I. Photon noise and selection criteria”, Astron. Astrophys., 527, A29. [DOI], [ADS], [arXiv:1011.4380 [astro-ph.SR]] (Cited on page 12.)
Brandenburg, A. and Dobler, W., 2002, “Solar and stellar dynamos. latest developments”, Astron. Nachr., 323, 411–416. [DOI], [ADS], [astro-ph/0207393] (Cited on page 15.)
Braun, D.C., Birch, A.C., Benson, D., Stein, R.F. and Nordlund, Å., 2007, “Helioseismic Holography of Simulated Solar Convection and Prospects for the Detection of Small-Scale Subsurface Flows”, Astrophys. J., 669, 1395–1405. [DOI], [ADS], [arXiv:0708.0214] (Cited on page 6.)
Braun, D.C., Birch, A.C., Rempel, M. and Duvall, T.L., 2012, “Helioseismology of a Realistic Magnetoconvective Sunspot Simulation”, Astrophys. J., 744, 77. [DOI], [ADS] (Cited on page 6.)
Brown, B.P., Browning, M.K., Brun, A.S., Miesch, M.S., Nelson, N.J. and Toomre, J., 2007, “Strong Dynamo Action in Rapidly Rotating Suns”, in Unsolved Problems in Stellar Physics: A Conference in Honor of Douglas Gough, Cambridge, UK, 2 - 6 July 2007, (Eds.) Stancliffe, R.J., Houdek, G., Martin, R.G., Tout, C.A., vol. 948 of AIP Conference Proceedings, pp. 271–278, American Institute of Physics, Melville, NY. [DOI], [ADS], [arXiv:0801.1684 [astro-ph]] (Cited on page 15.)
Brown, B.P., Browning, M.K., Brun, A.S., Miesch, M.S. and Toomre, J., 2010, “Persistent Magnetic Wreaths in a Rapidly Rotating Sun”, Astrophys. J., 711, 424–438. [DOI], [ADS], [arXiv:1011.2831 [astro-ph.SR]] (Cited on page 15.)
Browning, M.K., Miesch, M.S., Brun, A.S. and Toomre, J., 2006, “Dynamo Action in the Solar Convection Zone and Tachocline: Pumping and Organization of Toroidal Fields”, Astrophys. J. Lett., 648, L157–L160. [DOI], [ADS], [arXiv:astro-ph/0609153] (Cited on page 15.)
Brun, A.S., Miesch, M.S. and Toomre, J., 2004, “Global-Scale Turbulent Convection and Magnetic Dynamo Action in the Solar Envelope”, Astrophys. J., 614, 1073–1098. [DOI], [ADS], [arXiv:astro-ph/0610073] (Cited on page 15.)
Bushby, P.J., Houghton, S.M., Proctor, M.R.E. and Weiss, N.O., 2008, “Convective intensification of magnetic fields in the quiet Sun”, Mon. Not. R. Astron. Soc., 387, 698–706. [DOI], [ADS], [arXiv:0804.1238] (Cited on pages 6, 14, and 27.)
Cameron, R., Gizon, L. and Daiffallah, K., 2007a, “SLiM: a code for the simulation of wave propagation through an inhomogeneous, magnetised solar atmosphere”, Astron. Nachr., 328, 313–318. [DOI], [ADS], [arXiv:1002.2344 [astro-ph.SR]] (Cited on page 31.)
Cameron, R., Schüssler, M., Vögler, A. and Zakharov, V., 2007b, “Radiative magnetohydrodynamic simulations of solar pores”, Astron. Astrophys., 474, 261–272. [DOI], [ADS] (Cited on page 37.)
Carlsson, M., Stein, R.F., Nordlund, Å. and Scharmer, G.B., 2004, “Observational Manifestations of Solar Magnetoconvection: Center-to-Limb Variation”, Astrophys. J. Lett., 610, L137–L140. [DOI], [ADS], [arXiv:astro-ph/0406160] (Cited on pages 12, 27, 29, and 31.)
Carlsson, M., Hansteen, V.H. and Gudiksen, B.V., 2010, “Chromospheric heating and structure as determined from high resolution 3D simulations”, in Chromospheric Structure and Dynamics: From Old Wisdom to New Insights, NSO Workshop #25, Sacramento Peak Observatory, Sunspot, NM, USA, August 31 - September 4, 2009, (Eds.) Tritschler, A., Reardon, K., Uitenbroek, H., vol. 81 of Mem. Soc. Astron. Ital., pp. 582–587, Italian Astronomical Society, Trieste. [ADS], [arXiv:1001.1546 [astro-ph.SR]] (Cited on page 14.)
Cattaneo, F., 1999, “On the Origin of Magnetic Fields in the Quiet Photosphere”, Astrophys. J. Lett., 515, L39–L42. [DOI], [ADS] (Cited on pages 6 and 14.)
Cattaneo, F., Emonet, T. and Weiss, N.O., 2003, “On the Interaction between Convection and Magnetic Fields”, Astrophys. J., 588, 1183–1198. [DOI], [ADS] (Cited on page 14.)
Cattaneo, F., Brummell, N.H. and Cline, K.S., 2006, “What is a flux tube? On the magnetic field topology of buoyant flux structures”, Mon. Not. R. Astron. Soc., 365, 727–734. [DOI], [ADS] (Cited on page 23.)
Centeno, R., Socas-Navarro, H., Lites, B., Kubo, M., Frank, Z., Shine, R., Tarbell, T., Title, A.M., Ichimoto, K., Tsuneta, S., Katsukawa, Y., Suematsu, Y., Shimizu, T. and Nagata, S., 2007, “Emergence of Small-Scale Magnetic Loops in the Quiet-Sun Internetwork”, Astrophys. J. Lett., 666, L137–L140. [DOI], [ADS], [arXiv:0708.0844] (Cited on pages 5 and 13.)
Charbonneau, P., 2010, “Dynamo Models of the Solar Cycle”, Living Rev. Solar Phys., 7, lrsp–2010–3. [ADS]. URL (accessed 19 March 2012): http://www.livingreviews.org/lrsp-2010-3 (Cited on pages 5 and 17.)
Cheung, M.C.M. and Cameron, R.H., 2012, “Magnetohydrodynamics of the Weakly Ionized Solar Photosphere”, Astrophys. J., 750, 6. [DOI], [ADS], [arXiv:1202.1937 [astro-ph.SR]] (Cited on page 41.)
Cheung, M.C.M., Schüssler, M. and Moreno-Insertis, F., 2007, “Magnetic flux emergence in granular convection: radiative MHD simulations and observational signatures”, Astron. Astrophys., 467, 703–719. [DOI], [ADS], [arXiv:astro-ph/0702666] (Cited on pages 6, 17, and 21.)
Cheung, M.C.M., Schüssler, M., Tarbell, T.D. and Title, A.M., 2008, “Solar Surface Emerging Flux Regions: A Comparative Study of Radiative MHD Modeling and Hinode SOT Observations”, Astrophys. J., 687, 1373–1387. [DOI], [ADS], [arXiv:0810.5723] (Cited on page 17.)
Cheung, M.C.M., Rempel, M., Title, A.M. and Schüssler, M., 2010, “Simulation of the Formation of a Solar Active Region”, Astrophys. J., 720, 233.244. [DOI], [ADS], [arXiv:1006.4117 [astro-ph.SR]] (Cited on pages 17, 20, 22, 23, 24, 31, 37, and 38.)
Danilovic, S., Beeck, B., Pietarila, A., Schüssler, M., Solanki, S.K., Martínez Pillet, V., Bonet, J.A., del Toro Iniesta, J.C., Domingo, V., Barthol, P., Berkefeld, T., Gandorfer, A., Knölker, M., Schmidt, W. and Title, A.M., 2010, “Transverse Component of the Magnetic Field in the Solar Photosphere Observed by SUNRISE”, Astrophys. J. Lett., 723, L149–L153. [DOI], [ADS], [arXiv:1008.1535 [astro-ph.SR]] (Cited on pages 12 and 13.)
De Pontieu, B., Carlsson, M., Stein, R.F., Rouppe van der Voort, L., Löfdahl, M., van Noort, M., Nordlund, Å. and Scharmer, G., 2006, “Rapid Temporal Variability of Faculae: High-Resolution Observations and Modeling”, Astrophys. J., 646, 1405–1420. [DOI], [ADS] (Cited on page 13.)
de Wijn, A.G., Rutten, R.J. and Haverkamp, 2005, “DOT tomography of the solar atmosphere. IV. Magnetic patches in internetwork areas”, Astron. Astrophys., 441, 1183–1190. [DOI], [ADS], [arXiv:0706.2008] (Cited on page 20.)
de Wijn, A.G., Stenflo, J.O., Solanki, S.K. and Tsuneta, S., 2009, “Small-Scale Solar Magnetic Fields”, Space Sci. Rev., 144, 275–315. [DOI], [ADS], [arXiv:0812.4465] (Cited on pages 5 and 10.)
Deinzer, W., Hensler, G., Schüssler, M. and Weisshaar, E., 1984, “Model calculations of magnetic flux tubes. II. Stationary results for solar magnetic elements”, Astron. Astrophys., 139, 435–449. [ADS] (Cited on pages 24 and 37.)
Dobler, W., Stix, M. and Brandenburg, A., 2006, “Magnetic Field Generation in Fully Convective Rotating Spheres”, Astrophys. J., 638, 336–347. [DOI], [ADS], [arXiv:astro-ph/0410645] (Cited on page 15.)
Dorch, S.B.F. and Nordlund, Å., 2000, “The Solar Dynamo: Flux Pumping by Stratified Convection”, in The Solar Cycle and Terrestrial Climate, Proceedings of the 1st Solar and Space Weather Euroconference: 25 - 29 September 2000, Instituto de Astrofísica de Canarias, Santa Cruz de Tenerife, Tenerife, Spain, (Ed.) Wilson, A., vol. SP-463 of ESA Conference Proceedings, pp. 305–308, ESA Publications Division, Nordwijk. [ADS] (Cited on page 17.)
Dorch, S.B.F. and Nordlund, Å., 2001, “On the transport of magnetic fields by solar-like stratified convection”, Astron. Astrophys., 365, 562–570. [DOI], [ADS], [arXiv:astro-ph/0006358] (Cited on pages 14 and 17.)
Drobyshevskii, E.M., Kolesnikova, E.N. and Iuferev, V.S., 1980, “The rate of magnetic field penetration through a Bénard convection layer”, J. Fluid Mech., 101, 65–78. [DOI], [ADS] (Cited on page 17.)
Emonet, T. and Cattaneo, F., 2001, “Small-Scale Photospheric Fields: Observational Evidence and Numerical Simulations”, Astrophys. J. Lett., 560, L197–L200. [DOI], [ADS] (Cited on pages 6, 14, and 20.)
Evershed, J., 1909, “Radial movement in sun-spots”, Mon. Not. R. Astron. Soc., 69, 454–458. [ADS] (Cited on page 39.)
Fabbian, D., Khomenko, E., Moreno-Insertis, F. and Nordlund, Å., 2010, “Solar Abundance Corrections Derived Through Three-dimensional Magnetoconvection Simulations”, Astrophys. J., 724, 1536–1541. [DOI], [ADS], [arXiv:1006.0231 [astro-ph.SR]] (Cited on page 6.)
Fan, Y., 2009, “Magnetic Fields in the Solar Convection Zone”, Living Rev. Solar Phys., 6, lrsp–2009–4. [ADS]. URL (accessed 22 March 2012): http://www.livingreviews.org/lrsp-2009-4 (Cited on pages 5, 14, and 17.)
Gizon, L. and Birch, A.C., 2005, “Local Helioseismology”, Living Rev. Solar Phys., 2, lrsp–2005–6. [ADS]. URL (accessed 26 March 2012): http://www.livingreviews.org/lrsp-2005-6 (Cited on page 5.)
Grossmann-Doerth, U., Schüssler, M. and Steiner, O., 1998, “Convective intensification of solar surface magnetic fields: results of numerical experiments”, Astron. Astrophys., 337, 928–939. [ADS] (Cited on pages 6, 24, and 27.)
Gudiksen, B.V., Carlsson, M., Hansteen, V.H., Hayek, W., Leenaarts, J. and Martínez-Sykora, J., 2011, “The stellar atmosphere simulation code Bifrost: Code description and validation”, Astron. Astrophys., 531, A154. [DOI], [ADS] (Cited on pages 9, 14, and 41.)
Guglielmino, S.L., Martínez Pillet, V., Bonet, J.A., del Toro Iniesta, J.C., Bellot Rubio, L.R., Solanki, S.K., Schmidt, W., Gandorfer, A., Barthol, P. and Knölker, M., 2012, “The Frontier between Small-scale Bipoles and Ephemeral Regions in the Solar Photosphere: Emergence and Decay of an Intermediatescale Bipole Observed with SUNRISE/IMaX”, Astrophys. J., 745, 160. [DOI], [ADS], [arXiv:1110.1405 [astro-ph.SR]] (Cited on pages 5 and 13.)
Hansteen, V.H., Carlsson, M. and Gudiksen, B., 2007, “3D Numerical Models of the Chromosphere, Transition Region, and Corona”, in The Physics of Chromospheric Plasmas, Coimbra, Portugal, 9–13 October 2006, (Eds.) Heinzel, P., Dorotović, I., Rutten, R.J., vol. 368 of ASP Conference Series, pp. 107–114, Astronomical Society of the Pacific, San Francisco. [ADS], [arXiv:0704.1511 [astro-ph]] (Cited on page 14.)
Harvey, J.W., Branston, D., Henney, C.J. and Keller, C.U. [SOLIS and GONG Teams], 2007, “Seething Horizontal Magnetic Fields in the Quiet Solar Photosphere”, Astrophys. J. Lett., 659, L177–L180. [DOI], [ADS], [arXiv:astro-ph/0702415] (Cited on page 10.)
Hathaway, D.H., 2010, “The Solar Cycle”, Living Rev. Solar Phys., 7, lrsp–2010–1. [ADS]. URL (accessed 22 March 2012): http://www.livingreviews.org/lrsp-2010-1 (Cited on pages 5, 10, and 11.)
Hayek, W., Asplund, M., Carlsson, M., Trampedach, R., Collet, R., Gudiksen, B.V., Hansteen, V.H. and Leenaarts, J., 2010, “Radiative transfer with scattering for domain-decomposed 3D MHD simulations of cool stellar atmospheres. Numerical methods and application to the quiet, non-magnetic, surface of a solar-type star”, Astron. Astrophys., 517, A49. [DOI], [ADS] (Cited on page 41.)
Heinemann, T., Nordlund, Å., Scharmer, G.B. and Spruit, H.C., 2007, “MHD Simulations of Penumbra Fine Structure”, Astrophys. J., 669, 1390–1394. [DOI], [ADS], [arXiv:astro-ph/0612648] (Cited on pages 31 and 38.)
Hirzberger, J. and Wiehr, E., 2005, “Solar limb faculae”, Astron. Astrophys., 438, 1059–1065. [DOI], [ADS] (Cited on page 13.)
Hotta, H., Rempel, M., Yokoyama, T., Iida, Y. and Fan, Y., 2012, “Numerical calculation of convection with reduced speed of sound technique”, Astron. Astrophys., 539, A30. [DOI], [ADS], [arXiv:1201.1061 [astro-ph.SR]] (Cited on page 14.)
Hurlburt, N.E. and Rucklidge, A.M., 2000, “Development of structure in pores and sunspots: flows around axisymmetric magnetic flux tubes”, Mon. Not. R. Astron. Soc., 314, 793–806. [DOI], [ADS] (Cited on page 14.)
Hurlburt, N.E. and Toomre, J., 1988, “Magnetic fields interacting with nonlinear compressible convection”, Astrophys. J., 327, 920–932. [DOI], [ADS] (Cited on page 20.)
Ishikawa, R. and Tsuneta, S., 2009, “Comparison of transient horizontal magnetic fields in a plage region and in the quiet Sun”, Astron. Astrophys., 495, 607–612. [DOI], [ADS], [arXiv:0812.1631] (Cited on pages 5, 12, and 14.)
Ishikawa, R. and Tsuneta, S., 2010, “Spatial and Temporal Distributions of Transient Horizontal Magnetic Fields with Deep Exposure”, Astrophys. J. Lett., 718, L171–L175. [DOI], [ADS] (Cited on pages 10 and 20.)
Ishikawa, R., Tsuneta, S. and Jurčák, J., 2010, “Three-Dimensional View of Transient Horizontal Magnetic Fields in the Photosphere”, Astrophys. J., 713, 1310–1321. [DOI], [ADS], [arXiv:1003.1376 [astro-ph.SR]] (Cited on pages 5, 13, and 14.)
Isobe, H., Proctor, M.R.E. and Weiss, N.O., 2008, “Convection-driven Emergence of Small-Scale Magnetic Fields and their Role in Coronal Heating and Solar Wind Acceleration”, Astrophys. J. Lett., 679, L57–L60. [DOI], [ADS] (Cited on page 20.)
Jacoutot, L., Kosovichev, A.G., Wray, A. and Mansour, N.N., 2008, “Realistic Numerical Simulations of Solar Convection and Oscillations in Magnetic Regions”, Astrophys. J. Lett., 684, L51–L54. [DOI], [ADS] (Cited on page 14.)
Keller, C.U., Schüssler, M., Vögler, A. and Zakharov, V., 2004, “On the Origin of Solar Faculae”, Astrophys. J. Lett., 607, L59–L62. [DOI], [ADS] (Cited on pages 12, 13, 27, and 30.)
Khomenko, E.V. and Collados, M., 2012, “Heating of the Magnetized Solar Chromosphere by Partial Ionization Effects”, Astrophys. J., 747, 87. [DOI], [ADS], [arXiv:1112.3374 [astro-ph.SR]] (Cited on page 41.)
Khomenko, E.V., Shelyag, S., Solanki, S.K. and Vögler, A., 2005, “Stokes diagnostics of simulations of magnetoconvection of mixed-polarity quiet-Sun regions”, Astron. Astrophys., 442, 1059–1078. [DOI], [ADS] (Cited on page 6.)
Kitiashvili, I.N., Jacoutot, L., Kosovichev, A.G., Wray, A.A. and Mansour, N.N., 2009, “Numerical Modeling of Solar Convection and Oscillations in Magnetic Regions”, in Stellar Pulsation: Challenges for Theory and Observation, Santa Fe, NM, 31 May - 5 June 2009, (Eds.) Guzik, J.A., Bradley, P.A., vol. 1170 of AIP Conference Proceedings, pp. 569–573, American Institute of Physics, Melville, NY. [DOI], [ADS] (Cited on page 6.)
Kitiashvili, I.N., Kosovichev, A.G., Mansour, N.N. and Wray, A.A., 2010, “Numerical MHD Simulations of Solar Magnetoconvection and Oscillations in Inclined Magnetic Field Regions”, Solar Phys., 268, 283–291. [DOI], [ADS], [arXiv:1011.5527 [astro-ph.SR]] (Cited on pages 17 and 37.)
Knölker, M., Grossmann-Doerth, U., Schüssler, M. and Weisshaar, E., 1991, “Some developments in the theory of magnetic flux concentrations in the solar atmosphere”, Adv. Space Res., 11, 285–295. [DOI], [ADS] (Cited on page 24.)
Krijger, J.M. and Roudier, T., 2003, “Photospheric flows measured with TRACE II. Network formation”, Astron. Astrophys., 403, 715–723. [DOI], [ADS] (Cited on page 20.)
Langangen, O., Carlsson, M., Rouppe van der Voort, L. and Stein, R.F., 2007, “Velocities Measured in Small-Scale Solar Magnetic Elements”, Astrophys. J., 655, 615–623. [DOI], [ADS], [astro-ph/0611741] (Cited on page 37.)
Lites, B.W., 2009, “The Topology and Behavior of Magnetic Fields Emerging at the Solar Photosphere”, Space Sci. Rev., 144, 197–212. [DOI], [ADS] (Cited on page 23.)
Lites, B.W., Scharmer, G.B., Berger, T.E. and Title, A.M., 2004, “Three-Dimensional Structure of the Active Region Photosphere as Revealed by High Angular Resolution”, Solar Phys., 221, 65–84. [DOI], [ADS] (Cited on page 13.)
Lites, B.W., Kubo, M., Socas-Navarro, H., Berger, T., Frank, Z., Shine, R., Tarbell, T., Title, A.M., Ichimoto, K., Katsukawa, Y., Tsuneta, S., Suematsu, Y., Shimizu, T. and Nagata, S., 2008, “The Horizontal Magnetic Flux of the Quiet-Sun Internetwork as Observed with the Hinode Spectro-Polarimeter”, Astrophys. J., 672, 1237–1253. [DOI], [ADS] (Cited on page 12.)
Maltby, P., 2000, “Sunspots: Wilson Effect”, in Encyclopedia of Astronomy and Astrophysics, (Ed.) Murdin, P., Institute of Physics Publishing, Bristol. [DOI], [ADS] (Cited on pages 6 and 27.)
Martínez González, M.J. and Bellot Rubio, L.R., 2009, “Emergence of Small-scale Magnetic Loops Through the Quiet Solar Atmosphere”, Astrophys. J., 700, 1391–1403. [DOI], [ADS], [arXiv:0905.2691 [astroph. SR]] (Cited on pages 5, 13, and 14.)
Martínez-Sykora, J., Hansteen, V. and Carlsson, M., 2008, “Twisted Flux Tube Emergence From the Convection Zone to the Corona”, Astrophys. J., 679, 871–888. [DOI], [ADS], [arXiv:0712.3854] (Cited on page 17.)
Martínez-Sykora, J., Hansteen, V. and Carlsson, M., 2009, “Twisted Flux Tube Emergence from the Convection Zone to the Corona. II. Later States”, Astrophys. J., 702, 129–140. [DOI], [ADS], [arXiv:0906.5464 [astro-ph.SR]] (Cited on page 17.)
Martínez-Sykora, J., De Pontieu, B. and Hansteen, V.H., 2012, “2D Radiative MHD Simulations of the Importance of Partial Ionization in the Chromosphere”, Astrophys. J., 753, 161. [DOI], [ADS], [arXiv:1204.5991 [astro-ph.SR]] (Cited on page 41.)
Meneguzzi, M., Frisch, U. and Pouquet, A., 1981, “Helical and nonhelical turbulent dynamos”, Phys. Rev. Lett., 47, 1060.1064. [DOI], [ADS] (Cited on page 14.)
Miesch, M.S., 2005, “Large-Scale Dynamics of the Convection Zone and Tachocline”, Living Rev. Solar Phys., 2, lrsp–2005–1. [ADS]. URL (accessed 22 March 2012): http://www.livingreviews.org/lrsp-2005-1 (Cited on pages 14 and 15.)
Miesch, M.S. and Toomre, J., 2009, “Turbulence, Magnetism, and Shear in Stellar Interiors”, Annu. Rev. Fluid Mech., 41, 317–345. [DOI], [ADS] (Cited on pages 14 and 17.)
Miesch, M.S., Brun, A.S., De Rosa, M.L. and Toomre, J., 2008, “Structure and Evolution of Giant Cells in Global Models of Solar Convection”, Astrophys. J., 673, 557–575. [DOI], [ADS], [arXiv:0707.1460] (Cited on page 14.)
Miesch, M.S., Brown, B.P., Browning, M.K., Brun, A.S. and Toomre, J., 2011, “Magnetic Cycles and Meridional Circulation in Global Models of Solar Convection”, in Astrophysical Dynamics: From Stars to Galaxies, Nice, France, June 21 - 25, 2010, (Eds.) Brummell, N.H., Brun, A.S., Miesch, M.S., Ponty, Y., vol. 271 of Proc. IAU, pp. 261–269, Cambridge University Press, Cambridge; New York. [DOI], [ADS], [arXiv:1009.6184 [astro-ph.SR]] (Cited on page 14.)
Moradi, H., Baldner, C., Birch, A.C., Braun, D.C., Cameron, R.H., Duvall, T.L., Gizon, L., Haber, D., Hanasoge, S.M., Hindman, B.W., Jackiewicz, J., Khomenko, E.V., Komm, R., Rajaguru, P., Rempel, M., Roth, M., Schlichenmaier, R., Schunker, H., Spruit, H.C., Strassmeier, K.G., Thompson, M.J. and Zharkov, S., 2010, “Modeling the Subsurface Structure of Sunspots”, Solar Phys., 267, 1–62. [DOI], [ADS], [arXiv:0912.4982 [astro-ph.SR]] (Cited on page 31.)
Muller, R., Hulot, J.C. and Roudier, T., 1989, “Perturbation of the granular pattern by the presence of magnetic flux tubes”, Solar Phys., 119, 229–243. [DOI], [ADS] (Cited on page 6.)
Nordlund, Å., 1982, “Numerical simulations of the solar granulation. I. Basic equations and methods”, Astron. Astrophys., 107, 1–10. [ADS] (Cited on pages 9 and 14.) Nordlund, Å., 1986, “3-D Model Calculations”, in Small Scale Magnetic Flux Concentrations in the Solar Photosphere, Workshop held in Göttingen, 1 - 3 October 1985, (Eds.) Deinzer, W., Knölker, M., Voigt, H.H., vol. 38 of Abhandlungen der Akademie der Wissenschaften zu Göttingen. Mathematisch-Physikalische Klasse, p. 83, Vandenhoeck & Ruprecht, Göttingen. [ADS] (Cited on pages 6 and 27.)
Nordlund, Å., Brandenburg, A., Jennings, R.L., Rieutord, M., Ruokolainen, J., Stein, R.F. and Tuominen, I., 1992, “Dynamo action in stratified convection with overshoot”, Astrophys. J., 392, 647–652. [DOI], [ADS] (Cited on pages 6 and 17.)
Nordlund, Å., Stein, R.F. and Asplund, M., 2009, “Solar Surface Convection”, Living Rev. Solar Phys., 6, lrsp–2009–2. [ADS]. URL (accessed 22 March 2012): http://www.livingreviews.org/lrsp-2009-2 (Cited on pages 5 and 7.)
Ossendrijver, M., 2003, “The solar dynamo”, Astron. Astrophys. Rev., 11, 287–367. [DOI], [ADS] (Cited on page 17.)
Parker, E.N., 1978, “Hydraulic concentration of magnetic fields in the solar photosphere. VI. Adiabatic cooling and concentration in downdrafts”, Astrophys. J., 221, 368–377. [DOI], [ADS] (Cited on pages 6 and 27.)
Parnell, C.E., DeForest, C.E., Hagenaar, H.J., Johnston, B.A., Lamb, D.A. and Welsch, B.T., 2009, “A Power-Law Distribution of Solar Magnetic Fields Over More Than Five Decades in Flux”, Astrophys. J., 698, 75–82. [DOI], [ADS] (Cited on pages 5, 10, 11, and 17.)
Petrovay, K. and Szakály, G., 1993, “The origin of intranetwork fields: a small-scale solar dynamo”, Astron. Astrophys., 274, 543–554. [ADS] (Cited on page 17.)
Pietarila Graham, J., Cameron, R. and Schüssler, M., 2010, “Turbulent Small-Scale Dynamo Action in Solar Surface Simulations”, Astrophys. J., 714, 1606–1616. [DOI], [ADS], [arXiv:1002.2750 [astro-ph.SR]] (Cited on pages 6, 14, and 15.)
Rempel, M., 2011, “Penumbral Fine Structure and Driving Mechanisms of Large-scale Flows in Simulated Sunspots”, Astrophys. J., 729, 5. [DOI], [ADS], [arXiv:1101.2200 [astro-ph.SR]] (Cited on pages 31, 38, 39, and 40.)
Rempel, M. and Schlichenmaier, R., 2011, “Sunspot Modeling: From Simplified Models to Radiative MHD Simulations”, Living Rev. Solar Phys., 8, lrsp–2011–3. [ADS]. URL (accessed 22 March 2012): http://www.livingreviews.org/lrsp-2011-3 (Cited on pages 31 and 37.)
Rempel, M., Schüssler, M., Cameron, R.H. and Knölker, M., 2009a, “Penumbral Structure and Outflows in Simulated Sunspots”, Science, 325, 171–174. [DOI], [ADS], [arXiv:0907.2259 [astro-ph.SR]] (Cited on pages 31, 37, and 38.)
Rempel, M., Schüssler, M. and Knölker, M., 2009b, “Radiative Magnetohydrodynamic Simulation of Sunspot Structure”, Astrophys. J., 691, 640–649. [DOI], [ADS], [arXiv:0808.3294] (Cited on pages 31 and 38.)
Rutten, R.J., Kiselman, D., Rouppe van der Voort, L. and Plez, B., 2001, “Proxy Magnetometry of the Photosphere: Why are G-Band Bright Points so Bright?”, in Advanced Solar Polarimetry - Theory, Observation, and Instrumentation, Proceedings of the 20th Sacramento Peak Summer Workshop, held at NSO/Sac, Sunspot, New Mexico, USA, 11–15 September 2000, (Ed.) Sigwarth, M., vol. 236 of ASP Conference Series, pp. 445–452, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 31.)
Sánchez Almeida, J., Asensio Ramos, A., Trujillo Bueno, J. and Cernicharo, J., 2001, “G-Band Spectral Synthesis in Solar Magnetic Concentrations”, Astrophys. J., 555, 978–989. [DOI], [ADS], [astroph/ 0103006] (Cited on page 31.)
Sánchez Almeida, J., Emonet, T. and Cattaneo, F., 2003, “Polarization of Photospheric Lines from Turbulent Dynamo Simulations”, Astrophys. J., 585, 536–552. [DOI], [ADS], [arXiv:astro-ph/0211175] (Cited on page 6.)
Schaffenberger, W., Wedemeyer-Böhm, S., Steiner, O. and Freytag, B., 2005, “Magneto-hydrodynamic Simulation from the Convection Zone to the Chromosphere”, in Chromospheric and Coronal Magnetic Fields, Proceedings of the International Scientific Conference, 30 August - 2 September 2005, Katlenburg-Lindau, Germany, (Eds.) Innes, D.E., Lagg, A., Solanki, S.A., Danesy, D., vol. SP-596 of ESA Conference Proceedings, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 14, 23, 24, 26, and 27.)
Scharmer, G.B., Nordlund, Å. and Heinemann, T., 2008, “Convection and the Origin of Evershed Flows in Sunspot Penumbrae”, Astrophys. J. Lett., 677, L149–L152. [DOI], [ADS], [arXiv:0802.1927] (Cited on pages 31 and 38.)
Schüssler, M., 2001, “Numerical Simulation of Solar Magneto-Convection”, in Advanced Solar Polarimetry — Theory, Observation, and Instrumentation, 20th Sacramento Peak Summer Workshop, Sunspot, New Mexico, USA, 11 - 15 September 2000, (Ed.) Sigwarth, M., vol. 236 of ASP Conference Series, pp. 343–354, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 14.)
Schüssler, M. and Rempel, M., 2005, “The dynamical disconnection of sunspots from their magnetic roots”, Astron. Astrophys., 441, 337–346. [DOI], [ADS], [arXiv:astro-ph/0506654] (Cited on page 38.)
Schüssler, M. and Vögler, A., 2006, “Magnetoconvection in a Sunspot Umbra”, Astrophys. J. Lett., 641, L73–L76. [DOI], [ADS], [astro-ph/0603078] (Cited on pages 31, 37, and 38.)
Schüssler, M. and Vögler, A., 2008, “Strong horizontal photospheric magnetic field in a surface dynamo simulation”, Astron. Astrophys., 481, L5–L8. [DOI], [ADS], [arXiv:0801.1250] (Cited on pages 6, 15, and 16.)
Shelyag, S., Schüssler, M., Solanki, S.K., Berdyugina, S.V. and Vögler, A., 2004, “G-band spectral synthesis and diagnostics of simulated solar magneto-convection”, Astron. Astrophys., 427, 335–343. [DOI], [ADS] (Cited on pages 12 and 31.)
Shelyag, S., Schüssler, M., Solanki, S.K. and Vögler, A., 2007, “Stokes diagnostics of simulated solar magneto-convection”, Astron. Astrophys., 469, 731–747. [DOI], [ADS], [arXiv:astro-ph/0703490] (Cited on page 6.)
Simon, G.W., Title, A.M. and Weiss, N.O., 2001, “Sustaining the Sun’s Magnetic Network with Emerging Bipoles”, Astrophys. J., 561, 427–434. [DOI], [ADS] (Cited on page 20.)
Skartlien, R., 2000, “A Multigroup Method for Radiation with Scattering in Three-Dimensional Hydrodynamic Simulations”, Astrophys. J., 536, 465–480. [DOI], [ADS] (Cited on page 9.)
Spruit, H.C., 1976, “Pressure equilibrium and energy balance of small photospheric fluxtubes”, Solar Phys., 50, 269–295. [DOI], [ADS] (Cited on pages 6, 12, 27, and 31.)
Spruit, H.C., 1977, “Heat flow near obstacles in the solar convection zone”, Solar Phys., 55, 3–34. [DOI], [ADS] (Cited on pages 12 and 31.)
Spruit, H.C., 1979, “Convective collapse of flux tubes”, Solar Phys., 61, 363–378. [DOI], [ADS] (Cited on pages 6 and 27.)
Stein, R.F. and Nordlund, Å., 1989, “Topology of convection beneath the solar surface”, Astrophys. J. Lett., 342, L95–L98. [DOI], [ADS] (Cited on page 5.)
Stein, R.F. and Nordlund, Å., 1998, “Simulations of Solar Granulation. I. General Properties”, Astrophys. J., 499, 914–933. [DOI], [ADS] (Cited on pages 5, 9, and 14.)
Stein, R.F. and Nordlund, Å., 2003, “Radiative Transfer in 3D Numerical Simulations”, in Stellar Atmosphere Modeling, Tübingen, Germany, 8–12 April 2002, (Eds.) Hubeny, I., Mihalas, D., Werner, K., vol. 288 of ASP Conference Series, pp. 519–532, Astronomical Society of the Pacific, San Francisco. [ADS], [arXiv:astro-ph/0209510] (Cited on page 9.)
Stein, R.F. and Nordlund, Å., 2004, “Magneto-Convection: Structure and Dynamics”, in Multi-Wavelength Investigations of Solar Activity, St. Petersburg, Russian Federation, June 14 - 19, 2004, (Eds.) Stepanov, A.V., Benevolenskaya, E.E., Kosovichev, A.G., vol. 223 of IAU Symposium, pp. 179–182, Cambridge University Press, Cambridge; New York. [DOI], [ADS] (Cited on pages 6 and 20.)
Stein, R.F. and Nordlund, Å., 2006, “Solar Small-Scale Magnetoconvection”, Astrophys. J., 642, 1246–1255. [DOI], [ADS] (Cited on pages 6, 14, 20, 23, 24, 26, 27, 31, and 37.)
Stein, R.F., Bercik, D.J. and Nordlund, Å., 2003, “Solar Surface Magneto-Convection”, in Current Theoretical Models and High Resolution Solar Observations: Preparing for ATST, 21st Sacramento Peak Workshop, held at the National Solar Observatory, Sunspot, New Mexico, 11 - 15 March 2002, (Eds.) Pevtsov, A.A., Uitenbroek, H., vol. 286 of ASP Conference Series, pp. 121–131, Astronomical Society of the Pacific, San Francisco. [ADS], [arXiv:astro-ph/0209470] (Cited on pages 14 and 31.)
Stein, R.F., Lagerfjärd, A., Nordlund, Å. and Georgobiani, D., 2010a, “Solar Flux Emergence Simulations”, Solar Phys., 268, 271–283. [DOI], [ADS], [arXiv:0912.4938 [astro-ph.SR]] (Cited on page 17.)
Stein, R.F., Lagerfjärd, A., Nordlund, Å. and Georgobiani, D., 2010b, “Emerging Flux Simulations and Proto-Active Regions”, in 4th Hinode Science Meeting: Unsolved Problems and Recent Insights, Proceedings of a Conference held at Mondello, Palermo, Italy, 11 - 15 October 2010, (Eds.) Bellot Rubio, L.R., Reale, F., Carlsson, M., vol. 455 of ASP Conference Series, pp. 133–142, Astronomical Societry of the Pacific, San Francisco. [ADS], [arXiv:1102.1049 [astro-ph.SR]] (Cited on pages 6, 17, and 31.)
Steiner, O., 2005, “Radiative properties of magnetic elements. II. Center to limb variation of the appearance of photospheric faculae”, Astron. Astrophys., 430, 691–700. [DOI], [ADS] (Cited on pages 13 and 31.)
Steiner, O., 2010, “Magnetic Coupling in the Quiet Solar Atmosphere”, in Magnetic Coupling between the Interior and Atmosphere of the Sun, ‘Centenary Commemoration of the Discovery of the Evershed Effect’ held in Bangalore, India, December 2 - 5, 2008, (Eds.) Hasan, S.S., Rutten, R.J., Astrophysics and Space Science Proceedings, pp. 166–185, Springer, Berlin; New York. [DOI], [ADS], [arXiv:0904.2026 [astro-ph.SR]] (Cited on pages 15 and 27.)
Steiner, O., Grossmann-Doerth, U., Knölker, M. and Schüssler, M., 1998, “Dynamical Interaction of Solar Magnetic Elements and Granular Convection: Results of a Numerical Simulation”, Astrophys. J., 495, 468–484. [DOI], [ADS] (Cited on pages 14, 20, and 37.)
Steiner, O., Hauschildt, P.H. and Bruls, J., 2001, “Radiative properties of magnetic elements. I. Why are..-band bright points bright?”, Astron. Astrophys., 372, L13–L16. [DOI], [ADS] (Cited on page 31.)
Tao, L., Proctor, M.R.E. and Weiss, N.O., 1998a, “Flux expulsion by inhomogeneous turbulence”, Mon. Not. R. Astron. Soc., 300, 907–914. [DOI], [ADS] (Cited on pages 6 and 20.)
Tao, L., Weiss, N.O., Brownjohn, D.P. and Proctor, M.R.E., 1998b, “Flux Separation in Stellar Magneto-convection”, Astrophys. J. Lett., 496, L39–L42. [DOI], [ADS] (Cited on page 14.)
Thornton, L.M. and Parnell, C.E., 2011, “Small-Scale Flux Emergence Observed Using Hinode/SOT”, Solar Phys., 269, 13–40. [DOI], [ADS] (Cited on pages 5, 10, 13, and 17.)
Title, A.M., Topka, K.P., Tarbell, T.D., Schmidt, W., Balke, C. and Scharmer, G.B., 1992, “On the differences between plage and quiet sun in the solar photosphere”, Astrophys. J., 393, 782–794. [DOI], [ADS] (Cited on page 6.)
Tobias, S.M., Brummell, N.H., Clune, T.L. and Toomre, J., 1998, “Pumping of Magnetic Fields by Turbulent Penetrative Convection”, Astrophys. J. Lett., 502, L177. [DOI], [ADS] (Cited on page 17.)
Tobias, S.M., Brummell, N.H., Clune, T.L. and Toomre, J., 2001, “Transport and Storage of Magnetic Field by Overshooting Turbulent Compressible Convection”, Astrophys. J., 549, 1183–1203. [DOI], [ADS] (Cited on pages 14 and 17.)
Trujillo Bueno, J., Shchukina, N. and Asensio Ramos, A., 2004, “A substantial amount of hidden magnetic energy in the quiet Sun”, Nature, 430, 326–329. [DOI], [ADS], [arXiv:astro-ph/0409004] (Cited on page 10.)
Unno, W. and Ando, H., 1979, “Instability of a thin magnetic tube in the solar atmosphere”, Geophys. Astrophys. Fluid Dyn., 12, 107–115. [DOI], [ADS] (Cited on pages 6 and 27.)
Ustyugov, S.D., 2010, “Realistic magnetohydrodynamical simulation of solar local supergranulation”, Phys. Scripta, T142, 014031. [DOI], [ADS], [arXiv:0906.5232 [astro-ph.SR]] (Cited on page 9.)
Vögler, A., 2004, “Effects of non-grey radiative transfer on 3D simulations of solar magneto-convection”, Astron. Astrophys., 421, 755–762. [DOI], [ADS] (Cited on page 9.)
Vögler, A., 2005, “On the effect of photospheric magnetic fields on solar surface brightness: Results of radiative MHD simulations”, Mem. Soc. Astron. Ital., 76, 842–849. [ADS] (Cited on pages 6 and 24.)
Vögler, A. and Schüssler, M., 2007, “A solar surface dynamo”, Astron. Astrophys., 465, L43–L46. [DOI], [ADS], [arXiv:astro-ph/0702681] (Cited on pages 6, 14, and 16.)
Vögler, A., Bruls, J.H.M.J. and Schüssler, M., 2004, “Approximations for non-grey radiative transfer in numerical simulations of the solar photosphere”, Astron. Astrophys., 421, 741–754. [DOI], [ADS] (Cited on page 9.)
Vögler, A., Shelyag, S., Schüssler, M., Cattaneo, F., Emonet, T. and Linde, T., 2005, “Simulations of magneto-convection in the solar photosphere. Equations, methods, and results of the MURaM code”, Astron. Astrophys., 429, 335–351. [DOI], [ADS] (Cited on pages 6, 14, 20, 23, 24, 27, and 31.)
Weiss, N.O., 1966, “The Expulsion of Magnetic Flux by Eddies”, Proc. R. Soc. London, Ser. A, 293, 310–328. [ADS] (Cited on pages 14 and 20.)
Weiss, N.O., 1991, “Magnetoconvection”, Geophys. Astrophys. Fluid Dyn., 62, 229-247. [DOI], [ADS] (Cited on page 14.)
Weiss, N.O., Proctor, M.R.E. and Brownjohn, D.P., 2002, “Magnetic flux separation in photospheric convection”, Mon. Not. R. Astron. Soc., 337, 293–304. [DOI], [ADS] (Cited on pages 6, 14, and 20.)
Yelles Chaouche, L., Cheung, M., Lagg, A. and Solanki, S.K., 2005, “Diagnostics of a Simulated Flux Tube Emergence”, in The Dynamic Sun: Challenges for Theory and Observations, Proceedings of the 11th European Solar Physics Meeting, 11 - 16 September 2005, Leuven, Belgium, (Eds.) Danesy, D., Poedts, S., De Groof, A., Andries, J., vol. SP-600 of ESA Conference Proceedings, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 17 and 27.)
Zhao, J., Georgobiani, D., Kosovichev, A.G., Benson, D., Stein, R.F. and Nordlund, Å., 2007, “Validation of Time-Distance Helioseismology by Use of Realistic Simulations of Solar Convection”, Astrophys. J., 659, 848–857. [DOI], [ADS], [astro-ph/0612551] (Cited on page 6.)
Acknowledgements
The author was supported by NSF grants AST 0605738 and AGS 1141921 and NASA grants NNX07AH79G and NNX08AH44G. The author’s calculations were performed on the Pleiades supercomputer of the NASA Advanced Supercomputing Division at NASA’s Ames Research Center.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
41116_2015_9156_MOESM1_ESM.mpg
mpg-Movie (37927878 KB) Still from a movie showing Log B showing multiple loops and several vertical flux concentrations, one of which has become a pore (see Section 4.4). The movie shows that most of the magnetic features are being pushed down by convective downflows, but some of the loops are rising toward the surface and in places loops have opened out through the top boundary leaving vertical “flux tubes” behind. Movie produced by Sandstrom, CSC, NASA Ames Res. Ctr.
Electronic supplementary material
41116_2015_9156_MOESM2_ESM.mov
mpg-Movie (194745724 KB) Still from a movie showing Rise and emergence of initially uniform, untwisted horizontal magnetic field continuously being advected into the computational domain by inflows in the centers of supergranule cells at the bottom. Left: |B| image and velocity vectors. Right: |B| image and magnetic field vectors both in a vertical plane. The boundary field strength was gradually increased from 0.2 kG with an e-folding time of 5 hrs until it reached 5 kG and thereafter held constant.
Electronic supplementary material
41116_2015_9156_MOESM3_ESM.mov
mpg-Movie (169942682 KB) Still from a movie showing Time sequence of emergent continuum intensity (left), vertical magnetic field at τRoss = 0.1 (right), for an initial twisted flux half torus driven into the computational domain at 7.5 Mm depth. The initial central field strength was 21 kG and total flux 7.6 × 1021 Mx. The domain is 92 × 49 Mm wide. Image reproduced by permission from Cheung et al. (2010), copyright by AAS.
Electronic supplementary material
41116_2015_9156_MOESM4_ESM.mov
mpg-Movie (108657227 KB) Still from a movie showing Emergent continuum intensity (left) and vertical magnetic field at τcont = 0.01 (right) from simulation with initial/boundary condition of convective inflows advecting 1 kG uniform, untwisted, horizontal field into the computational domain at 20 Mm depth. The intensity range is I/〈I〉 = [0.13, 2.5] and the magnetic field range is ± 3.5 kG. The pores may form spontaneously in vertical flux tubes from magnetic loops that have reached the surface and opened out through top boundary. Compare this with Figure 14 for the rise of a coherent twisted flux tube. (Movie shows the initial “pepper and salt” emergence, the horizontal advection of the field, its concentration into unipolar regions with cancellation where opposite polarities meet and merging of like polarities to form pores. Resolution was increased from 48 km to 24 km horizontally at time 51.7 hrs.)
Electronic supplementary material
41116_2015_9156_MOESM5_ESM.mpg
mpg-Movie (24956644 KB) Still from a movie showing Time sequence of temperature and density fluctuations during pore formation viewed from below (surface is at the bottom). Note the cooler temperatures extending downward from surface, followed by lower densities. Movie produced by Sandstrom, CSC, NASA Ames Res. Ctr. (For video see appendix)
Electronic supplementary material
41116_2015_9156_MOESM6_ESM.mpg
mpg-Movie (34719413 KB) Still from a movie showing Time sequence of log |B| during pore formation. The flux concentration forms first at the surface and then extends downward. Near the surface the pore’s field is filamentary, but at large depths it becomes mostly coherent. Movie produced by Sandstrom, CSC, NASA Ames Res. Ctr.
Electronic supplementary material
41116_2015_9156_MOESM7_ESM.mpg
mpg-Movie (34719413 KB) Still from a movie showing Time sequence of log |B| during pore formation. The flux concentration forms first at the surface and then extends downward. Near the surface the pore’s field is filamentary, but at large depths it becomes mostly coherent. Movie produced by Sandstrom, CSC, NASA Ames Res. Ctr.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Stein, R.F. Solar Surface Magneto-Convection. Living Rev. Sol. Phys. 9, 4 (2012). https://doi.org/10.12942/lrsp-2012-4
Published:
DOI: https://doi.org/10.12942/lrsp-2012-4